Как найти мощность вольтметра

Мощность в
электрических цепях постоянного тока
измеряют прямым и косвенным методами.
В первом случае для измерения мощности
используют ваттметр
(рисунок 8), во втором случае — амперметр
и вольтметр (рисунок 9).

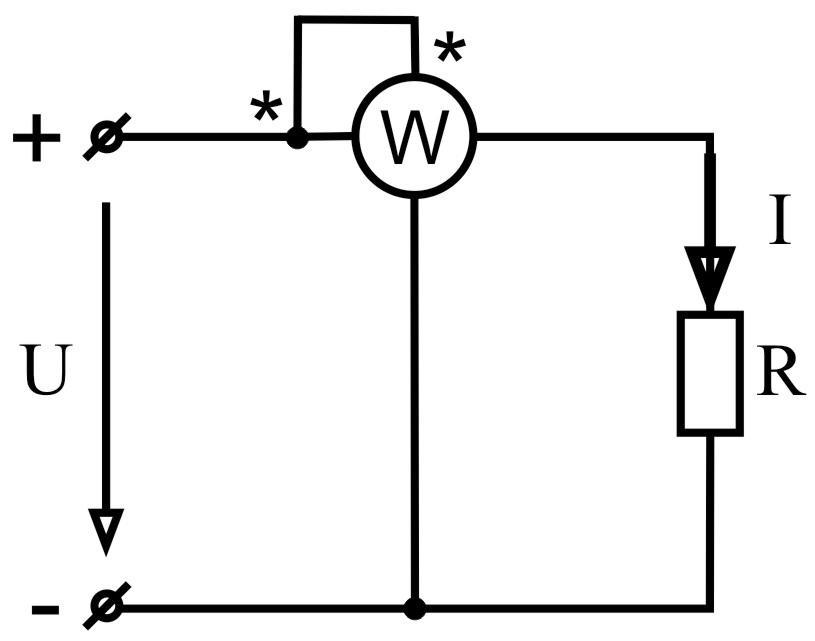
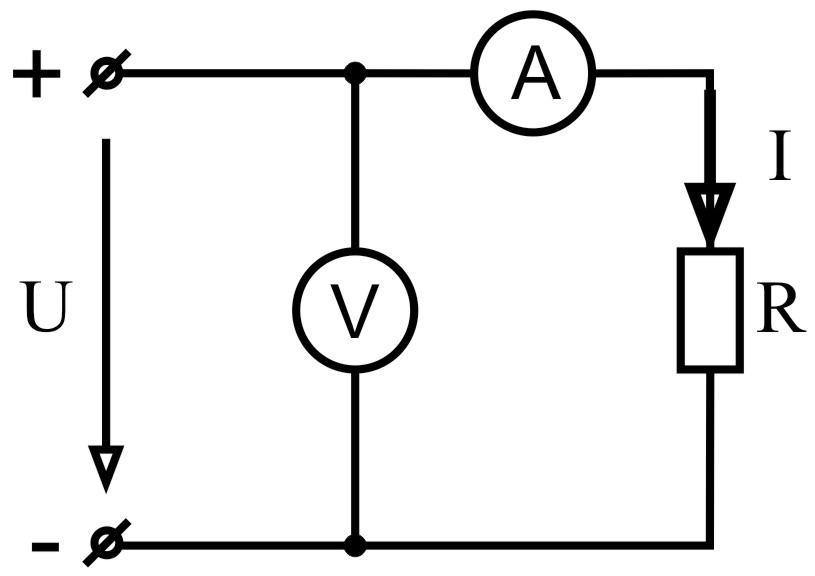
Рисунок 8 – Схема измерения мощности ваттметром	Рисунок 9 – Схема измерения мощности амперметром и вольтметром

В качестве
ваттметров обычно применяют
электродинамические приборы, у которых
имеются обмотки двух типов: последовательная
(или токовая)
обмотка
и параллельная
обмотка (или
обмотка
напряжения).
Токовую
обмотку
ваттметра включают
последовательно с приемником
,
то есть в цепь тока
,
а обмотку
напряжения
— параллельно
приемнику
,
то есть на напряжение
.
Начало токовой обмотки обозначено
,
начало обмотки напряжения
.
Начала обмоток образуют общую точку,
которую располагают на приборе.

Цена
деления ваттметра

определяется по следующим формулам:

,     , (10)

где
,
,

— конечные значения мощности, напряжения
и тока, указанные на приборе,

— число делений шкалы прибора.

При измерении
мощности постоянного тока косвенным
методом (рисунок 9) определяют амперметром
значение силы тока
,
вольтметром — значение напряжения

и вычисляют мощность по формуле

. (11)

2.1.4 Измерение электрического сопротивления постоянному току

Электрические
сопротивления
электротехнических устройств (катушек,
резисторов и т.д) постоянному току можно
условно разделить на малые
(до
Ома),
средние
(от

до
Ом)
и большие
(свыше
Ом).
Для измерения малых сопротивлений
применяют метод
амперметра–вольтметра
и мостовой.
Для измерения средних сопротивлений
применяют методы амперметра–вольтметра,
непосредственной
оценки
(омметры),
мостовой
(одинарные
мосты) и
компенсационный.
Для измерения больших сопротивлений
используют метод непосредственной
оценки, реализуемый мегаомметрами.

Метод
амперметра–вольтметра является наиболее
простым для измерения малых и средних
сопротивлений. В основе его лежит закон
Ома
,
из которого следует простой способ
определения сопротивления

по показаниям амперметра и вольтметра:

. (12)

На практике этот
метод может быть реализован двумя
экспериментальными схемами, изображенными
на рисунках 10 и 11.

Рисунок 10 – Схема измерения больших сопротивлений методом амперметра–вольтметра	Рисунок 11 – Схема измерения малых сопротивлений методом амперметра–вольтметра

В схеме рисунка
10 амперметр измеряет ток

в резисторе с сопротивлением
,
а вольтметр — напряжение
,
где

— напряжение на резисторе. Следовательно,
на основании закона Ома определяется
сумма сопротивлений резистора и
амперметра:
.
Действительное значение сопротивления
резистора

. (13)

Очевидно, что
ошибка
измерения будет тем меньше, чем меньше
сопротивление амперметра по отношению
к измеряемому сопротивлению
.
Схему рисунка 10, следовательно,
целесообразнее применять для измерения
больших сопротивлений.

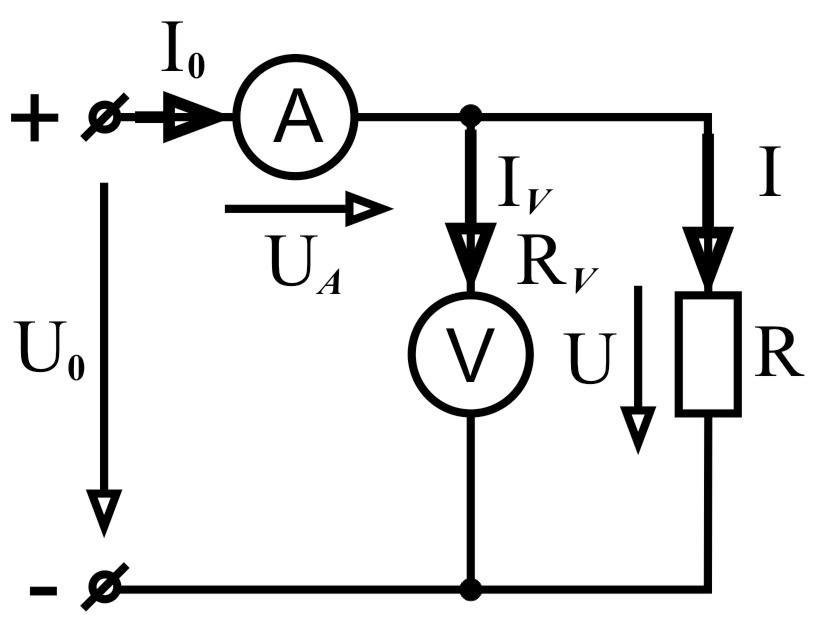
В схеме рисунка
11 вольтметр присоединен непосредственно
к выводам резистора и показывает
напряжение на нем, а амперметр измеряет
сумму токов в резисторе и цепи вольтметра:
.
Следовательно, на основании показаний
приборов в этом случае определяется
проводимость:
.
Действительное значение сопротивления
резистора

. (14)

Очевидно, что чем
больше
сопротивление вольтметра по отношению
к измеряемому сопротивлению
,
тем меньше поправка к результату
измерений.
Схему рисунка 11, следовательно,
целесообразно применять для измерения
малых сопротивлений.

Измерение
сопротивлений методом непосредственной
оценки используется в специальном
электроизмерительном приборе — омметре,
принципиальная схема которого приведена
на рисунке 12. Он состоит из
магнитоэлектрического измерительного
механизма ()
с собственным сопротивлением
,
шкала которого проградуирована в омах,
источника питания с напряжением
,
добавочного резистора

и имеет выходные зажимы «»,
к которым присоединяют объект с измеряемым
сопротивлением
.

Цена деления
омметра

определяется по следующей формуле:

, (15)

где

— конечное значение сопротивления,
указанное на приборе,

— число делений шкалы прибора.

Рисунок 12 – Принципиальная схема омметра

Омметры удобны в
практике, но имеют большую погрешность
(класс точности 2,5) из-за неравномерности
шкалы и нестабильности источника питания
(обычно батарея гальванических элементов).

Для измерения
средних по величине сопротивлений
применяют мостовой
метод.
Устройства, реализующие этот метод
измерения, называются измерительными
мостами.

Одинарный
(четырехплечий)
мост (рисунок 13) содержит четыре плеча
и две диагонали. В одно плечо моста
включают измеряемое сопротивление
,
а три остальных плеча образованы
резисторами
,

и
.
В одну диагональ моста (между зажимами
«»
и «»)
включают источник питания с ЭДС
,
а в другую (зажимы «»
и «»)
— индикатор
,
выполняющий функцию указателя равновесии
моста.

Рисунок 13 – Схема измерительного моста для определения сопротивления

Когда потенциалы
узлов «»
и «»
равны, ток в индикаторе
,
мост находится в состоянии равновесия
(признаком равновесия моста является
нулевое отклонение указателя
).
При этом справедливы следующие
соотношения:

;    ;         и    .

Разделив почленно
два последних уравнения друг на друга
и учтя равенства токов, получим

    или    .

Из последнего
выражения вычисляют искомое сопротивление
:

. (16)

Для измерения
сопротивления с повышенной точностью
используют компенсационный метод. Схема
измерительной цепи аналогична схеме
рисунка 4, используемой для измерения
компенсационным методом напряжения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Обновлено: 20.05.2023

1. Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Рис.1.

Измерение силы тока и напряжения амперметром и вольтметром.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R_V. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1, это условие записывается в виде:

Это условие означает, что ток: I_V = , протекающий через вольтметр, много меньше тока I = , который протекает по тестируемому участку цепи.

Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.

Амперметрпредназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением R_A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1. сопротивление амперметра должно удовлетворять условию R_A

Амперметр и вольтметр приборы, которые могут быть устроены на базе одно итого же прибора магнитоэлектрической системы, который называют гальванометром:

Рис.2.Гальванометр.

Любой гальванометр, имеет проволочную катушку, обладающую сопротивлением R_Г. Если к гальванометру подключить последовательно добавочное сопротивление, то его можно использовать как вольтметр, подключая его, вместе с добавочным сопротивлением, параллельно участку цепи:

Рис.3.Подключение добавочного сопротивления к гальванометру.

R_д = R_г(n – 1), где n = , отношение напряжения которое необходимо измерить к напряжению которое приходится на катушку гальванометра.

В соответствии с законами последовательного соединения и законом Ома для участка цепи имеем:

= , = ,

U ‒ U_г = R_д , ‒ 1 = , n ‒ 1 = ,

Если к гальванометру подключить параллельно сопротивление (шунт), то его можно использовать как амперметр, подключая его, вместе с шунтом, параллельно участку цепи:

Рис.4.Подключение шунта к гальванометру.

I_ш⋅ R_ш= I_г ⋅ R_г , (I ‒ I_г )⋅ R_ш= I_г ⋅ R_г, ( ‒1)⋅ R_ш= I_г ⋅ R_г,

R_ш = , где n = , отношение cилы тока которую необходимо измерить к силе тока которая приходит через катушку гальванометра.

2. Измерение мощности.

Мощность в электрической цепи можно измерить помощью амперметра и вольтметра.

Зная показания амперметра и вольтметра по формуле:

P = U∙I – определяем мощность в электрической цепи.

Мощность в электрической цепи можно определить, используя ваттметр электродинамической системы.

.

Рис.6.Схема соединения катушек Рис.7.Схема включения катушек

электродинамического ваттметра. электродинамического ваттметра.

Катушка вывод (вывод её обозначается *), которой подключается последовательно к источнику тока (генератору) называется токовой.

Катушка, которая подключается параллельно нагрузке, называется катушкой напряжения. Один из выводов этой катушки обозначается *и соединяется с выводом токовой катушки, обозначенной звёздочкой*. Шкала такого прибора проградуирована в ваттах (Вт).

Работа электрического тока в цепи определяется по формулам: $A = Uq$ и $A = UIt$. Но часто, кроме самой работы, нам важна скорость ее выполнения. В механике у нас была такая величина — мощность.

Что называют мощностью? Как рассчитать мощность?

Мощность — это физическая величина, равная отношению работы ко времени, за которое она была совершена. Она определяется по формуле: $N = frac$.

На данном уроке мы рассмотрим мощность как величину, характеризующую работу именно электрического тока.

Мощность тока и ее связь с напряжением и силой тока

В электричестве мощность обозначается буквой $P$, а не $N$. При этом смысл этой величины остается тем же. Эта величина численно равна работе, которая совершается в единицу времени:
$P = frac$, где $P$ — мощность электрического тока.

Как рассчитать мощность электрического тока через напряжение и силу тока?

Вы уже знаете, что работа электрического тока определяется по формуле: $A = UIt$. Подставим это выражение в определение мощности:
$P = frac = frac = UI$.

Мощность электрического тока — это величина, численно равная произведению напряжения на силу тока:
$P = UI$.

Единицы измерения мощности тока

Что принимают за единицу мощности?

Единицей мощности является $1 space ватт$ ($Вт$).

Как выражается единица мощности через единицы напряжения и силы тока?

Из формулы $P = UI$ следует:

$1 space ватт = 1 space вольт cdot 1 space ампер$,
$1 space Вт = 1 space В cdot А$.

Кратные единицы мощности

На практике часто используют кратные единицы мощности для удобства. К ним относятся гектоватт ($гВт$), киловатт ($кВт$) и мегаватт ($МВт$).

$1 space гВт = 100 space Вт$,
$1 space кВт = 1000 space Вт$,
$1 space МВт = 1 space 000 space 000 space Вт$.

Измерение мощности электрического тока

Мощность электрического тока напрямую зависит от напряжения и силы тока в цепи. Соответственно, для того, чтобы определить мощность тока, нам понадобится два прибора: амперметр и вольтметр. Умножив показания этих приборов друг на друга, мы получим численное значение мощности.

Также для измерения мощности напрямую существуют специальные приборы — ваттметры (рисунок 1). Они непосредственно измеряют мощность электрического тока в цепи.

Мощность, потребляемая некоторыми приборами

В таблице 1 представлены значения мощности для некоторых приборов. Для бытовых приборов она всегда указывается в паспорте каждого устройства.

Устройство	Потребляемая мощность $P$, $Вт$
Лампа карманного фонаря	1
Лампа накаливания	40-200
Холодильник	160
Кондиционер	800
Утюг	1200-2200
Стиральная машина	2200
Пылесос	1500-3000
Лампа звезды башни Кремля	5000
Электропоезд	6 500 000

Таблица 1. Значения мощности тока для некоторых приборов и устройств

Упражнения

Упражнение №1

В цепь с напряжением в $127 space В$ включена электрическая лампа, сила тока в которой равна $0.6 space А$. Найдите мощность тока в лампе.

Дано:
$U = 127 space В$
$I = 0.6 space А$

Посмотреть решение и ответ

Решение:

Мощность электрического тока в лампе рассчитывается по формуле: $P = UI$.

$P = 127 space В cdot 0.6 space А = 76.2 space Вт$.

Ответ: $P = 76.2 space Вт$.

Упражнение №2

Электроплитка рассчитана на напряжение $220 space В$ и силу тока $3 space А$. Определите мощность тока в плитке.

Дано:
$U = 220 space В$
$I = 3 space А$

Посмотреть решение и ответ

Решение:

Мощность электрического тока в плитке рассчитаем по формуле: $P = UI$.

$P = 220 space В cdot 3 space А = 660 space Вт$.

Ответ: $P = 660 space Вт$.

Упражнение №3

Пользуясь таблицей 1, вычислите, какую работу совершает за $1 space ч$ электрический ток в лампе карманного фонаря, осветительной лампе мощностью $200 space Вт$, в лампе звезды башни Кремля.

Дано:
$t = 1 space ч$
$P_1 = 1 space Вт$
$P_2 = 200 space Вт$
$P_3 = 5000 space Вт$

СИ:
$t = 3600 space с$

Посмотреть решение и ответ

Решение:

Мощность тока по определению равна работе, которую ток совершает за единицу времени: $P = frac$.

Выразим отсюда работу и рассчитаем ее для каждой лампы:
$A = Pt$.

Работа тока в лампе карманного фонаря:
$A_1 = P_1 t$,
$A_1 = 1 space Вт cdot 3600 space с = 3600 space Дж = 3.6 space кДж$.

Работа тока в осветительной лампе:
$A_2 = P_2 t$,
$A_2 = 200 space Вт cdot 3600 space с = 720 space 000 space Дж = 720 space кДж$.

Работа тока в лампе звезды башни Кремля:
$A_3 = P_3 t$,
$A_3 = 5000 space Вт cdot 3600 space с = 18 space 000 space 000 space Дж = 18 space МДж$.

Ответ: $A_1 = 3.6 space кДж$, $A_2 = 720 space кДж$, $A_3 = 18 space МДж$.

Упражнение №4

Рассмотрите один-два электроприбора, используемые в квартире. Найдите по паспорту приборов их мощность. Определите работу тока в них за $10 space мин$.

Если вы не можете найти паспорт прибора, внимательно рассмотрите его. Часто производители указывают мощность на самом устройстве. Мы возьмем пылесос мощностью $2000 space Вт$ и фен для волос мощностью $2200 space Вт$ (рисунок 2).

Дано:
$t = 10 space мин$
$P_1 = 2000 space Вт$
$P_2 = 2200 space Вт$

СИ:
$t = 600 space с$

Посмотреть решение и ответ

Решение:

Мощность тока по определению равна работе, которую ток совершает за единицу времени: $P = frac$.

Выразим отсюда работу и рассчитаем ее для каждого прибора:
$A = Pt$.

Работа тока в пылесосе, совершенная за $10 space мин$ его использования:
$A_1 = P_1t$,
$A_1 = 2000 space Вт cdot 600 space с = 1 space 200 space 000 space Дж = 1.2 space МДж$.

Работа тока в фене для волос, совершенная за $10 space мин$ его использования:
$A_2 = P_2t$,
$A_2 = 2200 space Вт cdot 600 space с = 1 space 320 space 000 space Дж = 1.32 space МДж$.

Чтобы определить мощность тока, возьмите амперметр и вольтметр, присоедините к аппарату-потребителю, мощность которого измеряется, и, сняв показания, рассчитайте ее числовое значение. В том случае, когда заранее известно сопротивление проводника, можно измерить только силу тока или напряжение и посчитать мощность тока. Ее также можно узнать прямым измерением.

• Как узнать мощность тока
• Как рассчитать потребляемый ток
• Как по току рассчитать мощность

• Для проведения измерений возьмите амперметр, вольтметр, ваттметр, омметр.

Прямое измерение мощности тока Возьмите ваттметр, присоедините его к потребителю, на котором необходимо измерить мощность. Подключите его клеммы к местам вывода потребителя в сеть. На шкале аналогового или экране цифрового ваттметра отобразится мощность данного потребителя. В зависимости от настроек прибора значение мощности можно будет получить в ваттах, киловаттах, милливаттах и т.д.

Изменение мощности с помощью вольтметра и амперметра Соберите цепь, включив в нее потребителя электрического тока и амперметр. Вольтметр присоедините параллельно потребителю. Измерительные приборы подключайте, соблюдая полярность, если ток постоянный. Пустите электрический ток, подключив источник, и снимите показания приборов с амперметра значение силы тока в амперах, а с вольтметра значение напряжения в вольтах. Умножьте значение силы тока на напряжение P=U•I. Результатом будет мощность потребителя в ваттах.

Определение мощности тока при известном сопротивлении потребителя Если сопротивление потребителя известно (найдите его значение на корпусе или измерьте омметром), и он рассчитан на известное напряжение, то его номинальную мощность можно найти, возведя это напряжение в квадрат и поделив на значение сопротивления (P=U²/R). Например, у лампочки с сопротивлением 484 Ома и при номинальном напряжении 220 В, мощность будет равна 100 Вт. Если напряжение источника тока не известно, включите последовательно в цепь потребителя амперметр. Измерьте с его помощью силу тока, идущего через потребитель. Для расчета мощности возведите силу тока в квадрат и умножьте на значение сопротивления (P=I²•R). Если сила тока измерена в амперах, а сопротивление в Омах, то значение мощности будет получено в ваттах.

Приветствую всех, сегодня в рамках курса “Основы электроники” мы рассмотрим основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр и амперметр.

Измерение тока. Амперметр.

И начнем с измерения тока. Прибор, используемый для этих целей, называется амперметр, и в цепь он включается последовательно. Рассмотрим небольшой пример:

Как видите, здесь источник питания подключен напрямую к резистору, символизирующему полезную нагрузку. Кроме того, в цепи присутствует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи:

Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 👍

Важным параметром этого прибора является его внутреннее сопротивление r_А . Почему это так важно? Смотрите сами – при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится общее сопротивление, и мы получим следующее значение:

Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.

При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:

В этой формуле n – это коэффициент шунтирования – число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.

Пусть максимальное значение, которое может измерить амперметр составляет 1 А. А схема, силу тока в которой нам нужно определить имеет следующий вид:

Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Напряжение в 1200 В взято исключительно ради примера, сокровенного практического смысла в этом нет ) Итак, из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:

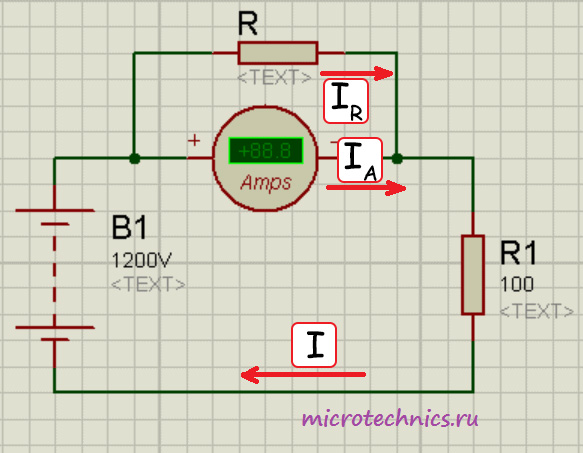
В данной задаче нам необходимо измерить ток I . Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и получим нужное значение. Для реализации задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:

В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.

Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:

Выразим ток шунта через ток амперметра:

Измеряемый ток равен:

Подставим в это уравнение предыдущее выражение для тока шунта:

Но сопротивление шунта нам также известно ( R = frac ). В итоге мы получаем:

Вот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нужно измерить.

С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.

Измерение напряжения. Вольтметр.

Прибор, предназначенный для измерения напряжения, называется вольтметр. И, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся, с чем это связано:

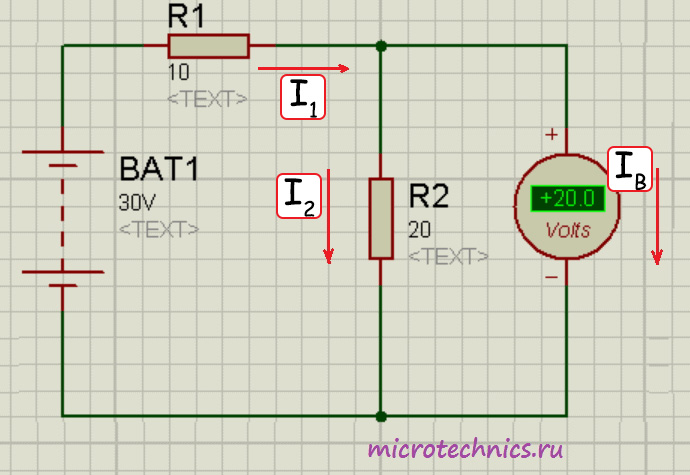
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:

Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с R_2 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток ( I_B = 0 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку r_В имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток. В связи с этим напряжение на резисторе R_2 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.

Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:

Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример:

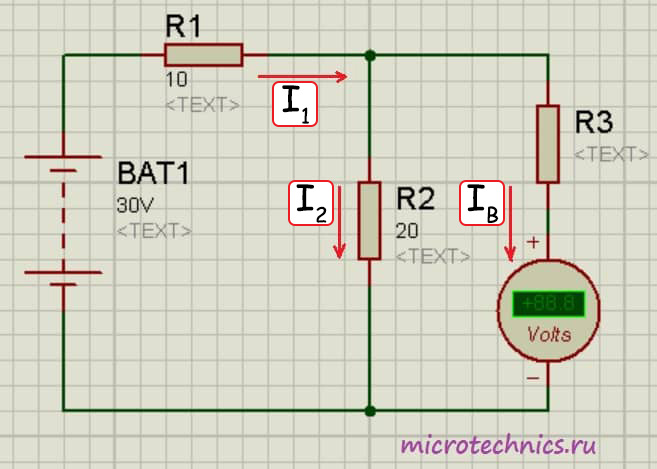
Здесь мы добавили в цепь добавочное сопротивление R_3 . Перед нами стоит задача измерить напряжение на резисторе R_2:medspace U_2 = R_2medspace I_2 . Давайте определим, какой результат при таком включении выдаст нам вольтметр:

Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:

Таким образом: U_В = frac . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно значительно увеличить пределы измерения вольтметра.

В завершении статьи пару слов об измерении сопротивления и мощности.

Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи (омметр) и мощности (ваттметр).

В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями!

Читайте также:

  

• Конституционное закрепление рф как социального государства кратко

  

• Кто является создателем народной музыки народных песен ответ кратко

  

• Объясните почему необходимо охранять природный комплекс мирового океана кратко

  

• Почему вода содержит в себе различные вещества кратко

  

• Почему трахейная воздухоносная система не может обеспечить воздухообмен у крупных организмов кратко

Как узнать мощность тока

Чтобы определить мощность тока, возьмите амперметр и вольтметр, присоедините к аппарату-потребителю, мощность которого измеряется, и, сняв показания, рассчитайте ее числовое значение. В том случае, когда заранее известно сопротивление проводника, можно измерить только силу тока или напряжение и посчитать мощность тока. Ее также можно узнать прямым измерением.

Вам понадобится

• Для проведения измерений возьмите амперметр, вольтметр, ваттметр, омметр.

Инструкция

Прямое измерение мощности тока Возьмите ваттметр, присоедините его к потребителю, на котором необходимо измерить мощность. Подключите его клеммы к местам вывода потребителя в сеть. На шкале аналогового или экране цифрового ваттметра отобразится мощность данного потребителя. В зависимости от настроек прибора значение мощности можно будет получить в ваттах, киловаттах, милливаттах и т.д.

Изменение мощности с помощью вольтметра и амперметра Соберите цепь, включив в нее потребителя электрического тока и амперметр. Вольтметр присоедините параллельно потребителю. Измерительные приборы подключайте, соблюдая полярность, если ток постоянный. Пустите электрический ток, подключив источник, и снимите показания приборов с амперметра значение силы тока в амперах, а с вольтметра значение напряжения в вольтах. Умножьте значение силы тока на напряжение P=U•I. Результатом будет мощность потребителя в ваттах.

Определение мощности тока при известном сопротивлении потребителя Если сопротивление потребителя известно (найдите его значение на корпусе или измерьте омметром), и он рассчитан на известное напряжение, то его номинальную мощность можно найти, возведя это напряжение в квадрат и поделив на значение сопротивления (P=U²/R). Например, у лампочки с сопротивлением 484 Ома и при номинальном напряжении 220 В, мощность будет равна 100 Вт. Если напряжение источника тока не известно, включите последовательно в цепь потребителя амперметр. Измерьте с его помощью силу тока, идущего через потребитель. Для расчета мощности возведите силу тока в квадрат и умножьте на значение сопротивления (P=I²•R). Если сила тока измерена в амперах, а сопротивление в Омах, то значение мощности будет получено в ваттах.

Видео по теме

Источники:

• мощность амперметра

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Методика измерений в электрических цепях

Измерение постоянного и переменного напряжения

Измерение как постоянного, так и переменного напряжения может производиться непосредственно вольтметрами, рассчитанными для работы соответствующего типа напряжения. В тех случаях, когда необходимо измерить напряжение больше того, на которое рассчитан вольтметр, необходимо последовательно с ним включить добавочный резистор. Тогда часть измеряемого напряжения будет падать на добавочный резистор, а часть — на прибор. Подбирая величину сопротивления добавочного резистора, можно в широких пределах расширять возможности измерения больших напряжений. Известно сопротивление вольтметра R_пp и выбран коэффициент расширения пределов расширения:

n = U_x/U_пp

где U_x — максимальное напряжение на входе схемы, подлежащее измерению; U_пp — максимальные пределы измерения непосредственно вольтметром.

Величина сопротивления добавочного резистора может быть найдена по следующей формуле:

R_доб = R_пр(n-1)

Обычно для удобства производства отсчетов коэффициент п выбирают кратным 2, 5 или 10.

Для измерения высоких значений переменных напряжений могут быть использованы так называемые измерительные трансформаторы напряжения.

Они представляют собой понижающие трансформаторы, т. е. такие, у которых число витков вторичной обмотки W₂, к которой подключается вольтметр, меньше числа витков W₁ первичной обмотки. Коэффициент расширения пределов измерения n = W₁/W₂. Схемы подключения вольтметров для измерения напряжения приведены на рис. 1.

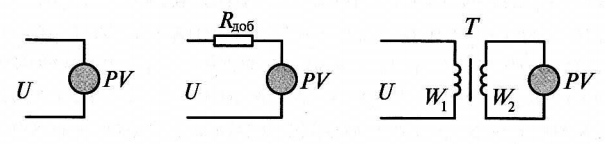
Рис. 1. Схемы измерения напряжения

Измерение электродвижущей силы (ЭДС)

Измерение Е имеет свои особенности. При подключении вольтметра к источнику ЭДС для ее измерения через него всегда будет проходить ток, а так как любой источник ЭДС обладает внутренним сопротивлением R_вн, то напряжение на таком источнике и вольтметр будет измерять величину меньшую, чем ЭДС Е.

U = E – IR_вн

Если нет требований к высокой точности измерения ЭДС, то для уменьшения тока можно воспользоваться вольтметром с большим внутренним сопротивлением, например электронным. В этом случае можно считать, что измеренное напряжение U ~ Е. Более точные методы измерения ЭДС связаны с использованием компенсационных схем (рис. 2).

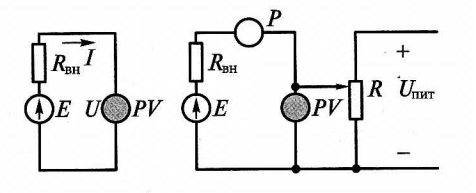
Рис. 2. Схемы измерения ЭДС

В них напряжение, измеряемое вольтметром PV, снимаемое с переменного резистора R, сравнивается с напряжением на источнике ЭДС.

Изменяя напряжение на выходе переменного резистора (потенциометра), можно добиться такого условия, когда измерительный прибор Р покажет отсутствие тока через источник ЭДС. В этом случае показания вольтметра будут точно соответствовать величине ЭДС источника, т. е. U = Е .

Измерение тока

Можно производить измерение тока непосредственно амперметром, включенным в разрыв измеряемой цепи (рис. 3, а).

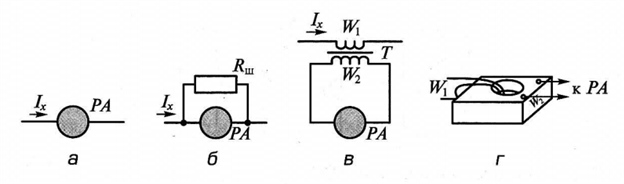
Рис. 3. Схемы измерения силы тока

При необходимости расширить пределы измерения амперметра необходимо параллельно амперметру включить резистор (рис. 3, б), который чаще всего называют шунтом. Тогда через амперметр будет проходить только часть тока, а остальная — через шунт. Так как сопротивление амперметров обычно небольшое, то для существенного расширения пределов измерения сопротивление шунта должно быть очень небольшим. Существуют формулы для расчета сопротивления шунта, но обычно на практике приходится вручную подгонять его сопротивление, контролируя ток эталонным амперметром.

Для измерения больших переменных токов часто используют измерительные трансформаторы токов (рис. 3, в). У них первичная обмотка, включаемая в разрыв измеряемой цепи, имеет число витков W₁ меньшее, чем число витков W₂ вторичной обмотки, т. е. трансформатор является повышающим по напряжению, но по току он понижающий. Амперметр подключается к выходу вторичной обмотки трансформатора тока. Часто лабораторные трансформаторы тока вообще не имеют изготовленной заранее первичной обмотки, а в их корпусе имеется широкое сквозное отверстие, через которое сам экспериментатор наматывает необходимое число витков (рис. 3, г). Зная число витков вторичной обмотки (оно обычно указано на корпусе трансформатора тока), можно выбрать коэффициент трансформации n = W₁/W₂ и определить измеряемый ток I_х по показаниям амперметра I_пр по следующей формуле:

I_х = I_пр/n

Совершенно по-иному производят измерение токов в электронных схемах, которые обычно спаяны, изготовлены на печатных платах; произвести какой-либо разрыв в них практически невозможно. Для измерения токов в этих случаях используют вольтметры (обычно электронные с большим внутренним сопротивлением для устранения влияния прибора на работу электронной схемы), подключая их к резисторам схемы, величины которых либо известны, либо могут быть предварительно измерены. Воспользовавшись законом Ома, можно определить силу тока:

I = U/R

Измерение сопротивлений

Часто при работе с электрическими установками или при наладке электронных схем необходимо производить измерение различных сопротивлений. Простейший способ измерения сопротивлений заключается в использовании двух измерительных приборов: амперметра и вольтметра. С их помощью измеряют напряжение и ток в сопротивлении R, подключенном к источнику питания, и по закону Ома находят величину искомого сопротивления:

R = U/I

Однако этот способ измерения сопротивлений не позволяет получить результаты измерения с высокой точностью, так как на результаты измерения оказывают влияние собственные внутренние сопротивления амперметра и вольтметра. Так, на изображенной на рис. 4, а схеме амперметр измеряет не только ток, проходящий через сопротивление, но и ток, проходящий через вольтметр, чем вносится методическая погрешность измерений.

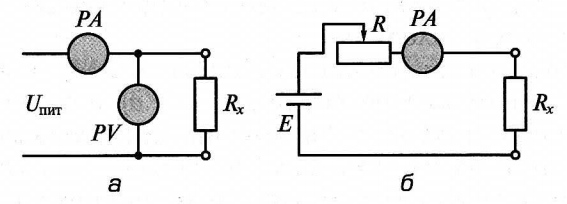
Рис. 4. Схема для измерения сопротивлений методом амперметра и вольтметра (а) и схема омметра (б)

Этим способом производят измерение обычно в тех случаях, когда нет специальных приборов — омметров. Одна из возможных схем омметра (рис. 4, б) — последовательная. Она состоит из автономного источника питания Е, переменного резистора R и миллиамперметра магнитоэлектрического типа РА. В качестве источника питания обычно используют сухие элементы или батареи напряжением 1,4…4,5 В. Если к выводам прибора подключить сопротивление R_x, величину которого необходимо определить, то по цепи пойдет ток, величина которого будет зависеть от величины сопротивления. Так как миллиамперметр измеряет этот ток, то его шкала может быть непосредственно отградуирована в омах. Шкала у такого омметра обратная, т. е. нуль находится в правой части шкалы, так как при сопротивлении на входе, равном нулю (режим короткого замыкания), через амперметр будет протекать максимальный ток. Если внешняя цепь разорвана, что соответствует бесконечно большому сопротивлению на входе, то стрелка миллиамперметра будет находиться в самой левой части шкалы, где стоит знак х . Шкала такого омметра резко нелинейная, что в какой-то мере затрудняет считывание результатов. Переменный резистор омметра служит для установки прибора на нуль перед началом работы с ним. Для этого замыкают выводы омметра накоротко и, вращая ручку переменного резистора, добиваются нулевых показаний прибора. Так как ЭДС элемента питания с течением времени за счет разряда уменьшается, такую установку нуля необходимо периодически контролировать. С помощью подобных омметров можно измерять сопротивления от нескольких омов до сотен килоомов.

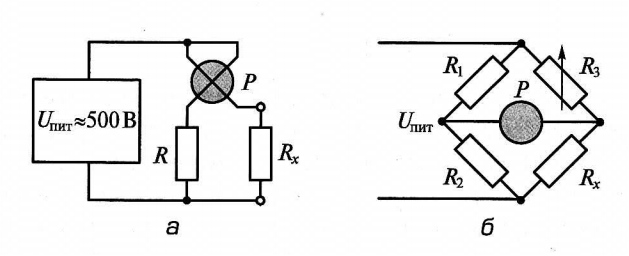
Рис. 5. Схемы мегометра (а) и электрического моста (б)

Измерение больших сопротивлений до 100 МОм обычно производят с помощью мегометров (рис. 5, а). В своем классическом виде он представляет собой комбинацию автономного источника питания и измерительного прибора — логометра. Логометр — разновидность магнитоэлектрического прибора, у которого вместо одной рамки имеются две, соединенные жестко между собой под некоторым утлом. Так же, как и в обычном магнитоэлектрическом приборе, с ними связана стрелка прибора и находятся они в магнитном поле постоянного магнита. При пропускании тока через обмотки рамок они создают вращающие моменты противоположных знаков, в результате чего положение стрелки будет зависеть от отношения токов в рамках. В цепь одной из рамок включен резистор R, а в цепь другой — сопротивление R_x, величина которого должна быть определена. Применение логометра объясняется тем, что его показания определяются только отношением токов в рамках и не зависят от изменения питающего напряжения U_пит. В качестве источника напряжения для мегометра используют либо индуктор, приводимый во вращение рукой оператора, либо аккумуляторную батарею с электронным преобразователем напряжения. Такая система питания определяется тем, что для работы прибора требуются большие напряжения — порядка 500 В, так как при меньших напряжениях токи в обмотках прибора были бы слишком малыми для его нормальной работы. Использование автономного источника питания диктуется тем, что мегометром часто измеряют сопротивление изоляции кабелей; при этом, естественно, напряжение в них бывает отключенным. Кроме того, с его помощью часто проводят измерения вне помещений, где нет электрической сети.

Измерение малых сопротивлений (меньше 1 Ом), а также измерения других сопротивлений в широком диапазоне значений с высокой точностью могут проводиться с помощью электрических мостов.

Электрический мост (рис. 5, б) представляет собой четыре сопротивления (одно из них — R_x подлежит измерению), включенные по кольцевой схеме. Каждое из сопротивлений образует плечо моста. В одну диагональ моста подают постоянное напряжение питания U_пит , а к другой подключают измерительный прибор — гальванометр Р. Он представляет собой высокочувствительный магнитоэлектрический прибор с нулем посередине шкалы. Его назначение — фиксировать момент, когда ток будет отсутствовать. Приборы подобного типа часто называются нуль-индикаторами. Одно или два сопротивления в плечах моста делаются переменными, и именно ими добиваются нулевых показаний прибора. Мост при этом считается сбалансированным. Как показывает теория электрических мостов, условие баланса достигается при равенстве произведения сопротивлений противоположных плеч, т. е. при условии R₁R_x = R₂R₃. Следовательно, после балансировки моста можно, зная величины всех сопротивлений, определить значение неизвестного сопротивления

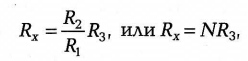
где N = R₂/R₁ — множитель.

Точность измерения с помощью мостов постоянного тока может быть очень велика. Результирующие значения сопротивлений могут иметь более пяти значащих цифр. В то же время мост не позволяет оперативно производить измерения, так как процесс балансировки требует определенного времени и навыка оператора.

Измерение емкостей

Определение емкости конденсатора или других устройств емкостного характера также может осуществляться различными способами. Простейший из них — метод амперметра-вольтметра (рис. 6, а).

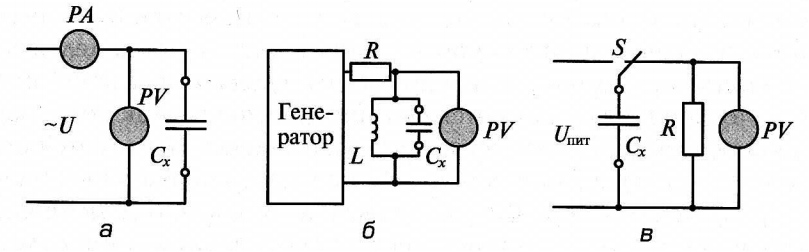
Рис. 6. Схемы измерения емкости

Он во многом аналогичен такому же методу измерения сопротивлений, с той только разницей, что схема питается переменным синусоидальным напряжением от генератора низкой или высокой частоты (или от сети). Емкостное сопротивление конденсатора определяется по следующей формуле:

где f – частота переменного напряжения.

Емкостное сопротивление находится по закону Ома по показаниям приборов

Измерение малых по величине емкостей удобнее производить методом резонанса (рис. 6, б). Измеряемый конденсатор С_х подключается к известной индуктивности L, образуя колебательный контур. На контур подается синусоидальное напряжение от генератора. С помощью электронного вольтметра измеряют напряжение на контуре. При резонансе оно достигает максимума.

Известно, что резонансная частота контура может быть выражена следующей формулой:

Следовательно, при известной величине индуктивности в контуре и определенной по максимальным показаниям вольтметра частоте резонанса можно найти искомое значение емкости С_х.

Измерение больших емкостей (например, электролитических конденсаторов) проще всего производить путем разряда конденсатора на известное сопротивление R. Известно, что за время, равное постоянной времени цепи разряда конденсатора, его напряжение уменьшается в е раз, где е = 2,71… — основание натурального логарифма. Постоянная времени цепи разряда конденсатора на резистор определяется соотношением

Схема измерения емкости этим методом (рис. 6, в) состоит из источника постоянного напряжения питания, известного по величине сопротивления резистора R, электронного вольтметра PV, переключателя S и клемм для подключения конденсатора. С помощью переключателя S конденсатор С_х заряжается до напряжения источника питания, а после переключения конденсатора на разряд с помощью секундомера измеряют время t, по истечении которого конденсатор разрядится до напряжения U_пит/е. Емкость конденсатора определяется по формуле

Емкости конденсаторов можно измерять также с помощью мостов переменного тока.

Измерение индуктивностей

Измерение индуктивностей несколько сложнее. Это связано с тем, что любая катушка (обмотка трансформатора и т. п.) имеет кроме индуктивности еще и резистивное сопротивление. Поэтому во многих случаях измеряют предварительно полное сопротивление катушки индуктивности:

Оно может быть определено методом амперметра и вольтметра путем измерения напряжения и тока измерительными приборами схемы на переменном напряжении (рис. 7, a) z = U/I. При подаче на схему постоянного напряжения (рис. 7, б), как уже рассматривалось выше, можно определить резистивное сопротивление катушки R.

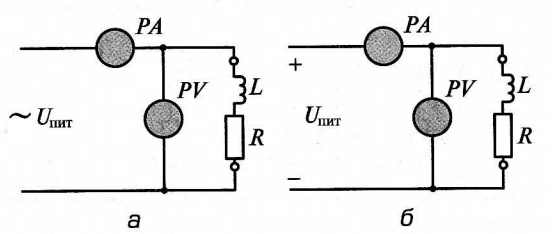
Рис. 7. Схемы измерения индуктивностей

Тогда

В свою очередь, индуктивное сопротивление

При известном значении частоты / напряжения питания легко найти величину искомого значения индуктивности

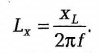
При малых значениях индуктивности (например, контурных катушек радиоэлектронных устройств) можно воспользоваться резонансной схемой, аналогичной схеме определения емкости резонансным методом.

Для измерения индуктивности можно использовать также мосты переменного тока, специальные измерительные приборы — ку- метры, позволяющие определять не только величину индуктивности, но и такую характеристику, как добротность катушки, характеризующие качество работы катушки в электронных схемах.

Измерение мощности

В электрических цепях измерение мощности удобнее рассматривать отдельно для цепей постоянного и переменного тока.

На постоянном токе основные формулы для определения мощности следующие:

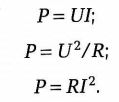
В соответствии с приведенными формулами мощность в каком-то сопротивлении нагрузки R можно измерить тремя способами: с помощью вольтметра и амперметра (рис. 8, а), только вольтметром (рис. 8, б) и только амперметром (рис. 8, в). Во всех случаях после снятия показаний с приборов необходимо провести математические расчеты для определения собственно мощности.

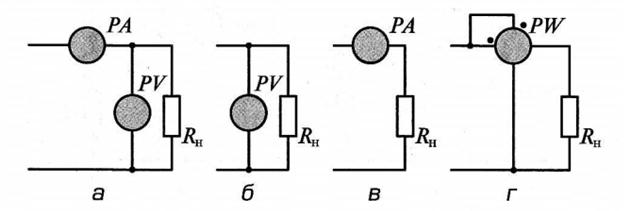
Рис. 8. Схемы измерения мощности в цепях постоянного тока

Этого можно избежать, если для измерения мощности воспользоваться специальным прибором ваттметром (рис. 8, г). Как правило, выпускаемые промышленностью ваттметры изготавливаются на базе ферродинамического прибора (см. рис. 2.105). У ваттметров имеются две обмотки и соответственно четыре вывода. Одна из обмоток является токовой, через нее проходит ток к нагрузке, расходуемая мощность в которой подлежит измерению, а вторая — обмоткой напряжения. Она подключается непосредственно к источнику питания.

Измерение мощности на переменном токе имеет свои особенности. Во-первых, здесь существуют три различные мощности:

полная мощность, В * А,

S= UI,

активная мощность, Вт,

Р = UIcosφ;

реактивная мощность, вар,

Q = UIsinφ.

В этих формулах (φ — угол сдвига по фазе между током и напряжением.

Чаще всего интересуются полной и активной мощностями. Знание полной мощности необходимо для расчета токов в нагрузке, выбора сечения проводов и предохранителей. Активная мощность важна потому, что именно она характеризует ту мощность, которая в нагрузке преобразуется в теплоту, свет, звук и т.д.

Измерение полной мощности обычно производят, измеряя напряжение и ток вольтметром и амперметром и перемножая полученные значения. Активную мощность чаще всего измеряют с помощью ферродинамических ваттметров, которые кроме напряжения и тока учитывают и так называемый коэффициент мощности cosφ.

При подключении обмоток ваттметра к нагрузке, так же как и при постоянном напряжении, ваттметр непосредственно произведет измерение активной мощности.

На переменном токе достаточно часто приходится решать задачу измерения активной мощности в трехфазных цепях. Трехфазные цепи могут быть двух типов: трехпроводные и четырехпроводные. В трехпроводных цепях к нагрузке подходят три провода, обозначаемые буквами А, В, С. Для измерения активной мощности в такой цепи при любом варианте подключения элементов нагрузки к проводам достаточно подключить только два ваттметра так, как это показано на рис. 9.

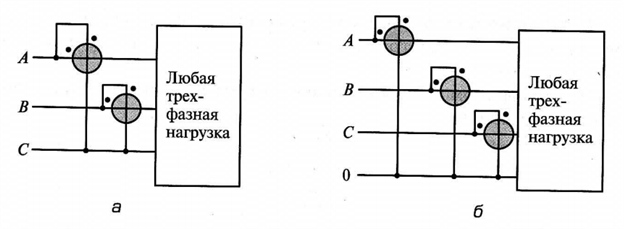
Рис. 9. Схемы измерения мощности на переменном токе: а — трехпроводная система; б — четырехпроводная система

При этом необходимо соблюсти определенные правила подключения ваттметров. Выводы обмоток ваттметра, обозначенные на его корпусе звездочками, должны быть обращены в сторону источника энергии. Поэтому эти выводы получили название генераторные (подключаются к проводам, идущим от генератора). Суммарная активная мощность такой трехфазной системы находится как алгебраическая сумма показаний двух ваттметров. При этом возможен вариант, когда показания одного из ваттметров могут быть отрицательными, т. е. его стрелка уйдет влево. Для снятия показаний с такого ваттметра необходимо поменять местами провода, подходящие к любой из обмоток, прочесть результат измерения, но в формулу подставить с отрицательным знаком.

Измерение активной мощности в четырехпроводных цепях требует использования трех ваттметров. Один из выводов каждого ваттметра здесь подключается к четвертому проводу, обычно называемому нулевым. Показания всех ваттметров могут быть только положительными, и суммарная активная мощность, потребляемая трехфазной цепью, будет равна сумме мощностей, измеряемых каждым из ваттметров:

Р_е = Р₁ + Р₂ + Р₃.

Один из наиболее простых методов измерения количества электричества — метод измерения с помощью так называемого баллистического гальванометра. Он представляет собой прибор магнитоэлектрической системы (см. рис. 2.103) с умышленно утяжеленной подвижной частью (с большим моментом инерции). Если на вход такого баллистического гальванометра подать кратковременный импульс напряжения, то подвижная часть прибора, получив как бы импульсный вращающий момент, начнет движение, причем уже после окончания входного импульса это движение еще будет продолжаться и стрелка прибора, двигаясь по инерции, отклонится до какого-то значения шкалы, а затем возвратится в исходное нулевое положение. В качестве отсчета на таком приборе необходимо отметить то максимальное отклонение стрелки α_mах от нулевого значения, которое наблюдалось во время ее движения по «баллистической траектории». Теория такого баллистического гальванометра показывает, что этот отсчет по максимальному отклонению стрелки оказывается пропорциональным количеству электричества, прошедшего через рамку такого прибора, т. е.

α_mах = Q/С₆,

где С_б—баллистическая постоянная, зависящая от конструктивных особенностей гальванометра.

Измерение количества электричества Q на обкладках предварительно заряженного конденсатора можно осуществить, разрядив его через баллистический гальванометр, и по максимальному отклонению его стрелки найти искомое значение количества электричества:

Q = С₆α_mах

При разработке новых сплавов, предназначенных для использования в электротехнических цепях, возникает необходимость в определении их удельного сопротивления. Под удельным сопротивлением понимают сопротивление проводника сечением 1 мм²

и длиной 1м. Соответственно такое удельное сопротивление р измеряется в единицах Ом – (мм^{2/м). Для его измерения выбирают отрезок проводника, желательно небольшого сечения, и измеряют его сопротивление любым из рассмотренных выше методов. После этого расчетным путем приводят величину этого сопротивления к сечению 1 мм2 и длине 1 м, что не представляет каких- либо трудностей, и получают значение удельного сопротивления. Для получения большей точности измерения желательно длину проводника брать по возможности большей.}

Для многих изоляционных материалов представляет определенную ценность определение их диэлектрической проницаемости ε. Одним из простейших способов ее измерения является способ косвенного измерения с последующим расчетом величины диэлектрической проницаемости. Известно, что емкость простейшего конденсатора, состоящего из двух одинаковых пластин площадью S, расположенных на расстоянии δ друг от друга, с диэлектриком, заполняющим все пространство между пластинами, определяется по формуле

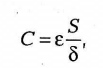
где ε — диэлектрическая проницаемость материала между пластинами.

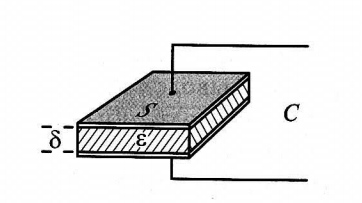
Рис. 10. Схема для измерения диэлектрической постоянной изоляционных материалов

Измерение диэлектрической проницаемости материала производят с помощью конденсатора (рис. 10), между пластинами которого помещают испытуемый материал, а также измерения емкости такого элементарного конденсатора любым из описанных выше методов. Численную величину диэлектрической проницаемости определяют по формуле

Развитие радиоэлектроники и установок для высокочастотного воздействия на материалы машиностроения привело к тому, что практически все пространство заполнено электромагнитными волнами.

В мире работают миллионы передающих радиостанций, многие из которых излучают значительные мощности (например, радиолокационные станции дальнего обнаружения, вещательные радиостанции и т. п.). Для оценки электромагнитных волн часто возникает необходимость определения их уровня. Обычно об уровне электромагнитных волн судят по напряженности электрического поля, величина которого аналитически может быть пересчитана в мощность электромагнитного поля. Напряженность электрического поля наиболее часто измеряют с помощью рамочной антенны (рис. 11), которая представляет собой плоскую катушку, намотанную на каркас Е из какого- либо диэлектрика. (На рис. 11 для простоты изображен только один виток.)

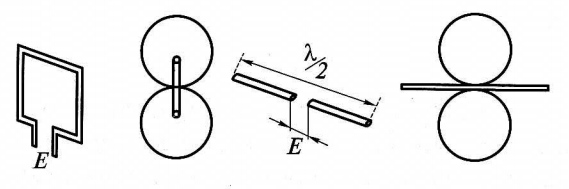
Рис. 11. Измерение напряженности электрического поля

Диаграмма направленности такой антенны показывает, что максимум принимаемого излучения идет со стороны, лежащей в плоскости витков катушки. Это позволяет не только производить измерение напряженности электрического поля, но и определять направление на источник высокочастотных излучений по максимальной величине напряжения на выходе рамки при ее поворотах относительно вертикальной оси. Напряженность электрического поля определяется по величине напряжения на выходе рамки по следующей формуле, В/м:

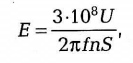
где U — напряжение на выходе рамки, В; f – частота принимаемого сигнала, Гц; n — число витков в рамке; S— площадь рамки, м^2.

Обычно на геометрические размеры рамки в зависимости от частоты сигнала напряженность поля которого определяется, накладываются определенные ограничения. В частности, на частотах более 30 МГц более точные результаты получаются, если вместо рамочной антенны использовать полуволновый диполь, представляющий собой проводник длиной в половину длины волны, разрезанный посередине. Напряжение с диполя снимается с центральной разрезанной части. Значение напряженности электрического поля можно определить по следующей формуле:

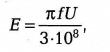
где f— частота, Гц; U— напряжение на выходе диполя, В.

Диполь, так же как и рамка, позволяет определять направление, с которого приходит сигнал, так как обладает определенной направленностью, что видно из диаграммы направленности. Максимум принимаемых сигналов определяется перпендикуляром к плоскости диполя. Именно так ориентированы телевизионные антенны по отношению к телевизионной вышке.

Напряжение на выходе рамки или диполя можно измерять с помощью электронного вольтметра непосредственно при сильных сигналах или применяя электронные усилители. В этом случае, используя селективные свойства усилителей, можно определить уровень напряженности электрического поля определенной частоты. Нужно учесть, что уровень сигнала на выходе рамки и частично диполя складывается из большого числа электромагнитных полей, существующих в пространстве в районе расположения приемного устройства от различных источников (передатчиков).

При необходимости определить частоту высокочастотного сигнала можно, если он сильный, используя непосредственное включение электронного частотомера на выход рамки или диполя. При слабых сигналах и использовании усилителей можно по их частотной настройке определять частоты сигналов, наведенные в рамке или диполе, т. е. так, как обычно по шкале радиоприемника можно определить длину волны или частоту принимаемой станции.