Задачи, тесты
С. Н.
Карташов
Мощность, выделяемая во внешней цепи с
потребителями
С.Н.КАРТАШОВ,
с. Маис, Пензенская обл.
Мощность, выделяемая во внешней
цепи с потребителями
Решение задач на экстремум с
компьютерной поддержкой
Предлагаемые задачи рассматриваются с
учениками 10-х и 11-х классов на заседании
школьного физического кружка. Они требуют знаний
по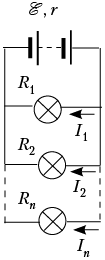
теме «Законы постоянного тока», умения
исследовать функции на экстремум при помощи
производной, а также навыков программирования на
компьютере.
ЗАДАЧА 1. Найдите зависимость мощности,
выделяемой во внешней цепи, от числа одинаковых
потребителей (лампочек), соединённых
параллельно. ЭДС источника ![]() , его внутреннее сопротивление r.
, его внутреннее сопротивление r.
Решение
Пусть сопротивления всех лампочек
одинаковы R1 = R2 = … = Rn,
P – мощность, выделяемая во внешней цепи, P1
– мощность, выделяемая на каждой лампочке.
Очевидно, что P = nP1; P1 = I12
R1, где I1 – ток, проходящий
через каждую лампочку.
Сила тока в неразветвлённой цепи:
![]()
(1)
Применяя первое правило Кирхгофа,
имеем
![]()
(2)
С учётом (2) имеем для мощности 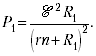
Полная мощность, выделяемая во внешней
цепи:
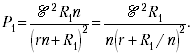 (3)
(3)
Нетрудно заметить , что если n ![]()
![]() , то P
, то P ![]() 0. Это означает, что при
0. Это означает, что при
неограниченном увеличении количества лампочек
мы не достигнем бесконечного увеличения
мощности, выделяемой во внешней цепи. Напротив,
мощность будет стремиться к нулю.
Из формулы (3) следует также, что если r
![]() 0, то P
0, то P ![]() n
n![]() 2/R. То есть, если
2/R. То есть, если
источник тока идеален (r = 0), то мощность
возрастает прямо пропорционально числу
потребителей в цепи. Но внутреннее сопротивление
источника тока не может быть равно нулю, поэтому
достигнуть бесконечного увеличения мощности во
внешней цепи за счёт увеличения числа
потребителей невозможно. Напротив, достигнув
максимума, мощность, выделяемая во внешней цепи,
начнёт уменьшаться с ростом потребителей.
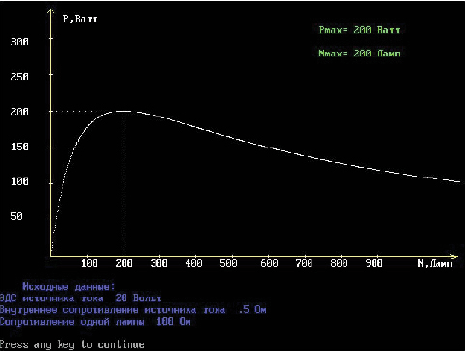
Для получения полной картины
зависимости мощности Р от количества
потребителей n, можно предложить учащимся
построить график зависимости P(n) на
компьютере (![]() = 20 В, r
= 20 В, r
= 0,5 Ом, R1 = 100 Ом). В рубрике
«Дополнительные материалы» на сайте газеты http://fiz.1september.ru приводим
авторскую компьютерную программу WATT для
построения вышеупомянутой зависимости (среда
программирования QBasic, компьютер Celeron1300).
Изменяя внутреннее сопротивление r
при неизменных ![]() и R1,
и R1,
делаем вывод: мощность P, выделяемая во
внешней цепи, убывает с ростом r. Изменяя R1
при неизменных ![]() и r,
и r,
делаем вывод: от сопротивления одной лампочки
максимум мощности P не зависит. Этот
максимум сдвигается вправо при увеличении R1
и сдвигается влево при уменьшении R1.
Число ламп в цепи, при котором наблюдается
максимум мощности, равно nmax = R1/r.
То есть мощность, выделяемая во внешней цепи,
максимальна, если внутреннее сопротивление
источника тока равно внешнему сопротивлению
цепи: r = R1/ nmax.
Расчётные результаты отлично согласуются с
результатами следующей, похожей, задачи.
ЗАДАЧА 2. При каком значении R
мощность, выделяемая во внешней цепи,
максимальна? ЭДС источника тока ![]() , внутреннее сопротивление r.
, внутреннее сопротивление r.
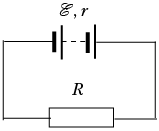
Решение
Получим формулу зависимости мощности P,
выделяемой во внешней цепи, от внешнего
сопротивления R и исследуем функцию P(r)
на экстремум при помощи производной.
По закону Ома для полной цепи, ток I
=![]() /(R + r),
/(R + r),
мощность, выделяемая во внешней цепи:
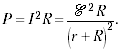
Дифференцируем P по R:
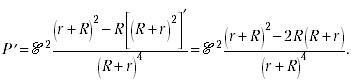

Найдём критические точки из условия P’
= 0:
(R + r)2 – 2R(R + r)
= 0;(R + r) · (R + r – 2R) =
0;(R + r) · (r – R) = 0.
Имеем две критические точки R = –r
и R = r . Но т.к. R > 0, то R = –r
не имеет смысла. Производная P’ меняет знак с
«+» на «–» в точке R = r, следовательно, R
= r – точка минимума.
Итак, мощность максимальна, если R
= r, т.е. внутреннее сопротивление источника
тока равно внешнему сопротивлению. Это означает,
что применительно к задаче 1 максимум мощности
наблюдается при R = r, но т.к.
сопротивление n одинаковых ламп равно R
= R1/n, то r = R1/n,
или n = nmax = R1/r.
Рассчитаем максимум мощности,
используя формулу (3) и условие r = R1/n:
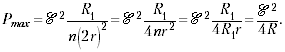
(4)
При ![]() = 12 В,
= 12 В,
r = 0,4 Ом и R1= 20 Ом имеем nmax
= R1/r = 50 ламп.
Согласно формуле (4), Pmax = 90
Вт. Всё это очень хорошо согласуется с
результатами компьютерного эксперимента. Кроме
того, из этой формулы следует, что максимум
мощности зависит от внутреннего сопротивления
обратно пропорционально, в чём легко убедиться,
используя компьютерную программу WATT,
приведённую на сайте газеты http://fiz.1september.ru.
В заключение необходимо сказать, что
все выше приведённые выкладки, а также
результаты, полученные с помощью компьютерной
программы для цепей постоянного тока,
справедливы и для цепей переменного тока.
Возможен более современный подход,
если использовать для моделирования таблицу МicrosoftExcel.
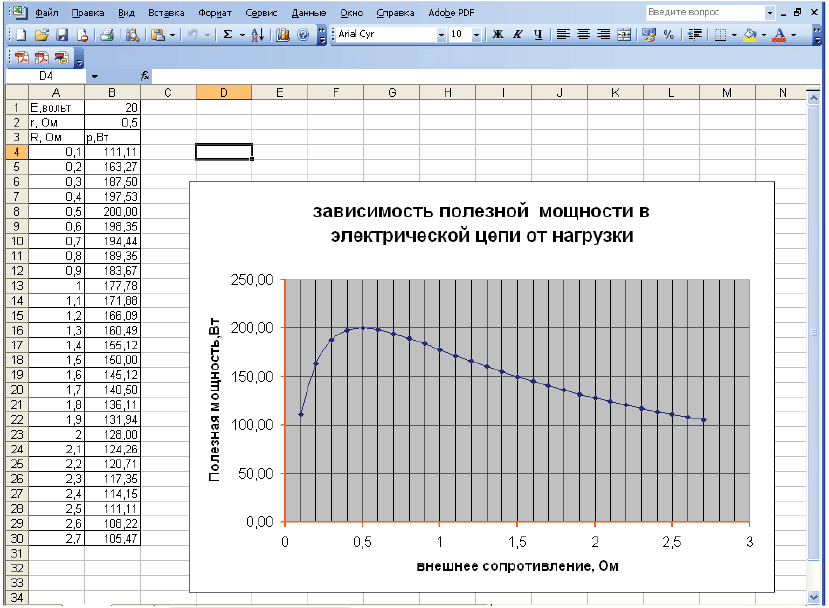
Если R – внешнее сопротивление цепи, то ![]() Построим график
Построим график
для тех же данных: 1 = 20 В, r = 0,5 Ом, меняя R
от 0,1 до 2,7 Ом с шагом 0,1 Ом. Для этого в ячейку B4
введём формулу =$B$1^2*A4/(A4+$B$2)^2 и скопируем её в
ячейки В5–В30. Графики, построенные с помощью
таблицы Excel и программы WATT, совпадают
(максимум мощности 200 Вт получается, если внешнее
сопротивление цепи равно внутреннему
сопротивлению источника тока). В рубрике
«Дополнительные материалы» к № 9/2008 на сайте
газеты приведена программа «Мощность»,
аналогичная программе WATT, но на более
продвинутом языке VisualBasic6.0, результат расчёта
с её помощью, а также таблица МicrosoftExcel.

Сергей Николаевич Карташов –
учитель физики высшей квалификационной
категории, выпускник физфака МПГУ им. В.И.Ленина
1993 г. Педагогический стаж 14 лет. Ученики Сергея
Владимировича занимают призовые места на
районных олимпиадах по физике и математике.
Педагогическое кредо: моделирование физических
процессов на компьютере, индивидуальная работа с
сильными детьми. Один закончил физфак МГУ им.
М.В.Ломоносова, ещё один учится в университете им.
Н.Э.Баумана. В 2002 г. Сергей Владимирович был
награждён почётной грамотой МОиН РФ. Женат, сыну
3,5 года. Хобби: шахматы, решение олимпиадных
задач по физике и математике, кулинария.
С.Н.КАРТАШОВ,
с. Маис, Пензенская обл.
maisscool1@mail.ru
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
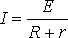 , (1)
, (1)
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
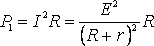 . (2)
. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®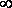 эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
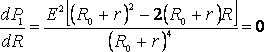 . (3)
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R0 = r. (4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи 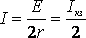 (5)
(5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
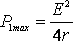 . (6)
. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
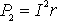 .
.  (7)
(7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
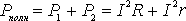 = I2(R+r) = IE (8)
= I2(R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен 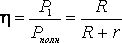 . (9)
. (9)
Из формулы (8) следует, что
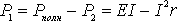 , (10)
, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 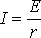 . Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
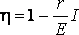 (11)
(11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.


Рис.1. I0 E/r
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Рис. 2.
Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой  э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку  в нижней части экрана) и амперметр (кнопка
в нижней части экрана) и амперметр (кнопка  там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр  , измеряющий напряжение на нагрузке.
, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода  внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой  . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Таблица 1. Исходные параметры электрической цепи
|
Номер варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Е, В |
10,0 |
9,5 |
9,0 |
8,5 |
8,0 |
8,5 |
9,0 |
9,5 |
|
r, Ом |
4,8 |
5,7 |
6,6 |
7,5 |
6,4 |
7,3 |
8,2 |
9,1 |
5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.
6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.
7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.
8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R).
9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.
Таблица 2. Результаты измерений и расчётов
|
R, Ом |
2,0 |
2,5 |
3,0 |
… |
20 |
||
|
U, В |
|||||||
|
I, А |
|||||||
|
P1, Вт |
|||||||
|
P2, ВТ |
|||||||
|
Pполн, ВТ |
|||||||
|
h |
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.
Рассмотрим полную цепь постоянного тока, состоящую из источника с электродвижущей силой Е, внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
Работа кулоновских сил ΔAкул, действующих во всей замкнутой цепи (внешней и внутренней) равна работе сторонних сил ΔAст, действующих внутри источника.
Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
Во внешней цепи выделяется мощность
Отношение
называется коэффициентом полезного действия источника.
На рисунке графически представлены зависимости мощности источника Pист , полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I.
Для источника с ЭДС, равной Е, и внутренним сопротивлением r ток в цепи может изменяться в пределах от I = 0 при R = ∞ , до
при R = 0.
Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока.
Из приведенных графиков видно, что максимальная мощность во внешней цепи Pmax, равная
достигается при R = r. При этом ток в цепи
а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
“Элементарная Физика” на YouTube – интересные факты, законы физики, примеры решения задач в доступной и увлекательной форме
Для
того чтобы поддерживать разность
потенциалов на концах проводника и,
следовательно, существование постоянного
электрического тока в проводнике и
постоянное тепловыделение, необходимы
источники электрической энергии
(электрического тока). В источниках
такого рода происходит разделение
зарядов разных знаков и на выходных
клеммах появляется разность потенциалов.
Подключим
какую-нибудь нагрузку (сопротивление)
к источнику электрической энергии.
Получим замкнутую цепь. Каким образом
движутся заряды вне и внутри источника
тока? Прежде всего, еще раз напомним,
что мы рассматриваем только стационарные
токи, т.е. заряды нигде не накапливаются,
а просто циркулируют по замкнутой цепи.
Вне источника (во внешней цепи) ток идет
от «плюса» к «минусу» (клемма «плюс» –
клемма с большим потенциалом, клемма
«минус» – клемма с меньшим потенциалом).
Таким образом, во внешней цепи заряды
движутся в направлении, в котором на
них действует электрическое поле внутри
проводника: положительные по полю,
отрицательные против поля. Внутри
источника электрической энергии (во
внутренней цепи) ток идет от «минуса»
к «плюсу», т.е. заряды движутся в
направлении, противоположном тому, в
котором на них действует электрическое
поле. Значит, внутри источника перемещение
зарядов вызывается не электрическим
полем, а какими-то иными причинами. Эти
причины (химические, механические,
световые, магнитные и т. д.) зависят от
природы источника тока.
Силы,
действующие внутри источника электрической
энергии, заставляющие заряды двигаться
против действия электрического поля,
называются сторонними
силами. При
этом часто при решении каких-то задач
природа этих сил значения не имеет и не
конкретизируется. Сторонние силы при
упорядоченном движении зарядов совершают
работу, за счет которой, например,
нагреваются сопротивления. Очевидно,
что полный запас энергии источника тока
равен работе, которую могут совершить
сторонние силы.
К
идее о необходимости действия в замкнутой
цепи сторонних сил полезно прийти и
иным образом. Представим себе, что на
свободные заряды в замкнутой цепи
действовали бы одни электрические силы.
Известно, что цепь при прохождении по
ней тока нагревается. Выделившееся
тепло тогда можно было бы рассматривать
только как результат работы электрических
сил (электрического поля). Но работа
электрического поля по перемещению
зарядов по замкнутой траектории (в
данном случае замкнутой цепи) равна
нулю (этот факт подробно обсуждался в
п.1.12). А значит, не могла бы нагреваться
и цепь, что явно противоречит опыту.
Следовательно, где-то в замкнутой цепи
обязательно должны действовать силы
не электростатического происхождения,
работа которых отлична от нуля, т.е.
сторонние силы. Место действия сторонних
сил в замкнутой цепи и можно назвать
источником электрической энергии или
источником тока.
Важнейшей
характеристикой источника тока является
электродвижущая сила (ЭДС). Можно дать
два эквивалентных определения ЭДС.
1)
ЭДС – разность потенциалов на выходных
клеммах источника тока при разомкнутой
внешней цепи
(или когда ток через источник не идет).
Далее мы покажем, что в случае разрядки
или зарядки источника тока разность
потенциалов на его выходных клеммах
соответственно меньше ЭДС и больше ЭДС.
2) ЭДС – работа
сторонних сил (источника) по разделению
единичного заряда (или просто при
прохождении через источник единичного
заряда):
![]() .
.
(2.12)
Из
(2.12) следует, что, зная ЭДС источника,
силу тока и время его протекания, можно
определить работу, совершенную сторонними
силами:
![]() .
.
(2.13)
Обсудим
вторую характеристику источника –
внутреннее сопротивление. Представим
себе, что мы замкнули клеммы источника
проводником с исчезающе малым
сопротивлением
![]() ,
,
другими словами, сделали короткое
замыкание источника. Тогда, если бы
источник был идеальным, т.е. на его
выходных клеммах разность потенциалов
была бы всегда равна ЭДС, то по закону
Ома мы получили бы![]() ,
,
т.е. источник давал бы бесконечный ток
и в единицу времени совершал бы бесконечно
большую работу (см. (2.13)), что невозможно.
Таким образом, при работе любого источника
обязательно должны существовать
какие-либо внутренние механизмы
ограничения максимального тока. Эти
механизмы могут быть различными в
зависимости от природы источника тока.
Однако все они могут быть смоделированы,
если ввести вторую характеристику
источника – внутреннее сопротивление![]() .
.
В этом случае при коротком замыкании
за счет конечного внутреннего сопротивления
источника мы получим конечный ток в
цепи, называемый током короткого
замыкания:![]() .
.
Это максимальный ток, который может
давать источник. Итак, внутреннее
сопротивление источника![]() – это характеристика, определяющая
– это характеристика, определяющая
ток короткого замыкания или максимальные
ток и мощность, которые может давать
источник.

Можно сделать
вывод, что какова бы ни была сложная
природа источника тока, его можно
охарактеризовать всего двумя параметрами
– электродвижущей силой (ЭДС) и внутренним
сопротивлением. Любой источник тока
можно представлять себе как «черный
ящик», состоящий из идеального источника
ЭДС
![]() ,
,
разность потенциалов на клеммах которого
всегда равна![]() ,
,
и последовательно соединенного
с ним сопротивленияr,
которое называется внутренним
сопротивлением источника тока.
Такая модель источника тока показана
на рис. 2.9.
На
этом же рис. 2.9 к клеммам источника
подключено некоторое, отличное от нуля
сопротивление R.
Поскольку внутреннее и внешнее
сопротивления соединены последовательно,
полное сопротивление цепи будет
![]() ,
,
и по цепи потечет ток:
 . (2.14)
. (2.14)
Последнее
равенство называется законом Ома для
полной цепи.
Уравнение
(2.14) легко преобразуется к виду:
![]() .
.
Правая часть этого равенства (а значит
и левая) есть напряжение на внешнем
сопротивленииR.
Это напряжение суть напряжение на
выходных клеммах источника тока, так
как сопротивление R
непосредственно к этим клеммам подключено.
Таким образом, при разрядке источника
током I
напряжение на его клеммах:
![]() .
.
(2.15)
Это
напряжение тем ближе к ЭДС, чем меньше
внутреннее сопротивление и ток разрядки.
При
![]() в соответствии с данным выше первым
в соответствии с данным выше первым
определением ЭДС из (2.15) получим![]() .
.
Пример
2.7. В схеме
на рис. 2.9
![]() В,
В,![]() Ом,
Ом,![]() Ом.
Ом.
-
Определить
силу тока в цепи. По закону Ома для
полной цепи (2.14) получим:
 А.
А. -
Определить
напряжение на клеммах источника тока.
Напряжение на клеммах источника суть
напряжение на нагрузке R:
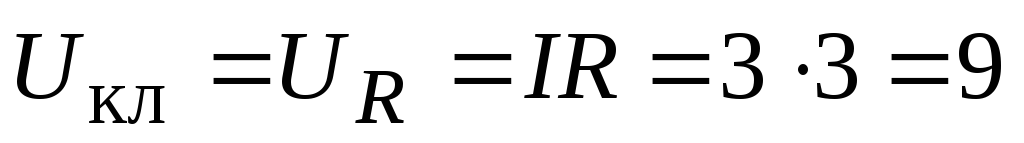 В. Естественно то же самое получается
В. Естественно то же самое получается
и по формуле (2.15). -
Определить
мощность, выделяющуюся во внешней цепи.
Мощность, выделяющаяся во внешней цепи,
есть мощность, выделяющаяся на нагрузке
R,
поэтому:
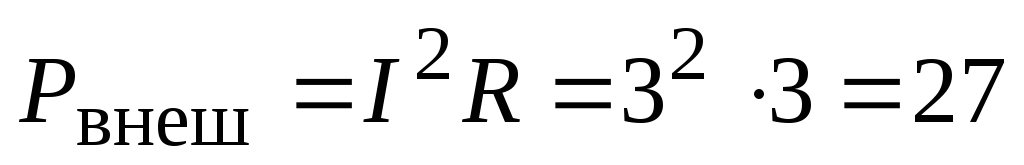 Вт.
Вт. -
Определить
мощность, выделяющуюся во внутренней
цепи. Конечно, при работе источника
тока нагревается не только внешняя
нагрузка, но и сам источник, поскольку
он обладает внутренним сопротивлением.
Мощность, выделяющаяся во внутренней
цепи, есть мощность, выделяющаяся на
сопротивлении r:
 Вт.
Вт. -
Определить
мощность источника тока (мощность,
развиваемую сторонними силами). Работа
источника тока расходуется на нагревание
как внешней нагрузки, так и самого
источника тока, поэтому:
 Вт. Можно рассуждать и по-другому,
Вт. Можно рассуждать и по-другому,
опираясь на уравнение (2.13): Вт.
Вт. -
Определить
КПД схемы. Полезной следует считать
часть мощности источника, которая
выделяется на внешнем сопротивлении,
поэтому:
![]() (или
(или
75%).
-
Определить
максимальный ток, который может давать
заданный источник. Ток будет максимален
при коротком замыкании источника (т.е.
при
 ):
):
 (А).
(А).
Пример
2.8. Каким
должно быть сопротивление
![]() при заданных параметрах источника тока
при заданных параметрах источника тока
и r
для того, чтобы во внешней цепи выделялась
максимальная мощность? Чему равна эта
максимальная мощность?
Решение.
Пользуясь законом Ома для полной цепи
(2.14) для мощности, выделяемой во внешней
цепи, можно записать:
 (2.16)
(2.16)
Рвнеш
![]()
R1
R=r
R2
R















Рис.
2.10. Зависимость мощности, выделяемой
во внешней цепи от сопротивления
График
зависимости функции
![]() показан на рис. 2.10. Ясно, что эта функция
показан на рис. 2.10. Ясно, что эта функция
должна иметь точку максимума (т.е.
значение
![]() ,
,
при котором мощность во внешней цепи
максимальна), поскольку из (2.16) следует,
что
![]() и
и![]() при
при![]() .
.
Найдем точку максимума функции![]() .
.
Для этого продифференцируем![]() по сопротивлению
по сопротивлению![]() и приравняем производную к нулю:
и приравняем производную к нулю:
![]() ,
,
откуда
получаем: ![]() .
.
Таким образом, мощность, выделяемая во
внешней цепи максимальна, когда внешнее
сопротивление равно внутреннему
сопротивлению источника (рис. 37).
По формуле (2.16)
рассчитаем максимальное значение
мощности, выделяемой во внешней цепи:
![]() .
.
Отметим,
что КПД схемы при этом равен всего на
всего 50%, т.е. половина мощности выделяется
во внешней цепи и половина – во внутренней:
![]() .
.
Анализируя
график на рис. 2.10, можно сделать вывод,
что какое-то требуемое значение мощности,
выделяемой во внешней цепи, можно
получить двумя способами: подключая к
источнику тока некоторые сопротивления
![]() и
и![]() ,
,
причем![]() ,
,
а![]() .
.
Какой вариант следует выбрать? Конечно,
предпочтение следует отдать второму
варианту (т.е. включить большее
сопротивление![]() ),
),
поскольку КПД схемы в этом случае будет
больше (см. вопрос 6 примера 2.5). При
подключении же сопротивления![]() КПД будет меньше 50%. Во внешней цепи мы
КПД будет меньше 50%. Во внешней цепи мы
тоже получим требуемую мощность, но при
этом еще большая мощность будет бесполезно
выделяться во внутренней цепи, т.е.
расходоваться на нагрев самого источника.
В результате источник быстрее израсходует
свой ресурс.
Соседние файлы в папке Методички_Общая физика
- #
- #
- #
- #
- #
- #
- #
- #
Коэффициент полезного действия источника тока.
Исследуем физические характеристики замкнутой электрической цепи, включающей внешнее сопротивление , называемое полезной нагрузкой, и источник тока с электродвижущей силой  и внутренним сопротивлением (рис. 3).При прохождении тока тепло выделяется как на внешнем, так и внутреннем сопротивлении. Полная тепловая мощность
и внутренним сопротивлением (рис. 3).При прохождении тока тепло выделяется как на внешнем, так и внутреннем сопротивлении. Полная тепловая мощность 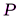 , выделяемая в цепи постоянного тока, складывается из полезной мощности
, выделяемая в цепи постоянного тока, складывается из полезной мощности
 , (6.17)
, (6.17)
выделяемой во внешней цепи, и мощности тепловых потерь  , выделяемой внутри источника тока, т.е.
, выделяемой внутри источника тока, т.е.
 . (6.18)
. (6.18)
Полная мощность развивается за счет сторонних сил, осуществляющих разделение зарядов в источнике тока. Используя закон Ома для замкнутой цепи [см. формулу (6.13)], выражения для полезной и полной тепловых мощностей можно записать в виде
 (6.19)
(6.19)
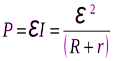 . (6.20)
. (6.20)
Коэффициент полезного действия(КПД) электрической цепи определяется как отношение полезной мощности  к полной мощности :
к полной мощности :
 . (6.21)
. (6.21)
Таким образом, КПД зависит от соотношения внутреннего сопротивления и сопротивления нагрузки.
Каким должно быть сопротивление нагрузки для того, чтобы получить максимальную полезную мощность и максимальный КПД? Ответ на этот вопрос получим, исследовав графически и аналитически выражения (6.19) и (6.21).
Полная мощность определяется формулой (12). Ее величина максимальна при  , т.е. при коротком замыкании источника. Как видно из формул (11) и (13), при этом равны нулю Рп и
, т.е. при коротком замыкании источника. Как видно из формул (11) и (13), при этом равны нулю Рп и  ( рис. 6.4.).
( рис. 6.4.).
При  полная мощность и сила тока равны половинам своих максимальных значений, КПД равен 0,5, а полезная мощность достигает своего максимального значения, равного половине полной мощности при этой нагрузке.
полная мощность и сила тока равны половинам своих максимальных значений, КПД равен 0,5, а полезная мощность достигает своего максимального значения, равного половине полной мощности при этой нагрузке.
Чтобы убедиться, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока полезная мощность действительно максимальна, преобразуем правую часть выражения (6.19) следующим образом:
 . (6.22)
. (6.22)

Полезная мощность максимальна, когда знаменатель выражения (6.22) минимален. Возьмем производную по R от этого знаменателя и приравняем ее нулю. В результате получим уравнение
 , (6.23)
, (6.23)
из которого следует, что условием максимума полезной мощности действительно является равенство внешнего и внутреннего сопротивлений.
Сам максимум полезной мощности определяется как
 , (6.24)
, (6.24)
то есть максимум полезной мощности равен четверти мощности короткого замыкания:
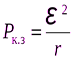 . (6.25)
. (6.25)
При неограниченном увеличении сопротивления нагрузки как полная мощность, так и полезная мощность стремятся к нулю, а КПД – к единице (рис.6.4).
Из рис. 6.4 видно, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального КПД противоречивы. Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и КПД, так как почти вся совершаемая источником тока работа идет на выделение теплоты на внутреннем сопротивлении r. Чтобы получить от данного источника тока максимальную полезную мощность, следует использовать согласованную нагрузку, т.е. нагрузку с сопротивлением  .
.
Докажите, что мощность, выделяемая на внешнем участке цепи, максимальна при равенстве электрического сопротивления внешнего
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Исследование зависимости мощности и КПД источника тока от внешней нагрузки
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
alt=»Статья 34 — Картинка 2″ />. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R® alt=»Статья 34 — Картинка 3″ />эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
alt=»Статья 34 — Картинка 4″ /> . (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи alt=»Статья 34 — Картинка 5″ /> (5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
alt=»Статья 34 — Картинка 6″ />. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
alt=»Статья 34 — Картинка 7″ /> . alt=»Статья 34 — Картинка 8″ /> (7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
alt=»Статья 34 — Картинка 9″ />= I 2 (R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен alt=»Статья 34 — Картинка 10″ />. (9)
Из формулы (8) следует, что
alt=»Статья 34 — Картинка 11″ />, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при alt=»Статья 34 — Картинка 12″ />. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
alt=»Статья 34 — Картинка 13″ /> (11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.
alt=»Статья 34 — Картинка 14″ />
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой alt=»Статья 34 — Картинка 17″ />э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку alt=»Статья 34 — Картинка 18″ />в нижней части экрана) и амперметр (кнопка alt=»Статья 34 — Картинка 19″ />там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр alt=»Статья 34 — Картинка 20″ />, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода alt=»Статья 34 — Картинка 21″ />внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой alt=»Статья 34 — Картинка 22″ />. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
