Price and Output Determination under Monopoly
Monopoly refers to a market structure in which there is a single producer or seller that has a control on the entire market.
This single seller deals in the products that have no close substitutes and has a direct demand, supply, and prices of a product.
Therefore, in monopoly, there is no distinction between an one organization constitutes the whole industry.
Demand and Revenue under Monopoly:
In monopoly, there is only one producer of a product, who influences the price of the product by making Change m supply. The producer under monopoly is called monopolist. If the monopolist wants to sell more, he/she can reduce the price of a product. On the other hand, if he/she is willing to sell less, he/she can increase the price.
As we know, there is no difference between organization and industry under monopoly. Accordingly, the demand curve of the organization constitutes the demand curve of the entire industry. The demand curve of the monopolist is Average Revenue (AR), which slopes downward.
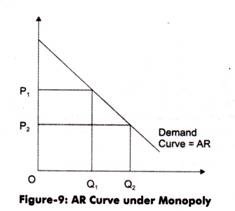
Figure-9 shows the AR curve of the monopolist:
In Figure-9, it can be seen that more quantity (OQ2) can only be sold at lower price (OP2). Under monopoly, the slope of AR curve is downward, which implies that if the high prices are set by the monopolist, the demand will fall. In addition, in monopoly, AR curve and Marginal Revenue (MR) curve are different from each other. However, both of them slope downward.
The negative AR and MR curve depicts the following facts:
i. When MR is greater than AR, the AR rises
ii. When MR is equal to AR, then AR remains constant
iii. When MR is lesser than AR, then AR falls
Here, AR is the price of a product, As we know, AR falls under monopoly; thus, MR is less than AR.
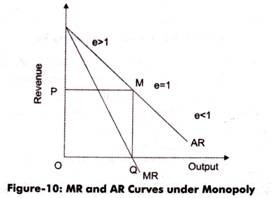
Figure-10 shows AR and MR curves under monopoly:
In figure-10, MR curve is shown below the AR curve because AR falls.
Table-1 shows the numerical calculation of AR and MR under monopoly:
As shown in Table-1, AR is equal to price. MR is less than AR and falls twice the rate than AR. For instance, when two units of
Output are sold, MR falls by Rs. 2, whereas AR falls by Re. 1.
Monopoly Equilibrium:
Single organization constitutes the whole industry in monopoly. Thus, there is no need for separate analysis of equilibrium of organization and industry in case of monopoly. The main aim of monopolist is to earn maximum profit as of a producer in perfect competition.
Unlike perfect competition, the equilibrium, under monopoly, is attained at the point where profit is maximum that is where MR=MC. Therefore, the monopolist will go on producing additional units of output as long as MR is greater than MC, to earn maximum profit.
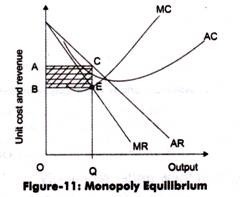
Let us learn monopoly equilibrium through Figure-11:
In Figure-11, if output is increased beyond OQ, MR will be less than MC. Thus, if additional units are produced, the organization will incur loss. At equilibrium point, total profits earned are equal to shaded area ABEC. E is the equilibrium point at which MR=MC with quantity as OQ.
It should be noted that under monopoly, price forms the following relation with the MC:
Price = AR
MR= AR [(e-1)/e]
e = Price elasticity of demand
As in equilibrium MR=MC
MC = AR [(e-1)/e]
Exhibit-2:
Determining Price and Output under Monopoly:
Suppose demand function for monopoly is Q = 200-0.4Q
Price function is P= 1000-10Q
Cost function is TC= 100 + 40Q + Q2
Maximum profit is achieved where MR=MC
To find MR, TR is derived.
TR= (1000-10Q) Q = 1000Q-10Q2
MR = ∆TR/∆Q= 1000 – 20Q
MC = ∆TC/∆Q = 40 + 2Q
MR = MC
1000 – 20Q = 40 + 2Q
Q = 43.63 (44 approx.) = Profit Maximizing Output
Profit maximizing price = 1000 – 20*44 = 120
Total maximum profit= TR-TC= (1000Q – 10Q2) – (100+ 40Q+Q2)
At Q = 44
Total maximum profit = Rs. 20844
Monopoly Equilibrium in Case of Zero Marginal Cost:
In certain situations, it may happen that MC is zero, which implies that the cost of production is zero. For example, cost of production of spring water is zero. However, the monopolist will set its price to earn profit.
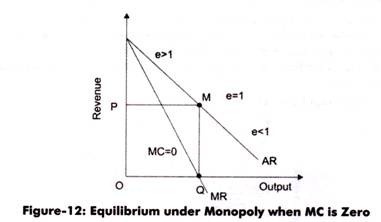
Figure-12 shows the monopoly equilibrium when MC is zero:
In Figure-12, AR is the average revenue curve and MR is the marginal revenue curve. In such a case, the total cost is zero; therefore, AR and MR are also zero. As shown in Figure-12, equilibrium position is achieved at the point where MR equals zero that is at output OQ and price P.We can see that point M is the mid-point of AR curve, where elasticity of demand is unity. Therefore, when MC = 0, the equilibrium of the monopolist is established at the output (OQ) where elasticity of demand is unity.
Short-Run and Long-Run View under Monopoly:
Till now, we have discussed monopoly equilibrium without taking into consideration the short-run and long- run period. This is because there is not so much difference under short run and long run analysis in monopoly.
In the short run, the monopolist should make sure that the price should not go below Average Variable Cost (AVC). The equilibrium under monopoly in long-run is same as in short-run. However, in long-run, the monopolist can expand the size of its plants according to demand. The adjustment is done to make MR equal to the long run MC.
In the long-run, under perfect competition, the equilibrium position is attained by entry or exit of the organizations. In monopoly, the entry of new organizations is restricted.
The monopolist may hold some patents or copyright that limits the entry of other players in the market. When a monopolist incurs losses, he/she may exit the business. On the other hand, if profits are earned, then he/she may increase the plant size to gain more profit.
Page load link
Go to Top

283
отрицательный наклон (рис. 11-1Б). Поэтому монополист может управлять ценой на свой товар, но тогда ему придется столкнуться с изменением величины спроса: чем цена выше, тем ниже спрос. Монополия – ценоискатель. Ее цель – установить такую цену (соответственно выбрать такой выпуск), при которой ее прибыль будет максимальна.
Общее правило: прибыль максимальна при таком выпуске, когда предельный доход равен предельным затратам – MR=MC (тема 10, п. 3) – остается верным и для монополии. Разница лишь в том, для совершенно конкурентной фирмы линия предельного дохода (MR) горизонтальна и совпадает с линией рыночной цены, по которой эта фирма может продать любое количество своей продукции (тема 10, п. 2). Иными словами, предельный доход конкурентной фирмы равен цене. Напротив, для монополии линия MR не горизонтальна и не совпадает с линией цены (кривой спроса).
Для обоснования этого вспомним, что предельный доход есть приращение выручки при увеличении выпуска на одну единицу: MR = ∆∆TRq .
Для примера исчисления предельного дохода возьмем самую простую функцию спроса на продукт монополии: P=10-q. Составим таблицу (табл.
11-1):
|
P |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|||||||||
|
q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||||
|
TR (P*q) |
0 |
9 |
16 |
21 |
24 |
25 |
24 |
21 |
16 |
9 |
0 |
|||||||||
|
MR (∆TR/∆q) |
9 |
7 |
5 |
3 |
1 |
-1 -3 |
-5 |
-7 |
-9 |
Из данных таблицы следует, что если монополист снижает цену с 10 до 9, спрос увеличивается с 0 до 1. Соответственно, выручка возрастает на 9. Это и есть предельный доход, получаемый при выпуске дополнительной единицы продукции. Увеличение выпуска еще одну единицу приводит к повышению выручки еще на 7. И т.д. В таблице значения предельного дохода расположены не строго под значениями цены и спроса, а между ними. В данном случае приращения выпуска не являются бесконечно
284
малыми, а потому предельный доход получается как бы «на переходе» от одной величины производства к другой.
В тот момент, когда предельный доход достигает нуля (последняя единица выпуска вовсе не увеличивает выручку), выручка монополии достигает максимума. Дальнейшее увеличение производства ведет к падению выручки, т.е. предельный доход становится отрицательным.
Данные таблицы позволяют сделать вывод, что величина предельного дохода, относящаяся к каждому значению выпуска (кроме нулевого), оказывается меньше соответствующего значения цены. Дело в том, что при выпуске дополнительной единицы продукции выручка увеличивается на цену этой единицы продукции (P). В то же время, чтобы продать эту дополнительную единицу выпуска, приходится снижать цену на величину
∆∆Pq . Но по новой цене продаются не только последняя, но и все
предыдущие единицы выпуска (q), прежде продававшиеся по более высокой цене. Поэтому монополист несет потери в выручке от снижения цены,
равные ∆∆Pq * q . Вычитая из выигрыша от роста выпуска потери от снижения
цены, получаем величину предельного дохода, который оказывается, тем самым, меньше новой цены:
MR = P + ∆∆Pq q
При бесконечно малых изменениях цены и спроса формула принимает вид:
MR = P + dPdq q ,
где dPdq – производная функции цены по спросу.
Вернемся к таблице. Пусть монополист на прошлой неделе установил цену 7, продав по ней 3 ед. товара. Пытаясь увеличить выручку, он снижает на этой неделе цену до 6, что позволяет ему продать 4 ед. товара. Значит, от расширения выпуска на одну единицу монополист получает 6 ед.

285
дополнительного дохода. Но от продажи первых 3 ед. товара он теперь получает только 18 ед. выручки, вместо 21 ед. на прошлой неделе. Потери монополиста от снижения цены равны, следовательно, 3. Поэтому предельный доход от расширения продаж при снижении цены составляет: 6-3=3 (см. таблицу 11-1).
Можно строго доказать, что при линейной функции спроса на продукт монополиста функция его предельного дохода также линейна, причем ее наклон двое больше наклона кривой спроса (рис. 11-3):
Рис. 11-3. Кривые спроса и предельного дохода монополиста
P
D
MR
q
Если функция спроса задана аналитически: P=P(q), то для определения функции предельного дохода проще всего сначала вывести функцию выручки от выпуска: TR=P(q)*q, а затем взять ее производную по выпуску: MR =TRq/ = dTRdq
Б. Максимизация монопольной прибыли
Соединим функции спроса, предельного дохода (MR), предельных (МС) и средних затрат (AС) монополиста на одном рисунке (рис. 11-4):
Рис. 11-4. Максимизация монопольной прибыли
P, MR,
MC, АС
|
Pm |
E |
MC |
AC |
|
|
C |
F |
|||
|
O |
MR |
D |
||
|
qm |
q |
286
Точка пересечения кривых MR и MC определяет выпуск (qm), при котором монополист получает максимальную прибыль. Предельный доход здесь равен предельным затратам. На кривой спроса находим монопольную цену, соответствующую этому выпуску (Pm). При такой цене (объеме выпуска) монополия находится в состоянии равновесия, ибо ей не выгодно ни повышать, ни снижать цену.
В данном случае в точке равновесия монополист получает экономическую прибыль (сверхприбыль). Она равна разнице между его выручкой и совокупными затратами:
П=TR-TC=Pm*qm-AC*qm
На рис. 11-4 выручка – это площадь прямоугольника OPmEqm, совокупные затраты – площадь прямоугольника OCFqm. Поэтому прибыль равна площади прямоугольника CPmEF.
Обращает на себя внимание то, что в условиях монопольного равновесия цена оказывается выше предельных затрат. В этом отличие от равновесия конкурентной фирмы: такая фирма выбирает выпуск, при котором цена в точности равна предельным затратам. О вытекающих отсюда проблемах речь пойдет в следующем вопросе.
Втеме «Совершенная конкуренция» (п. 4) говорилось о том, что в длительном периоде конкурентная фирма не в состоянии получать экономическую прибыль. В условиях монополии это не так. Коль скоро монополисту удается защитить свой рынок от вторжения конкурентов, он сохраняет экономическую прибыль в длительном периоде.
Вто же время обладание монопольной властью само по себе не гарантирует получение экономической прибыли даже в коротком периоде. Монополист может нести убытки, если спрос на его продукцию падает или увеличиваются его затраты – например, по причине роста цен на ресурсы или налогов (рис. 11-5):
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Равновесие в краткосрочном периоде
Согласно универсальному правилу 2, действуя в любой рыночной структуре, фирма производит такое количество q товара, при котором MR = MC. Фирма-монополист также будет стремиться выполнить данное условие; цена товара при этом будет определяться спросом на товар фирмы-монополиста (кривой спроса).
Раскрытие зависимости цены товара, производимого монополистом, от объемов выпуска проще сделать с использованием соответствующих графиков (см. рисунки С и D).
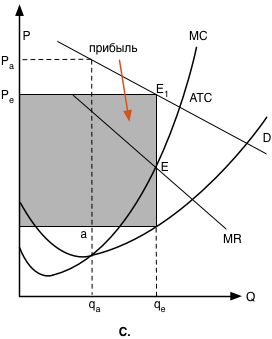
Максимизация прибыли фирмой-монополистом
Как видно из рисунков, фирма производит такой объем товара qе, при котором MR = MC. Цена Рe при этом определяется соответствующей точкой Е1 на кривой спроса D.
Если цена Рe превосходит средние суммарные издержки, т.е. находится выше кривой АТС (рисунок C), то фирма получает прибыль, равную заштрихованному прямоугольнику.
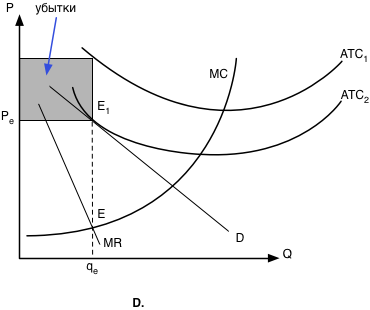
В том случае, если средние суммарные издержки при выпуске объема товаров qe равны цене (кривая АТС1 на рисунке D), то фирма полностью покрывает издержки упущенных возможностей и имеет нулевую прибыль.
Когда же суммарные издержки на единицу продукции превосходят цену (кривая АТС2 на рисунке D), фирма-монополист несет убытки (заштрихованная область).
Поскольку у фирмы-монополиста кривая MR лежит всегда ниже кривой спроса, то в отличие от совершенной конкуренции, где условием максимизации прибыли служит равенство Р = МС, при монополии универсальное правило 2 (МС = MR) выполняется, в АТС том случае, когда предельные издержки меньше цены товара (МС < Р) и точка пересечения кривых МС и MR находится ниже кривой D.
Обычно существуют типичные заблуждения в отношении принципов деятельности монополии.
Во-первых, бытует мнение, что фирма-монополист может установить любую цену на монопольно продаваемый ею товар. Однако цена производимого монополистом товара зависит от спроса на этот товар и при заданных значениях qe (когда МС = MR) имеет вполне конкретную (Рe на рисунках С и D) величину.
Во-вторых, считается, что монополист реализует с максимальной прибылью каждую единицу товара. Но внимательное изучение рисунка C показывает, что выпуская qa единиц товара (где суммарные издержки на единицу продукции минимальны), фирма имела бы более высокую прибыль на единицу продукции, чем в точке qe (цена Рa выше Рe, а средние суммарные издержки ниже).
Следовательно, монополист максимизирует суммарную прибыль, увеличивая выпуск до qe: теряя в «удельной» прибыли (на единицу продукции), он за счет расширения объемов производства повышает суммарную прибыль.
Наконец, в-третьих, с точки зрения обывателя, монополист обязательно имеет прибыль. Однако очевидно, что успехи монополиста всецело зависят от объективной рыночной ситуации: изменение спроса, рост издержек в связи с увеличением цен ресурсов могут привести к ситуации, отраженной на рисунке D, когда монополист несет убытки. Следовательно, монополизация отрасли вовсе не означает, что монополист будет иметь прибыль.
Даны функция спроса на продукцию монополиста
Q = 26 – 0,5 × P
и функция общих затрат
ТС = 120 – 8 × Q + Q2.
Найти максимальную прибыль и соответствующую цену.
Решение:
Запишем обратную функцию спроса:
P = 52 – 2 × Q.
Общий доход найдём по формуле:
TR = Р × Q = (52 – 2 × Q) × Q = 52 × Q – 2 × Q2.
Найдём предельный доход как производную от функции общего дохода:
MR = TR’ = (52 × Q – 2 × Q2)’ = 52 – 4 × Q.
Определим функцию предельных затрат, взяв производную от функции общих затрат:
MC = TC’ = (120 – 8 × Q + Q2)’ = – 8 + 2 × Q.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
– 8 + 2 × Q = 52 – 4 × Q
Q = 10 – оптимальный объём производства, при котором прибыль максимальна.
Цена на продукцию монополии будет соответственно равна
P = 52 – 2 × 10 = 32.
Прибыль вычислим по формуле:
П = TR – TC = P × Q – 120 + 8 × Q – Q2 = 32 × 10 – 120 + 8 × 10 – 102 = 180.