можно ли в Яндекс-картах измерить расстояние ПО КРИВОЙ? провести по дорогам линию и измерить её
Екатерина Скворцова
Мастер
(1230),
закрыт
11 лет назад
Лучший ответ
Дмитрий Сабаш
Мастер
(1063)
11 лет назад
да вкладка маршрут
Остальные ответы
Mkolhoz.mobi new game
Мастер
(1332)
11 лет назад
Да там даже можно расчитать маршруты! так как яндекс карты для навигаторов делают!
Техноторг Техноторг
Профи
(676)
11 лет назад
прокладываешь маршрут (там есть такой раздел) от точки А до точки Б. и потом с лева ты увидишь полную информацию об этом маршруте (и расстояние и время в пути и т. д.)
Похожие вопросы
| Ссылка на этот фрагмент: |
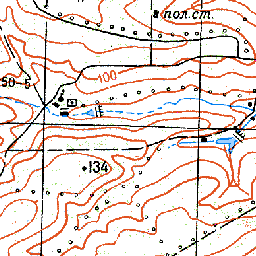
Кривой
Посмотрите, где находится Кривой на онлайн картах: топографических, старых, тематических и исторических. Это урочище расположено в Российской Федерации на территории Ростовской области на широте: 47.783 и долготе: 40.700. Данная область относится к Южному Федеральному Округу.
Кривой располагается на расстоянии 97 км. по прямой от центра региона и в 910 км. от центра Москвы. Высота местоположения над уровнем моря в центральной населённой части около: 78 м. В номенклатуре Советских карт эта местность относится к квадрату: L-37-10. Автомобильные коды в регионе: 61 и 161.
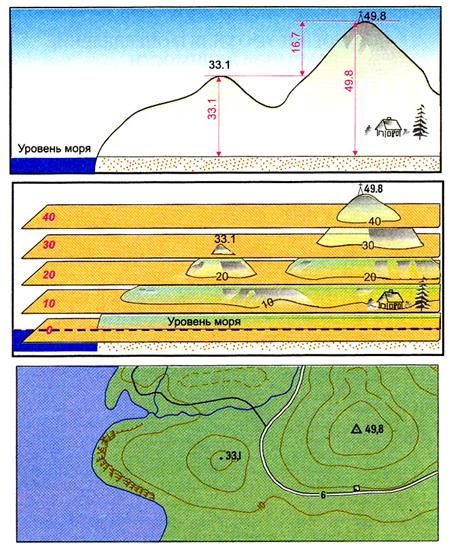
Отображение рельефа играет важную роль, так как он в значительной мере определяет характер всех остальных элементов содержания карт и планов. Кроме того, рельеф влияет на водный режим, на распределение растительности и на пространственное размещение большинства объектов местности. Без достаточно точного отображения рельефа и его детального изучения на карте или плане невозможно установить взаимосвязи между отдельными элементами ландшафта и, следовательно, рационально использовать природные ресурсы.
Традиционным представлением о рельефе местности на топографических картах и планах является его изображение горизонталями. Этот способ нагляден и дает однозначное представление о рельефе местности, позволяет быстро получать количественные характеристики рельефа и решать различные прикладные задачи.
Типы и формы рельефа местности
Рельеф — совокупность неровностей суши, дна океанов и морей, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития. Слагается из положительных (выпуклых) и отрицательных (вогнутых) форм. Основными формамирельефа являются: гора, котловина, хребет, лощина и седловина.
Кроме перечисленных форм рельеф имеет детали. К деталям рельефа относятся: овраги, промоины, курганы, насыпи, выемки, уступы, каменоломни и т. д. Все разновидности форм и деталей рельефа состоят из элементов. Основными элементами рельефа являются: основание (подошва), склон (скат), вершина (дно), высота (глубина), крутизна и направление ската, линии водораздела и водосбора (тальвег).
В военном деле под местностью понимают участок земной поверхности, на котором предстоит вести боевые действия. Неровности земной поверхности называются рельефом местности, а все расположенные на ней объекты, созданные природой или трудом человека (реки, населенные пункты, дороги и т. п.) — местными предметами.
Рельеф и местные предметы являются основными топографическими элементами местности, влияющими на организацию и ведение боя, применение боевой техники в бою, условия наблюдения, ведения огня, ориентирования, маскировки и проходимость, т. е. определяющими ее тактические свойства.
Топографическая карта является точным отображением всех наиболее важных в тактическом отношении элементов местности, нанесенных во взаимно точном расположении относительно друг друга. Она дает возможность изучить любую территорию в относительно короткий срок. Предварительное изучение местности и принятие решения для выполнения подразделением (частью, соединением) той или иной боевой задачи обычно производят по карте, а затем уже уточняют на местности.
Местность, оказывая влияние на боевые действия, в одном случае может способствовать успеху войск, а в другом оказывать отрицательное воздействие. Боевая практика убедительно показывает, что одна и та же местность может больше преимуществ дать тому, кто лучше ее изучит и более умело использует.
По характеру рельефа местность делится на равнинную, холмистую и горную.
Равнинная местность характеризуется небольшими (до 25 м) относительными превышениями и сравнительно малой (до 2°) крутизной скатов. Абсолютные высоты обычно небольшие (до 300 м).
Тактические свойства равнинной местности зависят главным образом от почвенно-растительного покрова и от степени пересеченности. Глинистые, суглинистые, супесчаные, торфяные грунты ее допускают беспрепятственное движение боевой техники в сухую погоду и значительно затрудняют движение в период дождей, весенней и осенней распутицы. Она может быть изрезана руслами рек, оврагами и балками, иметь много озер и болот, значительно ограничивающих возможности маневра войск и снижающих темпы наступления.
Холмистая местность характеризуется волнистым характером земной поверхности, образующей неровности (холмы) с абсолютными высотами до 500 м, относительными превышениями 25 — 200 м и преобладающей крутизной 2-3° (рис. 3, 4). Холмы обычно сложены твердыми породами, вершины и склоны их покрыты толстым слоем рыхлых пород. Понижения между холмами представляют собой широкие, ровные или замкнутые котловины.
Холмистая местность обеспечивает скрытое от наземного наблюдения противника передвижение и развертывание войск, облегчает выбор мест для огневых позиций ракетных войск и артиллерии, обеспечивает хорошие условия для сосредоточения войск и боевой техники. В целом она благоприятна как для наступления, так и для обороны.
Горная местность представляет собой участки земной поверхности, значительно приподнятые над окружающей местностью (имеющей абсолютные высоты 500 м и более). Она отличатся сложным и разнообразным рельефом, специфическими природными условиями. Основные формы рельефа — горы и горные хребты с крутыми скатами, часто переходящими в скалы и скалистые обрывы, а также лощины и ущелья, расположенные между горными хребтами. Горная местность характеризуется резкой пересеченностью рельефа, наличием труднодоступных участков, редкой сетью дорог, ограниченным количеством населенных пунктов, бурным течением рек с резкими колебаниями уровня воды, разнообразием климатических условий, преобладанием каменистых грунтов.
Боевые действия в горной местности рассматриваются, как действия в особых условиях. Войскам часто приходится использовать горные проходы, затрудняется наблюдение и ведение огня, ориентирование и целеуказание, в то же время она способствует скрытности расположения и передвижения войск, облегчает устройство засад и инженерных заграждений, организацию маскировки.
Сущность изображения рельефа на картах горизонталями
Рельеф является важнейшим элементом местности, определяющим ее тактические свойства.
Изображение рельефа на топографических картах дает полное и достаточно подробное представление о неровностях земной поверхности, форме и взаимном расположении, превышениях и абсолютных высотах точек местности, преобладающей крутизне и протяженности скатов.
Рельеф на топографических картах изображается горизонталями в сочетании с условными знаками обрывов, скал, оврагов, промоин, каменных рек и т. п. Изображение рельефа дополняется отметками высот характерных точек местности, подписями горизонталей, относительных высот (глубин) и указателями направления скатов (бергштрихами). На всех топографических картах рельеф изображается в Балтийской системе высот, то есть в системе исчисления абсолютных высот от среднего уровня Балтийского моря.
Виды горизонталей
Горизонталь — замкнутая кривая линия на карте, которой соответствует на местности контур, все точки которого расположены на одной и той же высоте над уровнем моря.
Различают следующие горизонтали:
- основные (сплошные) — соответствующие высоте сечение рельефа;
- утолщенные — каждая пятая основная горизонталь; выделяется для удобства чтения рельефа;
- дополнительные горизонтали (полугоризонтали) — проводятся прерывистой линией при высоте сечения рельефа, равной половине основной;
- вспомогательные — изображаются короткими прерывистыми тонкими линиями, на произвольной высоте.
Расстояние между двумя смежными основными горизонталями по высоте называют высотой сечения рельефа. Высоту сечения рельефа подписывают на каждом листе карты под ее масштабом. Например: «Сплошные горизонтали проведены через 10 метров».
Для облегчения счета горизонталей при определении высот точек по карте все сплошные горизонтали, соответствующие пятой кратной высоте сечения, вычерчиваются утолщенно и на ней ставится цифра, указывающая высоту над уровнем моря.
Для того чтобы при чтении карты можно было быстро определить характер неровностей поверхности на картах, применяются специальные указатели направления скатов — бергштрихи — в виде коротких черточек, расставленных на горизонталях (перпендикулярно им) по направлению покатостей. Они помещаются на изгибах горизонталей в наиболее характерных местах, преимущественно у вершин седловин или на дне котловин.
Дополнительные горизонтали (полугоризонтали) применяются для отображения характерных форм и деталей рельефа (перегибов склонов, вершин, седловин и т. п.), если они не выражаются основными горизонталями. Кроме того, применяют для изображения равнинных участков, когда заложения между основными горизонталями очень велики (более 3 — 4 см на карте).
Вспомогательные горизонтали применяют для изображения отдельных деталей рельефа (блюдец в степных районах, западин, отдельных бугров на плоскоравнинной местности), которые не передаются основными или дополнительными горизонталями.
Изображение горизонталями типовых форм рельефа
Рельеф на топографических картах изображается кривыми замкнутыми линиями, соединяющими точки местности, имеющие одинаковую высоту над уровенной поверхностью, принятой за начало отсчета высот. Такие линии называются горизонталями. Изображение рельефа горизонталями дополняется подписями абсолютных высот, характерных точек местности, некоторых горизонталей, а также числовых характеристик деталей рельефа — высоты, глубины или ширины.
Определение на карте абсолютных высот и относительных превышений точек местности
Профиль — чертеж, изображающий разрез местности вертикальной плоскостью.
Для большей выразительности рельефа местности вертикальный масштаб профиля принимается в 10 или более раз крупнее горизонтального.
В связи с этим профиль, передавая взаимное превышение точек, искажает (увеличивает) крутизну скатов.
Для построения профиля нужно:
- прочертить на карте профильную линию (маршрут движения), приложить к ней лист разграфленной (миллиметровой) бумаги, перенести на ее край короткими черточками места горизонталей, точки перегиба скатов и местные предметы, которые сечет профильная линия, и подписать их высоты;
- подписать на листе разграфленной бумаги у горизонтальных линий высоты, соответствующие высотам горизонталей на карте, приняв условно промежутки между этими линиями за высоту сечения (установить вертикальный масштаб);
- от всех черточек, обозначающих места пересечения профильной линии с отметками высот горизонталей, точек перегиба скатов и местных предметов, опустить перпендикуляры до пересечения их с соответствующими по отметкам параллельными линиями и отметить полученные точки пересечения;
- соединить точки пересечения плавной кривой, которая и изобразит профиль местности (подъемы и спуски на маршруте движения).
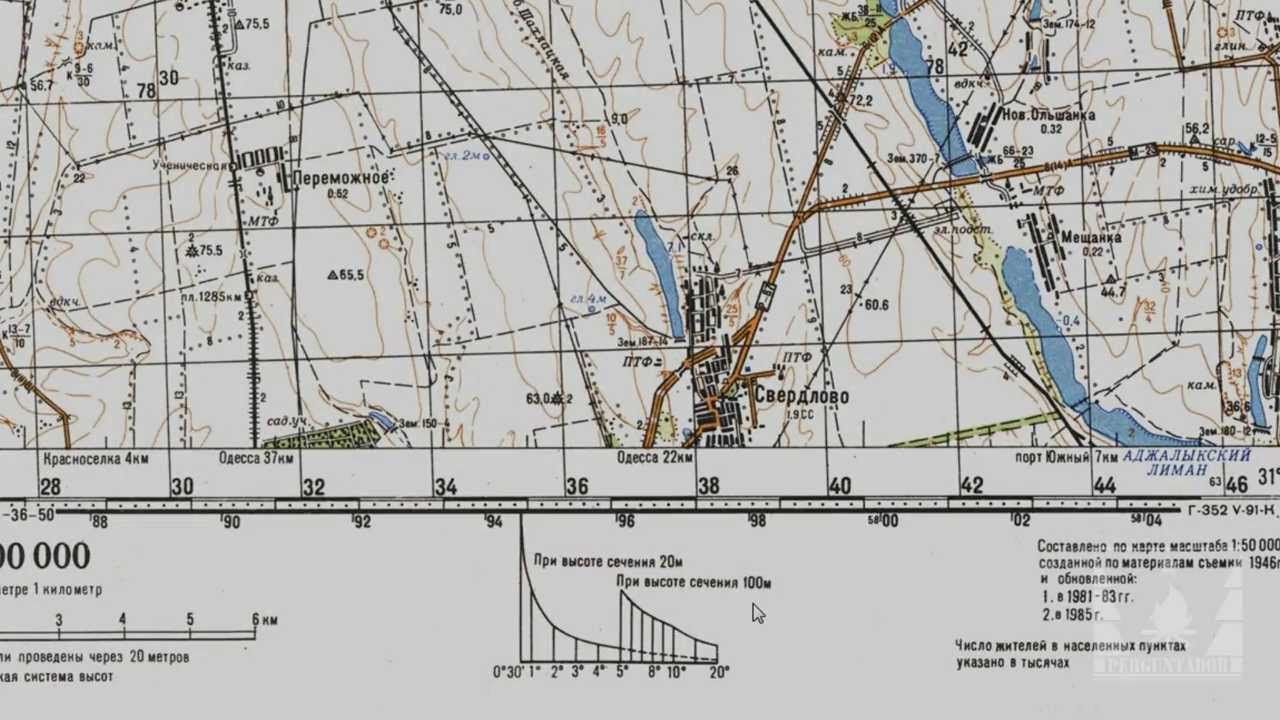
Определение на карте крутизны скатов
Крутизна ската на карте определяется по заложению — расстоянию между двумя смежными основными или утолщенными горизонталями; чем меньше заложение, тем круче скат.
Для определения крутизны ската надо измерить расстояние между горизонталями циркулем, найти соответствующий отрезок на графике заложений и прочитать число градусов.
На крутых скатах это расстояние измеряется между утолщенными горизонталями, и крутизна ската определяется по графику, расположенному справа.
-
-
May 17 2014, 17:46
- Россия
- Cancel
КАРТПРОСВЕТ | Выпуск первый. Кривая линейка Яндекс.Карт
Встречайте новую познавательную рубрику о картографии от моего сокурсника (картографический факультет МИИГАиК) 
Оригинал взят у 
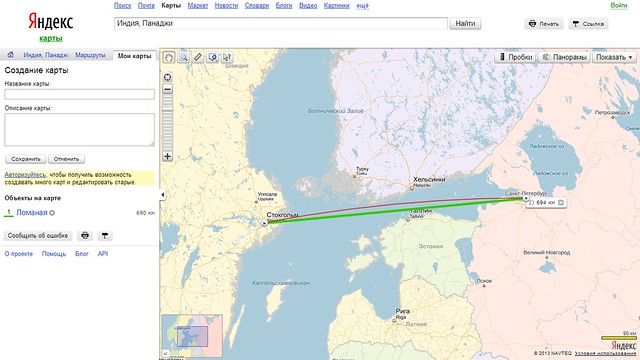
Вчера, находясь на работе в режиме ожидания, я полубессознательно тыкал линейкой в разные точки на Яндекс.Карте. Ткнул в Санкт-Петербург, ткнул в Стокгольм и…
(1)
…И сам на пару секунд оторопел. А потом обрадовался: вот, есть тема для первого выпуска обещанного Картпросвета.
***
Казалось бы, расстояние между двумя точками измеряется по отрезку прямой линии, проходящей через них. Чтобы измерить это расстояние, мы берём прямую линейку, а не кривое лекало.
А тут — нате вам. Сравните красную линию, по которой Яндекс измерил расстояние, и зелёный отрезок прямой, который я сам нарисовал.
Хотите более острых ощущений? Измерьте расстояние от Москвы до Владивостока. Той же линейкой.
Почему так происходит? Постараюсь объяснить под катом.
Прежде всего, небольшая вводная. Земля, как мы знаем, — шар1, а не плоская пратчеттовская фигура. И кратчайшим расстоянием между двумя точками на её поверхности будет не отрезок прямой линии, а ортодромия.
(2)
Посмотрите на схему. Точка O — центр Земли. Точки A и B находятся на поверхности Земли.
Круг, полученный при пересечении шара плоскостью, проходящей через его центр, называется больши́м. На схеме голубым цветом показан большой круг, проходящий также через наши точки A и B.
Эти наши точки делят окружность, ограничивающую большой круг, на две дуги — бо́льшую и меньшую.
Так вот, меньшая дуга большого круга, проходящего через точки A и B, и будет ОРТОДРОМИЕЙ, кратчайшим расстоянием между двумя этими точками. На схеме ортодромия показана тёмно-зелёной линией
Теперь посмотрите вот на эту картинку. Та же предыдущая схема, только с нанесёнными меридианами.
(3)
Посмотрите: наша ортодромия пересекает меридианы (тонкие тёмно-синие линии) под разными углами. Запомним этот факт и пойдём дальше.
Если же у вас под рукой есть глобус, можете сами построить произвольный большой круг с помощью ниточки и воочию убедиться, что он будет пересекать меридианы под разными углами.
А дальше мы приходим уже к Яндекс.Картам.
Яндекс.Карта составлена в равноугольной цилиндрической проекции Меркатора. То есть, и меридианы, и параллели на этой карте являются отрезками прямых, пересекающихся под прямым углом:
(4)
Теперь давайте рассуждать таким образом. Меридианы на этой проекции являются параллельными отрезками прямых. Следовательно, любая прямая линия, начерченная на этой карте, пересекала бы меридианы под одним и тем же углом (см. зелёную линию на самой первой картинке). Но ортодромия пересекает меридианы под разными углами. А линия, пересекающая параллельные прямые под разными углами, прямой быть ну никак не может. Она будет как раз-таки кривой.
Кстати, линия, пересекающая меридианы под одним и тем же углом, называется локсодромией. На цилиндрических проекциях локсодромии как раз-таки прямые.
А бывают ли, всё-таки, ортодромии, которые отобразятся на Яндекс.Карте отрезками прямых? Бывают-бывают.
Например, есть одна-единственная параллель, ограничивающая большой круг. Это экватор.
Судите сами: во-первых, это линия, ограничивающая большой круг. Во-вторых, это параллель. А параллели в цилиндрической проекции являются параллельными прямыми линиями, пересекающими меридианы под одним и тем же (прямым, ага) углом. Следовательно, дуги большого круга (в том числе и ортодромии) на экваторе будут прямыми.
(5)
И ещё один частный случай ортодромии, которая на Яндекс.Карте отобразится отрезком прямой линии. Это ортодромии, лежащие на меридианах. Ведь меридианы тоже являются дугами большого круга, это очевидно из рисунка (3). Эксперимент с меридианами, если хотите, проведите сами.
***
Ещё раз, кратко:
- Кратчайшим расстоянием между двумя точками на поверхности Земли будет ОРТОДРОМИЯ, то есть меньшая из дуг соответствующего большого круга — круга, проходящего через центр Земли и две этих точки.
- Ортодромия пересекает меридианы под разными углами.
- Яндекс.Карта составлена в цилиндрической проекции, где меридианы являются отрезками параллельных прямых.
- Ортодромия пересекает меридианы под разными углами. Следовательно, она не может быть прямой.
- Исключения — ортодромии, лежащие на меридианах или экваторе, то есть, линиях, ограничивающих большие круги. Они на Яндекс.Карте будут прямыми.
Вот и всё. Интересно? Если хотите, в следующем выпуске я расскажу, как самим построить ортодромию на Яндекс.Карте между любыми двумя городами. Главное, чтобы они были как можно дальше друг от друга. Для наглядности — не менее тысячи километров.
Также ближайшие выпуски Картпросвета будут посвящены более подробному рассмотрению фигуры Земли. И про картографические проекции расскажу.
______________________________________________
1 Ну, на самом деле, не шар. Всё намного сложнее и интереснее. Я про фигуру Земли потом расскажу, а пока пусть Земля будет шаром.
Расчет кривой одного радиуса приведен в табл. 10.
В графу 1 этой таблицы даются номера делений (точек). Отрицательные деления в этой графе получились потому, что деления 0, 10, 20 и т.д. было целесообразно совместить с пикетами.
В графу 2 выписываются данные пикетажа. В нее же при расчете выписываются значения СК (середины кривой) НПК, КПК и др.
В графу 3 выписываются из журнала съемки кривой величины измеренных стрел в миллиметрах. Если выписать сюда удвоенную величину измеренных стрел, освобождаясь тем самым от половинок миллиметров, то величины в графах 4, 5 и последующих будут также удвоены и, следовательно, в графе 9 будут получены величины сдвижек и тогда надобность в графе 10 отпадет.
В графе 4 подсчитывается последовательно сумма стрел. Сумма стрел для последнего деления должна равняться итогу графы 3.
В графе 5 подсчитывается момент стрел (сумма сумм стрел). Для этого нулевое значение из графы 4 (против деления — 3) выписывают в графу 5 на одну строку ниже (против деления — 2).
Затем величины граф 4 и 5 этой строки (против деления — 2) суммируют — 2 + 0 = —2 и записывают в графу 5 на одну строку ниже (против деления — 1); то же делают для следующей строки +8 — 2 = 6 и так до конца.
При суммировании нужно учитывать знак у отрицательных стрел.
Величина момента стрел относительно последней точки М52 (которая не выписывается) должна быть равна итогу графы 4. Подсчитывают также итог графы 5 (1 446 401).
В графах с 6 по 10 выписываются расчетные данные.
Прежде чем определять расчетную величину стрелы круговой кривой в графе 6, необходимо выяснить, с какой кривой мы имеем дело: одного ли она радиуса или составная, есть ли переходные кривые и одинаковая ли их длина.
Представление о кривой может сложиться из рассмотрения данных графы 3 и более наглядно — по графику стрел.
Наколку графика стрел на миллиметровке достаточно делать частично, на участках, где происходит резкое изменение величин стрел: на участках переходных кривых и в местах изменения радиуса составных кривых.
В нашем примере можно считать, что кривая описана одним радиусом с переходными кривыми длиной около 5 делений в начале и около 4 делений в конце (рис. 51):
Поэтому определяем общий угол поворота кривой и ее середину по формулам (III. 24) и (III. 34):

Предварительно расчетную величину стрелы изгиба можно определить как
среднее значение на участке круговой кривой между делениями 5 и 45, а именно:
С большим приближением при натурных переходных кривых расчетную стрелу изгиба можно определить по формуле:

гдеМа
— момент стрел относительно точки
а на участке круговой кривой;
Мб
— то же, относительно точки б;
Мср—то же, относительно средней точки между а
и б;
n
— число делений между точками а
и б
(аналогично рис. 42).
Выбирая участок, например, между точками
5 и
45, будем иметь:
Определенная по формуле (III. 38) величина стрелы несколько отличается от среднего значения.
Необходимо заметить, что формула (III. 38) не учитывает влияния переходной кривой на длину круговой кривой: уменьшения ее длины за счет сдвижки или соответственно увеличения расчетной стрелы изгиба.
Для достижения минимальных рихтовок
следует назначать такую расчетную длину переходных кривых, чтобы она была близка натурной их длине.
Полагая, что по условиям движения длину переходной кривой в нашем случае можно принять не менее 80 м, т.е. l = 8 делений, что больше натурной длины переходных кривых, находим сдвижку круговой кривой по формуле (III. 37):
Теперь имеются все данные для того, чтобы определить окончательно длину круговой кривой (в пределах НК — КК; рис. 51) и по ней величины стрел в каждом делении.
Эта длина, в которой уже учитываются проектные переходные кривые, определяется по формулам:
Подставляя величины в формулу, найдем:
Расчетная стрела изгиба для такой длины круговой кривой согласно формуле (III.30) будет равна:
Радиус круговой кривой определится по формуле (III.28):
Находим положение начала переходной кривой:
Положение НПК отмечаем в графе 2.
Определяем положение конца (начала) второй переходной кривой:

Зная положение переходных кривых, легко находим величины стрел изгиба в их пределах. Так как величина стрелы в пределах переходной кривой изменяется по закону прямой, то расчетные стрелы, очевидно, будут равны:

Концевая переходная кривая
Аналогично для концевой переходной кривой:

Такой подсчет целесообразно делать на логарифмической линейке.
Читайте продолжение в следующей статье.
§