Математика
5 класс
Урок №80
Представление дробей на координатном луче
Перечень рассматриваемых вопросов
– изображение дробей на координатном луче;
– запись координаты дроби;
– решение текстовых задач с опорой на смысл понятия координаты числа;
– применение дроби для выражения единиц измерения длины, массы, времени в более крупных единицах.
Тезаурус
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Координатная ось – это прямая, с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта.
Координата данной точки – это число, которое соответствует данной точке на координатной оси.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямую с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта называют координатным лучом.
Начало отсчёта – точка 0.
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Координатный луч обычно располагают горизонтально и направляют вправо.
На координатном луче можно изобразить дробь.
Изобразим дробь
Для этого единичный отрезок разделим на q частей.
Возьмём 
Точку, изображающую на координатном луче дробь p/q, называют точкой с координатой p/q или короче – точкой p/q
Например, точка А имеет координату три пятых. Пишем A (3/5).
Точка В имеет координату семь пятых, выраженную неправильной дробью или одна целая две пятых, выраженную смешанным числом. Пишем В (7/8) или В(1 2/5)
Положительные дроби называют ещё положительными рациональными числами, а точки, изображающие их на луче, называют положительными рациональными точками.
3/5, 7/5,1 2/5 – положительные дроби, или положительные рациональные числа.
Если а и с – два положительных рациональных числа и с > a, то:
- точка c на координатном луче находится правее точки а;
- расстояние между точками а и c равно c – а;
- точка (a + c) : 2 является серединой отрезка, соединяющего точки а и с.
Докажем, что точка (a + c) : 2 является серединой отрезка, соединяющего точки а и с:
Рассмотрим задачу.
Найдём длину отрезка, соединяющего точки:
и с = 1, и координату середины этого отрезка.
Решение
3/7 < 1, поэтому точка 1 находится правее 3/7.
Значит, длина отрезка, соединяющего точки а и с, равна:
Середина этого отрезка будет иметь координату:
Таким способом можно вычислить координату середины отрезка, соединяющего любые две рациональные точки.
Т. е. между любыми двумя рациональными точками находится ещё хотя бы одна рациональная точка.
Число (a + c) : 2 называется средним арифметическим чисел а и с.
Например:
Если необходимо вычислить среднее арифметическое нескольких чисел, нужно найти частное от деления суммы этих чисел на число слагаемых.
Например:
Рассмотрим, как применять дроби для выражения единиц измерения длины, массы и времени в более крупных единицах.
Известно, что для измерения массы используют единицы измерения: граммы, килограммы, центнеры, тонны. Если масса тела небольшая, используют г или кг. Если тело более крупное, то массу измеряют в тоннах.
Мы знаем, что 1 кг = 1000 г. А как узнать, сколько килограмм в грамме? Для этого нужно один разделить на тысячу, получим одну тысячную, т. е. в одном грамме содержится одна тысячная килограмма.
Рассмотрим единицы измерения времени. Время измеряют в секундах, минутах, часах. Вы знаете, что в одном часе шестьдесят минут, следовательно, минута будет равна одной шестидесятой часа.
Рассмотрим единицы измерения длины.
Длину измеряют в метрах, километрах, сантиметрах.
Тренировочные задания
№ 1. Подставьте к изображению координаты середин отрезков АВ, ВС и СК.
Варианты ответов:
Координаты середины отрезка определяются по формуле (a + c) : 2, где а и с – координаты концов отрезка.
Найдём середину отрезка АВ. Для этого сложим координаты точки А и В, поделим на два и получим:
Значит, 1 – это середина отрезка АВ.
Найдём середину ВС. Для этого сложим координаты точки В и С, поделим на два и получим:
Значит, 2 – это середина отрезка ВС.
Найдём середину СК. Для этого сложим координаты точки С и К, поделим на два и получим:
Значит, 3 – это середина отрезка СК.
№ 2. Найдите среднее арифметическое чисел 11, 14 и 17. В ответе напишите только число: __
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
У нас три слагаемых, значит, сложим числа 11, 14 и 17 и полученную сумму разделим на 3.
(11 + 14 + 17) : 3 = 42 : 3 = 14
Правильный ответ:14.
Найди верный ответ на вопрос ✅ «Найдите на отрезке длиной 6 клеток (3 см) дроби 7 6 (ых) и 5 3 (ых). Это неправильные дроби, как найти их на отрезке? …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Математика » Найдите на отрезке длиной 6 клеток (3 см) дроби 7 6 (ых) и 5 3 (ых). Это неправильные дроби, как найти их на отрезке?
Что такое неправильные дроби? Чем они отличаются от правильных обыкновенных дробей, каковы их особенности? Давайте узнаем.
Знакомство с неправильными дробями
Две подруги, Лена и Марина, ели бутерброды, и тут к ним подошла бездомная и голодная собака Шарик. Девочки разломили свои бутерброды на две половинки (рисунок 1, а) и дали Шарику по половинке (рисунок 1, б).
В итоге у Шарика получается целый бутерброд!
$$frac{1}{2} + frac{1}{2} = frac{2}{2}$$
$$frac{2}{2}=1$$
Потом к девочкам подошёл их одноклассник Андрей, у которого тоже был с собой бутерброд, увидел Шарика и тоже захотел его угостить. Он также отломил от своего бутерброда половину и отдал собаке.
Итого у Шарика стало три половинки бутерброда (рисунок 2)
$$frac{1}{2} + frac{1}{2}+ frac{1}{2}=frac{3}{2}$$
Количество бутерброда превысит единицу. Числитель дроби станет больше знаменателя.
Но возможно ли это? Да, конечно. Такая дробь будет называться неправильной. Но это совсем не значит, что она ошибочна, и так писать нельзя. Просто эта дробь не такая, как правильная.
Сравнение правильных и неправильных дробей
Дробь, в которой числитель меньше знаменателя, называют правильной дробью.
Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
Также легко узнать, какая у нас дробь, если сравнить её с единицей. Помните, что знаменатель показывает, на сколько частей поделили целое, а числитель — какое количество частей взяли. Если числитель равен знаменателю, то у нас получается целое, как если бы его и не делили. А если числитель больше знаменателя, то получившаяся дробь больше, чем целое (как в примере с тремя половинками бутерброда).
Правильная дробь меньше единицы, а неправильная дробь больше или равна единице.
Предлагаем вам следующее упражнение для тренировки.
В этом упражнении все числа заменены условными обозначениями. За ними могут скрываться любые цифры.
Число «кружок» меньше, чем число «капля», а «капля» меньше, чем число «звезда».
Правильные и неправильные дроби на координатном луче
Если мы расположим на координатном луче неправильные дроби, то все они будут располагаться на отрезке между началом координатного луча и единицей, так как все они будут меньше одного. Начиная с отметки «1» будут идти неправильные дроби.
На рисунке 6 зелёными точками отмечены правильные дроби, красными — неправильные.
Содержание:
- § 1 Определение правильной и неправильной дроби
- § 2 Дроби на координатном луче
§ 1 Определение правильной и неправильной дроби
В этом уроке Вы познакомитесь с определением правильных и неправильных дробей, а также расположением их на координатном луче.
Рассмотрим следующую задачу:
На ужин купили две пиццы. Разделили каждую на 8 частей-долей.
Такие дроби называют правильными.
Такие дроби называют неправильными.
Получили определение правильных и неправильных дробей:
Дробь, в которой числитель меньше знаменателя, называют правильной дробью. Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
Давайте выполним следующее задание:
Решение:
Кстати, если числитель и знаменатель дроби равны, то такая дробь равна 1.
В самом деле, вспомним задачу про пиццу.
Таким образом, можно сделать вывод, что любая правильная дробь меньше единицы, а неправильные дроби больше или равны единице.
§ 2 Дроби на координатном луче
Как же отметить дробь на координатном луче?
А как Вы думаете, где расположены точки, отмеченные правильными и неправильными дробями на координатном луче относительно единицы?
Начертим координатный луч с единичным отрезком 8 клеток.
Значит:
Правильные дроби, которые меньше единицы, лежат левее 1 на координатном луче, а неправильные дроби, которые больше единицы, лежат правее 1.
Те дроби, у которых числитель и знаменатель равны, совпадают с единицей.
Таким образом, на этом уроке Вы узнали, что правильной дробью является дробь, у которой числитель меньше знаменателя, и на координатном луче она располагается левее 1, а неправильной дробью называется дробь, у которой числитель больше или равен единице, и на координатном луче она лежит правее 1 или совпадает с ней.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009
Смешанные числа. Изображение обыкновенных дробей на координатном луче
Число, состоящее из целой части и дробной части, называется смешанным числом.
Чтобы неправильную дробь представить в виде смешанного числа, надо разделить числитель дроби на знаменатель, тогда неполное частное будет целой частью смешанного числа, остаток – числителем дробной части, а знаменатель останется тот же.
Чтобы представить смешанное число в виде неправильной дроби, нужно умножить целую часть смешанного числа на знаменатель, к полученному результату прибавить числитель дробной части и записать в числителе неправильной дроби, а знаменатель оставить тот же.
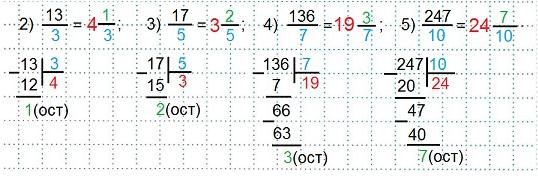
Примеры.
Дробная часть означает знак деления. В столбик разделим числитель13 на знаменатель 3. Частное 4 будет целой частью смешанного числа, остаток 1 станет числителем дробной части, а знаменатель 3 останется тот же.
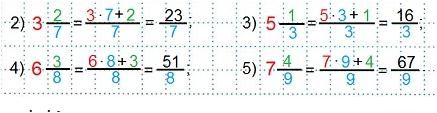
Записать смешанное число в виде неправильной дроби:
Число 3 — целую часть смешанного числа умножают на знаменатель 7 дробной части, к полученному произведению прибавляют число 2— числитель дробной части смешанного числа; результат 23 станет числителем неправильной дроби, а знаменатель 7 останется тот же.
Изображение обыкновенных дробей на координатном луче
Для удобного изображения дроби на координатном луче важно правильно выбрать длину единичного отрезка.
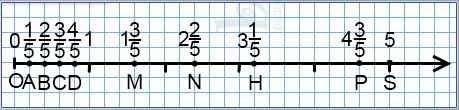
Самый удобный вариант отметить на координатном луче дроби — взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Например, если требуется изобразить на координатном луче дроби со знаменателем 5, единичный отрезок лучше взять длиной в 5 клеточек:
В этом случае изображение дробей на координатном луче не вызовет затруднений: 1/5 — одна клеточка, 2/5 — две, 3/5 — три, 4/5 — четыре.
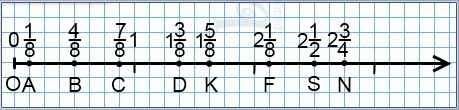
Если требуется отметить на координатном луче дроби с разными знаменателями, желательно, чтобы число клеточек в единичном отрезке делилось на все знаменатели. Например, для изображения на координатном луче дробей со знаменателями 8, 4 и 2 удобно взять единичный отрезок длиной в восемь клеточек. Чтобы отметить на координатном луче нужную дробь, единичный отрезок разбиваем на столько частей, каков знаменатель, и берем таких частей столько, каков числитель. Чтобы изобразить дробь 1/8, единичный отрезок разбиваем на 8 частей и берем 7 из них. Чтобы изобразить смешанное число 2 3/4, отсчитываем от начала отсчета два целых единичных отрезка, а третий разбиваем на 4 части и берем три из них:
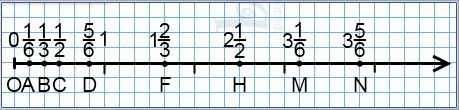
Еще один пример: координатный луч с дробями, знаменатели которых равны 6, 2 и 3. В этом случае в качестве единичного удобно взять отрезок длиной шесть клеточек:
Вопросы к конспектам
Даны точки и
. Найдите длину отрезка АВ.
На координатном луче даны точки В(а-3) и А(а+5) 7. Найдите длину отрезка АВ.
Запишите неправильную дробь в виде смешанного числа:
Запишите смешанное число в виде неправильной дроби: