Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.
Как найти гипотенузу?
Как найти гипотенузу, зная катеты?
Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.
Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).
Например:
Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:
c² = 3² + 4² <=> c² = 9 + 16 <=> c² = 25 <=> c = √25 <=> c = 5.
Ответ: длина гипотенузы 5 см (или x = 5).
Как найти катет в прямоугольном треугольнике
По той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:
Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:

Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.
Применяем формулу b = √c² — a² ⇔
b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.
Как найти гипотенузу, зная катет и угол?
Если есть противолежащий катет — теорема синусов
Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).
Формула:
Например:
Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.
∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).
Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.
Значит: ∠c = 180º — (90º + 45º) = 45º.
Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:
BC/sin90º = AC/sin45º = AB/sin45º
В таблице вы найдёте значения для синуса:
| sin 45º | √2/2 |
| sin 60º | √3/2 |
| sin 90º | 1 |
В условии задачи нам дано: 𝐴𝐶 = √2, значит:
BC/sin90º = √2/sin45º = AB/sin45º
Подставляем значения синуса из таблицы:
BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔
BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)
Если хотите вычислить катет, уже зная другой катет и гипотенузу:
AB/(√2/2) = 2 ⇔ AB = √2
Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.
Если есть прилежащий катет — по косинусу
Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).
Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.
Например:
Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).
Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.
Смотрим в таблице, чему равен cos 45º.
BC = 1/ (√2/2) = √2
Ответ: гипотенуза BC равна √2 см.
Как найти гипотенузу равнобедренного треугольника
В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).
Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.
Например:
Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.
Формула b = √2a². Подставляем:
b = √2*7² = √2*49 ≈ √98 ≈ 9.899
Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):
c² = a² + b²
c² = 7² + 7²
c² = 49 + 49
c² = 98
c = √98
c ≈ 9.899
Ответ: гипотенуза равна 9.899.
Узнайте больше про Теорему Пифагора, Теорему косинусов, а также, что такое Тангенс и Аксиома.
Расчет гипотенузы треугольника
Гипотенуза треугольника – это самая длинная сторона прямоугольного треугольника, лежащая против его прямого угла.
Формула расчета гипотенузы:
c = √(a 2 + b 2 ), где
a – катет;
b – катет;
c – гипотенуза.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета гипотенузы прямоугольного треугольника, если известны его катеты. С помощью этой программы вы в один клик сможете рассчитать гипотенузу треугольника.
Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² – 4² = √ 25 – 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
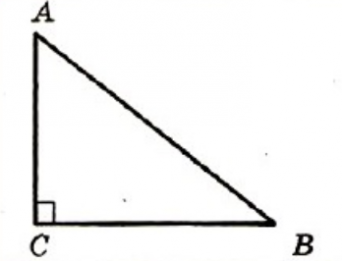
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
- В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .
Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
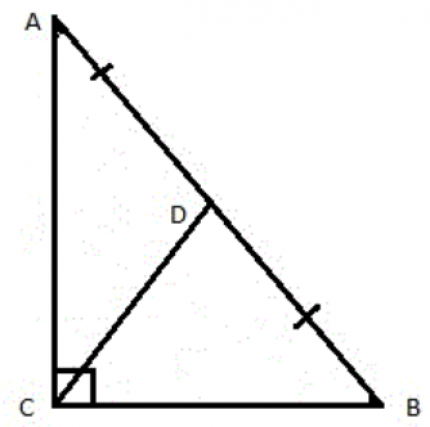
- Медиана, проведенная к гипотенузе, равна её половине.
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
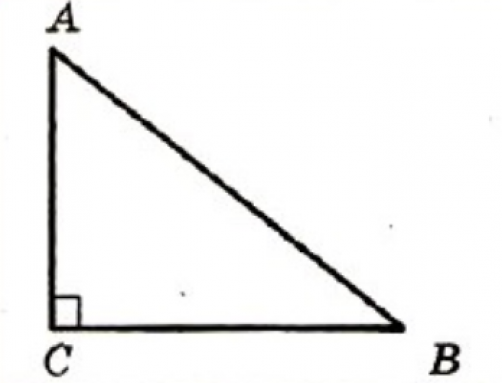
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.
Египетский треугольник
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.
[spoiler title=”источники:”]
http://poschitat.online/storony-pryamougolnogo-treugolnika
[/spoiler]
Гипотенуза — это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Поскольку в треугольнике напротив бОльшей стороны лежит и бОльший угол, а прямой угол в прямоугольном треугольнике является наибольшим, то гипотенуза является самой длинной стороной.
Традиционно гипотенузу обозначают строчной латинской буквой c.
автор вопроса выбрал этот ответ лучшим
88SkyWalker88
[428K]
5 лет назад
Гипотенузу можно обнаружить в прямоугольном треугольнике.
Представим прямоугольный треугольник:
две стороны (на рисунке это а и b), которые образуют прямой угол будут называться катетами.
Третья сторона (на рисунке это с) – будет гипотенузой.
Вили Борисович
[26.5K]
5 лет назад
Гипотенуза в переводе с греческого языка означает, как “натянутая”. Гипотенуза это геометрический термин. Гипотенузой называют длиннейшую сторону в прямоугольном треугольнике. Один из углов этого треугольника должен быть равен 90 градусов. Другие две стороны, называют катетами.
terli4eno4ka
[75.3K]
5 лет назад
Гипотенуза – это сторона прямоугольного треугольника, расположенная напротив прямого угла или угла, равного 90 градусов. Гипотенуза является самой длинной стороной треугольника. Как правило, она обозначается латинской буквой “с”.
Ксарфакс
[156K]
5 лет назад
Гипотенуза – это геометрический термин, который пришёл к нам из греческого языка.
В геометрии под гипотенузой понимается одна из сторон прямоугольного треугольника – она находится (лежит) напротив угла в 90 градусов.
Стоит отметить, что длина гипотенузы всегда больше длины катетов.
Как найти гипотенузу?
Чтобы определить, чему равна гипотенуза в прямоугольном треугольнике, можно воспользоваться теоремой Пифагора.
Пусть катеты равны a и b, гипотенуза равна c.
a² + b² = c².
Соответственно, гипотенуза будет равна квадратному корню от суммы катетов.
c = √(a² + b²).
Например, катеты равны 5 и 7 см. Длина гипотенузы в этом случае составляет: √(5² + 7²) = √74.
moreljuba
[62.5K]
5 лет назад
Сразу стоит отметить тот факт, что такое понятие как “гипотенуза” имеет место быть только в прямоугольных треугольниках. Так вот под гипотенузой подразумевается самая длинная сторона прямоугольного треугольника, располагающаяся против прямого угла.
Skiyers
[121K]
8 лет назад
Гипотенуза бывает только в прямоугольных треугольниках, то есть тех, один угол которых равен 90 градусам. Сторона, которая лежит напротив прямого угла, “косая” и самая длинная сторона такого треугольника является его гипотенузой.
Wertep75
[1.5K]
5 лет назад
В прямоугольном треугольнике есть, как и в обычном треугольнике, три стороны: две из них называются катетами, третья сторона – это и есть та самая гипотенуза.
Найти ее просто, ведь она расположена прямо напротив угла в 90 градусов. А ещё она самая длинная.
При этом помните, что сумма двух катетов обязательно будет больше гипотенузы.
И ещё одна любопытная деталь: катеты в квадрате равны гипотенузе, тоже в квадрате.
Бархатные лапки
[382K]
5 лет назад
Гипотенуза – это понятие из такой науки, как геометрия, изучать начинают примерно в 7 классе.
Гипотенуза бывает только в прямоугольном треугольнике, это сторона треугольника, которая находиться напротив угла равного 90 градусов.
Гипотенуза это большая сторона треугольника, две другие стороны носят название – катеты, так вот они меньше, нежели гипотенуза.
mychange
[73.1K]
5 лет назад
Термин “гипотенуза” относится к основам геометрии, первоначальные элементарные понятия – стороны прямоугольного треугольника называются катетами и гипотенузой. Катеты непосредственно граничат с прямым углом такого треугольника, гипотенуза с ним не граничит, она находится напротив прямого угла, гипотенуза длиннее катетов.
Елена Никитюк
[1.4K]
6 лет назад
Любой человек, который проходил школьную программу, учил термин “гипотенуза”. Гепотенузой в геометрии называют длинейшую сторону треугольника, которая находится напротив прямого угла. А стороны которые исходят из этого прямого угла называют катетами.
Знаете ответ?
Как найти гипотенузу прямоугольного треугольника
Геометрия – наука не простая. Она может пригодиться как для школьной программы, так и в реальной жизни. Знание многих формул и теорем упростит геометрические вычисления. Одна из наиболее простых фигур в геометрии – это треугольник. Один из разновидностей треугольников, равносторонний, имеет свои особенности.
1
Особенности равностороннего треугольника
Согласно определению, треугольник – это многогранник, который имеет три угла и три стороны. Это плоская двумерная фигура, ее свойства изучаются в средней школе. По типу угла различают остроугольные, тупоугольные и прямоугольные треугольники. Прямоугольный треугольник – такая геометрическая фигура, где один из углов равен 90º. Такой треугольник имеет два катета (они создают прямой угол), и одну гипотенузу (она находится напротив прямого угла). В зависимости от того, какие величины известны, существует три простых способа вычислить гипотенузу прямоугольного треугольника.
2
Первый способ найти гипотенузу прямоугольного треугольника. Теорема Пифагора
Теорема Пифагора – древнейший способ вычислить любую из сторон прямоугольного треугольника. Звучит она так: “В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”. Таким образом, чтобы вычислить гипотенузу, следует вывести квадратный корень из сумы двух катетов в квадрате. Для наглядности приведены формулы и схема.
3
Второй способ. Вычисление гипотенузы с помощью 2-х известных величин: катета и прилегающего угла
Одно из свойств прямоугольного треугольника гласит, что отношение длины катета к длине гипотенузы, равносильно косинусу угла между этиv катетом и гипотенузой. Назовем известный нам угол α. Теперь, благодаря известному определению, можно легко сформулировать формулу для вычисления гипотенузы: Гипотенуза = катет/cos(α)
4
Третий способ. Вычисление гипотенузы с помощью 2х известных величин: катета и противолежащего угла
Если известен противолежащий угол, возможно снова воспользоваться свойствами прямоугольного треугольника. Отношение длины катета и гипотенузы равносильно синусу противолежащего угла. Снова назовем известный угол α. Теперь для вычислений применим немного другую формулу:
Гипотенуза = катет/sin (α)
5
Примеры, которые помогут разобраться с формулами
Для более глубокого понимания каждой из формул, следует рассмотреть наглядные примеры. Итак, предположим, дан прямоугольный треугольник, где есть такие данные:
- Катет – 8 см.
- Прилегающий угол cosα1 – 0.8.
- Противолежащий угол sinα2 – 0.8.
По теореме Пифагора: Гипотенуза = корень квадратный из (36+64) = 10 см.
По величине катета и прилежащего угла: 8/0.8 = 10 см.
По величине катета и противолежащего угла: 8/0.8 = 10 см.
Разобравшись в формуле, можно с легкостью вычислить гипотенузу с любыми данными.
Видео: Теорема Пифагора
| О нас |
| Демоверсии |
| Учебные пособия |
| Справочник по математике |
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Фигура | Рисунок | Формулировка |
| Прямоугольный треугольник |  |
Треугольник, у которого один из углов равен 90°, называют прямоугольным треугольником. Сторону, лежащую против угла в 90°, называют гипотенузой, две другие стороны называют катетами. |
| Катеты прямоугольного треугольника | Длины катетов прямоугольного треугольника меньше длины гипотенузы. | |
| Равнобедренный прямоугольный треугольник |  |
Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.Острые углы равнобедренного прямоугольного треугольника равны 45°. |
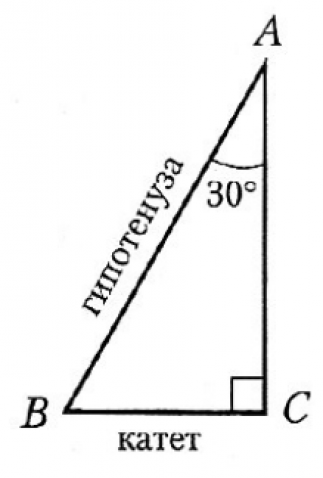
| Прямоугольный треугольник с углом в 30° |  |
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. |
| Катет, равный половине гипотенузы | Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°. | |
| Медиана, проведённая к гипотенузе прямоугольного треугольника |  |
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.Посмотреть доказательство |
| Медиана треугольника, равная половине стороны, к которой она проведена | Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. | |
| Центр описанной окружности |  |
Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.Посмотреть доказательство |
| Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. | ||
| Теорема Пифагора |  |
|
| Обратная теорема Пифагора | Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным |
| Прямоугольный треугольник |

|
| Равнобедренный прямоугольный треугольник |

|
| Прямоугольный треугольник с углом в 30° |
|
| Медиана, проведённая к гипотенузе прямоугольного треугольника |
|
| Центр описанной окружности |
|
| Теорема Пифагора |
|
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник: https://www.resolventa.ru/demo/traininggia.htm
Как найти гипотенузу в прямоугольном треугольнике: самые простые и запоминающиеся формулы для учеников

Как найти гипотенузу по катетам?
Вспомним немного теории: прямоугольным треугольником называют плоскую фигуру, у которой есть три угла. Один из них имеет величину 90º, а стороны называют катетами и гипотенузой.
Та сторона, которая противолежит прямому углу, и есть гипотенуза, а остальные две – это прилежащие катеты. Главная игра сторон проявляется в теореме Пифагора, согласно которой гипотенуза равняется сумме квадратов катетов.
Однако это лишь кажется запутанным, ведь на самом деле все гораздо проще.
Свойства геометрической фигуры
Перед тем, как найти гипотенузу треугольника, необходимо разобраться, какие особенности имеет данная фигура. Рассмотрим главные из них:
- В прямоугольном треугольнике оба острых угла в сумме будут равны 90º.
- Катет, лежащий против угла в 30º, будет равен ½ от величины гипотенузы.
- Если катет равен ½ от значения гипотенузы, тогда второй угол будет иметь такую же величину – 30º.
Найти гипотенузу в прямоугольном треугольнике можно несколькими способами. Самым простым решением является вычисление через катеты. Допустим, вам известны значения катетов сторон А и В.
Тогда на выручку приходит теорема Пифагора, повествующая нам, что если поставить каждую величину катета в квадрат и просуммировать полученные данные, мы узнаем чему равна гипотенуза.
Таким образом, нам необходимо просто извлечь значение квадратного корня:
Как найти гипотенузу через угол?
Еще одним способом, который поможет узнать, чему равна гипотенуза в прямоугольном треугольнике, является вычисление через заданный угол. Для этого нам потребуется вывести величину через формулу синуса. Допустим, нам известна величина катета (А) и значение противолежащего угла (α). Тогда все решение заключается в одной формуле: С=А/sin(α).
- Например, если длина катета 40 см, а угол составляет 45°, тогда длину гипотенузы можно вывести следующим образом:
- 40/sin(45°) = 40/0,71 = 56,33.
Определить искомую величину можно также через косинус заданного угла. Допустим, нам известно значение одного катета (В) и острого прилежащего угла (α). Тогда для решения задачи понадобится одна формула: С=В/ cos(α).
- К примеру, если длина катета имеет значение 50 см, а угол составляет 45°, тогда гипотенузу можно вычислить следующим образом:
- 50/cos(45°) = 50/0,71 = 80,42.
Таким образом, мы рассмотрели основные способы как узнать гипотенузу в треугольнике. В ходе решения задания важно сконцентрировать внимание на имеющихся данных, тогда найти неизвестную величину будет достаточно просто. Необходимо знать всего пару формул и процесс решения задач станет простым и приятным.
Источник: https://otvetkak.ru/other/kak-najti-gipotenuzu-v-pryamougolnom-treugolnike.html
Гипотенуза в прямоугольном треугольнике
Гипотенуза – это самая длинная сторона прямоугольного треугольника. Она лежит напротив прямого угла. Длина гипотенузы может быть найдена различными способами.
Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы.
Соответственно длина гипотенузы в прямоугольном треугольнике вычисляется по формуле:
К примеру: катет a = 3 см, катет b = 4 см.
Чтобы найти длину гипотенузы в прямоугольном треугольнике, подставим числа в формулу. =5 см
Преобразовав эту формулу можно найти и длину одного неизвестного катета.
,
В случае если известна длина катета A и гипотенузы C, угол α можно определить по формуле:
Второй угол будет вычисляться так: β = 180°-90°-α. Зная, что сумма всех углов составляет 180°, вычитаем прямой угол и уже известный.
К примеру: A = 3 см, C=5 см, подставляем значения в формулу: =0,6
По таблицу синусов угол α будет приблизительно равен 36°, соответственно угол β = 54°.
Если по условиям даны параметры двух катетов, то можно найти острый угол по следующей формуле:
К примеру: A = 3 см, B = 4 см
Подставляем значения в формулу =0,75
По таблице тангенсов угол α будет равняться 36°, соответственно угол β = 54°.
Также стороны прямоугольного треугольника можно найти по различным формулам в зависимости от количества известных переменных.
A
B
C
При расчете параметров прямоугольного треугольника важно обращать внимание на известные значения и решать задачу по самой простой формуле.
Источник: https://2mb.ru/matematika/geometriya/gipotenuza-v-pryamougolnom-treugolnike/
Формула гипотенузы равнобедренного прямоугольного треугольника
1001student.ru > Геометрия > Формула гипотенузы равнобедренного прямоугольного треугольника
В повседневной жизни каждому человеку время от времени приходится решать задачи из школьной программы.
Несмотря на то что многие в детстве считали эти знания ненужными, сейчас все понимают, что были неправы.
Например, в любой момент может понадобиться найти длину гипотенузы равнобедренного треугольника, формулу расчета которой несложно вывести самостоятельно. Для этого следует вспомнить законы геометрии.
Законы геометрии
В первую очередь надо определиться с терминами. Чтобы в дальнейшем было понятно, что означают те или иные геометрические понятия, необходимо вспомнить следующие определения:
- треугольник;
- сторона;
- угол;
- бедро;
- равнобедренный;
- равносторонний;
- прямоугольный;
- гипотенуза;
- катет;
- теорема.
Треугольник – это замкнутая геометрическая фигура, состоящая из трех точек, соединенных последовательно тремя отрезками, которые являются сторонами этой фигуры. Прямые, исходящие из одной точки, образуют угол.
Каждый треугольник состоит из трех сторон. Исходящие из одной вершины стороны называются бедрами, поэтому фигура, у которой минимум две стороны имеют равную длину, называется равнобедренной. В случае когда все стороны фигуры равны, она называется равносторонним треугольником.
Треугольник, в котором есть прямой угол, называется прямоугольным. Прямым в геометрии называется угол в 90 градусов. Поскольку в каждой треугольной фигуре сумма всех углов равна 180 градусов, то в ней может быть только один прямой угол. Гипотенуза в переводе с греческого языка означает «натянутая» – это сторона треугольника, которая лежит напротив прямого угла.
Катет – это одна из двух других сторон прямоугольного треугольника, тоже греческое слово, которое в переводе означает опущенный, отвесный или перпендикуляр. Катеты одновременно являются бедрами, а в равнобедренном прямоугольном треугольнике гипотенуза служит еще и основанием.
Теорема – это истина, которую надо доказать. Одно из самых известных и значимых правил геометрии – это теорема Пифагора.
Теорема Пифагора
Древнегреческий математик и философ Пифагор, если верить историкам, первым нашел правильный расчет соотношения размеров длин катетов и гипотенузы. Согласно теореме Пифагора, длина гипотенузы в квадрате равна сумме длин катетов, возведенных в квадрат. Можно кратко описать теорему, обозначив гипотенузу буквой Г, а катеты — К1 и К2:
Г2 =К12 + К22
Как вычислить формулу
Если довериться логике и Пифагору, то легко высчитать, что размер самой длинной стороны треугольника будет равен квадратному корню из суммы квадратов двух меньших сторон. Если учесть, что в равнобедренном треугольнике катеты равны, то формулу можно усовершенствовать.
Гипотенузу равнобедренного треугольника можно рассчитать путем вычисления квадратного корня из квадрата длины катета, умноженного на два.
Вопрос на засыпку
Чтобы ответить на вопрос, как найти гипотенузу равностороннего треугольника, надо вспомнить, чему равен каждый его угол.
При любой длине сторон в этой фигуре, сумма всех углов неизменна и равна 180 градусов, соответственно каждый из них в этой фигуре равен 60 градусов.
Прямого угла в такой фигуре не может быть по определению, поэтому нет и гипотенузы. Значит, поставленный вопрос некорректен и не имеет ответа.
Практическое применение
В каких сферах повседневной жизни может понадобиться знание формулы? Эта тема находит практическое применение в архитектуре, строительстве, физике, математике, астрономии и других областях народного хозяйства, например:
- Для дизайнера, работающего над планировкой дома или квартиры, важно знать, является ли конкретный угол прямым. Высчитав длину всех сторон, можно сделать вывод о размере угла.
- В организациях, занимающихся оптовой торговлей или транспортными услугами, для правильного построения логистической схемы распределения товара между розничными точками порой необходимо рассчитывать самые краткие и оптимальные пути передвижения между различными объектами.
- На даче или огороде можно правильно рассчитать длину лестницы, необходимой для установки на определенную высоту под определенным углом, чтобы легко взбираться на мансарду или чердак.
Если внимательно оглядеться вокруг, можно различить большое количество разнообразных геометрических фигур.
Где геометрия, там и возможности использовать ее правила и формулы расчетов, в том числе и формулу длины гипотенузы.
Источник: https://1001student.ru/geometriya-2/formula-gipotenuzy-ravnobedrennogo-pryamougolnogo-treugolnika.html
Свойство медианы прямоугольного треугольника
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Пусть СМ — медиана прямоугольного треугольника АВС с прямым углом С.
Проведем через вершину В прямую m, параллельную катету АС.
Через вершину А проведем прямую n, параллельную катету ВС.
Прямые m и n пересекаются в точке К.
Мы получили прямоугольник АКВС (параллелограмм, в котором угол С – прямой).
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
Задача ЕГЭ по теме «Медиана прямоугольного треугольника»
В треугольнике ABC угол ACB равен , угол B равен , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD – равнобедренный, CD = BD. Тогда
Источник: https://ege-study.ru/mediana-pryamougolnogo-treugolnika
Гипотенуза и угол “α” прямоугольного треугольника
Если в прямоугольном треугольнике известна гипотенуза и угол α, то можно сразу вычислить катеты и угол β из свойства суммы углов треугольника и отношений синуса и косинуса. (рис. 79.1)
β=90°-α
a=c sinα
b=c cosα
Периметр, заданный суммой катетов и гипотенузы, можно представить в виде суммы известной гипотенузы и выраженных через нее катетов.
P=a+b+c=c sinα+c cosα+c=c(sinα+cosα+1)
Площадь любого прямоугольного треугольника равна половине произведения катетов, следовательно, чтобы рассчитать площадь через гипотенузу и угол α, необходимо также заменить неизвестные на соответствующие выражения.
S=ab/2=(sinα cosα)/2
Треугольник, в котором один угол прямой, будет иметь всего одну высоту, опущенную на гипотенузу. Из любого внутреннего прямоугольного треугольника, полученного с помощью дополнительного построения высоты, можно выразить ее, как произведение катета и синуса угла. (рис. 79.2)
h=b sinα=c cosα sinα
Найти медиану прямоугольного треугольника проще всего, если она опущена на гипотенузу, в таком случае она будет равна ее половине. Медианы катетов вычисляются по стандартным формулам с заменой переменных через гипотенузу. (рис.79.
3)
m_с=c/2
m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4 〖c^2 sin^2〗α+〖c^2 cos^2〗α )/2=(с√(3 sin^2α+1))/2
m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4 〖c^2 cos〗^2α+sin^2α )/2=(с√(3 cos^2α+1))/2
Рассчитать биссектрисы прямоугольного треугольника тоже достаточно просто, если использовать специальные формулы, зная гипотенузу и угол α. Преобразуя выражения, можно упростить их до следующих тождеств. (рис. 79.
4)
l_с=(ab√2)/(a+b)=(c sinα cosα √2)/(sinα+cosα )
l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(c cosα √(2c(c cosα+c) ))/(c cosα+c)=(c cosα √(2(cosα+1) ))/(cosα+1)
l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(c sinα √(2c(c sinα+c) ))/(c sinα+c)=(c sinα √(2(sinα+1) ))/(sinα+1)
Проведенная средняя линия прямоугольного треугольника создает внутри него еще один подобный треугольник в два раза меньше первоначального, поэтому сама она равна половине параллельной ей стороны. (рис. 79.7)
M_a=a/2=(c sinα)/2
M_b=b/2=(c cosα)/2
M_c=c/2
Прямоугольный треугольник может быть вписан в окружность и описан вокруг нее.
Радиус вписанной окружности внутри треугольника можно вычислить, сложив катеты за вычетом гипотенузы, и разделив полученное число на два.
Рассчитать радиус описанной окружности для прямоугольного треугольника через гипотенузу еще проще, так как он равен ее половине. (рис. 79.5, 79.6)
r=(a+b-c)/2=(c sinα+c cosα-c)/2=c/2 (sinα+cosα-1)
R=c/2
Источник: https://geleot.ru/education/math/geometry/calc/triangle/hypotenuse_and_angle_a