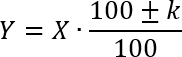|
Найти начальное число |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Формула простого процента: как найти исходное значение
13 ноября 2013
В этом коротком видеоуроке мы научимся решать задачи на проценты с помощью специальной формулы, которая так и называется: формула простого процента. Давайте оформим эту формулу в виде теоремы.
Теорема о простом проценте. Предположим, что есть некая исходная величина x, которая затем меняется на k%, и получается новая величина y. Тогда все три числа связаны формулой:
Плюс или минус перед коэффициентом k ставится в зависимости от условия задачи. Если по условию величина x возрастает, то перед k стоит плюс. Если же величина уменьшается, то перед коэффициентом k стоит минус.
Несмотря на кажущуюся мудреность этой формулы, многие задачи с ее помощью решаются очень быстро и красиво. Давайте попробуем.
Задача. Цена на товар была повышена на 10% и составила 2970 рублей. Сколько рублей стоил товар до повышения цены?
Чтобы решить эту задачу с помощью формулы простых процентов, нам необходимы три числа: исходное значение x, проценты k и итоговое значение y. Из всех трех чисел нам известны проценты k = 10 и итоговое значение y = 2970. Обратите внимание: 2970 — это именно итоговая цена, т.е. y. Потому что по условию задачи исходная цена на товар неизвестна (ее как раз требуется найти). Но затем она была повышена, и только тогда составила 2970 рублей.
Итак, нам нужно найти x, т.е. исходное значение. Что ж, подставляем наши числа в формулу и получаем:
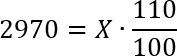
Складываем числа в числителе и получаем:
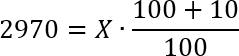
Сокращаем по одному нулю в числителе и знаменателе, а затем умножаем обе части уравнения на 10. Получим:
11x = 29 700
Чтобы найти x из этого простейшего линейного уравнения, нужно разделить обе стороны на 11:
x = 29 700 : 11 = 2700
Как видите, это довольно большие числа, поэтому в уме такие вычисления не провести. В случае, если такая задача встретится вам на ЕГЭ, придется делить уголком. При этом все разделилось без остатка, и мы получили значение x:
x = 2700
Именно столько стоил товар до повышения цены. И именно это число нам требовалось найти по условию задачи. Поэтому все: задача решена. Причем решена не «напролом», а с помощью формулы простого процента — быстро, красиво и наглядно.
Разумеется, эту задачу можно было решать по-другому. Например, через пропорции. Или экзотическим методом коэффициентов. Но будет гораздо лучше и надежнее, если у вас на вооружении будет несколько приемов для решения любой задачи на проценты. Так что обязательно попрактикуйтесь в использовании данной формулы.
А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: неизвестно начальное значение (метод пропорции)

- Формула простого процента: неизвестно конечное значение

- Решение ЕГЭ-2011: вариант 1, часть B

- Метод коэффициентов, часть 1

- Деление многочленов уголком

- Сфера, вписанная в куб

Последовательность, почти всегда возвращающая простые числа
Возможно, самым интересным в теории чисел является раздел, посвященный простым числам. При этом он один из самых малоизученных. Из простейшего определения понятия простого числа — это число, которое делится на себя и единицу, — вытекает множество загадок, многие из которых удалось разгадать сравнительно недавно, а некоторые еще ждут своего разрешения. Разгадав некоторые из них, человечество продвинется далеко вперед, а возможно, спровоцирует мировой кризис.
О важности простых чисел в математике говорит основная теорема арифметики: любое число можно представить в виде произведения простых множителей. Вся математика опирается на простые числа, но закономерности появления их в натуральном ряду так никто еще и не объяснил.
Математики всего мира не раз пытались найти ту формулу, при вычислениях по которой всегда получались бы простые числа. Если в этой фразе отбросить слово «всегда», то таких формул удастся привести довольно много, например: f(n)=n2 + n + 17; f(n) = n2 – n + 41; f(n) = 2n2 + 29.
Последовательно подставляя, например, в первую формулу вместо n натуральные числа, получим числа 19, 23, 29, 37. Все они являются простыми, но торжествовать рано — уже f(16) = 289 = 172, то есть получилось составное число.
Эти формулы порождают много простых чисел, но это «много» еще не означает «всегда»! Более того, можно доказать, что никакой многочлен с целыми коэффициентами не может для всякого натурального значения n равняться простому числу.
На самом деле для простых чисел не существует никакой формулы, никакой комбинации алгебраических операций над n, выполняя которые можно было бы получить очередное nное простое число. Многие люди впадали в заблуждение на этот счет, достигнув некоторых первоначальных успехов.
Полотно Улама
Так чем же объясняются закономерности в распределении простых чисел? Пока ответа на этот вопрос нет, но все же есть множество визуальных наблюдений. Одну из таких закономерностей случайно открыл Станислав Улам, американский математик, поляк по происхождению. Сидя както на скучной лекции, он, ни о чем не думая, начал рисовать решетку из горизонтальных и вертикальных линий. В одной из полученных таким образом клеток он поставил 1 и стал нумеровать остальные клетки по спирали, расходящейся от первой клетки:
5 4 3
6 1 2
7 8 9
Когда спираль совершила несколько оборотов, Улам начал обводить кружками простые числа, не преследуя никакой определенной цели. Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел.
Составление формулы простого числа
Чтобы увидеть всё своими глазами, а не полагаться только на слова, составим простую компьютерную программу, которая бы рисовала точку в центре, а вокруг нее по спирали располагала бы все числа натурального ряда. Программа будет отмечать черным цветом точки, соответствующие простым числам, а серыми — составные. Вот что мы получим:
У самого центра диаграммы одна такая закономерность пролегает сверху вниз и слева направо. Она состоит из последовательности чисел: 7, 23, 47, 79… Оказывается, эту последовательность можно описать квадратичной функцией р = 4х2 + 4х – 1.

С помощью этого графика можно задать формулой любую последовательность простых чисел. Рассмотрим, например, последовательность, берущую свое начало из точки 5 и идущую справа налево сверху вниз. Следующее число в этой последовательности 19, затем идут 41, 71… Попробуем описать ее рекуррентной формулой. Для этого сначала рассмотрим каждый квадрат, состоящий из точек. У любого такого квадрата на восемь точек больше, чем у вложенного в него, — это очень легко доказать. Значит, разность между любыми двумя точками, лежащими в соседних квадратах по одному правилу, будет увеличиваться на восемь по сравнению с предыдущими. Для определенности за отношение «лежать по одному правилу» примем точки, лежащие в соседних квадратах, причем из точки, лежащей в меньшем квадрате, можно перейти к точке из большего квадрата, если перейти в другой квадрат по кратчайшему расстоянию и затем сместиться на число t, где t целое, причем t — постоянное число для данного правила. В нашем случае t = 1.
Если разность между точками, лежащими в 1м и 2м квадратах от центра, равна 14, то разность между точками 2го и 3го квадратов возрастет на 8 и будет равна 22. Теперь можно составить формулу: следующий член последовательности будет отличаться от предыдущего на 14 + 8·n, где n — номер члена последовательности, то есть номер квадрата от центра. Если считать 5 нулевым членом и каждый член больше предыдущего на 8·(n – 1), где n — номер квадрата, то получим:
xn = xn – 1 + 14 + 8(n – 1)
xn = xn – 1 + 8n + 6
Это и есть формула данной последовательности.
И таким образом можно составить сколько угодно формул последовательностей простых чисел, но всегда на какомто номере окажется, что число вовсе не простое. Примечательно, что если в качестве начальной точки взять число не 1, а 41, то мы увидим последовательность, состоящую из 41 простого числа!
Никакая целая рациональная функция от х с целыми коэффициентами не может для любого натурального значения х равняться простому числу (теорема Гольбаха).
САПР и графика 1`2010
Ольга Зайцева
Гуру
(2967)
5 лет назад
Два решения будут, если b>-1/4:
a=(1+sqrt(1+4b))/2
a=(1-sqrt(1+4b))/2
Одно решение будет, если b=-1/4:
a=1/2
При b<-1/4 вещественных решений нет, только два комплексно сопряженных решения:
a=(1+i*sqrt(|1+4b|))/2
a=(1-i*sqrt(|1+4b|))/2
Александр Титов
Гений
(50766)
5 лет назад
Просто решить уравнение относительно a с параметром b.
Это квадратное уравнение a^2 – a – b = 0, где первый и второй коэффициенты равны 1 и -1 соответственно, а свободный член равен -b.
Корней (или “начальных чисел”) может быть два, один или ни одного.
Краеугольный камень псевдослучайности: с чего начинается поиск чисел
Время на прочтение
7 мин
Количество просмотров 8.4K

(с)
Случайные числа постоянно генерируются каждой машиной, которая может обмениваться данными. И даже если она не обменивается данными, каждый компьютер нуждается в случайности для распределения программ в памяти. При этом, конечно, компьютер, как детерминированная система, не может создавать истинные случайные числа.
Когда речь заходит о генераторах случайных (или псевдослучайных) чисел, рассказ всегда строится вокруг поиска истинной случайности. Пока серьезные математики десятилетиями ведут дискуссии о том, что считать случайностью, в практическом отношении мы давно научились использовать «правильную» энтропию. Впрочем, «шум» — это лишь вершина айсберга.
С чего начать, если мы хотим распутать клубок самых сильных алгоритмов PRNG и TRNG? На самом деле, с какими бы алгоритмами вы не имели дело, все сводится к трем китам: seed, таблица предопределенных констант и математические формулы.
Каким бы ни был seed, еще есть алгоритмы, участвующие в генераторах истинных случайных чисел, и такие алгоритмы никогда не бывают случайными.
Что такое случайность
Первое подходящее определение случайной последовательности дал в 1966 году шведский статистик Пер Мартин-Лёф, ученик одного из крупнейших математиков XX века Андрея Колмогорова. Ранее исследователи пытались определить случайную последовательность как последовательность, которая проходила все тесты на случайность.
Основная идея Мартина-Лёфа заключалась в том, чтобы использовать теорию вычислимости для формального определения понятия теста случайности. Это контрастирует с идеей случайности в вероятности; в этой теории ни один конкретный элемент пространства выборки не может быть назван случайным.
«Случайная последовательность» в представлениях Мартина-Лёфа должна быть типичной, т.е. не должна обладать индивидуальными отличительными особенностями.
Было показано, что случайность Мартина-Лёфа допускает много эквивалентных характеристик, каждая из которых удовлетворяет нашему интуитивному представлению о свойствах, которые должны иметь случайные последовательности:
- несжимаемость;
- прохождение статистических тестов для случайности;
- сложность создания прогнозов.
Существование множественных определений рандомизации Мартина-Лёфа и устойчивость этих определений при разных моделях вычислений свидетельствуют о том, что случайность Мартина-Лёфа является фундаментальным свойством математики.
Seed: основа псевдослучайных алгоритмов
Первые алгоритмы формирования случайных чисел выполняли ряд основных арифметических действий: умножить, разделить, добавить, вычесть, взять средние числа и т.д. Сегодня такие мощные алгоритмы, как Fortuna и Yarrow (используется в FreeBSD, AIX, Mac OS X, NetBSD) выглядят как генераторы случайных чисел для параноиков. Fortuna, например, это криптографический генератор, в котором для защиты от дискредитации после выполнения каждого запроса на случайные данные в размере 220 байт генерируются еще 256 бит псевдослучайных данных и используются в качестве нового ключа шифрования — старый ключ при этом каждый раз уничтожается.
Прошли годы, прежде чем простейшие алгоритмы эволюционировали до криптографически стойких генераторов псевдослучайных чисел. Частично этот процесс можно проследить на примере работы одной математической функции в языке С.
Функция rand () является простейшей из функций генерации случайных чисел в C.
#include <stdio.h>
#include <stdlib.h>
int main()
{
int r,a,b;
puts("100 Random Numbers");
for(a=0;a<20;a++)
{
for(b=0;b<5;b++)
{
r=rand();
printf("%dt",r);
}
putchar('n');
}
return(0);
}В этом примере рандома используется вложенный цикл для отображения 100 случайных значений. Функция rand () хороша при создании множества случайных значений, но они являются предсказуемыми. Чтобы сделать вывод менее предсказуемым, вам нужно добавить seed в генератор случайных чисел — это делается с помощью функции srand ().
Seed — это стартовое число, точка, с которой начинается последовательность псевдослучайных чисел. Генератор псевдослучайных чисел использует единственное начальное значение, откуда и следует его псевдослучайность. Генератор истинных случайных чисел всегда имеет в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
#include <stdio.h>
#include <stdlib.h>
int main()
{
unsigned seed;
int r,a,b;
printf("Input a random number seed: ");
scanf("%u",&seed);
srand(seed);
for(a=0;a<20;a++)
{
for(b=0;b<5;b++)
{
r=rand();
printf("%dt",r);
}
putchar('n');
}
return(0);
}srand() принимает число и ставит его в качестве отправной точки. Если seed не выставить, то при каждом запуске программы мы будем получать одинаковые случайные числа.
Вот пример простой формулы случайного числа из «классики» — книги «Язык программирования C» Кернигана и Ричи, первое издание которой вышло аж в 1978 году:
int rand() { random_seed = random_seed * 1103515245 +12345;
return (unsigned int)(random_seed / 65536) % 32768; }Эта формула предполагает существование переменной, называемой random_seed, изначально заданной некоторым числом. Переменная random_seed умножается на 1 103 535 245, а затем 12 345 добавляется к результату; random_seed затем заменяется этим новым значением. Это на самом деле довольно хороший генератор псевдослучайных чисел. Если вы используете его для создания случайных чисел от 0 до 9, то первые 20 значений, которые он вернет при seed = 10, будут такими:
44607423505664567674Если у вас есть 10 000 значений от 0 до 9, то распределение будет следующим:
0 — 10151 — 10242 — 10483 — 9964 — 9885 — 10016 — 9967 — 10068 — 9659 — 961
Любая формула псевдослучайных чисел зависит от начального значения. Если вы предоставите функции rand() seed 10 на одном компьютере, и посмотрите на поток чисел, которые она производит, то результат будет идентичен «случайной последовательности», созданной на любом другом компьютере с seed 10.
К сожалению, у генератора случайных чисел есть и другая слабость: вы всегда можете предсказать, что будет дальше, основываясь на том, что было раньше. Чтобы получить следующее число в последовательности, мы должны всегда помнить последнее внутреннее состояние генератора — так называемый state. Без state мы будем снова делать одну и ту же математическую операцию с одинаковыми числами, чтобы получить тот же ответ.
Как сделать seed уникальным для каждого случая? Самое очевидное решение — добавить в вычисления текущее системное время. Сделать это можно с помощью функции time().
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int r,a,b;
srand((unsigned)time(NULL));
for(a=0;a<20;a++)
{
for(b=0;b<5;b++)
{
r=rand();
printf("%dt",r);
}
putchar('n');
}
return(0);
}Функция time() возвращает информацию о текущем времени суток, значение, которое постоянно изменяется. При этом метод typecasting гарантирует, что значение, возвращаемое функцией time(), является целым числом.
Итак, в результате добавления «случайного» системного времени функция rand() генерирует значения, которые являются более случайными, чем мы получили в первом примере.
Однако в этом случае seed можно угадать, зная системное время или время запуска приложения. Как правило, для приложений, где случайные числа являются абсолютно критичными, лучше всего найти альтернативное решение.
В .net framework есть функция System.Security.Cryptography.RandomNumberGenerator, где в расчетах учитываются следующие факторы:
- ID текущего процесса;
- текущий ID потока;
- количество отсчетов с момента загрузки;
- текущее время;
- различные высокоточные счетчики производительности процессора;
- MD4-хэш среды пользователя (имя пользователя, имя компьютера и т.д.).
Но опять же, все эти числа не случайны.
Лучшее, что вы можете сделать с детерминированными генераторами псевдослучайных чисел — добавить энтропию физических явлений.
Период (цикл) генератора
Одними из наиболее часто используемых методов генерации псевдослучайных чисел являются различные модификации линейного конгруэнтного метода, схема которого была предложена Дерриком Лемером еще в 1949 году:
Xn+1 = (aXn + c) mod m, где m — модуль, a — множитель, c — приращение, mod — операция взятия остатка от деления. Причем m > 0, 0 < a ≤ m, 0 < c ≤ m, также задается начальное значение X0: 0 < X0 ≤ m.
Линейный конгруэнтный метод дает нам повторяющиеся последовательности — конгруэнтная последовательность всегда образует «петли». Этот цикл (период), повторяющийся бесконечное число раз — свойство всех последовательностей вида Xn+1 = f(n).
В языке С линейно-конгруэнтный метод реализован в уже знакомой вам функции rand():
#define RAND_MAX 32767
unsigned long next=1;
int rand(void)
{ next=next*1103515245+12345;
return((unsigned int)(next/65536)%RAND_MAX);}
void srand(unsigned int seed)
{ next=seed; } Что вообще такое цикл с точки зрения случайных чисел? Период — это количество чисел, которое генерируется до того, как они вернутся в той же последовательности. Для примера число периодов в шифре А5 в среднем составляет 223, а сложность атаки 240, что позволяет взломать его на любом персональном компьютере.
Рассмотрим случай, когда seed равен 1, а период — 100 (на языке Haskell):
random i = (j, ans)
where j = 7 * i `mod` 101
ans = (j — 1) `mod` 10 + 1 — just the ones place, but 0 means 10В результате мы получим следующий ответ:
random 1 —> ( 7, 7)
random 7 —> (49, 9)
random 49 —> (40, 10)
random 40 —> (78, 8)
random 78 —> (41, 1)
random 41 —> (85, 5)
random 85 —> (90, 10)
random 90 —> (24, 4)
random 24 —> (67, 7)
random 67 —> (65, 5)
random 65 —> (51, 1)Это лишь пример и подобную структуру в реальной жизни не используют. В Haskell, если вы хотите построить случайную последовательность, можно воспользоваться следующим кодом:
random :: StdGen —> (Int, StdGen)Выбор случайного Int дает вам обратно Int и новый StdGen, который вы можете использовать для получения более псевдослучайных чисел. Многие языки программирования, включая Haskell, имеют генераторы случайных чисел, которые автоматически запоминают свое состояние (в Haskell это randomIO).
Чем больше величина периода, тем выше надежность создания хороших случайных значений, однако даже с миллиардами циклов крайне важно использовать надежный seed. Реальные генераторы случайных чисел обычно используют атмосферный шум (поставьте сюда любое физическое явление — от движения мыши пользователя до радиоактивного распада), но мы можем и схитрить программным методом, добавив в seed асинхронные потоки различного мусора, будь то длины интервалов между последними heartbeat потоками или временем ожидания mutual exclusion (а лучше добавить все вместе).
Истинная случайность бит
Итак, получив seed с примесью данных от реальных физических явлений (либо максимально усложнив жизнь будущему взломщику самым большим набором потоков программного мусора, который только сможем придумать), установив state для защиты от ошибки повтора значений и добавив криптографических алгоритмов (или сложных математических задач), мы получим некоторый набор данных, который будем считать случайной последовательностью. Что дальше?
Дальше мы возвращаемся к самому началу, к одному из фундаментальных требований — тестам.
Национальный институт стандартов и технологий США вложил в «Пакет статистических тестов для случайных и псевдослучайных генераторов чисел для криптографических приложений» 15 базовых проверок. Ими можно и ограничиться, но этот пакет вовсе не является «вершиной» проверки случайности.
Одни из самых строгих статистических тестов предложил профессор Джордж Марсалья из Университета штата Флорида. «Тесты diehard» включают 17 различных проверок, некоторые из них требуют очень длинных последовательностей: минимум 268 мегабайт.
Случайность можно проверить с помощью библиотеки TestU01, представленной Пьером Л’Экуйе и Ричардом Симардом из Монреальского университета, включающей классические тесты и некоторые оригинальные, а также посредством общедоступной библиотеки SPRNG.
Еще один полезный сервис для количественного измерения случайности.