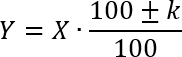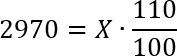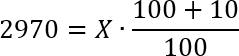Как найти начальное число от процента

Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью Excel]

Проценты, скажу я вам, это не только что-то «скучное» на уроках математики в школе, но еще и архи-нужная и прикладная вещь в жизни 👌 (встречаемая повсюду: когда берете кредит, оцениваете скидку, считаете прибыль и т.д.).

И на мой взгляд, при изучении темы «процентов» в той же школе — этому уделяется чрезвычайно мало времени. Возможно, из-за этого, некоторые люди попадают в не очень приятные ситуации (многие из которых можно было бы избежать, если бы вовремя прикинуть что там и как. ).

Собственно, в этой статье хочу разобрать наиболее популярные задачи с процентами, которые как раз встречаются в жизни (разумеется, рассмотрю это как можно на более простом языке с примерами). Ну а предупрежден — значит вооружен 😉 (думаю, что знание этой темы позволит многим сэкономить и время, и деньги).

И так, ближе к теме.

Как посчитать проценты: примеры

Вариант 1: расчет простых чисел в уме за 2-3 сек.

В подавляющем большинстве случаев в жизни требуется быстро прикинуть в уме, сколько там это будет скидка в 10% от какого-то числа (например). Согласитесь, чтобы принять решение о покупке, вам ненужно высчитывать все вплоть до копейки (важно прикинуть порядок).

Наиболее распространенные варианты чисел с процентами привел в списке ниже, а также, на что нужно разделить число, чтобы узнать искомую величину.

• 1% от числа = разделить число на 100 (1% от 200 = 200/100 = 2);
• 10% от числа = разделить число на 10 (10% от 200 = 200/10 = 20);
• 25% от числа = разделить число на 4 или два раза на 2 (25% от 200 = 200/4 = 50);
• 33% от числа ≈ разделить число на 3;
• 50% от числа = разделить число на 2.

Задачка! Например, вы хотите купить технику за 197 тыс. руб. Магазин делает скидку в 10,99%, если вы выполняете какие-нибудь условия. Как это быстро прикинуть, стоит ли оно того?

Пример решения. Да просто округлить эти пару чисел: вместо 197 взять сумму в 200, вместо 10,99% взять 10% (условно). Итого, нужно-то 200 разделить на 10 — т.е. мы оценили размер скидки, примерно в 20 тыс. руб. (при определенном опыте расчет делается практически на автомате за 2-3 сек.).

Точный расчет : 197*10,99/100 = 21,65 тыс. руб.

Диаграмма с процентами / в качестве примера

Вариант 2: используем калькулятор телефона на Андроид

Когда результат нужен более точный, можно воспользоваться калькулятором на телефоне (в статье ниже приведу скрины с Андроида). Пользоваться им достаточно просто.

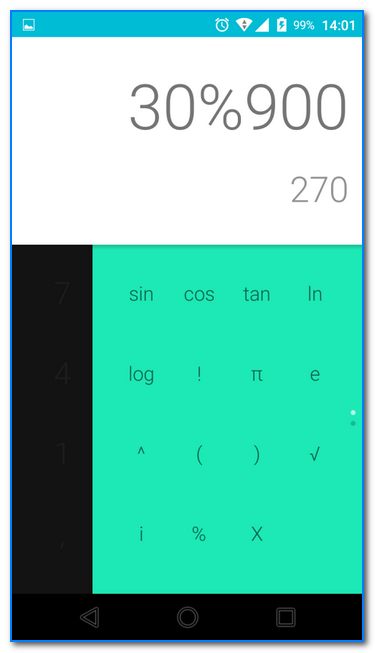
Например, вам нужно найти 30% от числа 900. Как это сделать?

Да достаточно легко:

• открыть калькулятор;
• написать 30%900 (естественно, процент и число может быть отличными);
• обратите внимание, что внизу под вашим написанным «уравнением» вы увидите число 270 — это и есть 30% от 900.

30% от числа 900 (калькулятор Андроид)

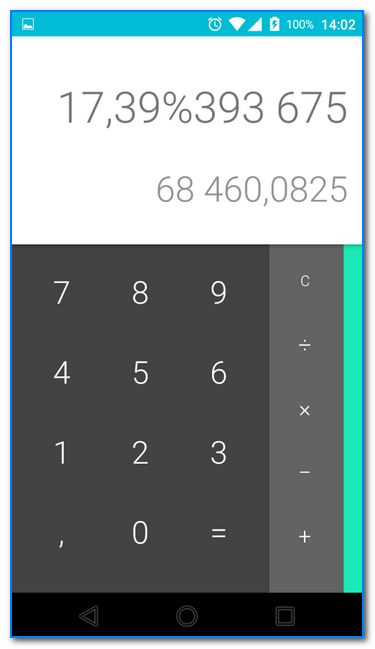
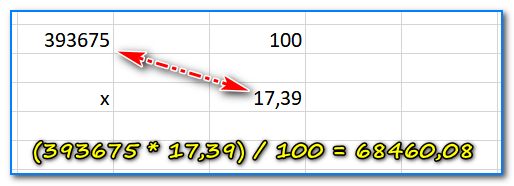
Ниже представлен более сложный пример. Нашли 17,39% от числа 393 675 (результат 68460,08).

еще один пример

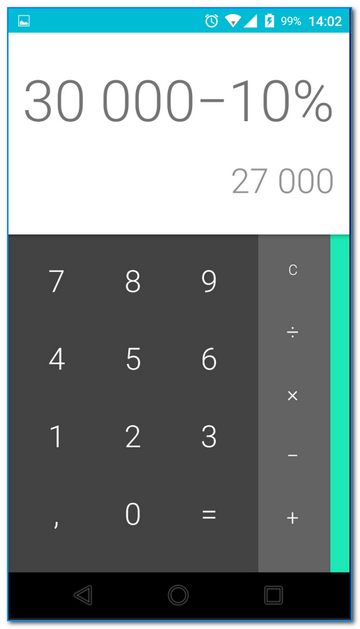
Если вам нужно, например, от 30 000 отнять 10% и узнать сколько это будет, то вы можете так это и написать (кстати, 10% от 30 000 — это 3000).

Таким образом, если от 30 000 отнять 3000 — будет 27000 (что и показал калькулятор). 👇

От числа отнимаем 10% (еще один пример)

В общем-то, весьма удобный инструмент, когда нужно просчитать 2-3 числа и получить точные результаты, вплоть до десятых/сотых.

Вариант 3: считаем процент от числа (суть расчета + золотое правило)

Не всегда и не везде можно округлять числа и высчитывать проценты в уме. Причем, иногда требуется не только получить какой-то точный результат, но и понять саму «суть расчета» (например, чтобы просчитать сотню/тысячу различных задачек в Excel).

В этих случаях рекомендую запомнить одно «золотое» правило столбика. Если вы поймете его — то без проблем сможете всегда решать задачки с процентами.

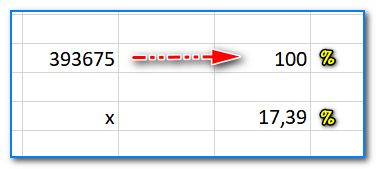
Допустим нам необходимо найти 17,39% от числа 393 675. Решим эту простую задачку.

1. сначала запишите на листочке число 393675 и напротив него напишите 100% (т.е. число, от которого мы пытаемся найти какой-то процент — считаем за 100%) ;
2. далее под 100% напишите, тот процент, который хотите найти (т.е. 17,39 в нашем примере); под самим числом — поставьте «X» (т.е. то число, что нужно найти, см. скрин ниже). Здесь главное число писать под числом, проценты под процентами (и не путать между собой их)!

Записываем числа для расчета процентов

Крест на крест (считаем проценты)

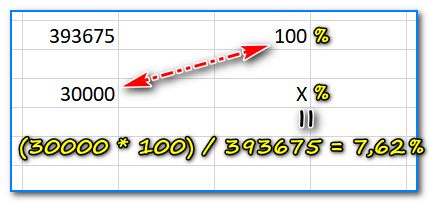
Чтобы снять все точки на «Й», рассмотрю обратную задачу. Например, сколько процентов составляет число 30 000 от числа 393 675.

1. сначала записываем столбиком также 393 675 и напротив него ставим 100%;
2. далее под самим числом 393 675 пишем 30 000, а напротив него ставим X (т.е. то, что нам нужно найти);
3. далее (30 000 * 100)/393675 и получаем 7,62 % (можете проверить 👌). Т.е. работает тоже правило: перемножаем крест на крест (т.е. там, где в диагонали известны два числа) и делим на оставшееся. Таким образом легко найти неизвестное.

Обратная задачка с процентами

Вариант 4: считаем проценты в Excel

Excel хорош тем, что позволяет производить достаточно объемные расчеты: можно одновременно просчитывать десятки самых различных таблиц, связав их между собой. Да и вообще, разве вручную просчитаешь проценты для десятков наименований товаров, например.

Ниже покажу парочку примеров, с которыми наиболее часто приходится сталкиваться.

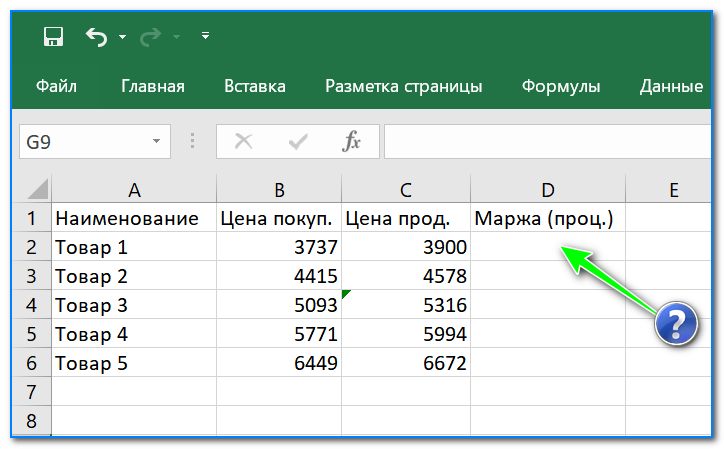
Задачка первая. Есть два числа, например, цена покупки и продажи. Надо узнать разницу между этими двумя числами в процентах (насколько одно больше/меньше другого).

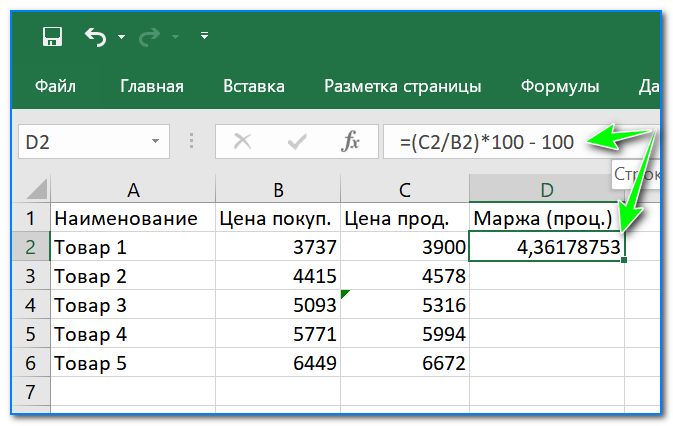
1. Сначала оформляем все это в Excel в форме таблички (пример см. ниже: в моем случае будем считать проценты для столбика «Маржа» по цене покупки и цене продажи товара) ;

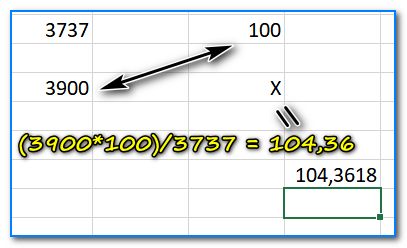
Как определить, насколько одно число больше другого в процентах

Второе число составляет 104% от первого

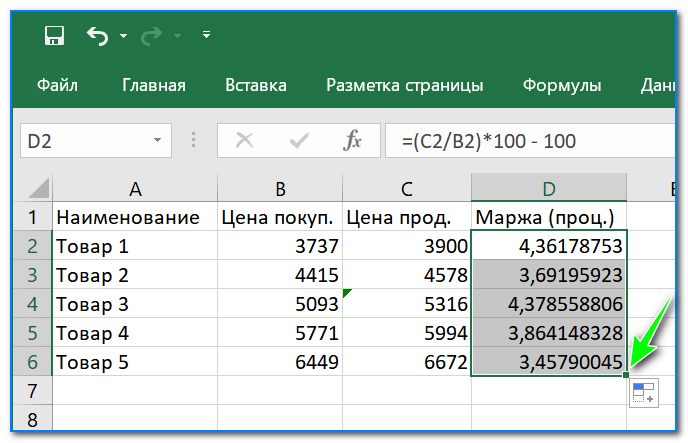
Формулу растянули — проценты посчитаны для всего столбца

Для более точного понимания, приведу еще один пример. Другая задачка: есть цена покупки и желаемый процент прибыли (допустим 10%). Как узнать цену продажи. Вроде бы все просто, но многие «спотыкаются».