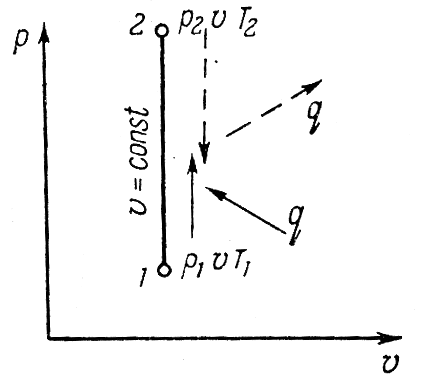
Исследования изохорного процесса идеальных газов.
Изменение
состояния рабочего тела при постоянном
объеме называется изохорным процессом.
Напишем уравнение состояния для 1 кг
газа. p1v=RT1-для
начального состояния, p2v=RT2–для
конечного состояния. Разделив почленно
и учитывая v =const
получим
В изохорном процессе давление газа
прямо пропорционально температуре.
Изменение внутренней энергии
∆u=u2-u1=cv(T2-T1).
Внешняя работа при изохорном процессе
не совершается, т.к. v=const,
dv=0. => l=0.
Тепло
участвующее в процессе определяют по
формуле q= ∆u=
cv(T2-T1).
Все подведенное тепло в изохорном
процессе расходуется на изменение
внутренней энергии газа. Коэффициент
α=1, т.к. q= ∆u.
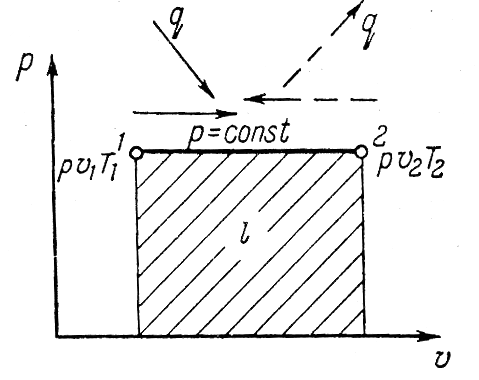
Исследование изобарного процесса идеальных газов.
Изменения
состояния рабочего тела при постоянном
давлении называется изобарным процессом.
Напишем уравнение состояния для 1 кг
газа. p1v=RT1-для
начального состояния, p2v=RT2–для
конечного состояния. Разделив почленно
и учитывая p =const
получим
В изобарном процессе объемы газа прямо
пропорциональны температуре. Изменение
внутренней энергии ∆u=u2–u1=cv(T2–T1).
Внешняя работа
,
т.к. p=const,
то
или l=R(T2–T1).
Если принять что температура увеличивается
на 1К, то l=R.,
Из этого следует, что газовая постоянная
R численно равна работе
расширения 1кг газа при нагреве его в
изобарном процессе на 1К.
Тепло участвующее в процессе определяют
по формуле q=
cp(T2–T1).
Уравнение первого закона термодинамики
для этого процесса примет вид q=∆u
+l=
u2–u1+p(v2-v1)
или q=(u2+pv2)-(u1+pv1)
Т.к. u+pv=i
то q=i2-i1.
Все подведенное тепло в изобарном
процессе расходуется на увеличение его
энтальпии. Коэффициент
, принимая, что для двухатомных газов
k=1.4, α=5/7. =>
5/7 теплоты идет на увеличение внутренней
энергии газа, 2/7 на совершение работы
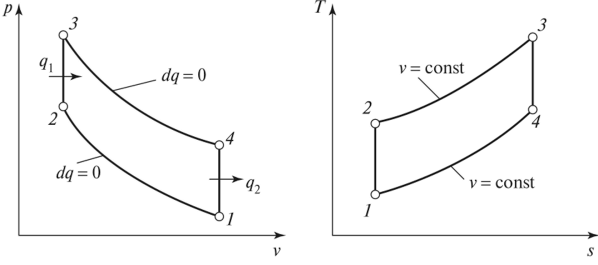
Исследование адиабатного процесса идеальных газов
Процесс
изменения состояния рабочего тела,
протекающий при отсутствии теплообмена
между газом и внешней средой, называется
адиабатным процессом. Пользуясь дифф.
уравнением П.З.Т., учитывая dq=0
уравнение процесса можно представить
в виде dq=du+dl=0.
Подставив du=сVdT,
dl=pdv =>
cVdT+pdv=0.
Т.к. сV=R/(k-1)
получим
.
Продифференцировав уравнение идеального
газа pv=RT
получим pdv+vdp=RdT/
Подставляя
получим vdp+kpdv=0.
Разделим на pv получим
.
Интегрируя и полагая k=cons.
Получим ln p
+klnv=const =>
pvk=const.
Адиабатный процесс в pv
отображается кривой. Т.к. k>1
адиабата круче изотермы и падение
давления происходит быстрее. Соотношения
между p,v,T^:

Изменение
внутренней энергии ∆u=сV(T2-T1).
Работа может быть определена из q=∆u+l=0,
т.к. q=0 =>
l=–∆u=–
сV(T2-T1)=
сV(T1-T2)=
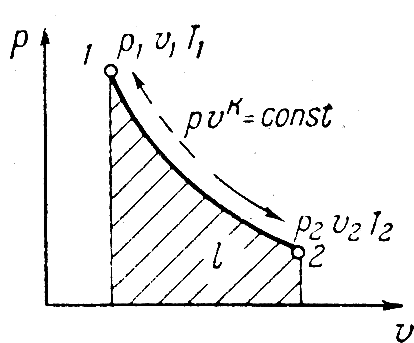
.
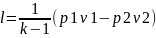
Видно, что
при адиабатном расширении газа
положительная работа происходит за
счет уменьшения внутренней энергии
газа. При адиабатном сжатии газа вся
работа идет на увеличение внутренней
энергии.
Исследования изотермического процесса идеальных газов.
Процесс,
протекающий при постоянной температуре
называют изотермическим. Уравнение
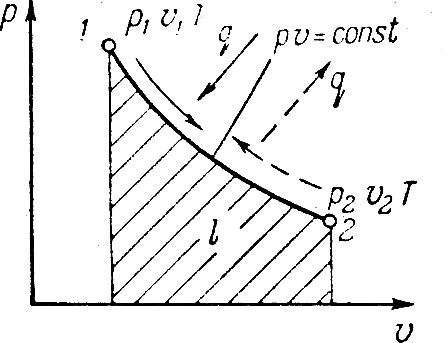
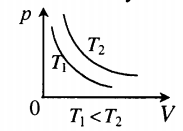
изотермического процесса pv=const.
На графике обозначается кривой
представляющей равнобокую гиперболу.
Связь между параметрами в начале и конце
процесса получается из уравнения
В изотермическом процессе объемы газа
обратно пропорциональны давлениям
газа, а изменение внутренней энергии
равно нулю. Внешнюю работу в этом процессе
определяют
,
т.к. p=RT/v.
.
Теплоту,
затраченную на совершение процесса,
определяют из уравнения

В иотермическом
процессе при
коэффициент α=
=0.
Теплота
подводимая к га зу в изотермическом
процессе расширения расходуется на
внешнюю работу.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изохорный (изохорический) процесс относится к основным процессам термодинамики и возможен исключительно при постоянном объеме. При этом два других параметра, а именно, давление и температура, изменяются.
В термодинамике давление, объем и температуру называют макроскопическим параметрами. В каждом из трех изопроцессов один из макроскопических параметров остается неизменным.
Изопроцессами, в свою очередь, называют изменение термодинамических систем макроскопических тел.
Как уже отмечалось, в изохорном процессе неизменен объем, в изотермическом постоянной остается температура, в изобарическом – давление.
Наиболее удобно рассматривать термодинамические процессы на примере идеальных газов.
Условие осуществления изохорного процесса в идеальном газе
Необходимым и достаточным условием для протекания изопроцесса в идеальном газе или жидкости является постепенное изменение – увеличение или уменьшение – температуры вещества, в котором происходит процесс. Первоначальный объем вещества должен оставаться неизменным, для чего вещество помещается в замкнутое пространство, т. е. в закрытый сосуд.
Зависимость температуры и давления идеального газа в изохорном процессе
В изохорном процессе давление идеального газа всегда прямо пропорционально его температуре. В реальных газах эта зависимость не выполняется.
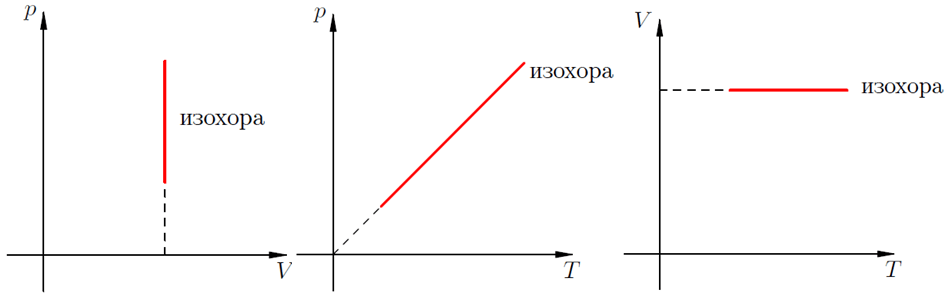
На графиках такое физическое явление как изохорный нагрев (охлаждение) отображает изохора. Это линия, связывающая три физических параметра:
- температуру рабочего тела (вещества) – T;
- объем рабочего тела (вещества) – V;
- внутренне давление – Р.
Для идеальных газов изохоры всегда являются прямыми линиями.
Возникновение и развитие теории изохорного процесса
В 1702 году французский физик-механик, член Французской Академии наук, Гийом Амонтон опубликовал свою работу «Парижские мемуары». В ней ученый подробно описал свои наблюдения за поведением фиксированного объема идеального газа в «стабильном воздушном термометре», в котором жидкость, под влиянием энергии газа в резервуаре и атмосферного давления, находилась в равновесии. При постепенном нагревании давление газа увеличивалось пропорционально температуре, и жидкость вытеснялась, заполняя следующий выступающий столб.
Дальнейшее развитие изучение изохорного процесса газа получило благодаря экспериментам английского физика Джона Дальтона. В своих экспериментах ученый определил, что при совпадающих начальных и конечных показателях, а также при постоянном давлении, все газы и пары при изменении температуры сжимаются или расширяются одинаково. Результаты исследований Джон Дальтон опубликовал в 1801 году.
Через некоторое время полученные Дальтоном результаты смог подтвердить и член Французской Академии наук, физик Жозеф Луи Гей-Люссак. Ученый провел свои независимые опыты и также выявил одинаковое распределение различных газов с практически тем же коэффициентом, что и Дальтон. Свои исследования Гей-Люссак объединил с законом Бойля-Мариотта, благодаря чему впоследствии удалось более подробно описать изохорный процесс. А закон пропорциональной зависимости объема газа от температуры в изохорическом процессе получил название закона Гей-Люсака.
Первый закон термодинамики для изохорного процесса
Формула
Формула первого закона термодинамики имеет следующий вид:
[boldsymbol{Q=Delta U+A}]
Где Q – количество теплоты, [boldsymbol{Delta U}] – сумма изменения внутренней энергии, A – работа системы.
Закон подразумевает, что для каких-либо изменений внутри системы необходимо приложить внешние усилия. Таким образом, можно предложить следующую простейшую формулировку первого закона термодинамики: для изменения внутренней энергии некоторой системы требуется внешнее воздействие. Именно этот закон доказывает невозможность изобретения вечного двигателя, над которым так долго бились ведущие ученые разных стран.
Изохорный процесс:
- Процесс, происходящий с газом неизменной массы при постоянном объеме называется изохорным.
- Закон Шарля: при изохорном нагревании газа относительное изменение его давления пропорционально конечной температуре.
[frac{p V}{T}=text { const }\frac{p_{1}}{T_{1}}=frac{p_{2}}{T_{2}}]
Как уже отмечалось, изохорным процессом в термодинамике считается физическое явление, протекающее при постоянном объеме. То есть при изменении температуры некоторого газа, находящегося внутри сосуда, его объем не изменится. Следовательно, работа, совершаемая газом при [V=c o n s t], равна нулю, т.е. A=0.
Формула
Таким образом, первый закон термодинамики для изохорного процесса выражается следующей формулой:
[boldsymbol{Q=Delta U=Uleft(T_{2}right)-Uleft(T_{1}right)}]
Где [boldsymbol{Uleft(T_{1}right)}] – внутренняя энергия идеального газа при начальной температуре, [boldsymbol{Uleft(T_{2}right)}] – внутренняя энергия идеального газа при конечной температуре.
При изохорном нагреве внутренняя энергия газа возрастает за счет поглощения тепла [(Q>0)], а при охлаждении газ отдает тепло и его внутренняя энергия уменьшается [(Q<0)].
Изучения термодинамических изменений подразумевает под собой определение следующих параметров: работы, которая была совершена в данном процессе, изменения внутренней энергии и количества теплоты. Также определяется взаимосвязь некоторых величие, характеризующих состояние газа.
Исследование изохорических процессов проводится по следующему методу:
- устанавливается взаимосвязь показателями рабочего тела на начальный и конечный момент, то есть выводится физическое уравнение;
- определяется работа, совершаемая газом, при изменении объема;
- определяется количество подводимой/отводимой теплоты;
- вычисляется изменение внутренней энергии и энтропии (функции состояния исследуемой системы).
Нет времени решать самому?
Наши эксперты помогут!
Эффект изохорного процесса и его применение
Свойства изохорного процесса, так же как и свойства изобарного и изотермического процессов, широко применяются в современных изобретениях.
Главный эффект изохорного процесса заключается в том, что при неизменном объеме теплоемкость значительно ниже, чем при постоянном давлении. Теплоемкость – величина, показывающая, какое количество теплоты необходимо для нагрева тела на один градус.
В изохорном процессе при изменении температуры система не совершает никакой работы, и, следовательно, вся подведенная теплота расходуется на изменение тепловой энергии: [d U=D q].
Согласно закону Шарля, в идеальном газе при изохорном процессе изменение давления прямо пропорционально изменению температуры. Однако для неидеальных газов закон Шарля не применим. Так как в этом случае некоторая часть теплоты, сообщаемой газу, расходуется на увеличение энергетического потенциала взаимодействия элементарных частиц.
В бензиновом двигателе внутреннего сгорания, в работе которого в максимальном приближении внедрен идеальный цикл Отто, такты 2-3 и 4-1 являются изохорными процессами. 2-3 – изохорный подвод тепла, 4-1 – изохорный отвод тепла. Работа, которая совершается на выходе мотора, равна разности основных работ. То есть разности между работой, совершаемой газом во время рабочего хода (над поршнем во время третьего такта), и работой, затрачиваемой поршнем на сжатие газа во втором такте. Принудительное сжигание смеси, используемое в таких двигателях, позволяет увеличить степень сжатия газа в 7-12 раз.
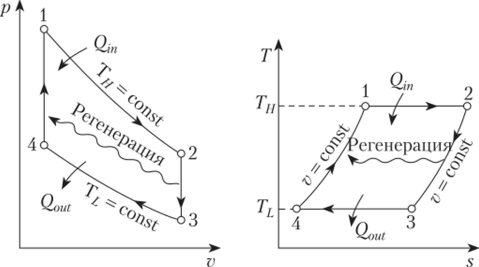
Изохорные такты также присутствуют в двигателях с циклом Стирлинга. В таких двигателях установлен регенератор, обеспечивающий выполнение изохорного процесса в двух тактах. Проходя через наполнитель в одну сторону, газ передает регенератору тепловую энергию рабочего тела. Двигаясь в обратном направлении, газ снова возвращает энергию рабочей системе. КПД и обратимость идеального цикла Стирлинга равны показателям цикла Карно.
Также изохорный подвод тепла используется в циклах ГТУ – газотурбинных установок.
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Изохорический или изохорный процесс — один из основных термодинамических процессов, который происходит исключительно при постоянном объёме.
Рисунок 1. Изохорный процесс. Автор24 — интернет-биржа студенческих работ
Для осуществления изохорного процесса в идеальном газе или жидкости достаточно постепенно нагревать или охлаждать действующее вещество в сосуде, который не изменяет своего изначального объёма и находится в замкнутом пространстве.
При изохорическом процессе общее давление идеального газа будет всегда прямо пропорционально его начальной температуре. Графики, которые изображают указанное физическое явление линиями, называются изохоры.
Для идеального газа они являются прямыми и стабильными во всех диаграммах, которые связывают такие основные параметры:
- $T$ (температура рабочего тела);
- $V$ (объем исследуемого вещества);
- $P$ (внутреннее давление).
История возникновения теории изохорного процесса
Наиболее часто первые научные исследования изохорного процесса связывают с физиком-теоретиком Гийомом Амонтоном . В своей первой работе «Парижские мемуары», которая была выпущена в 1702 году, изобретатель детально описал поведение идеального газа в фиксированном объёме внутри так называемого «воздушного стабильного термометра». Жидкость в нём находится всегда в равновесии под влиянием атмосферного давления и энергии исследуемого элемента в резервуаре. При постепенном нагревании давление и объем в замкнутом пространстве увеличивается, и жидкость вытесняется в следующий, выступающий столб.
«Изохорный процесс в термодинамике» 👇
В начале 1801 года физик Джон Дальтон в двух своих известных эссе опубликовал новый эксперимент, в котором определил, что все пары и газы, исследованные при неизменном давлении, одинакового расширяются и уменьшаются при изменении температуры, если соответствующий начальный и конечный показатель были одинаковы. Данный закон получил в науке название закона Гей-Люссака, так как именно этот исследователь вскоре смог провести самостоятельные опыты и подтвердил одинаковое распределение различных газов, получив в итоге практически тот самый коэффициент, что и Дальтон. Впоследствии ученый объединил свою теорию с законом Бойля — Мариотта, что позволило более понятно описывать в том числе и сам изохорный процесс.
Первый закон термодинамики для изохорного процесса
Рисунок 2. Закон Шарля. Автор24 — интернет-биржа студенческих работ
Простая формулировка первого термодинамического закона может звучать приблизительно так: изменение внутренней энергии той или иной концепции возможно только при наличии внешнего воздействия.
То есть иными словами, чтобы в системе произошли любые изменения необходимо приложить усилия извне. Именно первый закон термодинамики устанавливает, почему все многочисленные попытки исследователей потерпели неудачу, ведь ученые так и не смогли изобрести «вечный двигатель», существование которого считается абсолютно невозможным согласно этому самому закону.
Замечание 1
Формула первого закона термодинамики записывается таким образом: $Q = ΔU + A$, где $Q$ –количество теплоты, $ΔU$ – сумма изменения внутренней энергии и $A$ – работа системы.
Изохорным процессом в термодинамике называют физическим процесс, происходящий при постоянном, равномерном объеме. То есть, если в газе или жидкости нагреть определенное вещество в сосуде, произойдет изучаемое явление, так как объем элементов в такой системе останется неизменным. Это условие имеет существенное влияние и на первый термодинамический закон термодинамики, проходящий в основном при изохорном процессе.
В изохорном процессе объем рабочих тел $V$ является постоянной константой, следовательно, газ работы не совершает $A = 0$.
Из этого возможно вывести следующую формулу: $Q = ΔU = U (T_2) – U (T_1)$. Здесь $U (T_1)$ и $U (T_2)$ – внутренние энергии идеального газа, которые были зафиксированы в начальном и конечном положениях. Внутренняя энергия исследуемого элемента напрямую зависит только от первостепенной температуры (закон Джоуля).
При изохорном систематическим нагревании все тепло материального тела поглощается газом $(Q > 0)$, и его внутренняя энергия постепенно увеличивается. При охлаждении тепло будет отдаваться внешним элементам $(Q $
Метод исследования данного процесса заключается в следующем:
- изначально выводится уравнение физического явления (взаимосвязь между начальными и конечными показателями рабочего тела);
- вычисляется дальнейшая работа изменения объема газа;
- устанавливается точное количество теплоты, отведенное или подведенной к исследуемому объекту;
- определяется изменение внутренней энергии и энтропии концепции в процессе.
Поскольку внутренняя энергия является главной функцией состояния материального тела, то формулы изохорного процесса справедливы для любого термодинамического процесса идеального газа.
Применение эффекта изохорного процесса
Рисунок 3. Уравнение состояния. Автор24 — интернет-биржа студенческих работ
Изохорный процесс зачастую осуществляется в жидкостях и газах, расположенных в замкнутом сосуде с постоянным объемом. При этом явлении система не выполняет работы, и подведённая теплота $Q$ полностью расходуется на изменение тепловой энергии: $dU = Dq$.
Замечание 2
Следовательно, теплоёмкость при неизменном объёме будет всегда значительно меньше аналогичного параметра при постоянном давлении.
В идеальном газе в ходе изохорного процесса давление прямо пропорционально температуре – закон Шарля. Для неидеального газа закон Шарля невозможно применить, так как часть сообщённой газу теплоты идет строго на увеличение энергетического потенциала взаимодействия элементарных частиц.
При идеальном цикле Отто, который максимально приближённо внедрен в бензиновый двигатель внутреннего сгорания, такты 2—3 и 4—1 считаются изохорными процессами. Совершаемая на выходе мотора работа равна разности основных работ, которую производит газ над конкретным поршнем во время третьего такта и рабочего хода, включающий поршень на сжатие действующего вещества во время второго такта. Так как в указанном цикле используются принципы принудительного зажигания смеси, то происходит увеличение сжатия газа в 7—12 раз.
В другом цикле, под названием Стирлинг, также присутствуют два главных изохорных такта. Для его осуществления в устройстве добавлен мощный регенератор. Газ, проходя через наполнитель в одну сторону, отдаёт тепловую энергию от рабочего тела к регенератору, а при обратном движении возвращает его рабочей системе. Идеальный цикл Стирлинга достигает стопроцентной обратимости, а затем и тех же величин, что и цикл Карно.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Изопроцессы – виды графиков, формулы законов и уравнения
Трактовка понятий
Газ является одним из существующих агрегатных состояний вещества, для которого характерна слабая связь между компонентами и большая подвижность частиц. Последние передвигатся хаотично и свободно. При их столкновения изменяется характер движения.
Реальный газ считается высоко перегретым паром. Его свойства несколько отличаются от идеального компонента. В термодинамики различаются два состояния:
- насыщенные пары либо системы с двумя фазами;
- перегретые пары либо однофазовые системы.
Газы, как и жидкости, обладают текучестью. Они хорошо сопротивляются деформации. В отличие от воды, газ не имеет фиксированного объёма. Он стремится заполнить весь сосуд. Изопроцессы в газах подчиняются законам, которые определяют зависимость между двумя параметрами вещества при постоянном значении третьего. Так как уравнение справедливо для любой смеси, поэтому формула изотермического процесса (ИЗ) выражается следующим образом: T=const.
Само понятие ИЗ трактуется как новое состояние вещества, которое протекает при неизменной температуре. Процесс соответствует закону Бойля — Мариотта: для газа определённой массы произведение объёма на давление постоянно, если не изменяется температура. Равенство отображается на графике изопроцессов с помощью гиперболы и координат. Отдельно отмечаются изотермы при разных значениях температуры. В последнем случае соблюдается неравенство: Т1 23 молекул. Это считается числом Авогадро.
По закону Дальтона, давление смеси равно сумме парциальных P, входящих в состав. Выражение записывается следующим образом: P cm=P1+P2+…Pn. Последний показатель Pn является давлением газа, который бы занимал весь объёмом сосуда.
Чаще в старших классах физике рассматриваются изохорические процессы, когда переходит идеальный газ из одного состояния в другое, при этом не изменяется его объёмом. Явление впервые рассмотрел француз Жак Шарль. Закон записывается следующим образом: PV=vRT. Так как v= const и V=const, поэтому для любых разных состояний веществ используется равенство: P1/T1=P2/T2=….Pn/Tn. Закон Шарля математически записывается так: P/T=const.
Из выражения следует, что между температурой и давлением наблюдается прямо пропорциональная связь. Если увеличивается P, тогда повышается T, и наоборот. График зависимости данных величин называется изохорой. На промежутке абсолютного нуля для кривых предусмотрена условная зависимость. Прямая доводится до начала координат с помощью пунктирных линий.
Подобная зависимость T от P и V при изобарных и изохорных процессах определяет точность и эффективность измерения температуры газовыми термометрами. Первыми ученые открыли эти явления, которые считаются частными случаями уравнения состояния. Позже физики утвердили закон Клапейрона и Менделеева.
Если следовать хронологии, сначала изучались процессы, которые протекали при постоянной температуре, а затем при одном объеме. Последними рассматривались изобарические процессы. Редким и интересным явлением считается изоэнтропия, когда изменяется термодинамическая система при условии постоянной энтропии. Последнее записывается как S=const.
Примером подобного считается адиабатический обратимый процесс. Чтобы вычислить идеальный газ, используется уравнение: pV γ = const, где γ — показатель адиабаты (определяется типом газа). Для адиабатического явления характерно отсутствие теплоприёма и теплоотдачи. Физики считают такие процессы быстро протекающими.
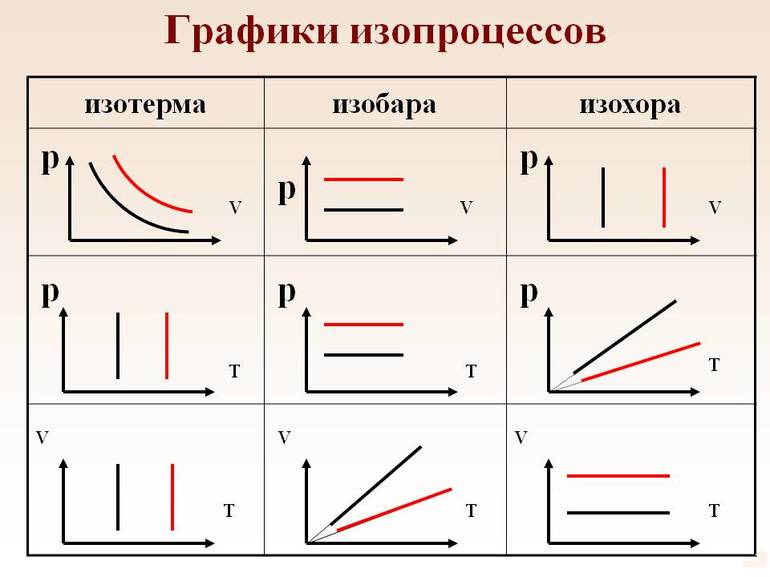
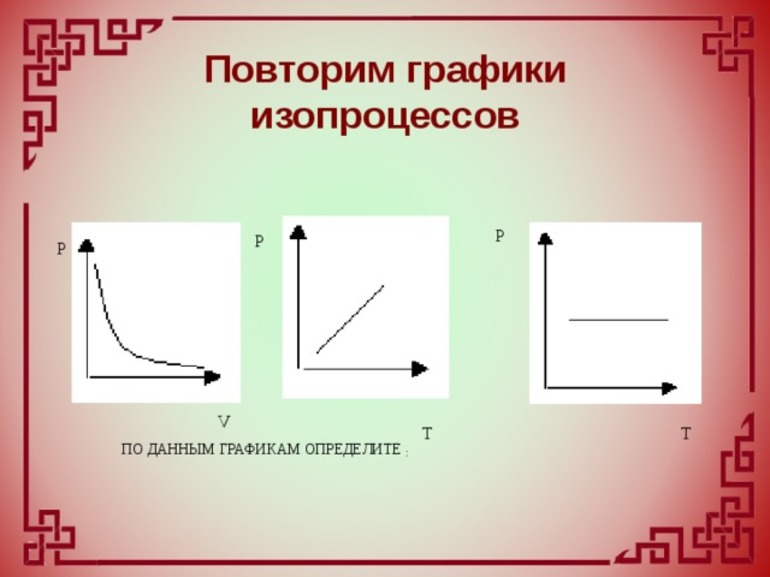
Изопроцессы в газах.
Изопроцессами называются процессы, протекающие при неизменном значении одного из параметров: давления (p), объема (V), температуры (T).
Изопроцессами в газах являются термодинамические процессы, на протяжении течения которых количество вещества и давление, объём, температура либо энтропия не поддаются изменениям. Таким образом, при изобарном процессе не изменяется давление, при изохорном – объём, при изотермическом – температура, при изоэнтропийном – энтропия (к примеру, обратимый адиабатический процесс). И линии, которые отображают перечисленные процессы на некой термодинамической диаграмме, называют, соответственно, изобара, изохора, изотерма и адиабата. Все эти изопроцессы являются частными случаями политропного процесса.
В идеальном газе эти процессы подчиняются газовым законам.
Газовыми законами называются количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра.
Изобарный процесс.
Изобарный (или изобарический) процесс — это изменение термодинамической системы с условием не изменения давления (P = const). Изобарой называют линию, которая отображает изобарический процесс на графике. Этот процесс описывает закон Гей-Люссака.
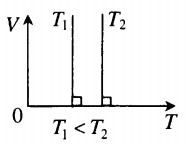
Изохорный процесс.
Изохорный (или изохорический) процесс — это изменение термодинамической системы с условием не изменения объема (V = const). Изохорой называют линию, которая отображает изохорический процесс на графике. Этот процесс описывает закон Шарля.
Изотермический процесс.
Изотермический процесс — это изменение термодинамической системы с условием не изменения температуры (T = const). Изотермой называют линию, которая отображает изотермический процесс на графике. Этот процесс описывает закон Бойля-Мариотта.
Изоэнтропийный процесс.
Изоэнтропийный процесс — это изменение термодинамической системы с условием не изменения энтропии (S = const). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:
где γ — показатель адиабаты, определяемый типом газа.
Объединенный газовый закон и изопроцессы
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:
При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:
p V T . . = c o n s t и л и p 1 V 1 T 1 . . = p 2 V 2 T 2 .
Объединенный газовый закон применительно к изопроцессам
Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.
Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.
Изотермический процесс. Закон Бойля — Мариотта.
Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:
Для изотермического процесса действует закон Бойля — Мариотта:
Закон Бойля — Мариотта
Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.
Изохорный процесс. Закон Шарля.
Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:
Для изохорного процесса действует закон Шарля:
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
p T . . = c o n s t ( p 1 T 1 . . = p 2 T 2 . . )
Изобарный процесс. Закон Гей-Люссака.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
V T . . = c o n s t ( V 1 T 1 . . = V 2 T 2 . . )
Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Так как газ нагревают, то:
Запишем закон Шарля применительно к данному случаю:
p T 1 . . = 1 , 6 p 240 + T 1 . .
Сделаем некоторые преобразования и вычислим начальную температуру:
p T 1 . . = 1 , 6 p 240 + T 1 . .
240 + T 1 = 1 , 6 T 1
T 1 = 240 0 , 6 . . = 400 ( К )
Подсказки к задачам на газовые законы
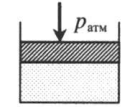
Газ под невесомым поршнем:
p — давление газа;
pатм — давление, оказываемое на газ со стороны поршня.
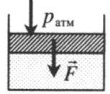
На невесомый поршень действует сила:
p = p а т м + F S . .
F — сила, действующая на поршень;
S — площадь поршня.
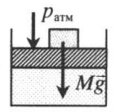
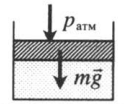
На невесомый поршень поставили груз. В данном случае на поршень дополнительно будет действовать сила тяжести:
p = p а т м + F т я ж S . . = p а т м + M g S . .
Fтяж — сила тяжести, действующая на поршень со стороны груза;
g — ускорение свободного падения.
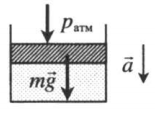
Газ под массивным поршнем. В данном случае на него дополнительно будет действовать сила тяжести поршня:
p = p а т м + m g S . .
m — масса поршня.
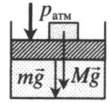
На массивный поршень поставили груз. В данном случае на поршень дополнительно будут действовать силы тяжести со стороны поршня и груза:
p = p а т м + M g S . . + m g S . .
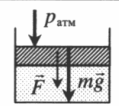
На массивный поршень действует сила. В данном случае газ сдавливается как атмосферным давлением, так и силой тяжести поршня, а также силой, которая на него действует:
p = p а т м + m g S . . + F S . .
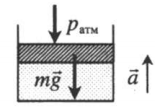
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вверх. Когда ускорение движения лифта противоположно направлено ускорению свободного падения, вес тел увеличивается. Поэтому:
p = p а т м + m g S . . + m a S . .
a — модуль ускорения, с которым движется лифт.
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вниз. Когда ускорение движения лифта направлено в сторону вектора ускорения свободного падения, вес тел уменьшается. Поэтому:
p = p а т м + m g S . . − m a S . .
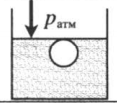
«Пузырек у поверхности воды» — на пузырек действует только атмосферное давоение:
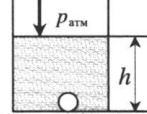
«Пузырек на глубине» — на пузырек действует атмосферное давление и давление столба жидкости:
ρ — плотность жидкости; h — глубина, на которой находится пузырек.
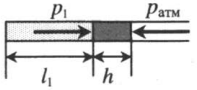
Газ, находящийся в горизонтальной пробирке, отделен от атмосферы столбиком ртути. Объем газа можно вычислить, используя параметры пробирки:
V1— объем газа; l1 — длина части пробирки, которую занимает газ; S — площадь поперечного сечения пробирки. Давление газа равно атмосферному давлению:
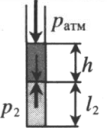
Пробирку поворачивают открытым концом вверх. В этом случае кроме атмосферного давления на газ давит давление со стороны ртути:
Объем газа можно вычислить, используя параметры пробирки:
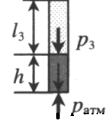
Пробирку поворачивают открытым концом вниз. В этом случае сумма давлений газа и ртути в пробирке равна атмосферному давлению. Отсюда давление газа равно:
Объем газа можно вычислить, используя параметры пробирки:
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
 |
|||||||||||||||||
| Шар или понтон поднимается вверх в воздухе или жидкости | Архимедова сила больше силы тяжести:
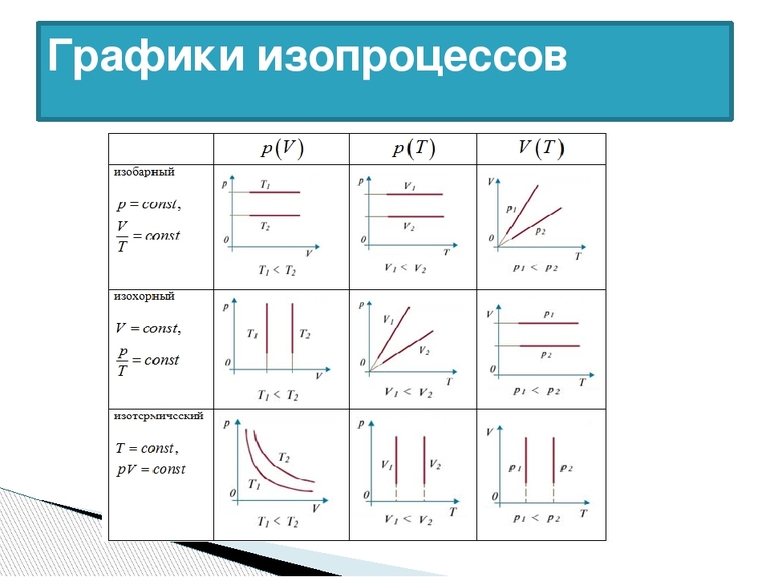
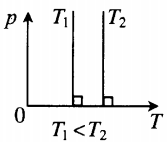
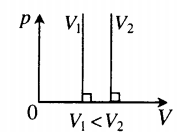
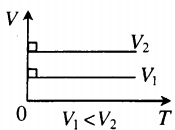
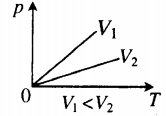
Пример №2. Поршень площадью 10 см 2 массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с 2 ? Изменение температуры газа не учитывать. 10 см 2 = 10 –3 м 2 100 кПа = 10 5 Па Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем: p 1 = p а т м + m g S . . Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх: p 2 = p а т м + m g S . . + m a S . . Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно: Объемы в 1 и 2 случае будут определяться формулами: h1 — расстояние от нижнего края поршня до дна сосуда в первом случае. h2 — та же самая величина, но во втором случае (искомая величина). Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов: p 1 V 1 = S h 1 ( p а т м + m g S . . ) p 2 V 2 = S h 2 ( p а т м + m g S . . + m a S . . ) Так как это изотермический процесс, правые части уравнений можно приравнять: S h 1 ( p а т м + m g S . . ) = S h 2 ( p а т м + m g S . . + m a S . . ) Графики изопроцессовИзопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.
|
Какой процесс называется изохорным, условия протекания
Определение
Изохорным процессом называют термодинамический процесс, протекающий при условии постоянного объема.
Изохорный процесс можно наблюдать опытным путем. Для этого необходимо повышать или понижать температуру вещества в газообразном или жидком состоянии, находящегося в сосуде и сохраняющего стабильность объема. В случае, когда манипуляции производят с идеальным газом, его давление и температура будут изменяться прямо пропорционально, согласно закону Шарля. Для реальных газов данная закономерность не применима.
История возникновения теории, кто открыл, формула
Изучение изохорного процесса связывают с Гийомом Амонтоном. Работа ученого под названием «Парижские мемуары», написанная в 1702 году, посвящена исследованию характеристик газообразного вещества, помещенного в фиксированный объем, который составляет часть «воздушного термометра». Равновесие жидкости в данных условиях объясняется воздействием на нее давления газа, находящегося в сосуде, и атмосферного давления. Если температура среды повышается, показатели давления в резервуаре возрастают. При этом определенный объем жидкости вытесняется в выступающую трубку. Зависимость между такими характеристиками процесса, как температура и давление, представлена на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В 1801 году были опубликованы два эссе исследователя Джона Дальтона с описанием эксперимента, результаты которого демонстрируют одинаковое расширение всех газов и паров при постоянном давлении и изменении температуры, когда начальная и конечная температура одинакова. В итоге был сформулирован закон Гей-Люссака. Ученый, в честь которого явление получило название, экспериментальным путем подтвердил одинаковое расширение различных газообразных веществ и вывел коэффициент, практически равный коэффициенту, полученному Дальтоном. Благодаря объединению данной закономерности с законом Бойля-Мариотта, был описан изохорный процесс.
График изохорного процесса в идеальном газе
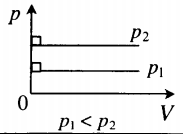
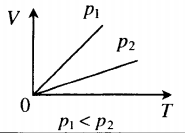
Зависимость характеристик при изохорном процессе можно представить схематично. График на диаграмме в системе координат будет иметь следующий вид:
В случае идеального газа графически изохорные процессы будут изображены следующим образом:
Первый закон термодинамики для изохорного процесса
В условиях термодинамического процесса формула элементарной работы имеет следующий вид:
(delta A=PdV)
Преобразование данного выражения позволит рассчитать величину полной работы процесса:
(A=int_{V_{1}}^{V_{1}}{PdV})
В случае, когда объем сохраняет стабильность, то есть (dV=0), значение интеграла будет нулевым. Исходя из этого, в изохорном процессе работа газа не наблюдается:
(A=0)
Изменение внутренней энергии для идеального газа рассчитывается по формуле:
(Delta U=frac{i}{2}nu RDelta T)
где i представляет собой количество степеней свободы, зависящее от числа атомов, которыми обладает молекула газа. В качестве примера можно рассмотреть такие вещества:
- одноатомная молекула неона обладает тремя степенями;
- пять степеней характерно для двухатомной молекулы кислорода;
- в молекуле с тремя и более атомами, как у водяного пара, насчитывается 6 степеней.
Формула внутренней энергии выходит из понятия и уравнения теплоемкости, представляет собой следующее отношение:
(Delta U=nu c_{upsilon }^{mu }Delta T)
где (c_{upsilon }^{mu }) является молярной теплоемкостью в условиях постоянного объема.
Расчет количества теплоты выполняют с помощью первого начала термодинамики в условиях термодинамического процесса:
(Q=Delta U+A)
Следует учитывать, что в условиях изохорного процесса газообразное вещество не выполняет работу. Исходя из этого, можно вывести формулу:
(Q=Delta U=nu c_{upsilon }^{mu }Delta T)
Согласно уравнению, газ получает теплоту. Она полностью расходуется, чтобы изменять внутреннюю энергию газообразного вещества.
Изменения термодинамических параметров в изохорном процессе
В условиях изохорного процесса наблюдается теплообмен с внешней средой. Данное явление называют изменением энтропии. Из его понятия следует уравнение:
(dS=frac{delta Q}{T})
где (delta Q) является элементарным количеством теплоты.
Преобразуя уравнение для расчета количества теплоты в дифференциальный вид, получают следующую формулу:
(delta Q=nu c^{mu }_{upsilon }dT)
где (nu) является количеством вещества, а (nu c^{mu }_{upsilon }) обозначает молярную теплоемкость в условиях постоянного объема.
Формула микроскопического изменения энтропии в условиях протекания изохорного процесса имеет вид:
(dS=frac{nu c^{mu }_{upsilon }dT}{T}dy/dx dy/dx)
Если проинтегрировать последнюю формулу, то расчет полного изменения энтропии выполняют таким образом:
(int_{S_{1}}^{S_{2}}{dS}=nu int_{T_{1}}^{T_{2}}frac{c^{mu }_{upsilon }dT}{T}Rightarrow Delta S=nu int_{T_{1}}^{T_{2}}frac{c^{mu }_{upsilon }dT}{T})
В этой ситуации не представляется возможным вынести определение молярной теплоемкости в условиях стабильного объема за интеграл, так как оно представлено в виде функции, зависящей от температуры.
Применение эффекта изохорного процесса
Идеальный цикл Отто приближенно воспроизведен в конструкции мотора внутреннего сгорания, работающего на бензине. Такты 2-3 и 4-1 при его функционировании представляют собой изохорные процессы. На выходе двигателя совершается работа. Она рассчитывается, как разность работ. К одной из них относят работу, производимую газообразным веществом над поршнем в процессе третьего такта или рабочего хода, к другой – работу, затраченную поршнем во время сжатия газа при втором такте. Таким образом, на примере двигателя, функционирующего, согласно принципу Отто, в системе принудительного сжигания смеси, газообразное вещество сжимается до 7-12 раз.
На рисунке изображен классический двигатель Стирлинга с конструкцией бета-типа, для которой характерно расположение рабочего и вытеснительного поршня в одном цилиндре.
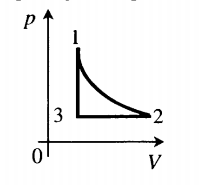
Динамику цикла Отто можно представить в следующем виде:
Цикл Стирлинга также характеризуется наличием двух изохорных тактов. Процесс протекает при дооснащении конструкции двигателя Стирлинга регенератором. Во время прохождения газообразного вещества в одном направлении через наполнитель осуществляется передача тепла от рабочего тела к регенератору. Если газ проходит в обратную сторону, то тепловая энергия передается на рабочее тело. Идеальный цикл Стирлинга достигает обратимости и характеризуется теми же параметрами КПД, что и цикл Карно.
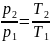

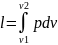


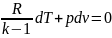

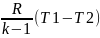



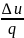





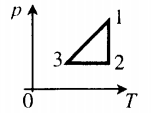
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.