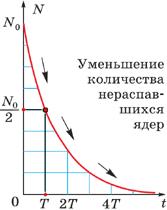
Появление «ручных» сцинтилляционных счетчиков и, главным образом, счётчиков Гейгера–Мюллера, которые помогли автоматизировать подсчёты частиц (см. § 15-е), привело физиков к важному выводу. Любой радиоактивный изотоп характеризуется самопроизвольным ослабеванием радиоактивности, выражающимся в уменьшении количества распадающихся ядер в единицу времени.
Построение графиков активности различных радиоактивных изотопов приводило учёных к одной и той же зависимости, выражающейся показательной функцией (см. график). По горизонтальной оси отложено время наблюдения, а по вертикальной – количество нераспавшихся ядер. Кривизна линий могла быть различной, однако сама функция, которой выражались описываемые графиками зависимости, оставалась одной и той же:
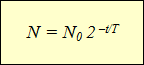 |
N – количество нераспавшихся ядер N0 – начальное количество ядер t – время наблюдения, с T – период полураспада, с |
Эта формула выражает закон радиоактивного распада: количество нераспавшихся с течением времени ядер определяется как произведение начального количества ядер на 2 в степени, равной отношению времени наблюдения к периоду полураспада, взятой с отрицательным знаком.
Как выяснилось в ходе опытов, различные радиоактивные вещества можно охарактеризовать различным периодом полураспада – временем, за которое количество ещё нераспавшихся ядер уменьшается вдвое (см. таблицу).
| Йод-129 | 15 млн лет | Углерод-14 | 5,7 тыс лет | |
| Йод-131 | 8 дней | Уран-235 | 0,7 млрд лет | |
| Йод-135 | 7 часов | Уран-238 | 4,5 млрд лет |
Период полураспада – общепринятая физическая величина, характеризующая скорость радиоактивного распада. Многочисленные опыты показывают, что даже при очень длительном наблюдении за радиоактивным веществом его период полураспада постоянен, то есть не зависит от числа уже распавшихся атомов. Поэтому закон радиоактивного распада нашёл применение в методе определения возраста археологических и геологических находок.
Метод радиоуглеродного анализа. Углерод – очень распространённый на Земле химический элемент, в состав которого входят стабильные изотопы углерод-12, углерод-13 и радиоактивный изотоп углерод-14, период полураспада которого составляет 5,7 тысяч лет (см. таблицу). Живые организмы, потребляя пищу, накапливают в своих тканях все три изотопа. После прекращения жизни организма поступление углерода прекращается, и с течением времени его содержание убывает естественным путём, за счёт радиоактивного распада. Поскольку распадается только углерод-14, с течением веков и тысячелетий изменяется соотношение изотопов углерода в ископаемых останках живых организмов. Измерив эту «углеродную пропорцию», можно судить о возрасте археологической находки.
Метод радиоуглеродного анализа применим и для геологических пород, а также для ископаемых предметов быта человека, но при условии, что соотношение изотопов в образце не было нарушено за время его существования, например, пожаром или действием сильного источника радиации. Неучёт подобных причин сразу после открытия этого метода приводил к ошибкам на несколько веков и тысячелетий. Сегодня применяются «вековые калибровочные шкалы» для изотопа углерода-14, исходя из его распределения в долгоживущих деревьях (например, в американской тысячелетней секвойе). Их возраст можно подсчитать весьма точно – по годовым кольцам древесины.
Предел применения метода радиоуглеродного анализа в начале XXI века составлял 60 000 лет. Для измерения возраста более древних образцов, например горных пород или метеоритов, используют аналогичный метод, но вместо углерода наблюдают за изотопами урана или других элементов в зависимости от происхождения исследуемого образца.
|
При всем разнообразии реакций самопроизвольного (спонтанного) распада ядер в этом процессе наблюдается общая закономерность, которую можно описать математически. Интересно, что зависимость количества распавшихся ядер от времени задается одной и той же функцией для различных ядер, участвующих в распаде. Перейдем к количественному описанию процессов радиоактивного распада. |
Большинство изотопов любого химического элемента превращается в более устойчивые изотопы путем радиоактивного распада. Каждый радиоактивный элемент распадается со своей, присущей только ему «скоростью». При этом для каждого радиоактивного ядра существует характерное время, называемое периодом полураспада , спустя которое в исходном состоянии остается половина имевшихся ядер. Таким образом, периодом полураспада
называется промежуток времени, за который распадается половина начального количества
радиоактивных ядер. Другая половина ядер превращается в более устойчивые изотопы посредством распада.
Отметим, что период полураспада не зависит от того, в каком состоянии находится вещество: твердом, жидком или газообразном. Кроме того, период полураспада радиоактивного вещества не зависит от его количества, от времени, места и условий, в которых оно находится. Поэтому количество радиоактивных ядер «тогда» и «сейчас»
непосредственно определяет промежуток времени
, прошедший с момента уменьшения числа ядер от
до
.
Невозможно точно предсказать, когда произойдет распад данного ядра. Однако можно оценить среднее число ядер, которые распадутся за данный промежуток времени. Таким образом, закон радиоактивного распада является статистическим и он справедлив только при достаточно большом количестве радиоактивных ядер.
Для записи закона радиоактивного распада будем считать, что в начальный момент времени () число радиоактивных ядер
. Через промежуток времени, равный периоду полураспада, это число будет
, еще через такой же промежуток времени —
(рис. 218). Спустя промежуток времени, равный n периодам полураспада
, радиоактивных ядер останется:
|
|
(1) |
Это соотношение выражает закон радиоактивного распада, который можно сформулировать следующим образом:
число нераспавшихся радиоактивных ядер убывает с течением времени по закону, представленному соотношением (1).
Закон радиоактивного распада позволяет найти число нераспавшихся ядер в любой момент времени. Полученное выражение хорошо описывает распад радиоактивных ядер, если их количество достаточно велико.
Приведем экспериментальные результаты, которые показывают, что при малом количестве радиоактивных ядер это выражение неприменимо. На рисунке 219 изображен график распада 47 ядер изотопа фермия , период полураспада которого
. Из рисунка 219 видно, что пока ядер было достаточно много — от 47 до 12, то показательная функция хорошо описывала закон распада. Однако при меньшем числе ядер истинная зависимость существенно отличается от показательной функции.
Периоды полураспада некоторых радиоактивных изотопов веществ приведены в таблице 11.
| Таблица 11. Периоды полураспада радиоактивных изотопов веществ | |
| Вещество | Период полураспада |
| 30,17 лет | |
| 5,3 года | |
| 8,04 суток | |
| 24 390 лет | |
| 1600 лет | |
| 3,8 суток | |
| 700 млн лет | |
| 4,5 млрд лет |
|
Впервые процесс радиоактивного распада для измерения промежутков времени был использован в 1904 г. Резерфордом. По отношению концентрации урана и его дочернего продукта распада (гелия) он определил возраст урановой породы. Эта работа положила начало ядерной геохронологии — определению возраста различных минералов Земли по радиоактивным долгоживущим веществам. В дальнейшем исследование процессов ядерного синтеза позволило перейти к ядерной космохронологии, т.е. к определению продолжительных промежутков времени, прошедших с момента образования элементов в масштабах Галактики и Вселенной. В основу ядерной космохронологии положена неизменность «скорости» радиоактивного распада. В 1927 г. американский ученый Г. Блюмгарт, используя изотоп В 1934 г. венгерский ученый Дьердь фон Хевеши, используя дейтерий, впервые установил, что в организме человека вода полностью обновляется в течение 14 суток. В 1943 г. Дьердь фон Хевеши была присуждена Нобелевская премия по химии «за работу по использованию изотопов в качестве меченых атомов при изучении химических процессов». |
 |
Тема: Определить число радиоактивных ядер в свежеприготовленном препарате (Прочитано 5443 раз)
0 Пользователей и 1 Гость просматривают эту тему.
11.8. Определить число радиоактивных ядер в свежеприготовленном препарате 82Br, если известно, что через сутки его активность стала равной 7,4∙109 Бк (0,20 Ки). Сделать рисунок.
Записан
Решение.
Активность – число ядер радиоактивного препарата, распадающихся за единицу времени.
Активность в начальный момент наблюдения определим по формуле
А0 = λ∙N0 (1).
λ – постоянная распада, постоянную распада определим по формуле
[ lambda =frac{ln 2}{T} (2).
]
Т – период полураспада (табличная величина) для 82Br период полураспада равен 36 часов.
N0 – количество ядер в начальный момент наблюдения N – количество ядер через время одни сутки от начала наблюдения.
Активность излучения изменяется по закону:
[ begin{align}
& A={{A}_{0}}cdot {{e}^{-lambda cdot t}} (3),A=lambda cdot {{N}_{0}}cdot {{e}^{-frac{ln 2}{T}cdot t}},{{N}_{0}}=frac{A}{lambda cdot {{e}^{-frac{ln 2}{T}cdot t}}},{{N}_{0}}=frac{Acdot {{e}^{frac{ln 2}{T}cdot t}}}{lambda },{{N}_{0}}=frac{Acdot {{e}^{frac{ln 2}{T}cdot t}}cdot T}{ln 2}. \
& {{N}_{0}}=frac{7,4cdot {{10}^{9}}cdot {{e}^{frac{ln 2cdot 24}{36}}}cdot 36}{ln 2}=2,3cdot {{10}^{15}}. \
end{align} ]
Ответ: 2,3∙1015.
« Последнее редактирование: 19 Февраля 2018, 06:26 от alsak »
Записан
8. Примеры решения задач
1. Зная постоянную
распада ядра, определить вероятность
Р того, что ядро распадается за промежуток
времени от 0 до t.
Решение.
Процесс радиоактивного распада носит
статистический характер, а это значит,
что если многократно повторять опыты
с радиоактивным препаратом, содержащим
достаточно большое начальное число
ядер
,
то за промежуток времени от 0 до t
распадается каждый раз одна и та же доля
ядер
.
Эта величина, характеризующая относительную
частоту события – распада ядра, и
принимается за вероятность Р распада
ядра в течение данного промежутка
времени. Таким образом
где – число нераспавшихся ядер
к моменту времени t.
Подставив в это равенство вместо N
его значение по закону радиоактивного
распада и произведя сокращение, получим
ответ:
.
2. Определить,
сколько ядер в
=1,0
мг радиоизотопа церия распадается в
течение промежутков времени:
1)
=1с;
2)
=1 год.
Период полураспада церия Т=285
сут.
Решение. Задача
решается с помощью закона радиоактивного
распада.
1. Так как
,
то можно считать, что в течение всего
промежутка
число
нераспавшихся ядер остается практически
постоянным и равным их начальному числу
.
Тогда для нахождения числа распавшихся
ядер
применим закон радиоактивного распада,
записав его так:
или учитывая, что период полураспада
Т и постоянная распада связаны
соотношением
Чтобы определить начальное число
ядер (атомов)
,
умножим постоянную Авогадро
на число молей
,
содержащихся в данном препарате:
где
– начальная масса препарата,
–
молярная масса изотопа
,
численно равная (приблизительно) его
массовому числу. С учетом предыдущего
выражения получим
.
Выразим числовые значения
величин, входящих в полученную формулу,
в единицах СИ:
Произведя
вычисления с учетом того, что ln2
= 0,693, найдем
.
2. Так как теперь
–
величины одного порядка, то дифференциальная
форма закона радиоактивного распада
здесь неприменима. Поэтому для решения
задачи воспользуемся интегральной
формой закона, справедливой для любого
промежутка
.
Тогда получим
.
Или
.
Так как
,
то уравнение принимает более простой
вид
.
Произведя вычисления, получим
.
3. Радиоизотоп
с постоянной распада
превращается в радиоизотоп
с постоянной распада
.
Считая, что в начальный момент препарат
содержал только ядра изотопа
,
найти, через сколько времени активность
радиоизотопа
достигнет максимума?
Решение.
Активность препарата пропорциональна
числу наличных ядер N
этого препарата. Поэтому активность а
радиоизотопа
достигнет максимума тогда, когда
максимальным будет число ядер
этого радиоизотопа. Закон изменения со
временем числа ядер
выражается формулой (3). Для отыскания
промежутка времени t,
которому соответствует максимум функции
,
продифференцируем эту функцию по времени
и приравняем к нулю производную:
Отсюда
Решив это уравнение относительно
t,
найдем искомое время
9. Активность радиоактивного препарата
Активность любого радиоактивного
препарата, в котором ежесекундно
распадается N
радиоактивных атомов, выражается
формулой
|
|
(9.1) |
Единица активности в СИ –
беккерель
(Бк).
1 Бк – это активность, при
которой за 1с происходит один распад
ядра.
Часто используется внесистемная
единица активности – кюри
(Ки),
1Ки=3,71010
Бк.
Активность радиоактивного
препарата уменьшается со временем по
экспоненциальному закону
|
|
(9.2) |
Для долгоживущих радиоактивных
элементов с большим периодом полураспада
удельная активность (активность единицы
массы) вычисляется по формуле
|
|
(9.3) |
где
–
число Авогадро; M
– атомная масса радиоактивного элемента,
в а.е.м.; N
– число ядер в 1 кг этого элемента.
Активность образца C
с массой m
кг, атомной массой M
а.е.м. и периодом полураспада
определяется формулой
|
|
(9.4) |
Если радиоизотоп
с постоянной распада
превращается в радиоизотоп
с постоянной распада
, то число ядер радиоизотопа изменяется
со временем по закону
|
|
(9.5) |
где
–
число ядер радиоизотопа
в момент t=0.
10. Примеры решения задач
1. Найти активность
радона, образовавшегося из
=
1,0 г радия
за
одни сутки. Найти также максимальную
активность радона. Периоды полураспада
радия и радона соответственно равны
лет,
сут.
Решение. Используя
соотношения (8) и (10), запишем для искомой
активности
.
Входящие сюда величины
выразим через данные
,
,
по формулам:
и
.
Тогда, произведя сокращения,
имеем
.
Это общая формула, выражающая
закон изменения со временем активности
одного радиоизотопа (дочернего),
полученного в процессе распада другого
(материнского). Если учесть вытекающие
из условия соотношения
и
,
эту формулу можно упростить. Из первого
неравенства следует, что можно пренебречь
величиной
в разности
–
.
В силу второго неравенства можно принять
за единицу первый член, стоящий в скобках.
Тогда найдем
.
Произведя расчет, получим
расп/с,
или
Ки
=0 б17 Ки.
Анализируя полученную приближенную
формулу, с учетом неравенств
и
,
видим, что с ростом времени t
величина, стоящая в скобках, приближается
по экспоненте к единице. Следовательно,
расп/с=1б0 Ки.
2. Определить начальную
активность радиоактивного препарата
магния-27 массой 0,2 мкг, а также его
активность через время 6 часов.
Решение. Активность А
изотопа характеризует скорость
радиоактивного распада и определяется
отношением числа dN ядер, распавшихся
за интервал времени dt, к этому
интервалу
А = –
, (1)
знак
“-” показывает, что число N
радиоактивных ядер с течением времени
убывает.
Для того, чтобы найти dN/dt,
воспользуемся законом радиоактивного
распада
N = No e–t, (2)
где
N – число радиоактивных ядер,
содержащихся в изотопе, в момент времени
t, No – число радиоактивных
ядер в момент времени, принятый за
начальный (t=0),
– постоянная радиационного распада.
Продифференцируем выражение
(2) по времени
dN/dt = –Noe–
t. (3)
Исключив из формул (1) и (3) dN/dt,
находим активность препарата в момент
времени t
А =Noe–
t
. (4)
Начальную активность Ао
препарата получим при t = 0
Ао =
No
. (5)
Постоянная радиоактивного
распада
связана с периодом полураспада Т1/2
соотношением
. (6)
Число No радиоактивных
ядер, содержащихся в изотопе, равно
произведению постоянной Авогадро NA
на количество вещества
данного изотопа
No =
NA
=
NA
. (7)
где
m – масса изотопа,
– молярная масса.
С учетом вырaжений (6) и (7) формулы
(5) и (4) принимают вид:
Ао =
NA
, (8)
A =
NA
. (9)
Произведя вычисления и учитывая,
что Т1/2 = 600 с; ln2 = 0,693; t
= 6 ч = 63,6.103 с =
2,16.104 с, получим
Ао=Бк
= 5,13 . 1012 Бк =
=
Ku ,
Бк
= 46.10-10 Ku.
3. При археологических
раскопках были обнаружены сохранившиеся
деревянные предметы, активность 6С14
которых оказалась равной 106
распадов в минуту на 1 г содержаще-гося
в них углерода. В живом дереве происходит
в среднем 14,5 распадов за минуту на 1 г
углерода. Исходя из этих данных, определить
время изготовления обнаруженных
предметов.
Решение.
Известно, изотоп 6С14
является радиоактивным, его период
полураспада Т1/2(6С14)
= 5700 лет.
Найдем число атомов 6С14
в 1 г.
N = (m/A)
NA
= (1/14) 6,02·1023
=0,42·1023.
t0
– настоящий момент времени,
t*
– момент времени, когда были изготовлены
деревянные предметы.
Число распадающихся атомов 6С14
в момент t0
и t*
за 1 мин равно ∆N0
= λ·N0·∆t;
∆N*
= λ·N·∆t;
Активность пропорциональна
числу атомов a0
= λ·N0
Активность радионуклида со
временем изменяется по экспоненте a*
= a0·exp(-λ·t*).
Отсюда ln(a0/a*)=λ·t*=(ln2/Т1/2)·t*.
Численное значение t*
равно t*
= ln(a0/a*)·Т1/2/ln2
= ln(14,5/10)
5700/0,693 = 3056 лет.
Ответ: деревянные
предметы были изготовлены примерно за
3056 лет до настоящего времени.
6. В результате
атмосферных испытаний и связанных с
ними глобальных выпадений радионуклидов
содержание цезия-137 в оленине в северных
районах СССР к 1964 г. достигло 1628 Бк/кг.
Сколько лет должна храниться такая
оленина в холодильниках, чтобы ее
удельная активность снизилась до 592
Бк/кг – предельно допустимого загрязне-ния
мясных продуктов цезием-137, регламентированного
белорусскими нормативами 1990 – 91 г.
Целесообразно ли столь длительное
хранение оленины?
Решение.
Активность изменяется по экспоненте
a =
a0·exp(-λ·t).
Следовательно, (a0/a*)
= exp(λ·t*).
Отсюда время хранения оленины в
холодильнике равно
t*
= ln(a0/a*)×T1/2/ln2
= ln(628/592)·30,2/0,693
= 44 года.
Ответ: столь
продолжительное время хранения оленины
в холодильнике для снижения удельной
активности цезия следует считать
экономически нецелесообразным.
7. Согласно
белорусским нормативам 1990 – 91 г активность
цезия-137 в пшенице (зерне) должна быть
на уровне 370 Бк/кг. Сколько времени
пшеница урожая 1990 г, имеющая предельно
допустимую активность, должна храниться
в элеваторе, чтобы ее активность снизилась
до 0,06 Бк/кг –средней активности по
цезию-137, произведенной в 1963 г. в СССР?
Целесообразно ли такое хранение?
Решение.
Удельная активность зерна, содержа-щего
радионуклид цезий-137, изменя-ется по
экспоненте a
= a0·exp(-λ·t).
В конкретном случае имеем такое
соотношение: a0/aСР
= exp(λ·tСР),
где tСР–среднее
время хранения зерна на элеваторе.
Отсюда
tСР
= ln(a0/aСР)·T1/2/ln2
= ln(370/0,06)
30,2/ln2
= 380 лет.
Ответ: такое
зерно хранить не следует.
11. Радиоактивный распад
Альфа-распадом
называется испускание ядрами некоторых
химических элементов
-частиц.
Альфа-распад является свойством тяжелых
ядер с массовыми числами А>200
и зарядами ядер Ze>82.
Внутри таких ядер происходит образование
обособленных
-частиц,
состоящих каждая из двух протонов и
двух нейтронов.
При
–
радиоактивности заряд ядра уменьшается
на 2 единицы, а масса – на 4 единицы,
например:
Термином бета-распад
обозначают три типа ядерных превращений:
электронный
(-)
и позитронный
(+)
распады, а также электронный
захват. Первые два типа
превращения состоят в том, что ядро
испускает электрон (позитрон) и электронное
антинейтрино (электронное нейтрино).
Эти процессы происходят путем превращения
одного вида нуклона в ядре в другой:
нейтрона в протон или протона в нейтрон.
В случае электронного захвата превращение
заключается в том, что исчезает один из
электронов в ближайшем к ядру слое.
Протон, превращаясь в нейтрон, как бы
“захватывает” электрон; отсюда
произошел термин “электронный захват”.
Электронный захват в отличие от
±-захвата
сопровождается характеристическим
рентгеновским излучением.
-распад
происходит у естественно-радиоактивных,
а также искусственно-радиоактивных
ядер;
+-распад
характерен только для явления искусственной
радиоактивности.
При
-распаде
заряд ядра увеличивается на единицу, а
масса остается неизменной, например:
– излучением называется
электромагнитное излучение, возникающее
при переходе атомных ядер из возбужденных
в менее возбужденные или основное
состояния.
– излучение обычно сопровождает ядерные
реакции. Длины волн
– излучения лежат в диапазоне
10-10210-13м,
а энергия
– квантов лежит в пределах от
10кэВ до 5МэВ.
При
–
распаде превращения
элементов не происходит, но внутренняя
энергия ядра уменьшается:
Продукты распада могут быть, в
свою очередь радиоактивными.
12. Примеры решения задач
1. Ядро радиоактивного
элемента подвергнувшись ряду превращений,
потеряло 5
–
частиц и 3
-частицы
и превратилось в ядро элемента
.
Определить исходный радиоактивный
элемент.
Решение. Потеря
–
частиц приводит к уменьшению числа
Менделеева на
единиц, а потеря
-частиц
приводит к увеличению этого числа на
единиц. Таким образом,
откуда
.
На изменение массового числа
влияет только потеря
–
частиц, Каждая из которых имеет массовое
число 4:
,
отсюда
.
После подстановки численных
значений, получим:
=
83 +2*5-3=90;
=212+5*5=232.
Из таблицы Д.И.Менделеева
определяем искомый изотоп:
2. Ядро какого
элемента образуется после пяти
последовательных α-превращений 92U234?
Решение.
Cогласно
правилу радиоактивного смещения при
α-распаде образуется новый радиоактивный
элемент, смещенный в таблице Менделеева
на две клетки влево.
1) 92U234
→α→
90X230
+ 2He4,
X ≡ Th (торий);
2) 90Th230
→α→
88Y226
+ 2He4,
Y ≡ Ra (радий);
3) 88Ra226
→α→
86Z222
+ 2He4,
Z
≡ Rn (радон);
4) 86Rn222
→α→
84Q218
+ 2He4,
Q ≡ Po (полоний);
5) 84
Po218
→α→
82D214
+ 2He4,
D ≡ Pb (Свинец).
Ответ: в
результате пяти α-распадов образуется
изотоп 82Pb214.
13. 3акон ослабления пучка моноэнергетического
γ – излучения или β –
частиц
При
прохождении радиоактивного излучения
через вещество плотность его потока
уменьшается. 3акон ослабления пучка
моноэнергетического γ – излучения или
β – частиц имеет вид
,
где
j0
– плотность потока частиц, падающих на
поверхность вещества, j
– плотность потока на глубине х,
μ – линейный
коэффициент ослабления.
Интенсивность
γ
– излучения I
после прохождении слоя вещества толщиной
x
можно определить по формуле
,
где
I0
– интенсивность γ – излучения, падающего
на поверхность вещества.
Рисунок 13.1.
На
рисунке 13.1 приведена зависимость
линейного коэффициента ослабления от
энергии γ
– фотонов
для разных веществ.
14. Энергия связи ядра. Дефект массы ядра
Энергия связи ядра определяется
величиной той работы, которую нужно
совершить, чтобы расщепить ядро на
составляющие его нуклоны без придания
им кинетической энергии.
Из закона сохранения энергии
следует, что при образовании ядра должна
выделяться такая же энергия, какую нужно
затратить при расщеплении ядра на
составляющие его нуклоны. Энергия связи
ядра является разностью между энергией
всех свободных нуклонов, составляющих
ядро, и их энергией в ядре.
При образовании ядра происходит
уменьшение его массы: масса ядра меньше,
чем сумма масс составляющих его нуклонов.
Уменьшение массы ядра при его образовании
объясняется выделением энергии связи
|
или
|
где
– массы протона, нейтрона и ядра
соответственно;
–
дефект массы ядра,
представляющий собой разность между
суммой масс покоя частиц, составляющих
ядро, и массой покоя ядра.
Масса ядра измеряется в атомных
единицах массы (а.е.м.) или мегаэлектронвольтах
(МэВ). 1 а.е.м. равна
массы
атома углерода – 12 и составляет
кг
или 931,4812 МэВ (931,5
МэВ).
В таблицах обычно приводятся
массы атомов
,
которые связаны с массами ядер соотношением
,
где
–
масса электрона.
Поэтому дефект массы ядра
выражается следующим образом
|
|
Здесь
– масса атома водорода (протон + электрон);
–
масса нейтрона;
–
масса атома (протоны + электроны); с –
скорость света;
– энергия связи.
Дефект массы на 1 нуклон
рассчитывается по формуле
|
|
(14.1) |
Энергией связи нуклона
в ядре называется физическая величина,
равная той работе, которую нужно совершить
для удаления нуклона из ядра без сообщения
ему кинетической энергии.
Удельной энергией связи ядра
называется энергия связи,
приходящаяся на один нуклон. Удельная
энергия связи ядра составляет в среднем
8 МэВ/нуклон. По мере увеличения числа
нуклонов в ядре удельная энергия связи
убывает.
Критерием устойчивости
атомных ядер является
соотношение между числом протонов и
нейтронов в устойчивом ядре для данных
изобар (А=const).
Конспект урока: Радиоактивность. Закон радиоактивного распада. Причины радиоактивности. Альфа- и бета-распады. Правила смещения
Ядерная физика
Радиоактивность. Закон радиоактивного распада
План урока
- Радиоактивность
- Закон радиоактивного распада
Цели урока
- Знать, что такое радиоактивность
- Знать, что называют периодом полураспада
- Знать закон радиоактивного распада
- Уметь рассчитывать количество ядер, оставшихся к моменту времени t, в результате радиоактивного распада
Разминка
- Что такое энергия связи ядра?
- Как рассчитывается дефект масс?
- Что такое изотоп?
Радиоактивность
Не всякое атомное ядро, состоящее из протонов и нейтронов, удерживаемых ядерными силами притяжения, может существовать неограниченно долго. Таким образом в природе существует немалое количество нестабильных изотопов, которые с течением времени спонтанно превращаются в ядра других элементов с одновременным испусканием различных частиц и энергии. Как нам уже известно, подобные превращения называются радиоактивностью.
Радиоактивность
– это самопроизвольное (спонтанное) превращение атомных ядер, которое сопровождается испусканием различных частиц (например, альфа-частиц, электронов, фотонов, нейтронов, протонов и т.д.) и энергии.
Опыт большого количества наблюдений показывает, что радиоактивность – процесс вероятностный. Среднее время жизни ядер определённого изотопа, вычисленное по наблюдению за очень большим числом распадающихся ядер, не зависит от способа получения ядер этого изотопа, температуры, давления и т.п.
При исследовании явления радиоактивности было установлено, что для каждого радиоактивного вещества существует определённый промежуток времени, по истечении которого распадается половина от начального (достаточно большого) числа ядер. Этот промежуток времени называют
периодом полураспада T
.
За время, равное периоду полураспада, интенсивность радиоактивных излучений часто также уменьшается в 2 раза.
Закон радиоактивного распада
Распад большого количества любого радиоактивного изотопа подчиняется одному закону, который может быть выражен в следующей математической форме:
N=N0·2-tT.
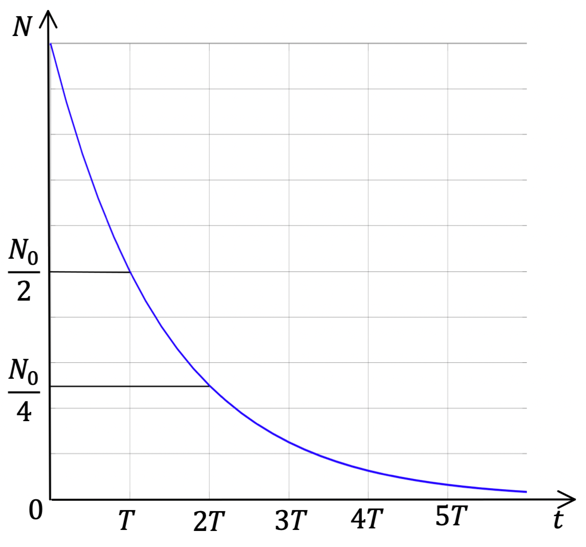
Рис. 1. Закон радиоактивного распада
Это уравнение носит название закона радиоактивного распада. В нём N0 означает начальное количество радиоактивных ядер в момент времени, с которого начинаются наблюдения (t=0). Число ядер, не испытавших распада до некоторого произвольного момента времени t, обозначено N. Символом T обозначена постоянная величина, зависящая от типа радиоактивного изотопа – период полураспада. Через промежуток времени, равный периоду полураспада (t=T), исходное количество радиоактивных ядер убывает вдвое.
На рисунке 1 по оси ординат отложено количество радиоактивных ядер в момент времени t, время отсчитывается по оси абсцисс.
Закон радиоактивного распада
N=N0·2-tT,
где N0 – начальное количество радиоактивных ядер в начальный момент времени, T – период полураспада.
Пример 1
Сколько процентов ядер радиоактивного иода I 53131 с периодом полураспада T=8 суток останется через 16 суток?
Решение
1. Обозначим начальное количество ядер величиной N0.
2. Воспользуемся законом радиоактивного распада:
N=N0·2-tT;
N=N0·2-168=N04=0,25·N0.
Ответ: 25%.
Упражнение 1
1. Активность радиоактивного элемента уменьшилась в 4 раза за 8 суток. Найти период полураспада.
2. Период полураспада изотопа стронция S 3881r равен 30 мин. В некоторый момент времени имелось 10 г этого изотопа. Определите массу этого изотопа через 3 ч.
Контрольные вопросы
1. Какие ядра называются нестабильными?
2. Что называют радиоактивностью?
3. Что такое период полураспада?
4. Сформулируйте закон радиоактивного распада.
5. Зависит ли период полураспада от способа получения ядер данного изотопа и внешних условий?
Ответы
Упражнение 1
1. 4 сут.
2. ≈ 0,16 г.
Предыдущий урок
Ядерные реакции. Ядерная энергетика
Ядерная физика
Следующий урок
Методы регистрации ионизирующих радиоактивных ядерных излучений. Биологическое действие радиоактивных излучений. Дозиметрия
Ядерная физика