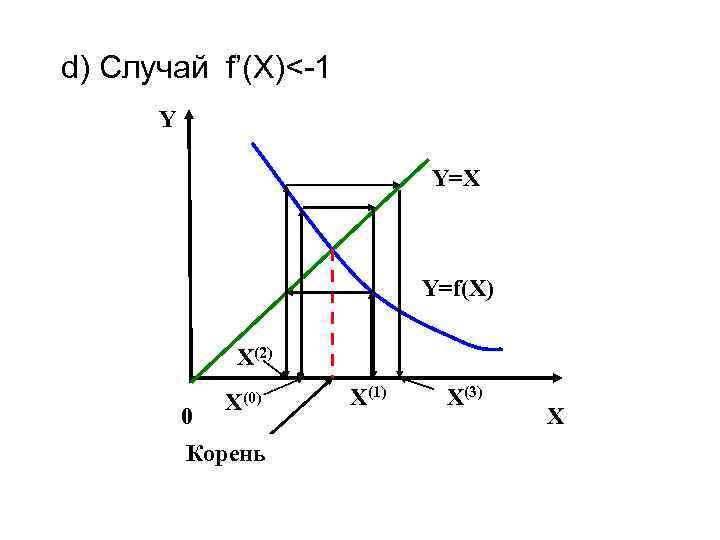
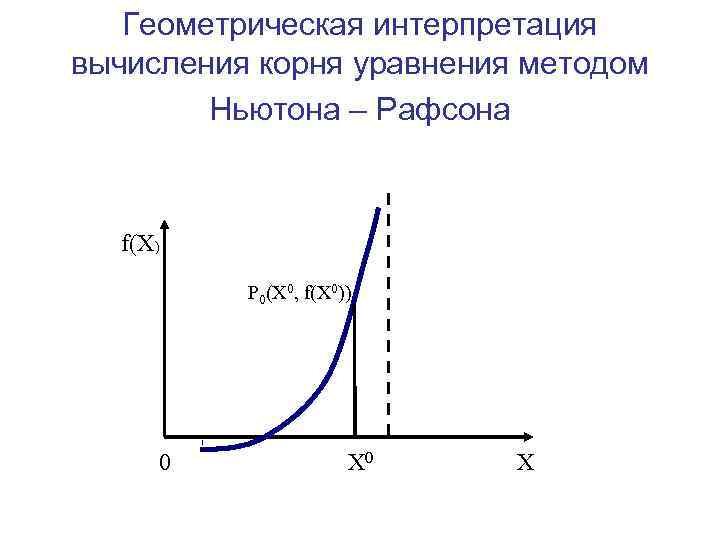
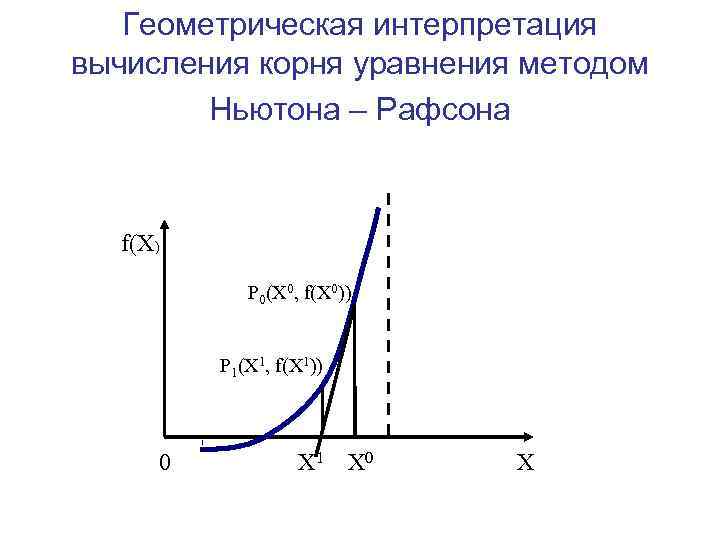
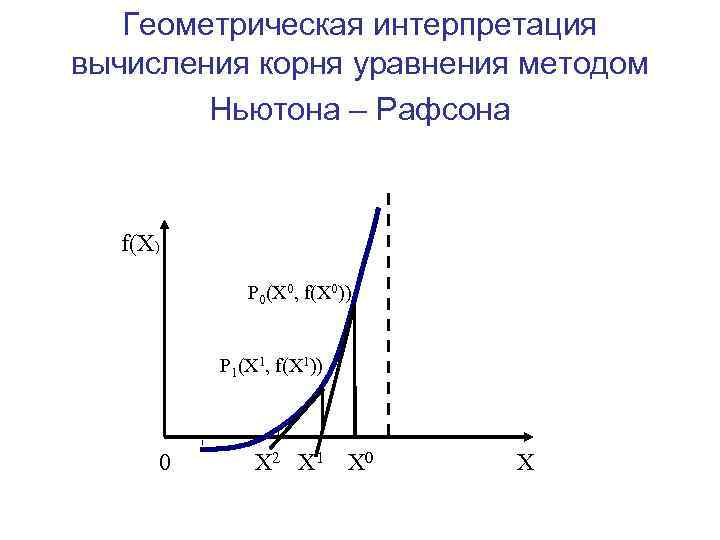
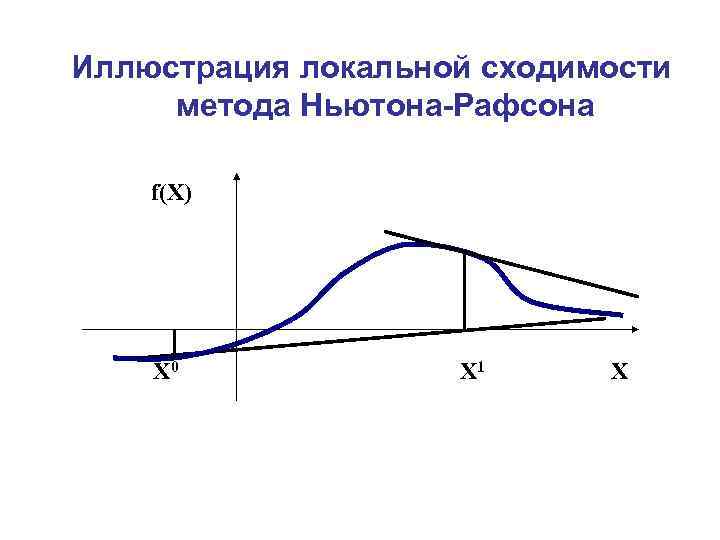
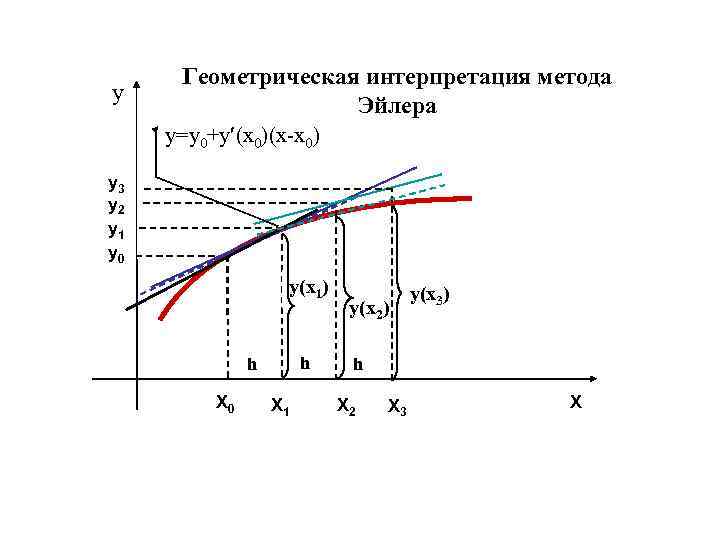
Численные методы: решение нелинейных уравнений
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.
В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.
В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.
В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.
Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.
Нам нужно найти такое значение при котором такие называются корнями функции
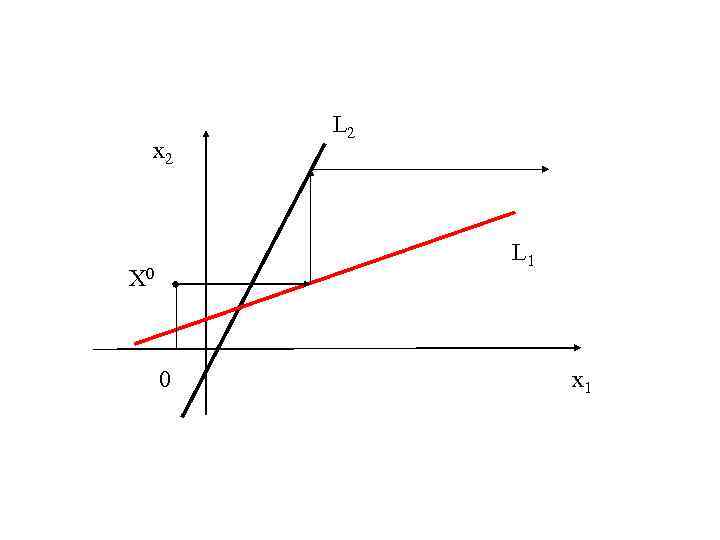
Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.
Метод деления пополам
Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.
Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем.
Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .
Поделим отрезок пополам и введем среднюю точку .
Тогда либо , либо .
Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.
Заметьте, описанный алгоритм применим для любой непрерывной функции.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Метод Ньютона: теоретические основы
Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .
Уравнение касательной к функции в точке имеет вид:
В уравнении касательной положим и .
Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2.
Таким образом, сходимость метода касательных Ньютона очень быстрая.
Запомните этот замечательный факт!
Без всяких изменений метод обобщается на комплексный случай.
Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.
Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).
Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Визуализация метода Ньютона
Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:
1) функция y= f(x) определена и непрерывна при ;
2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка.
Рассмотрим метод Ньютона на конкретном примере.
Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f ”(x) = 2 > 0.
Уравнение касательной в общем виде имеет представление:
В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.
Точка пересечения касательной и оси Ox: x1 =
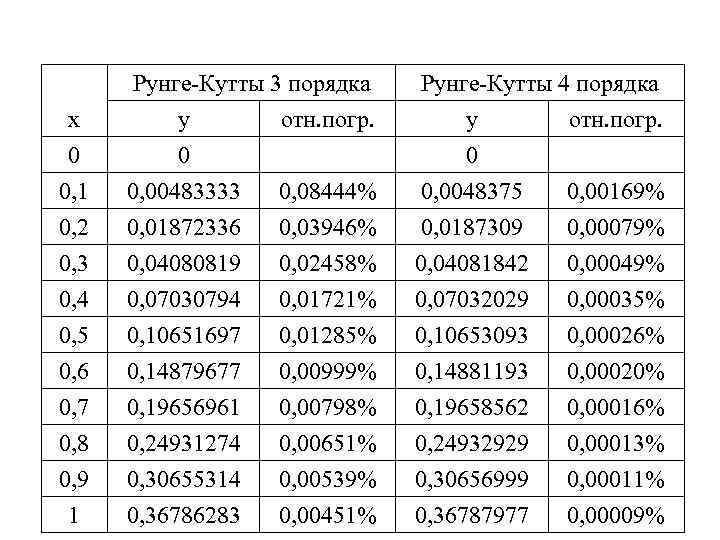
Рисунок 2. Результат первой итерации
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2.
Точка пересечения касательной и оси Ox: x2 = .
Рисунок 3. Вторая итерация метода Ньютона
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее.
В3 = ()
Рисунок 4. Третий шаг метода касательных
Первое приближение корня определяется по формуле:
= 1.5.
Второе приближение корня определяется по формуле:
=
Третье приближение корня определяется по формуле:
Таким образом, i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e – до выполнения неравенства |xi–xi-1|
using namespace std;
float f(double x) //возвращает значение функции f(x) = x^2-2
float df(float x) //возвращает значение производной
float d2f(float x) // значение второй производной
int _tmain(int argc, _TCHAR* argv[])
int exit = 0, i=0;//переменные для выхода и цикла
double x0,xn;// вычисляемые приближения для корня
double a, b, eps;// границы отрезка и необходимая точность
cin>>a>>b; // вводим границы отрезка, на котором будем искать корень
cin>>eps; // вводим нужную точность вычислений
if (a > b) // если пользователь перепутал границы отрезка, меняем их местами
if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня
cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?
xn = x0-f(x0)/df(x0); // считаем первое приближение
cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять
xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона
> while (exit!=1); // пока пользователь не ввел exit = 1
Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.
Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.
Рис. 4. Решение ошибки компиляции проекта
Мы будем искать корни у функции f(x) = x2-2.
Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.
У нас появилось окно приложения:
Рис. 5. Ввод входных данных
Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.
Рис. 6. Ошибка «На этом отрезке корней нет!»
Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».
Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.
Рис. 7. Вычисление корня с необходимой точностью
Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.
Чтобы выйти из приложения, введем «Exit?» => 1.
Метод секущих
Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:
/
Итерационный процесс имеет вид:
где .
Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .
Эта замечательная величина называется золотым сечением:
Убедимся в этом, считая для удобства, что .
Таким образом, с точностью до бесконечно малых более высокого порядка
Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .
После подстановки имеем: и
Для сходимости необходимо, чтобы было положительным, поэтому .
Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.
Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.
Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.
Такая процедура определения момента окончания итераций называется приемом Гарвика.
Метод парабол
Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .
Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .
В форме Ньютона она имеет вид:
Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .
Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.
Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.
Этот метод очень удобен для поиска корней многочленов высокой степени.
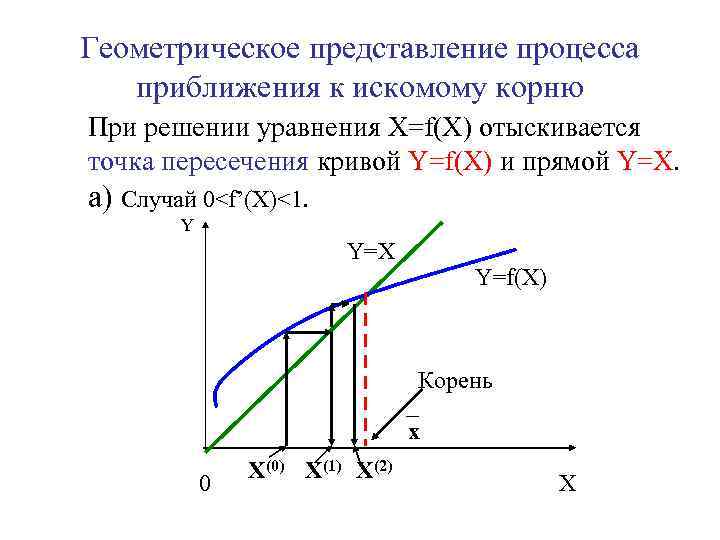
Метод простых итераций
Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.
Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).
По теореме Банаха существует и единственна неподвижная точка
Она может быть найдена как предел простой итерационной процедуры
где начальное приближение — произвольная точка промежутка .
Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа
Таким образом, если производная меньше единицы, то является сжатием.
Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.
Рассмотрим уравнение: .
Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .
Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .
Эти итерации сходятся к неподвижной точке для любого начального приближения :
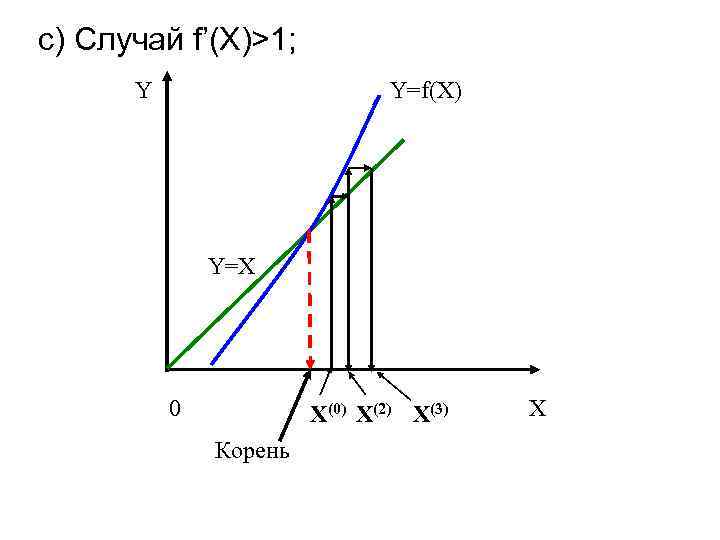
Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.
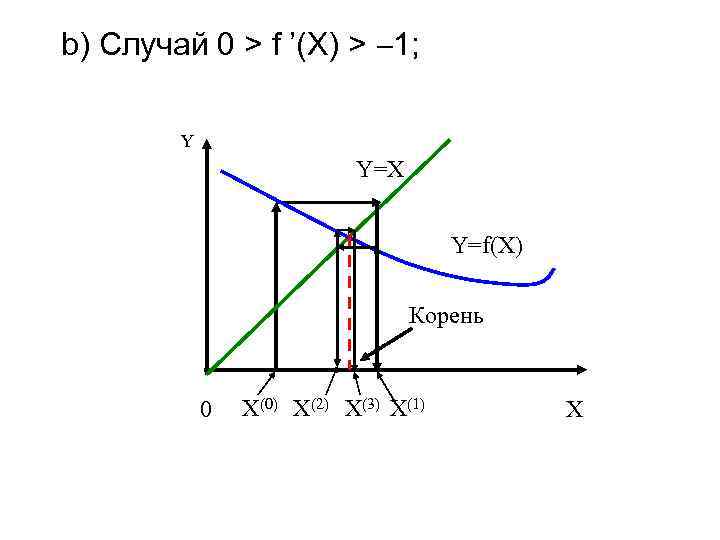
Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.
т.е. такой итерационный процесс всегда сходится.
Метод Ньютона представляет собой частный случай метода простых итераций.
Здесь нетрудно убедиться, что при существует окрестность корня, в которой .
то если корень кратности , то в его окрестности и, следовательно,.
Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).
Поскольку , то
Таким образом, сходимость метода Ньютона очень быстрая.
Нахождение всех корней уравнения
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.
Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.
Для поиска других корней используется метод удаления корней.
Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.
Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.
Повторяя указанную процедуру, можно найти все корни с учетом кратности.
Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.
Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.
Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.
5.1. Приближённое решение систем нелинейных уравнений. Метод Ньютона
Рассмотрим нелинейную систему уравнений
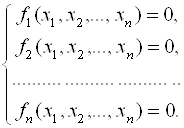
С действительными левыми частями. Систему (5.1) можно представить в матричном виде

Здесь приняты следующие обозначения:


Для решения системы (5.2) воспользуемся методом последовательных приближений. Предположим, что найдено Р-ое приближение Xp = (X1(P), X2(P) , . Xn(P)) одного из изолированных корней X = (X1, X2, X3, . Xn) векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

Где 
Подставив выражение (5.3) в (5.2), получим

Предположим, что функция F(X) – непрерывно дифференцируема в некоторой выпуклой области, содержащей X и X(P). Тогда левую часть уравнения (5.4) разложим в ряд Тейлора по степеням малого вектора ε(P), ограничиваясь линейными членами:

Или в развернутом виде:

Из анализа формул (5.5) и (5.6) следует, что под производной F¢(X) следует понимать матрицу Якоби системы функций F1 , F2, . Fn, относительно переменных X1, X2, X3, . Xn, то есть:

Выражение (5.7) в краткой записи можно представить:

Выражение (5.6) представляет собой линейную систему относительно поправок 

Отсюда, предполагая, что матрица W(X(P)) – неособенная, получим:

Теперь, подставив выражение (5.10) в формулу (5.3), окончательно получим:

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения X(0) можно взять приближенное (грубое) значение искомого корня.
Пример 5.1. Рассмотрим применение метода Ньютона на примере системы двух нелинейных уравнений

Прежде чем разбирать конкретные шаги по решению системы (5.12), распишем в общем виде якобиан для системы из двух уравнений
Здесь A, B, C, D – функционалы от переменных X1, x2. Нас фактически интересует W-1. Пусть матрица W– неособенная, тогда обратная матрица вычисляется
Теперь вернемся к системе (5.12). Графическое решение этой системы дает две точки пересечения: М1 (1.4; -1.5) и М2 (3.4; 2.2). Зададим начальное приближение:
Как найти начальное приближение нелинейного уравнения
Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |xn – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при и нахождение участков возрастания и убывания функции.
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
Найдем производную f / (x)=3x 2 -12x+3.
Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;
X1== 0.268;
X2== 3.732;
Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x1)= 3x1 2 -12x1+3=11.39; на интервале – убывает до f(x2)= 3x2 2 -12x2+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.
[spoiler title=”источники:”]
http://matica.org.ua/metodichki-i-knigi-po-matematike/chislennye-metody-iu-ia-katcman/5-1-priblizhennoe-reshenie-sistem-nelineinykh-uravnenii-metod-niutona
http://nickolay.info/study/methods/01.html
[/spoiler]
У этого термина существуют и другие значения, см. Метод (значения).
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить ноль первой производной либо градиента в случае многомерного пространства.
Описание метода[править | править код]
Обоснование[править | править код]
Чтобы численно решить уравнение 


Для наилучшей сходимости метода в точке очередного приближения 


В предположении, что точка приближения «достаточно близка» к корню 


С учётом этого функция 
При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение.
В этом случае алгоритм нахождения численного решения уравнения 
По теореме Банаха последовательность приближений стремится к корню уравнения 
Иллюстрация метода Ньютона (синим изображена функция 



Геометрическая интерпретация[править | править код]
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть 1) вещественнозначная функция 

2) существует искомая точка 

3) существуют 

для ![{displaystyle xin (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260bb1d0fcbae53c2e7a917c0ada3962ebf17bdd)
и
для 
4) точка 

Тогда формула итеративного приближения 
может быть выведена из геометрического смысла касательной следующим образом:
где 
к графику
в точке 
Следовательно (в уравнении касательной прямой полагаем 

Если 

Если 



до тех пор, пока точка «не вернётся» в область поиска

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения 
2) Случаи граничного (в точке 


3) С геометрической точки зрения равенство
означает, что касательная прямая к графику
в точке

параллельна оси
и при
не пересекается с ней в конечной части.
4) Чем больше константа 

тем для
пересечение касательной к графику 


то есть тем ближе значение 

Итерационный процесс начинается с некоторого начального приближения

причём между
и искомой точкой
не должно быть других нулей функции

то есть «чем ближе
к искомому корню 
тем лучше». Если предположения о нахождении 
Для предварительно заданных 
итерационный процесс завершается если


В частности, для матрицы дисплея 

исходя из масштаба отображения графика 
то есть если 



Алгоритм[править | править код]
- Задается начальное приближение
.
- Пока не выполнено условие остановки, в качестве которого можно взять
или
(то есть погрешность в нужных пределах), вычисляют новое приближение:
.
Пример[править | править код]
Иллюстрация применения метода Ньютона к функции  с начальным приближением в точке с начальным приближением в точке  . .
|
|
|---|---|
|
График последовательных приближений. |
График сходимости. |
| Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум. |
Рассмотрим задачу о нахождении положительных 








Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
Условия применения[править | править код]
Иллюстрация расхождения метода Ньютона, применённого к функции 

Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры[править | править код]
-
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём ноль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст ноль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
График производной функции 

-
- Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.
Рассмотрим функцию:
Тогда 

В окрестности корня производная меняет знак при приближении 


Таким образом 

-
- Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.
Рассмотрим пример:
Тогда 


На очередном шаге имеем 
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и 
-
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда 

Ограничения[править | править код]
Пусть задано уравнение 

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы 
на
, то есть
сут и не равна нулю;
на
, то есть
ограничена;
на
, и
;
Причём длина рассматриваемого отрезка 
- на
существует корень
уравнения
;
- если
, то итерационная последовательность сходится к этому корню:
;
- погрешность может быть оценена по формуле
.
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию 
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная
равномерно отделена от нуля;
- её вторая производная
должна быть равномерно ограничена.
Историческая справка[править | править код]
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения 

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений 
В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
Обобщения и модификации[править | править код]
Иллюстрация последовательных приближений метода одной касательной, применённого к функции 

Метод секущих[править | править код]
Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

Таким образом, основная формула имеет вид
Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618…
Замечания. 1) Для начала итерационного процесса требуются два различных значения


2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только
(и в ходе вычислений — временно 

для метода секущих требуется сохранение




3) Применяется, если вычисление 
(например, требует большого количества машинных ресурсов: времени и/или памяти).
Метод одной касательной[править | править код]
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения 
При таком выборе 

и если отрезок, на котором предполагается наличие корня 






Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.
Метод Ньютона-Фурье[править | править код]
Метод Ньютона-Фурье – это расширение метода Ньютона, выведенное Жозефом Фурье для получения оценок на абсолютную ошибку аппроксимации корня, в то же время обеспечивая квадратичную сходимость с обеих сторон.
Предположим, что f(x) дважды непрерывно дифференцируема на отрезке [a, b] и что f имеет корень на этом интервале. Дополнительно положим, что f′(x), f″(x) ≠ 0 на этом отрезке (например, это верно, если f(a) < 0, f(b) > 0, и f″(x) > 0 на этом отрезке). Это гарантирует наличие единственного корня на этом отрезке, обозначим его α. Эти рассуждения относятся к вогнутой вверх функции. Если она вогнута вниз, то заменим f(x) на −f(x), поскольку они имеют одни и те же корни.
Пусть x0 = b будет правым концом отрезка, на котором мы ищем корень, а z0 = a – левым концом того же отрезка. Если xn найдено, определим
которое выражает обычный метод Ньютона, как описано выше. Затем определим
где знаменатель равен f′(xn), а не f′(zn). Итерации xn будут строго убывающими к корню, а итерации zn – строго возрастающими к корню. Также выполняется следующее соотношение:
,
таким образом, расстояние между xn и zn уменьшается квадратичным образом.
Многомерный случай[править | править код]
Обобщим полученный результат на многомерный случай.
Пусть необходимо найти решение системы:
Выбирая некоторое начальное значение ![{displaystyle {vec {x}}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ae4aca0e44306357efc8a4653f758b4d984a42f)
![{displaystyle {vec {x}}^{[j+1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/731295798153991209f20aaf78929acff1a3a6fa)
где ![{displaystyle {vec {x}}^{[j]}=(x_{1}^{[j]},;x_{2}^{[j]},;ldots ,;x_{n}^{[j]}),quad j=0,;1,;2,;ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/84da9bf66616a56d35d1971525796f1cd57fab79)
Применительно к задачам оптимизации[править | править код]
Пусть необходимо найти минимум функции многих переменных 

где 

В более удобном итеративном виде это выражение выглядит так:
В случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
Метод Ньютона — Рафсона[править | править код]
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где
Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением ![{displaystyle H(f({vec {x}}^{[0]}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deb9b2bfeb49d385250170d0ec25c37a5772da8b)

Применительно к задачам о наименьших квадратах[править | править код]
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где 



Тогда очередной шаг 
Метод Гаусса — Ньютона[править | править код]
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое 



Таким образом, когда норма 



Обобщение на комплексную плоскость[править | править код]
Бассейны Ньютона для полинома пятой степени 
До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексной переменной. При этом процедура остаётся неизменной:
Особый интерес представляет выбор начального приближения 
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Реализация[править | править код]
Scala[править | править код]
object NewtonMethod { val accuracy = 1e-6 @tailrec def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = { val x1 = x0 - f(x0) / dfdx(x0) if (abs(x1 - x0) < e) x1 else method(x1, f, dfdx, e) } def g(C: Double) = (x: Double) => x*x - C def dgdx(x: Double) = 2*x def sqrt(x: Double) = x match { case 0 => 0 case x if (x < 0) => Double.NaN case x if (x > 0) => method(x/2, g(x), dgdx, accuracy) } }
Python[править | править код]
from math import sin, cos from typing import Callable import unittest def newton(f: Callable[[float], float], f_prime: Callable[[float], float], x0: float, eps: float=1e-7, kmax: int=1e3) -> float: """ solves f(x) = 0 by Newton's method with precision eps :param f: f :param f_prime: f' :param x0: starting point :param eps: precision wanted :return: root of f(x) = 0 """ x, x_prev, i = x0, x0 + 2 * eps, 0 while abs(x - x_prev) >= eps and i < kmax: x, x_prev, i = x - f(x) / f_prime(x), x, i + 1 return x class TestNewton(unittest.TestCase): def test_0(self): def f(x: float) -> float: return x**2 - 20 * sin(x) def f_prime(x: float) -> float: return 2 * x - 20 * cos(x) x0, x_star = 2, 2.7529466338187049383 self.assertAlmostEqual(newton(f, f_prime, x0), x_star) if __name__ == '__main__': unittest.main()
PHP[править | править код]
<?php // PHP 5.4 function newtons_method( $a = -1, $b = 1, $f = function($x) { return pow($x, 4) - 1; }, $derivative_f = function($x) { return 4 * pow($x, 3); }, $eps = 1E-3) { $xa = $a; $xb = $b; $iteration = 0; while (abs($xb) > $eps) { $p1 = $f($xa); $q1 = $derivative_f($xa); $xa -= $p1 / $q1; $xb = $p1; ++$iteration; } return $xa; }
Octave[править | править код]
function res = nt() eps = 1e-7; x0_1 = [-0.5,0.5]; max_iter = 500; xopt = new(@resh, eps, max_iter); xopt endfunction function a = new(f, eps, max_iter) x=-1; p0=1; i=0; while (abs(p0)>=eps) [p1,q1]=f(x); x=x-p1/q1; p0=p1; i=i+1; end i a=x; endfunction function[p,q]= resh(x) % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1; p=-25*x.^4+16*x.^3-36*x.^2+22*x-2; q=-100*x.^3+48*x.^2-72*x+22; endfunction
Delphi[править | править код]
// вычисляемая функция function fx(x: Double): Double; begin Result := x * x - 17; end; // производная функция от f(x) function dfx(x: Double): Double; begin Result := 2 * x; end; function solve(fx, dfx: TFunc<Double, Double>; x0: Double): Double; const eps = 0.000001; var x1: Double; begin x1 := x0 - fx(x0) / dfx(x0); // первое приближение while (Abs(x1-x0) > eps) do begin // пока не достигнута точность 0.000001 x0 := x1; x1 := x1 - fx(x1) / dfx(x1); // последующие приближения end; Result := x1; end; // Вызов solve(fx, dfx,4));
C++[править | править код]
#include <stdio.h> #include <math.h> #define eps 0.000001 double fx(double x) { return x * x - 17;} // вычисляемая функция double dfx(double x) { return 2 * x;} // производная функции typedef double(*function)(double x); // задание типа function double solve(function fx, function dfx, double x0) { double x1 = x0 - fx(x0) / dfx(x0); // первое приближение while (fabs(x1 - x0) > eps) { // пока не достигнута точность 0.000001 x0 = x1; x1 = x0 - fx(x0) / dfx(x0); // последующие приближения } return x1; } int main () { printf("%fn", solve(fx, dfx, 4)); // вывод на экран return 0; }
C[править | править код]
typedef double (*function)(double x); double TangentsMethod(function f, function df, double xn, double eps) { double x1 = xn - f(xn)/df(xn); double x0 = xn; while(abs(x0-x1) > eps) { x0 = x1; x1 = x1 - f(x1)/df(x1); } return x1; } //Выбор начального приближения xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A; double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная //Пример вызова функции double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1)
Haskell[править | править код]
import Data.List ( iterate' ) main :: IO () main = print $ solve ( x -> x * x - 17) ( * 2) 4 -- Функция solve универсальна для всех вещественных типов значения которых можно сравнивать. solve = esolve 0.000001 esolve epsilon func deriv x0 = fst . head $ dropWhile pred pairs where pred (xn, xn1) = (abs $ xn - xn1) > epsilon -- Функция pred определяет достигнута ли необходимая точность. next xn = xn - func xn / deriv xn -- Функция next вычисляет новое приближение. iters = iterate' next x0 -- Бесконечный список итераций. pairs = zip iters (tail iters) -- Бесконечный список пар итераций вида: [(x0, x1), (x1, x2) ..].
Литература[править | править код]
- Акулич И. Л. Математическое программирование в примерах и задачах : Учеб. пособие для студентов эконом. спец. вузов. — М. : Высшая школа, 1986. — 319 с. : ил. — ББК 22.1 А44. — УДК 517.8(G).
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров : Учеб. пособие. — М. : Высшая школа, 1994. — 544 с. : ил. — ББК 32.97 А62. — УДК 683.1(G). — ISBN 5-06-000625-5.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М. : Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М. : Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М. : Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М. : Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М. : Наука, 1970. — С. 575—576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М. : МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
См. также[править | править код]
- Метод простой итерации
- Двоичный поиск
- Метод дихотомии
- Метод секущих
- Метод Мюллера
- Метод хорд
- Метод бисекции
- Фрактал
- Численное решение уравнений
- Целочисленный квадратный корень
- Быстрый обратный квадратный корень
Ссылки[править | править код]
- «Бассейны Ньютона» на сайте fractalworld.xaoc.ru
- «Исаак Ньютон» на сайте www.scottish-wetlands.org
- «Математические работы Канторовича» на сайте Института математики СО РАН
- Hazewinkel, Michiel, ed. (2001), Newton method, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W. Newton’s Method (англ.) на сайте Wolfram MathWorld.
- Newton’s method, Citizendium.
- Mathews, J., The Accelerated and Modified Newton Methods, Course notes.
- Wu, X., Roots of Equations, Course notes.
Пусть
нам известно начальное приближение к
корню
(вопрос выбора начального приближение
будет подробно рассмотрен ниже). Проведем
в этой точке касательную к кривой
(рис. 2.8). Эта касательная пересечет ось
абсцисс в точке
,
которую будем рассматривать в качестве
следующего приближения. Значение
легко найти из рисунка:

выражая
отсюда
,
получим

Аналогично
могут быть найдены и следующие приближения.
Формула для k+1-го
приближения имеет вид

(2.15)
Из
формулы (2.15) вытекает условие применимости
метода: функция
должна быть дифференцируемой и
в окрестности корня не должна менять
знак.
Для
окончания итерационного процесса могут
быть использованы условия (2.12) или
(2.14).
ØЗамечание 1. В
методе Ньютона, в отличие от предыдущих
методов, не обязательно задавать отрезок
,
содержащий корень уравнения, а достаточно
найти некоторое начальное приближение
корня
.<
ØЗамечание 2.
Формула метода Ньютона может быть
получена и из других соображений.
Зададимся некоторым начальным приближением
корня
.
Заменим функциюf(x)
в окрестности точки
отрезком ряда Тейлора:
,
и
вместо нелинейного уравнения
решим линеаризованное уравнение
рассматривая
его решение как следующее (первое)
приближение к искомому значению корня.
Решение этого уравнение очевидно:
Повторяя
это процесс приходим к формуле Ньютона
(2.15).<
Сходимость
метода Ньютона. Выясним основные
условия сходимости последовательности
значений
,
вычисляемых по формуле (2.15), к корню
уравнения (2.1). Предполагая, что
дважды непрерывно дифференцируема,
разложим
в ряд Тейлора в окрестностиk-го
приближения

Разделив
последнее соотношение на
и перенеся часть слагаемых из левой
части в правую, получим:
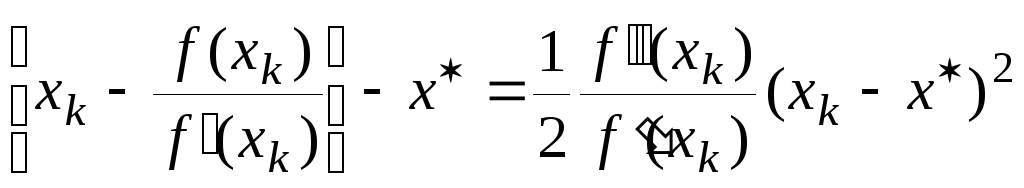
Учитывая,
что выражение в квадратных скобках
согласно (2.15) равно
,
переписываем это соотношение в виде

Отсюда

(2.16)
Из
(2.16) следует оценка

(2.17)
где
,
.
Очевидно,
что ошибка убывает, если

(2.18)
Полученное
условие означает, что сходимость зависит
от выбора начального приближения.
Оценка
(2.17) характеризует скорость убывания
погрешности для метода Ньютона: на
каждом шаге погрешность пропорциональна
квадрату погрешности на предыдущем
шаге. Следовательно, метод Ньютона
обладает квадратичной сходимостью.
В
начального приближения в методе Ньютона.Как следует из условия (2.18) сходимость
итерационной последовательности,
получаемой в методе Ньютона, зависит
от выбора начального приближения
.
Это можно заметить и из геометрической
интерпретации метода. Так, если в качестве
начального приближения взять точку
(рис. 2.9), то на сходимость итерационного
процесса рассчитывать не приходится.
Если
же в качестве начального приближения
выбрать точку
,
то получим сходящуюся последовательность.
В
общем случае, если задан отрезок
,
содержащий корень, и известно, что
функция
монотонна на этом отрезке, то в качестве
начального приближения
можно выбрать ту границу отрезка
,
где совпадают знаки функции
и второй производной
.
Такой выбор начального приближения
гарантирует сходимость метода Ньютона
при условии монотонности функции на
отрезке локализации корня.
Соседние файлы в папке Курсовая работа_ф_3
- #
- #
- #
02.04.2015207.87 Кб12Ведомость КР _11-12_фак_3.xls
- #
02.04.201525.09 Кб14График выполнения КР.xls
- #
- #
Как найти начальное приближение корня уравнения
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 — e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
- Для выражения с несколькими корнями, например x 2 — 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) — g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
- Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как найти начальное приближение корня уравнения
Глава 4. Решение уравнений
4.1 Функция root
Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.
Обращение к функции осуществляется следующим образом:
root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).
Уравнение
начальное приближение
решение
или 

другие корни 



Задан интервал поиска корней


Рис. 4. 1 Использование функции root
Функция f ( x ) и аргумент x должны быть скалярами, то есть результат вычисления функции – число, а не вектор или матрица. Функция root использует метод секущих. Корень уравнения – ближайшее к начальному приближению значение x , обращающее функцию f ( x ) в нуль. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:
root ( f ( x ), x , а, b ),
где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.

Если уравнение не имеет действительных корней, то есть на графике функция f ( x ) нигде не равна нулю, то для вывода комплексных корней надо ввести начальное приближение в комплексной форме (рис. 4.2) .
Если функция имеет мнимый корень,
то начальное приближение задается комплексным числом










Рис. 4. 2 Решение уравнения с комплексными корнями

Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:
где x 1, x 2 , , xn – корни уравнения. Начальное приближение можно задать только для первого корня. В качестве функции f ( x ) нужно взять

где 









Рис. 4. 3 Определение трех корней уравнения
Если функция f ( x ) имеет малый наклон вблизи искомого корня, то функция root ( f ( x ), x ) может сходиться к значению, довольно далеко отстоящему от корня. В таком случае для уточнения корня необходимо уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL . Для этого:
1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);
2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).
Чем меньше константа TOL , тем ближе к нулю будет значение функции при найденном корне уравнения, но тем больше будет время вычисления корня.
Для повышения точности расчета корня можно заменить f ( x ) на

Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:
1) выделить график, щелкнув левой кнопкой мыши внутри графика;
2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);
3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;
4) в открытом окне X – Y Zoom (Масштаб по осям X – Y ) нажать кнопку Zoom .
Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:
1) Выделите график, щелкнув левой кнопкой мыши внутри графика,
2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),
3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,
4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).
5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер
6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.


Рис. 4. 4 Определение корня уравнения по графику
В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.

Численные методы: решение нелинейных уравнений
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.
В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.
В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения 

В простейшем случае у нас имеется функция 
Каждому значению x из этого отрезка мы можем сопоставить число 
Нам нужно найти такое значение 


Визуально нам нужно определить точку пересечения графика функции 
Метод деления пополам
Простейшим методом нахождения корней уравнения 
Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем.
Предположим, мы нашли две точки 




Поделим отрезок 

Тогда либо 

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.
Заметьте, описанный алгоритм применим для любой непрерывной функции.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Метод Ньютона: теоретические основы
Классический метод Ньютона или касательных заключается в том, что если 




Уравнение касательной к функции 

В уравнении касательной положим 

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2.
Таким образом, сходимость метода касательных Ньютона очень быстрая.
Запомните этот замечательный факт!
Без всяких изменений метод обобщается на комплексный случай.
Если корень 
Упражнение 1. Найти с помощью метода касательных решение уравнения 
Упражнение 2. Найти с помощью метода касательных решение уравнения 
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие 
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Визуализация метода Ньютона
Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень 
1) функция y= f(x) определена и непрерывна при 
2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка.
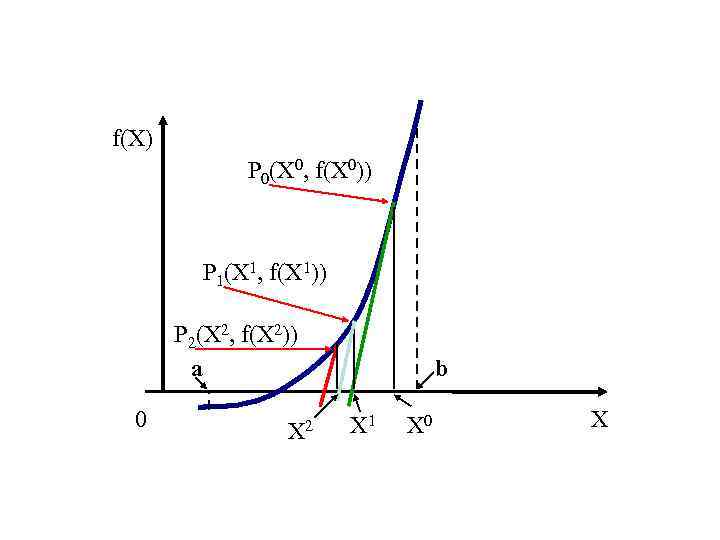
Рассмотрим метод Ньютона на конкретном примере.
Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.
Уравнение касательной в общем виде имеет представление:
В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.
Точка пересечения касательной и оси Ox: x1 =
Рисунок 2. Результат первой итерации
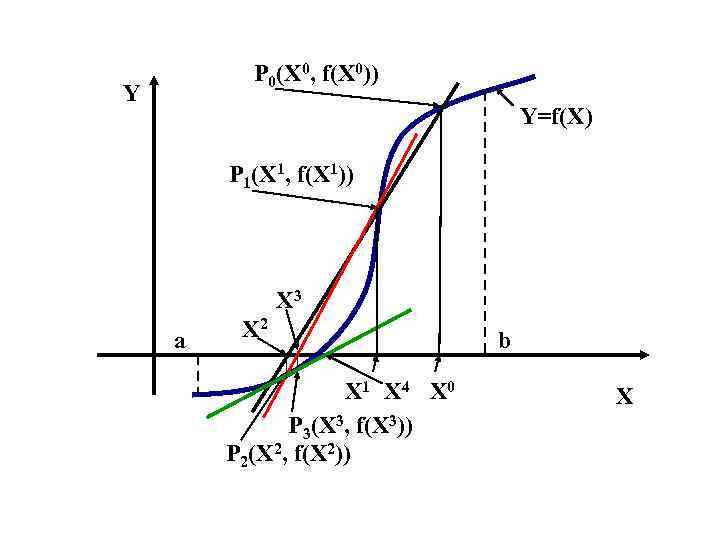
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2.
Точка пересечения касательной и оси Ox: x2 = 
Рисунок 3. Вторая итерация метода Ньютона
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее.
В3 = (
Рисунок 4. Третий шаг метода касательных
Первое приближение корня определяется по формуле:

Второе приближение корня определяется по формуле:

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|
using namespace std;
float f(double x) //возвращает значение функции f(x) = x^2-2
float df(float x) //возвращает значение производной
float d2f(float x) // значение второй производной
int _tmain(int argc, _TCHAR* argv[])
int exit = 0, i=0;//переменные для выхода и цикла
double x0,xn;// вычисляемые приближения для корня
double a, b, eps;// границы отрезка и необходимая точность
cin>>a>>b; // вводим границы отрезка, на котором будем искать корень
cin>>eps; // вводим нужную точность вычислений
if (a > b) // если пользователь перепутал границы отрезка, меняем их местами
if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня
cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?
xn = x0-f(x0)/df(x0); // считаем первое приближение
cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять
xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона
> while (exit!=1); // пока пользователь не ввел exit = 1
Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.
Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.
Рис. 4. Решение ошибки компиляции проекта
Мы будем искать корни у функции f(x) = x2-2.
Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.
У нас появилось окно приложения:
Рис. 5. Ввод входных данных
Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.
Рис. 6. Ошибка «На этом отрезке корней нет!»
Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».
Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.
Рис. 7. Вычисление корня с необходимой точностью
Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.
Чтобы выйти из приложения, введем «Exit?» => 1.
Метод секущих
Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

Итерационный процесс имеет вид:
где 
Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня 
Эта замечательная величина называется золотым сечением:
Убедимся в этом, считая для удобства, что 
Таким образом, с точностью до бесконечно малых более высокого порядка
Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде 
После подстановки имеем: 
Для сходимости необходимо, чтобы 

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.
Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое 

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.
Такая процедура определения момента окончания итераций называется приемом Гарвика.
Метод парабол
Рассмотрим трехшаговый метод, в котором приближение 



Для этого заменим, аналогично методу секущих, функцию 



В форме Ньютона она имеет вид:
Точка 

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.
Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если 

Этот метод очень удобен для поиска корней многочленов высокой степени.
Метод простых итераций
Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: 

Пусть 




По теореме Банаха существует и единственна неподвижная точка
Она может быть найдена как предел простой итерационной процедуры
где начальное приближение 

Если функция 

Таким образом, если производная меньше единицы, то 
Условие 



Рассмотрим уравнение: 
Если в качестве 




Однако можно в качестве 


Эти итерации сходятся к неподвижной точке для любого начального приближения 
Действительно, в первом случае 




Рассмотрим 
т.е. такой итерационный процесс всегда сходится.
Метод Ньютона представляет собой частный случай метода простых итераций.
Здесь 


то если 



Если 
Поскольку 
Таким образом, сходимость метода Ньютона очень быстрая.
Нахождение всех корней уравнения
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.
Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.
Для поиска других корней используется метод удаления корней.
Пусть 







Применяя тот или иной метод нахождения корней к функции 



Повторяя указанную процедуру, можно найти все корни 
Заметим, что когда мы производим деление на тот или иной корень 


Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции 
Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.
источники:
http://www.math.mrsu.ru/text/courses/mcad/4.1.htm
http://statistica.ru/branches-maths/chislennye-metody-resheniya-uravneniy/
Приближение функций
Пример. Получить приближение функции f(x) для аргумента x=1, 5 методом Лагранжа. x y Х 0 Y 0 0 0 Х 1 Y 1 1 1 Х 2 Y 2 2 4 Х 3 Y 3 3 9
x y Х 0 Y 0 0 0 Х 1 Y 1 1 1 Х 2 Y 2 2 4 Х 3 Y 3 3 9
Пример. Необходимо оценить погрешность приближения f(x)= x в точке x=116 на отрезке [a, b], где a=100, b=144 с помощью интерполяционного многочлена Лагранжа L 2(X), построенного с узлами X 0=100, X 1=121, X 2=144.
Решение. Так как n=2, необходимо найти максимальное значения производной 3 го порядка функции f(x)=x½. Производные заданной функции до третьего порядка включительно: Функция f (X) на отрезке [100, 144] принимает максимальное значение в точке Х=100:
На основании оценки
В силу оценки :
Геометрическая интерпретация приближения функции с использованием аппроксимирующего многочлена y Результаты измерений yn y 0 Х 0 Х 1 Х 2 Хn Х
Геометрическая интерпретация приближения функции с использованием аппроксимирующего многочлена f(Х) –истинное поведение функции y yn y 0 Х 0 Х 1 Х 2 Хn Х
Геометрическая интерпретация приближения функции с использованием интерполирующего многочлена y φ(Х) – интерполирующая функция f(Х) – истинное поведение функции yn y 0 Х 0 Х 1 Х 2 Хn Х
Геометрическая интерпретация приближения функции с использованием аппроксимирующего многочлена f(Х) – истинное поведение функции y yn Рm(Х) – аппроксимирующий многочлен y 0 Х 0 Х 1 Х 2 Хn Х
Численное интегрирование
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников Y fn fn-1 А 1 f 0 А 0 0 x x 0=a x 1 x 2 xn=b
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников y fn Аn А 1 f 0 А 2 А 0 0 x x 0=a x 1 x 2 xn=b
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников Аn y fn-1 А 1 f 0 А 2 А 0 0 x x 0=a x 1 x 2 xn=b
Геометрическая интерпретация решения задачи численного интегрирования методом левых прямоугольников Аn y fn-1 А 1 f 0 А 2 А 0 0 x x 0=a x 1 x 2 xn=b , где (6. 4)
Принимаемые обозначения fi=f(хi) значение подынтегральной функции в узле интегрирования, хi-½ = середины частичных отрезков [хi – хi-1], fi-½ = f(хi-½) значение функции для середины частичного отрезка [xi-1, xi], hi = хi – хi-1 длины частичных отрезков. Обычно шаг интегрирования h величина постоянная, т. е. hi=h=const.
Квадратурная формула для метода левых прямоугольников: (6. 5)
Пример 1. Получить численное значение определённого интеграла по формуле левых прямоугольников если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9 Точное значение интеграла
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9 Точное значение интеграла
Геометрическая интерпретация решения задачи численного интегрирования методом y правых прямоугольников fn f 1 f 0 0 x x 0=a x 1 x 2 xn=b Квадратурная формула для метода правых прямоугольников : (6. 6)
Пример 2. Получить численное значение определённого интеграла по формуле правых прямоугольников если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9 Точное значение интеграла
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9 Точное значение интеграла
Геометрическая интерпретация решения задачи численного интегрирования методом центральных прямоугольников f(x) fn-½ f 3/2 f½ 0 x a x½ x 2 xn-½ b Квадратурная формула для приближённого вычисления интеграла методом центральных прямоугольников (6. 7)
Пример 3. Получить численное значение определённого интеграла по формуле центральных прямоугольников если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9
Метод трапеций y Аn fn-1 f 0 0 А 1 А 2 А 0 h h h x Площадь фигуры, ограниченной ломаной: (6. 8)
Формула трапеций:
Пример 4. Получить численное значение определённого интеграла по формуле трапеций, если подынтегральная функция задана таблицей (h=1): i 0 1 2 3 4 x f(x)=fi -1 1 0 0 1 1 2 4 3 9
h=0, 5 i 0 1 2 3 4 5 6 7 8 x f(x)=fi -1 1 -0, 5 0, 25 0 0 0, 5 0, 25 1 1 1, 5 2, 25 2 4 2, 5 6, 25 3 9 Точное значение интеграла
Формула Симпсона На частичных отрезках [хi-1, хi+1] (i=1, …, n) подынтегральная функция f(х) приближается интерполяционным многочленом Лагранжа второго порядка. Для частичного отрезка [х0, х2] такой многочлен : (6. 14)
Геометрическая интерпретация квадратичной интерполяции подынтегральной функции для частичного отрезка [хi-1, хi+1]. y Mi fi fi-1 Mi- fi+1 1 0 y=L 2(x) Mi+1 xi-1 xi xi+1 y=f(x) x
Из математического анализа известно: Площадь криволинейной трапеции, ограниченной параболой с осью, параллельной оси Оy (т. е. графиком квадратного трёхчлена y=Аx 2+Bx+C), равна произведению основания этой трапеции на сумму крайних ординат (ул и уп) и учетверённой средней ординаты параболы (ус): (6. 15)
y y= Аx 2+Bx+C ус ул уп 0 a c= b x График функции у=Аx 2+Bx+C.
Рассмотрим решение поставленной задачи для отрезка интегрирования произвольной длины. Заданный отрезок [a, b] разделим на чётное число (2 n) равных отрезков точками x 1, x 2, …, x 2 n-1. Длина каждого частичного отрезка равна Точки деления определяются формулами: x 1=a+h, x 2=a+2 h, …, xk=a+kh, …. Объединяя построенные отрезки попарно, будем рассматривать отрезки удвоенной длины : [x 0, x 2], [x 2, x 4], …, [x 2 n-2, x 2 n], x 0=а, x 2 n=b. Значения функции в точках x 0, x 1, x 2, … обозначим f 0, f 1, f 2, …, соответственно.
К каждому из членов этой суммы применим формулу (6. 15) и получим:
Формула Симпсона или формула парабол
Геометрическая интерпретация решения задачи численного интегрирования методом Симпсона. f(x) f 0 f 1 f 2 f 3 f 4 f 2 n-2 f 2 n-1 f 2 n 0 x a=x 0 x 1 x 2 x 3 x 4 x 2 n=b
Формула Гаусса для численного интегрирования
Задача. При заданном числе N+1 узлов построить квадратурную формулу, точную для многочленов наиболее высокой степени. Формулы, удовлетворяющие этому условию, называются квадратурными формулами Гаусса. Сначала строят формулы Гаусса (1) для стандартного отрезка [-1, 1].
Откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. Сделаем линейную замену переменной и преобразуем исходный интеграл к интегралу со стандартным промежутком интегрирования [ 1, 1]: (2)
Формула (1) точна для многочленов степени m тогда и только тогда, когда она точна для функций f(t) = 1, t, t 2, . . . , tm. Это эквивалентно тому, что узлы ti и веса Ai в (1) должны удовлетворять системе нелинейных уравнений k = 0, 1, . . . , m. (3) Система (3) имеет единственное решение A 0, A 1, . . . An, t 0, t 1, . . . tn (ti [-1, 1]) тогда и только тогда, когда число уравнений системы совпадает с числом неизвестных, т. е. m = 2 N + 1.
Пример. Построим функцию Гаусса с двумя узлами. В этом случае N =1, m = 3. Система (3) примет вид: (4)
Решая систему (4), получим: A 0 =A 1 =1; t 0 =-1/ , t 1 =1/. Т. о. получаем квадратурную формулу Гауссa, Для квадратурной формулы Гаусса справедлива следующая оценка погрешности:
Методы решения нелинейных алгебраических уравнений
Метод половинного деления (частный случай метода дихотомии)
Основная идея метода состоит в следующем: для нахождения корня, принадлежащего отрезку [ , ], делим отрезок пополам, то есть выбираем начальное приближение Если f( X(0) )=0, то X(0) является корнем уравнения. Если f(X(0) ) 0, то выбирается тот из отрезков [ (0), X(0) ] или [X(0) , (0)], на концах которого функция f(X) имеет противоположные знаки. Новый отрезок будем обозначать [ (1), (1)].
Неограниченное продолжение итерационного процесса дает последовательность отрезков: [ (1), (1)], [ (2), (2)], . . . , [ (n), (n)], . . . , содержащих искомый корень. Середина n-го отрезка точка (1) дает приближение к корню оценку погрешности: , имеющее (2) .
f(x) [α, β] α 2 0 β 2 х α 0 β 0 Геометрическая интерпретация итерационного процесса приближения к корню уравнения методом половинного деления.
f(x) [α 1, β 1] α 2 0 β 2 х α β 1 1 Геометрическая интерпретация итерационного процесса приближения к корню уравнения методом половинного деления.
f(x) [α 2, β 2] α 2 0 β 2 х α β 2 2 Геометрическая интерпретация итерационного процесса приближения к корню уравнения методом половинного деления.
Пример. Решить уравнение x 2+2=0 методом половинного деления с точностью ε=0, 5 для поиска корня на интервале (0, 6). α=α 1=0; β= β 1=6. [0; 6] f( α 1)= 02+2=2; f( β 1)= 62+2= 34. f( α 1) f(β 1)=2 ( 34 )<0 Корень есть! X 1=(0+6)/2=3; f(X 1)= 32+2= 7. f( α 1) f(Х 1)=2 ( 7) <0 Корень есть! α 2=α 1=0; β 2=Х 1=3. [0; 3] X 2=(0+3)/2=1, 5; f(X 2)= 1, 52+2= 0, 25. |X 1 X 2|= |3 1, 5|=1, 5>0, 5 Продолжать! f( α 2) f(Х 2)=2 ( 0. 25) <0 Корень есть! α 3=α 2=0; β 3= β 2=Х 2 =1, 5. [0; 1, 5]
α 3=α 2=0, β 3= β 2=Х 2 =1, 5. [0; 1, 5] X 3=(0+1, 5)/2=0, 75; f(X 3)= 0, 752+2 0, 56. | X 2 X 3 |= |1, 5 0, 56 |=0, 94>0, 5 Продолжать! f( α 3)= 02+2=2; f(X 3 )= 0, 56. f( α 3) f(X 3 )=2 0, 56 >0 Корня нет! f(β 3)= 1, 52+2= 0, 25. f(β 3) f(X 3 )= 0, 25 0, 56 <0 Корень есть! α 4= X 3 = 0, 75; β 4= β 3=1, 5. [0, 75; 1, 5] X 4=(0, 75+1, 5)/2=1, 125 1, 13; f(X 4)= 1, 132+2 0, 72. | X 3 X 4 |= |0, 75 1, 13|=0, 38 < 0, 5 КОНЕЦ!!! КОРЕНЬ= X 4 =1, 13.
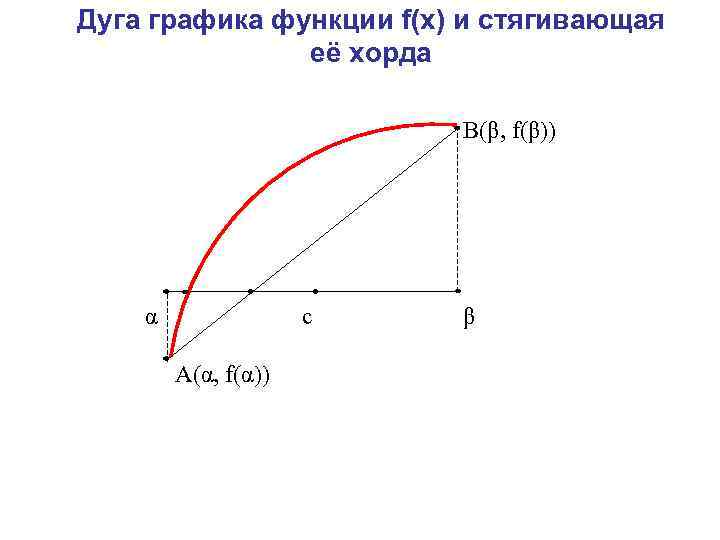
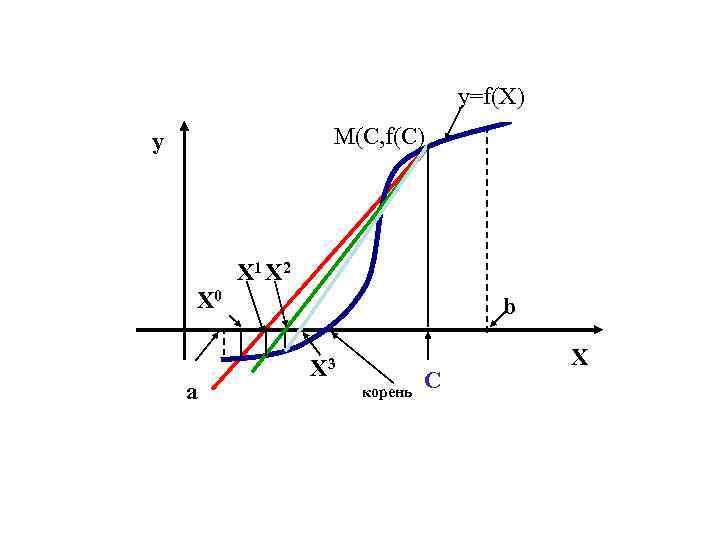
Метод хорд В методе половинного деления получение очередного приближения к корню осуществляется по жёстко заданному плану и не учитывает вычисляемые на каждом шаге значения функции. Можно достичь лучших результатов, если отрезок [ , ] делить точкой с на части не пополам, а пропорционально величинам ординат f( ) и f( ) графика заданной функции f(х). Т. е. точку с следует находить как абсциссу точки пересечения оси Ох с прямой, проходящей через точки А( , f( )) и В( , f( )), иными словами, с хордой АВ дуги АВ.
Дуга графика функции f(x) и стягивающая её хорда B(β, f(β)) α с β А(α, f(α))
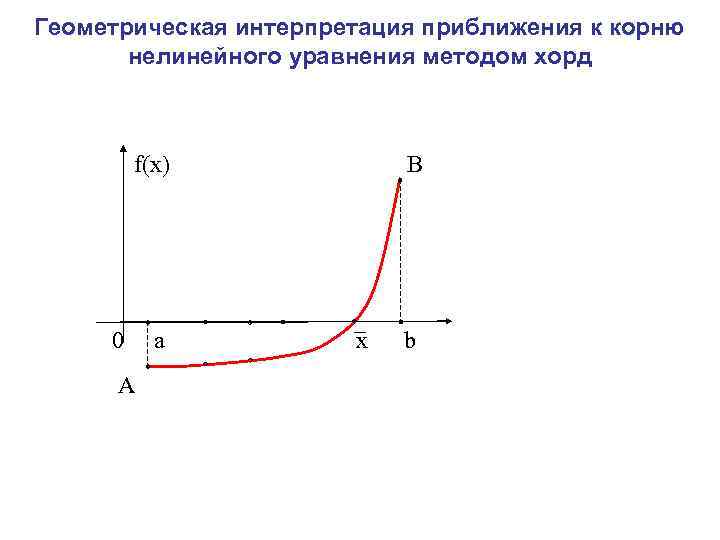
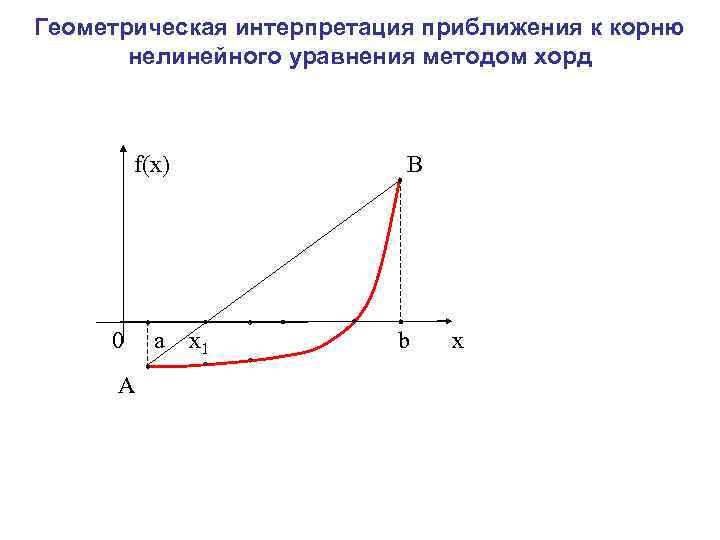
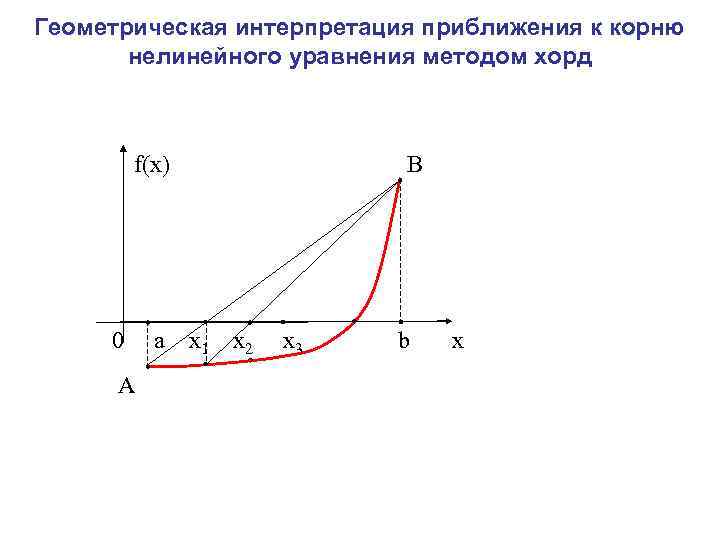
Уравнение прямой, проходящей через две заданные точки А и В имеет вид: Полагая y=0 и х=с (обозначение искомой точки пересечения прямой АВ с осью Ох), находим Метод, получающийся из метода дихотомии таким фиксированием точки деления очередного отрезка, называется методом хорд.
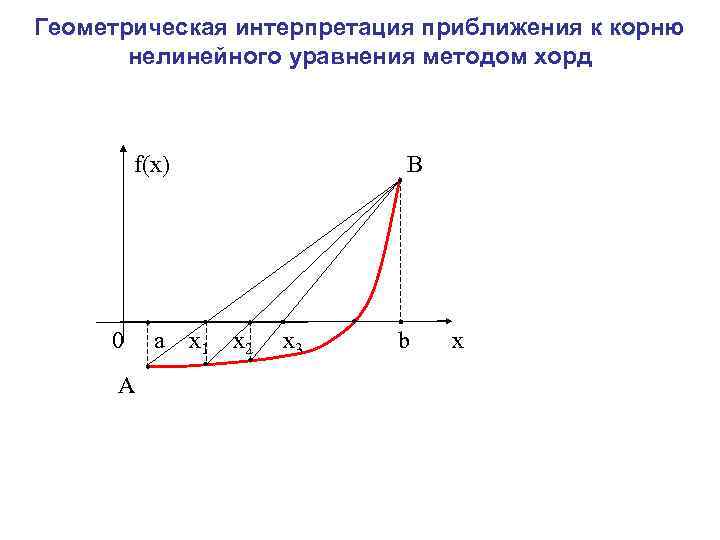
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 x b А
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 b x А
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 b x А
Геометрическая интерпретация приближения к корню нелинейного уравнения методом хорд f(x) В 0 a x 1 x 2 x 3 b x А
Метод последовательных приближений (метод простой итерации) Предположим, что уравнение вида: F(X)=0 (1) преобразовано к виду: X=f(Х). (2) Пусть X(0) является исходным приближенным значением корня. Тогда в качестве первого приближения примем X(1) = f(X(0)), в качестве второго X(2) = f(X(1)) и т. д. Основная расчетная формула в таком случае имеет вид: X(n) = f(X(n-1)). (3)
Геометрическое представление процесса приближения к искомому корню При решении уравнения X=f(X) отыскивается точка пересечения кривой Y=f(X) и прямой Y=X. а) Случай 0
b) Случай 0 > f ’(X) > 1; Y Y=X Y=f(X) Корень Х(0) Х(2) Х(3) Х(1) 0 X
c) Случай f’(X)>1; Y Y=f(X) Y=X 0 X X(0) X(2) X(3) Корень
d) Cлучай f’(X)<-1 Y Y=X Y=f(X) X(2) 0 X(0) Корень X(1) X(3) X
Метод Ньютона – Рафсона Описание классического метода Ньютона – Рафсона Предположим, что уравнение f(X)=0 имеет один корень на интервале [ , ], f’(X) и f’’(X) определены, непрерывны и сохраняют постоянные знаки на отрезке [ , ].
Геометрическая интерпретация вычисления корня уравнения методом Ньютона – Рафсона f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) 0 X 2 X 1 X 0 X
Геометрическая интерпретация вычисления корня уравнения методом Ньютона – Рафсона f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) 0 X 2 X 1 X 0 X
Геометрическая интерпретация вычисления корня уравнения методом Ньютона – Рафсона f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) 0 X 2 X 1 X 0 X
Уравнение касательной, проходящей через точку P 0, имеет вид: Y = f (X 0) + f’(X 0)(X – X 0). Полагая Y=0, найдем абсциссу X 1 точки пересечения касательной и OX Следующие приближения найдем по формулам: …
Процесс вычисления приближений необходимо прекратить при выполнении условия: где m 1 – наименьшее значение |f’(X)| на отрезке [ , ], M 2 – наибольшее значение |f’’(X)| на том же отрезке. При этом будет выполняться равенство: где ε – предельная абсолютная погрешность корня.
Иллюстрация локальной сходимости метода Ньютона-Рафсона f(X) X 0 X 1 X
Модификации метода Ньютона Упрощенный метод Ньютона Если производная f’(X) непрерывна, то ее значение вблизи простого корня почти постоянно. Поэтому можно попытаться вычислить f’(X) лишь однажды в точке X(0), а затем заменить f’(X(n-1)) постоянной f’(X(0)). В результате получим упрощенную формулу метода Ньютона: n 0
f(X) P 0(X 0, f(X 0)) P 1(X 1, f(X 1)) P 2(X 2, f(X 2)) а b 0 X X 1 X 0 X 2
Метод ложного положения В основе этой и следующей модификаций метода Ньютона лежит приближенное равенство: (1) Оно верно при условии известности Zn и Xn и следует из определения производной: (2)
Пусть C фиксированная точка, расположенная в окрестности простого корня. Заменим в расчетной формуле производную правой частью формулы (1), полагая, что Zn=C. В результате приходим к формуле ложного положения: (3)
y=f(X) M(C, f(C) y X 1 X 2 X 0 a b X 3 корень С X
Метод секущих Замена в формуле метода Ньютона производной f’(X) приближением: приводит к расчетной формуле для метода секущих: Метод двухшаговый, то есть необходимо задать два начальных приближения: X 0 и X 1
P 0(X 0, f(X 0)) Y Y=f(X) P 1(X 1, f(X 1)) Х 3 a X 2 X 1 Х 4 X 0 3 3 P 3(X , f(X )) 2 2 P 2(X , f(X )) b X
Уточнение метода Ньютона для случая кратного корня Корень X уравнения f(X) = 0 называется простым, если f’( X) 0. В противном случае, то есть если f’( X)=0 – кратным. Целое число m называется кратностью корня X, если f (k)( X) = 0 для k = 1, 2, . . . , m – 1 и f(m)( X) 0.
Для вычисления корня уравнения f (X) = 0 кратности m >1 можно использовать и стандартный метод Ньютона. Однако в этом случае скорость его сходимости является только линейной q = 1 – 1/m. Чтобы сохранить квадратичную скорость сходимости, метод Ньютона нужно модифицировать следующим образом:
Решение ОДУ
Основная идея метода Эйлера Решается дифференциальное уравнение с начальным условием y(x 0)=y 0. В процессе решения составляется таблица значений yk =y(xk). где [a, b] отрезок, на котором ищется решение.
Геометрическая интерпретация метода Эйлера Т. к. в точке x 0 известно значение решения y(x 0)=y 0 и значение его производной y (x 0)=F(x 0, y 0), можно записать уравнение касательной к графику искомой функции y=y(x) в точке (x 0, y 0): y=y 0+ F(x 0, y 0) (x х0). (8. 8)
y Геометрическая интерпретация метода Эйлера y=y 0+y (x 0)(x-x 0) y 3 y 2 y 1 y 0 y(x 1) y(x 2) y(x 1) h h Х 0 Х 1 y(x 3) h Х 2 Х 3 Х
Суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой, являющейся касательной к графику функции y=y(x) в точке (xi, y(хi)), т. е. yi+1=yi+ F(xi, yi)h, i=0, 1, …, n. График решения y=y(x) задачи Коши представляется ломаной, составленной из отрезков приближённых касательных.
Пример, иллюстрирующий применение метода Эйлера для решения следующей задачи Коши: y’= x y; (x 0=y 0=0) на сетке с шагом h=0, 1 на интервале [0, 1]. Решение. Данное уравнение уже записано в стандартном виде, разрешенном относительно производной искомой функции, т. е. y =F(x, y). Поэтому, для решаемого уравнения имеем F(x, y)=x y.
Примем шаг интегрирования равным шагу сетки h=0, 1. При этом для каждого узла сетки будет вычислено только одно значение (N=1). Для первых четырех узлов сетки получим следующие результаты: y 1=y(0, 1) y 0+h. F(x 0, y 0)=0+0, 1(0 0)=0; y 2=y(0, 2) y 1+h. F(x 1, y 1)=0+0, 1(0, 1 0)=0, 01; y 3=y(0, 3) y 2+h. F(x 2, y 2)=0, 01+0, 1(0, 2 0. 01)= =0, 029; y 4=y(0, 4) y 3+h. F(x 3, y 3)=0, 029+0, 1(0, 3 0, 029)= =0, 0561 и т. д.
х Точное решение h 0, 1 N 2 4 0, 000000 0, 05 0, 025 0 0, 00000 1 0, 000000 0, 1 0, 00483 0, 000000 0, 002500 0, 003688 0, 2 0, 3 0, 4 0, 01873 0, 04081 0, 07032 0, 010000 0, 029000 0, 056100 0, 014506 0, 016652 0, 035092 0, 037998 0, 063420 0, 066920 0, 5 0, 6 0, 7 0, 8 0, 9 1 0, 10653 0, 14881 0, 19658 0, 24932 0, 30657 0, 36787 0, 090490 0, 131441 0, 178297 0, 230467 0, 287420 0, 348678 0, 098737 0, 140360 0, 187675 0, 240127 0, 297214 0, 358486 y(х)=e-x+x 1 0, 102688 0, 144642 0, 192186 0, 244783 0, 301945 0, 363232
Относительные погрешности вычисленных значений функции для различных шагов сетки (h) и числа отрезков интегрирования (N) h 0, 1 0, 05 0, 025 x N 1 2 4 0, 1 100, 00% 48, 32% 23, 76% 0, 2 46, 61% 22, 55% 11, 10% 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 28, 95% 20, 22% 15, 06% 11, 67% 9, 30% 7, 57% 6, 25% 14, 03% 9, 81% 7, 32% 5, 68% 4, 53% 3, 69% 3, 05% 6, 91% 4, 83% 3, 61% 2, 80% 2, 24% 1, 82% 1, 51% 1 5, 22% 2, 55% 1, 26%
Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений n -го порядка Применение метода Эйлера для решения дифференциального уравнения n-го порядка
Уравнение сводится к системе n обыкновенных дифференциальных уравнений первого порядка заменой производных y’, y’’, …. , y(n-1) на независимые функции P 1(x), P 2(x), Pn-1(x), соответственно.
В результате такой замены получим систему n дифференциальных уравнений 1 -го порядка: причем исходные начальные условия преобразуются в следующую совокупность начальных условий:
Пример решения типовой задачи Пусть необходимо решить, применяя метод Эйлера, дифференциальное уравнение второго порядка: y 2 y +sin(xy)+x=0, для которого заданы начальные условия: x 0=0, y 0=y(x 0)=1, y 0=y (x 0)=1.
Сначала необходимо понизить порядок дифференциального уравнения. Введём в рассмотрение новую функцию Р(x, y)= y (x, y). Тогда исходное уравнение может быть представлено системой из двух дифференциальных уравнений 1 -го порядка: y (x, y)=P(x, y) P (x, y)=2 P(x, y) sin(xy) x. Начальные условия для уравнений этой системы: x 0=0, y 0=1, Р 0=1.
Расчётные формулы для получения решения методом Эйлера имеют вид: yi+1=yi+h Pi , Pi+1=Pi+h (2 Pi sin(xi yi) xi). Начальные условия: x 0=0, y 0=1, Р 0=1.
Результаты вычислений по расчётным формулам x y(x) P(x, y) 0, 1 1, 2 0, 2 1, 22 1, 42 0, 3 1, 36 1, 66 0, 4 1, 53 1, 92 0, 5 1, 72 2, 21 0, 6 1, 94 2, 52 0, 7 2, 19 2, 88 0, 8 2, 48 3, 28 0, 9 2, 81 3, 77 1 3, 19 4, 37 Иллюстрация решения задачи Коши для дифференциального уравнения второго порядка
Алгоритм Рунге-Кутты третьего порядка (погрешность порядка h 3) где
Алгоритм Рунге-Кутты четвертого порядка (погрешность порядка h 4) На каждом шаге вычисления выполняются по формуле где
Пример. Используя алгоритм Рунге-Кутты третьего и четвертого порядков решить ДУ y’=x-y x 0=0, y 0=0 с шагом h=0. 1: Решение. Для алгоритма третьего порядка (для узла x=0. 1) вычисления таковы: k 1=hf(x 0, y 0)=0. 1(0 -0)=0 k 2=hf(x 0+h/2, y 0+k 1/2)=0. 1[(0+0. 05)-(0+0/2]=0. 005 k 3=hf(x 0+h/2, y 0+2 k 1 -k 0)=0. 1[(0+0. 1)-(0+2 0. 005 -0]=0. 009 y 1=y 0+1/6(k 1+4 k 2+k 3)=1/6(0+4 0. 005+0. 009)=0. 0048333
Для алгоритма четвертого порядка (для узла x=0. 1) вычисления таковы: k 1=hf(x 0, y 0)=0. 1(0 -0)=0 k 2=hf(x 0+h/2, y 0+k 1/2)=0. 1[(0+0. 05)-(0+0/2]=0. 005 k 3=hf(x 0+h/2, y 0+k 2/2)=0. 1[(0+0. 05)-(0+ 0. 005/2)]= =0. 00475 k 4=hf(x 0+h, y 0+k 3)=0. 1[(0+0. 1)-(0+0. 00475)]= =0. 009525 y 1=y 0+1/6(k 1+2 k 2+2 k 3+k 4)= =1/6(0+2 0. 005+2 0. 00475+0. 009525)=0. 0048375
x 0 0, 1 Рунге-Кутты 3 порядка y отн. погр. 0 0, 00483333 0, 08444% Рунге-Кутты 4 порядка y отн. погр. 0 0, 0048375 0, 00169% 0, 2 0, 3 0, 4 0, 5 0, 6 0, 7 0, 8 0, 9 1 0, 01872336 0, 04080819 0, 07030794 0, 10651697 0, 14879677 0, 19656961 0, 24931274 0, 30655314 0, 36786283 0, 0187309 0, 04081842 0, 07032029 0, 10653093 0, 14881193 0, 19658562 0, 24932929 0, 30656999 0, 36787977 0, 03946% 0, 02458% 0, 01721% 0, 01285% 0, 00999% 0, 00798% 0, 00651% 0, 00539% 0, 00451% 0, 00079% 0, 00049% 0, 00035% 0, 00026% 0, 00020% 0, 00016% 0, 00013% 0, 00011% 0, 00009%
Пример решения типовой задачи Пусть необходимо, применяя метод Рунге. Кутты, решить дифференциальное уравнение второго порядка: y 2 y +sin(xy)+x=0, для которого заданы начальные условия: x 0=0, y 0=y(x 0)=1, y 0=y (x 0)=1.
Понизим порядок дифференциального уравнения. Введём в рассмотрение новую функцию Р(x, y)= y (x, y). Тогда исходное уравнение может быть представлено системой из двух дифференциальных уравнений 1 -го порядка: y (x, y)=P(x, y) P (x, y)=2 P(x, y) sin(xy) x. Начальные условия для уравнений этой системы: x 0=0, y 0=1, Р 0=1.
Расчётные формулы для получения решения методом Рунге-Кутты имеют вид:
Для нашего примера расчётные формулы имеют вид: т. е. Формула Эйлера
Правило двойного пересчёта (правило Рунге) Пусть значение в точке Xi найдено и равно Yi. 1) Обозначим через Yhi+1 приближение Yi+1 к Y(Xi+1), найденное с помощью некоторого одношагового метода: Yhi+1 =Yi+1= Yi+hi+1 Ф(Xi, Yi, hi+1), (1) который имеет порядок точности р. Уменьшим шаг интегрирования вдвое, положив
2) Вычислим приближение к значению в точке Xi+1 с помощью то же одношагового метода, но с половинным шагом hi+1/2 : Yi+1/2= Yi + hi+1/2 Ф(Xi, Yi, hi+1/2), Yi+1= Yi+1/2 + hi+1/2 Ф(Xi+1/2, Yi+1/2, hi+1/2 ), Полученное таким образом значение Yhi+1/2= Yi+1 будет отличаться от значения, найденного по формуле (1).
3) Для оценки локальной (Li+1) погрешности значения Yhi+1/2 принимается приближенное равенство: Li+1=Yi+1(Xi+1) Yhi+1/2 ≈(Yhi+1/2 Yhi+1)/(2 p 1), называемое правилом двойного пересчёта или правилом Рунге.
Методы решения систем линейных алгебраических уравнений
Метод Гаусса (метод последовательного исключения неизвестных) Решение системы линейных алгебраических уравнений с помощью метода Гаусса состоит из двух основных этапов: 1) Прямого хода; 2) Обратного хода (обратной подстановки).
Прямой ход заключается в последовательном исключении неизвестных из системы a 11 x 1+a 12 x 2+…+a 1 mxm =b 1 a 21 x 1+a 22 x 2+…+a 2 mxm =b 2 …………… (1) am 1 x 1+am 2 x 2+…+ammxm=bm. для преобразования её к эквивалентной системе линейных алгебраических уравнений с верхней треугольной матрицей: Вычисление значений неизвестных производят на этапе обратного хода.
9. 4. 1 Схема единственного деления. Прямой ход решения состоит из (m– 1)го шага исключения неизвестных. 1 -й шаг. Целью этого шага является исключение неизвестного х1 из уравнений с номерами i = 2, 3, …, m. Предположим, что коэффициент a 11 0. Главный (ведущий) элемент 1 -го шага
Множители 1 -го шага Найдём величины i 1 = ai 1 / a 11, ( i = 2, …, m), Вычтем последовательно из 2 -го, 3 -го, …, m-го уравнений системы (1) первое уравнение, умноженное соответственно на 21, 31, …, m 1. Это позволит обратить в нуль коэффициенты при неизвестном х1 во всех уравнениях системы, кроме первого уравнения.
В результате получим эквивалентную систему линейных алгебраических уравнений: a 11 x 1 + a 12 x 2 + … + a 1 mxm = b 1 a(1)22 x 2 +… + a(1)2 mxm = b(1)2 a(1)32 x 2 +… + a(1)3 mxm = b(1)3 (2) …………………………. a(1)m 2 x 2 +… + a(1)mmxm = b(1)m, где a(1)ij = aij – i 1 a 1 j , b(1)i = bi – i 1 b 1. (3)
2 -й шаг. Целью этого шага является исключение неизвестного х2 из уравнений с номерами i = 3, 4, …, m. Множители второго шага исключения: i 2 = a(1)i 2 / a(1)22 , (i = 3, 4, …, m). Вычтем последовательно из третьего, четвертого, …, m-го уравнений системы (2) второе уравнение, умноженное соответственно на 32, 42, …, m 2.
В результате получим систему: a 11 x 1 + a 12 x 2 + … + a 1 m xm = b 1 a(1)22 x 2 +… +a(1)2 mxm = b(1)2 a(2)33 x 3 +… + a(2)3 mxm = b(2)3 ……………………… (4) a(2)m 3 x 3 +… + a(2)mmxm= b(2)m, где a(2)ij = a(1)ij – i 2 a(1)2 j , b(2)i = b(1)i – i 2 b(1)2. (5)
k-й шаг. В предположении, что главный элемент k – го шага a(k-1)kk≠ 0, вычислим множители: ik = a(k-1)ik / a(k-1)kk , (i = k+1, …, m) и вычтем из (k+1)-го, (k+2)-го, …, m -го уравнений полученной на предыдущем шаге системы k-ое уравнение, умноженное соответственно на k+1, k; k+2, k; … ; mk.
После (m-1)-го шага получим: a 11 x 1 + a 12 x 2 + … + a 1 m xm = b 1 a(1)22 x 2 +… + a(1)2 mxm = b(1)2 a(2)33 x 3 +… + a(2)3 mxm = b(2)3 …………… (6) a(m-1)mmxm= b(m-1)m, Матрица А(m-1) является треугольной.
Обратный ход Из последнего уравнения системы (6) находим значение неизвестного xm. Подставляя найденное значение в предпоследнее уравнение, получаем значение xm-1. Осуществляя обратную подстановку, далее последовательно находим xm-2, xm-1, …, x 1. Вычисление неизвестных здесь проводится по формулам: b(m-1)m xm = ——— ; a(m-1)mm (7) b(k-1)k – a(k-1)k, k+1 xk+1 – … – a(k-1)kmxm xk = ———————– ; a (k-1)kk k = m-1, …, 1.
Итерационные методы решения систем линейных алгебраических уравнений Метод простой итерации
Приведение системы уравнений к виду, удобному для итераций АХ = Р (1) А – квадратная невырожденная матрица Необходимо предварительно преобразовать эту систему к виду: Х = ВХ + С. (2) Здесь В – квадратная матрица с элементами bij (i, j [1, m]), С – вектор-столбец с элементами сi (i [1, m]).
Самый простой способ приведения системы к виду (2) состоит в следующем: Из первого уравнения системы (1) выразим неизвестное x 1: х1 = (р1 – а 12 х2 – а 13 х3–…–а 1 mхm) / а 11 ; Из второго уравнения – неизвестное х2 : х2 = (р2 – а 22 х2 – а 23 х3–…– а 2 mхm) / а 22 , и т. д.
В результате получим систему в виде (3): х1 = b 12 x 2 +b 13 x 3+…+b 1, m-1 xm-1+ b 1 mxm +c 1 х2 = b 21 x 1 +b 23 x 3+… + b 2, m-1 xm-1+ b 2 mxm + c 2 …………… хm = bm 1 x 1+bm 2 x 2 +… +bm, m-1 xm-1 +cm.
В главной диагонали матрицы В находятся нулевые элементы. Остальные элементы вычисляются по формулам: (4)
Описание метода Выбираем некоторое начальное приближение вектора решения: Х(0) = (х1(0), х2(0), …, хm(0))Т. Подставляя его в правую часть системы (2) и вычисляя полученное выражение, находим первое приближение: Х(1)= ВХ(0) + С. Подставляя приближение Х(1) в правую часть системы (2), получим: Х(2) = ВХ(1) + С, и. т. д.
Таким образом, основная расчетная формула имеет вид: Х(k+1) = ВХ(k) + С. (5) В случае, когда используется система (3) с коэффициентами, вычисляемыми по формуле (4), метод простой итерации называется методом Якоби.
Метод Зейделя для решения систем линейных алгебраических уравнений Описание метода Пусть система (1) приведена к виду (3) с коэффициентами, вычисленными по формуле (4). Метод Зейделя можно рассматривать как модификацию метода Якоби. Основная идея метода состоит в том, что при вычислении очередного( k+1) – го приближения к неизвестному xi при i > 1 используют уже найденные ( k+1)–е приближения к неизвестным х1, х2, …, хi-1, а не k –е, как в методе Якоби
Основная идея метода Зейделя состоит в том, что при вычислении очередного( k+1) – го приближения к неизвестному xi при i > 1 используют уже найденные ( k+1)–е приближения к неизвестным х1, х2, …, хi-1, а не k –е, как в методе Якоби
х1(k+1) = b 12 x 2 (k) + b 13 x 3 (k) +… +b 1 mxm (k) х2 (k+1) = b 21 x 1 (k+1) + c 1 + b 13 x 3 (k) +… +b 1 mxm (k) + c 2 х3 (k+1)= b 31 x 1 (k+1)+ b 32 x 2 (k+1) +… +b 1 mxm (k) + c 3 …………………………… хm (k+1) = bm 1 x 1 (k+1) + … …………. +bm, m-1 xm-1 (k+1) + cm
Введём верхнюю и нижнюю треугольные матрицы: В 1 = и В 2 = .
Тогда расчетная формула примет компактный вид: Х(k+1) = В 1 Х(k+1) + В 2 Х(k) + С. Заметим, что матрица В = В 1 + В 2 и поэтому решение X системы удовлетворяет равенству: X= В 1 + В 2 X+ С. Метод Зейделя иногда называют методом Гаусса – Зейделя или процессом Либмана, или методом последовательных замещений.
Геометрическая интерпретация метода Зейделя a 11 x 1 + a 12 x 2 = b 1 – прямая L 1; a 21 x 1 + a 22 x 2 = b 2 – прямая L 2. Расчётные формулы для решения этой системы имеют вид: х1(k+1) = b 12 x 2(k) + c 1 х2(k+1) = b 21 x 2 k+1) + c 2,
x 2 L 1 X 01, Х 02 X 12 0 L 2 Х 11 Х 01 Х 1
x 2 X 0 0 L 2 L 1 x 1














![{displaystyle x_{n}in (a,,x^{*}-delta ]cup [x^{*}+delta ,,b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5f21fd665315688b00234e990e4e815e427b5b)




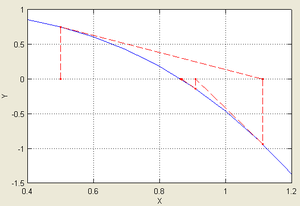





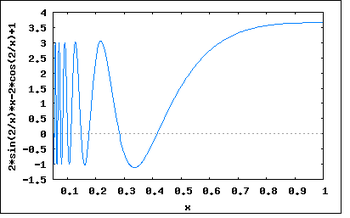





![[a,;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e682a8a7d3222e237401e57d673fd362523662cd)



![{displaystyle f(x)=0colon exists x^{*}in [a,;b]colon f(x^{*})=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15d9c34f877cd2e534419376c36f93e258c15801)














![{displaystyle f_{i}+sum _{k=1}^{n}{frac {partial f_{i}}{partial x_{k}}}(x_{k}^{[j+1]}-x_{k}^{[j]})=0,qquad i=1,;2,;ldots ,;m,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc7f4c706fe7cadefee1e80477d0e3648a358b7f)
![{displaystyle nabla f({vec {x}}^{[j]})+H({vec {x}}^{[j]})({vec {x}}^{[j+1]}-{vec {x}}^{[j]})=0,quad j=1,;2,;ldots ,;n,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a93eebcf171c9964de5dc34316c1c362df1d719)
![{displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7746807ee2e9f155ca9bc3d0d82822e9d0ba810)
![{displaystyle {vec {x}}^{[j+1]}={vec {x}}^{[j]}-lambda _{j}H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c868e602fce2d22f00f7113f6c4c2af899e1578)
![{displaystyle lambda _{j}=arg min _{lambda }f({vec {x}}^{[j]}-lambda H^{-1}({vec {x}}^{[j]})nabla f({vec {x}}^{[j]})).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c90586d6156feccbfe6a6d006966c3b1b5b276d)



![left[J^{T}({vec {x}})J({vec {x}})+sum _{{i=1}}^{m}f_{i}({vec {x}})H_{i}({vec {x}})right]{vec {p}}=-J^{T}({vec {x}}){vec {f}}({vec {x}}).](https://wikimedia.org/api/rest_v1/media/math/render/svg/98c37fe7b2533841a5672c30db2a479588a0b887)





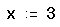
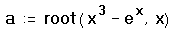
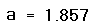
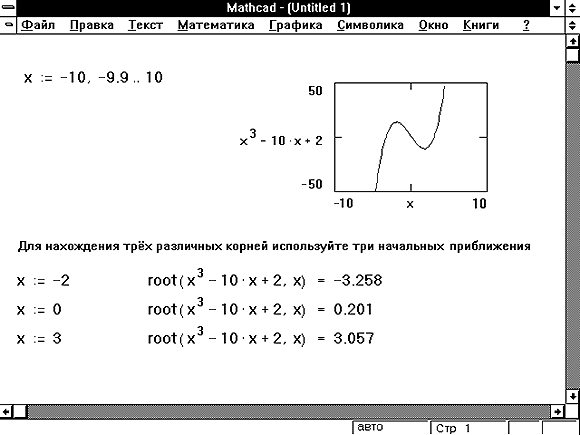
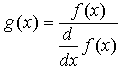






























































![Пример. Необходимо оценить погрешность приближения f(x)= x в точке x=116 на отрезке [a, b], Пример. Необходимо оценить погрешность приближения f(x)= x в точке x=116 на отрезке [a, b],](https://present5.com/presentation/15751739_91860122/image-4.jpg)

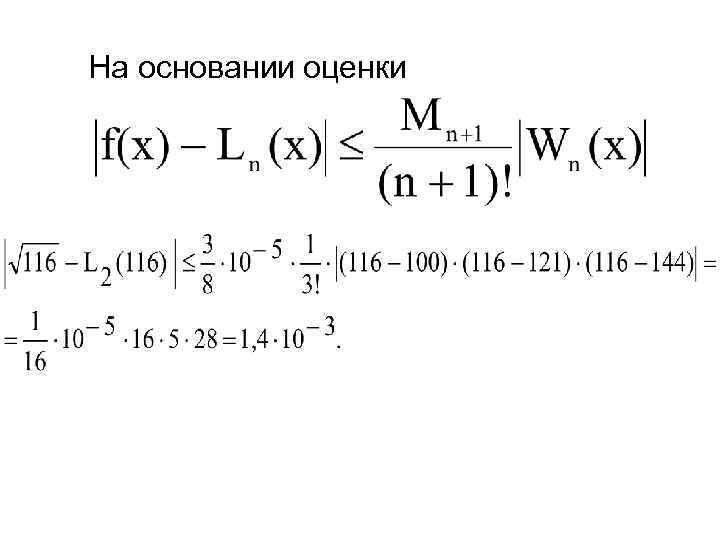
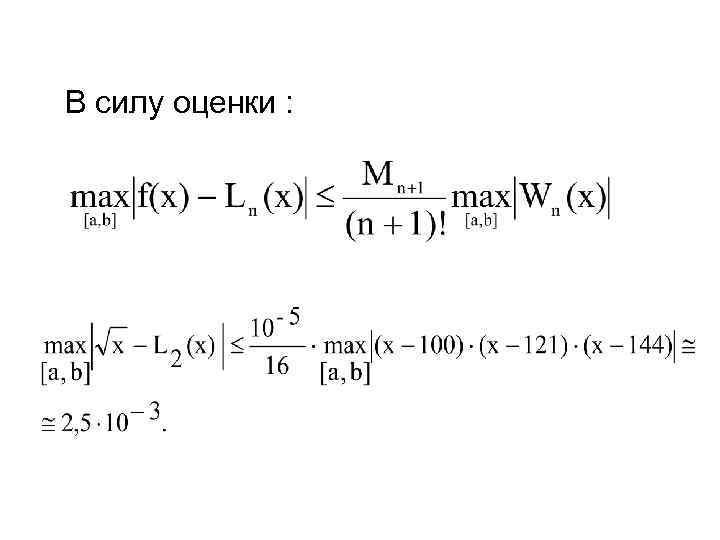
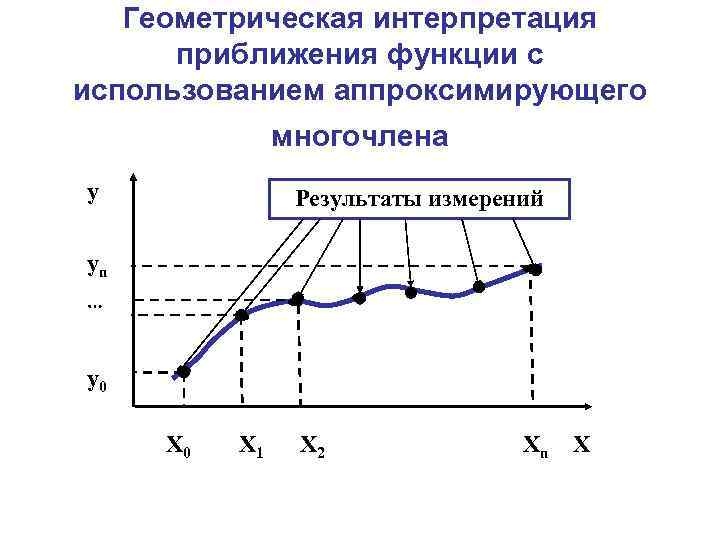
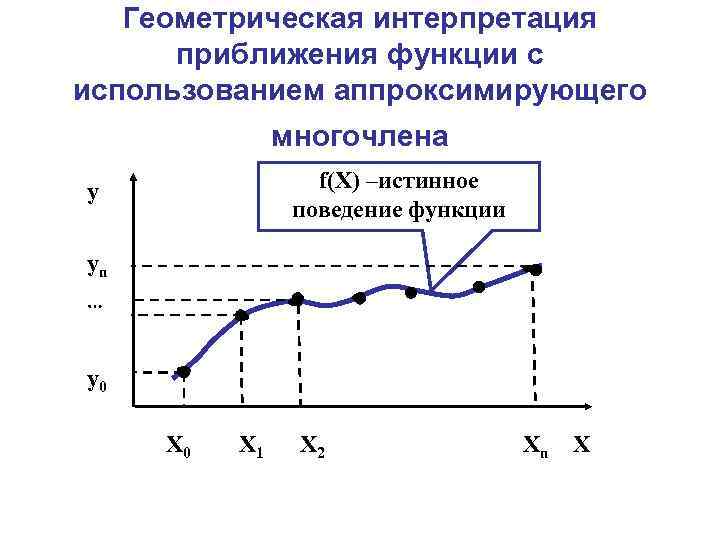
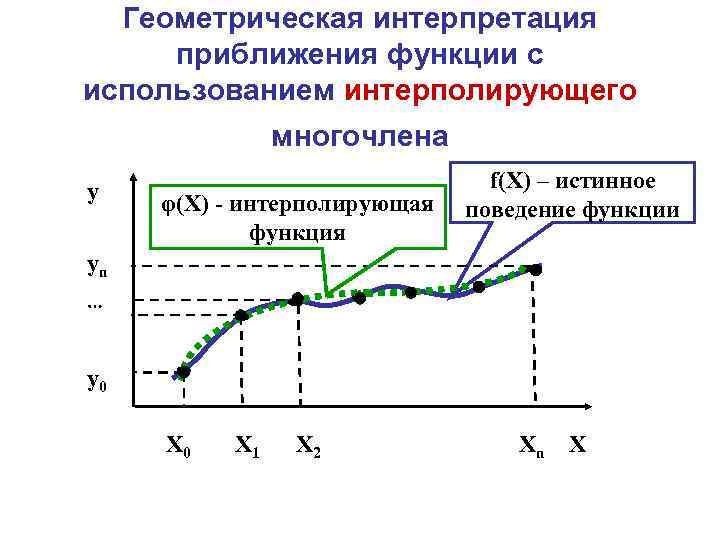
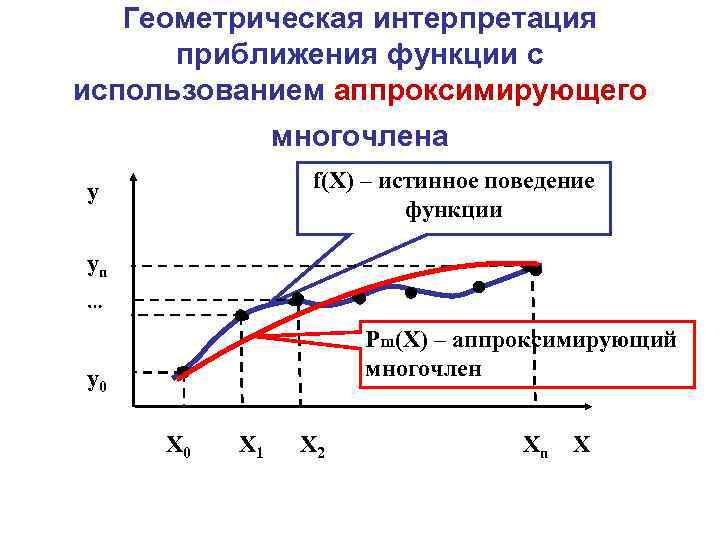

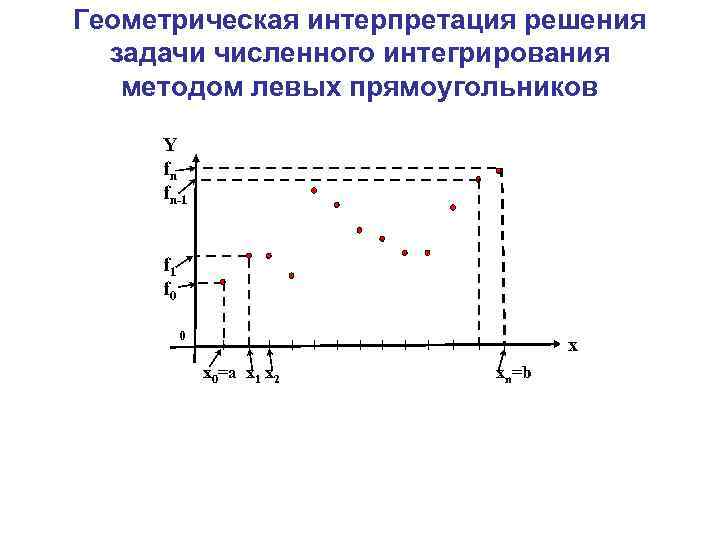
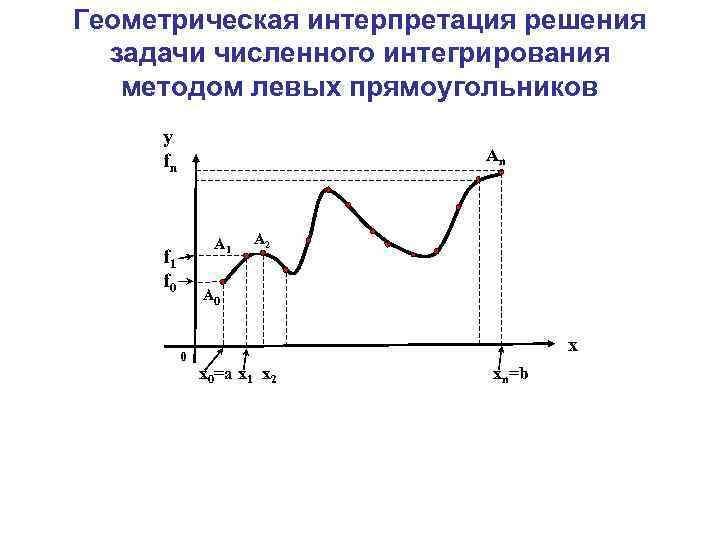
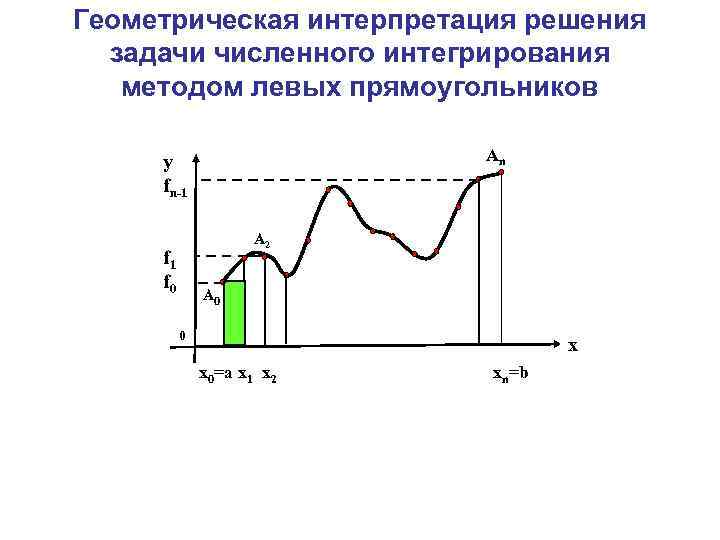
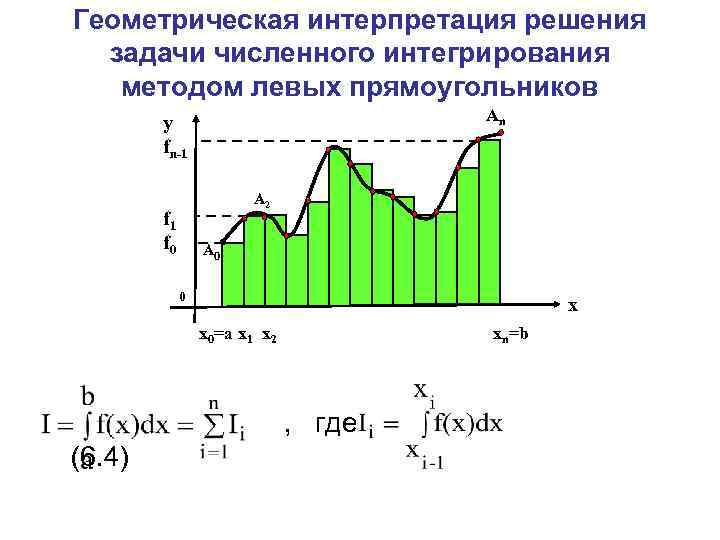




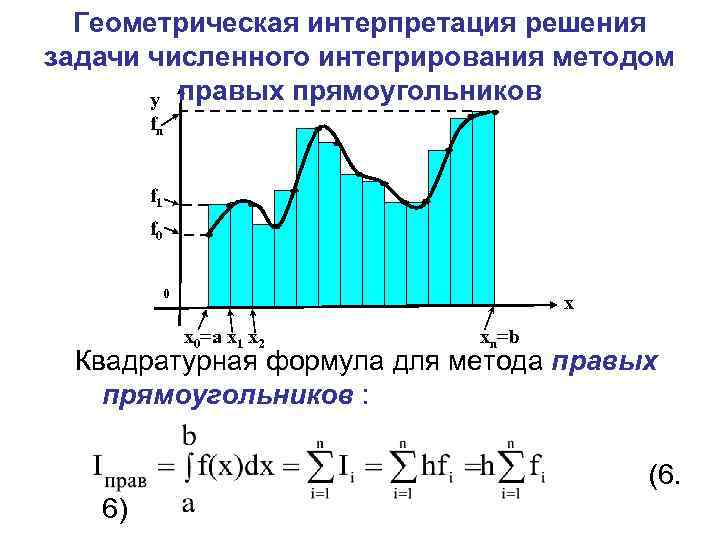


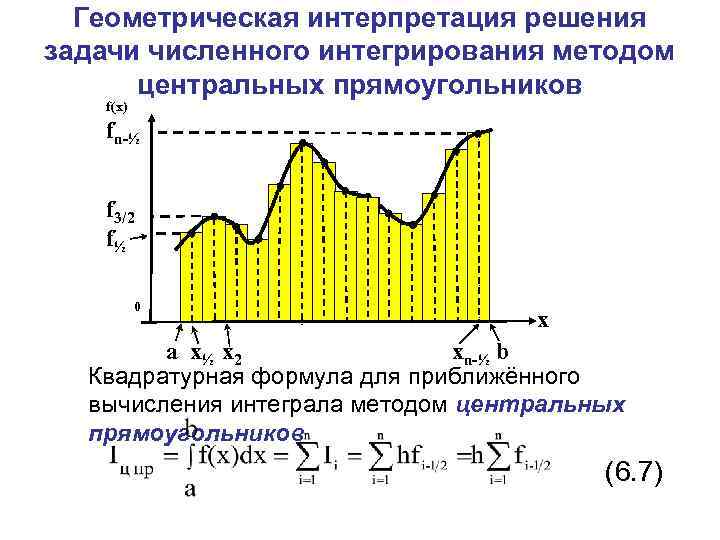


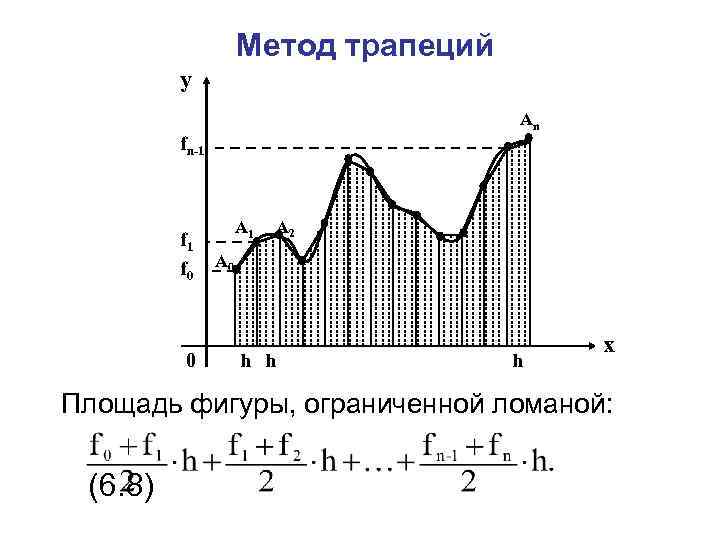



![Формула Симпсона На частичных отрезках [хi-1, хi+1] (i=1, …, n) подынтегральная функция f(х) приближается Формула Симпсона На частичных отрезках [хi-1, хi+1] (i=1, …, n) подынтегральная функция f(х) приближается](https://present5.com/presentation/15751739_91860122/image-31.jpg)
![Геометрическая интерпретация квадратичной интерполяции подынтегральной функции для частичного отрезка [хi-1, хi+1]. y Mi fi Геометрическая интерпретация квадратичной интерполяции подынтегральной функции для частичного отрезка [хi-1, хi+1]. y Mi fi](https://present5.com/presentation/15751739_91860122/image-32.jpg)

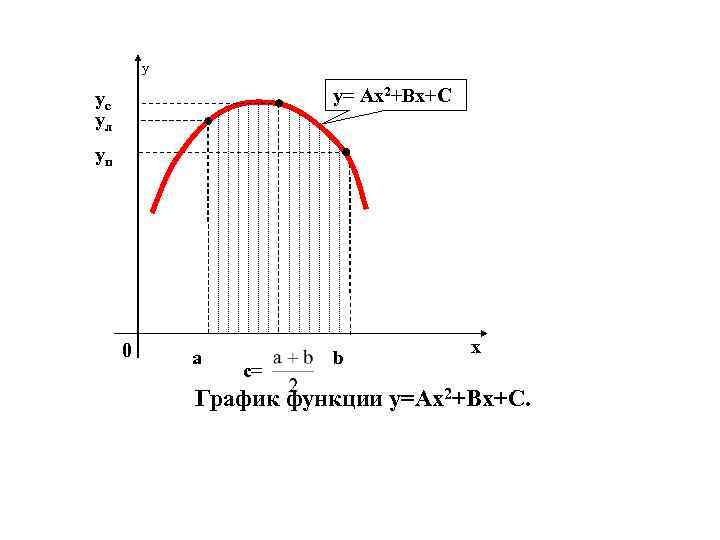
![Рассмотрим решение поставленной задачи для отрезка интегрирования произвольной длины. Заданный отрезок [a, b] разделим Рассмотрим решение поставленной задачи для отрезка интегрирования произвольной длины. Заданный отрезок [a, b] разделим](https://present5.com/presentation/15751739_91860122/image-35.jpg)


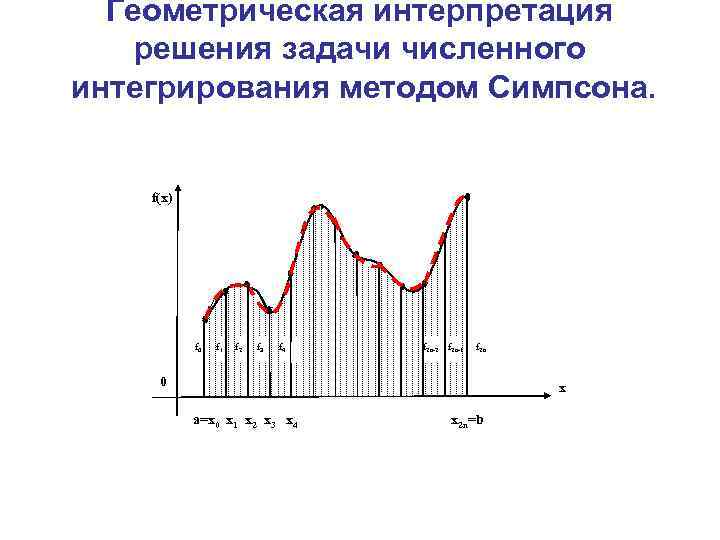


![Откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. Сделаем линейную замену Откажемся от равномерного распределения узлов xi на промежутке интегрирования [a, b]. Сделаем линейную замену](https://present5.com/presentation/15751739_91860122/image-41.jpg)





![Основная идея метода состоит в следующем: для нахождения корня, принадлежащего отрезку [ , ], Основная идея метода состоит в следующем: для нахождения корня, принадлежащего отрезку [ , ],](https://present5.com/presentation/15751739_91860122/image-47.jpg)
![Неограниченное продолжение итерационного процесса дает последовательность отрезков: [ (1), (1)], [ (2), (2)], . Неограниченное продолжение итерационного процесса дает последовательность отрезков: [ (1), (1)], [ (2), (2)], .](https://present5.com/presentation/15751739_91860122/image-48.jpg)
![f(x) [α, β] α 2 0 β 2 х α 0 β 0 Геометрическая f(x) [α, β] α 2 0 β 2 х α 0 β 0 Геометрическая](https://present5.com/presentation/15751739_91860122/image-49.jpg)
![f(x) [α 1, β 1] α 2 0 β 2 х α β 1 f(x) [α 1, β 1] α 2 0 β 2 х α β 1](https://present5.com/presentation/15751739_91860122/image-50.jpg)
![f(x) [α 2, β 2] α 2 0 β 2 х α β 2 f(x) [α 2, β 2] α 2 0 β 2 х α β 2](https://present5.com/presentation/15751739_91860122/image-51.jpg)

![α 3=α 2=0, β 3= β 2=Х 2 =1, 5. [0; 1, 5] X α 3=α 2=0, β 3= β 2=Х 2 =1, 5. [0; 1, 5] X](https://present5.com/presentation/15751739_91860122/image-53.jpg)