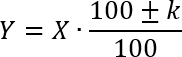Как узнать начальную сумму если известна скидка и сумма со скидкой
Ученик
(107),
на голосовании
7 лет назад
Голосование за лучший ответ
Tikkkk
Гуру
(3139)
7 лет назад
сначала было 100% сделали скидку 30 и получилось 3200, значит 3200 = 70% от начальной суммы, 3200 делишь на 70, узнаешь 1% и умножаешь на 100, получаешь 100%
Даня Тараканов
Ученик
(113)
5 месяцев назад
Вид литературы Количество проданных книг
Художественная литература 60
Научно-популярная литература 36
Справочная литература 30
Учебная литература 54
В таблице приведены данные по продажам в книжном магазине за день. Пользуясь данными таблицы, определите, какую долю проданных книг составляет художественная литература.
В этом уроке мы узнаем, как найти первоначальную цену, учитывая цену продажи и процентную скидку.
Правила поиска первоначальной цены с учетом цены продажи и процентной скидки
Сначала рассмотрим неизвестную первоначальную цену как « х ».
Тогда рассмотрим ставку дисконта.
Чтобы найти фактическую скидку, умножьте ставку дисконта на исходную сумму « х ».
Чтобы найти продажную цену, вычтите фактическую скидку из первоначальной суммы « х » и сравните ее с данной продажной ценой.
Решите уравнение и найдите исходную сумму « х ».
Письменный стол продается со скидкой 36%. Цена продажи составляет $ 496. Какова была его первоначальная цена?
Шаг 1:
Пусть первоначальная цена будет = х
Дисконтная ставка = 36%
Шаг 2:
Скидка = 36% от х = 0,36 х х = 0,36 х
Цена продажи = Первоначальная цена – Скидка = x – 0.36 x = 0.64 x
Шаг 3:
Цена продажи = $ 496 = 0,64 х
Решение для х
x = $ frac {496} {0.64} = $ 775
Итак, первоначальная цена = 775 $
Если Play Station была куплена за 558 долларов США со скидкой 10%, какова была первоначальная цена Play Station?
Шаг 1:
Пусть первоначальная цена будет = х
Дисконтная ставка = 10%
Шаг 2:
Скидка = 10% от х = 0,10 × х = 0,1 х
Цена продажи = Первоначальная цена – Скидка = х – 0,1 х = 0,9 х
Шаг 3:
Цена продажи = $ 558 = 0,9 х
Решение для х
x = $ frac {558} {0.9} = $ 620
Итак, первоначальная цена = 620 $
Формула простого процента: как найти исходное значение
13 ноября 2013
В этом коротком видеоуроке мы научимся решать задачи на проценты с помощью специальной формулы, которая так и называется: формула простого процента. Давайте оформим эту формулу в виде теоремы.
Теорема о простом проценте. Предположим, что есть некая исходная величина x, которая затем меняется на k%, и получается новая величина y. Тогда все три числа связаны формулой:
Плюс или минус перед коэффициентом k ставится в зависимости от условия задачи. Если по условию величина x возрастает, то перед k стоит плюс. Если же величина уменьшается, то перед коэффициентом k стоит минус.
Несмотря на кажущуюся мудреность этой формулы, многие задачи с ее помощью решаются очень быстро и красиво. Давайте попробуем.
Задача. Цена на товар была повышена на 10% и составила 2970 рублей. Сколько рублей стоил товар до повышения цены?
Чтобы решить эту задачу с помощью формулы простых процентов, нам необходимы три числа: исходное значение x, проценты k и итоговое значение y. Из всех трех чисел нам известны проценты k = 10 и итоговое значение y = 2970. Обратите внимание: 2970 — это именно итоговая цена, т.е. y. Потому что по условию задачи исходная цена на товар неизвестна (ее как раз требуется найти). Но затем она была повышена, и только тогда составила 2970 рублей.
Итак, нам нужно найти x, т.е. исходное значение. Что ж, подставляем наши числа в формулу и получаем:
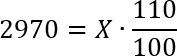
Складываем числа в числителе и получаем:
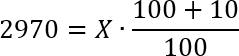
Сокращаем по одному нулю в числителе и знаменателе, а затем умножаем обе части уравнения на 10. Получим:
11x = 29 700
Чтобы найти x из этого простейшего линейного уравнения, нужно разделить обе стороны на 11:
x = 29 700 : 11 = 2700
Как видите, это довольно большие числа, поэтому в уме такие вычисления не провести. В случае, если такая задача встретится вам на ЕГЭ, придется делить уголком. При этом все разделилось без остатка, и мы получили значение x:
x = 2700
Именно столько стоил товар до повышения цены. И именно это число нам требовалось найти по условию задачи. Поэтому все: задача решена. Причем решена не «напролом», а с помощью формулы простого процента — быстро, красиво и наглядно.
Разумеется, эту задачу можно было решать по-другому. Например, через пропорции. Или экзотическим методом коэффициентов. Но будет гораздо лучше и надежнее, если у вас на вооружении будет несколько приемов для решения любой задачи на проценты. Так что обязательно попрактикуйтесь в использовании данной формулы.
А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: неизвестно начальное значение (метод пропорции)

- Формула простого процента: неизвестно конечное значение

- Решение ЕГЭ-2011: вариант 1, часть B

- Метод коэффициентов, часть 1

- Деление многочленов уголком

- Сфера, вписанная в куб

Калькулятор процентов онлайн. Как найти процент от числа
Используя калькулятор процентов Вы сможете производить всевозможные расчеты с использованием процентов. Округляет результаты до нужного количества знаков после запятой.
Сколько процентов составляет число X от числа Y. Какое число соответствует X процентам от числа Y. Прибавление или вычитание процентов из числа.
Калькулятор процентов
очистить форму
Сколько составляет % от числа
Расчет
0% от числа 0 = 0
Калькулятор процентов
очистить форму
Сколько % составляет число от числа
Расчет
Число 15 от числа 3000 = 0.5%
Калькулятор процентов
очистить форму
Прибавить % к числу
Расчет
Прибавить 0 % к числу 0 = 0
Калькулятор процентов
очистить форму
Вычесть % из числа
Расчет
Вычесть 0 % из числа 0 = 0
Сохранить расчет
Округлять до
знаков после запятой
очистить всё
Калькулятор разработан специально для расчета процентов. Позволяет выполнять разнообразные расчеты при работе с процентами. Функционально состоит из 4-х разных калькуляторов. Примеры вычислений на калькуляторе процентов смотрите ниже.
Процентом в математике называют сотую часть числа. К пример 5% от 100 равно 5.
Данный калькулятор позволит точно посчитать посчитать процент от заданного числа. Имеются различные режимы расчета. Вы сможете производить различные расчёты с использованием процентов.
- Первый калькулятор нужен когда вы хотите рассчитать процент от суммы. Т.е. Вы знаете значение процента и суммы
- Второй — если нужно посчитать сколько процентов составляет Х от Y. X и Y это числа, а вы ищете процент первого во втором
- Третий режим — прибавление процента от указанного числа к данному числу. К примеру у Васи 50 яблок. Миша принёс Васе ещё 20% от яблок. Сколько яблок у Васи?
- Четвёртый калькулятор противоположен третьему. У Васи 50 яблок, а Миша забрал 30% яблок. Сколько яблок осталось у Васи?
Частые задачи
Задача 1. Индивидуальный передприниматель получает каждый месяц 100 тыс рублей. Он работает по упрощенке и платит налогов 6% в месяц. Сколько ИП должен заплатить налогов в месяц?
Решение: Пользуемся первым калькулятором. Вводим в первое поле ставку 6, в второе 100000
Получаем 6000 руб. — сумма налога.
Задача 2. У Миши 30 яблок. 6 он отдал Кате. Сколько процентов от общего числа яблок Миша отдал Кате?
Решение: Пользуемся вторым калькулятором — в первое поле вводим 6, во второе 30. Получаем 20%.
Задача 3. У банка Тинькофф за пополнение вклада из другого банка вкладчик получает 1% сверху от суммы пополнения. Коля пополнил вклад переводом из другого банка на сумму 30 000. На какую итоговую сумму будет пополнен вклад Коли.
Банковские калькуляторы процентов
Если вам нужно посчитать проценты по вкладу или кредиту, рекомендуем воспользоваться калькуляторами нашего проекта, которые представлены н
Выше. Также рекомендуем посмотреть калькулятор сложных процентов с пополнением
Алгоритмы расчета
Как посчитать скидку, зная цену со скидкой и без?
Допустим имеем начальную цену товара 50 р(А), цену со скидкой 30(B). Для расчета, сколько составила скидка нужно сделать следующее
- Отнять от начальной цены конечную и определить скидку в рублях C = 50 – 30 = 20
- Скиду в рублях С поделить на начальную цену А и умножить на 100%, Процент скидки = 100* 20/50 = 40%
Как добавить процент от числа к числу?
Чтоб добавить процент от числа к числу, нужно сначала определить этот процент, а потом сложить с числом.
Допустим, нужно добавить 7%(C) к 50(A) рублям. Алгоритм будет следующий:
- Шаг 1: Определяем 7% от 50, для этого умножаем 50 на 7% и делим на 100%: Х = 50*7/100 = 3.5
- Шаг 2: Складываем Х и А, т.е. сумму и процент от суммы получаем B = 50 + 3.5 = 53.5
Как отнять процент от числа?
Чтоб отнять процент от числа(А), нужно сначала посчитать величину этого процента, а потом получить разность между числом и этой величиной.
Допустим, нужно отнять 7%(C) от 50(A) рублей. Алгоритм будет следующий:
- Определяем 7% от 50 руб., для этого умножаем 50 на 7% и делим на 100%: Х = 50*7/100 = 3.5
- Отнимаем от А величину Х, т.е. получаем B = 50 – 3.5 = 46.5 рублей
Как посчитать процент одного числа от другого?
Для расчета процента одного числа от другого нужно первое число поделить на второе и умножить на 100%
К примеру: сколько процентов составляет 5 от числа 25
Считаем: Процент = 100* 5/25 = 20%
1 миллиард минус 13 процентов сколько будет?
В одной из лотерей счастливчик выиграл 1 миллиард рублей. Вопрос – сколько налогов он заплатит и сколько получит на руки
Для ответа на этот вопрос, можно воспользоваться калькулятором или посчитать вручную согласно алгоритма выше. Один миллиард – это тысяча миллионов.
- Шаг 1. Считаем 13% от 1 миллиарда: 1 000 000 000 * 13/100 = 130 000 000 или 130 миллионов налогов
- Шаг 2. Находим разницу: 1000 000 000 – 130 000 000 = 870 000 000 или 870 миллионов – сумма на руки
Вычисление исходного числа по известному проценту от числа
Формула вычисления числа по его проценту.
Если дано число B которое составляет P процентов от числа A и необходимо найти значение числа A, то
Для вывода этого соотношения используем методику решения задач с процентами через пропорции
“все“”часть” =100%”часть в %“ =>
“все” = “часть” · “100%“часть в %
Примеры вычисления исходного числа по известному проценту от числа
Пример 1.
Найти исходное число, если 5% от этого числа равно 40.
Решение:
Ответ: 800.
Пример 2.
На заводе работает 270 женщины. Это 30% от всех работников. Сколько человек работает на заводе?
Решение:
Ответ: На заводе работает 900.
Пример 3.
Какую сумму нужно положить на депозит под 10% годовых, чтобы через год получить прибыль 1000 рублей.
Решение:
Ответ: на депозит необходимо положить 10000 рублей.
При изучении процентов вам также будут полезны: