Как найти начальную длину пружины по жесткости

На этой странице сайта вы найдете ответы на вопрос Как найти L0(начальная длина пружины) если известны L, масса и коофицент жесткости пружины?,
относящийся к категории Физика. Сложность вопроса соответствует базовым
знаниям учеников 5 – 9 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) )  – начальная длина пружины;

( L left(text{м} right) )  – конечная длина растянутой пружины;

( Delta L left(text{м} right) )  – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

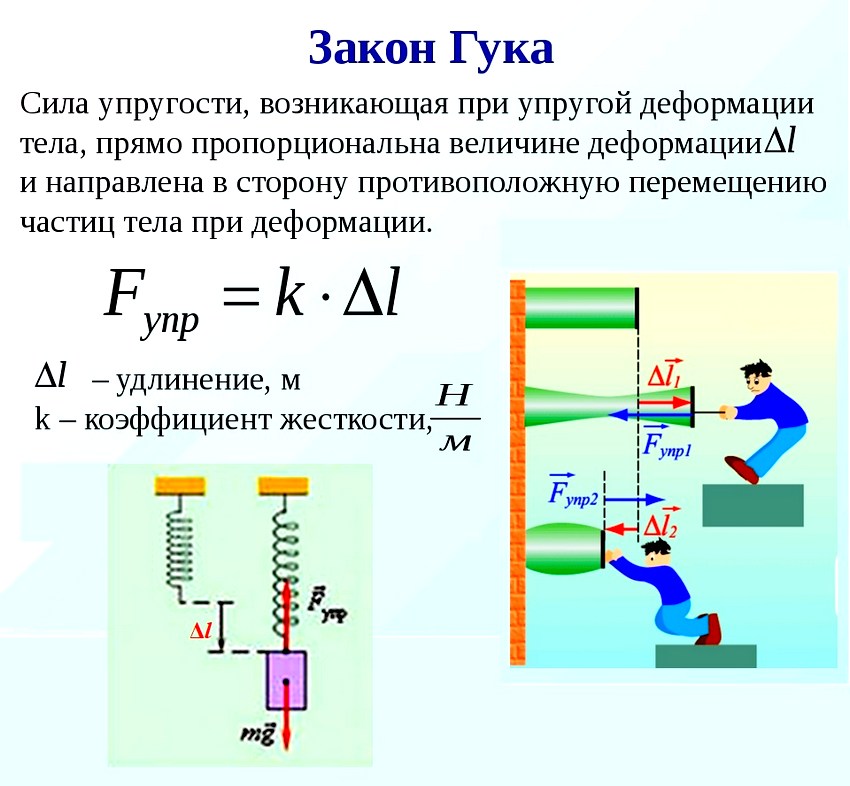
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу,  например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot  left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) )  – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) )  – коэффициент жесткости (упругости) пружины.

Выводы

1. Упругие тела – такие, которые сопротивляются деформации;
2. Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
3. Деформация – изменение формы, или размеров тела;
4. Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
5. Удлинение пружины – это разность ее конечной и начальной длин;
6. Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
7. Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
8. Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
9. А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Найти начальную длину пружинки с жесткостью 100 Н/м, если на ней висит m=500 г и конечная длина пружинки 30 см.

Согласно закону Гука: 

$F=-kx=-k(x-x_0)$            (1)                   

$x=x_0+Delta x$                 (2)

где $F,;k,;Delta x,;x,;x_0$ – соответственно сила реакции пружины, коэффициент жесткости пружины, размер удлинения (сжатия) пружины, длина растянутой (сжатой)  пружины, начальная длина пружины.  Знак “минус” говорит о том, что сила реакции пружины направлена против направления деформации пружины.

Поскольку пружина растянулась и далее пребывает в состоянии покоя, то согласно 3 закону Ньютона сила реакции пружины равна по модулю силе тяжести. Можем записать:

$mg=k(x-x_0)$              $x_0=frac{kx-mg}{k}$

$x_0=frac{100*0,3-0,5*10}{100}=0,25$ м                 

Ответ: 0,25 м  или 25 см

Задачи на силу упругости с решениями

Формулы, используемые на уроке «ЗАДАЧИ на силу упругости с решениями»

Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Под действием груза в 200 Н пружина динамометра удлинилась на 0,5 см. Каково удлинение пружины под действием груза в 700 Н?

ОТВЕТ: 1,75 см.

Задача № 2.
Под действием силы давления вагона 50 кН буферные пружины между вагонами сжимаются на 1 см. С какой силой давит вагон, если пружины сжались на 4 см?

ОТВЕТ: 200 кН.

Задача № 3.
Резиновая лента удлинилась на 10 см под действием силы 10 Н. Какова ее жесткость?

ОТВЕТ: 100 Н/м.

Задача № 4.
Пружина без нагрузки длиной 20 см имеет коэффициент жесткости 20 Н/м. Какой станет длина пружины под действием силы 2 Н?

ОТВЕТ: на 0,1 м.

Задача № 5.
На сколько удлинится пружина под нагрузкой 12,5 Н, если под нагрузкой в 10 Н пружина удлинилась на 4 см?

ОТВЕТ: на 5 см.

Задачи на силу упругости

Задача № 6.
Какой груз нужно подвесить к пружине, жесткость которой 1000 Н/м, чтобы растянуть ее на 10 см?

ОТВЕТ: m ≈ 10 кг.

Задача № 7.
Грузовик взял на буксир легковой автомобиль «Волга» массой m = 2 т и, двигаясь равноускоренно, за 50 с проехал путь 400 м. На сколько удлинился при этом трос, соединяющий автомобили, если его жесткость 2 • 10⁶ Н/м? Трением пренебречь.

ОТВЕТ: на 0,32 мм.

Задача № 8.
На рисунке приведен график зависимости удлинения резинового жгута от модуля приложенной к нему силы. Найти жесткость жгута.

ОТВЕТ: 10 Н/м.

Задача № 9.
Две пружины равной длины, скрепленные одними концами, растягивают за свободные концы руками. Пружина жесткостью 200 Н/м удлинилась на 4 см. Какова жесткость второй пружины, если ее удлинение равно 2 мм?

ОТВЕТ: 4000 Н/м.

Краткая теория к теме
«Задачи на силу упругости»

В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации. Виды упругих деформаций: растяжение, сжатие, кручение, изгиб, сдвиг, срез.

Силы упругости — силы, возникающие при деформации тела и направленные в сторону, противоположную деформации. При небольших деформациях растяжения или сжатия силу упругости можно определить по закону Гука: F_упр = –kx, где x — удлинение/сжатие тела (всегда положительное значение), k — коэффициент пропорциональности (коэффициент упругости), названный жесткостью тела Знак «минус» в законе означает, что сила упругости всегда направлена в сторону, противоположную деформации. Единицы измерения жесткости тела в СИ: 1 Н/м.

В некоторых учебниках и задачниках закон Гука выражают формулой F_упр = k • Δl. В этом случае: Δl — удлинение/сжатие тела (всегда отрицательное значение), k — коэффициент упругости (жесткость) тела.

Иногда, силу упругости, возникающую при деформации опоры, называют силой реакции опоры и обозначают буквой N. Силу упругости, возникающую при деформации нити или каната, называют силой натяжения нити (каната) и обозначают буквой Т.

Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела. Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным. Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.

Конспект урока по физике «ЗАДАЧИ на силу упругости». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:

• Вернуться к Списку конспектов по физике для 7-11 классов
• Найти конспект через Кодификатор ОГЭ по физике
• Найти конспект через Кодификатор ЕГЭ по физике