
Пример решения задачи на расчет деформаций участков и изменение общей длины стального стержня при его растяжении-сжатии.
Задача
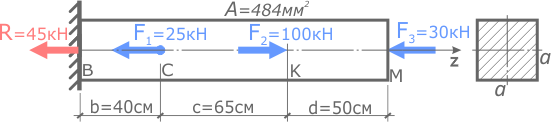
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Другие примеры решений >
Помощь с решением задач >
Модуль продольной упругости стали E=200ГПа.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций,
- Построение эпюр внутренних продольных сил,
- Подбор размеров поперечного сечения стержня,
- Построение эпюр нормальных напряжений.
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
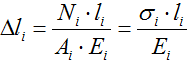
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.
Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).
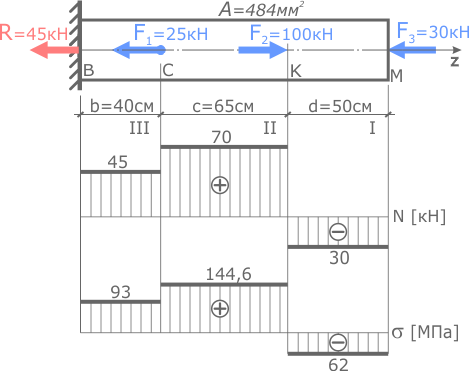
По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Рассчитаем их:
Деформация I участка (KM)
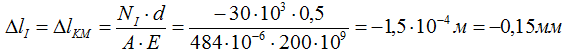
II участок (CK)
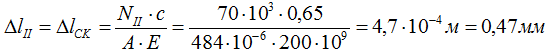
Удлинение третьего участка BC
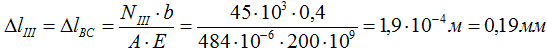
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
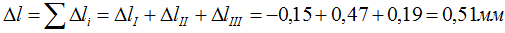
В результате деформации общая длина стержня увеличится на 0,51мм.
Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Помогите решить задачу.
Анастасия Конькова
Знаток
(329),
на голосовании
7 лет назад
Найти Первоначальную длину стержня L0, если в момент растяжения длина равняется L1, относительное удлинение равно Lp%.
Голосование за лучший ответ
ВК
Просветленный
(32923)
7 лет назад
Lp=(L1-L0)/L0*100
отсюда находите L0
Анастасия КоньковаЗнаток (329)
7 лет назад
А как найти L0????
ВК
Просветленный
(32923)
Извините, подсказываю бесплатно, но решаю за плату, пишите на е-майл. Хотя, конечно, с этим вполне сами можете справиться.
vk.com/termehsopromat
Просветленный
(32398)
7 лет назад
Определение относительного удлинения почитайте.
Похожие вопросы
ОБЩИЕ ПОЛОЖЕНИЯ
6.1. Расчетную (эффективную) длину
рекомендуется принимать для расчета,
главным образом, стержневых конструкций
при проверке несущей способности их
отдельных стержней.
Использование понятия расчетной длины
предполагает разделение стержневых
систем на отдельные элементы, при этом
необходимо учитывать взаимодействие
рассматриваемого элемента с основанием
и другими элементами (в первую очередь,
примыкающими к нему в узлах).
Расчетные длины сжатых, внецентренно-сжатых
и сжато-изгибаемых элементов стержневых
и рамных систем необходимо устанавливать
в случаях, когда выполнить расчет
конструкций как единых систем по
деформированной схеме с учетом
пластических деформаций не представляется
возможным.
6.2 (6.8).
Под расчетной длиной стержня обычно
понимают условную длину однопролетного
стержня, критическая сила которого при
шарнирном закреплении его концов такая
же, как для заданного стержня [18].
По физическому смыслу расчетная длина
стержня с произвольными закреплениями
концов является наибольшим расстоянием
между двумя точками перегиба изогнутой
оси, определяемым из расчета этого
стержня на устойчивость по методу
Эйлера.
Согласно этому определению для
установления расчетной длины необходимо
применять метод расчета на устойчивость
систем с прямыми стержнями при приложении
нагрузок в узлах в предположении упругих
деформаций [19].
При этом следует учитывать продольные
усилия в стержнях и, как правило, исключать
из рассмотрения поперечные нагрузки и
эксцентриситеты, вызывающие изгиб
стержней.
При проектировании расчетную длину
стержня
![]()
обычно определяют по формуле
![]()
,
(50)
где
– коэффициент расчетной длины, зависящий
от условий закрепления концов стержня
и вида нагрузки;
l – геометрическая длина рассматриваемого
стержня.
Для плоских стержневых систем расчетную
длину сжатых стержней следует определять
как в плоскости, так и из плоскости
системы (перпендикулярной ей).
6.3. При подборе сечений стержней обычно
выполняется поэлементный расчет,
требующий определения расчетной длины
для каждого стержня. При этом необходимо
принимать такие расчетные схемы, которые
отражают действительные условия
нагружения стержней и закрепления их
концов с учетом неравномерности
распределения нагрузок между стержнями
и различия их жесткостей, наличие
конструктивных элементов, обеспечивающих
ту или иную форму потери устойчивости
здания или сооружения.
В частности, при практическом определении
расчетной длины стоек многоэтажных рам
в нормах, как правило, используется
приближенная расчетная схема в виде
простейшей ячейки независимо от числа
этажей и соотношения продольных сил в
стойках.
Следует отметить, что применение такой
расчетной схемы не предполагает
пропорционального возрастания нагрузок
на систему в целом.
6.4. В СНиП
II-23-81* значения расчетной длины
стержней для различных систем приведены,
как правило, для наиболее неблагоприятных
случаев нагружения и работы системы,
т.е. зачастую с некоторым запасом. Поэтому
в дальнейшем, наряду с разъяснением
требований норм, будут приведены также
и более строгие расчетные схемы для
определения и уточнения значений
расчетной длины на основе учета
действительной работы системы и схемы
загружения.
Расчетная длина стержней одной и той
же системы различна при разных сочетаниях
нагрузок, хотя в п.
6.11* СНиП II-23-81* по этому поводу
имеется упрощающее разрешение. В связи
с этим при проектировании возможно
уточнение значений расчетной длины в
соответствии с тем сочетанием нагрузок,
при котором выполняется подбор сечений
некоторых стержней.
ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ДЛИН ЭЛЕМЕНТОВ
6.5 (6.9*).
Коэффициенты
для определения расчетной длины элементов
постоянного сечения в зависимости от
условий закрепления концов и характера
нагружения следует принимать по табл.
21 и
2
2.
Таблица 21
──────┬──────────────────────────────────────────┬────────────────
N
п/п│ Расчетная схема стержня
│ Коэффициент мю
──────┴──────────────────────────────────────────┴────────────────
1
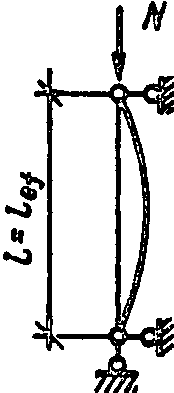
1,0
──────────────────────────────────────────────────────────────────
2
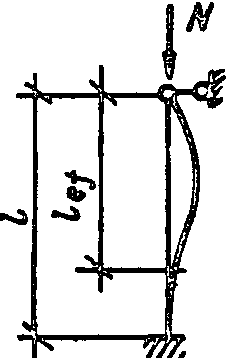
0,7
──────────────────────────────────────────────────────────────────
3
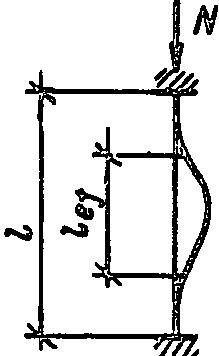
0,5
──────────────────────────────────────────────────────────────────
4
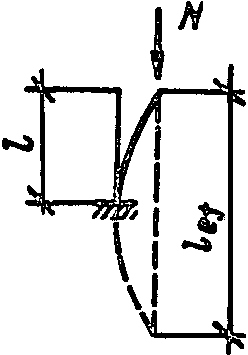
2,0
──────────────────────────────────────────────────────────────────
5

2,0
──────────────────────────────────────────────────────────────────
6
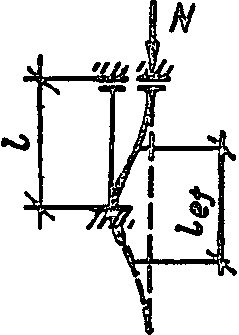
1,0
Таблица 22
──────┬──────────────────────────────────────────┬────────────────
N
п/п│ Расчетная схема стержня
│ Коэффициент мю
──────┴──────────────────────────────────────────┴────────────────
1
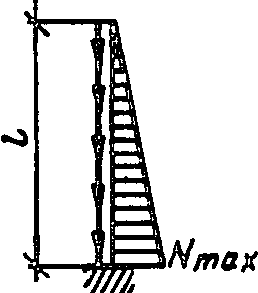
1,12
──────────────────────────────────────────────────────────────────
2
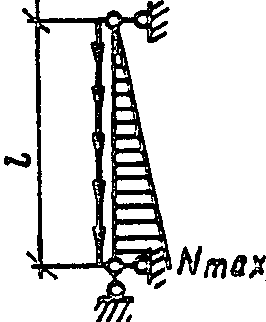
0,73
──────────────────────────────────────────────────────────────────
3
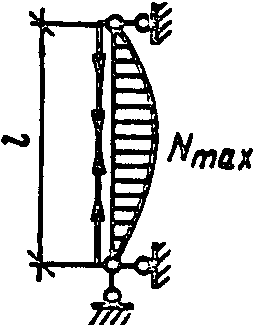
0,69
──────────────────────────────────────────────────────────────────
4
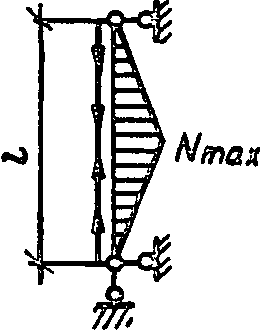
0,56
6.6. Коэффициенты
для установления расчетной длины
элементов постоянного сечения с упругими
закреплениями концов следует определять
по формулам табл. 23.
Таблица 23
Обозначения, принятые в табл. 23:
![]()
;
![]()
;
![]()
–
коэффициент жесткости упругого
защемления, равный значению реактивного
момента, возникающего в опорном сечении
при повороте его на угол, равный 1,0;
![]()
–
коэффициент жесткости упругой опоры,
равный значению реактивной силы,
возникающей в опорном сечении при
смещении его на 1,0.
В табл. 24 приведены примеры определения
коэффициентов
и
.
Таблица 24
──────────┬───────────────────────────────┬───────────────────────
N
п/п │ Расчетная схема системы │
Определение
│ │ мю
= l /l
│ │ ef
│ │ по
формуле табл.
23
──────────┴───────────────────────────────┴───────────────────────
1
(VI) при
![]()
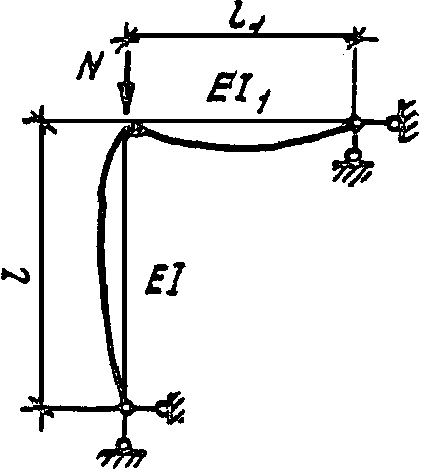
──────────────────────────────────────────────────────────────────
2
(VI) при
![]()
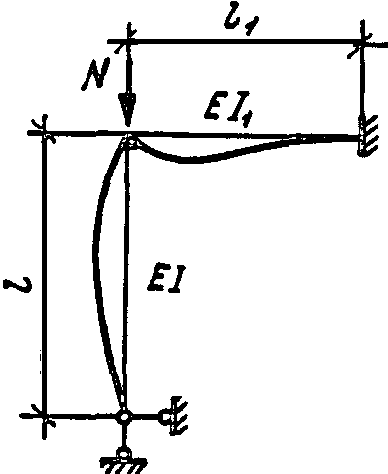
──────────────────────────────────────────────────────────────────
3
(V) при
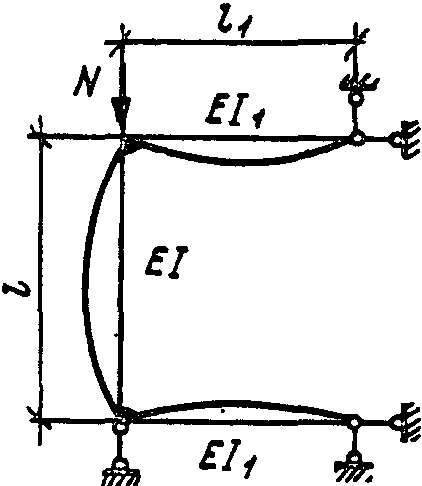
──────────────────────────────────────────────────────────────────
4
(I) при
![]()
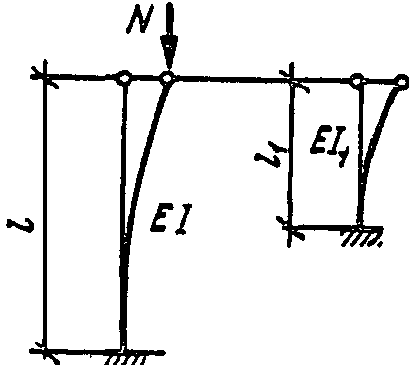
──────────────────────────────────────────────────────────────────
5
(IV) при
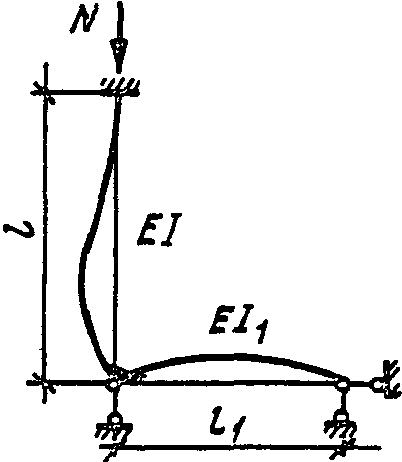
──────────────────────────────────────────────────────────────────
6
(IV) при

──────────────────────────────────────────────────────────────────
7
(IV) при
![]()

──────────────────────────────────────────────────────────────────
8
(III) при
![]()
=![]()

──────────────────────────────────────────────────────────────────
6.7 (6.3*).
Коэффициенты
и
![]()
для установления расчетной длины
![]()
пересекающихся элементов постоянного
сечения в зависимости от конструктивной
схемы узла пересечения следует определять
по формулам табл. 25.
Таблица 25
Приведенные в табл. 25 расчетные схемы
соответствуют следующим случаям
загружения и конструкции пересечения
элементов в узле:
1) оба элемента не прерываются,
поддерживающий элемент сжат;
2) оба элемента не прерываются,
поддерживающий элемент растянут;
3) рассматриваемый элемент не прерывается,
поддерживающий элемент сжат, прерывается
и перекрывается фасонкой;
4) рассматриваемый элемент не прерывается,
поддерживающий элемент растянут,
прерывается и перекрывается фасонкой;
5) рассматриваемый элемент прерывается
и перекрывается фасонкой, поддерживающий
элемент растянут и не прерывается.
На рис.
13 приведено сопоставление значений
коэффициентов
и
пересекающихся стержней, определенных
по формулам
табл. 25 и по
табл. 12 СНиП II-23-81*. Как следует из
рис. 13, коэффициенты, согласно
СНиП II-23-8
1*,
не зависят от соотношения усилий в
стержнях и совпадают с точными значениями
только при неработающем поддерживающем
стержне.
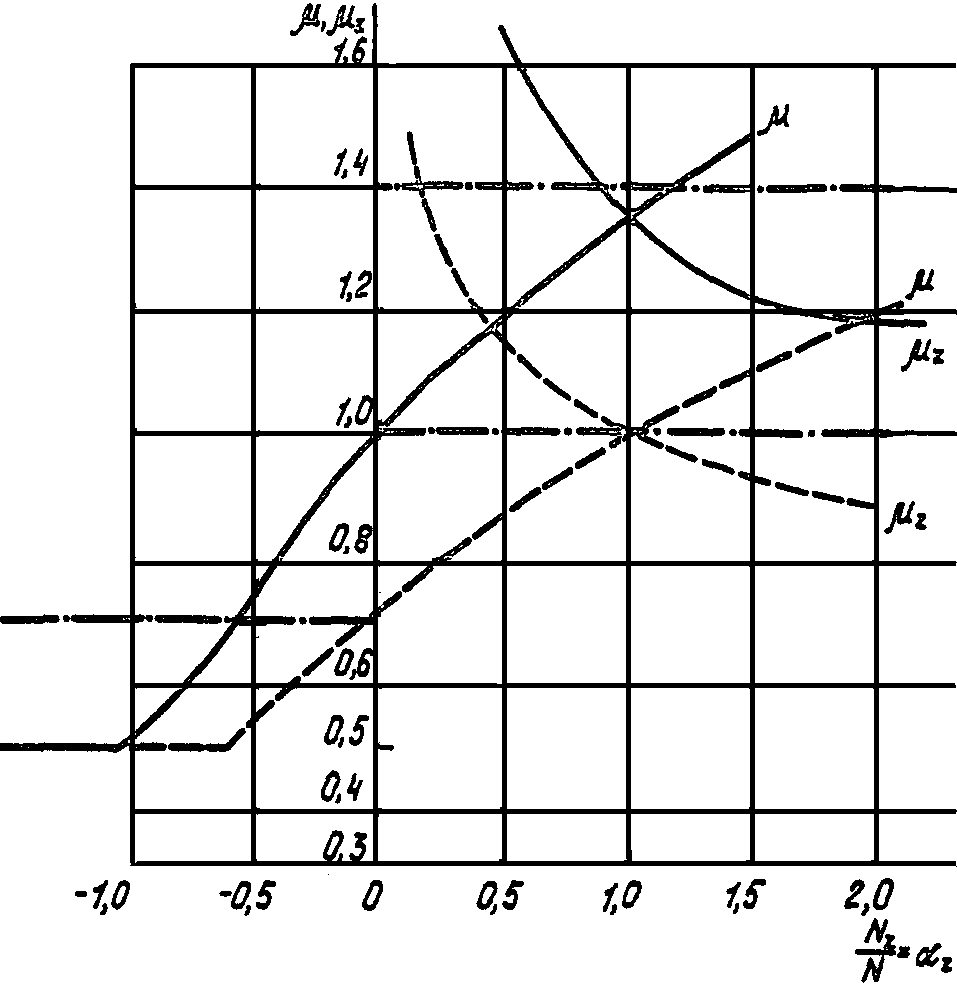
Условные обозначения:
![]()
–
по
СНиП II-23-81
*
![]()
–
по схемам 1 и 2
табл. 2
5
![]()
–
по схемам 3 и 4
табл. 2
5
Рис. 13. График для определения значений
коэффициентов
расчетных длин пересекающихся стержней
(при равных длинах
и жесткостях) при различных усилиях в
них
6.8. Расчетные длины
![]()
неразрезных стержней постоянного
сечения с различными сжимающими или
растягивающими усилиями в пролетах как
в плоскости, так и из плоскости конструкции
можно определять по формулам табл. 26.
Граничные условия, приведенные в поз.
1 и 2 табл. 26, соответствуют расчетной
схеме верхнего пояса фермы, а в поз. 3 и
4 – подкрановой ветви решетчатой колонны.
При вычислении параметра
по поз. 2 и 4 табл. 26 растягивающие усилия
в стержнях необходимо принимать со
знаком “минус”.
Таблица 26
6.9 (6.10*).
Коэффициенты расчетной длины
колонн постоянного сечения свободных
рам в плоскости рамы при жестком креплении
ригелей к колоннам и при одинаковом
нагружении верхних узлов следует
определять по формулам
табл. 17, а СНиП II-23-81*. При этом
вместо
формул (70, а) и
(70, б
)
при предельных значениях параметров p
и n допускается пользоваться формулами
табл. 27.
Таблица 27
─────────────────┬────────────────┬────────────────────────────────────────
p
│ n │ Формулы для определения
коэффициента мю
─────────────────┴────────────────┴────────────────────────────────────────
![]()
От
0,03 до 0,2 ![]()
———————————————————-
Св.
0,2 ![]()
───────────────────────────────────────────────────────────────────────────
0
От 0,03 до 0,2 ![]()
———————————————————-
Св.
0,2 ![]()
───────────────────────────────────────────────────────────────────────────
0,03
<= p <= 50
![]()
6.10. Коэффициенты расчетной длины
![]()
колонн постоянного сечения несвободных
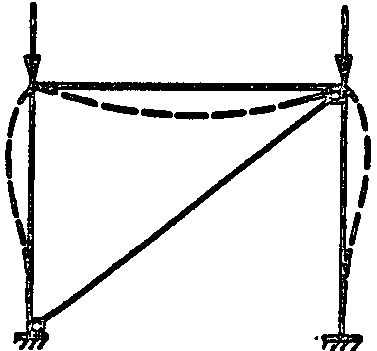
рам (рис.
14) в плоскости рамы при жестком
креплении ригелей к колоннам и при
одинаковом нагружении верхних узлов
следует определять по
формуле 70,
в
СНиП II-23-81*. При этом в частных случаях
эта формула может быть упрощена:
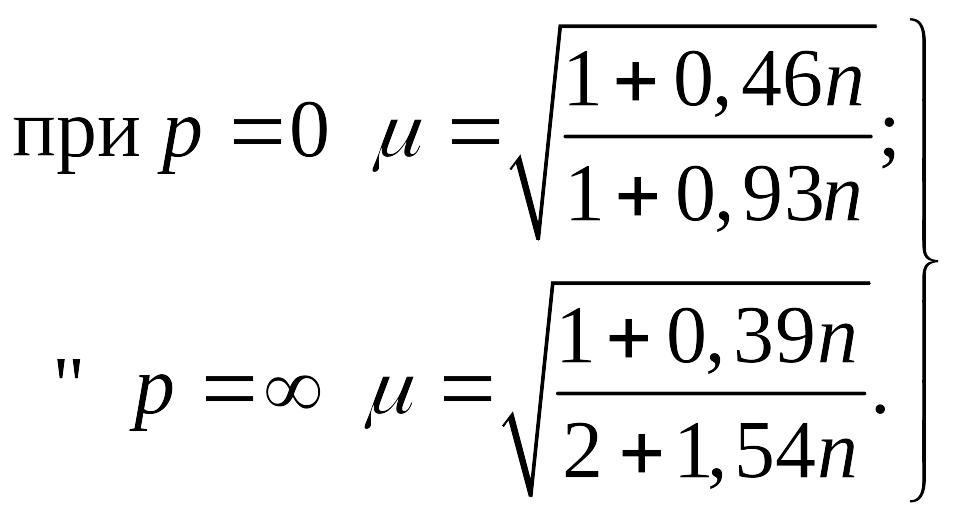
(51)
а)
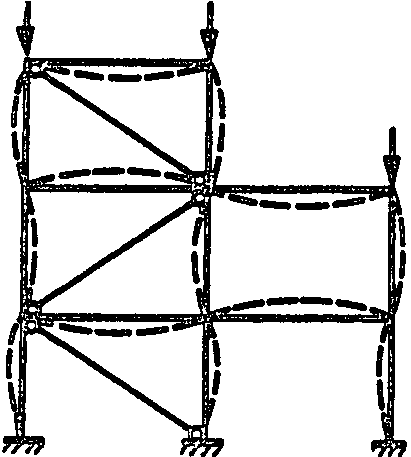
б)

в)
Рис. 14. Схемы деформаций несвободных
рам
а – одноэтажных; б – многоэтажных; в –
многопролетных
6.11. При наличии жесткого диска покрытия
или продольных связей по верху колонн
в расчетный блок допускается включать
по две рамы с каждой стороны, перпендикулярной
плоскости рассматриваемой рамы. При
этом коэффициент
![]()
расчетной длины наиболее нагруженной
колонны постоянного сечения в
производственном здании с кранами
(мостовыми или подвесными) при неравномерном
распределении нагрузок от крана следует
определять по формуле
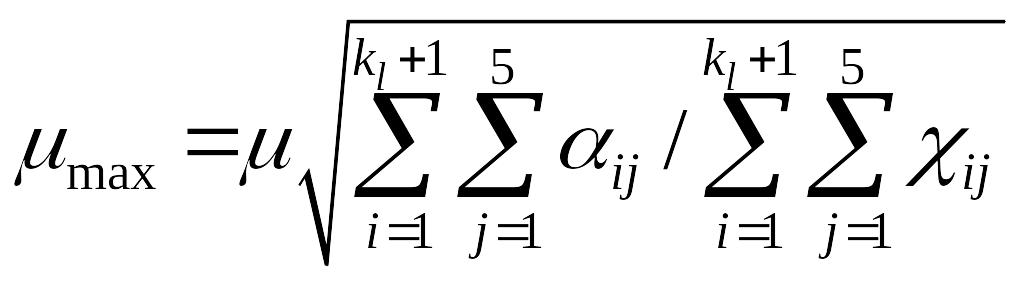
;
(52)
(но не менее 0,7
),
где
– коэффициент расчетной длины
рассматриваемой колонны одно- и
многопролетного здания при равномерном
нагружении узлов, определенный согласно
пп. 6.9 и
6.1
0;
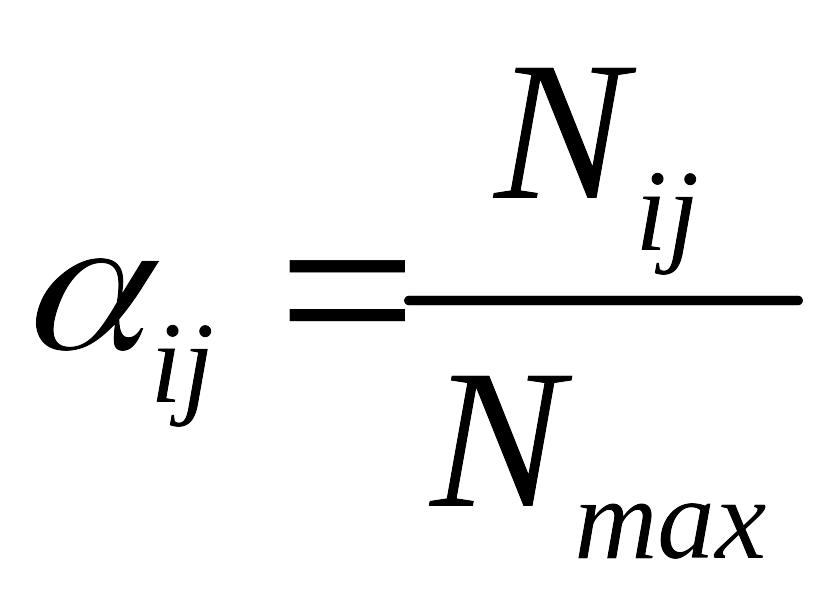
;
здесь
![]()
– усилие в наиболее нагруженной колонне
рассматриваемой плоской рамы;
![]()
–
усилия во всех колоннах (в том числе в
рассматриваемой) расчетного блока;
![]()
;
![]()
–
момент инерции наиболее нагруженной
колонны рассматриваемой плоской рамы;
![]()
–
моменты инерции всех колонн расчетного
блока;
i = 1, 2,…,
![]()
– номер колонны в плоскости рамы (![]()
– число пролетов);
j = 1, 2, 3, 4, 5 – номер рамы.
6.12 (6.11*).
Коэффициенты
![]()
расчетной длины нижнего участка
одноступенчатых колонн при различном
креплении их верхних концов следует
определять в зависимости от соотношения
нагрузок, длины и жесткостей верхнего
и нижнего участков по формулам табл.
28, в которой приведены конструктивные
схемы производственных зданий,
соответствующие различным расчетным
схемам колонн, и
табл. 2
9.
Таблица 28
Обозначения, принятые в табл. 28:
![]()
;
![]()
;
![]()
;
![]()
;
![]()
.
Таблица 29
Обозначения, принятые в табл. 29:
;
.
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ РАСЧЕТНЫХ ДЛИН
СТОЕК РАМ
Пример 1. Рассмотрим случаи определения
коэффициентов
расчетной длины стоек при предельных
значениях n и p.
При n и p, стремящихся к бесконечности,
по формулам табл.
27 находим:
а) при p =
![]()
и n = 0,2
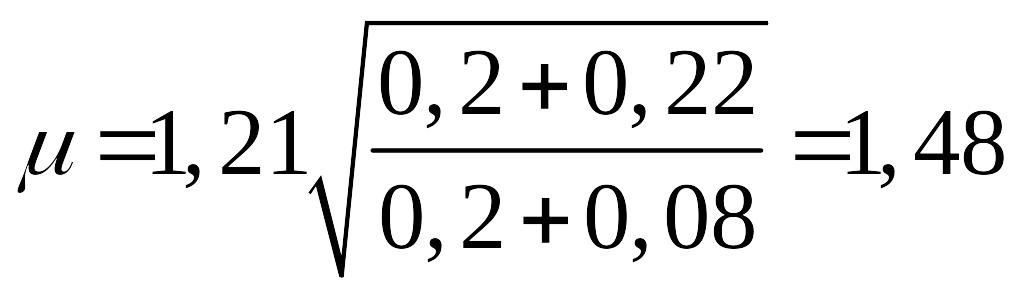
;
б) при p =
и n = 5,0
![]()
.
При p = 50 и n = 0,2 и n = 5,0 согласно п.
6.10* СНиП II-23-81* получим соответственно
= 1,49 и
= 1,03.
В случае шарнирного закрепления в
фундаменте стойки одного яруса рамы
рекомендуется пользоваться формулами
табл.
27 при p = 0 и n > 0,2. Откуда находим:
а) при p = 0 и n = 1,0
![]()
;
б) при p = 0 и n =
![]()
.
Пример 2. Требуется определить значения
коэффициентов расчетной длины
средних колонн многопролетных и
многоэтажных зданий.
1. Исходные данные. Двухпролетная
одноэтажная рама с жестким закреплением
колонн в фундаментах и жестким креплением
ригелей к колоннам постоянного сечения.
Здесь и далее в примерах принимаем
![]()
;
![]()
(одинаковые пролеты и сечения ригелей);
![]()
= 3;
![]()
= 0,2;
а) здание, нагруженное силами N во всех
узлах по верху колонн.
При k = 2 и ![]()
вычислим
![]()
;
по табл.
17, а СНиП II-23-81*
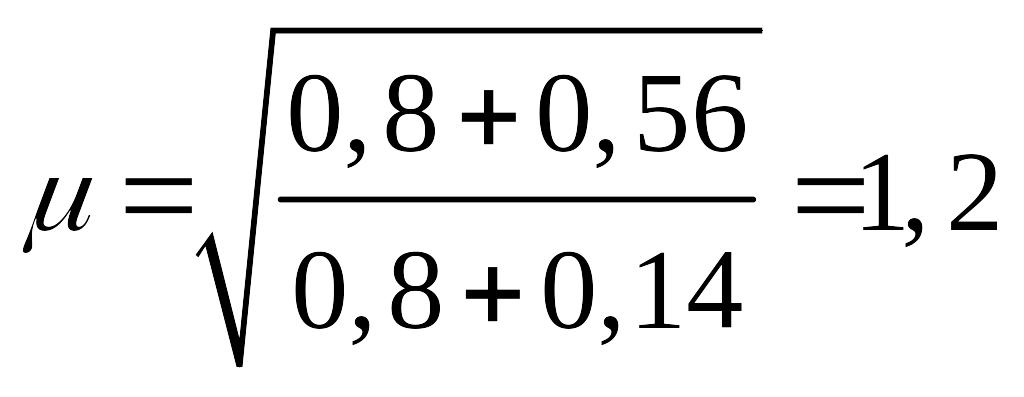
;
б) здание при неравномерном нагружении
узлов в плоскости рамы (одной колонны
силой N, а двух других – силами 0,5N).
По формуле
(52) при
![]()
= 1 + 0,5 + 0,5 = 2 и
![]()
= 3
![]()
;
в) здание при наличии продольных связей
в конструкции и нагружении в расчетном
блоке (из пяти рам) одной колонны в
средней раме силой N и двух других колонн
в средней раме силами 0,5N, а остальных
колонн в четырех рамах – силами 0,3N.
Тогда
= 12 x 0,3 + 2 x 0,5 + 1 = 5,6 и
= 15.
По формуле
(52)
![]()
;
г) здание при нагружении одной колонны
в средней раме силой N, двух других колонн
силами 0,3N и всех колонн в оставшихся
четырех рамах расчетного блока силами
0,1N.
При
= 12 x 0,1 + 2 x 0,3 + 1 = 2,8 и
= 15.
по формуле
(52)
![]()
.
Так как вычисленное
< 0,7, следует принять
= 0,7 (см.
поз. 2 табл.
21);
д) конструкция обеспечена от возможности
боковой потери устойчивости системы в
целом и ее можно отнести к категории
несвободной рамы.
При n = 0,8 по формуле
(51)
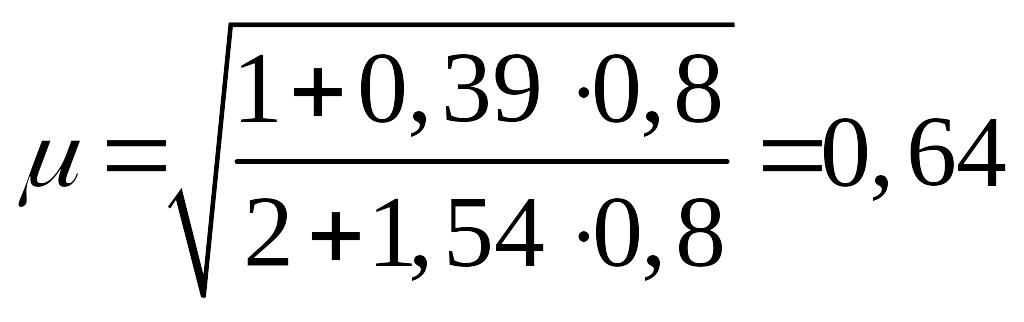
.
2. Исходные данные. Десятипролетная
одноэтажная рама с жестким закреплением
колонн в фундаментах и жестким креплением
ригелей равных пролетов и сечений к
колоннам постоянного сечения нагружена
силой N во всех узлах:
а)
= 3;
= 0,2.
При k = 10 и
![]()
![]()
;
по табл.
17, а СНиП II-23-81*
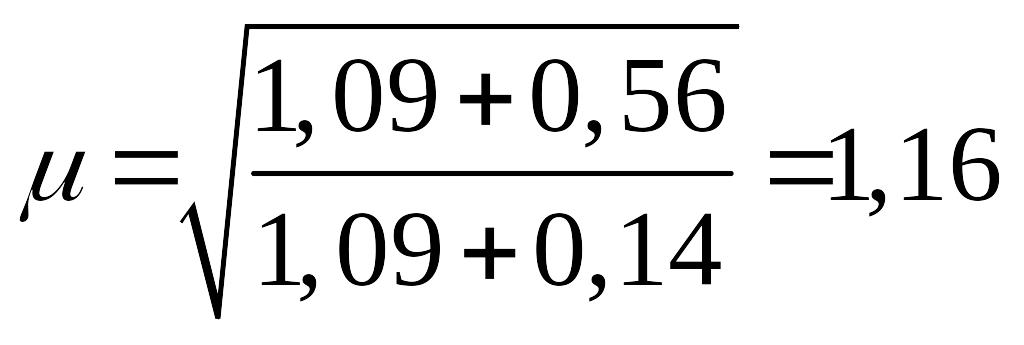
;
б)
= 3;
= 2.
При k = 10 и
![]()
![]()
;
по табл.
17, а СНиП II-23-81*
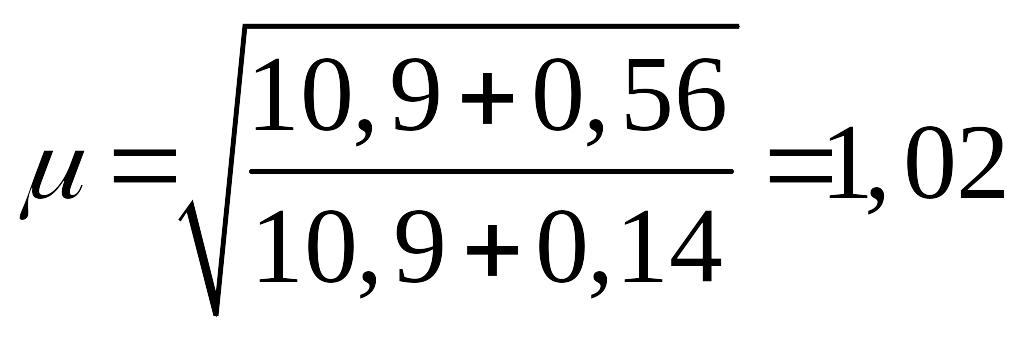
.
Пример 3. Требуется определить значения
коэффициентов
расчетной длины нижнего участка
одноступенчатых колонн при различных
значениях параметров, приведенных в
табл. 28 и
2
9:
1) для схемы 1 при
![]()
= 0,2, m = 2,0,
![]()
= 0,5, n = 0,25 вычислим
![]()
= 1,6; при 1,35 – 035
![]()
= 0,91 > n по формуле поз.
1 табл. 28
![]()
= 3,28;
2) для схемы 1 при
![]()
= 0 и m = 2,0,
= 0,5, n = 0,25 вычислим
= 8,0; при 1,35 – 0,35
= 0,36 > n по формуле поз.
1 табл. 28
= 7,15;
3) для схемы 2 при
= 0,2, m = 2,0,
= 0,5, n = 0,25 вычислим
= 1,6; при 1,35 – 0,35
= 0,91 > n по формуле поз.
2 табл. 28
= 2,12;
4) для схемы 2 при
= 0,8, m = 2,0,
= 1,2 > 1, n = 0,6 вычислим
= 2,7; при 1,35 – 0,35
= 0,78 > n по формуле поз.
2 табл. 28
= 2,59;
5) для схемы 3 при
![]()
= 0 и
= 0, m = 2,0;
= 0,04, n = 0,02 по формуле поз.
5 табл. 29
= 1,86;
6) для схемы 3 при
= 0 и
= 1,0, m = 0,1,
= 1,0, n = 10,0 по формуле поз.
6 табл. 29
= 0,77;
7) для схемы 4 при
= 0 и
= 0, m = 2,0;
= 0,04, n = 0,02 по формуле поз.
7 табл. 29
= 1,83;
8) для схемы 4 при
= 0 и
= 1,0, m = 0,1,
= 1,0, n = 10,0 по формуле поз.
8 табл. 29
= 0,55.
6.13 (6.15*).
Ограничения гибкостей сжатых стержней
вводятся с целью повышения экономичности
и надежности стальных конструкций. В
определенной мере это реализуется за
счет более полного использования
прочностных свойств стали как материала,
поскольку с увеличением гибкости
стержней уровень использования прочности
стали уменьшается. Отсюда следует, что
применять высокопрочные стали при
больших гибкостях экономически
нецелесообразно. Ограничения гибкостей
способствуют также уменьшению искривлений
стержней при изготовлении, транспортировании
и монтаже. Для стержней, сечения которых
назначаются по предельным гибкостям,
допускается увеличить предельную
гибкость в соответствии со СНиП
II-23-81*.
Абсолютное удлинение стержня формула
Формула абсолютного удлинения стержня, связывающая продольную силу, длину стержня и жесткость, имеет вид:
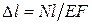
Формулу абсолютного удлинения стержня иногда называют законом Гука, но не для материала, а для всего стержня, а стоящее в знаменателе произведение 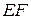 – жесткостью стержня при растяжении (сжатии).
– жесткостью стержня при растяжении (сжатии).
Определение расчетной длины стержней



В момент потери устойчивости сжатый стержень выпучивается, поворачивается вокруг центров соответствующих узлов и вследствие жесткости фасонок заставляет поворачиваться и изгибаться в плоскости фермы остальные стержни.
Примыкающие стержни сопротивляются изгибу и повороту узла и
Препятствуют свободному изгибу стержня, теряющего устойчивость.
Наибольшее сопротивление повороту узла оказывают растянутые стержни. Сжатые стержни слабо сопротивляются изгибу.
Таким образом, чем больше растянутых стержней примыкает к сжатому стержню и чем они мощнее (больше их погонная жесткость), тем выше степень защемления стержня и меньше его расчетная длина; влиянием сжатых стержней на защемление можно пренебречь.
Сжатый пояс оказывается слабо защемленным в узлах, так как с каждой стороны к нему примыкает только по одному растянутому раскосу, погонная жесткость которых значительно меньше погонной жесткости пояса. Поэтому защемлением сжатого пояса в запас устойчивости можно пренебречь и принимать его расчетную длину равной расстоянию между смежными узлами.
Таким образом, при большей степени защемления меньше расчетная длина стержня фермы
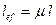 , (9.4)
, (9.4)
где 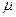 — коэффициент приведения длины, зависящий от степени защемления;
— коэффициент приведения длины, зависящий от степени защемления;
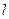 — расстояние между центрами узлов.
— расстояние между центрами узлов.
По нормам коэффициент приведения длины “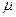 ” элементов решетки из
” элементов решетки из
уголков в плоскости фермы равен 0,8. Тогда расчетная длина 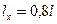 в плоскости фермы определяется с некоторым запасом, в особенности для средних раскосов, жесткость которых по сравнению с примыкающими стержнями невелика.
в плоскости фермы определяется с некоторым запасом, в особенности для средних раскосов, жесткость которых по сравнению с примыкающими стержнями невелика.
Исключение составляет опорный восходящий раскос, условия работы которого в плоскости фермы такие же, как и у верхнего пояса, поэтому расчетная длина опорного раскоса в плоскости фермы принимается равной расстоянию между центрами узлов.
Расчетная длина пояса в плоскости, перпендикулярной плоскости фермы, принимается равной расстоянию между узлами, закрепленными связями от смещения из плоскости фермы.
В беспрогонных покрытиях верхний пояс стропильных ферм закреплен в плоскости кровли плитами или панелями настила, прикрепленными к поясам ферм в каждом узле. В этом случае за расчетную длину пояса из плоскости фермы принимают ширину одной плиты.
Расчетная длина стержней решетки при выгибе их из плоскости фермы принимается равной расстоянию между геометрическими центрами узлов, так как фасонки очень гибки и рассматриваются как листовые шарниры.
В трубчатых фермах с бесфасонными узлами расчетная длина раскоса, как в плоскости фермы, так и из нее, с учетом повышенной крутильной жесткости замкнутых сечений применятся равной 0,9.
В других случаях расчетная длина элементов ферм принимается по нормали.
Источник
25. Определение расчетных длин
От правильности задания расчётных длин элементов конструкций зависит надежность принятых конструктивных решений.
В большинстве случаев определение расчетных длин происходит согласно нормативных документов. Но нормативные документы рассматривают далеко не все возможные случаи.
В качестве примера рассматривается каркасное здание пролётом 10 метров с колоннами из двутавра 40К1 и ригелями из двутавра 40Б1 (рис. 1).
Рис. 1. Расчётная модель здания. ПК ЛИРА 10.
Дл я определения расчетных длин кол онн с определенной погрешностью можно использовать формулу 142 таблицы 31 СП 16.13330.2011, а для ригелей, которые в таких рамах, наряду с изгибом, испытывают также и сжатие, нормы не дают ответа по определению расчетной длины.
Поэтому, для определения расчетных длин элементов рамы в плоскости, воспользуемся подсистемой «устойчивость». Для этого возьмем плоскую раму и зададим на нее нагрузку для определения свободных длин (рис. 2).
Для анализа устойчивости схемы проектировщик должен составить характерное загружение, или характерную комбинацию загружений (РСН), по которой будет происходить определение расчетных длин элементов. Характерных загружений, или комбинаций загружений может быть несколько, для различных групп элементов. При этом следует руководствоваться п. 10.3.2 СП 16.13330.2011, согласно которому при определении расчетных длин следует брать сочетание, создающее наибольшие значения продольных сжимающих сил N в рассматриваемых элементах, и полученные расчетные длины использовать при проверке устойчивости для всех возможных комбинаций РСУ. Таким образом, для нашего объекта характерная комбинация загружений для определения расчетных длин включает (со своими коэффициентами сочетаний) все постоянные, длительные и снеговые загружения, но не включает ветер.
Рис. 2. Плоская рама для определения расчётных длин. ПК ЛИРА 10
В редакторе загружений выбираем Выполнять Анализ устойчивости (рис. 3).
Рис. 3. Настройка параметров для расчёта устойчивости
Далее переходим в результаты расчёта и выбираем результаты по устойчивости.
Необходимо смотреть на первую форму потери устойчивости, дающую максимальные расчётные длины. Расчёт устойчивости по характерной комбинации загружений подтвердил, что первой, наиболее опасной, формой потери устойчивости ожидаемо является кососимметричная форма (рис. 4).
Рис. 4. Первая форма потери устойчивости. ПК ЛИРА 10
Если в этом режиме нажать левой кнопкой мыши на элемент, то появиться таблица с характеристиками расчётной длины этого элемента (рис. 5).
При определении расчетных длин следует также иметь в виду, что для анализа устойчивости принято, чтобы продольные сжимающие силы N в пределах рассматриваемых участков были неизменными. В нашем случае, как для колонн, так и для ригелей имеется равномерно-распределённая составляющая нагрузки вдоль стержня, обеспечивающая плавное изменение усилия N, что не вполне корректно. Соответственно, меняется и расчётная длина элемента на различных участках. Чем больше сжимающая сила, тем меньше получается расчётная длина. Здесь проектировщик должен обращать внимание на то, чтобы эта равномерно-распределённая составляющая нагрузка вдоль стержня не играла бы решающую роль в работе стержня, а разброс расчётных длин в пределах конструктивного элемента был бы несущественным. Далее, следуя логике пункта 10.3.2 норм СП 16.13330.2011, расчётную длину элемента следует брать в том месте, где сила N максимальная, т. е. там, где расчётная длина минимальна. Однако, подозревая, что максимальный эффект от совместного действия силы N и момента Му в месте жёсткого соединения ригеля с колонной, мы бы рекомендовали брать величину расчётной длины как для колонны, так и для ригеля именно в этом месте.
Окончательный же выбор остаётся за автором расчёта.
Получаем для колонн расчётную длину 14.1 м, а для ригелей 13.3 м (рис. 6).
Если считать по формуле (142), расчётная длина колонны получилась бы 11.7 м. Однако, формула (142) не учитывает двускатную форму ригеля, а это при значительных уклонах может существенно повлиять на результат.
Рис. 5. Расчетная длина колонн. ПК ЛИРА 10
Рис. 6. Расчётная длина ригелей. ПК ЛИРА 10
Теперь, задав эти параметры в редакторе конструирования (рис. 7), можем производить расчёт конструирования и получать точные результаты по подбору и проверке МК.
Рис. 7. Задание параметров конструирования для колонн и ригелей. ПК ЛИРА 10
Более подробно методика определения расчетных длин и другие вопросы рассматриваются на наших курсах обучения. Будем рады видеть вас среди наших учеников.
Источник
Центрально-растянутые элементы
где γс – коэффициент условия работы
Центрально-сжатые элементы
N / φ · A ≤ Ry · γс
где φ – коэффициент продольного изгиба, учитывающий снижение несущей способности гибкого элемента; зависит от гибкости элемента λ = lef / i и расчётного сопротивления стали (табл. 72 СНиП II-23);
lef – расчётная длина элемента (табл. 11,12,13,14,16,17 СНиП II-23).
Для колонн, стоек lef = μ· l; l – расчётная длина колонны, отдельного её участка или высоты этажа; μ – коэффициент расчётной длины, зависит от условий закрепления на опорах и вида нагрузки.
Для предварительных расчётов коэффициент φ принимается в пределах φ = 0,5…0,9, для поясов ферм, опорных подкосов и колонн – в пределах φ = 0,7…0,9, для прочих элементов φ = 0,5…0,6.
Пример 1. Подобрать сечение стержня решетки стальной фермы, работающей в климатическом районе II4. На стержень действует растягивающее усилие N =200 кН (нагрузка статическая). Геометрическая длина стержня (расстояние между узлами) l = 3000 мм. Предельная гибкость λmax = 400. Толщина фасонки t =10 мм.
Решение.
1. Учитывая климатический район (http://map.teploov.ru/ ) и то, что фермы относятся к конструкциям группы 2 (табл. 50* СНиП II-23-81*), принимаем из рекомендованных сталей сталь С245.
2. Находим расчетное сопротивление стали по пределу текучести (табл. 2.2): Ry = 240 МПа = 24,0 кН/см 2 (при толщине проката 2−20 мм).
3. Определяем коэффициент условий работы γс = 0,95 (табл. 2.3).
4. Определяем расчетные длины стержня (см. табл. 11 СНиП II-23-81*):
расчетная длина в плоскости фермы:
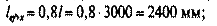
расчетная длина в плоскости, перпендикулярной плоскости фермы:
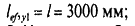
5. Находим требуемую площадь сечения стержня:
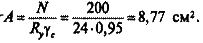
6. По сортаменту прокатной угловой стали (Приложение 1, табл. 3) подбираем уголки, при этом учитываем, что сечение стержня состоит из двух уголков; площадь одного уголка будет равна:
А1у= 8,77/2 = 4,39 см 2 ; принимаем 2 уголка 50 х 50 х 5; А1у=4,8 см 2 ; ix =1,92 см; iyl= 2,45 см.
7. Проверяем принятое сечение:
а) проверяем прочность:

б) проверяем гибкость:
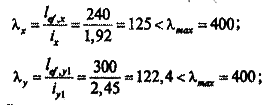
гибкость в пределах норм.
Вывод. Принимаем сечение стержня из двух уголков 50 х 50 х 5, сталь С245.
Пример 2. Подобрать сечение стержня решетки фермы (рис. 9.12), работающей в климатическом районе II4. На стержень действует сжимающее усилие N = 359 кН (нагрузка статическая). Геометрическая длина стержня l = 4520 мм. Предельная гибкость λmax = 210 − 60α, (см. табл. 5.4). Толщина фасонки t = 10 мм.
Решение.
1. Учитывая, что климатический район строительства II4, фермы относятся к конструкциям группы 2 (табл. 50* СНиП II-23-81*), из допускаемых к использованию сталей принимаем сталь С345-1.
2. Находим расчетное сопротивление стали по пределу текучести Rу = 335 МПа = 33,5 кН/см 2 (при толщине проката 2−10 мм, табл. 2.2).
3. Определяем коэффициент условий работы (табл. 2.3): предполагая, что гибкость стержня будет больше 60, принимаем по п. 3 табл. 2.3 γс = 0,8; также для нашего случая подходит коэффициент условия работы по п. 6а табл. 2.3, γс = 0,95; принимаем в расчет меньшее значение коэффициента γс =0,8.
4. Определяем расчетные длины стержня: расчетная длина в плоскости фермы lef,x = 0,8l = 0,8 ∙ 4520 = 3616 мм; расчетная длина в плоскости, перпендикулярной плоскости фермы, lef,y1= l =4520 мм (табл. 11 СНиП II-23-81*).
5. Находим требуемую площадь сечения стержня из формулы устойчивости; для этого предварительно принимаем гибкость стержня λ= 100 и по гибкости находим коэффициент продольного изгиба φ = 0,493 (табл. 5.3):

6. Определяем требуемые радиусы инерции:
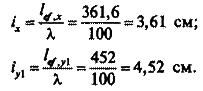
7. По сортаменту (Приложение 1, табл. 2) подбираем уголки по трем параметрам: A, ix, iy1; при подборе уголков не забываем, что площадь стержня состоит из двух уголков; требуемая площадь одного уголка А1y = 27,17/2 = 13,59 см 2 ; принимаем уголки: 2 уголка 100 x 8; А1y = 15,6 см 2 ; ix,= 3,07 см; iy1= 4,47 см (принятое сечение имеет площадь больше требуемой, а радиусы инерции имеют значения меньше, но близкие к требуемым).
8. Проверяем принятое сечение:
а) определяем гибкости:
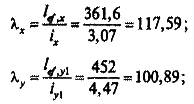
б) по наибольшей гибкости λ =117,59 определяем (табл. 5.3) коэффициент продольного изгиба φ = 0,473;
в) находим значение коэффициента α:
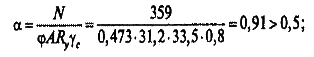
так как значение коэффициента получилось больше 0,5, принимаем величину коэффициента α = 0,91;
г) определяем предельную гибкость:
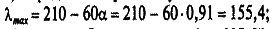
наибольшая гибкость стержня λх = 117,59, что меньше предельной гибкости λmax = 155,4, следовательно, гибкость стержня в пределах нормы;
д) проверяем устойчивость:
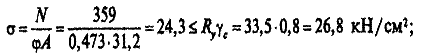
Вывод. Принимаем сечение стержня из двух уголков 100 x 8, сталь С345-1.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ №2
Задача 1. Подобрать сечение растянутого стержня решётки стальной фермы. На стержень действует усилие N=…кН, Геометрическая длина стержня l=…мм. Предельная гибкость λ=400. Толщина фасонки t=…мм.
Задача 2. Подобрать сечение сжатого стержня решётки стальной фермы. На стержень действует усилие N=…кН. Геометрическая длина стержня l=…мм. Предельная гибкость λmax=210-60α. Толщина фасонки t=…мм.
Таблица 1 Исходные данные
| № варианта | Марка стали | Усилие | Длина стержня | Толщина фасонки |
| 1 | С245 | 100 | 3000 | 8 |
| 2 | С345 | 120 | 3200 | 10 |
| 3 | С245 | 140 | 3300 | 12 |
| 4 | С345 | 150 | 3400 | 14 |
| 5 | С245 | 160 | 3500 | 16 |
| 6 | С345 | 170 | 3600 | 12 |
| 7 | С245 | 180 | 3700 | 14 |
| 8 | С345 | 200 | 3800 | 16 |
| 9 | С245 | 210 | 3900 | 12 |
| 10 | С345 | 220 | 4000 | 10 |
| 11 | С245 | 230 | 4100 | 14 |
| 12 | С345 | 240 | 4050 | 15 |
| 13 | С245 | 250 | 4150 | 10 |
| 14 | С345 | 260 | 4200 | 12 |
| 15 | С245 | 270 | 3950 | 14 |
| 16 | С345 | 280 | 4250 | 16 |
| 17 | С245 | 290 | 4300 | 10 |
| 18 | С345 | 300 | 5350 | 12 |
| 19 | С245 | 310 | 4400 | 14 |
| 20 | С345 | 320 | 4450 | 16 |
| 21 | С245 | 330 | 4500 | 10 |
| 22 | С345 | 340 | 4520 | 12 |
| 23 | С245 | 350 | 4530 | 14 |
| 24 | С345 | 360 | 4540 | 16 |
| 25 | С245 | 370 | 4550 | 10 |
| 26 | С345 | 380 | 4560 | 12 |
| 27 | С245 | 290 | 4570 | 14 |
| 28 | С345 | 400 | 4580 | 16 |
| 29 | С245 | 410 | 4590 | 10 |
| 30 | С345 | 420 | 4600 | 12 |
ПРАКТИЧЕСКАЯ РАБОТА №3
Тема: Расчёт колонны сплошного сечения
В результате выполнения работы студент должен:
ü знать работу сжатых конструкций под нагрузкой и особенности их работы в зависимости от материала; возможный характер потери несущей способности;;
ü уметь рассчитать, т.е. подобрать сечение или проверить несущую способность стальной колонны из прокатного двутавра или трубы.
Теоретическое обоснование:
При расчёте стержня колонны строительные нормы предписывают выполнение следующих расчётов: по прочности, по потере общей устойчивости, а также при этом необходимо ограничивать гибкость.
Расчёт прочности выполняют по формуле
Расчёт на устойчивость выполняют по формуле
Проверка гибкости выполняется по формуле
Из приведённых формул можно решать два типа задач: определять размеры сечения колонн (тип 1) или проверять несущую способность (тип 2).
Общий порядок подбора сечения стержня колонны (тип 1)
1. Определяют нагрузку на колонну.
2. Устанавливают расчётную схему.
3. Находят расчётную длину колонны по формуле
4. Назначают тип поперечного сечения стержня колонны: труба, прокатный двутавр, составное сечение из прокатных профилей и т.д.
5. Принимают сталь для колонны: выбор стали зависит от конструкции колонны, величины нагрузок, климатического района и условий эксплуатации, экономического обоснования. Для рассматриваемых примеров будем принимать любую из сталей: С235, С245, С275, С345.
6. Для принятой стали определяют расчётное сопротивление по пределу текучести Rу.
7. Определяют коэффициент условия работы колонны γс.
8. Определяют требуемую площадь поперечного сечения стержня.
Поскольку в формуле два неизвестных – А и φ, то одной из величин необходимо задаться, т.е. принять предварительно, а затем выполнить проверочный расчёт.
9. Определяют требуемый радиус инерции
10. По найденным площади и радиусу инерции сечения, пользуясь сортаментом прокатных профилей, принимают сечение стержня колонны и выписывают фактические характеристики принятого сечения.
11. Проводят проверку принятого сечения и при необходимости выполняют уточнение его размеров.
Проверку устойчивости производят по формуле
А – принятая площадь сечения. Сортамент прокатных профилей не позволяет подобрать площадь, в точности равную требуемой, поэтому коэффициент продольного изгиба определяется заново по наибольшей фактической гибкости подобранного сечения колонны.
Наибольшую гибкость колонны находят по формуле
По таблице в зависимости отRу и λmax находят действительный коэффициент продольного изгиба φ.
При условии σ = NφА ≤ Rуγс несущая способность колонны обеспечена (перенапряжение недопустимо, недонапряжение не превышает 5%).
12. Независимо от выполненного расчёта необходимо, чтобы гибкость колонны не превышала предельной λпред. Предельные гибкости сжатых элементов принимаются по табл. 19 СНиП II-3-81 (для основных колонн они определяются по формуле λпред =180−60α, где коэффициент α = N/φА Rуγс ≥ 0,5).
Проверка насущей способности(задача 2 типа) является составной частью решения задачи по подбору сечения (необходимо выполнить пп. 2, 3, 6, 7, 11, 12 порядка расчёта).
Пример 1. Используя данные примера 7 (практическая работа №2),стальную колонну рассчитать для здания магазина. Колонна выполнена из прокатного двутавра с параллельными гранями полок. Нагрузка N =566,48 кН.Коэффициент надёжности по ответственности принимаем γn =0,95; нагрузка с учётом коэффициента надёжности по ответственности N =566,48∙0,95 =538,16кН. Колонна фактически выполняется высотой в два этажа, но расчётная длина принимается равной высоте одного этажа, так как учитывается её закрепление в перекрытии lef = 3,6м.
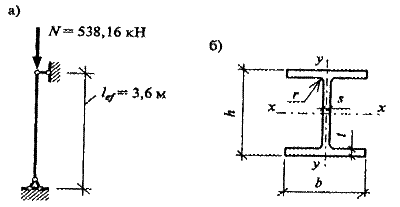
Решение.
1. Определяем группу конструкций по табл. 50 (СНиП). Принимаем сталь С245 по ГТСО 27772-88 (см. Приложение 1, табл. 2)
3. При расчётах на устойчивость принимаем коэффициент условия работы γ = 1 (табл.2.3). Задаёмся гибкостью колонны λ = 100, что соответствует коэффициенту продольного изгиба φ ≈ 0,488 (табл. 5.3). Определяем требуемую площадь:
4. Определяем требуемый минимальный радиус инерции (по заданной гибкости λ = 100): i = lef//λ = 360/100 = 3,6см.
5. По требуемым площади и радиусу инерции сечения подбираем двутавр по сортаменту двутавров с параллельными гранями полок. Ближе всего подходит двутавр 23Ш1. Который имеет следующие характеристики: А =4 6,08см 2 ; ix =9,62см; iy = 3,67см.
6. Проверяем подобранное сечение:
· определяем наибольшую фактическую гибкость (наибольшая гибкость будет относительно оси y-y, так как радиус инерции сечения относительно оси y-y меньше радиуса инерции сечения относительно оси x-x, а расчётные длины относительно этих осей одинаковы):
· по наибольшей гибкости определяем фактическое значение коэффициента продольного изгиба φ, с интерполяцией φ = 0,566 (см. табл. 5.3);
· проверяем условие, чтобы гибкость была не больше предельной гибкости, установленной СНиП II-23-81. Для основных колонн предельная гибкость определяется по формулеλпред =180−60α
λпред = 180-60α = 180-60α = 180-60∙0,875 = 127,5;
λ y = 98,09‹λпред = 127,5, гибкость в пределах нормы;
Вывод: несущая способность стержня колонны обеспечена. Принимаем в качестве стержня двутавр 23Ш1.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ №3
Задача 1. Подобрать сечение основной стальной колонны, выполненной из прокатного двутавра: коэффициент надёжности по нагрузке γn=0,95, коэффициент условия работы γс = 1. Исходные данные см. табл. 1.
Задача 2. Определить несущую способность стальной второстепенной колонны, выполненной из прокатного двутавра; коэффициент условия работы γс = 1. Исходные данные см. табл. 1.
Таблица 1 Исходные данные
№варианта
Задача 1
Задача 2
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4
Тема: Расчёт и конструирование сборной железобетонной колонны
поперечных стержней. Конструирование каркаса.
В результате выполнения работы студент должен:
ü знать работу сжатых конструкций под нагрузкой и особенности их работы в зависимости от материала; возможный характер потери несущей способности и предпосылки для расчёта; правила конструирования колонн;
ü уметь рассчитать, т.е. подобрать сечение или проверить несущую способность железобетонной колонны квадратного сечения (со случайным эксцентриситетом).
Теоретическое обоснование:
Основная расчётная формула для центрально сжатых колонн прямоугольного (квадратного) сечения имеет вид: N ≤ φ[ Rsс ( As+ As ’ ) + Rb γ b2 bh],
гдеRsc – расчётное сопротивление сжатой арматуры (табл. 2.8);
Rb – расчётное сопротивление бетона сжатию (табл. 2.6);
b и h – размеры поперечного сечения колонны, см;
As и As ’ – площади сечения арматуры, соответственно по одной стороне сечения и по другой;
φ – коэффициент продольного изгиба колонны:
где φb иφsb определяются по табл. 5.6 в зависимости от отношения расчётной длины колонныl0 к меньшей стороне сечения колонны h и от отношения нагрузок – соответственно длительной части нагрузки ко всей нагрузке Nl / N.
При расчёте колонн гражданских зданий расчётную длину можно принимать равной высоте этажа l0 = Hэт.(в общем случае l0= μ l):
где μ – коэффициент армирования:
На основании базовой формулы решаются 2 типа задач: подбор сечения арматуры (тип 1) и проверка несущей способности колонны (тип 2).
Общий порядок подбора сечения рабочей арматуры (тип 1)
1. Определяют нагрузку, если она не задана по условию задачи (полное значение нагрузки N и её длительную часть Nl ).
2. Устанавливают расчётную схему.
3. Принимают расчётную длину колонны l0.
4. Задаются следующими значениями:
а) принимают размеры поперечного сечения b, h(рекомендуется размеры сечения принимать не менее 30см и далее кратно 5,0см);
б) принимают материалы для колонны:
· обычно принимают тяжёлый бетон классов прочности В20−В35 и находят расчётное сопротивление бетона сжатииRb ;
· принимают класс арматуры, обычно А-III, А-II, и находят расчётное сопротивление арматуры сжатию Rsc;
5. Определяют коэффициент α s.
6. Определяют коэффициент продольного изгиба φ: если значения lo/ h и Nl / N не совпали с табличными, необходимо провести интерполирование.
7. Определяют требуемую площадь арматуры по формуле
· если в результате получают отрицательное значение, это говорит о том, что бетон один (без арматуры) справляется с нагрузкой (в этом случае иногда возможно уменьшить размеры поперечного сечения колонны и заново произвести расчёт или колонна армируется конструктивно, учитывая, что арматуру необходимо ставить обязательно, чтобы обеспечить минимальный процент армирования);
· если получают положительное значение требуемой площади арматуры, то по полученной площади назначаем диаметр арматуры (Приложение 3);
· для армирования принимают 4 стержня арматуры (приh ≤ 400 мм) и располагают их по углам колонны (возможно армировать и большим количеством стержней);
· при подборе арматуры следует учитывать, что диаметр продольных стержней монолитных колонн должен быть не менее 12мм; в колоннах с размером меньшей стороны сечения ≥ 250 ммдиаметр продольных стержней рекомендуется назначать не менее 16 мм;диаметр продольных стержней обычно принимают не более40мм.
8. Проверяют действительный процент армирования:
Если действительный процент армирования находится в пределах от μ min до 3%, то на этом заканчивается подбор арматуры, в противном случае необходимо скорректировать принятую арматуру или сечение элемента.
10. Назначают шаг поперечных стержней s:
s ≤ 20 ds в сварных каркасах, но не более 500мм;
s ≤ 15 ds в вязаных каркасах, но не более 500мм.
11. Конструируют каркас колонны.
Проверка несущей способности колонны (тип 2) сводится к проверке условия
Решение.
1. Для расчёта колонны собираем расчётную нагрузку (её полное значение Nи длительную часть нагрузки Nl):
· нагрузка от собственного веса железобетонной колонны:
Nколонны = N n γf =16,31∙1,1 = 17,94 кН;
· нагрузка на низ колонны
· находим длительную часть нагрузки на низ колонныNl , для чего необходимо из всей нагрузки вычесть кратковременную часть нагрузки
В соответствии с табл. 3.3 длительная нормативная нагрузка на перекрытие торговых залов составляет pl n =1,4 кПа,а полное значение нормативной нагрузки на перекрытие
p n = 4,0 кПа и коэффициент надёжности по нагрузке γа = 1,2, следовательно
N1 = N – 0,5 sAгр − p n γfAгр + pl n γfAгр = 563,7 − 0,5 ∙ 2,1∙27 − 4∙1,2∙27 + 1,4∙1,2∙27 = 451,11 кН;
· с учётом коэффициента γ n=0,95 нагрузка равна:
N = 563,7∙0,95 = 535,52 кН;
N1 = 451,11∙0,95 = 428,55 кН
2. Задаёмся материалами колонны: бетон тяжёлый класса В20;γ b2= 0,9;продольная арматура класса А-III; поперечная арматура класса Вр-I; расчётные сопротивления: Rb = 11,5 МПа; Rsc = 365 МПа.
3. Определяем расчётную длину колонны; расчётная длина колонны принимается равной высоте этажа: l0 = 3,6м.
4. Находим отношения:
10. Проверяем процент армирования:
μ=(As+ As ’ )100/ bh = 8,04 ∙ 100/30 ∙ 30 = 0,893%,что больше минимального значения μ min= 0,4% и меньше максимального значения μ max = 3,0%;
принятая арматура обеспечивает необходимый процент армирования.
11. Назначаем диаметры и шаг постановки поперечных стержней: dsw ≥ 0,25ds=0,25 ∙ 16 = = 4мм; принимаем поперечную арматуру Ø4 Bр-I; шаг поперечных стержней s: s ≤20ds=20∙16=320мм, округляем и принимаем шаг s=300мм.
12. Конструируем сечение колонны.
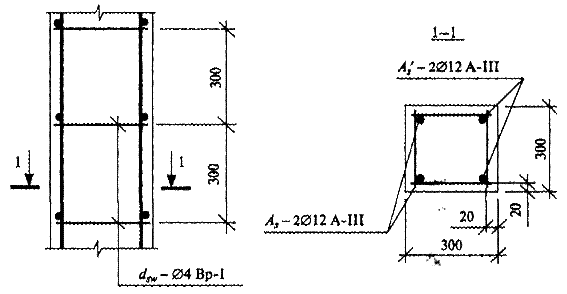
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ №4
Задачи №1,2,3 решить согласно условиям, а задачу № 4 – взять исходные данные из таблицы 1согласно варианта.
Задача 1. Подобрать класс арматуры и диаметры поперечных стержней для железобетонной колонны, определить их шаг, если продольные стержни каркаса колонны приняты диаметром 25 мм, А-III.
Задача 2. Рассчитать железобетонную колонну. Нагрузка, действующая на колонну, N = 640 кН; Nl =325 кН. Коэффициент надежности по ответственности γn = 0,95. Нагрузка приложена со случайным эксцентриситетом. Сечение колонны 350 х 350 мм, армирование симметричное. Высота колонны Н =4,9 м, закрепление концов колонны шарнирное. Арматура — продольная класса А-II; поперечная Вр-I. Бетон тяжелый класса В20; γb2 =0,9.
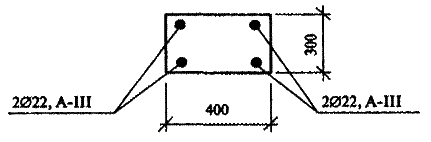
Задача 3. Проверить несущую способность железобетонной колонны, на которую действует нагрузка N =250 кН. Нагрузка приложена со случайным эксцентриситетом; длительная часть нагрузки Nl = 125 кН; коэффициент надежности по ответственности γn = 0,95. Расчетная длина колонны l0 = 3,0 м. Армирование симметричное AS = A’ S =(2 Ø22 мм). Арматура класса А-III. Бетон тяжелый, класс прочности бетона В20; γb2 = 0,9. Сечение колонны 300 x 400 мм (рис. 2).
Задача 4. Подобрать арматуру железобетонной колонны со случайным эксцентриситетом. Коэффициент надежности по ответственности γn = 1,0. Коэффициент условия работы бетона γb2 = 0,9. Исходные данные в таблице 1
Таблица 1 Исходные данные
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5
Тема: Расчёт кирпичного центрально сжатого армированного столба
В результате выполнения работы студент должен:
ü знать работу сжатых конструкций под нагрузкой и особенности их работы в зависимости от материала; возможный характер потери несущей способности и предпосылки для расчёта; правила конструирования колонн;
ü уметь рассчитать, т.е. подобрать сечение или проверить несущую способность кирпичного столба не армированного и с сетчатым армированием.
Теоретическое обоснование:
Источник



