Переменный синусоидальный ток
Колебания маятника также
подчиняются закону синуса.
Если
записать проекцию траектории
движения математического
маятника на
движущуюся бумажную ленту —
получится синусоида.
Синусоидальным
током называется периодический переменный
ток, который с течением времени изменяется
по закону синуса.
Синусоидальный ток —
элементарный, то есть его невозможно
разложить на другие более простые
переменные токи.
Переменный
синусоидальный ток выражается формулой:
,
где
—
амплитуда
синусоидального тока;
—
некоторый угол,
называемый фазой
синусоидального тока.
Фаза синусоидального
тока 
изменяется
пропорционально времени 
.
Множитель 
,
входящий в выражение фазы 
—
величина постоянная, называемая угловой
частотой переменного
тока.
Угловая
частота 
синусоидального
тока зависит от частоты 
этого
тока и определяется формулой:
,
где
—
угловая частота
синусоидального тока;
—
частота синусоидального
тока;
— период синусоидального
тока;
—
центральный
угол окружности,
выраженный в радианах.
Зависимость
синусоидального тока от времени
Зависимость
синусоидального тока от угла ωt
Периоду 
соответствует
угол 
,
половине периода 
угол 
и
так далее…
Исходя
из формулы 
,
можно определить размерность угловой
частоты:
,
где
— время в секундах,
—
угол в радианах,
является безразмерной величиной.
Фаза 
синусоидального
тока измеряется радианами.
1
радиан = 57°17′, угол 90° = 
радиан,
угол 180° = 
радиан,
угол 270° = 
радиан,
угол 360° = 
радиан,
где 
радиан; 
— число
«Пи», ° — угловой
градус и ′ — угловая
минута.
Формула 
описывает
случай, когда наблюдение за изменением
переменного синусоидального тока
начинается с момента времени 
при 
.
Если 
не
равен нулю, тогда формула для определения
мгновенного значения переменного
синусоидального тока примет следующий
вид:
,
где
— фаза переменного
синусоидального тока;
— угол,
называемый начальной
фазой переменного синусоидального
тока.
Начальная
фаза переменного тока 
Начальная
фаза переменного тока 
Если
в формуле 
принять 
,
то будем иметь
, 
и 
.
Начальная
фаза — это фаза синусоидального тока
в момент времени 
.
Начальная
фаза переменного синусоидального тока
может быть положительной 
или
отрицательной 
величиной.
При 
мгновенное
значение синусоидального тока в момент
времени 
положительно,
при 
—
отрицательно.
Если
начальная фаза 
,
то ток определяется по формуле 
.
Мгновенное значение его в момент
времени 
равно
,
то есть равно положительной амплитуде
тока.
Если
начальная фаза 
,
то ток определяется по формуле 
.
Мгновенное значение его в момент
времени 
равно
,
то есть равно отрицательной амплитуде
тока.
9. Идеальные элементы
электрической цепи синусоидального
тока
11.
Неразветвленная
цепь синусоидального тока. Резонанс
напряжений
Резонанс
напряжений –
резонанс, происходящий в
последовательном колебательном
контуре при
его подключении к источнику
напряжения, частота которого
совпадает с собственной
частотой контура.
Описание явления
Пусть
имеется колебательный контур с частотой
собственных колебаний f,
и пусть внутри него работает генератор
переменного тока такой же частоты f.
В
начальный момент конденсатор контура
разряжен, генератор не работает. После
включения напряжение на генераторе
начинает возрастать, заряжая конденсатор.
Катушка в первое мгновение не пропускает
ток из-за ЭДС самоиндукции. Напряжение
на генераторе достигает максимума,
заряжая до такого же напряжения
конденсатор.
Далее:
конденсатор начинает разряжаться на
катушку. Напряжение на нем падает с
такой же скоростью, с какой уменьшается
напряжение на генераторе.
Далее:
конденсатор разряжен до нуля, вся энергия
электрического поля, имевшаяся в
конденсаторе, перешла в энергию магнитного
поля катушки. На клеммах генератора в
этот момент напряжение нулевое.
Далее:
так как магнитное поле не может
существовать стационарно, оно начинает
уменьшаться, пересекая витки катушки
в обратном направлении. На выводах
катушки появляется ЭДС индукции, которое
начинает перезаряжать конденсатор. В
цепи колебательного контура течет ток,
только уже противоположно току заряда,
так как витки пересекаются полем в
обратном направлении. Обкладки
конденсатора перезаряжаются зарядами,
противоположными первоначальным.
Одновременно растет напряжение на
генераторе противоположного знака,
причем с той же скоростью, с какой катушка
заряжает конденсатор.
Далее:
катушка перезарядила конденсатор до
максимального напряжения. Напряжение
на генераторе к этому моменту тоже
достигло максимального.
Возникла
следующая ситуация. Конденсатор и
генератор соединены последовательно
и на обоих напряжение, равное напряжению
генератора. При последовательном
соединении источников питания их
напряжения складываются.
Следовательно,
в следующем полупериоде на катушку
пойдет удвоенное напряжение (и от
генератора, и от конденсатора), и колебания
в контуре будут происходить при удвоенном
напряжении на катушке.
В
контурах с низкой добротностью напряжение
на катушке будет ниже удвоенного, так
как часть энергии будет рассеиваться
(на излучение, на нагрев) и энергия
конденсатора не перейдет полностью в
энергию катушки). Соединены как бы
последовательно генератор и часть
конденсатора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Переменный синусоидальный ток
Переменный ток – это ток, который периодически изменяется как по модулю, так и по направлению. Появляется переменный ток благодаря электромагнитной индукции. Электромагнитная индукция это явление возникновения тока в замкнутом контуре при изменении магнитного потока проходящего через него. Чтобы понять, как именно возникает ток, представим себе рамку (кусочек проволоки прямоугольной формы), которая находится под воздействием магнитного поля B.
Пока рамка находится в покое, тока в ней нет. Но как только мы начнём её поворачивать, электроны, которые находятся в рамке, начнут перемещаться вместе с ней, то есть двигаться в магнитном поле. Вследствие этого магнитное поле начинает действовать на электроны, заставляя их двигаться по рамке. Чем больше линий магнитного поля пронизывает рамку, тем сила действующая на электроны больше, следовательно, и электрический ток тоже. Получается, что ток достигает максимума в момент, когда рамка перпендикулярна магнитному полю (наибольшее количество линии пронизывает рамку) и равен нулю, когда параллельна (наименьшее количество линии пронизывает рамку). Соответственно и сила, которая действует на электроны, тоже изменяется. После прохождения момента, когда рамка параллельна вектору магнитной индукции B, ток в ней начинает течь в обратную сторону.
Ток, который получается при вращении рамки, изменяясь во времени, описывает синусоиду, то есть является синусоидальным. Переменный синусоидальный ток является частным случаем периодического переменного тока. Закон, описывающий изменение тока, имеет вид:
Амплитуда Im – это наибольшая абсолютная величина, которую принимает периодически изменяющийся ток.
Начальная фаза ψ – аргумент синусоидального тока (угол), отсчитываемый от точки перехода тока через нуль к положительному значению.
Время, за которое ток в проводнике дважды изменяет своё направление, называют периодом T. Период измеряется в секундах.
Циклической частотой f называется величина обратная периоду . Измеряется в Герцах, в домашней розетке циклическая частота тока равна 50 Гц, её также называют промышленной частотой. При такой частоте период тока равен 
, это значит, что за две сотых секунды ток в нашей розетке меняет свое направление два раза.
Угловая частота ω показывает с какой скоростью изменяется фаза тока и определяется как
Среднее значение Iср синусоидального тока за период Т определяют из геометрических представлений: площадь прямоугольника с основанием T/2 и высотой Iср приравнивают площади ограниченной кривой тока:
После упрощения получаем формулу:
Действующее значение синусоидального тока определяется из энергетических представлений: действующий ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как и данный ток i. То есть действующее значение, это своеобразная аналогия между переменным и постоянным током.
Для синусоидального тока действующее значение определяется по формуле:
или
Это основное что нужно знать о переменном синусоидальном токе.
Читайте также – Мгновенная мощность
Мгновенное значение синусоидального тока определяется выражением
где 
— максимальное значение или амплитуда тока. Аргумент синуса 
называется фазой. Угол ψ равен фазе в начальный момент времени (t=0) и поэтому называется начальной фазой. Фаза с течением времени непрерывно растет. После ее увеличения на 2π весь цикл изменения тока повторяется. Поэтому, когда говорят о фазе для какого-либо момента времени, обычно отбрасывают целое число 2π так, чтобы значение фазы находилось в пределах 
или в пределах, от 0 до 2π. В течение периода Т фаза увеличивается на 2π. Величина 2π/Т показывает скорость изменения фазы и обозначается буквой ω. Принимая во внимание, что f=1/Т, можно написать
Это выражение, связывающее ω и f, послужило основанием называть ω угловой частотой. Измеряется w числом радианов, на которое увеличивается фаза в секунду. Так, например, при f=50 Гц имеем ω=314 рад/с. Введя в (3.1) обозначение ω для угловой частоты, получим
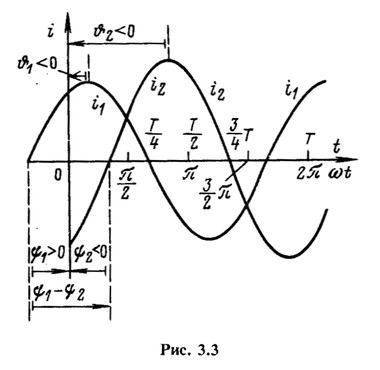На рис. 3.3 построен график синусоидальных токов одинаковой частоты, но с различными амплитудами и начальными фазами:
По оси абсцисс отложены время t и пропорциональная времени величина ωt.
Начальная фаза отсчитывается всегда от момента, соответствующего началу синусоиды (нулевое значение синусоидальной величины при переходе ее от отрицательных к положительным значениям), до момента начала отсчета времени t=0 (начало координат). При 
начало синусоиды тока 
сдвинуто влево, а при 
для тока 
— вправо от начала координат.
Мгновенное значение синусоидального тока можно представить и в виде косинусоидальной функции времени
где 
Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты относительно друг друга по фазе. Сдвиг фаз измеряется разностью фаз, которая, очевидно, равна разности начальных фаз. На рис. 3.3, например, 
, т.е. ток 
опережает по фазе ток 
на угол 
, или, что то же самое, ток 
отстает по фазе от тока 
на угол 
.
Если у синусоидальных функций одной и той же частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе, если разность их фаз равна 
, то говорят, что они противоположны по фазе, и, наконец, если разность их фаз равна 
, то говорят, что они находятся в квадратуре.
Тема 3. Цепи синусоидального тока
- Общие сведения и определения
- Комплексная амплитуда
- Действующие значения синусоидальной функции
- Изображение синусоидальных функций векторами. Векторная диаграмма
- Изображение синусоидальной функции комплексными числами
- Закон Ома в комплексной форме
- Уравнения элементов в комплексной форме
- § 3.1. Общие сведения и определения:
Переменный ток имеет большее распространение, чем постоянный.
Объясняют это:
- конструкция электродвигателей и генераторов переменного тока гораздо проще;
- генераторы переменного тока могут быть выполнены для более высокого напряжения;
- переменный ток легко преобразовывается с помощью трансформатора, что необходимо при распределении электроэнергии и т.д.
Переменный ток – ток, периодически меняющий свое значение и направление. Наибольшее значение переменного тока – его амплитуда.
Переменный ток характеризуется:
- амплитудой;
- периодом;
- частотой;
- фазой.
Амплитуда – наибольшие (положительные или отрицательные) величины.
Период – время, в течение которого происходит полное колебание тока в проводнике.
Частота – обратно периоду.
Фаза – характеризует состояние переменного тока в любой момент времени.
Основным видом переменного тока является синусоидальный (гармонический) ток. Закон изменения такого тока описывается синусоидальной функцией.
В линейных электрических цепях, в которых действуют синусоидальные источники, все электрические параметры изменяются по синусоидальному закону.
ЭДС: 
.
Напряжение: 
.
Ток: 
;
где:
e(t), u(t), i(t) – мгновенные значения;
εm,Um,Im – амплитуды;
(ωt + ψ) – фаза, [рад];
ω = 2π – угловая частота, [рад/с];
ƒ = 1Т – циклическая частота, [Гц];
Т – период, [с];
ψe, ψu, ψi – начальная фаза, [рад].
Любую синусоидальную функцию можно изобразить в виде графика, который называется графиком временных значений или временной диаграммой.
Любая синусоидальная функция задается тремя величинами: амплитудой, частотой и начальной фазой.
В разных электрических цепях частота может быть разной.
Автономные линейные электрические цепи – частота изменения тока, напряжения и ЭДС одинаковы.
Электрические цепи, в которых действуют синусоидальные ЭДС, напряжения и токи называются цепями синусоидального тока.
- § 3.2. Комплексная амплитуда:
Расчет цепей синусоидального тока с использованием мгновенных значений требует громоздкой вычислительной работы и применим для простейших электрических цепей.
Для расчета цепей синусоидального тока синусоидальную функцию заменяют эквивалентной величиной.
где j = √ — 1 – мнимая единица.
– комплексная амплитуда.
– сопряженная комплексная амплитуда.
– поворотный множитель.
Последняя запись означает, что синусоидальное напряжение можно представить на комплексной плоскости в виде двух векторов, длина которых равна Um и которые равномерно вращаются со скоростями, равными ω в противоположные стороны.
- § 3.3. Действующие значения синусоидальной функции:
Действующее значение синусоидальной функции – ее количественная оценка.
Действующие значения – среднеквадратичные за период значения синусоидальной функции, то есть, если:
то действующее значение:
Аналогично и для тока I и ЭДС ε.
Часто используются выражения, связывающие между собой амплитуду и действующее значение:
Действующее значение – это постоянная величина, которую обычно обозначают той же буквой, что и амплитуду, только без индекса m.
Действующее значение тока оказывает такое же тепловое действие на проводник с сопротивлением R, что и переменный ток, в течение времени, равном периоду. Поэтому большинство электроизмерительных приборов фиксируют и реагируют на действующие значения.
- § 3.4. Изображение синусоидальных функций векторами. Векторная диаграмма:
Электрическое состояние переменного тока описывается уравнениями Кирхгофа. Радиус-вектор, длина которого равна Am, вращается в декартовой плоскости координат xy против часовой стрелки с частотой ω и поворачивается за время одного оборота на угол 2π, то есть 2T = 2π. Положение радиус-вектора относительно оси x в момент начала (t = 0) определяется углом ψa. За отрезок времени t1 радиус-вектор повернется на угол ωt1 и его положение относительно оси x определяет угол ψ1 = ψa + ωt1. За время t2 радиус-вектор переместится на угол ψ2 = ψa + ωt2 и займет положение, определяемое углом и т.д. В соответствии с определением синуса проекция вращающегося радиус-вектора на ось y определяется:
где a – проекция вектора на ось y в момент времени t.
При:
рис. а рис. б
Любому равномерно вращающемуся радиус-вектору соответствует некоторая синусоидальная функция, и наоборот.
Посмотрим, как условный графический образ синусоидальной функции – радиус-вектор – может быть применим при расчетах цепей переменного тока. Определим ток:
i = i1 + i2,
если: 
и 
.
Как известно, сумма двух синусоид одинаковой частоты ω представляет собой также синусоиду частотой ω, то есть i = Imsin(ωt + ψ) и, следовательно, задача сводится к нахождению амплитуды Im и начальной фазы Ψ суммарного тока i. Искомые параметры Im и Ψ можно найти, воспользовавшись известными тригонометрическими преобразованиями.
Проведем решение задачи с помощью радиус-векторов I1m и I2m , вращающихся с частотой ω, положение которых для момента времени t = 0 показаны на рисунке ниже и осуществим геометрическое суммирование этих радиус-векторов по правилу параллелограмма. Результирующий радиус-вектор Im будет вращаться с частотой ω и является изображением некоторой синусоидальной функцией времени.
Следовательно, i = i1 + i2 – геометрическое изображение искомого тока.
Измерив дугу суммарного радиус-вектора и, зная выбранный масштаб, можно определить амплитуду Im тока. Непосредственно по чертежу определяется и начальная фаза Ψ.
Рассмотренная совокупность радиус-векторов, изображающих синусоидальные функции времени, называется векторной диаграммой.
- § 3.5. Изображение синусоидальной функции комплексными числами:
Для введения комплексного изображения перенесем радиус-вектор, изображающий синусоидальную функцию времени в декартовой плоскости на плоскость комплексных чисел. Для чего совместим ось x с осью действительных чисел Re, а ось y – с Im.
Любому вектору A, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах:
Все три формы записи в соответствии с формулой Эйлера равнозначны:
Переход от одной формы записи к другой:
где a1 – действительная часть;
a2 – мнимая часть.
Запишем в трех формах выражение для единичных действительных и мнимых комплексных чисел ( A = 1):
где с1 = a1 + b1, а с2 = a2 + b2 .
где C = AB.
Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется комплексным сопротивлением:
Модуль комплексного сопротивления, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока, а аргумент Ψ комплексного сопротивления – разности начальных фаз напряжения и тока:
Закон Ома в комплексной форме соответственно для амплитудных и действительных значений:
.
