Как найти начальную координату по графику скорости - Сайт, где вы сможете решить свои вопросы

Формула координаты тела при равномерном прямолинейном движении

Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.

Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:

Формула координаты тела при прямолинейном равномерном движении

x₀ — координата тела в начальный момент времени,

x — координата тела в текущий момент времени,

t — время движения,

V — скорость тела

Таким образом, необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат:

Механическое движение

О чем эта статья:

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

тело отсчета
система координат
часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

Время — в международной системе единиц СИ измеряется в секундах [с].
Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

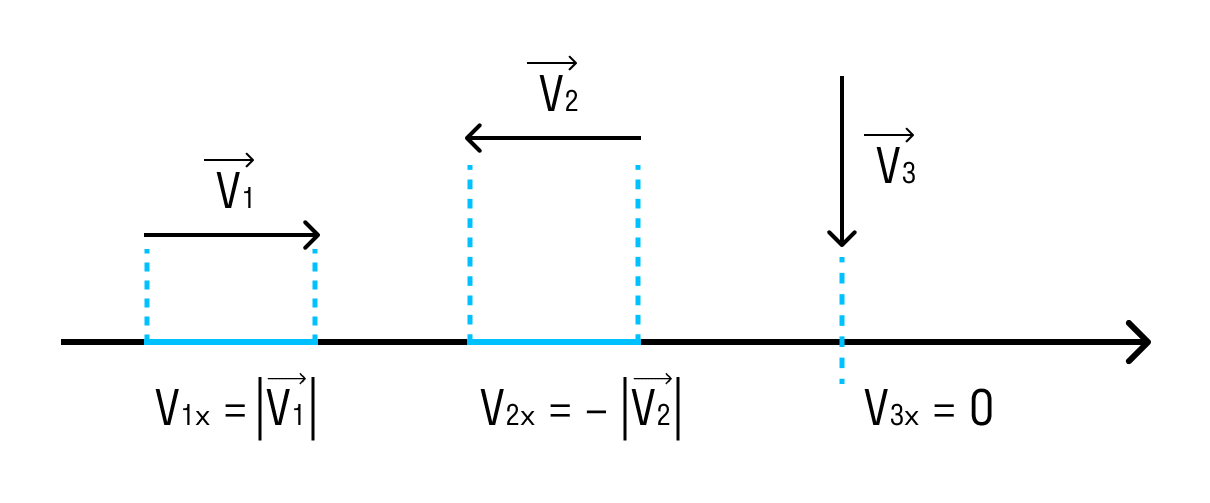
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Уравнение движения, графики равномерного прямолинейного движения

п.1. Прямолинейное равномерное движение на координатной прямой

Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.

Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:

t, c	0	1	2	3	4
x, м	20	30	40	50	60

Стартуя с точки x₀=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:

t, c	0	1	2	3	4
x, м	20	10	0	-10	-20

В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x₀ в любой момент времени t.

п.2. Уравнение прямолинейного равномерного движения

Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.

При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.

Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.

п.4. График движения x=x(t)

Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).

В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).

Построим графики зависимости координаты от времени для нашего примера:

x=20+10t – машина движется вправо (в направлении оси OX)
x=20-10t – машина движется влево (в направлении, противоположном оси OX)
x=20 – машина стоит

п.5. Как найти уравнение движения по графику движения?

п.6. График скорости v_x=v_x(t)

Для рассмотренного примера:

п.7. Как найти путь и перемещение по графику скорости?

Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:

Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.

Проекция перемещения может быть как положительной, так и отрицательной или равной 0.

п.8. Задачи

Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?

По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с – постоянная величина, её график:

$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м

Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?

а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).

Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.

б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.

в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с

[spoiler title=”источники:”]

http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie

http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/

[/spoiler]

Источник

3.2.1. Как правильно понимать условия задачи?

Скорость тела увеличилась в n раз:

Скорость уменьшилась в n раз:

Скорость увеличилась на 2 м/с:

Во сколько раз увеличилась скорость?

Во сколько раз уменьшилась скорость?

Как изменилась скорость?

На сколько увеличилась скорость?

На сколько уменьшилась скорость?

Тело достигло наибольшей высоты: nu_y=0.

Тело прошло половину расстояния:

Тело бросают с земли: y_0=0, (последнее условие часто ускользает из вида — если у тела скорость равна нулю, например у ручки, лежащей на столе, оно может полететь само вверх?), начальная скорость направлена вверх.

Тело бросают вниз: начальная скорость направлена вниз.

Тело бросают вверх: начальная скорость направлена вверх.

В момент падения на землю: y=0.

Тело выпадает из аэростата (воздушного шара): начальная скорость равна скорости аэростата (воздушного шара) и направлена в ту же самую сторону.

3.2.2. Как по графику скорости определить ускорение?

Закон изменения скорости имеет вид:

Графиком этого уравнения является прямая линия. Так как a_x — коэффициент перед t, то a_x является угловым коэффициентом прямой.

Для графика 1:

То, что график 1 «поднимается вверх», означает — проекция ускорения положительна, т. е. вектор veca направлен в положительном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.

Для графика 2:

То, что график 2 «опускается вниз», означает — проекция ускорения отрицательна, т. е. вектор veca направлен в отрицательном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.

Для определения и Delta t выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

3.2.3. Как по графику скорости определить пройденный путь и перемещение?

Как сказано в пункте 3.1.6 путь можно как площадь под графиком зависимости скорости от ускорения. Простой случай показан в пункте 3.1.6. Рассмотрим более сложный вариант, когда график скорости пересекает ось времени.

Напомним, что путь может только увеличиваться, поэтому путь, который проехало тело в примере на рисунке 9 равен:

где S_1, S_2 и S_3 — площади фигур, закрашенных на рисунке.

Для определения перемещения нужно заметить, что в точках t_1 и t_2 тело меняет направление движения. Проезжая путь S_1, тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Проезжая путь S_2, тело движется в обратную сторону, в отрицательном направлении оси Ox так как график лежит под осью времени. Проезжая путь S_3 , тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Таким образом, перемещение равно:

Еще раз обратим внимание:

1) пересечение с осью времени означает поворот в обратную сторону;

2) площадь графика, лежащего под осью времени положительна и входит со знаком «+» в определение пройденного пути, но со знаком «−» в определении перемещения.

3.2.4. Как из графика зависимости ускорения от времени определить зависимость скорости от времени и координаты от времени?

Для того, чтобы определить требуемые зависимости необходимы начальные условия — значения скорости и координаты в момент времени t=0. Без начальных условий решить однозначно данную задачу невозможно, поэтому, как правило, в условии задачи они даны.

В данном примере постараемся привести все рассуждения в буквах, для того, чтобы частном примере (при подстановке цифр) не потерять суть действий.

Пусть в момент времени t=0, скорость тела равна нулю nu_0=0, и начальная координата x_0=0.

1) От 0 до t=t_1.

Начальные значения скорости и координаты определяем из начальных условий, а ускорение из графика:

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

К концу данного промежутка времени ( t=t_1 ) скорость ( nu_k1 ) и координата ( x_k1 ) будут равны (вместо времени в формулы и нужно подставить t_1 ):

2) От t=t_1 до t=t_2.

Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

К концу данного промежутка времени ( t=t_2 ) скорость ( nu_k2 ) и координата ( x_k2 ) будут равны (вместо времени в формулы и нужно подставить t_2 ):

3) От t=t_2 до t=t_3.

следовательно, движение равноускоренное и закон изменения скорости имеет вид:

К концу данного промежутка времени ( t=t_3 ) скорость ( nu_k3 ) и координата ( x_k3 ) будут равны (вместо времени в формулы и нужно подставить t_3 ):

Для лучшего понимания построим полученные результаты на графике (см. рис.)

На графике скорости:

1) От 0 до t=t_1: прямая линия, «поднимающаяся вверх» (т. к. );

2) От t=t_1 до t=t_2: горизонтальная прямая линия (т. к. a=0 );

3) От t=t_2 до t=t_3 : прямая линия, «опускающаяся вниз» (т. к. ).

На графике координаты:

1) От 0 до t=t_1 : парабола, ветви которой направлены вверх (т. к. );

2) От t=t_1 до t=t_2 : прямая линия, поднимающаяся вверх (т. к. a=0 );

3) От t=t_2 до t=t_3 : парабола, ветви которой направлены вниз (т. к. ).

3.2.5. Как из графика закона движения записать аналитическую формулу закона движения?

Пусть дан график равнопеременного движения.

Закон равнопеременного движения имеет вид:

В этой формуле три неизвестные величины: x_0, nu_0x и a_x.

Для определения x_0 достаточно посмотреть на значение функции при t=0. Для определения двух других неизвестных выбираем две точки на графике, значения которых мы можем точно определить — вершины клеток. Получим систему:

При этом считаем, что x_0 нам уже известно. Умножим 1-ое уравнение системы на t_2, а 2-ое уравнение на t_1 :

Вычтем из 1-го уравнения 2-ое, после чего получаем:

Полученное из данного выражения значение a_x подставим в любое из уравнений системы (3.67) и решим полученное уравнение относительно nu_0x :

3.2.6. Как по известному закону движения определить закон изменения скорости?

Закон равнопеременного движения имеет вид:

Это его стандартный вид для данного типа движения и никак иначе он выглядеть не может, поэтому его стоит запомнить.

В данном законе коэффициент перед t — это значение начальной скорости, коэффициент пред — это ускорение, деленное пополам.

Например, пусть дан закон:

Тогда

И уравнение скорости имеет вид:

Таким образом, для решения подобных задач, необходимо точно помнить вид закона равнопеременного движения и смысл коэффициентов, входящих в это уравнение.

Однако можно пойти и иным путем. Вспомним формулу:

В нашем примере:

3.2.7. Как определить место и время встречи?

Пусть даны законы движения двух тел:

В момент встречи тела оказываются в одной координате, то есть x_1=x_2 и необходимо решить уравнение:

Перепишем его в виде:

Это квадратное уравнение, общее решение которого приводить не будем, в силу его громоздкости. Квадратное уравнение либо не имеет решений, что означает — тела не встретились; либо имеет одно решение — одна единственная встреча; либо имеет два решения — две встречи тел.

Полученные решения необходимо проверять на физическую реализуемость. Самое главное условие: и то есть время встречи должно быть положительным.

3.2.8. Как определить путь за -ую секунду?

Пусть тело начинает движение из состояния покоя и за -ую секунду проходит путь S_m. Требуется найти, какой путь проходит тело за n-ую секунду.

Для решения этой задачи необходимо воспользоваться формулой (3.25):

Обозначим Тогда

Поделим уравнение на и получим:

3.2.9. Как движется тело, брошенное вверх с высоты h?

Тело, брошено вверх с высоты h со скоростью nu_0.

Уравнение координаты y в произвольный момент времени:

Уравнение проекции скорости в произвольный момент времени:

Время подъема до наивысшей точки полета t_1 определяется из условия nu_y=0 :

Для нахождения максимальной высоты H необходимо в необходимо подставить t=t_1 :

Время всего полета t_2 определяется из условия y=0. Получаем уравнение:

Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате y=0 только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:

Скорость в момент падения:

3.2.10. Как движется тело, брошенное вниз с высоты h?

Тело, брошено вверх с высоты h со скоростью nu_0.

Уравнение координаты y в произвольный момент времени:

Уравнение проекции скорости в произвольный момент времени:

Время всего полета t_1 определяется из уравнения:

Скорость в момент падения:

3.2.11. Как движется тело брошенное вверх с поверхности земли?

Тело брошено вверх с поверхности земли со скоростью nu_0.

Уравнение координаты y в произвольный момент времени:

Уравнение проекции скорости в произвольный момент времени:

Время подъема до наивысшей точки полета t_1 определяется из условия nu_y=0:

Для нахождения максимальной высоты H необходимо в (3.89) необходимо подставить t=t_1:

Время всего полета t_2 определяется из условия y=0. Получаем уравнение:

Скорость в момент падения:

Заметьте, что что означает — время подъема равно времени падения на ту же высоту.

Также получили: то есть — с какой скоростью бросили, с такой же скоростью тело упало. Знак «−» в формуле указывает, что скорость в момент падения направлена вниз, то есть против оси Oy.

3.2.12. Тело побывало на одной высоте дважды…

При бросании тела оно может дважды оказаться на одной высоте — первый раз при движении вверх, второй — при падении вниз.

1) Когда тело оказывается на высоте h?

Для тела, брошенного вверх с поверхности земли справедлив закон движения:

Когда тело окажется на высоте h его координата будет равна y=h. Получаем уравнение:

решение которого имеет вид:

2) Известны времена t_1 и t_2, когда тело оказалось на высоте h. Когда тело окажется на максимальной высоте?

Время полета с высоты h назад до высоты h равно Как уже было показано, время подъема равно времени падения до той же высоты, поэтому время полета от высоты h до максимальной высоты равно:

Тогда время полета от начала движения до максимальной высоты:

3) Известны времена t_1 и t_2, когда тело оказалось на высоте h. Чему равно время полета тела?

Все время полета равно:

4) Известны времена t_1 и t_2, когда тело оказалось на высоте h. Чему равна максимальная высота подъема?

3.2.13. Как движется тело, брошенное горизонтально с высоты h?

Тело, брошено горизонтально с высоты h со скоростью nu_0.

Проекции начальной скорости на оси:

Проекции ускорения:

Проекции скорости в произвольный момент времени t:

Модуль скорости в произвольный момент времени t:

Координаты тела в произвольный момент времени t:

Время полета t_1 определяется из условия y=0:

Для определения дальности полета необходимо в уравнение для координаты x вместо t подставить t_1:

Для определения скорости тела в момент падения необходимо в уравнение вместо t подставить t_1:

Угол, под которым падает тело на землю:

3.2.14. Как движется тело, брошенное под углом α к горизонту с высоты h?

Тело, брошено под углом α к горизонту с высоты h со скоростью nu_0.

Проекции начальной скорости на оси:

Проекции ускорения:

Проекции скорости в произвольный момент времени t:

Модуль скорости в произвольный момент времени t:

Координаты тела в произвольный момент времени t:

Время полета до наивысшей точки t_1 определяется из условия nu_y=0:

Скорость в наивысшей точке полета nu_2:

Максимальная высота H определяется при подстановке в закон изменения координаты y времени t_1:

Все время полета t_2 находится из условия y=0, получаем уравнение:

Если подставим в закон изменения координаты x время t_2, то получим дальность полета L:

Скорость в момент падения t_2:

Угол, который образует вектор скорости с горизонталью в произвольный момент времени:

Угол падения:

3.2.15. Как движется тело, брошенное под углом α к горизонту земли?

Тело, брошено под углом α к горизонту с поверхности земли со скоростью nu_0.

Проекции начальной скорости на оси:

Проекции ускорения:

Проекции скорости в произвольный момент времени t:

Модуль скорости в произвольный момент времени t:

Координаты тела в произвольный момент времени t:

Время полета до наивысшей точки t_1 определяется из условия nu_y=0:

Скорость в наивысшей точке полета nu_2:

Максимальная высота H определяется при подстановке в закон изменения координаты y времени t_1:

Все время полета t_2 находится из условия y=0, получаем уравнение:

Получаем

Снова получили, что то есть еще раз показали, что время подъема равно времени падения.

Если подставим в закон изменения координаты x время t_2, то получим дальность полета L:

Скорость в момент падения t_2:

Угол, который образует вектор скорости с горизонталью в произвольный момент времени:

Угол падения:

то есть

3.2.16. Что такое настильная и навесная траектории?

Решим следующую задачу: под каким углом нужно бросить тело с поверхности земли, чтобы тело упало на расстоянии L от точки броска?

Дальность полета определяется формулой:

Отсюда

Из физических соображений ясно, что угол α не может быть больше 90°, поэтому, из серии решений уравнения подходят два корня:

Траектория движения, для которой называется настильной траекторией. Траектория движения, для которой называется навесной траекторией.

3.2.17. Как пользоваться треугольником скоростей?

Как было сказано в 3.6.1 треугольник скоростей в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.

Тело бросили с вершины башни со скорость nu_0 так, что дальность полета максимальна. К моменту падения на землю скорость тела равна nu. Сколько длился полет?

Построим треугольник скоростей (см. рис.). Проведем в ней высоту, которая, очевидно, равна Тогда площадь треугольника скоростей равна:

Здесь мы воспользовались формулой (3.121).

Найдем площадь этого же треугольника по другой формуле:

Так как это площади одного и того же треугольника, то приравняем формулы и :

Откуда получаем

Как видно из формул для конечной скорости, полученных в предыдущих пунктах, конечная скорость не зависит от угла, под которым бросили тело, а зависит только значения начальной скорости и начальной высоты. Поэтому дальность полета по формуле зависит только от угла между начальной и конечной скоростью β. Тогда дальность полета L будет максимальной, если примет максимально возможное значение, то есть

Таким образом, если дальность полета максимальна, то треугольник скоростей будет прямоугольным, следовательно, выполняется теорема Пифагора:

Откуда получаем

Свойством треугольника скоростей, который только что был доказан, можно пользоваться при решении других задач: треугольник скоростей является прямоугольным в задаче на максимальную дальность полета.

3.2.18. Как пользоваться треугольником перемещений?

Как было сказано в 3.6.2, треугольник перемещений в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.

Тело бросают под углом β к поверхности горы, имеющей угол наклона α. С какой скоростью нужно бросить тело, чтобы оно упало ровно на расстоянии L от точки бросания?

Построим треугольник перемещений — это треугольник ABC (см. рис. 19). Проведем в нем высоту BD. Очевидно, что угол DBC равен α.

Выразим сторону BD из треугольника BCD:

Выразим сторону BD из треугольника ABD:

Приравняем и :

Откуда находим время полета:

Выразим AD из треугольника ABD:

Выразим сторону DC из треугольника BCD:

Но Получаем

Подставим в это уравнение, полученное выражение для времени полета :

Окончательно получаем

3.2.19. Как решать задачи с помощью закона движения? (по горизонтали)

Как правило, в школе при решении задач на равнопеременное движение применяются формулы

Однако такой подход к решению трудно применить к решению многих задач. Рассмотрим конкретный пример.

Опоздавший пассажир подошёл к последнему вагону поезда в тот момент, когда поезд тронулся, начав движение с постоянным ускорением Единственная открытая дверь в одном из вагонов оказалась от пассажира на расстоянии Какую наименьшую постоянную скорость он должен развить, чтобы успеть сесть в поезд?

Введем ось Ox, направленную вдоль движения человека и поезда. За нулевое положение примем начальное положение человека («2»). Тогда начальная координата открытой двери («1») L:

Дверь («1»), как и весь поезд, имеют начальную скорость равную нулю. Человек («2») начинает движение со скоростью nu_0:

Дверь («1»), как и весь поезд, движется с ускорением a. Человек («2») движется с постоянной скоростью:

Закон движения и двери и человека имеет вид:

Подставим условия и в уравнение для каждого из движущихся тел:

Мы составили уравнение движения для каждого из тел. Теперь воспользуемся уже известным алгоритмом для нахождения места и времени встречи двух тел — нам нужно приравнять и :

Откуда получаем квадратное уравнение для определения времени встречи:

Это квадратное уравнение. Оба его решения имеют физический смысл — наименьший корень, это первая встреча человека и двери (человек с места может побежать быстро, а поезд не сразу наберет большую скорость, так что человек может обогнать дверь), второй корень — вторая встреча (когда уже поезд разогнался и догнал человека). Но наличие обоих корней означает — человек может бежать и медленнее. Скорость будет минимальна, когда уравнение будет иметь один единственный корень, то есть

Откуда находим минимальную скорость:

В таких задачах важно разобрать в условиях задачи: чему равны начальная координата, начальная скорость и ускорение. После этого составляем уравнение движения и думаем как дальше решать задачу.

3.2.20. Как решать задачи с помощью закона движения? (по вертикали)

Рассмотрим пример.

Свободно падающее тело прошло последние 10 м за 0,5 с. Найти время падения и высоту, с которой упало тело. Сопротивлением воздуха пренебречь.

Для свободного падения тела справедлив закон движения:

В нашем случае:

начальная координата: y_0=H;

начальная скорость:

Подставим условия в закон движения:

Подставляя в уравнение движения нужные значения времени, будем получать координаты тела в эти моменты.

В момент падения t_0 координата тела y=0:

За с до момента падения, то есть при координата тела y=h:

Уравнения и составляют систему уравнений, в которой неизвестны H и t_0. Решая эту систему, получим:

Итак, зная вид закона движения (3.30), и используя условия задачи для нахождения y_0 и nu_0y, получаем закон движения для данной конкретной задачи. После чего, подставляя нужные значения времени, получаем соответствующие значения координаты. И решаем задачу!

Источник

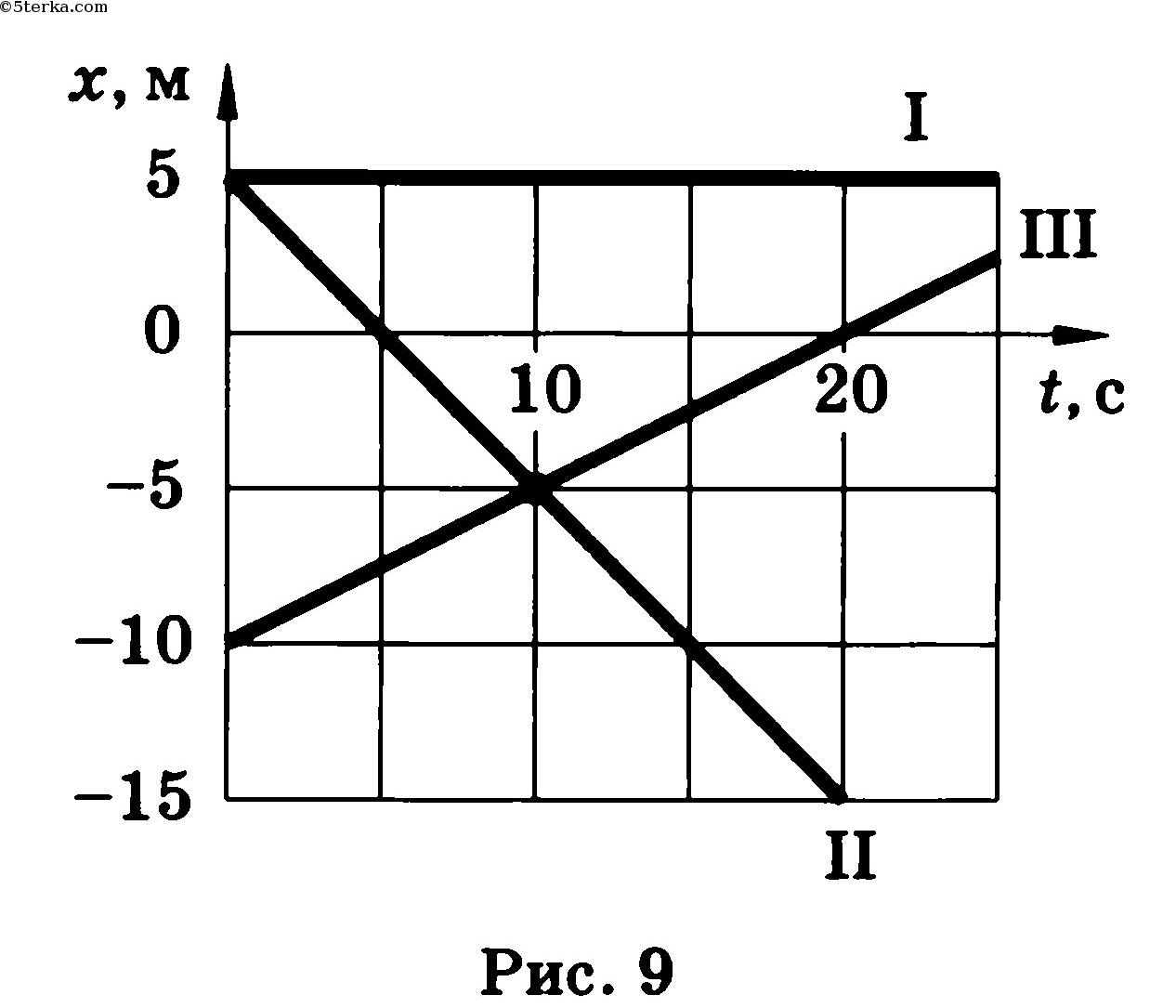
По графику видно, что начальные координаты I тела : 5 м, II: 5 м,

III: — 10 м. Скорости движения I:

II:

III:

Уравнения движения:

Т.к. движение равномерное вдоль оси Х, то найденные нами скорости v₁, v₂, v₃ являются проекциями на ось Х.

По графикам уравнения движения тел II и III видно, что они пересекутся в точке х = – 5 м в момент времени t = 10 с. Найдем это из уравнений движения.

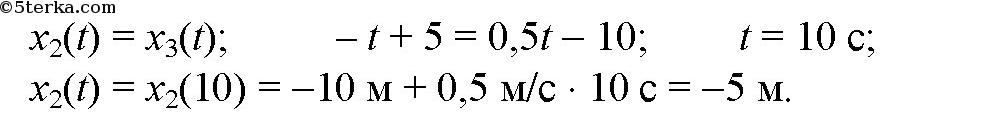
Источник:

Решебник

по

физике

за 10, 11 класс (А.П. Рымкевич, 2001 год),
задача №22
к главе «МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 2. Прямолинейное равномерное движение».

Все задачи

← №21. Движение грузового автомобиля описывается уравнением х1 = -270 + 12t, а движение пешехода по обочине того же шоссе — уравнением х2 = -1,5t. Сделать пояснительный рисунок (ось X направить вправо), на котором указать положение автомобиля и пешехода в м

№23. Движения двух велосипедистов заданы уравнениями: х1 = 5t, х2 = 150 – 10t. Построить графики зависимости x(t). Найти время и место встречи. →

Комментарии

Источник

Прямолинейное равномерное движение на координатной прямой
Уравнение прямолинейного равномерного движения
Удобная система отсчета для решения задачи о прямолинейном движении
График движения x=x(t)
Как найти уравнение движения по графику движения?
График скорости v_x=v_x(t)
Как найти путь и перемещение по графику скорости?
Задачи

п.1. Прямолинейное равномерное движение на координатной прямой

Составим таблицу перемещений за первые 4 секунды:

t, c	0	1	2	3	4
x, м	20	30	40	50	60

t, c	0	1	2	3	4
x, м	20	10	0	-10	-20

В этом случае координата x в любой момент времени t имеет вид: begin{gather*} x=x_0-st=x_0-vt\ x=20-10t end{gather*} Если же машина никуда не едет, её скорость v=0, и координата x=x₀ в любой момент времени t.

п.2. Уравнение прямолинейного равномерного движения

Основная задача механики – уметь определять положение тела в пространстве в любой момент времени.

Назовем проекцией вектора скорости (overrightarrow{x}) на параллельную ему ось координат OX величину (v_x=pm|overrightarrow{v}|=pm v).
Знак проекции определяется следующим правилом:

если направление вектора (overrightarrow{v}) совпадает с направлением оси OX, то (v_x=vgt 0)
если направление вектора (overrightarrow{v}) противоположно направлению оси OX, то (v_x=-vlt 0)

В любой момент времени t координата тела x(t) при прямолинейном равномерном движении описывается уравнением: $$ x(t)=x_0+v_x t $$ где (x_0) – координата в начальный момент времени, (v_x) – проекция вектора скорости движения.

Проекция перемещения (overrightarrow{r}) на параллельную ему ось координат OX в любой момент времени t определяется формулой: $$ triangle x=x(t)-x_0 $$ Знак (triangle x) указывает на направление совершенного перемещения:

если (triangle xgt 0), перемещение (overrightarrow{r}) произошло в направлении оси OX;
если (triangle xlt 0), перемещение (overrightarrow{r}) произошло противоположно направлению оси OX.

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

Прямолинейное движение описывается с помощью координатной прямой, параллельной направлению движения тела.

п.4. График движения x=x(t)

В осях (t) и (x) график (x(t)=x_0+v_x t) является прямой.
Эта прямая:

возрастает, если (v_xgt 0)
убывает, если (v_xlt 0)
постоянна (параллельна оси (t)), если (v_x= 0)

Построим графики зависимости координаты от времени для нашего примера:

п.5. Как найти уравнение движения по графику движения?

Шаг 1. Выбрать на прямой любые две точки (A(t_1,x_1)) и (B(t_2,x_2)).
Шаг 2. Найти проекцию скорости как отношение: $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{triangle x}{triangle t} $$ Шаг 3. Найти начальную координату по одной из формул: $$ x_0=x_1-v_x t_1 text{или} x_0=x_2-v_x t_2 $$ Шаг 4. Записать найденное уравнение движения: $$ x(t)=x_0+v_x t $$

п.6. График скорости v_x=v_x(t)

В осях (t) и (x) график (v_x(t)=v_x=const) является прямой, параллельной оси (t).
Эта прямая:

расположена над осью (t), если (v_xgt 0)
расположена под осью (t), если (v_xlt 0)
совпадает с осью (t), если (v_x=0)

Для рассмотренного примера:

Внимание!
В отличие от алгебры, в физике масштабы на осях, как правило, разные.
Поэтому обязательно нужно:
1) указывать обозначения и единицы измерения физических величин, которым соответствуют оси графика;
2) подбирать масштабы так, чтобы с графиком было удобно работать.

п.7. Как найти путь и перемещение по графику скорости?

На графике скорости путь, пройденный за промежуток времени (triangle t=t_2-t_1) равен площади прямоугольника, длина которого равна (triangle t), а ширина (triangle |v_x|): $$ s=|v_x|triangle t $$

На графике скорости проекция перемещения на ось OX за промежуток времени (triangle t=t_2-t_1) равна площади (v_xtriangle t), с учетом знака: $$ triangle x=v_xtriangle t $$

Проекция перемещения может быть как положительной, так и отрицательной или равной 0.

п.8. Задачи

По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin{gather*} x_1=x(5)=8cdot 5=40 text{(м)}\ x_2=x(10)=8cdot 10=80 text{(м)} end{gather*}
б) Скорость (v_x=8) м/с – постоянная величина, её график:

$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text{(м)} $$ Ответ: а) 40 м и 80 м; б) 40 м

а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).

Найдем скорость корабля (v_x): $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{56-38}{2-1}=18 (text{тыс.км/ч}) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text{тыс.км/ч}) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.

б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.

в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text{тыс.км}) $$
г) Переведем скорость в км/с: $$ 18000frac{text{км}}{text{ч}}=frac{18000 text{км}}{1 text{ч}}=frac{18000 text{км}}{3600 text{c}}=5 text{км/c} $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с

Источник

движение тела задано графиком координаты (зависимости координаты от времени). по графику определите: а) начальную координату тела б) проекцию скорости тела в) направление движения тела (по ост х или против оси х) г) запишите уравнение координаты

помогите пожалуйста!!!!

Остались вопросы?

Новые вопросы по предмету Физика

Источник

Формула координаты тела при равномерном прямолинейном движении

Формула координаты тела при прямолинейном равномерном движении

Механическое движение

Механическое движение

Прямолинейное равномерное движение

Скалярные величины (определяются только значением)

Векторные величины (определяются значением и направлением)

Проецирование векторов

Уравнение движения

Прямолинейное равноускоренное движение

Уравнение движения и формула конечной скорости

Движение по вертикали

Уравнение движения, графики равномерного прямолинейного движения

п.1. Прямолинейное равномерное движение на координатной прямой

п.2. Уравнение прямолинейного равномерного движения

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

п.4. График движения x=x(t)

п.5. Как найти уравнение движения по графику движения?

п.6. График скорости vx=vx(t)

п.7. Как найти путь и перемещение по графику скорости?

п.8. Задачи

п.1. Прямолинейное равномерное движение на координатной прямой

п.2. Уравнение прямолинейного равномерного движения

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

п.4. График движения x=x(t)

п.5. Как найти уравнение движения по графику движения?

п.6. График скорости vx=vx(t)

п.7. Как найти путь и перемещение по графику скорости?

п.8. Задачи

Остались вопросы?

Новые вопросы по предмету Физика

Вам также может понравиться

Как найти электропроводку в стенах квартиры

Как найти любовника моей жене

Как найти драйвер на официальный сайт

Добавить комментарий Отменить ответ

п.6. График скорости v_x=v_x(t)

п.6. График скорости v_x=v_x(t)