В данной статьи изложены мысли, которые возникали при решении задач с сайта “Решу ЕГЭ” в разделе – https://phys-ege.sdamgia.ru/test?theme=204. Рисунки взяты оттуда же.
1. Общий подход
Анализ и использование данного графика базируется на формуле перемещения тела S, м:
Как видно из формулы площадь под графиком равна перемещению тела. Например, тело с 1 по 2 секунду на графике, представленном на рис. 1 прошло S = V * t = 2м/с * (2с – 1с) = 2м/с *1с = 2м
2. Чуть посложнее
Если мы захотим найти перемещение тела с начала движения t = 0c до 4-ой секунды движения тела согласно графику на рис. 2, то нам необходимо найти сумму площадей трех геометрических фигур: с 0с по 1с – треугольник, с 1с по 2с прямоугольник, со 2с по 4с – трапеция.
S треугольника = (1/2) * длину высоты треугольника * длину сторону треугольника, к которой проведена высота =
=(1/2) * 2м/с * (1с – 0с) = 1/2 * 2м/с * 1с = 1м
S прямоугольника мы находили в начале статьи = 2м
S трапеции = (1/2) * сумму оснований трапеции * высоту трапеции =
=(1/2) * (2м/с + 6м/с) * (4с – 2с) = (1/2) * 8м/с * 2с = 8м
Итого S = 1м + 2м + 8м = 11м
3. А если скорость равна нулю?
Не стоит пугаться нулевых скоростей на каком-либо интервале времени. Например с 3с по 5с на графике, представленном на рис. 3 перемещение тела равно 0м, т. к. площадь фигуры с 3с по 5с равна 0.
4. А если скорость ушла “в минус”?
А вот отрицательная скорость может вызвать некоторые затруднения. Здесь надо очень внимательно читать задание и не перепутать очень похожие физические величины: путь и перемещение. Путь – величина скалярная и поэтому для ее нахождения с помощью графика на рис. 4 надо зеркально отобразить отрицательные участки скорости и сложить площади фигур (см. Рис. 5)
Перемещение – величина векторная и поэтому при определении этой величины необходимо учитывать знак площади. Например, если нужно найти перемещение тела с 0с по 10с (см. рис. 5), то нужно площадь треугольника с 0с по 4с сложить с площадью треугольника с 8с по 10с и из полученного результата вычесть площадь треугольника с 4с по 8с.
5. Когда можно и не считать!
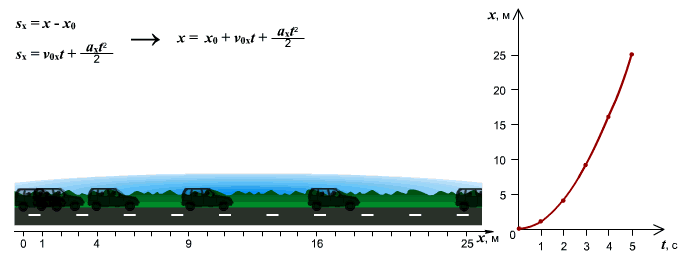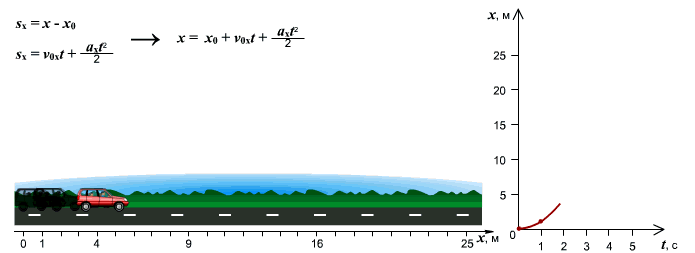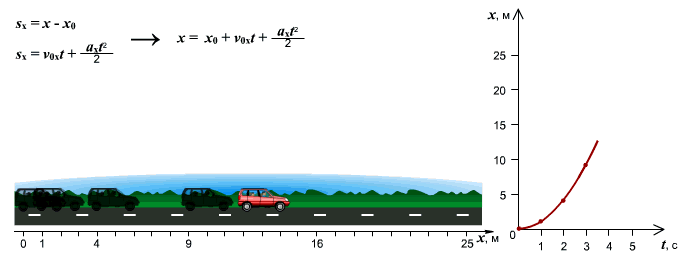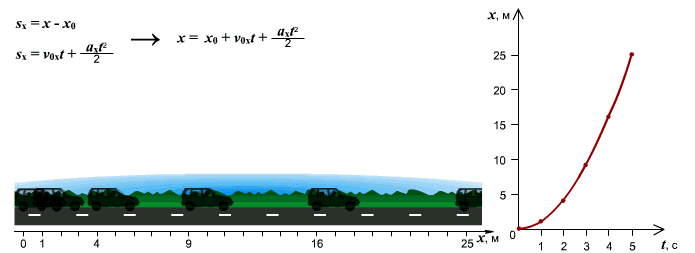
Иногда требуется визуальный анализ графиков. Например, необходимо определить какой автомобиль из 4-х с 0с до 15с проехал наибольшее расстояние?
Рассматривая площади геометрических фигур под графиками (см. рис. 6) видим, что площадь больше у графика (и машины) №3.
6. Переходим к ускорению
До сих пор мы на линейных графиках с координатами скорости и времени (см. рис. 7) видели скорость, время и перемещение (или путь).
А тут ещё прячется ускорение. Давайте попробуем его найти. Вспоминаем формулу равноускоренного движения
Рассматривая график на рис. 7 определим Vo при t = 0с => Vo = 2м/с.
А теперь возьмём на графике точку в момент времени t = 1c и определим по графику скорость в этот момент времени => V = 4м/с.
Подставляем найденные значения в формулу 2 =>
4м/с = 2м/с + a * 1c => а = (4м/с – 2м/с) / 1с = 2м/с2
Возвращаемся к графику (см. рис. 8)
Теперь мы можем сказать, что на рис. 8 представлен график линейного уравнения V = Vo + a*t = 2 + 2*t. Эти знания расширяют область использования графика на рис. 8. Например мы можем сказать, что при
t = 10c скорость будет равна V = 2м/с + 2м/с2*10с = 22м/с
7. Ищем ускорение на произвольном прямолинейном участке графика
Нас могут попросить найти ускорение тела на произвольном прямолинейном участке графика. Например с 6с по 10с на графике, представленном на рис. 9.
Для этого получим формулу для ускорения, усложнив формулу 2 заменив t на (t – to):
Возвращаемся к поиску ускорения:
а = (5м/с – (-5м/с))/(10с – 6с) = 10м/с / 4с = 2.5м/с2
8. Ищем координаты тела
Зная начальные координаты тела, начальную скорость, ускорение тела и время перемещения можем найти координаты тела в любой момент времен (формула 4)
9. Ищем скорость в пространстве
Мы можем знать значение проекций скорости на оси: х, y и z. Нас могут попросить найти модуль скорости. Ищем по формуле 5:
Для понимания формулы 5 можно представить модуль скорости диагональю параллелепипеда, а проекции скорости сторонами параллелепипеда (см. рис. 11)
Заключение
Пока, это все мысли, которые появлялись во время решения задач в разделе сайта “Решу ЕГЭ” по адресу https://phys-ege.sdamgia.ru/test?theme=204. Пишите в комментариях, если что-то напрашивается добавить.
Автор с благодарностью примет любые пожертвования на развитие канала “От сложного к простому” https://money.yandex.ru/to/4100170126360.
Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
 |
Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t – машина движется вправо (в направлении оси OX)
x=20-10t – машина движется влево (в направлении, противоположном оси OX)
x=20 – машина стоит
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:
По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с – постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
Как найти уравнение скорости по графику зависимости
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V (t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) – прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) – наклонная линия :
Из графика видно, что проекция скорости равна:
Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Vx — Скорость тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Sx — Перемещение тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
Vx — Скорость тела при равноускоренном движении по прямой
ax — Ускорение тела
t — Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
– если известны начальная, конечная скорости движения и ускорение.
– если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V(t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:
В координатах зависимость имеет вид:
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_<0>) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_<0>]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_<0>), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_ <0>+ v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_ <0>+ a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec) и (vec) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
[spoiler title=”источники:”]
http://www.sites.google.com/site/opatpofizike/teoria/teoria-10-klass/graficeskoe-predstavlenie-dvizenia
[/spoiler]
Загрузить PDF
Загрузить PDF
Скорость является функцией времени и определяется как абсолютной величиной, так и направлением.[1]
Часто в задачах по физике требуется найти начальную скорость (ее величину и направление), которой изучаемый объект обладал в нулевой момент времени. Для вычисления начальной скорости можно использовать различные уравнения. Основываясь на данных, приведенных в условии задачи, вы можете выбрать наиболее подходящую формулу, которая позволит легко получить искомый ответ.
-
1
Используйте подходящее уравнение. При решении физической задачи необходимо знать, какая формула вам понадобится. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, ускорение и время, для определения начальной скорости удобно использовать следующее соотношение:
- Vi = Vf – (a * t)
- В эту формулу входят следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- a — ускорение
- t — время
- Обратите внимание, что это стандартная формула, используемая для вычисления начальной скорости.
-
2
Подставьте в формулу известные величины. Выписав все исходные данные и записав необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Если вы где-либо допустили ошибку, то легко сможете найти ее, просмотрев свои записи.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для получения искомого результата. Если можно, используйте калькулятор, чтобы снизить вероятность просчетов при вычислениях.
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
- Запишем исходные данные:
- Vi = ?, Vf = 200 м/с, a = 10 м/с2, t = 12 с
- Умножим ускорение на время: a * t = 10 * 12 =120
- Вычтем полученное значение из конечной скорости: Vi = Vf – (a * t) = 200 – 120 = 80 Vi = 80 м/с на восток
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Предположим, что объект, двигаясь на восток с ускорением 10 метров в секунду в квадрате в течение 12 секунд, разогнался до конечной скорости 200 метров в секунду. Необходимо найти начальную скорость объекта.
-
1
Используйте подходящую формулу. При решении какой-либо физической задачи необходимо выбрать соответствующее уравнение. Для этого первым делом следует записать все данные, приведенные в условии задачи. Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- Vi = (d / t) – [(a * t) / 2]
- В эту формулу входят следующие величины:
- Vi — начальная скорость
- d — пройденное расстояние
- a — ускорение
- t — время
-
2
Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Допустив ошибку в решении, вы сможете без труда найти ее, просмотрев свои записи.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь стандартными преобразованиями для нахождения ответа. Если возможно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
- Запишем исходные данные:
- Vi = ?, d = 150 м, a = 7 м/с2, t = 30 с
- Умножим ускорение на время: a * t = 7 * 30 = 210
- Поделим произведение на два: (a * t) / 2 = 210 / 2 = 105
- Поделим расстояние на время: d / t = 150 / 30 = 5
- Вычтем первую величину из второй: Vi = (d / t) – [(a * t) / 2] = 5 – 105 = -100 Vi = -100 м/с в западном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, в нашем случае метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Допустим, объект движется в западном направлении с ускорением 7 метров в секунду в квадрате в течение 30 секунд, пройдя при этом 150 метров. Необходимо вычислить его начальную скорость.
-
1
Используйте подходящее уравнение. Для решения физической задачи необходимо выбрать соответствующую формулу. Первым делом следует записать все начальные данные, указанные в условии задачи. Если известны конечная скорость, ускорение и пройденное расстояние, для определения начальной скорости удобно использовать следующее соотношение:
- Vi = √ [Vf2 – (2 * a * d)]
- Эта формула содержит следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- a — ускорение
- d — пройденное расстояние
-
2
Подставьте в формулу известные величины. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Важно внимательно изучить условие задачи и аккуратно записывать каждый шаг при ее решении.
- Допустив где-либо ошибку, вы сможете без труда найти ее, просмотрев ход решения.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. По возможности используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
- Запишем исходные данные:
- Vi = ?, Vf = 12 м/с, a = 5 м/с2, d = 10 м
- Возведем в квадрат конечную скорость: Vf2= 122 = 144
- Умножим ускорение на пройденное расстояние и на 2: 2 * a * d = 2 * 5 * 10 = 100
- Вычтем результат умножения из квадрата конечной скорости: Vf2 – (2 * a * d) = 144 – 100 = 44
- Извлечем квадратный корень из полученного значения: = √ [Vf2 – (2 * a * d)] = √44 = 6,633 Vi = 6,633 м/с в северном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Предположим, объект движется в северном направлении с ускорением 5 метров в секунду в квадрате и, преодолев 10 метров, имеет конечную скорость 12 метров в секунду. Необходимо найти его начальную скорость.
-
1
Выберите подходящую формулу. При решении физической задачи необходимо использовать соответствующее уравнение. Прежде всего следует записать все данные, приведенные в условии задачи. Если известны конечная скорость, время и пройденное расстояние, для определения начальной скорости можно использовать следующее соотношение:
- Vi = Vf + 2 (t – d)
- В данную формулу входят следующие величины:
- Vi — начальная скорость
- Vf — конечная скорость
- t — время
- d — пройденное расстояние
-
2
Подставьте в формулу известные значения. После того, как вы выписали все исходные данные и записали необходимое уравнение, можно подставить в него известные величины. Внимательно изучите условие задачи и аккуратно записывайте каждый шаг при ее решении.
- Допустив ошибку, вы сможете без труда найти ее, просмотрев решение.
-
3
Решите уравнение. Подставив в формулу известные значения, воспользуйтесь необходимыми преобразованиями для получения ответа. Если можно, используйте калькулятор, чтобы уменьшить вероятность просчетов при вычислениях.
- Допустим, объект преодолел расстояние 15 метров (49,2 фута) в течение 45 секунд, и его конечная скорость составляет 17 метров (55,8 фута) в секунду. Найдем начальную скорость объекта.
- Запишем исходные данные:
- Vi = ?, Vf = 17 м/с, t = 45 с, d = 15 м
- Вычтем расстояние из времени: (t – d) = (45 – 15) = 30
- Умножим полученное значение на 2: 2 ( t – d) = 2 (45 – 15) = 60
- Прибавим к этой величине конечную скорость: Vf + 2 (t – d) = 17 + 60 = 77 Vi = 77 м/с в южном направлении
- Запишите ответ в правильном виде. Необходимо указать единицы измерения, то есть метры в секунду, или м/с, а также направление движения объекта. Если вы не укажете направление, ответ будет неполным, содержа лишь величину скорости без информации о том, в каком направлении движется объект.
Реклама
- Допустим, объект преодолел расстояние 15 метров (49,2 фута) в течение 45 секунд, и его конечная скорость составляет 17 метров (55,8 фута) в секунду. Найдем начальную скорость объекта.
Что вам понадобится
- Карандаш
- Бумага
- Калькулятор (необязательно)
Об этой статье
Эту страницу просматривали 149 347 раз.
Была ли эта статья полезной?
Определение кинематических характеристик движения с помощью графиков
- Подробности
- Обновлено 13.08.2018 21:14
- Просмотров: 912
«Физика – 10 класс»
Чем отличается равномерное движение от равноускоренного?
Чем отличается график пути при равноускоренном движении от графика пути при равномерном движении?
Что называется проекцией вектора на какую-либо ось?
В случае равномерного прямолинейного движения можно определить скорость по графику зависимости координаты от времени.
Проекция скорости численно равна тангенсу угла наклона прямой x(t) к оси абсцисс. При этом, чем больше скорость, тем больше угол наклона.
Прямолинейное равноускоренное движение.
На рисунке 1.33 изображены графики зависимости проекции ускорения от времени для трёх разных значений ускорения при прямолинейном равноускоренном движении точки. Они представляют собой прямые линии, параллельные оси абсцисс: ах = const. Графики 1 и 2 соответствуют движению, когда вектор ускорения направлен вдоль оси ОХ, график 3 — когда вектор ускорения направлен в противоположную оси ОХ сторону.
При равноускоренном движении проекция скорости зависит от времени линейно: υx = υ0x + axt. На рисунке 1.34 представлены графики этой зависимости для указанных трёх случаев. При этом начальная скорость точки одинакова. Проанализируем этот график.
Проекция ускорения 
За один и тот же промежуток времени при разных ускорениях скорость изменяется на разные значения.
При положительном значении проекции ускорения за один и тот же промежуток времени проекция скорости в случае 2 увеличивается в 2 раза быстрее, чем в случае 1. При отрицательном значении проекции ускорения на ось ОХ проекция скорости по модулю изменяется на то же значение, что и в случае 1, но скорость уменьшается.
Для случаев 1 и 3 графики зависимости модуля скорости от времени будут совпадать (рис. 1.35).
Используя график зависимости скорости от времени (рис. 1.36), найдём изменение координаты точки. Это изменение численно равно площади заштрихованной трапеции, в данном случае изменение координаты за 4 с Δx = 16 м.
Мы нашли изменение координаты. Если необходимо найти координату точки, то к найденному числу нужно прибавить её начальное значение. Пусть в начальный момент времени х0 = 2 м, тогда значение координаты точки в заданный момент времени, равный 4 с, равно 18 м. В данном случае модуль перемещения равен пути, пройденному точкой, или изменению её координаты, т. е. 16 м.
Если движение равнозамедленное, то точка в течение выбранного интервала времени может остановиться и начать двигаться в направлении, противоположном начальному. На рисунке 1.37 показана зависимость проекции скорости от времени для такого движения. Мы видим, что в момент времени, равный 2 с, направление скорости изменяется. Изменение координаты будет численно равно алгебраической сумме площадей заштрихованных треугольников.
Вычисляя эти площади, мы видим, что изменение координаты равно -6 м, это означает, что в направлении, противоположном оси ОХ, точка прошла большее расстояние, чем по направлению этой оси.
Площадь над осью t берём со знаком «плюс», а площадь под осью t, где проекция скорости отрицательна, — со знаком «минус».
Если в начальный момент времени скорость некоторой точки была равна 2 м/с, то координата её в момент времени, равный 6 с, равна -4 м. Модуль перемещения точки в данном случае также равен 6 м — модулю изменения координаты. Однако путь, пройденный этой точкой, равен 10 м — сумме площадей заштрихованных треугольников, показанных на рисунке 1.38.
Изобразим на графике зависимость координаты х точки от времени. Согласно одной из формул (1.14) кривая зависимости координаты от времени — x(t) — парабола.
Если движение точки происходит со скоростью, график зависимости которой от времени изображён на рисунке 1.36, то ветви параболы направлены вверх, так как ах > 0 (рис. 1.39). По этому графику мы можем определить координату точки, а также скорость в любой момент времени. Так, в момент времени, равный 4 с, координата точки равна 18 м.
Для начального момента времени, проводя касательную к кривой в точке А, определяем тангенс угла наклона α1, который численно равен начальной скорости, т. е. 2 м/с.
Для определения скорости в точке В проведём касательную к параболе в этой точке и определим тангенс угла α2. Он равен 6, следовательно, скорость равна 6 м/с.
График зависимости пути от времени — такая же парабола, но проведённая из начала координат (рис. 1.40). Мы видим, что путь непрерывно увеличивается со временем, движение происходит в одну сторону.
Если движение точки происходит со скоростью, график зависимости проекции которой от времени изображён на рисунке 1.37, то ветви параболы направлены вниз, так как аx < 0 (рис. 1.41). При этом моменту времени, равному 2 с, соответствует вершина параболы. Касательная в точке В параллельна оси t, угол наклона касательной к этой оси равен нулю, и скорость также равна нулю. До этого момента времени тангенс угла наклона касательной уменьшался, но был положителен, движение точки происходило в направлении оси ОХ.
Начиная с момента времени t = 2 с, тангенс угла наклона становится отрицательным, а его модуль увеличивается, это означает, что движение точки происходит в направлении, противоположном начальному, при этом модуль скорости движения увеличивается.
Модуль перемещения равен модулю разности координат точки в конечный и начальный моменты времени и равен 6 м.
График зависимости пройденного точкой пути от времени, показанный на рисунке 1.42 отличается от графика зависимости перемещения от времени (см. рис. 1.41).
Как бы ни была направлена скорость, путь, пройденный точкой, непрерывно увеличивается.
Выведем зависимость координаты точки от проекции скорости. Скорость υx = υ0x + axt, отсюда
В случае x0 = 0, ах > 0 и υx > υ0x график зависимости координаты от скорости представляет собой параболу (рис. 1.43).

При этом, чем больше ускорение, тем ветвь параболы будет менее крутой. Это легко объяснить, так как, чем больше ускорение, тем меньше расстояние, которое должна пройти точка, чтобы скорость увеличилась на то же значение, что и при движении с меньшим ускорением.
В случае ах < 0 и υ0x > 0 проекция скорости будет уменьшаться. Перепишем уравнение (1.17) в виде 
Ускоренное движение.
По графикам зависимости проекции скорости от времени можно определить координату и проекцию ускорения точки в любой момент времени при любом типе движения.
Пусть проекция скорости точки зависит от времени так, как показано на рисунке 1.45. Очевидно, что в промежутке времени от 0 до t3 движение точки вдоль оси X происходило с переменным ускорением. Начиная с момента времени, равного t3, движение равномерное с постоянной скоростью υDx. По графику мы видим, что ускорение, с которым двигалась точка, непрерывно уменьшалось (сравните угол наклона касательной в точках В и С).
Изменение координаты х точки за время t1 численно равно площади криволинейной трапеции OABt1, за время t2 — площади OACt2 и т. д. Как видим по графику зависимости проекции скорости от времени можно определить изменение координаты тела за любой промежуток времени.
По графику зависимости координаты от времени можно определить значение скорости в любой момент времени, вычисляя тангенс угла наклона касательной к кривой в точке, соответствующей данному моменту времени. Из рисунка 1.46 следует, что в момент времени t1 проекция скорости положительна. В промежутке времени от t2 до t3 скорость равна нулю, тело неподвижно. В момент времени t4 скорость также равна нулю (касательная к кривой в точке D параллельна оси абсцисс). Затем проекция скорости становится отрицательной, направление движения точки изменяется на противоположное.
Если известен график зависимости проекции скорости от времени, можно определить ускорение точки, а также, зная начальное положение, определить координату тела в любой момент времени, т. е. решить основную задачу кинематики. По графику зависимости координаты от времени можно определить одну из самых важных кинематических характеристик движения — скорость. Кроме этого, по указанным графикам можно определить тип движения вдоль выбранной оси: равномерное, с постоянным ускорением или движение с переменным ускорением.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика – Физика, учебник для 10 класса – Класс!ная физика
Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»
I. Механика
Тестирование онлайн
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают
Графики равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) – прямая линия, параллельная оси времени.
Правило определения пути по графику v(t): Численное значение перемещения (пути) – это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График s(t) – наклонная линия.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости 


Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости 

График движения при 
График движения при 
Сравнительная таблица графиков