Равнозамедленное движение. Формула равнозамедленного движения. График равнозамедленного движения
Что такое равнозамедленное движение?
Равнозамедленное движение определение
Определение равнозамедленного движения:
Если укорение отрицательно, то модуль скорости равномерно уменьшается.
График скорости равнозамедленного движения
Пример графика скорости равнозамедленного движения, здесь начальная скорость равна 2 м/с, ускорение отрицательно и модуль его равен 0,3 м/с 2 :
(Этот график я построил с помощью построителя графиков. Выбрал в нём вид функции «Линейная: y = k * x + b» установил k = -0.3, b = 2 и нажал кнопку «Построить график».)
Чем больше отрицательное ускорение, тем быстрее будет падать скорость в нашем примере, т.е. если задать большее ускорение, то график круче пойдёт вниз.
Равнозамедленное движение формула
Формула скорости равнозамедленного движения (прямолинейного):
в этой формуле все величины являются скалярами, а не векторами.
Из формулы скорости равнозамедленного движения видно, что если увеличить ускорение, то быстрее будет падать скорость.
В момент времени t1 скорость падает до нуля, а после этого момента скорость нарастает, тело движется равноускоренно, но с отрицательной скоростью.
Формулы равномерного и равноускоренного движения
Равномерное движение (движение тела с постоянной скоростью)
Формула скорости движения при равномерном движении: 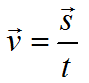
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: 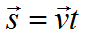
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле: 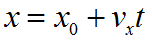
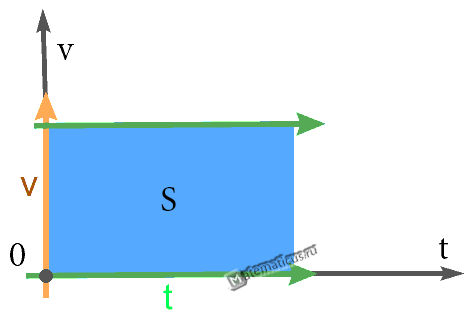
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении: 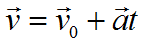
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с 2
Формула для нахождения перемещения при равноускоренном движении: 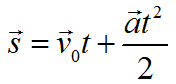
или 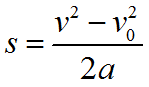
Уравнение равноускоренного движения в проекции на оси координат: 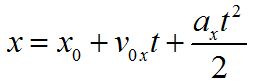
Формула для определения ускорения при равноускоренном прямолинейном движении: 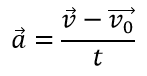
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения: 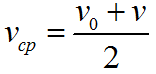
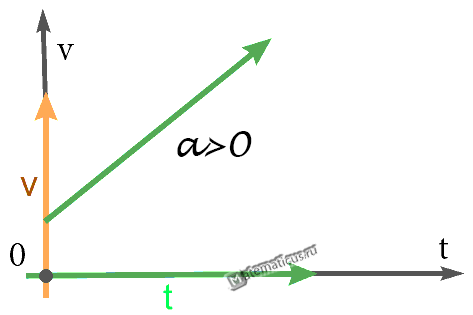
График — Равноускоренное движение при a>0
Равнозамедленное движение
Равнозамедленное движение — это движение тела, при котором модуль скорости равномерно уменьшается с течением времени, а вектор ускорения остается постоянным как по модулю, так и по направлению.
Формула скорости при равнозамедленном движении: 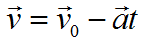
Формула перемещения при равнозамедленном движении: 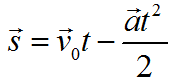
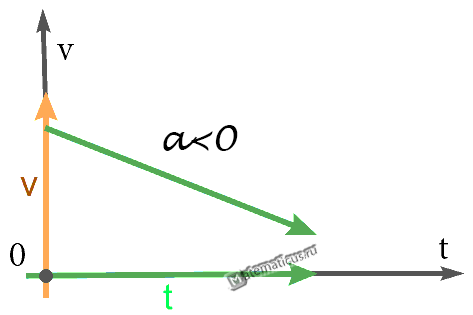
График — Равнозамедленное движение при a 2
Формула для вычисления скорости при свободном падении тела: 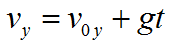
Формула для вычисления перемещения при свободном падении тела: 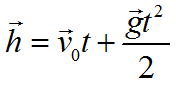
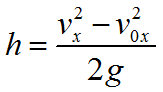
Формула координаты при свободном падении тела: 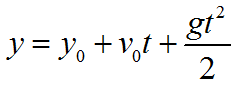
Формула высоты с которой тело свободно падает: 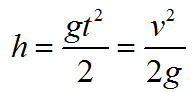
Формула для определения скорости тела в конце свободного падения: 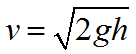
Время свободного падения тела равно: 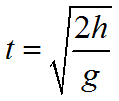
Уравнение пути при равнозамедленном движении
§ 25. Равнозамедленное движение. Формула пути
1. Понятие равнозамедленного движения. Формула пути.
Определение. Прямолинейное движение называется равнозамедленным , если за любые равные промежутки времени модуль скорости уменьшается на одну и ту же величину.
Это движение также является частным случаем движения с постоянным ускорением, поэтому любую задачу на это движение можно решать с помощью известных формул проекций скорости и координат движения с постоянным ускорением. Но иногда для более быстрого решения задач можно использовать формулы модуля скорости и пути.
Вначале найдём время, в течение которого тело движется равнозамедленно до остановки.
Получим теперь формулу модуля скорости равнозамедленного движения.
, где , то есть .
Из формулы координаты движения с постоянным ускорением можно получить формулу пути равнозамедленного движения.
, где .
2. График пути равнозамедленного движения.
Графиком пути при равнозамедленном движении является ветвь параболы; вершина параболы расположена в конце времени движения.
2а. Тело двигалось равнозамедленно, остановилось, а затем вновь начало двигаться (равноускоренно) в противоположном направлении: например, мяч, брошенный вертикально вверх.
График пути в этом случае будет выглядеть так.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
[spoiler title=”источники:”]
http://education-for.narod.ru/bas/kinematika/p25.html
[/spoiler]
Skip to content
Равномерное движение (движение тела с постоянной скоростью)
Формула скорости движения при равномерном движении:
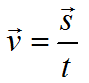
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении:
![]()
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле:
![]()

График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении:
![]()
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с2
Формула для нахождения перемещения при равноускоренном движении:
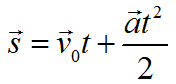
или
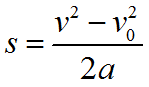
Уравнение равноускоренного движения в проекции на оси координат:
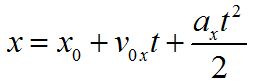
Формула для определения ускорения при равноускоренном прямолинейном движении:
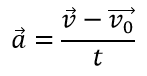
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:
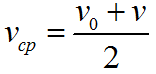

График — Равноускоренное движение при a>0
Равнозамедленное движение
Равнозамедленное движение — это движение тела, при котором модуль скорости равномерно уменьшается с течением времени, а вектор ускорения остается постоянным как по модулю, так и по направлению.
Формула скорости при равнозамедленном движении:
![]()
Формула перемещения при равнозамедленном движении:
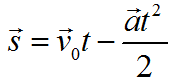

График — Равнозамедленное движение при a<0
Свободное падение
Постоянная величина скорости свободного падения тела равна g=9,8 м/с2
Формула для вычисления скорости при свободном падении тела:
![]()
Формула для вычисления перемещения при свободном падении тела:
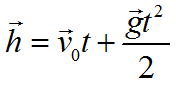
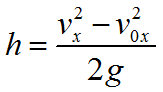
Формула координаты при свободном падении тела:
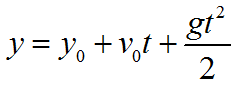
Формула высоты с которой тело свободно падает:
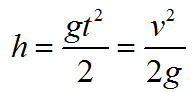
Формула для определения скорости тела в конце свободного падения:
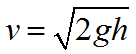
Время свободного падения тела равно:
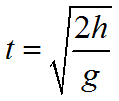
![]() 61133
61133
Что такое равнозамедленное движение?
Равнозамедленное движение определение
Определение равнозамедленного движения:
Равнозамедленное движение – движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению.
Если укорение отрицательно, то модуль скорости равномерно уменьшается.
График скорости равнозамедленного движения
Пример графика скорости равнозамедленного движения, здесь начальная скорость равна 2 м/с, ускорение отрицательно и модуль его равен 0,3 м/с2: 
(Этот график я построил с помощью построителя графиков. Выбрал в нём вид функции «Линейная: y = k * x + b» установил k = -0.3, b = 2 и нажал кнопку «Построить график».)
Чем больше отрицательное ускорение, тем быстрее будет падать скорость в нашем примере, т.е. если задать большее ускорение, то график круче пойдёт вниз.
Равнозамедленное движение формула
Формула скорости равнозамедленного движения (прямолинейного):
v = v0 — at
в этой формуле все величины являются скалярами, а не векторами.
Из формулы скорости равнозамедленного движения видно, что если увеличить ускорение, то быстрее будет падать скорость.
В момент времени t1 скорость падает до нуля, а после этого момента скорость нарастает, тело движется равноускоренно, но с отрицательной скоростью.
Формула закона равнозамедленного движения:
S = S0 + v0t — (at2)/2
-
Неравномерное
прямолинейное движение. -
Путь,
пройденный в неравномерном прямолинейном
движении. -
Ускорение.
-
Равнопеременное
движение. -
Равноускоренное
прямолинейное движение. -
Равнозамедленное
прямолинейное движение. -
Перемещение
в равноускоренном прямолинейном
движении. -
Перемещение
в равнозамедленном прямолинейном
движении. -
Средняя
скорость в равноускоренном движении. -
Формулы,
устанавливающие связь между скоростью,
ускорением и пройденным путём в
равноускоренном движении. -
График
зависимости координаты (перемещения)
от времени в равноускоренном прямолинейном
движении. -
Свободное
падение тел. -
Движение
тела, брошенного под углом к горизонту,
высота и дальность полёта.
1

.Неравномерное
прямолинейное движение
– это движение, при котором тело,
перемещаясь вдоль прямой линии, за
равные промежутки времени проходит
разные перемещения, т.е. скорость меняется
по величине с течением времени и является
функцией времени V
(t).
График зависимости величины скорости
от времени, т. е. график функции V
(t)
представлен на Рис.17
2
.
Путь, пройденный
в неравномерном прямолинейном движении.
Разобьём
всё время движения на очень малые
интервалы
,
в течение которых скорость можно считать
приближенно постоянной и равной средней
скорости
![]()
движения в течение времени
.
Тогда путь![]()
![]()
, пройденный за время
с постоянной скоростью
вычислим по формуле:
=
.
На Рис.17 этот путь равен площади
заштрихованной фигуры, которую ввиду
малости
можно считать прямоугольником со
сторонами
и
.
Складывая отрезки пути
получим площадь фигуры, образованной
графиком скорости осью времени.
И
так,
путь, пройденный телом при неравномерном
прямолинейном движении численно равен
площади графиком зависимости скорости
движения тела от времени.
3. Ускорение. При произвольном
движении точки модуль и направление
скорости непрерывно меняются Рис.18.
Совместим начала векторов
и
,
тогда вектор
![]()
=
–
есть изменение скорости точки и пусть
![]()
интервал времени,в течение которого
это изменение произошло Рис.19.
Средним ускорением
называют отношение изменение скорости
к интервалу времени, в течение которого
это изменение произошло:
![]()
=
![]()
.
В системе СИ
ускорение измеряется в (![]()
),
ускорение векторная величина.
Мгновенное
ускорение – среднее ускорение за
бесконечно малый интервал времени:
=
![]()
![]()
.
4. Равнопеременное
движение –
движение с постоянным по модулю
направлению ускорением
=
.
В этом случае скорость точки за равные
интервалы времени изменяется на одну
и ту же величину, а ускорение вычисляется
по формуле:
=
![]()
![]()
=
t
где
=
![]()
изменение скорости за время t,
![]()
– начальная скорость точки в момент
времени t=0,
–
конечная скорость точки в момент t,
т.е.
![]()
.
Теперь можно записать:
=
t
и далее
=
+
t
.
Если ускоренное
началось из состояния покоя, т.е.
= 0, то
=
t
.
5. Равноускоренное прямолинейное
движение – движение, при котором
траектория есть прямая линия , ускорение
постоянная величина и направлено вдоль
прямой причём направления скорости и
ускорения совпадают, т.е.
![]()
. В этом случае модуль скорости возрастает
со временем. Прямолинейность траектории
позволяет все вычисления с модулями
скорости и ускорения по формулам:
![]()
+
аt
и
![]()
,
если
=0.
Таким образом, в
прямолинейном равноускоренном движении
модуль скорости возрастает пропорционально
времени. График зависимости скорости
от времени представлен Рис. 20.

6. Равнозамедленное
прямолинейное движение
– прямолинейное движение с постоянным
по модулю и направлению ускорением, при
этом векторы скорости и ускорения
противонаправлены, т. е. антипараллельны
![]()
.
В этом случае все вычисления также
можно проводить с модулями скорости и
ускорения, учитывая , что ускорение
отрицательно
![]()
.
И
так,
скорость в прямолинейном равнозамедленном
движении линейно убывает с течением
времени. Зависимость скорости от времени
в равнозамедленном прямолинейном
движении представлена графиком на
Рис.21.
7. Перемещение
в равноускоренном прямолинейном
движении.
Уравнение
прямолинейного равноускоренного
движения.
Пусть материальная точка движется по
оси
х
и пусть в начальный момент времени
t=0
она имела начальную скорость
.
Перемещение, пройденное точкой за время
t
численно равно площади под графиком
зависимости скорости от времени, т.е.
площади трапеции с основаниями
и
+аt
и высотой t
Рис.20
![]()
=

![]()
+![]()
![]()
,
если
![]()
,
то
.
Учитывая, что
![]()
получим закон равноускоренного
прямолинейного движения:

.
Совмещая начальное положение тела с
началом отсчёта на оси х, т.е.
полагая
![]()
получим:

.
Если же движение началось из состояния
покоя, т.е.
![]()
,
закон равноускоренного прямолинейного
запишем в виде:
![]()
.
8. Перемещение
в равнозамедленном прямолинейном
движении.
Для равнозамедленного движения ускорение
отрицательно а< 0 и перемещение
вычисляется по формуле:
![]()
,
а закон движения записывается в
виде:
![]()
,
если
,
то![]()
.
Если
,
то координата х
численно равна пройденному пути.
Поэтому путь, пройденный в равноускоренном
движении, вычисляется по формуле:
![]()
и
![]()
при
![]()
Для равнозамедленного
движения а < 0 и
![]()
9.Средняя скорость
в равноускоренном движении получается
делением пройденного пути на время
движения

Учитывая, что
![]()
получим
![]()
.
Таким образом средняя скорость в
равноускоренном движении (равнопеременном)
равна среднему арифметическому начальной
и конечной скоростей. Если
,
то
![]()
.
10. Формулы,
устанавливающие связь между ускорением,
скоростью и пройденным путём в
равноускоренном (равнопеременном)
движении. Пусть тело, имея начальную
скорость
и двигаясь с ускорением а, за время t
достигло скорости
и
прошло путь S.
Тогда S=![]()
.
Подставляя сюда
![]()
,
t=![]()
получим
S=![]()
.
Если
,
то
![]()
и далее получим
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим прямолинейное движение тела вдоль оси (одномерный случай) и пусть при этом скорость тела изменяется.
Когда скорость изменяется, появляется ускорение. Ускорение, в свою очередь, тоже может меняться.
Если изменяется и ускорение, и скорость тела – движение сложное, например, колебательное;
Движение равнопеременное — если изменяется только скорость, а ускорение постоянное.
Термин «равнопеременное» применяют потому, что за одинаковые интервалы времени перемещение изменяется на одну и ту же величину.
При этом, если скорость увеличивается – движение называют равноускоренным, а если скорость уменьшается – равнозамедленным.
Примечание: Вместо слов «ускорение постоянное» можно произнести «ускорение не меняется», или «ускорение одно и то же».
Рекомендую предварительно ознакомиться с основными терминами для описания движения.
Будем выбирать направления для векторов скорости и ускорения относительно оси. Разберем несколько возможных вариантов.
Равноускоренное движение
Пусть при движении по прямой скорость тела увеличивается. Обратим внимание на перемещение тела.
Примечание: Движение равноускоренное, значит, за одинаковые интервалы времени перемещение будет увеличиваться на одну и ту же величину.
Этот факт иллюстрирует рисунок 1. Из рисунка видно: по сравнению с первой секундой, за вторую секунду пути перемещение увеличивается на небольшой отрезок, а за третью секунду – на два таких отрезка.

Рис. 1. Перемещение увеличивается на одну и ту же величину при равноускоренном движении
Считаем, что векторы скорости и ускорения сонаправлены с осью, вдоль которой движется тело (рис. 2).

Рис.2. Векторы скорости и ускорения направлены в одну и ту же сторону, скорость увеличивается
Примечание: Скорость увеличивается, когда вектор ускорения сонаправлен с вектором скорости.
В начальный и в конечный моменты времени скорости будут различаться.
Формулы можно записать в скалярном виде, так как движение происходит вдоль одной прямой и направления векторов известны.
Связь между начальной и конечной скоростью выглядит так:
[ v = v_{0} + a cdot t ]
Уравнение движения выглядит так:
[ S = v_{0} cdot t + a cdot frac{t^2}{2} ]
Или так:
[ x – x_{0} = v_{0} cdot t + a cdot frac{t^2}{2} ]
Кроме уравнения движения теперь есть связь между скоростями. Поэтому, решая задачи, в которых скорость увеличивается, используем систему, состоящую из двух таких уравнений:
[ large boxed{ begin{cases} v = v_{0} + a cdot t \ S = v_{0} cdot t + a cdot frac{t^2}{2} end{cases} } ]
Примечание: Перемещение тела можно вычислить, не обладая информацией о времени движения, зная только начальную и конечную скорость тела и его ускорение. Об этом подробно написано в статье о формуле пути без времени.
Равнозамедленное движение
Пусть теперь тело движется по прямой и его скорость уменьшается. Рассмотрим перемещение тела.
Примечание: Движение равнозамедленное, значит, за одинаковые интервалы времени перемещение будет уменьшаться. При чем, на одну и ту же величину.

Рис. 3. Перемещение уменьшается на одну и ту же величину при равнозамедленном движении
На рисунке 3 представлено изменение перемещения. Видно, что по сравнению с первой секундой, за вторую секунду перемещение уменьшается на небольшой отрезок, а за третью секунду – на два таких отрезка.
Примечание: Скорость будет уменьшаться, когда вектор ускорения направлен противоположно вектору скорости.

Рис. 4. Векторы скорости и ускорения направлены в противоположные стороны, скорость уменьшается
Пусть вектор скорости сонаправлен с осью, вдоль которой движется тело, а вектор ускорения – направлен против этой оси.
В начале и в конце пути скорости будут различаться.
Формулы можно записывать в скалярном виде, так как движение происходит вдоль одной прямой. Будем использовать знаки проекций векторов на ось.
Связь между скоростями выглядит так:
[ v = v_{0} — a cdot t ]
А уравнение движения имеет такой вид:
[ S = v_{0} cdot t — a cdot frac{t^2}{2} ]
Заменив перемещение разностью конечной и начальной координат ( S = x — x_{0}), получим:
[ x – x_{0} = v_{0} cdot t — a cdot frac{t^2}{2} ]
Значит, когда скорость уменьшается, для решения задач нужно использовать систему из двух таких уравнений:
[ large boxed{ begin{cases} v = v_{0} — a cdot t \ S = v_{0} cdot t — a cdot frac{t^2}{2} end{cases} } ]
Расшифруем теперь, к примеру, словосочетание «прямолинейное равнозамедленное движение» — это движение по прямой, ускорение есть, оно не меняется. Скорость тела уменьшается, так как вектор ускорения направлен противоположно вектору скорости.
Примечание: Перемещение замедляющегося тела можно вычислить не используя время. Потому, что существует запись формулы пути без времени для случая, когда скорость тела уменьшается.
Скорость направлена против оси, а ускорение – по оси
Дополнительно рассмотрим случай, когда скорость и ускорение направлены в противоположные стороны, ускорение – по оси, а скорость – против оси (рис. 5).

Рис. 5. Векторы скорости и ускорения направлены в противоположные стороны, скорость направлена против оси, модуль скорости уменьшается
При такой направленности векторов (vec{v}) и (vec{a}), с течением времени модуль скорости будет уменьшаться до нуля. Это движение будет равнозамедленным.
А если тело продолжит движение, то начнет двигаться в обратную сторону и модуль его скорости начнет увеличиваться. Поэтому, такое движение будет равноускоренным и будет сонаправленным с вектором ускорения.
Когда скорость направлена против оси, ее проекция на ось отрицательна и в уравнение она войдет со знаком минус. Ускорение же, напротив, совпадает с направлением оси, поэтому, войдет в уравнение со знаком «+».
Запишем связь между скоростями:
[ v = — v_{0} + a cdot t ]
Уравнение движения для рассмотренного случая имеет такой вид:
[ x – x_{0} = — v_{0} cdot t + a cdot frac{t^2}{2} ]
Для выбранного направления векторов в итоге получим такую систему уравнений:
[ large boxed{ begin{cases} v = — v_{0} + a cdot t \ x – x_{0} = — v_{0} cdot t + a cdot frac{t^2}{2} end{cases} } ]
Решая задачи на движение, иногда вычисляют мгновенную и среднюю скорости.
Термины «мгновенная скорость» и «средняя скорость» применяют для случаев, когда скорость изменяется – то есть, для неравномерного движения.
Мгновенная скорость
Мгновенная скорость – это скорость тела в какое-то мгновение. Когда скорость тела меняется, то в различные мгновения (моменты времени) скорости будут различаться.
Мгновенную скорость v вычисляют, вместо символа t подставляя в формулу интересующее нас время:
[ v = v_{0} pm a cdot t ]
Знак ускорения зависит его направления.
Средняя скорость
Средняя скорость тела – скорость, с которой нужно двигаться равномерно, чтобы пройти тот же путь за то же время.
Другими словами, средняя скорость помогает понять, с какой постоянной скоростью могло бы двигаться тело, чтобы пройти весь пройденный путь за такое же время.
Примечания:
- Выражение «скорость постоянная» можно заменить словами «неизменная», «одна и та же».
- Вместо фразы «за такое же время» в учебниках напишут «за выделенный интервал времени».
- Если скорость изменяется, появляется ускорение.
Формула для расчета средней скорости:
[ large boxed { v_{text{средняя}} = frac{S_{text{весь}}}{t_{text{полное}}}} ]
( S_{text{весь}}(text{м}) )– полный путь, пройденный телом;
( t_{text{полное}} left( c right)) – время, за которое тело прошло весь путь.
