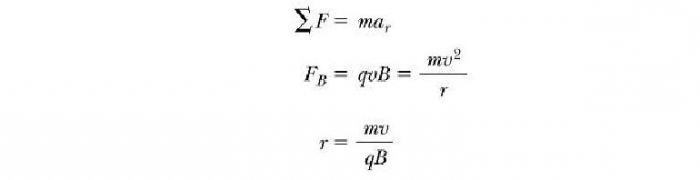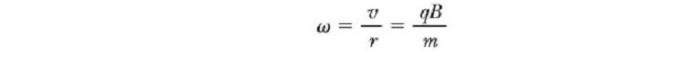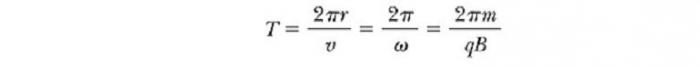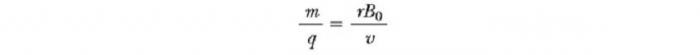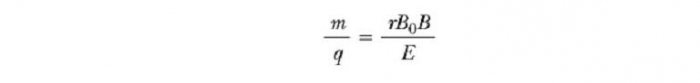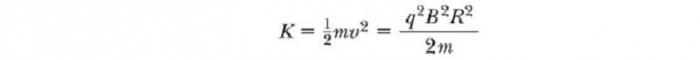Как найти начальную скорость протона

Элементарная
работа сил электрического поля по
перемещению электрического заряда на
dr,

Если
перемещение заряда q₂
было совершено из точки, находящейся
на расстоянии r₁
от центра заряда, создающего поля в
точку, расположенную на расстоянии r₂
от него, то работа, совершаемая силами
электрического поля

.

Из
выражения видно, что работа не зависит
от траектории перемещения, а определяется
только начальным и конечным положениями
перемещаемого заряда. Кроме того, работа,
по перемещению электрического заряда
во внешнем электрическом поле по любому
замкнутому пути ℓ , равна нулю, т.е.

Это
подтверждает, что электрическое поле
является потенциальным, а электрические
силы-консервативными.

Работа сил
электрического поля совершается за
счет изменения (уменьшение) потенциальной
энергии

A=W_p1-W_p2=-DW_p.

Принято
считать потенциальную энергию системы
зарядов равной нулю в том случае, когда
один из них удален от другого на
бесконечность, т.е., например, W_p2=W_p=0.
Тогда W_p1=A.

Потенциальная
энергия заряда, находящегося в
электрическом поле другого заряда,
измеряется работой, которую совершают
силы электрического поля по удалению
одного из зарядов из данной точки поля
в бесконечность:

.

при
r₂=,
W_p2=0,

В общем случае

Разность
потенциалов между двумя точками
электрического поля, которое создано
бесконечно длинным равномерно заряженным
стержнем (цилиндром) с линейной плотностью
заряда t:

где
r₁ и
r₂-соответственно
расстояние от оси стержня (цилиндра) до
рассматриваемых точек электрического
поля.

Разность
потенциалов между двумя точками
электрического поля, которое создано
бесконечно длинной, равномерно заряженной
плоскостью с поверхностной плотностью
заряда s:

где
r₂-r₁=d-расстояние
между рассматриваемыми точками. Разность
потенциалов между двумя точками поля,
которое создано равномерно заряженной
сферической поверхностью радиусом R,
расстояние от рассматриваемых точек
до центра сферы r₁>R
и r₂>R:

Если
принять r₁₌r
и r₂=,
то потенциал поля вне сферической
поверхности что совпадает с ранее
полученным соотношением для потенциала
поля точечного заряда.

.

Внутри сферической
поверхности потенциал всюду одинаков
и равен

Разность
потенциалов между двумя точками поля,
которое создано равномерно заряженным
по объёму шаром радиусом R, если расстояние
от рассматриваемых точек поля до центра
шара r₁>R
и r₂>R
, объёмная плотность заряда r:

Если
принять r₂=и r₁=R
, то потенциал поля в этом случае:

На
поверхности шара (r=R)

В
центре шара (R=0): j=0.

Эквипотенциальные
поверхности – поверхности равного
потенциала.

Так
как A=q(j₁–j₂),
то при перемещении заряда по
эквипотенциальной поверхности работа
не совершается (A=0). Работа совершается
лишь тогда, когда перемещение заряда
происходит с одной эквипотенциальной
поверхности на другую. В этом случае
j₁¹j₂

A=q(j₁-j₂).

1.3.1. Примеры решения задач

1.3.1.1.
Задача. Какой скоростью сближения должны
обладать протоны, находясь на расстоянии
5 см, чтобы они могли сблизиться друг с
другом до расстояния 10^-11
см?

Решение.
При решении задачи можно рассматривать
один протон неподвижным, а второй –
движущимся по направлению к первому.

Так
как между протонами существуют силы
отталкивания, то движение второго
протона будет замедленным. Его скорость
уменьшится от искомой скорости v₁
до скорости v₂=0
в момент остановки протона. При этом
будет уменьшаться и кинетическая энергия
протона от начального значения T₁
до значения T₂=0
в момент остановки протона.

За счет кинетической
энергии протона будет совершена работа
против сил поля. На основании закона
сохранения энергии

А=DT,

или

e(j₁-j₂)=T₂-T₁,(1)

где
e – заряд протона,

j₁
и j₂
– потенциалы поля, созданного неподвижными

протонами
в точках, соответствующих начальному
и конечному положению движущегося
протона.

Приняв
во внимание, что T₂=0,
и поменяв знаки в обеих частях равенства
(1) на обратные, получим:

e
(j₁-j₂)=T₁.

Подставим в формулу
(2) выражения потенциала, создаваемого
точечным зарядом, и кинетической энергии:

или

Отсюда

Подставив
числовые значения, произведя вычисления,
будем иметь:

v₁=1,66×10⁶
(м/с).

1.3.1.2.
Задача. Определить начальную скорость
v_o
сближения протонов, находящихся на
достаточно большом расстоянии друг от
друга, если минимальное расстояние
r_мин,
на которое они могут сблизиться, равно
10^-11
см.

Решение.
Между двумя протонами действуют силы
отталкивания, вследствие чего движение
протонов будет замедленным. Поэтому
задачу можно решить как в инерциальной
системе отсчета (связанной с центром
масс двух протонов), так и в неинерциальной
(связанной с одним из ускоренно движущихся
протонов). Во втором случае законы
Ньютона не могут быть применимыми.
Применение же принципа Даламбера
затруднительно из-за того, что ускорение
системы будет переменным. Поэтому удобно
рассмотреть задачу в инерциальной
системе отсчета.

Поместим
начало координат в центр масс протонов.
Поскольку мы имеем дело с одинаковыми
частицами, то центр масс будет находиться
в точке, делящей пополам отрезок,
соединяющий частицы. Относительно
центра масс частицы будут иметь в любой
момент времени одинаковые по абсолютной
величине скорости v₁
и v₂.
Скорость каждой частицы будет равна
половине скорости сближения

v₁=v₂=v/2.
(1)

Для
решения задачи применим закон сохранения
энергии, согласно которому полная
механическая энергия E изолированной
системы постоянна, т.е.

E=T+П,

где
T – кинетическая энергия;

П
– потенциальная энергия.

Выразим
потенциальную энергию в начальный и
конечный моменты движения.

В
начальный момент, согласно условию
задачи, протоны находились на большом
расстоянии, поэтому потенциальной
энергией можно пренебречь. Следовательно,
для начального момента полная энергия
будет равна кинетической энергии T₀
протонов, т.е.

E=T₀.
(2)

В
конечный момент, когда протоны максимально
сблизятся, скорость и кинетическая
энергия равны нулю, а полная энергия E
будет равна потенциальной энергии П_кон:

E=П_кон.
(3)

Приравняв правые
части равенств (2) и (3), получим

T₀=П_кон.
(4)

Кинетическая
энергия равна сумме кинетических энергий
протонов

.
(5)

Потенциальная
энергия системы двух зарядов q₁
и q₂,
находящихся в вакууме, определяется по
формуле:

где
r – расстояние между зарядами.

Воспользовавшись
этой формулой, получим

(6)

С учетом выражений
(5) и (6) формула (4) примет вид

.

Откуда

.

Подставив числовые
значения, получим

v₀=
2,35×10⁶
(м/с).

1.3.1.3.
Задача. Определить ускоряющую разность
потенциалов U, которую должен пройти в
электрическом поле электрон, обладающий
скоростью v₁=10⁶
м/с, чтобы скорость его возросла в n=2
раза.

Решение.
Ускоряющую разность потенциалов можно
найти, вычислив работу A сил
электростатического поля. Эта работа
определяется произведением заряда
электрона e на разность потенциалов U:

A=eU.
(1)

Работа
сил электростатического поля в данном
случае равна изменению кинетической
энергии электрона:

,
(2)

где
T₁
и T₂
– кинетические энергии электрона до и
после прохождения ускоряющего поля;

m-масса
электрона;

v₁
и v₂
– начальная и конечная его скорости.

Приравняв правые
части равенств (1) и (2), получим

или

где
n=v₂/v₁.

Отсюда искомая
разность потенциалов

(3)

Подставив
численные значения физических величин
и выполнив вычисления, будем иметь:

U=8,53
(В).

1.3.1.4.
Задача. Электрическое поле создается
двумя зарядами Q₁=4
мкКл и Q₂=-2
мкКл, находящимися на расстоянии а=0,1 м
друг от друга. Определить работу А_1,2
сил поля по перемещению заряда Q=50 нКл
из точки 1 в точку 2.

Решение.
Для определения работы А_1,2
сил поля воспользуемся соотношением

А_1,2=Q(j₁
– j₂).

Применяя
принцип суперпозиции электрических
полей, определим потенциалы j₁
и j₂
точек 1 и 2
поля:

Тогда

Подставив числовые
значения величин в единицах системы
СИ, произведя вычисления, получим

А_1,2=14,3
(мДж).

1.3.1.5.
Задача. С поверхности бесконечного
равномерно заряженного (t=50
нКл/м) прямого цилиндра вылетает a-частица
(v₀=0).
Определить кинетическую энергию T₂
a-частицы
(кэВ) в точке на расстоянии 8R от поверхности
цилиндра.

Решение.
Так как силы электростатического поля
являются консервативными, то для
определения кинетической энергии
a-частицы
в заданной точке воспользуемся законом
сохранения энергии, записанном в виде

E₁=E₂,

где
E₁
– полная энергия -частицы
на поверхности цилиндра;

E₂-полная
энергия -частицы
в заданной точке.

Так как

E₁=T₁+U₁;
E₂=T₂+U₂,

где
T₁
и T₂
– кинетические энергии a-частицы в
соответствующих состояниях;

U₁
и U₂
– потенциальные энергии -частицы
в соответствующих состояниях.

Учитывая,
что T₁=0
(v₀=0),
можно записать

U₁=T₂+U₂,

откуда

T₂=U₁
– U₂=Q(j₁
– j₂),

где
Q – заряд a-частицы;

j₁
и j₂–
потенциалы на поверхности цилиндра и
в рассматриваемой точке.

Используя решение
примера (1.5), для разности потенциалов,
будем иметь

Тогда

Подставив все
величины в единицах системы СИ, произведя
вычисления, получим

T₂=3,96
(кэВ).

1.3.1.6.
Задача. Две частицы, обладающие массами
m₁,
m₂
и зарядами q₁
и q₂,
движутся навстречу друг другу, имея
вдалеке относительную скорость vотн.
На какое минимальное расстояние сблизятся
частицы?

Решение.
Эту задачу можно решить тремя способами,
различающимися выбором системы отсчета:

1.
Рассмотрим движение частиц в какой-либо
“лабораторной” системе отсчета,
например связанной с Землей. Полагая
систему двух заряженных частиц
изолированной, воспользуемся законом
сохранения энергии

W=const,
(1)

где
W-полная энергия частиц, которые в каждый
момент времени обладают кинетической
энергией, а также потенциальной знергией
кулоновского взаимодействия.

Когда
частицы находятся вдалеке друг от друга,
то, как это следует из формулы

их потенциальной
энергией можно пренебречь.

Тогда полная
энергия системы

W₁₌m₁
v₁
²/2+m₂v₂²/2,
(2)

где
v₁,
v₂-скорости
частиц в выбранной системе отсчета.

Так
как векторы v₁
и v₂
направлены противоположно, то значения
v₁
и v₂
связаны с заданной величиной v_отн
соотношением

v_отн=ôv₁-v₂ô=v₁+v₂.
(3)

При
сближении частиц потенциальная энергия
их кулоновского взаимодействия
(отталкивания), будучи величиной
положительной, начнет увеличиваться.
Следовательно, суммарная кинетическая
энергия частиц станет уменьшаться.
Частицы не могут, как угодно близко
подойти друг к другу, иначе их потенциальная
энергия оказалась бы больше полной
энергии W₁,
что противоречит условия (1).

При
наибольшем сближении частиц, когда
расстояние между ними равно r_мин,
полная энергия

.
(4)

Чтобы
найти кинетическую энергию T_мин
системы, учтем, что в момент наибольшего
сближения частиц их скорости будут
одинаковыми: v_1мин=v_2мин=v.
Действительно, когда скорости частиц
неодинаковые, расстояние между ними
растет или уменьшается и, следовательно,
не является минимальным.

Применив к системе
закон сохранения импульса, запишем:

m₁
v₁
– m₂v₂=(m₁+m₂)v,
(5)

где
(m₁
v₁-m₂v₂)-импульс
удаленных частиц;

(m₁+m₂)v-импульс
системы при наибольшем сближении частиц.

При
этом вектор v
предположительно выбран совпадающим
по направлению с вектором v₁
(очевидно, при подсчете кинетической
энергии направление скорости
несущественно). Из уравнения (5) имеем

v=(m₁
v₁
– m₂v₂)/(m₁+m₂).

Тогда
для величины T_мин,
получим

Подставив
это значение T_мин
в формулу (4), приравняв на основании
закона сохранения энергии правые части
формул (2) и (4), а также учитывая соотношение
(3), найдем

2.
Выберем систему отсчета, связанную с
центром инерции системы двух частиц.
Пусть скорости частиц в этой системе
отсчета равны v₁
‘ и v₂‘.
Сначала выразим каждую из величин v₁
‘ и v₂‘
через относительную скорость v_отн.
Так как частицы движутся навстречу друг
другу, то

v_отн=v₁
‘+v₂‘.
(1)

Поскольку
в данной системе отсчета скорость центра
инерции частиц равна нулю, то, согласно
утверждению, что импульс системы
материальных точек равен произведению
массы M системы на скорость движения v_с
ее центра инерции, суммарный импульс
частиц p=0. Тогда, применив к системе
частиц закон сохранения импульса и
учитывая противополжные направления
векторов v₁
и v₂,
получим

m₁
v₁
‘ – m₂v₂‘=0.
(2)

Решив
систему (1) и (2) относительно v₁
‘ и v₂‘,
найдем:

v₁‘=[m₂/(m₁+m₂)]v_отн;
v₂‘=[m₁/(m₁+m₂)]v_отн.

Полная
энергия системы частиц в начальный
момент равна сумме их кинетических
энергий. В момент наибольшего сближения
частицы имеют одинаковые по модулю и
направлению скорости. При этом каждая
из скоростей равна нулю, так как в
противном случае оказалось бы нарушенным
условие p=0. Следовательно, частицы будут
сближаться до тех пор, пока вся кинетическая
энергия не превратится в энергию
кулоновского взаимодействия. Таким
образом,

.

Подставив
сюда найденные значения v₁‘
и v₂‘,
получим

3.
Выберем систему отсчета, движущуюся
поступательно вместе с одной из заряженных
частиц, например с первой. Эта система
отсчета является неинерциальной. В ней
первая частица неподвижна, а вторая
движется навстречу первой с начальной
скоростью vотн. Теперь начальная энергия
системы частиц равна кинетической
энергии второй частицы:

(1)

а
конечная энергия (при r=r_мин)
равна лишь потенциальной энергии
кулоновского взаимодействия, т.е.

(2)

поскольку в момент
наибольшего сближения вторая частица
имеет нулевую скорость.

В
данном случае система взаимодействующих
частиц является незамкнутой, так как
на нее действуют силы инерции, которые
следует считать внешними по отношению
к системе. Поэтому ни полный импульс,
ни полная энергия системы частиц в
неинерциальной системе отсчета не
сохраняются.

Согласно
закону сохранения энергии, изменение
энергии системы, должно быть равно
работе A силы инерции F_ин,
действующей на частицу m₂
во время ее приближения к частице m₁:

W₂-W₁=A,
(3)

и задача сводится
к нахождению величины A. Для силы инерции,
имеем

F_ин=-m₂a₁,
(4)

где
a₁-ускорение
частицы m₁
в инерциальной системе отсчета.

Это ускорение
можно определить с помощью второго
закона Ньютона и закона Кулона:

.

Поскольку
ускорение a₁
первой частицы, обусловленное кулоновской
силой отталкивания, направлено в одну
сторону, то сила инерции, как это следует
из (4), направлена в другую и равна

(5)

Так
как частица m₂
перемещается в сторону противоположную
направлению силы инерции, то сила инерции
совершает над ней отрицательную работу,
значение которой найдем, учитывая
соотношение (5):

.
(6)

Подставив
в (3) значения W₁,
W₂,
A из уравнений (1), (2), (6), найдем

1.4.
Проводники и диэлектрики в электрическом
поле. Электроемкость. Конденсаторы и
их емкость. Энергия электрического поля

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
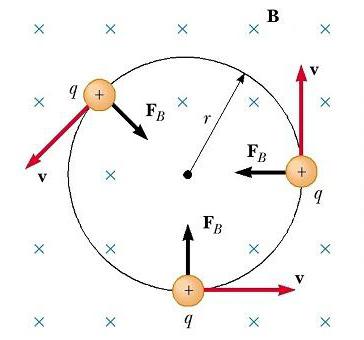
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

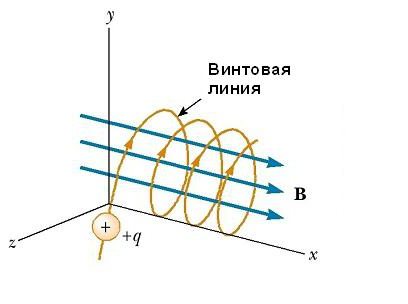
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

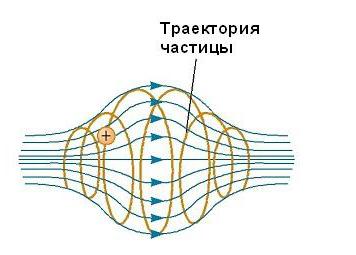
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

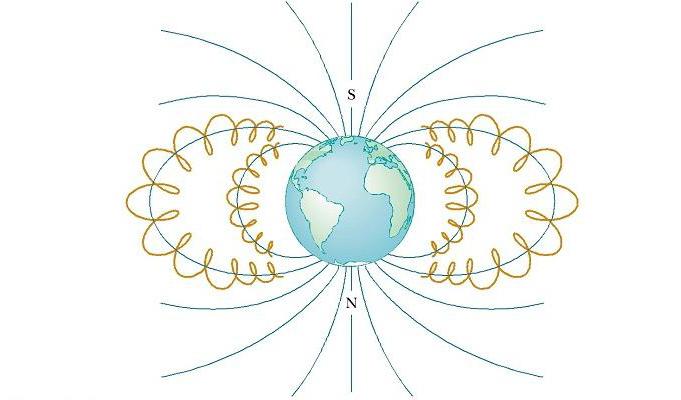
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

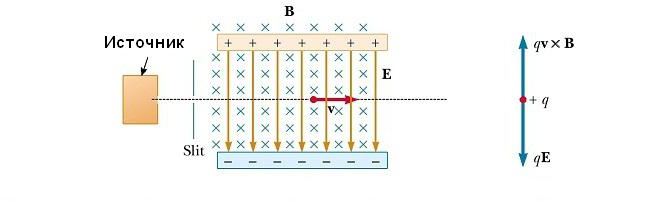
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

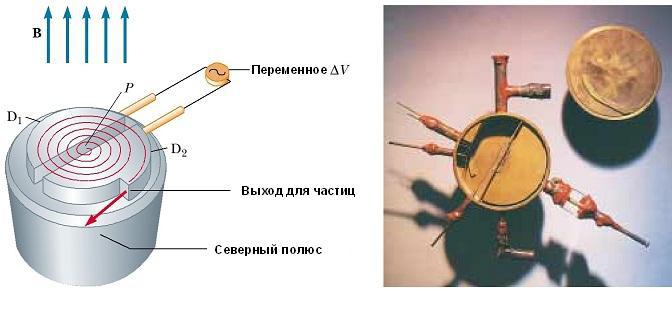
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Движение протона по окружности в магнитном поле

Задание 17. Протон движется по окружности в однородном магнитном поле между полюсами магнита под действием силы Лоренца. Как изменятся по сравнению с протоном модуль силы Лоренца и период обращения α-частицы, если она будет двигаться в этом же поле по окружности с той же скоростью?

Для каждой величины определите соответствующий характер изменения:

На α-частицу со стороны магнитного поля действует сила Лоренца , где q – заряд частицы; v – скорость частицы; B – напряженность магнитного поля. Так как α-частица движется по окружности, то магнитное поле направлено перпендикулярно его движению, то есть и сила Лоренца в данном случае запишется в виде

.

В соответствии со вторым законом Ньютона, силу Лоренца также можно записать как , где – центростремительное ускорение. Получаем значение для радиуса окружности R:

.

Теперь вычислим изменение радиуса окружности для альфа-частицы, движущейся с той же скоростью. Альфа-частица имеет в своем составе два протона и два нейтрона, то есть ее масса в 4 раза больше массы протона, а заряд в 2 раза больше заряда протона. В итоге получаем:

,

то есть радиус окружности увеличится в 2 раза. Так как период обращения T – это время одного полного оборота, а радиус увеличился в 2 раза при сохранении той же скорости, то период возрастет.

Модуль силы Лоренца возрастает, так как заряд α-частицы выше заряда протона.

5.3. Движение заряда в однородном магнитном поле

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

из которого легко получить выражение для угловой скорости частицы

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

Кинетическая энергия протона будет

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).

[spoiler title=”источники:”]

http://self-edu.ru/ege2019_phis_30.php?id=7_17

http://online.mephi.ru/courses/physics/electricity/data/course/5/5.3.html

[/spoiler]

Вы открыли страницу вопроса Чему равна начальная скорость протона, если он остановился, пролетев в электрическом поле между точками с разностью потенциалов 200В?. Он относится к категории
Физика. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Физика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.