Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
![]()
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
![]()
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
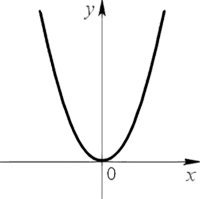
Также парабола может быть перевернутой.
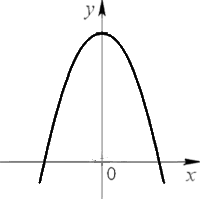
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.

- Координаты вершины параболы
Запомните!

Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».
- Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!

Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
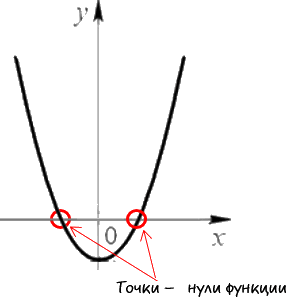
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.

- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
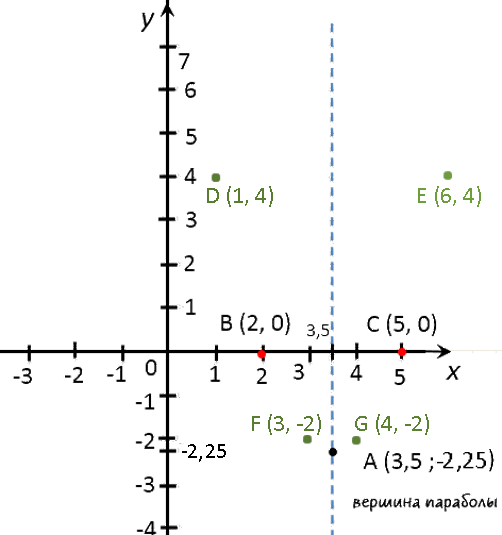
Теперь мы готовы построить график.
На забудьте после построения подписать график функции.
- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
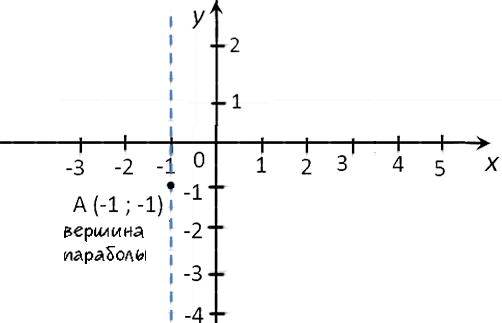
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
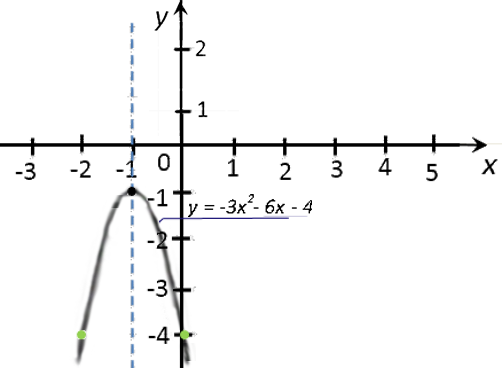
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0. 
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
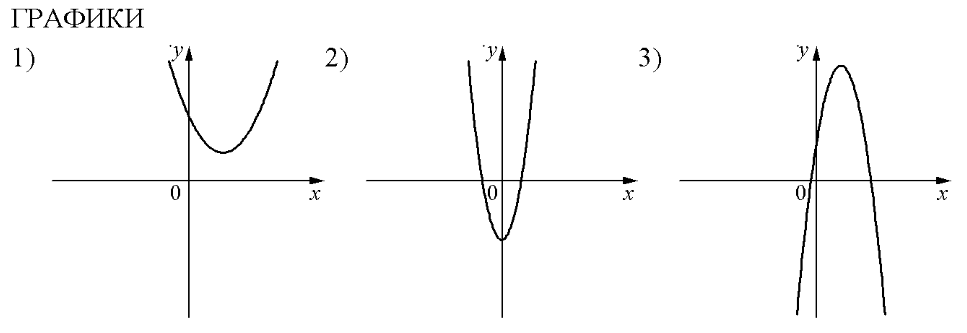
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
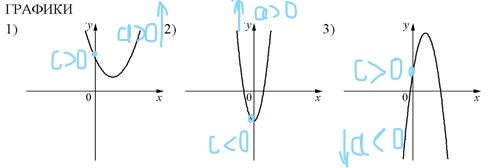
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
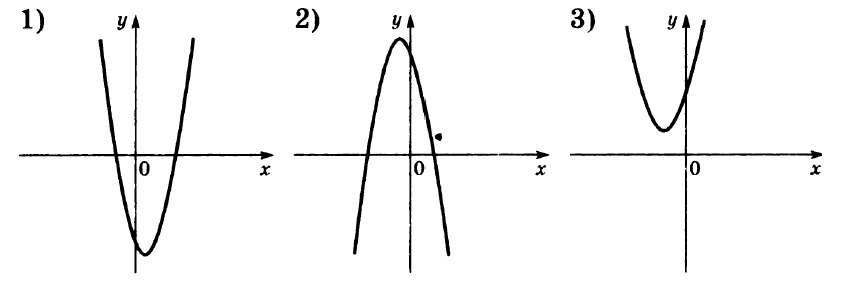
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.6k
Вершина параболы
Содержание:
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Что такое вершина параболы
Определение
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.
Чтобы найти ВП, необходимо применить формулу:
(lbrackfrac{-b}{2a};-frac{b^2-4ac}{4a}rbrack)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Исходя из координат, можно узнать расположение вершины параболы и построить ее.
Вывод формулы координат вершины параболы
Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:
(y;=;ax^2;+;bx;+;c)
Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y.
Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:
(y;=;f(x;+;l);+;m)
Делают это с помощью метода выделения полного квадрата, то есть (left(a+bright)^2) преобразуют в (a^2+2ab+b^2.)
Функции вида (y;=;f(x;+;l);+;m) отличаются от (y;=;f(x)) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:
(frac{-b}{2a}, а frac{left(4ac-b^2right)}{4a})
Получается, что l и m — это координаты x0 и y0.
Приведем доказательство:
- Соединяем первые два члена многочлена: (y;=;(ax^2;+;bx);+;c.)
- Выносим коэффициент a за скобку, b при этом делим на a: (y=aleft(x^2+frac baxright)+c.)
- Представляем, что у нас есть квадрат суммы, в котором x является слагаемым, а из выражения в скобках необходимо рассчитать его полный квадрат суммы. Одночлен (frac bax) умножаем на два и делим на два одновременно. Далее прибавляем и вычитаем квадрат второго слагаемого квадрата суммы. Получаем: (y=aleft(x^2+2frac b{2a}x+frac{b^2}{4a^2}-frac{b^2}{4a^2}right)+c.)
- Выделяем квадрат суммы: (y=aleft(left(x+frac b{2a}right)^2-frac{b^2}{4a}right)+c.)
- Умножаем на a: (y=aleft(x+frac b{2a}right)^2-frac{b^2}{4a}+c.)
- Приводим свободные члены к общему знаменателю: (y=aleft(x+frac b{2a}right)^2-frac{b^2+4ac}{4a}.)
- Меняем знак: (y=aleft(x+frac b{2a}right)^2+frac{b^2-4ac}{4a}.)
Мы привели функцию (y;=;ax^2;+;bx;+;c) к виду (y;=;a{(x;+;l)}^2;+;m,) что соответствует (y;=;f(x;+;l);+;m,) где (f(x);=;ax^2. )
Как найти координаты, основные способы
Существует несколько способов нахождения координат ВП:
- (x_0=frac{-b}{2a}) — подходит в том случае, если дискриминант квадратного уравнения равен нулю.
- (y_0=-frac{b^2-4ac}{4a}) — это формула дискриминанта, поделенная на 4а.
- (x_0=frac{x_1+x_2}2) — среднее арифметическое между нулями функции. Можно использовать, если в выражении есть нули.
- Если функция имеет вид (y=aleft(x-x_0right)^2+y_0), то в ее вершиной совпадают координаты (left(x_0;y_0right).)
Примеры решения задач
Задача №1
Найти вершину параболы для уравнения: (y=x^2-5x+7.)
Решение: В выражение (x=-frac b{2a}) подставляем известные числа и получаем (x=frac52=2,5). Теперь подставляем x в исходное уравнение: (2,5^2-5times2,5+7=0,75.)
Ответ: (2,5; 0,75).
Задача №2
Найти ВП для уравнения: y=5(x-1)(x+7).
Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.
Подставляем и получаем: (x_0=frac{x_1+x_2}2=frac{1+left(-7right)}2=-3.)
Второе: (y_0=5timesleft(-3-1right)left(-3+7right)=-80.)
Ответ: (-3; -80).
Задача №3
Найти вершину параболы для уравнения: (y=x^2-7x+3 ).
Решение: (х_0=-frac b{2a}=-frac{left(-7right)}{2times1}=3,5.)
Второе: (y_0=3,5^2-7times3,5+3=-9,25.)
Ответ: (3,5; -9,25).
Насколько полезной была для вас статья?
Рейтинг: 2.50 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Загрузить PDF
Загрузить PDF
Вершина параболы квадратного уравнения — это самая высокая или самая низкая ее точка. Чтобы найти вершину параболы, вы можете воспользоваться специальной формулой или методом дополнения до полного квадрата. Ниже описано, как это сделать.
-

1
Найдите величины a, b, и c. В квадратном уравнении коэффициент при x2 = a, при x = b, постоянная (коэффициент без переменной) = c. Например, возьмем уравнение: y = x2 + 9x + 18. Здесь a = 1, b = 9, and c = 18.[1]
-

2
Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a. Подставьте в нее соответствующие значения для вычисления x.
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
-

3
Подставьте найденное значение x в исходное уравнение для вычисления значения y. Теперь, когда вам известно значение x, просто подставьте его в исходное уравнение для нахождения y. Таким образом, формулу для нахождения вершины параболы можно записать в виде функции: (x, y) = [(-b/2a), f(-b/2a)]. Это значит, что для нахождения y необходимо сначала найти x по формуле, а затем подставить значение x в исходное уравнение. Вот, как это делается:
- y = x2 + 9x + 18
- y = (-9/2)2 + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 – 162 + 72)/4
- y = -9/4
-

4
Запишите значения x и y в виде пары координат. Теперь, когда вам известно, что x = -9/2, а y = -9/4, запишите их как координаты в виде: (-9/2, -9/4). Вершина параболы находится по координатам (-9/2, -9/4). Если вам нужно нарисовать эту параболу, то ее вершина лежит в нижней точке, так как коэффициент при x2 положительный.
Реклама
-

1
Запишите уравнение. Дополнение до полного квадрата — еще один способ найти вершину параболы. Применив этот метод, вы найдете координаты x и y сразу, без необходимости подставлять x в исходное уравнение. Например, дано уравнение: x2 + 4x + 1 = 0.[2]
-

2
Разделите каждый коэффициент на коэффициент при x2. В нашем случае коэффициент при x2 равен 1, поэтому мы можем пропустить этот шаг. Деление на 1 ничего не изменит.
-

3
Перенесите постоянную в правую часть уравнения. Постоянная — коэффициент без переменной. Здесь это 1. Перенесите 1 вправо путем вычитания 1 из обеих частей уравнения. Вот, как это сделать:[3]
- x2 + 4x + 1 = 0
- x2 + 4x + 1 -1 = 0 – 1
- x2 + 4x = – 1
-

4
Дополните до полного квадрата левую часть уравнения. Для этого просто найдите (b/2)2 и прибавьте результат к обеим частям уравнения. Подставьте 4 вместо b, так как 4x — это коэффициент b нашего уравнения.
- (4/2)2 = 22 = 4. Теперь прибавьте 4 к обеим частям уравнения и получите:
- x2 + 4x + 4 = -1 + 4
- x2 + 4x + 4 = 3
- (4/2)2 = 22 = 4. Теперь прибавьте 4 к обеим частям уравнения и получите:
-

5
Упрощаем левую часть уравнения. Мы видим, что x2 + 4x + 4 — полный квадрат. Он может быть записан в виде: (x + 2)2 = 3
-

6
Используйте его для нахождения координат x и y. Вы можете найти x, просто приравняв (x + 2)2 к 0. Теперь, когда (x + 2)2 = 0, вычисляем x: x =-2. Координата y — это постоянная в правой части полного квадрата. Итак, y = 3. Вершина параболы уравнения x2 + 4x + 1 = (-2, 3)
Реклама
Советы
- Правильно определяйте a, b, и c.
- Записывайте предварительные вычисления. Это не только поможет в процессе работы, но и позволит увидеть, где сделаны ошибки.
- Не нарушайте порядок вычислений.
Реклама
Предупреждения
- Проверьте ваш ответ!
- Удостоверьтесь, что вы знаете, как определить коэффициента a, b, и c. Если вы не знаете, ответ будет неправильным.
- Не паникуйте — решение таких задач требует практики.
Реклама
Что вам понадобится
- Бумага или компьютер
- Калькулятор
Об этой статье
Эту страницу просматривали 508 414 раз.
Была ли эта статья полезной?
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.

Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.




Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .


Квадратный корень
Функция y = x имеет следующий график:

Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
