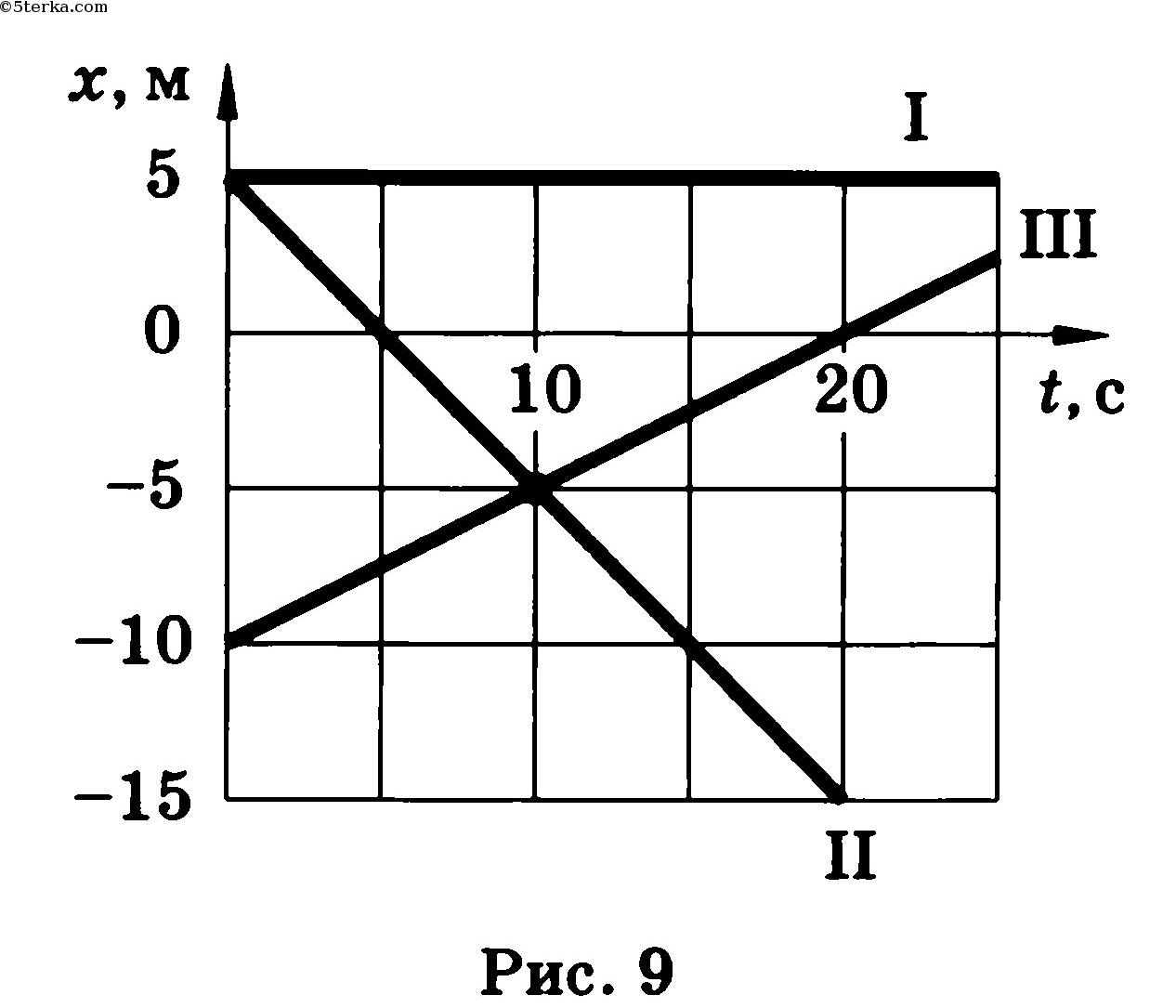
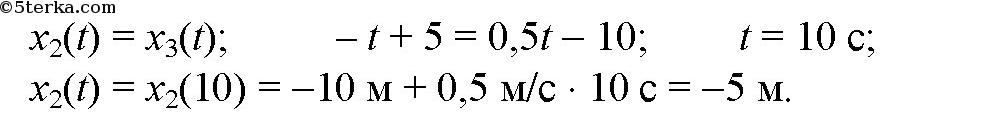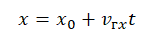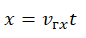По графику видно, что начальные координаты I тела : 5 м, II: 5 м,
III: — 10 м. Скорости движения I:
II:
III:
Уравнения движения:
Т.к. движение равномерное вдоль оси Х, то найденные нами скорости v1, v2, v3 являются проекциями на ось Х.
По графикам уравнения движения тел II и III видно, что они пересекутся в точке х = – 5 м в момент времени t = 10 с. Найдем это из уравнений движения.
Источник:
Решебник
по
физике
за 10, 11 класс (А.П. Рымкевич, 2001 год),
задача №22
к главе «МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 2. Прямолинейное равномерное движение».
Все задачи
← №21. Движение грузового автомобиля описывается уравнением х1 = -270 + 12t, а движение пешехода по обочине того же шоссе — уравнением х2 = -1,5t. Сделать пояснительный рисунок (ось X направить вправо), на котором указать положение автомобиля и пешехода в м
№23. Движения двух велосипедистов заданы уравнениями: х1 = 5t, х2 = 150 – 10t. Построить графики зависимости x(t). Найти время и место встречи. →
Комментарии
Физика. Кинематика
Равноускоренное движение по прямой и под углом к горизонту
Как определить положение тела в пространстве? И для чего нужны координаты?
Школьный курс физики начинается с раздела кинематика. Именно она закладывает фундамент для дальнейшего изучения, все остальные разделы так или иначе будут соприкасаться с этим разделом.
Что же такое кинематика? Это раздел физики, который изучает движение некоторого тела в пространстве. При это мы НЕ рассматриваем, что вызывает это движение, что является его причиной. У нас просто есть какое-то двигающееся тело и мы пытаемся его изучить. А на вопрос почему происходит движение, кинематика нам ответа не дает, это мы будем изучать в следующих разделах физики.
Начнем с простого вопроса – что такое «тело»? Это может быть все, что угодно – машина, самолет, мячик, капля воды, планета и т.д., то есть любой движущийся объект. Любое тело в школьной физике мы будем представлять в виде материальной точки.
Определение. Материальная точка – это тело, размерами которого мы можем пренебречь в данной задаче.
Мы просто договариваемся, что любой объект, будь то ракета или песчинка с пляжа, мы представляем в виде точки. Это необходимо для того, чтобы размеры тела не оказывали влияния на наши задачи. Так, например, автобус, двигающийся из Москвы в Санкт-Петербург, можно считать материальной точкой. Его размеры очень малы по сравнению с расстоянием между этими городами. Но движение пассажиров при выходе из автобуса уже нельзя считать материальной точкой, потому что пассажиры относительно автобуса не такие уж и маленькие. Такое школьное допущение (а в физике допущений будет много) упростит нам жизнь. При более глубоком изучении физики вы будете учитывать все эти допущения, в том числе и размеры тела, но в школе вам это, как правило, не нужно.
Задача кинематики – предсказать или описать при помощи законов физики, как этот объект будет двигаться в будущем, например, через час, если ничего не изменится.
Зачем нам это? Очень просто: если мы знаем, по каким законам двигается машина, мы легко сможем предсказать будущее и узнать, где она будет через какое-то время и с какой скоростью будет двигаться. Естественно, мы можем точно так же предсказывать движение брошенного камня и любых других объектов. Например, зная начальную скорость камня и как вы его кинули, можно предсказать, как далеко или высоко он улетит, или через сколько времени и с какой скоростью он упадет на землю.
Траектория, путь и перемещение. Что это такое и чем они отличаются?
Перед тем, как писать формулы, познакомимся еще с несколькими определениями, которые нам понадобятся в дальнейшем. Представим, что человек идет из пункта (А) в пункт (В) (см Рис.1.).
Рис.1. Траектория (зеленая линия). Путь(длина зеленой линии). Перемещение(фиолетовая стрелка)
- Траектория – линия, вдоль которой движется тело. На рис.1 показана зеленой линией.
- Путь – длина траектории. Обычно обозначается буквой (S).
- Перемещение – вектор, соединяющий начальную и конечную точки (фиолетовая линия). О том, что такое вектор, мы поговорим чуть позже. А на нашем рисунке перемещение – это длина отрезка (АВ), кроме длины перемещение еще показывает куда движется тело из начальной точки (А) в конечную (В).
Разберемся подробнее на примере. Если вы ходите по комнате с шагомером туда-сюда и вернетесь в итоге в исходную точку, то ваше перемещение будет равно 0, а путь будет расстоянием, которое вы находили, его покажет шагомер.
Что такое координаты и зачем они нужны?
Все это звучит здорово, но как нам определить положение тела в пространстве? Для этого люди придумали очень удобную штуку, которая называется координатная плоскость. С этим понятием вы должны были сталкиваться в курсе алгебры – построение графиков в осях (х) и (y). Помните, у вас были функции типа (y=x^2-3) и нужно было построить график этой функции по точкам? Вы брали какие-то значения (x) подставляли в (y=x^2-3) и получали значение (y). Потом отмечали получившуюся точку на координатной плоскости. Именно эта плоскость нас и будет интересовать.
Координаты используются людьми повсюду. Например, вся поверхность Земли расчерчена линиями, которые называются долгота и широта. Этих линий очень много, но указав пересечение некоторой долготы (37) с какой-то широтой (55), я укажу вполне конкретную точку на земной поверхности – это примерное расположение города Москва (37;55). Именно такой способ используется для определения положения любого объекта на Земле в географических картах и навигаторах – город, озеро, здание, машина, человек и т.д.
Для начала давайте рассмотрим одномерное движение – это такое движение, при котором машина может двигаться только вперед по дороге или назад, никуда свернуть она не может. (Рис.2.). Наложим на нашу дорогу ось Х, направленную вправо, как на рисунке. Теперь вся наша дорога размечена координатами. И мы можем определить положение машины, просто сказав ее координату. Начало координат мы можем выбрать как угодно, пусть оно будет в точке О. Тогда на рисунке наша машина находится в начальной координате (x_0=3). Из этой точки она может поехать влево (координата будет уменьшаться) или вправо (координата будет увеличиваться).
Расстояние можно измерять в различных единицах измерения: километры, метры, сантиметры, миллиметры и т.д. Пусть все координаты у нас измеряются в метрах, тогда можно сказать, что на рисунке машина находится на расстоянии 3 метра от точки О.
Итак, мы научились определять положение тела в пространстве при помощи координат.
Что такое скорость?
На интуитивном уровне это понятно. Но давайте попробуем вникнуть поглубже. В чем всегда измеряется скорость? В автомобиле это обычно километры в час (км/ч), измеряется при помощи спидометра. То есть спидометр машины показывает, сколько километров проедет машина за один час, если не будет менять скорость. Точно так же скорость можно измерять в метрах в секунду (м/с), километрах в секунду (км/с) и т.д. Значит, если я умножу скорость на количество часов, которые едет машина с этой скоростью, то получу расстояние, пройденное машиной за это время. Можно записать в виде известной формулы движения с постоянной скоростью:
$$S=V*t;$$
Итак, при движении с постоянной скоростью (V), можно посчитать расстояние (S), которое проходит тело за время (t).
Теперь давайте предположим, что машина двигается с постоянной скоростью 1 (м/с) влево из начальной точки с координатой (x_0=3(м)). Это означает, что машина за 1 секунду сдвинется на (S=V*t=1*1=1(м)) метр влево, то есть окажется в точке с координатой (2) (м). Через 2 секунды она пройдет расстояние (S=V*t=1*2=2(м)) и попадет в координату (1)(м), а через 6 секунд на (S=V*t=1*6=6(м)) и окажется в координате (-3)(м).
Скорость кроме величины еще имеет направление – в нашем случае это означает, что если машина едет вправо (туда же, куда направлена ось (х)), то скорость будет положительна, а если влево (в противоположную сторону направлению оси (х)), то скорость будет отрицательна.
Все, что имеет величину и направление, называется вектором. То есть скорость ни что иное, как вектор. Вектор – это ключевое понятие физики. Мы часто будем сталкиваться с величинами, у которых кроме числа есть еще и направление – ускорение, сила.
Немного отвлечемся, и обсудим, что такое вектор.
Вектор – это математический объект, у которого есть величина и направление.
В геометрии вектор – это направленный отрезок. Он имеет величину, равную длине отрезка, и направление.
Например, в случае двигающегося автомобиля принято показывать его направление движения стрелкой, а длина этой стрелки обычно указывает на величину скорости по модулю. Модуль, напомню, все отрицательные величины превращает в положительные. Чем больше длина стрелки, тем больше скорость машины. (См.Рис.3.)
В случае 1 стрелка у красной машины указывает нам на то, что автомобиль двигается вправо. Стрелка подписана сверху (vec{|V_1|}=90(км/ч)). Эта запись означает, что величина скорости красной машины по модулю равна (90(км/ч)).
Если я напишу вектор скорости красной машины без модуля, то он будет выглядеть вот так:
$$ vec{V_1}=+90(км/ч);$$
Знак плюс указывает на то, что скорость машины сонаправлена с выбранной нами осью (х).
В случае 2 синяя машина двигается влево. Ее вектор скорости запишется так:
$$vec{V_2}=-45(км/ч);$$
Знак минус указывает на то, что машина едет в противоположную сторону оси (х).
Как видите, по одной только записи вектора можно сразу сказать, куда едет машина и с какой скоростью – это очень удобно. Знак указывает на направление, а число – на величину.
Обратите внимание, что у красной машины вектор скорости длиннее, чем у синей, это означает, что красная едет быстрее. Не глядя на числа, мы можем с уверенностью сказать это, посмотрев на рисунок. Так принято обозначать. Это тоже удобно.
Равномерное движение
Любое движение с постоянной скоростью называется равномерным движением. Все, что мы рассматривали выше – это примеры равномерного движения.
Теперь мы готовы составить первые уравнения, описывающие равномерное движение. В кинематике нас будет интересовать уравнение, которое описывает положение тела в пространстве в зависимости от времени (изменение координаты тела со временем). Оно выглядит так:
$$ x(t)=x_0+V*t;$$
(x_0) – это начальная координата тела, где оно находилось в момент времени (t=0). Например, на рис.2. начальная координата автомобиля (x_0=3(м)).
(V) – это скорость, с которой двигается тело.
(t) – это время, которое прошло с момента начала движения.
(x(t)=x_{конечная}) – это конечная координата, то есть координата, где окажется тело через время (t). Я написал (x(t)), чтобы показать, что координата тела зависит от времени, ведь в разные моменты времени двигающееся тело находится в разных точках.
Разберем на примере, как работает это уравнение.
Пример 1
Автомобиль начал движение из координаты (x_0=-3(м)) со скоростью (V=5(м/с)) вправо. Где будет автомобиль через 3 секунды? Через какое время автомобиль окажется в точке с координатой (x=12(м))?
Решение: Первым делом всегда рисуем рисунок, он поможет правильно расставить знаки в уравнениях и лучше представить задачу. Чтобы ответить на поставленные вопросы, воспользуемся уравнением для координаты при равномерном движении (x(t)=x_0+V*t.)
Подставим известные величины:
$$x(t)=-3+5*t;$$
Обратите внимание, что скорость входит в уравнение со знаком (+), так как автомобиль едет по условию вправо, а это сонаправленно с осью (х). Если бы он ехал влево, то уравнение выглядело бы так: $$x(t)=-3-5t.$$
Получили уравнение, которое полностью задает движение автомобиля.
Действительно, если в это уравнение подставить некоторое время вместо (t), то можно узнать координату, где находится автомобиль в различные моменты времени.
Например, если (t=0), момент начала движения:
$$x(t=0)=-3+5*0=-3(м);$$
Логично, что в начале автомобиль находился в координате (x_0=-3). Чтобы узнать, где он будет через секунду, подставим (t=1(c)):
$$ x(t=1)=-3+5*1=-3+5=2(м);$$
Отрицательное время подставлять нет смысла, так как время не может быть отрицательным. А координата и скорость могут.
Теперь вспоминаем про задачу. Нам нужно узнать, где будет машина через 3 секунды. Просто подставляем в уравнение (t=3(с)):
$$ x(t=3)=-3+5*3=-3+15=12(м);$$
А как понять, через сколько по времени машина окажется в координате (x(t)=12(м))? Подставим:
$$12=-3+5*t;$$
Осталось решить простое линейное уравнение:
$$t=3(c).$$
Ответ: ( x(t=3)=12(м);) и (t=3(c)).
Равноускоренное движение
Если скорость не меняется, то все понятно. А что делать если скорость непостоянна?
В школе рассматривается случай, когда скорость у тела изменяется (увеличивается или уменьшается) равномерно, то есть за каждую следующую секунду скорость увеличивается/уменьшается на одну и ту же величину. Такое движение называют равноускоренным или равнозамедленным соответственно.
Пример такого движения. Представьте, что лыжник скатывается с горки из состояния покоя, при этом его скорость постоянно увеличивается, например, на 2 м/с ежесекундно. То есть:
$$V(t=0)=0(м/с);$$
$$V(t=1)=V(t=0)+2=0+2=2(м/с);$$
$$V(t=2)=V(t=1)+2=2+2=4(м/с);$$
$$V(t=3)=V(t=2)+2=4+2=6(м/с);$$
$$V(t=4)=V(t=3)+2=6+2=8(м/с);$$
Величина, на которую ежесекундно увеличивается/уменьшается скорость, называется ускорением и обозначается буквой (a).
Ускорение измеряется в (frac{м}{с^2}).
Разумеется, в жизни бывают случаи, когда скорость изменяется неравномерно. Но в школьном курсе такие задачи крайне редкие, и мы их рассматривать не будем.
Как выглядит уравнение, описывающие равноускоренное движение?
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
По сравнению с равномерным движением, у нас добавилось еще одно слагаемое (frac{a*t^2}{2}), которое отвечает за ускоренность/замедленность движения.
Так как скорость теперь переменная величина, для нее тоже можно записать уравнение:
$$V(t)=V_0+at;$$
- (x_0) – начальная координата тела;
- (V_0) – начальная скорость тела; скорость, с которой тело начало движение;
- (x(t)) – конечная координата;
- (V(t)) – конечная скорость;
- (a) – ускорение;
- (t) – время.
Уравнения для координаты и для скорости при равноускоренном движении являются основными уравнениями всей школьной кинематики. Если в них хорошо разобраться, то больше никаких формул учить не нужно. Все выводится из них. Я рекомендую пользоваться только этими двумя уравнениями и не забивать себе голову ничем посторонним.
Внимание! Вообще говоря, ускорение — это векторная величина, так же, как и скорость. Мы это обсуждали в начале темы. И помним, что если вектор сонаправлен с выбранным нами направлением оси координат, то ускорение положительно, а если нет, то отрицательно.
Если же вектора скорости и ускорения направлены в одну сторону, то тело ускоряется. А если в разные, то тормозит.
Посмотрите на рисунки:
В случае а) скорость сонаправлена с осью х, значит она будет положительна. Ускорение тоже сонаправлено с осью х, значит оно положительно. А раз вектора скорости и ускорения направлены в одну сторону, то это значит, что тело ускоряется.
Случай б): скорость положительна, ускорение отрицательно. Раз вектор скорости и вектор ускорения направлены в разные стороны, значит тело замедляется.
Случай в): скорость и ускорение отрицательны, но сонаправлены – тело ускоряется.
Случай г): скорость отрицательна, ускорение положительно – тело замедляется.
Со знаками разобрались, теперь давайте разберем пример.
Пример 2
Лыжник скатывается с горки с нулевой начальной скоростью ((V_0=0(м/с))). Через 5 секунд после начала движения его скорость была (V(t=5(c))=15(м/с)). Определите с каким ускорением движется лыжник и какое расстояние он проедет за 10 секунд?
Решение:
Рисуем рисунок, чтобы представить, что происходит, и правильно расставить знаки. Ось х выбираем, как угодно. Я направил вниз.
Как мы уже обсуждали выше, у нас есть всего два уравнения – для координаты и для скорости, которые полностью описывают любое движение:
$$x(t)=x_0+V_0*t+frac{a*t^2}{2};$$
$$V(t)=V_0+at;$$
Так как нам даны начальная и конечная скорости, то разумно воспользоваться уравнением для скорости. Не забываем про знаки скорости и ускорения – оба вектора сонаправлены с выбранной мною осью х, а значит, и скорость, и ускорение будут в уравнениях положительны.
$$V(t)=V_0+at;$$
$$15=0+a*5;$$
$$a=frac{15}{5}=3frac{м}{с^2};$$
Зная ускорение, с которым движется лыжник, мы можем найти, где будет лыжник через 10 секунд, используя уравнение для координаты:
$$x(t=10)=x_0+V_0*t+frac{a*t^2}{2}=0+0*10+frac{3*10^2}{2}=150(м);$$
Таким образом, мы получили, что лыжник за 10 секунд успеет проехать (150) метров, если будет двигаться с постоянным ускорением (a=3(frac{м}{с^2})).
Работа с графиками в кинематике
В ЕГЭ по физике кинематика часто встречается в самом первом задании и, как правило, там задача с графиками. Графики помогают нам визуально описывать поведение одной некоторой величины в зависимости от другой. В школе вы должны были часто строить графики зависимостей (y) от (x). В кинематике же обычно строят графики зависимости координаты или скорости от времени. Давайте построим пару таких графиков и обсудим, как их читать.
Главное, нужно понять, что перед вами не траектория и не картинка, на которой изображено, как движется тело. Это зависимость одной физической величины от другой. На наших рисунках изображены графики зависимостей координаты и скорости от времени некоторого объекта (пусть это будет велосипедист) при различных видах движения. Например, на графике ((в)) НЕ показано движение некоторого объекта в гору, а просто координата по мере движения увеличивается.
- На графике ((а)) показана зависимость координаты велосипедиста от времени. В моменты времени (t_1) и (t_2) велосипедист находится в одной и той же координате, а значит, он стоит на месте. То есть здесь велосипедист находится в покое.
- На графике ((б)) зависимость скорости от времени. Визуально он очень похож на график ((а)), но смысл совершенно другой. Так как тут показана скорость, мы видим, что в моменты времени (t_1) и (t_2) у велосипедиста была одна и та же скорость (V_0). А раз в различные моменты времени скорость одинаковая, то это равномерное движение или движение с постоянной скоростью. Более того, еще можно сделать вывод, что велосипедист движется вправо (туда, куда направлена ось (х)), потому что скорость положительна.
- В ((в)) линейная зависимость координаты тела от времени (то есть по прямой). Замечаем, что координата с течением времени увеличивается, а это значит, что объект движется вправо. Если бы координата уменьшалась, то движение было бы влево (в противоположную сторону оси (х)). Отметим на графике несколько точек через одинаковый интервал времени. В момент времени (t_1) велосипедист был в координате (x_1), а в момент (t_2) в (x_2). За время (Delta t=t_2-t_1) он прошел расстояние (Delta x=x_2-x_1). И за каждый следующий промежуток времени (Delta t) он будет проходит одинаковое расстояние (Delta x). Это означает, что он двигается с одной и той же скоростью – равномерное движение.
- График под пунктом ((г)) показывает нам линейный рост скорости от времени. Если посмотреть, какая скорость будет у велосипедиста через одинаковые промежутки времени, то мы увидим, что она все время растет на одинаковую величину (Delta V). Если скорость растет, то значит движение ускоренное, а если растет еще и линейно, то равноускоренное. Скорость здесь положительна, значит велосипедист едет вправо (туда, куда направлена ось (х)).
- График ((д)) – это зависимость координаты от времени. Видно, что каждый следующий промежуток времени координата успевает измениться на бОльшую величину – за время (t_4-t_3) он проходит бОльшее расстояние, чем за (t_2-t_1). Значит велосипедист ускоряется. Так как координата по ходу движения уменьшается, значит он двигается влево (противоположную сторону оси (х)).
- И на последнем графике ((е)) показана зависимость скорости от времени. Видим, что скорость с течением времени уменьшается, и каждый следующий промежуток времени скорость меняется быстрее, чем на предыдущем. Так как скорость положительна, велосипедист едет вправо (туда же, куда направлена ось х). Так как скорость уменьшается неравномерно, значит на рисунке показано замедленное движение с переменным ускорением.
Движение в поле тяжести Земли
Теперь рассмотрим движение объектов в поле тяжести нашей планеты Земли. Любое тело, свободно падающее (отпущенное с некоторой высоты без начальной скорости) на Земле, будет двигаться с ускорением свободного падения (g=9.8(м/с^2)). Важно помнить, что (g) всегда направлено к центру Земли.
Внимательно посмотрите на рисунок 8: на нем изображено движение камня, брошенного вертикально вверх с некоторой начальной скоростью (V_0). Сначала он будет двигаться равнозамедленно, пока не достигнет наивысшей точки подъема (H), там остановится (скорость (V=0)), и начнет падать обратно, постепенно набирая скорость, пока не упадет обратно к вам в руку со скоростью (V_к). Для того, чтобы лучше разобраться, представьте, что вы подбросили вверх камень – он будет двигаться именно так, как мы обсудили. Таким образом, задачи на движение в поле тяжести Земли ничем не отличаются от задач равноускоренного / равнозамедленного движения по дороге, только на этот раз нам всегда известно ускорение – (g=9.8 (м/с^2)).
Давайте составим уравнения, описывающие это движение. Как всегда, их будет два – для скорости и для координаты:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Что изменилось?
- Во-первых, координата теперь не (x), а (y) – тело двигается вдоль вертикальной оси, а ее принято обозначать за (Y).
- Вместо ускорения (a) мы теперь пишем (g) – ускорение свободного падения, оно нам известно.
Разбираемся со знаками: начальная скорость (V_0) направлена вверх (сонаправленно с осью (Y)). Ускорение во время всего движения направленно вниз к центру Земли (в противоположную сторону (Y)). Получаем, что в системе координат, выбранной на рисунке, начальная скорость будет с плюсом, а ускорение с минусом. Систему координат вы можете выбрать и другую, но тогда знаки будут меняться в соответствии с правилами расстановки знаков.
Обратите внимание!Не нужно писать отдельно уравнения для движения вверх и вниз. Уравнения сами учитывают, что тело после подъема полетит вниз.
Решим несколько задач и обсудим еще пару важных нюансов.
Пример 3
Пусть камень брошен вертикально вверх с начальной скоростью (V_0=10(м/с)). Найдите максимальную высоту подъема и время полета.
Решение
Для решения воспользуемся старым рисунком (рис.8).
Любая задача начинается с написания уравнений в общем виде:
$$y(t)=y_0+V_0*t-frac{g*t^2}{2};$$
$$V(t)=V_0-gt;$$
Выберем за начальное положение тела внизу, на Земле. А за конечное – наивысшую точку. Координата камня в наивысшей точке подъема будет – (y(t)=H), а скорость будет равна (V(t)=0 ) (смотрите на рисунок 8).
Важно! Скорость в наивысшей точке подъема будет равна 0 (камень останавливается), мы часто будем это использовать при решении подобных задач.
Начальная координата (y_0=0).
Начальная скорость (V_0=10(м/c)) из условия.
Получим уравнения:
$$H=10*t-frac{9.8*t^2}{2};$$
$$0=10-9.8*t;$$
Из уравнения для скорости можно найти время полета от Земли до наивысшей точки:
$$t=10/9.8=1.02 /,(с)$$
Подставим в первое уравнение:
$$H=10*1.02-frac{9.8*1.02^2}{2}=5.1 (м);$$
Обращаю ваше внимание, что (t) – время полета от Земли до наивысшей точки. А по условию задачи нам нужно найти время всего полета. Для этого нужно время подъема умножить на два.
Важно! Время подъема всегда равно времени падения.
$$T=2*t=1.02*2=2.04 c.$$
Ответ: (T=2.04 /,(с).)
Пример 4
Рассмотрим падение камня с некоторой высоты (H) вертикально вниз с начальной скоростью (V_0). Как тогда будут выглядеть уравнения, описывающие движение камня? (см. Рис.9.)
За конечное положение выберем Землю (y(t)=0), за начальное – высоту (y_0=H).
$$0=H-V_0*t-frac{g*t^2}{2};$$
$$-V_к=-V_0-gt;$$
Знаки расставлены с учетом направления осей координат.
Многие часто полагают, что при броске камня вниз, его конечная скорость у земли будет равна 0, ведь камень останавливается. Но это не так. К сожалению, уравнения кинематики не учитывают воздействие земли на камень, поэтому, говоря «конечная скорость», мы подразумеваем скорость за мгновение до удара о землю, и она, очевидно, не будет равна нулю.
Основные моменты
- В поле тяжести Земли вертикально брошенное тело всегда движется с ускорением свободного падения (g=9.8(м/с^2)).
- Если тело бросили с земли и оно упало обратно на землю, то время падения равно времени подъема.
- Скорость в верхней точке подъема всегда равно нулю.
Рассмотрим, как выглядят графики зависимостей координаты и скорости от времени при бросании камня.
Бросок тела вертикально вверх
Чтобы хорошо разобраться, рекомендую представить полет камня.
Скорость.При движении вверх скорость камня линейно уменьшается, он тормозит с ускорением (g), пока не остановится в верхней точке. После этого камень сразу начинает падать вниз, скорость увеличивается также с ускорением (g). Если же его бросили с земли, и он упал обратно на землю, то начальная скорость броска будет равна конечной скорости за мгновение до удара о землю. (Рис. 10 (б))
Координата. На рисунке 10 (а) изображено, как меняется координата (y(t)) в зависимости от времени полета. Обратите внимание на форму графика – это парабола. Не попадайтесь в визуальную ловушку, перед вами НЕ линия вдоль которой движется камень, в просто зависимость координаты от времени. Видно, что в начале полета тело успевает пройти за единицу времени большее расстояние, чем ближе к середине полета – координата растет сначала быстро, а потом все медленнее и медленнее, и останавливается в наивысшей точке подъема. Это связано с тем, что скорость в начале полета больше. Затем тело начинает падать, постепенно набирая скорость, и координата начинает изменяться все быстрее и быстрее, пока тело не упадет обратно на землю. (Рис. 10 (а))
Аналогичные рассуждения для броска камня вниз с нулевой начальной скоростью. (См. Рис.11)
Рис.10. Бросок камня вертикально вверх
Рис.11. Бросок тела вертикально вниз с нулевой начальной скоростью
Движение тела под углом к горизонту
До этого мы рассматривали одномерные задачи, где движение происходило вдоль одной прямой. В школьном курсе физики подавляющее большинство задач двумерны.
Рассмотрим классическую двумерную задачу кинематики – бросок камня под углом к горизонту в поле тяжести Земли. Представьте, что вы играете в игру, кто дальше кинет камень. Траектория камня будет похожа на параболу, зеленая линия. (См. Рис. 12) Именно такое движение мы и постараемся описать при помощи математики. Для этого нам понадобится двумерная система координат (XoY). Ось (X) будет отвечать за дальность полета, ось (Y) – за высоту. Точка (O) – точка начала движения. (V_0) – начальная скорость, скорость, которую мы придали камню в момент броска. Точка (А) – точка наивысшего подъема.
Рис.12. Движение под углом к горизонту
Для того, чтобы описать такое сложное двумерное движение, разобьем его на два – отдельно горизонтальное, и отдельно вертикальное движения. Мы можем представить, что наш камень в некоторый момент времени летит с вертикальной скоростью (V_y) и ускорением (a_y) вдоль оси (Y), и с горизонтальными скоростью (V_x) и ускорением (a_x) вдоль оси (X). Вместе эти два движения, если их наложить друг на друга, дают сложное двумерное движение по зеленой параболе с скоростью (V) и ускорением (a).
Скорость тела при двумерном движении в любой момент времени направлена по касательной к траектории. На рис.12. она показана красными стрелками в точках (О, А) и (В).
Рассуждая таким образом, мы можем записать уравнения для координаты и скорости по вертикали и потом по горизонтали – всего 4 уравнения, каждое из которых отвечает за свою ось.
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Возникает справедливый вопрос, откуда нам взять все горизонтальные и вертикальные скорости. Есть начальная скорость (V_0), одновременно направленная по обеим осям. Нам нужно как-то рассмотреть эту скорость, как совокупность двух отдельных скоростей – горизонтальной и вертикальной. Вот для этого нам понадобится некоторый математический прием – проекции.
Проекция вектора
Пусть у нас есть некоторый вектор (vec{a}). Напоминаю, что вектор – это направленный отрезок. У него есть начало – т.А, и конец – т.В. (см.Рис.13). Опустим перпендикуляры из точек А и В на ось (Х). Получим соответственно точки (A_x) и (B_x), который называются проекциями точек (A) и (В) на ось (Х). Получившийся отрезок ({A}_{x} {B}_{x}) будет называться проекцией вектора (vec{a}) на ось (Х). Для краткости записи обозначим ({A}_{x} {B}_{x}=a_x) Аналогичным образом получим проекцию (vec{a}) на ось (Y): ({A}_{y} {B}_{y}=a_y).
Посчитаем чему равны (a_x) и (a_y), если нам известен угол и длина вектора (vec{a}). Достроим наш вектор до прямоугольного треугольника с гипотенузой (vec{a}) и катетами (a_x) и (a_y) (На рис.13. показаны зеленым).
Напоминаю, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, а косинус – прилежащего катета к гипотенузе:
$$ sin{alpha}=frac{a_y}{a};$$
$$cos{alpha}=frac{a_x}{a};$$
Из этих формул можно выразить (a_x) и (a_y):
$$a_x=a*sin{alpha};$$
$$a_y=a*cos{alpha}.$$
Таким образом, зная длину вектора и угол, мы можем легко найти его проекции. Запомните это.
Вернемся к нашей задаче. Мы остановились на том, что нужно найти горизонтальную и вертикальную составляющие начальной скорости и ускорения. Оказывается, проекции начальной скорости (V_0) на оси (X) и (Y) и будут искомыми начальными скоростями по горизонтали и вертикали. (См. Рис. 12). Оранжевым показаны проекции (V_{0x})- начальная горизонтальная скорость, и (V_{0y})-вертикальная. Заметим, что (BB_x=V_{0y}) и (AB_x=V_{0x}). (См. Рис.14.). Из треугольника (ABB_x) получаем:
Рис.14. Проекция скорости на оси х и y
$$sin{alpha}=frac{BB_x}{AB}=frac{V_{0y}}{V_0};$$
$$cos{alpha}=frac{AB_x}{AB}=frac{V_{0x}}{V_0}.$$
Отсюда
$$V_{0y}=V_0*cos{alpha};$$
$$V_{0x}=V_0*sin{alpha}.$$
Зная угол к горизонту (alpha), под которым бросили тело, и его начальную скорость, мы можем по формулам выше найти начальные скорости для горизонтального и вертикального движений.
Разберемся теперь с каким ускорением движется тело по вертикали и горизонтали. Если вы бросаете камень на Земле, то у него будет вертикальное постоянное ускорение, направленное к центру Земли – ускорение свободного падения (g=9,8(м/с^2)). (См.Рис.12).
По горизонтали ускорение, оказывается, будет равно нулю. Другими словами, по горизонтали камень будет лететь равномерно, с постоянной скоростью. Это связано с тем, что в горизонтальном направлении на тело во время полета не действует никаких сил, то есть ничто не может изменить его скорость. А по вертикали действует сила притяжения Земли, которая вызывает ускорение свободного падения.
Можно просто запомнить, что по вертикали ускорение всегда (g), а по горизонтали ускорение 0.
Используем все наши рассуждения для записи системы уравнений, описывающих движение под углом к горизонту:
$$y(t)=y_0+V_{0y}*t+frac{a_{y}*t^2}{2};$$
$$V_{y}(t)=V_{0y}+a_{y}*t;$$
$$x(t)=x_0+V_{0x}*t+frac{a_{x}*t^2}{2};$$
$$V_{x}(t)=V_{0x}+a_{x}*t;$$
Подставим (V_{0x}=V_0*sin{alpha},, V_{0y}=V_0*cos{alpha},, a_x=0,,a_y=g):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Знания и понимания этих четырех уравнений достаточно, чтобы решить любую школьную задачу по кинематике. Часто в школах дают большое количество формул, связывающих расстояние, скорость и ускорение и т.п. Если вы разобрались, как были получены уравнения выше, то в этих формулах нет необходимости. Они легко выводятся.
Основные моменты движения тела, брошенного под углом к горизонту:
- Сложное двумерное движение разбиваем на два: горизонтальное и вертикальное.
- Ускорение по вертикали равно ускорению свободного падения и всегда направлено вниз, к центру Земли. Ускорение по горизонтали в отсутствии сопротивления воздуха равно 0. По горизонтали движение равномерное.
- Скорость полета тела всегда направлена по касательной к траектории полета. Скорость по горизонтали и вертикали можно найти соответственно из формул:
$$V_x=V*cos{alpha};$$
$$V_y=V*sin{alpha};$$ - Дальностью полета называют расстояние по горизонтали между точкой броска и точкой падения камня на землю. На рис.12. дальность показана буквой (S).
- Время подъема равно времени падения. При условии, что тело бросили с Земли и оно упало обратно на Землю.
- Скорость по вертикали в наивысшей точке подъема равна 0. Этот факт часто используют для нахождения времени подъема до наивысшей точки из уравнения для скорости по оси (y):
$$0=V_{0y}-gt.$$
Разберем несколько задач на движение под углом к горизонту.
Пример 5
Камень бросили под углом (alpha=30^о) к горизонту с начальной скоростью (V_0=20(м/с)). Найти дальность его полета. И максимальную высоту подъема.
Бросок камня под углом к горизонту
Решение
Первым делом выпишем все уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Начальная скорость направлена вверх и вправо, поэтому в уравнениях она будет со знаком плюс. Ускорение свободного падения направлено вниз – ставим минус.
Выбираем начальное и конечное положение тела, для которого будем записывать уравнение. Логично, что начальная точка – это момент броска с координатами (0;0), а за конечную выберем т.А ((S/2;H)) – наивысшую точку подъема, так как мы знаем, что скорость там по оси (y): (V_y=0).
Подставим координаты и известные величины в систему уравнений:
$$H=20*sin{30}*t-frac{9.8*t^2}{2};$$
$$0= 20*sin{30}-9.8*t;$$
$$S= 20*cos{30}*t;$$
$$V_{x}= 20*cos{30}.$$
Из уравнения для скорости по (y) (2-е уравнение) можно найти (t) – время подъема тела до наивысшей точки.
$$t=frac{20*sin{30}}{9.8}=1.02 (c);$$
Чтобы найти максимальную высоту подъема, подставим найденное время в первое уравнение для координаты (y). Камень будет в наивысшей точке через половину времени полета, потому что время подъема равно времени падения:
$$H=20*sin{30}*1.02-frac{9.8*1.02^2}{2}=5.1(м);$$
Полное время полета:
$$T=2*t=2.04 (c);$$
Найдем дальность, используя уравнения для координаты (x):
$$S= 20*cos{30}*2.04=35.3(м);$$
Мы решили задачу. Рассчитали высоту (H) и дальность полета камня (S), если бросить его под углом в (30^0) и с начальной скоростью (V_0=20(м/с)). Весь полет займет чуть больше 2-х секунд.
Ответ:(S=35.3(м)) и (H=5.1(м)) и (T=2.04(c)).
Пример 6
Камень бросили с балкона с высоты (y_0=20(м)), придав ему начальную скорость (V_0=10(м/с)) и под углом к горизонту (60^0).Найти дальность и максимальную высоту полета.
Бросок камня под углом к горизонту с некоторой высоты
Решение:
Запишем уравнения в общем виде:
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$x(t)=x_0+ V_0*cos{alpha}*t;$$
$$V_{x}(t)= V_0*cos{alpha}.$$
Подставим все данные в уравнения для координат, согласно условию задачи. За начальную точку выберем точку броска (x_0=0, . y_0=H_0), а за конечную точку падения (x(t)=S, . y(t)=0):
$$0=H_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$S= V_0*cos{alpha}*t;$$
С учетом данных в условии задачи
$$0=20+10*sin{60^0}*t-frac{g*t^2}{2};$$
$$S= 10*cos{60^o}*t;$$
Выразим время всего полета
$$20+5sqrt{3}*t-4.9*t^2=0;$$
Решаем через дискриминант квадратное уравнение и находим время всего полета
$$t=3.04(с);$$
Чтобы найти дальность полета, подставим найденное время в уравнение для координаты (х)
$$S= V_0*cos{alpha}*t;$$
$$S= 10*cos{60^0}*3.04=15.2(м);$$
Обращаю внимание, что в данной задаче время подъема не равно времени падения, так как задача несимметричная – камень бросают с балкона, а падает он на землю.
Для нахождения максимальной высоты подъема воспользуемся тем, что скорость по (Y) в верхней точке траектории равна (0), и найдем время полета до этой точки:
$$V_{y}(t)= V_0*sin{alpha}-g*t;$$
$$0= 10*sin{60^0}-g*t;$$
$$t=0.88(c);$$
Подставим найденное время в уравнение для координаты (у):
$$y(t)=y_0+V_0*sin{alpha}*t-frac{g*t^2}{2};$$
$$H=20+10*sin{60^0}*0.88-frac{9.8*0.88^2}{2}=28.65-3.79=24.86(м).$$
Ответ: (S=15.2(м)) и (H=24.86(м)).
Пример 7
Тело бросили ГОРИЗОНТАЛЬНО с балкона высотой 20 метров ((H_0=20м)) с начальной скоростью (V_0=10м/с). Найти под каким углом к горизонту будет направлена скорость тела через (t=0.5 с), время всего полета и дальность.
Рис.15. Бросок тела с некоторой высоты горизонтально
Как обычно, начинаем решение задачи с написания всех уравнений в общем виде:
$$y(t)=y_0+V_{0Y}*t-frac{g*t^2}{2};$$
$$V_{y}(t)= V_{0Y}-g*t;$$
$$x(t)=x_0+ V_{0X}*t;$$
$$V_{x}(t)= V_{0X}.$$
Найдем время всего полета и дальность. Начальная точка – это точка броска с координатами ((0;H_0)), конечная точка – падение на Землю ((L;0)).
Обратите внимание, что начальная скорость тела горизонтальна, а значит у нас нет вертикальной составляющей начальной скорости – мы не сообщаем телу начальную скорость по (Y). Поэтому (V_{0y}=0), а (V_{0x}=V_0).
Уравнение по (Y) принимает вид:
$$0=H_0-frac{g*t^2}{2};$$
$$0=20-frac{9.8*t^2}{2};$$
Находим время всего полета
$$t=sqrt{frac{2*20}{9.8}}=2,02(c);$$
Чтобы найти дальность, подставим найденное время в уравнение для координаты (х)
$$L=V_0*t=10*2.02=20.2(м);$$
И осталось ответить на последний вопрос – под каким углом к горизонту будет направлена скорость через (t=0,5(c)). Предположим, что тело в этот момент будет находиться в точке (А) (См.Рис.15). Скорость тела в любой момент времени направлена по касательной к траектории – (V_A).
Для решения этой задачи нам понадобится найти проекции (V_A) на оси (X) и (Y), на рисунке они показаны оранжевым цветом – (V_{AX};. V_{AY}).
Так как движение по горизонтали равномерное, то скорость по (X) в любой момент времени будет постоянна и равна начальной скорости (V_0).
Для нахождения (V_{AY}) запишем уравнение для скорости по (Y)
$$V_{y}(t)= V_{0Y}-g*t;$$
$$V_{0Y}=0;$$
$$V_{y}(t=0.5c)=-g*t;$$
$$V_{y}(t=0.5c)=-9.8*0.5=-4.9м/с;$$
Скорость получилась отрицательная, потому что она направлена вниз – в противоположную сторону оси (Y).
Рис.16. Проекции скорости в произвольной точки траектории
Зная проекции скорости (V_{AX}) и (V_{AY}) мы можем найти угол, под которым направлена скорость. Посмотрите на рис.16. Так как (ABCD) прямоугольник, то (AB=CD=V_{AX}). Тогда из треугольника (ADC) можно найти тангенс (alpha)
$$tg{alpha}=frac{V_{AY}}{V_{AX}}=frac{4.9}{10}=0.5;$$
$$alpha=27^0.$$
Ответ: (t=2.02(c);, L=20.2(м);, alpha=27^0.)
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec{a} =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec{a} =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_{0}) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_{0}]
Рис.1. Тело покоится, график координаты x(t) — горизонтальная прямая рис. б).
Скорость «v» и ускорение «a» — это прямые, лежащие на оси Ox. График скорости – рис. в). График ускорения – рис. г)
Скорость и ускорение неподвижного тела равны нулю:
[vec{v}=0]
[vec{a}=0]
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_{0} + v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
[ v = v_{0} = const ]
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
[ a = 0 ]
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Рис.3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Рис.4. Тело движется равноускорено – рис. а) по направлению оси Ox. Изменение координаты от времени x(t) описывается правой ветвью параболы – рис. б), график v(t) скорости изображен наклонной возрастающей прямой – рис. в), а график неизменного ускорения a(t) – рис. г) изображается горизонтальной прямой, лежащей выше оси времени
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_{0} + a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
[ a = const ]
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Рис.6. Тело движется равнозамедленно по оси Ox – рис. а), его координата растет по левой ветви параболы – рис. б), график скорости — убывающая наклонная прямая – рис. в), ускорение направлено против оси Ox, горизонтальный график ускорения — рис. г) лежит ниже оси времени
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Рис.7. Тело движется равнозамедлено против оси Ox – рис. а), его координата убывает по левой ветви параболы – рис. б), скорость отрицательная и уменьшается к нулю, график скорости — наклонная прямая – рис. в), ускорение направлено по оси Ox, горизонтальный график ускорения — рис. г) лежит выше оси времени
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
Уравнение координаты при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Уравнение координаты — зависимость координаты тела от времени:
Уравнение координаты при равноускоренном прямолинейном движении:
x0 — координата тела в начальный момент времени, v0x —проекция начальной скорости на ось ОХ, ax —проекция ускорения на ось ОХ, x — координата тела в момент времени t
Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:
Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v0 = 0 м/с.
В момент времени t = 10 c координата автомобиля равна:
Совместное движение двух тел
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.
Аналитический способ решения задачи на совместное движение тел
Чтобы найти место встречи двух тел, нужно:
- Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
- Построить уравнение вида x1 = x2.
- Найти время встречи двух тел tвстр.
- Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату xвстрч.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.
Составим уравнения для движения каждого из тел:
Приравняем правые части этих уравнений и найдем время t:
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Графический способ решения задачи на совместное движение тел
Существует графический способ решения данной задачи. Для этого нужно:
- Построить графики x1(t) и x2(t).
- Найти точку пересечения графиков.
- Пустить перпендикуляр из этой точки к оси ОХ.
- Значение точки пересечения — координата места пересечения двух тел.
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.
Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:
Приравняем правые части уравнений и вычислим t:
В результате получаем два
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.
В момент времени t=0 проекции её скорости υx и ускорения ax на ось Ох удовлетворяют соотношениям:
а)
б)
в)
г)
Алгоритм решения
- Определить характер движения материальной точки.
- Записать уравнение координаты материальной точки.
- С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.
Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 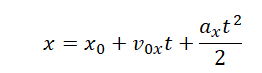
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Записать исходные данные.
- Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
- Выразить скорость грузовика из уравнения его движения.
- Записать уравнение движения мотоциклиста.
- Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
- Подставить время в формулу скорости грузовика и вычислить ее.
Решение
- Координата встречи грузовика и мотоциклиста: x = 150 м.
- Время запаздывания мотоциклиста: tзапазд = 5 с.
- Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .
Запишем уравнение движения грузовика:
Так как начальная координата равна нулю, это уравнение примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость движения грузовика равна:
Запишем уравнение движения мотоциклиста:
Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:
Найдем время, через которое грузовик и мотоциклист встретились:
Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Механическое движение
О чем эта статья:
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
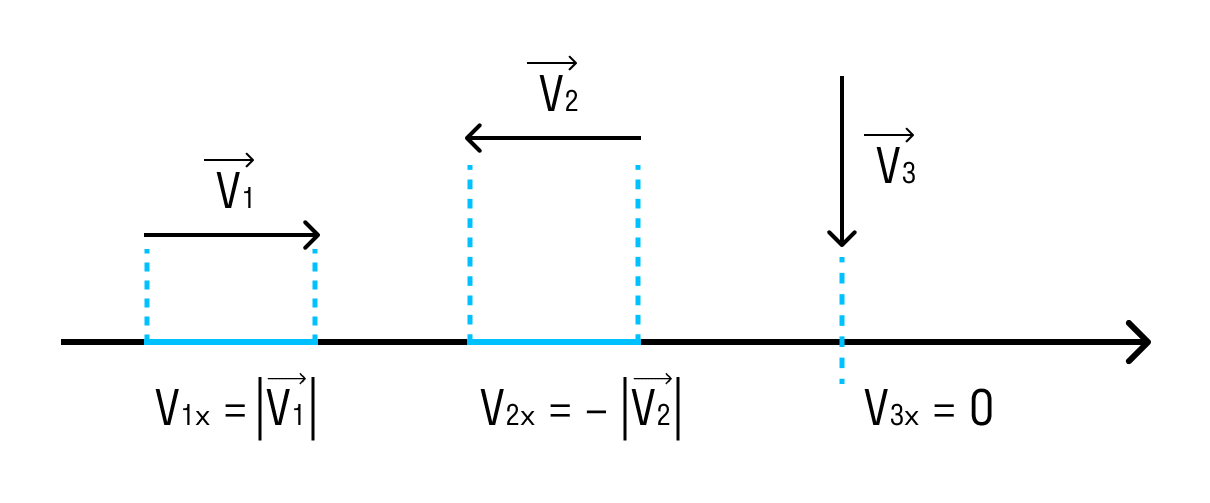
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Уравнение движения при движении против оси
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
Уравнение движения для равноускоренного движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с 2 ]
Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:
Формула конечной скорости
— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места, . Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt 2 /2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки:
км
Ответ: через полчаса координата автобуса будет равна 150 км.
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_<0>) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_<0>]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_<0>), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_ <0>+ v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_ <0>+ a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec) и (vec) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
источники:
http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie
http://formulki.ru/mehanika/grafiki-pryamolinejnogo-dvizheniya