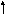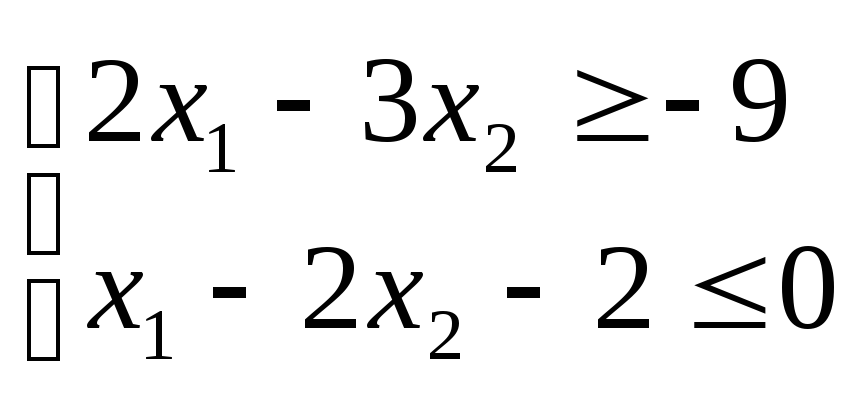Симплексный метод решения задач линейного программирования
Симплексный метод
– это метод последовательного улучшения
плана. Этим методом можно решать задачи
линейного программирования с любым
количеством переменных и ограничений.
Этот метод включает
в себя три основные этапа:
-
Построение
начального опорного плана. -
Правило перехода
к лучшему (точнее, нехудшему) решению. -
Критерий проверки
найденного решения на оптимальность.
При симплексном
методе выполняются вычислительные
процедуры (итерации) одного и того же
типа в определенной последовательности
до тех пор, пока не будет получен
оптимальный план задачи или станет
ясно, что его не существует.
1) Построение начального опорного плана.
Данную задачу
линейного программирования необходимо
сначала привести к каноническому виду;
при этом правые части ограничений должны
быть неотрицательными.
Признаком возможности
построения начального опорного плана
служит наличие в каждом ограничении-равенстве
с неотрицательной правой частью базисной
переменной.
Базисной
называют плановую переменную, которая
входит только в одно уравнение (а в
другие не входит), и при этом имеет
коэффициент, равный единице.
Пусть задача
линейного программирования приведена
к каноническому виду, и все уравнения
системы ограничений имеют свою базисную
переменную. Приравняв базисные переменные
к соответствующим правым частям
ограничений, а остальные переменные к
нулю, получим опорное или базисное
решение задачи.
Пример.
Для данной задачи линейного программирования
найти начальный опорный план (базисное
решение).
![]()
max

Решение. Изменим
знаки второго и третьего неравенств на
противоположные, умножив каждое из них
на –1. Система ограничений теперь будет
такой:

В
каждом ограничении слева добавим
положительную переменную
![]() ,
,
соответственно запишем канонический
вид задачи:
![]()
max

![]() .
.
Переменные
![]() базисные. Приравниваем их к правым
базисные. Приравниваем их к правым
частям ограничений:![]() Все остальные переменные – свободные,
Все остальные переменные – свободные,
приравниваем их к нулю:![]()
Запишем теперь
начальный опорный план
![]() (0;
(0;
0; 0; 0; 16; 4; 0).
2) Составление симплексных таблиц. Критерий оптимальности.
Симплексный метод
удобно применять, используя построение
симплексных таблиц. Первая симплексная
таблица, соответствующая начальному
плану, имеет вид:
|
Базис |
|
В |
|
|
… |
|
|
|
|
|
… |
|
||||
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
|
Здесь приняты
следующие обозначения.
Столбец
«Базис» – это базисные переменные.
Столбец
«![]() »
»
– это коэффициенты при базисных
переменных в целевой функции.
Столбец
«В» – правые части ограничений;
![]() –коэффициенты
–коэффициенты
при переменных в ограничениях;
![]() –коэффициенты
–коэффициенты
при переменных в целевой функции.
Последняя
строка в таблице (![]() )
)
– это проверочная или оценочная строка.
![]() –значение целевой
–значение целевой
функции, соответствующее построенному
начальному плану. Его находят так: каждый
элемент столбца
![]() умножают на соответствующий элемент
умножают на соответствующий элемент
столбца В и произведения складывают,
т.е.
![]() .
.
![]() –называют оценками
–называют оценками
или симплексными разностями и находят
так: элементы столбца
![]() умножают на соответствующие элементы
умножают на соответствующие элементы
столбца![]() ,
,
складывают результаты и вычитают![]() .
.
Например,
![]() .
.
Оценки
(![]() )
)
базисных переменных всегда равны нулю.
Признак
оптимальности опорного плана
состоит в следующем:
Опорный
план будет оптимальным тогда и только
тогда, когда все оценки
![]() для задачи на max
для задачи на max
и
![]() для задачи на min.
для задачи на min.
Если
критерии оптимальности не выполняются,
то нужно перейти к нехудшему опорному
плану, т.е. исключить из базиса некоторую
переменную и ввести вместо нее новую
из числа свободных переменных.
Переменная,
которую нужно ввести в базис, соответствует
той оценке
![]() ,
,
которая не удовлетворяет условию
оптимальности. Если таких оценок
несколько, то среди них выбирают
наибольшую по абсолютной величине и
соответствующую ей переменную вводят
в базис. Столбец с этой переменной
называютразрешающим.
Для
определения переменной, которую нужно
вывести из базиса, поступают так: элементы
столбца В делят только на положительные
элементы разрешающего столбца и находят
симплексные отношения
![]() .
.
Выбирают из![]() наименьшее. Оно называет ту переменную,
наименьшее. Оно называет ту переменную,
которую нужно ввести в базис. Соответствующая
строка таблицы называетсяразрешающей.
На
пересечении разрешающего столбца и
разрешающей строки находится разрешающий
элемент.
Теперь начинаем
заполнять следующую таблицу. Покажем
этот процесс на конкретном примере.
Пример.
Решить симплексным методом задачу
линейного программирования.
![]()
max

Решение.
1) Приводим задачу к каноническому виду,
т.е. из ограничений неравенств делаем
равенства.
![]()
max
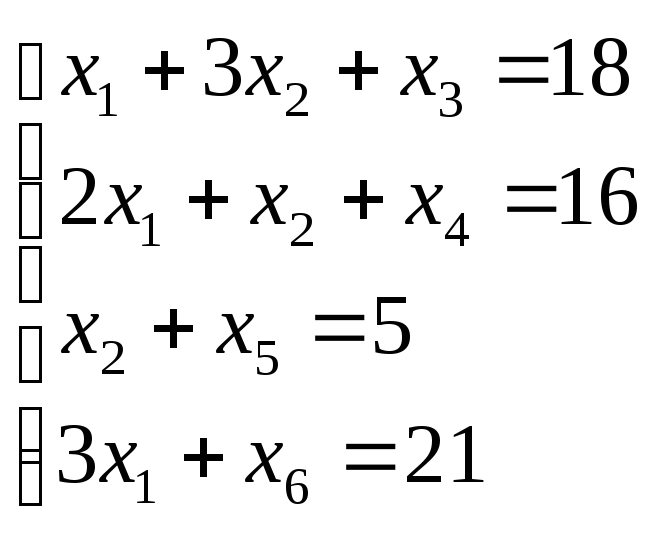
![]()
2)
Определяем базисные переменные – это
![]() .
.
3
 )
)
Заполняем первую таблицу
|
Базис |
|
В |
2 |
3 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||
|
|
0 |
18 |
1 |
3 |
1 |
0 |
0 |
0 |
|
|
|
0 |
16 |
2 |
1 |
0 |
1 |
0 |
0 |
|
|
|
0 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
0 |
21 |
3 |
0 |
0 |
0 |
0 |
1 |
– |
|
|
0 |
–2 |
–3 |
0 |
0 |
0 |
0 |
Здесь
![]() и
и![]() не удовлетворяют условию оптимальности,
не удовлетворяют условию оптимальности,
т. к. они меньше нуля. Выбираем среди
них большее по модулю. Это![]() .
.
Следовательно, столбец переменной![]() – разрешающий. Значит, в новый базис
– разрешающий. Значит, в новый базис
нужно ввести переменную![]() .
.
Находим
![]() :
:![]() ;
;![]() ;
;![]()
Наименьшее
из этих чисел – это число 5, что
соответствует строке базисной переменной
![]() .
.
Значит, строка базисной переменной![]() – разрешающая, следовательно, из базиса
– разрешающая, следовательно, из базиса
нужно вывести переменную![]() .
.
Элемент![]() =1
=1
– разрешающий. Новый базис:![]() .
.
Заполнение
следующей таблицы начинаем со столбцов
«Базис» и «![]() ».
».
Потом заполняем разрешающую строку,
разделив каждый ее элемент на разрешающий,
т.е. на 1. Все элементы разрешающего
столбца будут нулями, кроме разрешающего,
который всегда равен 1. Столбцы под![]() переписываем без изменения, т. к. эти
переписываем без изменения, т. к. эти
переменные остались в базисе. Остальные
элементы новой таблицы находим по
правилу прямоугольника. Например,
элемент![]() найдем из прямоугольника
найдем из прямоугольника
![]() =
=
![]()
Или
элемент
![]() =
=![]() из прямоугольника
из прямоугольника
Оценки
![]() для новой таблицы можно находить по
для новой таблицы можно находить по
этому же правилу.
В целом, решение данной задачи симплексным
целом, решение данной задачи симплексным
методом в виде таблиц будет иметь вид
|
Базис |
|
В |
2 |
3 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||
|
|
0 |
18 |
1 |
3 |
1 |
0 |
0 |
0 |
6 |
|
|
0 |
16 |
2 |
1 |
0 |
1 |
0 |
0 |
16 |
|
|
0 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
5 |
|
|
0 |
21 |
3 |
0 |
0 |
0 |
0 |
1 |
– |
|
|
0 |
–2 |
–3 |
0 |
0 |
0 |
0 |
таб. |
|
|
|
0 |
3 |
1 |
0 |
1 |
0 |
–3 |
0 |
3 |
|
|
0 |
11 |
2 |
0 |
0 |
1 |
–1 |
0 |
5,5 |
|
|
3 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
– |
|
|
0 |
21 |
3 |
0 |
0 |
0 |
0 |
1 |
7 |
|
|
15 |
–2 |
0 |
0 |
0 |
3 |
0 |
таб. |
|
Базис |
|
В |
2 |
3 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||
|
|
2 |
3 |
1 |
0 |
1 |
0 |
–3 |
0 |
– |
|
|
0 |
5 |
0 |
0 |
–2 |
1 |
5 |
0 |
1 |
|
|
3 |
5 |
0 |
1 |
0 |
0 |
1 |
0 |
5 |
|
|
0 |
12 |
0 |
0 |
–3 |
0 |
9 |
1 |
|
|
|
21 |
0 |
0 |
2 |
0 |
–3 |
0 |
таб. |
|
|
|
2 |
6 |
1 |
0 |
–0,2 |
0,6 |
0 |
0 |
|
|
|
0 |
1 |
0 |
0 |
–0,4 |
0,2 |
1 |
0 |
|
|
|
3 |
4 |
0 |
1 |
0,4 |
–0,2 |
0 |
0 |
|
|
|
0 |
3 |
0 |
0 |
0,6 |
–1,8 |
0 |
1 |
|
|
|
24 |
0 |
0 |
0,8 |
0,6 |
0 |
0 |
таб. |
О ценочная
ценочная
строка четвертой таблицы показывает,
что получен оптимальный план, так как
все![]() .
.
![]() –это значения
–это значения
![]() из столбца В, т.е.
из столбца В, т.е.![]() ,
,![]() ,
,![]() ,
,![]() .
.
Свободные
(небазисные) переменные
![]() .
.
Итак,
![]() =
=
(6; 4; 0; 0; 1; 3),
![]() =
=
![]() =
=
24.
Примечание:
При переходе от таблицы к таблице для
контроля сравнивают
![]() ,
,
которое должно быть не меньше предыдущего
для задачи на максимум и не больше
предыдущего – для задачи на минимум.
При использовании
симплексного метода возможны следующие
случаи.
1) Если
в оценочной строке симплекс-таблицы
оценка
![]() =
=
0 соответствует свободной переменной,
то это означает, что ЗЛП имеет не
единственный оптимальный план.
2) Если при переходе
от одного опорного плана к другому в
разрешающем столбце нет положительных
элементов, то это означает, что целевая
функция ЗЛП является неограниченной и
оптимальных планов не существует.
Задания
для самостоятельной работы.
Определить
оптимальный план задач, используя
симплексный метод решения задач линейного
программирования:
|
а) |
|
б) |
|
Калькулятор симплекс-метода
Количество переменных:
Количество ограничений:
Очистить
Решить
В двойственную
Выполнено действий:
Как пользоваться калькулятором
- Задайте количество переменных и ограничений
- Введите коэффициенты целевой функции
- Введите коэффициенты ограничений и выберите условия (≤, = или ≥)
- Выберите тип решения
- Нажмите кнопку “Решить”
Что умеет калькулятор симплекс-метода
- Решает основную задачу линейного программирования
- Позволяет получить решение с помощью основного симплекс-метода и метода искусственного базиса
- Работает с произвольным количеством переменных и ограничений
Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + … + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + … + an·xn v b, где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 … xn.
Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Пример 1
Привести к каноническому виду ограничения:
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 200
4·x1 + 6·x2 + 8·x3 ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 200
-4·x1 – 6·x2 – 8·x3 + x5 = -160
Формирование начального базиса
После того как задача приведена к каноническому виду, необходимо найти начальный базис для формирования первого опорного решения. Если в процессе приведения были добавлены дополнительные переменные, то они становятся базисными.
Иначе необходимо выделить среди коэффициентов ограничений столбец, который участвует в формировании единичной матрицы в заданной строке (например, если требуется определить вторую базисную переменную, то необходимо искать столбец, в котором второе число равно 1, а остальные равны нулю). Если такой столбец найден, то переменная, соответствующая этому столбцу, становится базисной.
В противном случае можно поискать столбец, в котором все значения кроме числа в заданной строке равны нулю, и, если он будет найден, то разделить все значения строки на число, стоящее на пересечении этих строки и столбца, тем самым образовав столбец, участвующий в формировании единичной матрицы.
Пример 2
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 – 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 – 4·x3 + 2·x5 = 30
Для ограничения с неравенством добавляем дополнительную переменную x6.
Перепишем ограничения в каноническом виде:
x1 – 2·x2 + 2·x3 + x6 = 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 – 4·x3 + 2·x5 = 30
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Столбец 4 является частью единичной матрицы. Переменная x4 входит в начальный базис
В пятом столбце все значения кроме третьего равны нулю. Поэтому в качестве третьей базисной переменной берём x5, предварительно разделив третью строку на 2.
Симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| ? | 2 | 1 | -4 | 0 | 2 | 0 | 30 |
После преобразования получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 1 |
1 2 |
-2 | 0 | 1 | 0 | 15 |
Если такой столбец отсутствует, то для формирования базиса необходимо применить исключение Гаусса для первого ненулевого столбца, который ещё не является базисным. Для этого вся строка делится на элемент в найденном столбце, а из остальных строк вычитается полученная строка, разделённая на значение, стоящее в этом же столбце. После этой операции все значения вне данной строки будут обнулены, и столбец можно будет считать базисным.
Пример 3
4·x1 + 5·x2 + 4·x3 → max
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 ≤ 200
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Перепишем ограничения в каноническом виде:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 + x5 = 200
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Начальная симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| ? | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
Для определения второй базисной переменной ищем первый ненулевой столбец, который ещё не является базисным. Первый столбец не нулевой и не является базисным. Выполняем исключение Гаусса: делим строку 2 на 4, а из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент в первом столбце.
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| x1 | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
После исключения получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 0 | 2 | 4 | 1 | 0 | 160 |
| x1 | 1 |
1 2 |
1 | 0 | 0 | 40 |
| x5 | 0 | 4 | 4 | 0 | 1 | 40 |
После того как базис сформирован, нужно построить начальную симплекс-таблицу. Она строится следующим образом:
- Для удобства в первой строке можно записать коэффициенты Ci целевой функции (для дополнительных переменных эти коэффициенты равны нулю)
- Вторая строка формирует шапку таблицы. В ней первый столбец называется базис, а остальные перечисляют основные переменные x1..xn и дополнительные xn+1..xn+k
- Затем построчно перечисляются базисные переменные и коэффициенты ограничений
Схематично начальная таблица будет выглядеть примерно так:
| C | с1 | c2 | … | cn | 0 | 0 | … | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| базис | x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+k | b |
| xe1 | a11 | a12 | … | a1n | a1n+1 | a1n+2 | … | a1n+k | b1 |
| xe2 | a21 | a22 | … | a2n | a2n+1 | a2n+2 | … | a2n+k | b2 |
| … | … | … | … | … | … | … | … | … | … |
| xem | am1 | am2 | … | amn | amn+1 | amn+2 | … | amn+k | bm |
Избавляемся от отрицательных свободных коэффициентов
После приведения к каноническому виду или после алгебраических преобразований при формировании базиса некоторые из свободных коэффициентов (bi) могли стать отрицательными, что не позволяет перейти к дальнейшим вычислениям. Чтобы избавиться от отрицательных значений b необходимо:
- Найти строку, в которой находится максимальное по модулю значение b. Пусть это будет строка i;
- Найти максимальный по модулю элемент в этой строке. Пусть он находится в столбце j;
- Строку i разделить на элемент, стоящий на пересечении i-ой строки и j-го столбца;
- Из каждой оставшейся строки k вычесть строку i, умноженную на элемент строки k и столбца j;
- Переменную, соответствующую найденному столбцу j, сделать базисной (добавить в базис вместо переменной, находящейся в строке i).
Этот шаг необходимо повторять до тех пор, пока все отрицательные b не станут положительными или в строке не останется отрицательных элементов. Если строка с максимальным по модулю bi не содержит отрицательных элементов, то такая задача не имеет решений и на этом алгоритм заканчивает свою работу. В противном случае все bi положительны и алгоритм переходит к следующему этапу — расчёту дельт.
Пример 4
20·x1 + 20·x2 + 10·x3 → min
4·x1 + 3·x2 + 2·x3 ≥ 33
3·x1 + 2·x2 + x3 ≥ 23
x1 + x2 + 2·x3 ≥ 12
Меняем знаки у ограничений с ≥, путём умножения на -1:
-4·x1 – 3·x2 – 2·x3 ≤ -33
– 3·x1 – 2·x2 – x3 ≤ -23
– x1 – x2 – 2·x3 ≤ -12
Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6.
Перепишем ограничения в каноническом виде:
– 4·x1 – 3·x2 – 2·x3 + x4 = -33
– 3·x1 – 2·x2 – x3 + x5 = -23
– x1 – x2 – 2·x3 + x6 = -12
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Начальная симплекс-таблица
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x4 | -4 | -3 | -2 | 1 | 0 | 0 | -33 |
| x5 | -3 | -2 | -1 | 0 | 1 | 0 | -23 |
| x6 | -1 | -1 | -2 | 0 | 0 | 1 | -12 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-33| находится в первой строке.
Максимальный по модулю элемент в первой строке = -4 находится в первом столбце.
В качестве базисной переменной x4 берём x1.
Делим первую строку на -4. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в первом столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
3 4 |
1 2 |
–
1 4 |
0 | 0 |
33 4 |
| x5 | 0 |
1 4 |
1 2 |
–
3 4 |
1 | 0 |
7 4 |
| x6 | 0 | –
1 4 |
–
3 2 |
–
1 4 |
0 | 1 | –
15 4 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-
| находится в третьей строке.
Максимальный по модулю элемент в третьей строке = –
находится в третьем столбце.
В качестве базисной переменной x6 берём x3.
Делим третью строку на –
. Из первой и второй строк вычитаем третью, умноженную на соответствующий элемент в третьем столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
2 3 |
0 | –
1 3 |
0 |
1 3 |
7 |
| x5 | 0 |
1 6 |
0 | –
5 6 |
1 |
1 3 |
1 2 |
| x3 | 0 |
1 6 |
1 |
1 6 |
0 | –
2 3 |
5 2 |
Расчёт дельт
Дельты — это параметры, на основании которых проверяется оптимальность текущего решения и улучшается функция. Они рассчитываются для каждой из переменных ограничений и записываются последней строкой таблицы.
Для расчёта дельт используется следующая формула: Δi = ce1·a1i + ce2·a2i + … + cem·ami – ci. Проще говоря, чтобы вычислить дельту по заданной i-ой переменной, нужно перемножить коэффициенты условий в i-ом столбце на коэффициенты целевой функции при соответствующих базисных переменных, сложить эти произведения и вычесть из полученной суммы коэффициент целевой функции столбца i.
Пример 5
Таблица:
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | –
4 5 |
36 5 |
Вычисляем дельты: Δi = C2·a1i + C4·a2i + C5·a3i – Ci
Симплекс-таблица с дельтами
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | –
4 5 |
36 5 |
| Δ | -3 | 0 | -2 | 0 | 0 | 6 | 0 |
Проверка плана на оптимальность
После того как дельты рассчитаны, необходимо проверить оптимальность текущего плана. Критерий оптимальности формулируется следующим образом:
При максимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют отрицательные дельты.
При минимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют положительные дельты.
Пример 6
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 – 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 – 4·x3 + x5 = 30
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Критерий оптимальности: план оптимален, если в таблице отсутствуют отрицательные дельты.
План не оптимален, так как ищется максимум функции, а Δ1 = -2 отрицательна.
Если текущий план оптимален, то алгоритм завершает свою работу. Значениям переменных соответствуют значения столбца свободных коэффициентов b. Если свободной переменной нет в базисе, то её значение считается нулевым. Значение целевой функции, принимаемой на данном наборе, находится в строке с дельтами в том же столбце. Если какое-либо из значений столбца b отрицательно, то решения задачи не существует.
Переход к более оптимальному решению
Если текущий план оказался не оптимальным, то алгоритм ищет столбец с наименьшей (с наибольшей, если ищется минимум) дельтой. После чего вычисляются симплекс-отношения Q. Для этого значения свободных коэффициентов делятся на ненулевые коэффициенты из найденного столбца. Если результат деления получается отрицательным, то такие отношение игнорируются.
Среди найденных симплекс-отношений ищется строка, в которой находится симплекс-отношение с наименьшим значением. Если таких отношений нет, то алгоритм останавливает свою работу, так как целевая функция не ограничена и решения не существует.
Пример 7
Симплекс-таблица с дельтами
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Проверяем план на оптимальность: план не оптимален, так как ищется минимум функции, а Δ2 = 1 положительна.
Определяем разрешающий столбец – столбец, в котором находится максимальная дельта: 2, Δ2: 1
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 | – |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 | – |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 | – |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Все значения второго столбца отрицательны. Функция не ограничена. Оптимальное решение отсутствует.
В противном случае строка с наименьшим отношением считается разрешающей и, аналогично избавлению от отрицательных свободных коэффициентов, делится на разрешающий элемент, расположенный в найденных столбце и строке, и из остальных строк вычитается найденная строка, разделённая на значения, стоящие в этом же столбце соответствующей строки. Переменная, стоящая в разрешающем столбце заменяет базисную переменную, находящуюся в найденной строке.
После этого вычисляются новые дельты и проверяется новый план. Так продолжается до тех пор пока не будет выполнен критерий оптимальности плана или не будет установлено, что решение не существует.
Пример 8
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -2 отрицательна.
Итерация 1
Определяем разрешающий столбец – столбец, в котором находится минимальная дельта: 3, Δ3: -9
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения третьего столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 3, строка 1.
На пересечении найденных строки и столбца находится разрешающий элемент: 2
В качестве базисной переменной x6 берём x3.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 | 1 | -2 | 2 | 0 | 0 | 1 | 6 | 6 / 2 = 3 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 | 24 / 1 = 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 | – |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Делим первую строку на 2. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в третьем столбце.
Вычисляем новые дельты: Δi = C3·a1i + C4·a2i + C5·a3i – Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | 3 |
| x4 |
1 2 |
3 | 0 | 1 | 0 | –
1 2 |
21 | 24 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | – |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Текущий план X: [ 0, 0, 3, 21, 42, 0 ]
Целевая функция F: 9·0 + 5·0 + 4·3 + 3·21 + 2·42 + 0·0 = 159
Проверяем план на оптимальность: план не оптимален, так как Δ2 = -6 отрицательна.
Итерация 2
Определяем разрешающий столбец – столбец, в котором находится минимальная дельта: 2, Δ2: -6
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 7, строка 2.
На пересечении найденных строки и столбца находится разрешающий элемент: 3
В качестве базисной переменной x4 берём x2.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | – |
| x2 |
1 2 |
3 | 0 | 1 | 0 | –
1 2 |
21 | 21 / 3 = 7 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | – |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Делим вторую строку на 3. Из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент во втором столбце.
Вычисляем новые дельты: Δi = C3·a1i + C2·a2i + C5·a3i – Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
2 3 |
0 | 1 |
1 3 |
0 |
1 3 |
10 | – |
| x2 |
1 6 |
1 | 0 |
1 3 |
0 | –
1 6 |
7 | 7 |
| x5 |
9 2 |
0 | 0 | 1 | 1 |
3 2 |
63 | – |
| Δ |
7 2 |
0 | 0 | 2 | 0 |
7 2 |
201 |
Текущий план X: [ 0, 7, 10, 0, 63, 0 ]
Целевая функция F: 9·0 + 5·7 + 4·10 + 3·0 + 2·63 + 0·0 = 201
Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.
Ответ: x1 = 0, x2 = 7, x3 = 10, x4 = 0, x5 = 63, F = 201
Метод искусственного базиса
Очень часто при решении задачи линейной оптимизации бывает довольно сложно выполнять алгебраические преобразования над коэффициентами ограничений для поиска начального базиса. Для упрощения вычислений существует альтернативный метод решения, называемый методом искусственного базиса. Его суть заключается в том, что вместо того, чтобы искать базис среди имеющихся основных и дополнительных переменных, ввести так называемые искусственные переменные, которые сформируют начальный базис. Возможно, звучит сложно и непонятно, но сейчас мы всё объясним.
Подготовительный этап
Аналогично базовому симплекс-методу для всех ограничений с неравентством вводятся дополнительные переменные, причём для ограничений с ≥ они берутся с коэффициентом -1, а для ограничений с ≤ с коэффициентом 1. Ограничения с равенством остаются без изменений. Если свободный коэффициент какого-либо из ограничений меньше нуля, то такое ограничение умножается на -1 (знак неравенства при этом меняется на противоположный). После этого приступают к поиску базиса.
Пример 9
3·x1 + 2·x2 + 3·x3 → min
-2·x1 – x2 – x3 ≥ -2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Меняем знаки у ограничений с отрицательными свободными коэффициентами, путём умножения на -1:
2·x1 + x2 + x3 ≤ 2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство с ≥. Базисная переменная для этого ограничения будет определена позднее.
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 3 | 2 | 3 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 2 |
| ?1 | 3 | 8 | 2 | 0 | -1 | 8 |
| ?2 | 2 | 0 | 1 | 0 | 0 | 1 |
Формирование начального базиса
Для того, чтобы сформировать начальный базис в первую очередь можно поискать столбец, у которого одно значение равно единице, а все значения остальные значения равны нулю, и сделать соответствующую переменную базисной для этой строки. Однако такое случается довольно редко, поэтому проще сразу перейти к следующему пункту. Для всех ограничений, не имеющих базисной переменной, добавляем искусственную переменную с коэффициентом 1. В целевую функцию добавляем эту же переменную с коэффициентов -M, если ищется максимум или с коэффициентом M, если ищется минимум. M всего лишь является очень большим числом.
Пример 10
x1 – x2 → min
2·x1 + x2 = 1
x1 – 3·x2 + x3 = 3
x1 + 11·x2 = 11
Ограничение 1 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Столбец 3 является частью единичной матрицы. Переменная x3 входит в начальный базис
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 1 | -1 | 0 | 0 |
| базис | x1 | x2 | x3 | b |
|---|---|---|---|---|
| ?1 | 2 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 3 |
| ?3 | 1 | 11 | 0 | 11 |
Для ограничения 1 добавляем искусственную переменную u1 и делаем её базисной.
Для ограничения 3 добавляем искусственную переменную u2 и делаем её базисной.
В целевую функцию добавляем искусственные пременные с коэффициентом M, где M — очень большое число.
Таблица с искусственными переменными
| C | 1 | -1 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | u1 | u2 | b |
|---|---|---|---|---|---|---|
| u1 | 2 | 1 | 0 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 0 | 0 | 3 |
| u2 | 1 | 11 | 0 | 0 | 1 | 11 |
Перепишем условие задачи с учётом добавленных искусственных переменных:
F = 1x1 -1x2 + Mu1 + Mu2 → min
2·x1 + x2 + u1 = 1
x1 – 3·x2 + x3 = 3
x1 + 11·x2 + u2 = 11
Расчёт дельт и проверка плана на оптимальность
После того, как начальный базис сформирован необходимо вычислить дельты. Дельты вычисляются полностью аналогично базовому методу: Δi = ce1·a1i + ce2·a2i + … + cem·ami – ci. Единственным отличием будет тот факт, что результат может содержать значения с M. Когда дельты будут получены необходимо проверить текущий опорный план на оптимальность (см. проверку плана на оптимальность в базовом симплекс-методе). Если план оптимален, то алгоритм завершает свою работу, иначе формирует более оптимальное решение и повторяет процесс.
Пример 11
Таблица с искусственными переменными
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
Вычисляем дельты: Δi = C4·a1i + C7·a2i + C8·a3i – Ci
Δ1 = C4·a11 + C7·a21 + C8·a31 – C1 = 0·2 + M·3 + M·0 – 3 = -3 + 3M
Δ2 = C4·a12 + C7·a22 + C8·a32 – C2 = 0·1 + M·0 + M·0 – 2 = -2
Δ3 = C4·a13 + C7·a23 + C8·a33 – C3 = 0·1 + M·2 + M·1 – 3 = -3 + 3M
Δ4 = C4·a14 + C7·a24 + C8·a34 – C4 = 0·1 + M·0 + M·0 – 0 = 0
Δ5 = C4·a15 + C7·a25 + C8·a35 – C5 = 0·0 + M·(-1) + M·0 – 0 = -M
Δ6 = C4·a16 + C7·a26 + C8·a36 – C6 = 0·0 + M·0 + M·(-1) – 0 = -M
Δ7 = C4·a17 + C7·a27 + C8·a37 – C7 = 0·0 + M·1 + M·0 – M = 0
Δ8 = C4·a18 + C7·a28 + C8·a38 – C8 = 0·0 + M·0 + M·1 – M = 0
Δb = C4·b1 + C7·b2 + C8·b3 – C9 = 0·2 + M·3 + M·1 – 0 = 4M
Симплекс-таблица с дельтами
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
| Δ | -3 + 3M | -2 | -3 + 3M | 0 | -M | -M | 0 | 0 | 4M |
Текущий план X: [ 0, 0, 0, 2, 0, 0, 3, 1 ]
Целевая функция F: 3·0 + 2·0 + 3·0 + 0·2 + 0·0 + 0·0 + M·3 + M·1 = 4M
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -3 + 3M положительна.

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Линейное программирование (ЛП) является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Линейное программирование
Создание Данцигом в конце 1940-х годов симплекс-метода стало началом современной эры в оптимизации. Этот метод позволил экономистам формулировать большие модели и систематически и эффективно анализировать их. Открытие Данцига совпало с появлением цифровых компьютеров, и симплекс-метод стал одним из первых примеров удачного использования этой новой революционной технологии. С тех пор реализация симплекс-метода постоянно совершенствуется. Сегодня линейное программирование и симплекс-метод — наиболее широко используемые средства оптимизации, и, несмотря на то что в настоящее время появились новые классы эффективных методов (например, метод внутренней точки), актуальность и важность симплекс-метода гарантированы в обозримом будущем.
Возможно эта страница вам будет полезна:
Постановка задачи линейного программирования. Общая, нормальная и каноническая формы записи
Задача оптимизации, в которой требуется найти числа 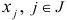 , обращающие в максимум (минимум) линейную форму
, обращающие в максимум (минимум) линейную форму
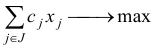
при линейных ограничениях (типа равенств и неравенств)
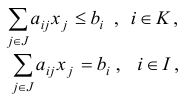
называется общей задачей линейного программирования (ЛП). Здесь . 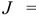
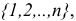
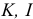 — некоторые заданные конечные наборы индексов;
— некоторые заданные конечные наборы индексов; 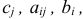
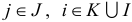 — заданные числа.
— заданные числа.
Задача, в которой требуется найти максимум линейной формы (1.1) при условиях (1.2) и условиях
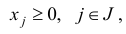
называется задачей линейного программирования в нормальной форме. В матричном виде задача в нормальной форме записи имеет вид
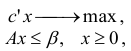
где 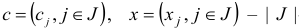 -векторы;
-векторы; 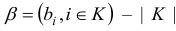 вектор;
вектор; 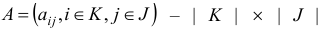 (-матрица; символом
(-матрица; символом 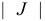 обозначено количество элементов множества
обозначено количество элементов множества 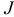 ; символом % (штрих) обозначается операция транспонирования.
; символом % (штрих) обозначается операция транспонирования.
Задача, в которой максимизируется линейная форма (1.1) при условиях (1.3) и (1.4), называется задачей линейного программирования в канонической форме записи.
В матричном виде задача в канонической форме записывается следующим образом
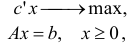
где 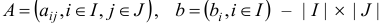 — матрица и
— матрица и 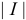 — вектор.
— вектор.
В задачах (1.5), (1.6) ограничения 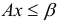 и
и 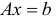 называются основными, ограничения вида
называются основными, ограничения вида 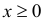 — прямыми. Линейная форма
— прямыми. Линейная форма 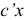 называется целевой функцией. Столбцы
называется целевой функцией. Столбцы 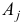 матрицы
матрицы 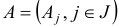 называются векторами условий.
называются векторами условий.
Вектор 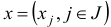 , удовлетворяющий всем ограничениям задачи линейного программирования, назовем ее планом. План
, удовлетворяющий всем ограничениям задачи линейного программирования, назовем ее планом. План 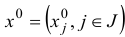 , обращающий в максимум линейную форму
, обращающий в максимум линейную форму 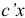 , называется оптимальным планом или решением задачи линейного программирования.
, называется оптимальным планом или решением задачи линейного программирования.
Задачу линейного программирования, заданную в любой форме, можно свести к задаче в канонической форме записи.
Покажем на простых примерах, как задачу, заданную в общей форме, можно свести к канонической.
Возможно эта страница вам будет полезна:
Задача №1
Привести к канонической форме записи задачу
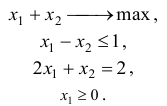
Решение:
Для того чтобы первое ограничение записать в форме равенства, введем неотрицательную переменную 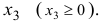 Заменим переменную
Заменим переменную 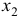 , на значения которой не наложено требование отрицательности, разностью двух неотрицательных переменных
, на значения которой не наложено требование отрицательности, разностью двух неотрицательных переменных
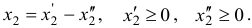
После этих преобразований исходная задача запишется в канонической форме
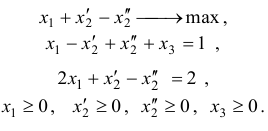
Задача №2
Привести к канонической форме задачу
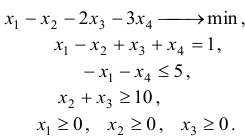
Решение:
Умножим коэффициенты целевой функции (а) на (-1), в результате вместо задачи минимизации получим задачу максимизации:
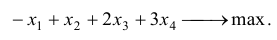
Введем дополнительные неотрицательные переменные 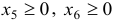 и запишем ограничения (с) и (d) в виде
и запишем ограничения (с) и (d) в виде
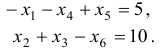
Исключим из задачи переменную 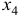 , на которую не наложено условие неотрицательности. Для этого из условия (Ь) выразим
, на которую не наложено условие неотрицательности. Для этого из условия (Ь) выразим 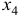 :
:
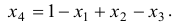
Подставив (h) в (f), (g), получим каноническую форму задачи :
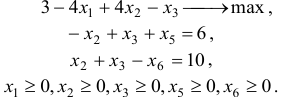
Отметим что задача максимизации функции (i) эквивалентна максимизации функции
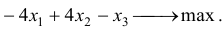
Задача линейного программирования в нормальной форме записи (1.5) приводится к канонической форме путем добавления неотрицательных переменных 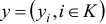 . В результате получим эквивалентную задачу в канонической форме
. В результате получим эквивалентную задачу в канонической форме
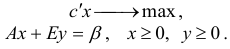
Здесь 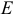 — единичная
— единичная 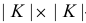 — матрица.
— матрица.
Теорема. Для того чтобы задача линейного программирования имела решение, необходимо и достаточно, чтобы множество ее планов было не пусто, а целевая функция ограничена сверху на множестве планов.
Таким образом, для построения решения задачи линейного программирования надо определить, какая из ситуаций 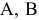 или
или 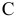 имеет для нее место, и, если реализовалась ситуация
имеет для нее место, и, если реализовалась ситуация 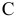 , то найти оптимальный план
, то найти оптимальный план 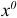 .
.
Возможно эта страница вам будет полезна:
Базисный план задачи линейного программирования
Выше показано, что любая задача линейного программирования может быть приведена к канонической форме. Поэтому далее основные теоремы и алгоритмы будут рассмотрены применительно к задаче (1.6), что не снижает общности рассмотрения.
Исследуем задачу линейного программирования в канонической форме (1.6), считая для определенности, что
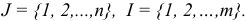
В дальнейшем, вплоть до подразд. 1.6, мы будем предполагать, что
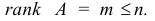
Очевидно, что при нарушении условия (1.8) система 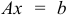 либо несовместна, либо содержит линейно зависимые условия, которые можно исключить из рассмотрения (см. подразд. 1.6).
либо несовместна, либо содержит линейно зависимые условия, которые можно исключить из рассмотрения (см. подразд. 1.6).
План 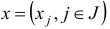 задачи (1.6) назовем базисным планом, если существует такое подмножество
задачи (1.6) назовем базисным планом, если существует такое подмножество 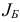 множества индексов
множества индексов 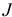 , что 1)
, что 1) 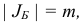 , 2)
, 2) 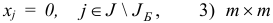 — матрица
— матрица 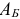 , построенная по правилу
, построенная по правилу 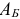
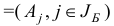 , не вырождена.
, не вырождена.
Напомним, что 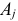 — это
— это 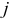 -й столбец матрицы
-й столбец матрицы 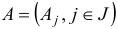 .
.
Множество 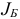 назовем базисом или множеством базисных индексов. Множество
назовем базисом или множеством базисных индексов. Множество 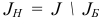 и будем называть множеством небазисных индексов, матрицу
и будем называть множеством небазисных индексов, матрицу 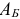 — базисной матрицей.
— базисной матрицей.
Иногда базисный план удобно обозначать в виде пары 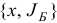 , состоящей из плана
, состоящей из плана 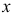 и соответствующего ему базиса
и соответствующего ему базиса 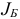 .
.
Базисный план считается невырожденным, если
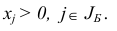
Отметим, что в общем случае плану 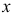 можно приписать несколько наборов базисных индексов
можно приписать несколько наборов базисных индексов
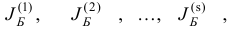
удовлетворяющих условиям 1) — 3). Базисному плану 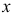 соответствует единственный набор базисных индексов
соответствует единственный набор базисных индексов 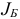 , если имеют место неравенства (1.9), т.е. базисный план является невырожденным.
, если имеют место неравенства (1.9), т.е. базисный план является невырожденным.
Легко проверить, что по заданному набору базисных индексов 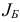 базисный план
базисный план 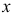 восстанавливается однозначно по правилу
восстанавливается однозначно по правилу
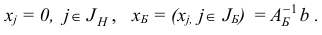
Здесь 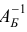 — матрица, обратная к базисной матрице
— матрица, обратная к базисной матрице 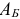 .
.
Далее будет показано, что симплекс-метод при решении задачи (1.6) генерирует последовательность планов 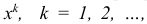 каждый из которых является базисным планом. Поскольку наша цель — построить последовательность планов, сходящихся к решению задачи (1.6), то итерации симплекс -метода будут иметь смысл только в том случае, если
каждый из которых является базисным планом. Поскольку наша цель — построить последовательность планов, сходящихся к решению задачи (1.6), то итерации симплекс -метода будут иметь смысл только в том случае, если
а) задача (1.6) имеет базисные планы;
б) существует оптимальный базисный план.
Оказывается, оба условия, а и б, верны при минимальных предположениях.
Теорема (основная теорема ЛП). Если для задачи (1.6) существует план, то для нее существует и базисный план. Если задача (1.6) имеет оптимальные планы, то хотя бы один из них базисный.
Возможно эта страница вам будет полезна:
Исследование базисного плана на оптимальность
Пусть 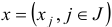 — базисный план задачи (1.6) с базисом
— базисный план задачи (1.6) с базисом 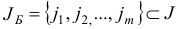 и базисной матрицей
и базисной матрицей 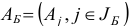 . Сформируем
. Сформируем 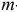 -вектор
-вектор 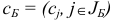 и подсчитаем
и подсчитаем 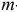 -вектор потенциалов
-вектор потенциалов 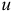 по правилу
по правилу
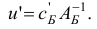
Вычислим оценки
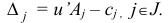
Отметим, что по построению
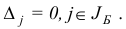
Для базисного плана 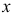 справедливы следующие утверждения.
справедливы следующие утверждения.
Утверждение 1. (Признак оптимальности базисного плана.) Базисный план х является решением задачи (1.6), если
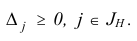
Утверждение 2. (Достаточное условие неограниченности сверху целевой функции.) Если существует индекс 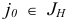 , для которого
, для которого 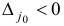 и все компоненты
и все компоненты 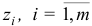 , вектора
, вектора
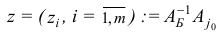
не положительны, то целевая функция задачи (1.6) не ограничена сверху на множестве планов.
Утверждение 3. (Возможность строгого улучшения плана.) Пусть 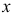 — невырожденный базисный план задачи (1.6) и для некоторого
— невырожденный базисный план задачи (1.6) и для некоторого 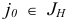 справедливы соотношения
справедливы соотношения
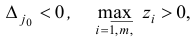
где вектор 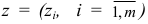 определен по формуле (1.10). Тогда существует базисный план
определен по формуле (1.10). Тогда существует базисный план 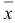 , для которого
, для которого 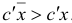 .
.
Компоненты нового базисного плана 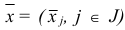 и соответствующий ему базис
и соответствующий ему базис 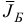 строятся по правилу
строятся по правилу
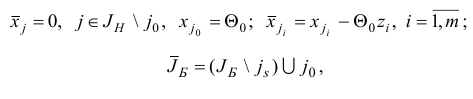
где
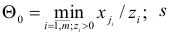
любой индекс из множества
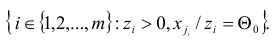
Задача №3
Исследовать на оптимальность план 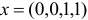 задачи
задачи
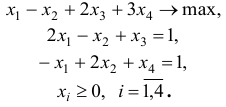
Решение:
В рассматриваемой задаче векторы условий 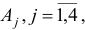 имеют вид
имеют вид
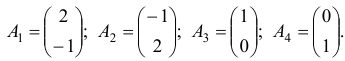
План 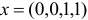 является невырожденным базисным планом с базисом
является невырожденным базисным планом с базисом 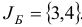 . Данному базису соответствует базисная матрица
. Данному базису соответствует базисная матрица

Для проверки плана 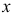 на оптимальность подсчитаем вектор потенциалов
на оптимальность подсчитаем вектор потенциалов 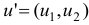 :
:
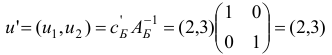
и оценки
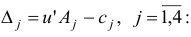
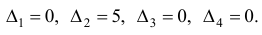
Поскольку все оценки 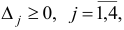 то, согласно утверждению 1, план
то, согласно утверждению 1, план 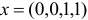 является оптимальным.
является оптимальным.
Возможно эта страница вам будет полезна:
Симплекс-метод. Общая итерация
Пусть 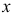 — некоторый базисный план задачи (1.6) с базисом
— некоторый базисный план задачи (1.6) с базисом 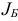 . В результате исследования, основанного на утверждениях 1-3, выясняется либо 1) оптимальность плана
. В результате исследования, основанного на утверждениях 1-3, выясняется либо 1) оптимальность плана 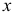 либо 2) неразрешимость задачи (1.6) в силу неограниченности сверху целевой функции на множестве планов, либо 3) возможность перехода к новому базисному плану
либо 2) неразрешимость задачи (1.6) в силу неограниченности сверху целевой функции на множестве планов, либо 3) возможность перехода к новому базисному плану 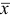 , для которого
, для которого 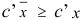 .
.
Последовательный переход от одного базисного плана к «лучшему» базисному плану вплоть до получения оптимального плана составляет основную идею симплекс-метода.
Для реализации симплекс-метода кроме исходных данных задачи (1.6) (векторов 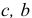 и матрицы
и матрицы 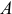 ) на каждой итерации необходимо знать следующие параметры:
) на каждой итерации необходимо знать следующие параметры:
текущий базисный план 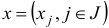 (достаточно знать только его базисные компоненты
(достаточно знать только его базисные компоненты 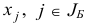 );
);
соответствующее плану 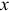 множество базисных индексов
множество базисных индексов 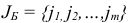 ;
; 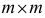 — матрицу
— матрицу 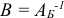 обратную к базисной матрице
обратную к базисной матрице 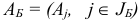 .
.
Опишем общую итерацию симплекс-метода по шагам. Шаг 1. Вычислим вектор потенциалов 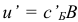 , где
, где 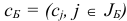 , и оценки
, и оценки
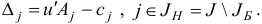
Шаг 2. Если 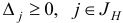 то STOP: вектор
то STOP: вектор 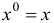 является оптимальным планом задачи (1.6). В противном случае переходим к шагу 3.
является оптимальным планом задачи (1.6). В противном случае переходим к шагу 3.
Шаг 3. Выберем индекс 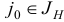 , для которого
, для которого 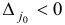 . Построим вектор
. Построим вектор 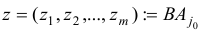 . Если
. Если 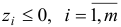 , то STOP: задача (1.6) не имеет решения в силу неограниченности сверху целевой функции на множестве планов. В противном случае перейдем к шагу 4.
, то STOP: задача (1.6) не имеет решения в силу неограниченности сверху целевой функции на множестве планов. В противном случае перейдем к шагу 4.
Шаг 4. Найдем минимум
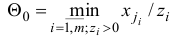
и выберем индекс 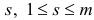 , для которого
, для которого 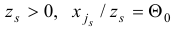 .
.
Шаг 5. Построим новый базисный план 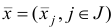 соответствующий ему базис
соответствующий ему базис 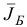 по правилам
по правилам
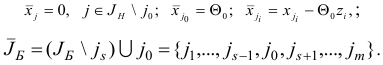
Шаг 6. Вычислим матрицу 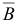 , обратную к новой базисной матрице
, обратную к новой базисной матрице 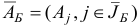 , по формуле
, по формуле 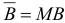 , где матрица
, где матрица 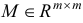 , отличается от единичной
, отличается от единичной 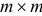 -матрицы только
-матрицы только 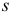 -м столбцом, который имеет вид
-м столбцом, который имеет вид
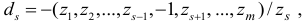
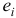 — единичный
— единичный 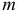 -вектор с единицей на
-вектор с единицей на 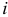 -м месте.
-м месте.
Переходим к следующей итерации, исходя из новых плана 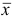 , базиса
, базиса 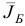 и матрицы
и матрицы 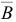 , обратной к новой базисной матрице
, обратной к новой базисной матрице 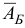 .
.
Замечания. 1. На шаге 3 выбирается индекс 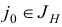 , для которого
, для которого 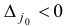 . В общем случае существует несколько индексов, удовлетворяющих этому условию. При численной реализации симплекс-метода для выбора
. В общем случае существует несколько индексов, удовлетворяющих этому условию. При численной реализации симплекс-метода для выбора 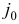 можно использовать дополнительные «уточняющие» правила, например, следующие:
можно использовать дополнительные «уточняющие» правила, например, следующие:
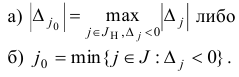
На шаге 4 выбирается индекс 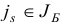 или
или 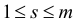 для которого
для которого 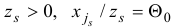 . В общем случае этот выбор может оказаться неоднозначным. Можно использовать дополнительные уточняющие правила, например, следующие:
. В общем случае этот выбор может оказаться неоднозначным. Можно использовать дополнительные уточняющие правила, например, следующие:
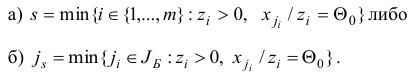
В современных версиях симплекс-метода для нахождения вектора потенциалов 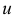 (см. шаг 1) и вектора
(см. шаг 1) и вектора 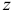 (см. шаг 3) решаются системы
(см. шаг 3) решаются системы 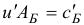 и
и 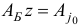 , соответственно. Для эффективного решения последних используется
, соответственно. Для эффективного решения последних используется 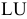 -разложение базисной матрицы
-разложение базисной матрицы 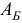 .
.
Легко подсчитать, что приращение целевой функции при переходе от начального базисного плана 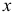 к новому базисному плану
к новому базисному плану 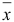 равно:
равно:

По построению,
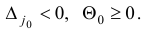
Следовательно, при 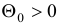 происходит «строгое улучшение» плана:
происходит «строгое улучшение» плана: 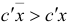 . Из описания шага 4 видно, что в случае невырожденности начального базисного плана
. Из описания шага 4 видно, что в случае невырожденности начального базисного плана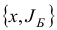 всегда верно неравенство
всегда верно неравенство 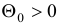 .
.
В случае, когда базисный план 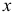 (с базисом
(с базисом 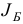 ) является вырожденным, может реализоваться ситуация:
) является вырожденным, может реализоваться ситуация: 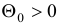 . При этом мы получаем
. При этом мы получаем 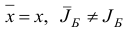 .
.
В этом случае не происходит улучшения целевой функции, но итерация может оказаться полезной, так как изменяется базис и новый базис может быть ближе к оптимальному базису, чем старый.
Задача №4
Решить задачу ЛП симплекс-методом
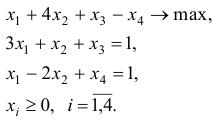
Решение:
Для данной задачи 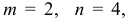 а векторы
а векторы 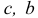 и матрица
и матрица 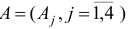 имеют вид
имеют вид 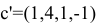 ;
;
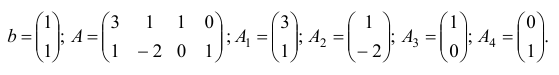
В качестве начального базисного плана возьмем вектор 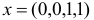 , которому соответствует базисное множество
, которому соответствует базисное множество 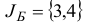 и базисная матрица
и базисная матрица
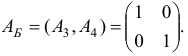
Используя
Очевидно, что
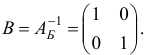
Используя
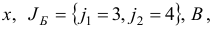
осуществим первую итерацию симплекс-метода. Шаг 1. Вычислим вектор потенциалов
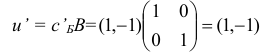
и оценки
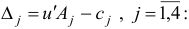
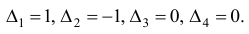
Шаг 2. Поскольку среди оценок 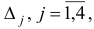 есть отрицательные, то переходим к шагу 3.
есть отрицательные, то переходим к шагу 3.
Шаг 3. Выберем в качестве индекса 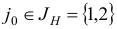 , для которого
, для которого 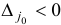 , индекс 2, т.е.
, индекс 2, т.е. 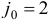 . Построим вектор
. Построим вектор
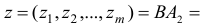
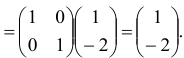
Поскольку среди компонент вектора 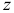 есть положительные, то перейдем к шагу 4. Шаг 4. Найдем минимум
есть положительные, то перейдем к шагу 4. Шаг 4. Найдем минимум
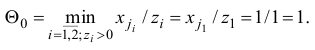
Очевидно, что в данном примере в качестве индекса 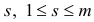 , для которого
, для которого 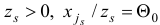 можно взять только индекс 1, т.е.
можно взять только индекс 1, т.е.
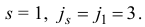
Шаг 5. Построим новый базисный план
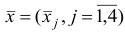
и соответствующий ему базис 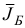 по правилам
по правилам
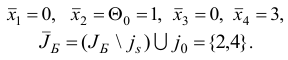
Шаг 6. Построим матрицу
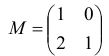
и найдем матрицу
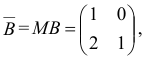
обратную к новой базисной матрице 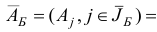
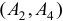 . Переходим ко второй итерации, исходя из новых плана
. Переходим ко второй итерации, исходя из новых плана 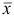 , базиса
, базиса 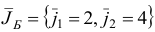 и матрицы
и матрицы 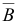 .
.
Осуществим вторую итерацию.
Шаг 1. Вычислим вектор потенциалов
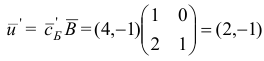
и оценки
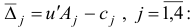
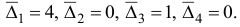
Шаг 2. Поскольку все оценки 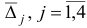 , неотрицательны, то алгоритм заканчивает свою работу: вектор
, неотрицательны, то алгоритм заканчивает свою работу: вектор 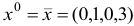 является оптимальным планом рассматриваемой задачи.
является оптимальным планом рассматриваемой задачи.
Возможно эта страница вам будет полезна:
Зацикливание. Конечные модификации симплекс- метода
Итерацию
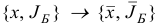
симплекс-метода назовем невырожденной, если 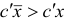 .
.
Ясно, что итерация 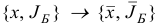 может оказаться вырожденной только в том случае, если базисный план
может оказаться вырожденной только в том случае, если базисный план 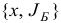 вырожденный, причем в случае вырожденности итерации справедливы соотношения:
вырожденный, причем в случае вырожденности итерации справедливы соотношения:
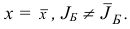
Теорема. При любом выборе начального базисного плана 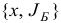 симплекс-метод за конечное число итераций строит оптимальный базисный план задачи (1.6) либо обнаруживает неограниченность сверху ее целевой функции на множестве планов, если в процессе его реализации не встречаются вырожденные итерации.
симплекс-метод за конечное число итераций строит оптимальный базисный план задачи (1.6) либо обнаруживает неограниченность сверху ее целевой функции на множестве планов, если в процессе его реализации не встречаются вырожденные итерации.
При наличии вырожденных итераций при реализации симплекс-метода может возникнуть такая ситуация, когда начиная с некоторого вырожденного базисного плана 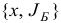 мы осуществляем последовательность вырожденных итераций
мы осуществляем последовательность вырожденных итераций
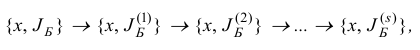
в которых меняются только базисы 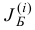 базисного плана
базисного плана 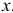 , причем при некотором конечном
, причем при некотором конечном 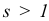 имеет место равенство
имеет место равенство 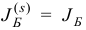 . Очевидно, что если мы продолжим операции симплекс-метода исходя из
. Очевидно, что если мы продолжим операции симплекс-метода исходя из 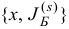 , то опять получим ту же последовательность итерации (1.12) и т. д. Такое явление получило название зацикливания.
, то опять получим ту же последовательность итерации (1.12) и т. д. Такое явление получило название зацикливания.
Первоначально считалось, что зацикливание — крайне редкое явление. Однако позже было замечено, что вероятность возникновения зацикливания увеличивается с ростом размеров задачи. Кроме того, зацикливание является типичным явлением для задач ЛП, возникающих при аппроксимации задач целочисленного программирования. В связи с этим возникла необходимость в разработке специальных приемов борьбы с зацикливанием. К настоящему времени известно много таких приемов. Опишем два из них.
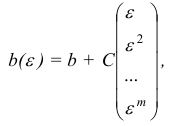
где 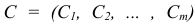 — некоторая невырожденная
— некоторая невырожденная 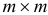 — матрица со столбцами
— матрица со столбцами 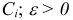 — достаточно малое число.
— достаточно малое число.
Возмущения в векторе 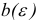 вызовут возмущения в базисных компонентах
вызовут возмущения в базисных компонентах 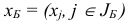 каждого базисного плана следующим образом:
каждого базисного плана следующим образом:
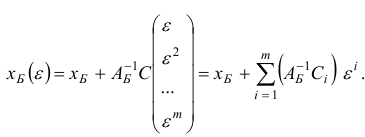
Матрица 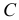 должна быть такой, что на первой итерации вектор
должна быть такой, что на первой итерации вектор 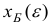 должен быть строго положительным при достаточно малых
должен быть строго положительным при достаточно малых 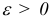 . Для этого достаточно положить
. Для этого достаточно положить 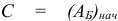 , где
, где 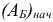 — базисная матрица, соответствующая начальному базису
— базисная матрица, соответствующая начальному базису 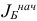 . Тогда для начального базисного плана имеем
. Тогда для начального базисного плана имеем
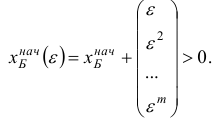
Предположим, что на текущей итерации имеется базисный план 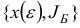 возмущенной задачи, для которого справедливы неравенства
возмущенной задачи, для которого справедливы неравенства 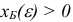 при достаточно малых
при достаточно малых 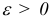 . Согласно данным подразд. 1.4, новый базисный план
. Согласно данным подразд. 1.4, новый базисный план 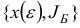 , построенный в результате одной итерации симплекс-метода из
, построенный в результате одной итерации симплекс-метода из 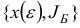 , будет также невырожденным, если не существует таких двух базисных индексов
, будет также невырожденным, если не существует таких двух базисных индексов 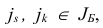 что
что 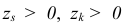 и
и
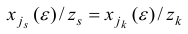
для всех достаточно малых 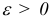 .
.
Последние соотношения могут иметь место только в том случае, если 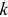 -я и
-я и 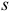 -я строки матрицы
-я строки матрицы 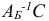 линейно зависимы. Однако это противоречит тому, что
линейно зависимы. Однако это противоречит тому, что 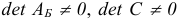 . Значит, соотношения (1.14) не могут иметь места и, следовательно, новый базисный план
. Значит, соотношения (1.14) не могут иметь места и, следовательно, новый базисный план 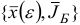 возмущенной задачи будет невырожденным при достаточно малых
возмущенной задачи будет невырожденным при достаточно малых 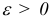 .
.
Таким образом, мы показали, что при достаточно малых 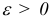 все итерации симплекс-метода для задачи с возмущенным вектором
все итерации симплекс-метода для задачи с возмущенным вектором 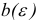 будут невырожденными и, следовательно, для возмущенной задачи симплекс- метод будет конечным. Кроме того справедлива следующая теорема.
будут невырожденными и, следовательно, для возмущенной задачи симплекс- метод будет конечным. Кроме того справедлива следующая теорема.
Теорема. Существует такое 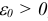 , что для любого
, что для любого 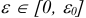 каждому базисному плану возмущенной задачи, порожденному базисом
каждому базисному плану возмущенной задачи, порожденному базисом 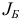 , соответствует базисный план (невозмущенной) исходной задачи, порожденный тем же базисом
, соответствует базисный план (невозмущенной) исходной задачи, порожденный тем же базисом 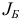 , а из оптимальности базиса
, а из оптимальности базиса 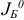 в возмущенной задаче следует его оптимальность в исходной задаче.
в возмущенной задаче следует его оптимальность в исходной задаче.
Покажем, как описанные выше результаты можно использовать для предотвращения зацикливания в исходной задаче (1.6).
Недостатком описанных выше рассуждений является то, что они верны только при достаточно малых 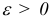 и заранее невозможно указать конкретное значение
и заранее невозможно указать конкретное значение 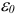 . Однако существуют правила (лексико-графическая стратегия), которые позволяют «мысленно» осуществить процедуру решения возмущенной задачи без явного выбора значения параметра
. Однако существуют правила (лексико-графическая стратегия), которые позволяют «мысленно» осуществить процедуру решения возмущенной задачи без явного выбора значения параметра 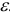 .
.
Пусть в начале текущей итерации для исходной задачи есть базисный план  , базис
, базис 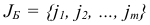 и соответствующая ему базисная матрица
и соответствующая ему базисная матрица 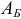 . Очевидно, что при достаточно малых
. Очевидно, что при достаточно малых 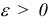 базис
базис 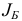 порождает базисный план
порождает базисный план 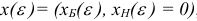 , где
, где 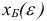 имеет вид (1.13), возмущенной задачи. Предположим, что мы осуществляем итерацию симплекс-метода для исходной и возмущенной задач, исходя из базисных планов
имеет вид (1.13), возмущенной задачи. Предположим, что мы осуществляем итерацию симплекс-метода для исходной и возмущенной задач, исходя из базисных планов 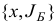 и
и 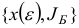 .
.
Ясно, что для обеих задач шаги 1-3 итерации будут полностью совпадать. Значит, совпадут и индексы 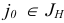 , подлежащие вводу в базис. Перейдем к шагу 4, на котором определяется индекс
, подлежащие вводу в базис. Перейдем к шагу 4, на котором определяется индекс 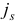 , подлежащий выводу из базиса
, подлежащий выводу из базиса 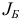 . Для возмущенной задачи индекс
. Для возмущенной задачи индекс 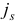 однозначно определяется из соотношений
однозначно определяется из соотношений
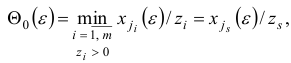
где 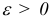 — достаточно малое число.
— достаточно малое число.
Легко проверить, что найти единственный индекс 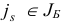 определяемый условием (1.15), можно по следующему правилу.
определяемый условием (1.15), можно по следующему правилу.
Положим
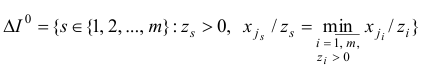
и построим множества 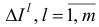 , по рекуррентным правилам
, по рекуррентным правилам
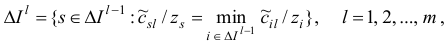
где
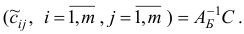
По построение,
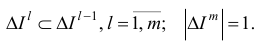
Обозначим через 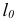 наименьший индекс
наименьший индекс 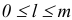 , при котором
, при котором 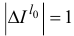 :
:
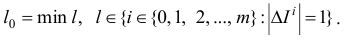
Пусть 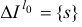 . Тогда индекс
. Тогда индекс 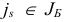 и совпадает с индексом, определяемым соотношениями (1.15).
и совпадает с индексом, определяемым соотношениями (1.15).
Ясно, что для исходной задачи любой индекс вида 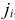 , где
, где  можно взять в качестве индекса, выводимого из базиса. Согласно (1.18)
можно взять в качестве индекса, выводимого из базиса. Согласно (1.18) 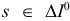 , следовательно, индекс
, следовательно, индекс 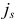 можно выводить из базиса в исходной задаче. Таким образом, в качестве нового базиса для исходной задачи можно взять базис
можно выводить из базиса в исходной задаче. Таким образом, в качестве нового базиса для исходной задачи можно взять базис
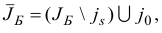
где индекс 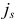 однозначно определяется по правилам (1.16)-(1.19). (Для возмущенной задачи новый базис (1.20) является единственно возможным).
однозначно определяется по правилам (1.16)-(1.19). (Для возмущенной задачи новый базис (1.20) является единственно возможным).
Из сказанного выше следует, что симплекс-метод будет конечным и для исходной задачи (1.6), если на шаге 4 индекс 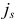 , подлежащий выводу из базиса, определять по правилам (1.16), (1.17), (1.19).
, подлежащий выводу из базиса, определять по правилам (1.16), (1.17), (1.19).
- Правило Блэнда. В 1977 г. Р. Блэнд предложил очень простое правило предотвращения зацикливания в симплекс- методе. Это правило сводится к следующему.
При реализации итерации симплекс-метода на шаге 3 индекс 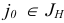 , подлежащий вводу в новый базис, однозначно определяется по правилу
, подлежащий вводу в новый базис, однозначно определяется по правилу
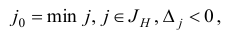
а на шаге 4 индекс 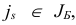 подлежащий выводу из базиса, однозначно определяется соотношениями
подлежащий выводу из базиса, однозначно определяется соотношениями
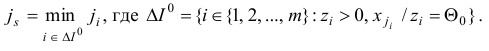
При использовании дополнительных правил (1.21), (1.22) симплекс-метод для любой задачи ЛП (с заданным начальным базисным планом) за конечное число итераций строит оптимальный базисный план либо обнаруживает неограниченность сверху целевой функции на множестве планов.
Первая фаза симплекс-метода
Все предыдущие утверждения и операции симплекс-метода были справедливы в предположении, что для задачи в канонической форме (1.6) выполнено условие (1.8).
Понятно, что для произвольной задачи (1.6) это условие может нарушаться. Поэтому, прежде чем применять описанный симплекс-метод необходимо исходную задачу (1.6) привести к такому виду, для которого выполняются соотношения (1.8).
Кроме того, из описания общей итерации симплекс-метода видно, что для начала его работы необходимо знать начальный базисный план 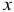 и начальный набор базисных индексов
и начальный набор базисных индексов 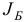 , для которых выполняются соотношения:
, для которых выполняются соотношения:
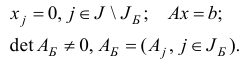
Проблема нахождения такой начальной информации может оказаться нетривиальной. Действительно, в общем случае по трудоемкости это проблема эквивалентна построению решения некоторой задачи линейного программирования. Для преодоления указанной трудности используется двухфазный симплекс-метод, общая схема которого состоит в следующем.
На первой фазе формируется вспомогательная задача ЛП, которая отличается от исходной задачи (1.6). Вспомогательная задача строится таким образом, что для нее выполняется условие (1.8), легко строится начальный базисный план и она имеет решение. Анализ решения вспомогательной задачи позволяет:
1) определить, совместны ли ограничения исходной задачи (1.6);
2) проверить, выполняется ли условие (1.8) для исходной задачи (1.6) и в случае его нарушения обнаружить линейно зависимые основные ограничения и удалить их из условий задачи;
3) в случае совместности ограничений задачи (1.6) построить для нее начальный базисный план 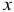 и базис
и базис 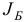 .
.
Если анализ решения вспомогательной задачи закончился построением начального базисного плана для исходной задачи, то переходим ко второй фазе алгоритма. Вторая фаза состоит в решении исходной задачи описанным выше симплекс-методом, при этом в качестве начальной используется информация, полученная на первой фазе.
Опишем подробнее первую фазу алгоритма. Без ограничения общности будем считать, что в задаче (1.6) вектор 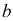 удовлетворяет неравенству
удовлетворяет неравенству 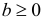 .
.
Тогда задачу первой фазы можно записать в виде
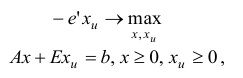
где 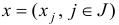 — исходные переменные,
— исходные переменные, 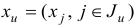 — искусственные переменные,
— искусственные переменные, 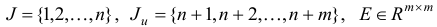 — единичная матрица,
— единичная матрица, 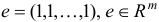 .
.
Легко проверить, что вектор 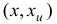 с компонентами
с компонентами
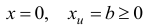
является базисным планом задачи (1.23) с базисом
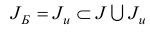
и базисной матрицей 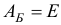 .
.
Решим задачу (1.23) симплекс-методом, описанным в подразд. 1.4, используя в качестве начального базисный план (1.24). Поскольку целевая функция задачи (1.23) ограничена сверху на множестве ее планов 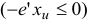 , то через конечное число итераций будет построен оптимальный базисный план
, то через конечное число итераций будет построен оптимальный базисный план 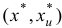 задачи (1.23) и соответствующий ему базис
задачи (1.23) и соответствующий ему базис 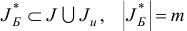 . Справедлива следующая теорема
. Справедлива следующая теорема
Теорема. Ограничения исходной задачи (1.6) совместны тогда и только тогда, когда компонента 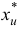 оптимального базисного плана задачи (1.23) равна нулю.
оптимального базисного плана задачи (1.23) равна нулю.
Проведем анализ решения задачи (1.23). Возможны случаи:
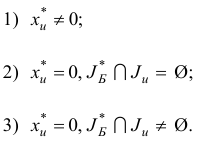
Пусть реализовался случай 1. Прекращаем исследование исходной задачи (1.6), так как согласно теореме она не имеет планов.
Рассмотрим случай 2. Легко проверить, что вектор 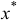 с базисным множеством
с базисным множеством 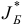 является базисным планом задачи (1.6). Переходим ко второй фазе алгоритма, исходя из этого плана.
является базисным планом задачи (1.6). Переходим ко второй фазе алгоритма, исходя из этого плана.
Исследуем случай 3. Ясно, что вектор 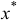 является планом задачи (1.6), но множество
является планом задачи (1.6), но множество 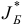 не является его базисом для задачи (1.6). Попытаемся построить базис для плана в задаче (1.6).
не является его базисом для задачи (1.6). Попытаемся построить базис для плана в задаче (1.6).
Пусть
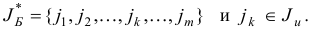
Обозначим
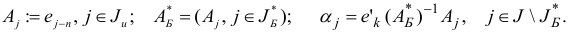
Возможны под случаи:
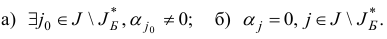
Если реализовался подслучай а, то оптимальному плану 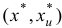 задачи (1.23) припишем новый базис
задачи (1.23) припишем новый базис
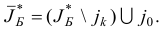
Очевидно, что по построению,
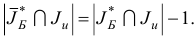
Снова проверяем, какая из ситуаций, 2 или 3, имеет место для оптимального плана 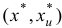 задачи (1.23) и нового базиса (1.26).
задачи (1.23) и нового базиса (1.26).
Подслучай б означает, что в исходной задаче (1.6) основное ограничение с индексом 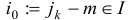 является линейно зависимым с остальными основными ограничениями этой задачи. Множество планов задачи (1.6) не изменится, если мы удалим это ограничение, т.е. заменим множество индексов
является линейно зависимым с остальными основными ограничениями этой задачи. Множество планов задачи (1.6) не изменится, если мы удалим это ограничение, т.е. заменим множество индексов 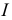 на
на 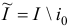 . Для преобразованной задачи (1.6) вспомогательная задача первой фазы получится из задачи (1.23) после удаления ограничения с индексом
. Для преобразованной задачи (1.6) вспомогательная задача первой фазы получится из задачи (1.23) после удаления ограничения с индексом 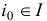 и искусственной переменной
и искусственной переменной 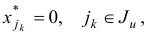 , т.е. заменой множеств
, т.е. заменой множеств 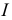 и
и 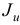 на
на
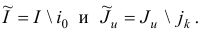
Очевидно, что для новой задачи первой фазы вектор
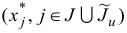
является оптимальным базисным планом с базисом
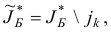
для которого
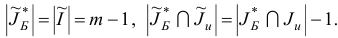
Для плана
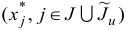
и новых множеств 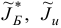 вновь проверяем, какая из ситуаций,
вновь проверяем, какая из ситуаций,
2 или 3, имеет место.
Ясно, что не более чем через 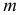 шагов из основных ограничений задачи (1.6) будут исключены все линейно зависимые ограничения и она будет сведена к задаче
шагов из основных ограничений задачи (1.6) будут исключены все линейно зависимые ограничения и она будет сведена к задаче
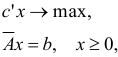
где
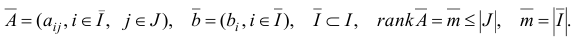
При этом для задачи (1.27) будет построен базисный план 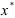 с некоторым базисом
с некоторым базисом
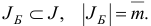
Дальнейшее решение задачи (1.27) осуществляем симплекс-методом, описанным в подразд. 1.4, используя в качестве начальных построений базисный план 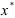 с базисом
с базисом 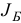 .
.
Возможно эта страница вам будет полезна:
Теория двойственности в линейном программировании
Определение двойственной задачи. Соотношения двойственности
Рассмотрим задачу линейного программирования, заданную в произвольной форме записи:
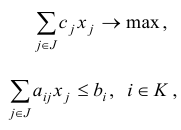
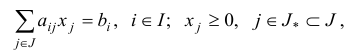
где 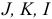 — некоторые конечные множества индексов. Задачу линейного программирования
— некоторые конечные множества индексов. Задачу линейного программирования
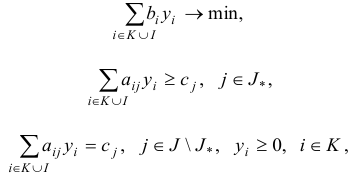
назовем двойственной по отношению к задаче (2.1). При этом задача (2.1) считается прямой.
Из приведенного определения следует, что для задачи линейного программирования в нормальной форме
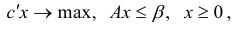
двойственной является задача
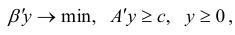
а для задачи в канонической форме
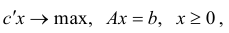
двойственная задача имеет вид
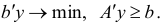
Легко проверить, что если в качестве исходной взять задачу линейного программирования (2.2), то двойственной к ней будет задача (2.1).
Сравнивая пары двойственных задач (2.1) и (2.2), приходим к следующему правилу построения двойственной задачи:
а) она не имеет ограничений на знак, если 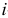 -е основное ограничение прямой задачи имело вид равенства;
-е основное ограничение прямой задачи имело вид равенства;
б) 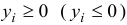 , если
, если 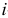 -е основное ограничение прямой задачи имело вид неравенства
-е основное ограничение прямой задачи имело вид неравенства 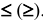 .
.
Каждой 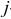 -й переменной
-й переменной 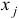 прямой задачи соответствует
прямой задачи соответствует 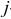 -е основное ограничение двойственной задачи. При этом вид
-е основное ограничение двойственной задачи. При этом вид 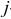 -го основного ограничения двойственной задачи определяется условиями:
-го основного ограничения двойственной задачи определяется условиями:
а) оно имеет вид равенства, если переменная 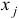 в прямой задаче не имеет ограничений на знак;
в прямой задаче не имеет ограничений на знак;
б) оно имеет вид неравенства 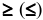 если в прямой задаче переменная
если в прямой задаче переменная 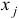 имела ограничение
имела ограничение 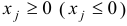 на знак.
на знак.
Рассмотрим общую задачу линейного программирования (2.1) и двойственную к ней задачу (2.2). Назовем эти задачи парой двойственных задач.
Теорема. Если одна из задач двойственной пары имеет решение, то другая задача также имеет решение. При этом для любых оптимальных планов
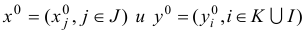
имеет место равенство
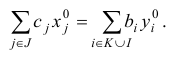
Следствие 1. Для разрешимости одной из задач двойственной пары необходимо и достаточно, чтобы каждая из задач этой пары имела хотя бы один план.
Следствие 2. Для того чтобы одна из задач двойственной пары имела планы, а множество планов другой задачи было пусто, необходимо и достаточно, чтобы целевая функция первой задачи была не ограничена на множестве ее планов.
Следствие 3. Для любых планов
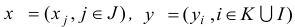
задач двойственной пары справедливо неравенство
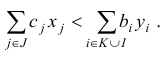
Следствие 4. Для оптимальности планов
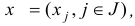
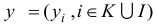
задач двойственной пары необходимо и достаточно выполнение равенства
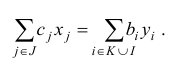
Задача №5
Записать задачу, двойственную к данной
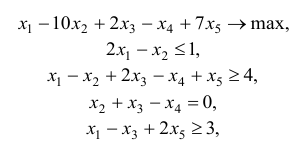
Решение:
Чтобы записать задачу, двойственную к данной, приведем систему к виду (2.1)
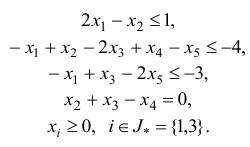
Теперь воспользуемся определением (2.2) и запишем задачу, двойственную к данной
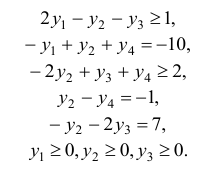
Базисный двойственный базисный план
Далее для определенности будем рассматривать пару двойственных задач (2.5), (2.6), в которой прямая задача имеет каноническую форму записи (2.5) с матрицей
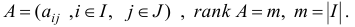
Вектор 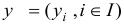 назовем двойственным планом, если
назовем двойственным планом, если 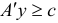 .
.
Двойственный план 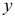 называется базисным двойственным планом, если существует такое множество
называется базисным двойственным планом, если существует такое множество 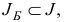 что
что
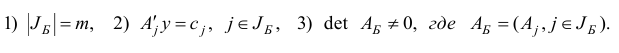
Как и раньше, множество 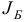 будем называть базисом или множеством базисных индексов, матрицу
будем называть базисом или множеством базисных индексов, матрицу 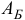 — базисной матрицей.
— базисной матрицей.
Отметим, что двойственный базисный план однозначно восстанавливается по заданному базису:
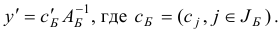
Базисный двойственный план у считается невырожденным, если
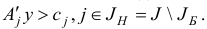
Пусть 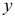 — базисный двойственный план с базисом
— базисный двойственный план с базисом 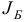 .
. 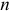 -вектор
-вектор 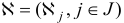 с компонентами, построенными по правилу
с компонентами, построенными по правилу
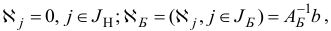
назовем псевдопланом задачи (2.5), соответствующим базису 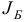 .
.
Утверждение 1. Если среди базисных компонент псевдоплана  нет отрицательных, т. е.
нет отрицательных, т. е.
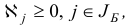
то псевдоплан 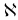 — оптимальный план
— оптимальный план
задачи (2.5). При этом базисный двойственный план 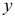 , определяющий псевдоплан
, определяющий псевдоплан 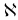 , является решением задачи (2.6).
, является решением задачи (2.6).
Утверждение 2. Пусть среди базисных компонент 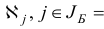
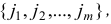 псевдоплана
псевдоплана 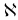 имеется отрицательная компонента
имеется отрицательная компонента 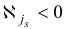 и выполняются неравенства
и выполняются неравенства
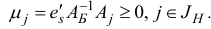
Тогда целевая функция двойственной задачи не ограничена снизу на множестве своих планов, а ограничения прямой задачи несовместны.
Утверждение 3. Пусть базисный двойственный план  (с базисом
(с базисом 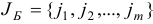 ) является невырожденным. Если среди базисных компонент псевдоплана
) является невырожденным. Если среди базисных компонент псевдоплана  , построенного по
, построенного по 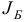 , есть отрицательная компонента
, есть отрицательная компонента 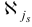 , для которой
, для которой 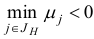 , то можно перейти к новому базисному двойственному плану
, то можно перейти к новому базисному двойственному плану 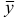 с лучшим значением двойственной целевой функции:
с лучшим значением двойственной целевой функции: 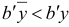 .
.
Новый базисный двойственный план 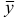 и соответствующий ему базис
и соответствующий ему базис 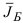 строятся по плану
строятся по плану
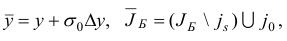
где
произвольный индекс из множества
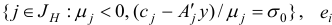
единичный 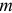 -вектор с единицей на
-вектор с единицей на 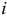 -м месте.
-м месте.
Возможно эта страница вам будет полезна:
Двойственный симплекс-метод
Метод решения канонической задачи линейного программирования, рассмотренный в разд. 1, впредь будем называть прямым симплекс-методом.
Опишем двойственный симплекс-метод, который является специальным алгоритмом построения оптимального плана задачи линейного программирования (2.5) посредством преобразования планов двойственной задачи (2.6).
Для решения задачи (2.5) двойственным симплекс-методом, кроме исходных данных  на каждой итерации необходимо знать следующие параметры:
на каждой итерации необходимо знать следующие параметры:
1) текущий базисный двойственный план 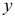 ;
;
2) соответствующий двойственному плану 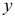 базис
базис
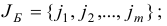
3) 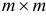 -матрицу
-матрицу 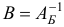 обратную к базисной матрице
обратную к базисной матрице
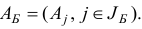
Опишем общую итерацию двойственного симплекс-метода по шагам. Шаг 1. Найдем базисные компоненты псевдоплана 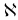 , соответствующего базису
, соответствующего базису
Шаг 2. Если выполняются неравенства
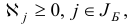
то STOP: вектор
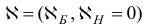
является оптимальным планом задачи (2.5), а вектор 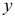 — оптимальным планом задачи (2.6). В противном случае перейдем к шагу 3.
— оптимальным планом задачи (2.6). В противном случае перейдем к шагу 3.
Шаг 3. Среди базисных индексов
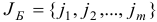
выберем индекс 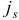 , для которого
, для которого 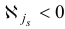 . Подставим
. Подставим 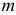 -вектор
-вектор 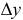 и числа
и числа 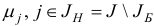 , по правилам
, по правилам
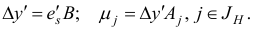
Если 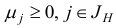 , то STOP: ограничения исходной задачи (2.5) несовместны, а целевая функция двойственной задачи (2.6) не ограничена снизу на множестве ее планов. В противном случае перейдем к шагу 4. Шаг 4. Найдем минимум
, то STOP: ограничения исходной задачи (2.5) несовместны, а целевая функция двойственной задачи (2.6) не ограничена снизу на множестве ее планов. В противном случае перейдем к шагу 4. Шаг 4. Найдем минимум
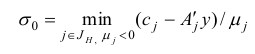
и выберем в качестве индекса 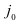 любой элемент из множества
любой элемент из множества
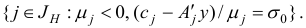
Шаг 5. Построим новый базисный двойственный план 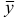 и соответствующий ему базис
и соответствующий ему базис 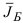 по правилам
по правилам
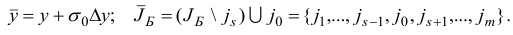
Шаг 6. Вычислим матрицу 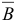 , обратную к новой базисной матрице
, обратную к новой базисной матрице
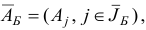
по правилам, описанным на шаге 6 итерации прямого симплекс-метода (см. подразд. 1.4).
Переходим к следующей итерации, исходя из новых значений для базисного двойственного плана 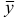 , базиса
, базиса 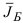 и матрицы
и матрицы 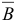 .
.
Замечания. 1. На шаге 3 выбор индекса 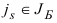 и на шаге 4 выбор индекса
и на шаге 4 выбор индекса 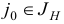 могут оказаться неоднозначным. Как и в прямом симплекс-методе, это может привести к зацикливанию алгоритма. Для предотвращения зацикливания рекомендуется использовать дополнительные правила, аналогичные приведенным в подразд. 1.6. Например, правило Блэнда для двойственного симплекс-метода сводится к следующему: на шаге 3 индекс
могут оказаться неоднозначным. Как и в прямом симплекс-методе, это может привести к зацикливанию алгоритма. Для предотвращения зацикливания рекомендуется использовать дополнительные правила, аналогичные приведенным в подразд. 1.6. Например, правило Блэнда для двойственного симплекс-метода сводится к следующему: на шаге 3 индекс 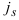 однозначно определяется условием
однозначно определяется условием
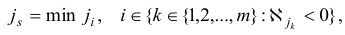
а на шаге 4 индекс 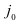 однозначно определяется соотношением
однозначно определяется соотношением
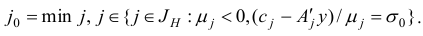
Легко проверить, что если базисный двойственный план 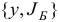 является невырожденным, то для нового базисного плана
является невырожденным, то для нового базисного плана 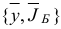 справедливо неравенство
справедливо неравенство 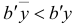 . (В общем случае верно неравенство
. (В общем случае верно неравенство 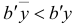 ).
).
Проблема построения начального базисного двойственного плана 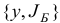 является нетривиальной. Для ее решения по аналогии с разделом 1 можно разработать двухфазный двойственный симплекс-метод.
является нетривиальной. Для ее решения по аналогии с разделом 1 можно разработать двухфазный двойственный симплекс-метод.
Задача №6
Решить задачу ЛП двойственным симплекс-методом
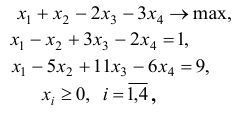
приняв в качестве начального базисного двойственного плана вектор
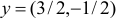
и базисное множество 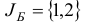 .
.
Решение:
Базису 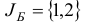 соответствует базисная матрица
соответствует базисная матрица
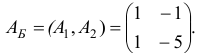
Построим матрицу
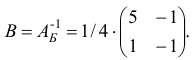
Используя
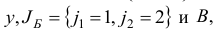
и осуществим первую итерацию.
Шаг 1. Найдем базисные компоненты псевдоплана 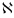 , соответствующего базису
, соответствующего базису 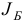 :
:
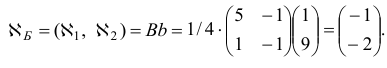
Шаг 2. Условие
не выполняется, следовательно, переходим к шагу 3.
Шаг 3. В качестве индекса
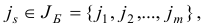
для которого 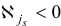 , выберем индекс
, выберем индекс 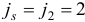 . Подсчитаем вектор
. Подсчитаем вектор 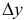 и числа
и числа 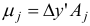 ,
, 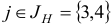 :
:
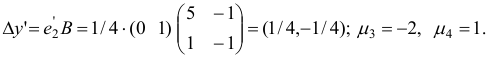
Поскольку среди чисел 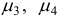 есть отрицательные, то переходим к шагу 4.
есть отрицательные, то переходим к шагу 4.
Шаг 4. Найдем минимум
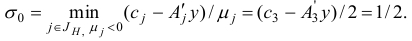
В данном примере в качестве индекса 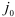 можно выбрать только индекс
можно выбрать только индекс 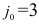 .
.
Шаг 5. Построим новый базисный двойственный план 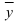 и соответствующий ему базис
и соответствующий ему базис 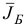 по правилам
по правилам
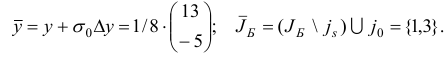
Шаг 6. По правилам, описанным на шаге 6 прямого симплекс-метода, вычислим матрицу
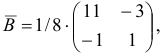
обратную к новой базисной матрице
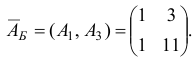
Переходим ко второй итерации, исходя из новых значений для базисного двойственного плана 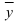 , базиса
, базиса
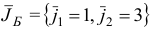
и матрицы 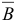 .
.
Осуществим вторую итерацию.
Шаг 1. Найдем базисные компоненты псевдоплана 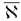 , соответствующего базису
, соответствующего базису 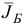 :
:
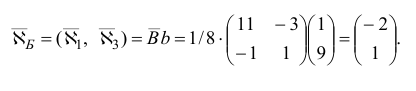
Шаг 2. Поскольку среди компонент
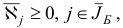
есть отрицательные, то переходим к шагу 3.
Шаг 3. На данной итерации в качестве индекса 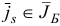 , для которого
, для которого 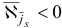 , можно выбрать только индекс
, можно выбрать только индекс 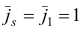 . Найдем
. Найдем
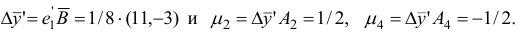
Поскольку среди чисел 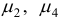 есть отрицательные, то переходим к шагу 4.
есть отрицательные, то переходим к шагу 4.
Шаг 4. Найдем
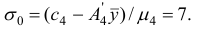
В качестве индекса 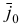 можно выбрать только индекс
можно выбрать только индекс 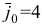 .
.
Шаг 5. Построим новый базисный двойственный план 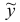 и соответствующий ему базис
и соответствующий ему базис 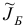 :
:
Шаг 6. Вычислим матрицу
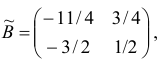
обратную к новой базисной
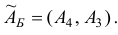
Переходим к третьей итерации, исходя из новых значений для базисного двойственного плана 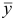 , базиса
, базиса 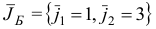 и матрицы
и матрицы  . Опишем третью итерацию.
. Опишем третью итерацию.
Шаг 1. Найдем базисные компоненты псевдоплана  , соответствующего базису
, соответствующего базису 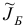 :
:
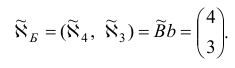
Шаг 2. Все компоненты 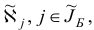 положительны, следовательно, вектор
положительны, следовательно, вектор
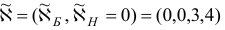
является оптимальным планом рассматриваемой задачи, а вектор  — ее оптимальным двойственным планом. Задача решена.
— ее оптимальным двойственным планом. Задача решена.
Возможно эти страницы вам будут полезны:
- Графическое решение задач линейного программирования
- Графический метод решения задач линейного программирования
- Заказать работу по линейному программированию
- Помощь по линейному программированию
- Контрольная работа по линейному программированию
- Линейное программирование в Excel
- Курсовая работа по линейному программированию

Этот метод является вариантом метода северо-западного угла, учитывающим специфику матрицы транспортных затрат С=. В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план, сокращая общее количество итераций по его дальнейшей оптимизации.
Формальное описание алгоритма. Элементы матрицы нумеруют, начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х0.
Пусть элементом с минимальным порядковым номером оказался . Возможные три случая: а) если , то оставшуюся часть -й строки заполняем нулями; б) если , то оставшуюся часть -го столбца заполняем нулями; в) если , то оставшуюся часть -й строки и -го столбца заполняем нулями.
Дале этот процесс повторяют с незаполненной частью матрицы Х1.
Пример 1. Найти начальный базисный план методом минимального элемента для Табл. 3. следующей задачи.
Таблица. 3.
|
Ai Bj |
1 |
2 |
3 |
4 |
Bj / ai |
|
1 |
7(10) |
8(11) |
5(7) |
3(5) |
11 |
|
2 |
2(3) |
4(4) |
5(8) |
9(12) |
11 |
|
3 |
6(9) |
3(4) |
1(1) |
2(2) |
8 |
|
Ai / bj |
5 |
9 |
9 |
7 |
bj ai |
Цифры в скобках указывают порядок заполнения элементов в матрице Х0 (табл. 3.4).
Соответствующее значение целевой функции равно
3*8 + 1*5 + 3*7 + 5*2 + 6*4 + 8*1 = 92
Таблица 4
|
Х0 |
|||||||

0 |
3 |
1 |
7 |
11 |
4 |
3 |
0 |
|
5 |
6 |
0 |
0 |
11 |
6 |
0 |
|
|
0 |
0 |
8 |
0 |
8 |
0 |
||
|
5 |
9 |
9 |
7 |
||||
|
0 |
3 |
1 |
0 |
||||
|
0 |
0 |
||||||
Решение транспортной задачи при вырожденном опорном плане
Опорный план называется вырожденным, если число его ненулевых перевозок k меньше ранга матрицы ограничений. В процессе построения начального плана или при его улучшении очередной план может оказаться вырожденным.
Рассмотрим два случая.
1. Вырожденный план является начальным Х0. Тогда выбирают некоторые нулевые элементы матрицы Х0 в качестве базисных так, чтобы при этом не нарушалось условие базисного плана. Число этих элементов равняется . Далее данные элементы заменяют на (где – произвольное, бесконечно малое число) и рассматривают их как обычные базисные элементы плана. Задачу решают как невырожденную, а в последнем оптимальном плане Хk вместо пишут нули.
2. Вырожденный план получается при построении плана Хk+1 на базе Хk, если цепочка в плане Хk содержит не менее двух минимальных нечетных элементов. В таком случае в матрице Хk+1 полагают равным нулю только один из этих элементов, а остальные заменяют на , и далее решают задачу как невырожденную. Если на k-м шаге , то при переходе от Хk к Хk+1 значение целевой функции не изменяется, а в базис вводится элемент , для которого перевозка станет равной .
Пример 2. Решим Т-задачу со следующими условиями (см. Табл.6)
Проверим условие баланса

Предварительный этап. Методом минимального элемента строим начальный базисный план Х0 (Табл. 5)
Таблица 5
|
C = |
ai bj |
4 |
6 |
8 |
6 |
|
6 |
2(5) |
2(4) |
3(6) |
4(11) |
|
|
8 |
6(12) |
4(10) |
3(9) |
1(3) |
|
|
10 |
1(1) |
2(6) |
2(7) |
1(2) |

Так как m + n – 1 = 6; k = 4, то план х0 – вырожденный; l = m+ n -1 – k = 2.
Два нулевых элемента Х0 делаем базисными так, чтобы не нарушить условие опорности. Выберем в качестве базисных элементов , и положим их равными ?.
Схема перевозок для плана Х0 показана на рис. 6.

Рис. 6.
Для вычисления предварительных потенциалов выберем начальный пункт А1 и допустим, что . Потенциалы всех остальных пунктов вычисляем по формулам
,
Для проверки оптимальности плана х0 строим матрицу С1, элементы которой вычисляем по соотношению

Так как в матрице С1 элемент С23 = – 3 < 0, то план Х0 – неоптимальный.

Первая итерация. Второй этап.
|
?* |
6* |
0 |
0 |
? |
6 |
0 |
0 |
||
|
X0 = |
0* |
?* |
8 |
0+ |
X1 = |
0 |
0 |
6 |
? |
|
4 |
0 |
0 |
6* |
?1 = ? |
4 |
0 |
0 |
6 |
|
В результате построения Х1 в базис вводим. План Х1 является вырожденным (в цепочке есть два минимальных элемента). Поэтому один из этих элементов, например , в плане Х1 заменяем на ?.
Вторая итерация. Первый этап
|
0 |
2 |
2 |
0 |
0 |
-1 |
2 |
||||
|
С1 = |
2 |
0 |
-3 |
+3 |
С2 = |
5 |
3 |
0 |
0 |
|
|
0 |
1 |
2 |
0 |
0 |
1 |
-1 |
0 |
|||
|
-3 |
Второй этап.
|
? |
6 |
0 |
0 |
? |
6 |
0 |
0 |
||
|
X1 = |
0 |
0 |
8* |
?* |
X2 = |
0 |
0 |
2 |
6 |
|
4 |
0 |
0+ |
6* |
?3 =min {8, 6}= 6 |
4 |
0 |
6 |
0 |
|
Третья итерация. Первый этап.
|
-1 |
2 |
+1 |
0 |
0 |
0 |
3 |
|||
|
С2 = |
5 |
3 |
С2 = |
4 |
2 |
0 |
0 |
||
|
1 |
-1 |
0 |
+1 |
0 |
1 |
0 |
1 |
||
|
-1 |
-1 |
Так как в матрице С3 нет отрицательных элементов, план Х2 – оптимальный.
Подробный разбор симплекс-метода +31
Из песочницы, Математика
Рекомендация: подборка платных и бесплатных курсов Java – https://katalog-kursov.ru/
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение:
Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
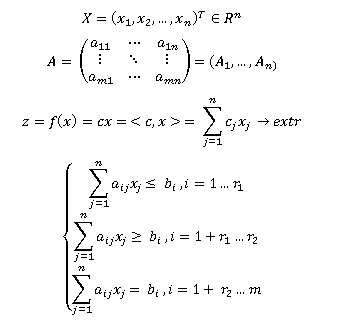
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
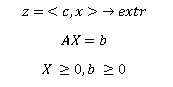
Замечание:
Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными $inline$b_i$inline$ умножаем на (-1).
- Если неравенство вида (?), то к левой части добавляем $inline$s_i$inline$ – добавочную переменную, и получаем равенство.
- Если неравенство вида (?), то из левой части вычитаем $inline$s_i$inline$, и получаем равенство.
- Делаем замену переменных:
- Если $inline$x_i ? 0$inline$, то $inline$x_i’= -x_i ? 0$inline$
- Если $inline$x_i$inline$ — любой, то $inline$x_i= x_i’ – x_i”$inline$, где $inline$x_i’, x_i”? 0$inline$
Замечание:
Будем нумеровать
$inline$s_i$inline$
по номеру неравенства, в которое мы его добавили.
Замечание: $inline$s_i$inline$
?0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение:
Точка
$inline$Х ? D$inline$
называется угловой точкой, если представление
$inline$ Х= ?Х^1+ (1-?) Х^2,где Х^1,Х^2 ?D;0< ?<1 $inline$
возможно только при
$inline$Х^1=Х^2 $inline$
.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит
$inline$Х$inline$
(т.е.
$inline$Х$inline$
– не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение:
Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
Необходимые условия для применения симплекс-метода:
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение:
Явно выделенным базисом будем называть вектора вида:
$inline$(..0100..)^T, (..010..)^T,(..0010..)^T…$inline$
, т.е. только одна координата вектора ненулевая и равна 1.
Замечание:
Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
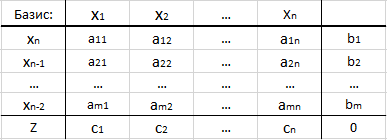
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание:
Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание:
Если ограничения в исходной задаче представлены неравенствами вида ?, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание:
Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание:
Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение:
Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение:
Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание:
Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение:
Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание:
Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.