Глава 8. зацепления зубчатые
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:
где z – число зубьев;
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
где t – шаг зацепления.
где h a – высота головки зуба, h a = m ; h f – высота ножки зуба, h f = 1,25 m .
Диаметр окружности выступов зубьев :
Диаметр окружности впадин :
Служит для передачи вращения при параллельных осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2 .
Служит для преобразования вращательного движения в возвратно-поступательное.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращательного движения между валами со скрещивающимися осями.
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при пересекающихся осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Как найти модуль зубчатого колеса?
История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес [4] .
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Чему равен модуль зубчатого колеса?
Модуль зубчатого колеса Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Для чего нужен модуль зубчатого колеса?
Что же такое модуль шестерни? это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Как определить параметры шестерни?
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр. Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как найти модуль зуба?
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2. Измеряем диаметр: Диаметр окружности выступов (De) равен 28,6 мм.
Какие бывают модули зубчатых колес?
Модуль — это линейная величина, в π раз меньшая шага зубьев p (окружного pt, осевого рx, нормального рn и других шагов) эвольвентного зубчатого колеса m = р/π. Соответственно различают модули: окружной mt, осевой mx, нормальный mn и др.
Цилиндрические зубчатые колёса
Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
Параметры эвольвентного зубчатого колеса:
- m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
-
- z — число зубьев колеса
- p — шаг зубьев (отмечен сиреневым цветом)
- d — диаметр делительной окружности (отмечена жёлтым цветом)
- da — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
- db — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
- df — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
- haP+hfP — высота зуба тёмного колеса, x+haP+hfP — высота зуба светлого колеса
Для целей стандартизации, удобства изготовления и замены зубчатых колёс в машиностроении приняты определённые значения модуля зубчатого колеса m, представляющие собой ряд из чисел на выбор: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 25; 32; 40; 50; 60; 80; 100.
Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).
Высота головки зуба — haP и высота ножки зуба — hfP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,25 m, то есть:
Отсюда получаем, что высота зуба h (на рисунке не обозначена):
Вообще из рисунка ясно, что диаметр окружности вершин da больше диаметра окружности впадин df на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:
Продольная линия зуба
Цилиндрические зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:
Прямозубые колёса
Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
Косозубые колёса
Зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. Также увеличена площадь контакта, что при тех же размерах с прямозубыми позволяет передавать больший крутящий момент. При работе косозубой пары зацепления возникает механическая осевая сила, направленная вдоль оси вращения каждого колеса и стремящаяся раздвинуть оба колеса в противоположные стороны от плоскости контакта, что обязательно требует применения упорных подшипников. Увеличенная площадь трения зубьев косозубого зацепления вызывает дополнительные потери мощности на нагрев. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.
Шевронные колеса
Изобретение шевронного профиля зуба часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка [6] . Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).
Колёса с круговыми зубьями
Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные колёса
Секторное колесо представляет собой часть обычного цилиндрического колеса с зубьями любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.
Зубчатые колёса с внешним и внутренним зацеплением
| Пара зубчатых колёс с ВНЕШНИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит противонаправлено. |
Пара зубчатых колёс с ВНУТРЕННИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит сонаправленно. |
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Реечная передача (кремальера)
Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Также реечная передача применяется в зубчатой железной дороге.
 Цевочная передача
Цевочная передача  Коронная шестерня
Коронная шестерня
Коронные колёса
Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.
Конические зубчатые колёса
Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Зубчатые передачи

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач

Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Почему шестерни часто выполняют заодно с валом?
Несмотря на это, в редукторах шестерню часто выполняют заодно с валом и даже при толщине, значительно превышающей указанные нормы. Это объясняется большей жесткостью и прочностью, а также технологичностью вала-шестерни, что в конечном итоге оправдывает ее стоимость.
Модуль зубьев зубчатого колеса: расчет, стандартные, определение

 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки

 Диаметр делительной окружностиd является одним из основных параметров, по которому производят расчет зубчатого колеса:
Диаметр делительной окружностиd является одним из основных параметров, по которому производят расчет зубчатого колеса:- d = m × z,
- где z – число зубьев;
- m – модуль.
- Модуль зацепленияm – это часть диаметра делительной окружности, приходящейся на один зуб:
- m = t / π,
- где t – шаг зацепления.
- Высота зуба:
- h = ha + hf,
- где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
- Диаметр окружности выступов зубьев:
- da = d + 2ha = m(z + 2).
- Диаметр окружности впадин:
- df = d – 2hf = m(z – 2,5).

- Служит для передачи вращения при параллельных осях валов.


- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.

- Служит для преобразования вращательного движения в возвратно-поступательное.


- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращательного движения между валами со скрещивающимися осями.
- ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
- Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
- Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращения при пересекающихся осях валов.
- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Зубчатые передачи
 Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев
 Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
Коррегирование зубчатого зацепления
 Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач

Степени точности зубчатых передач (DIN 3961…..3964)
Зубчатые передачи стартера
Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.
Модули зубчатых передач стартеров
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением.
Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х.
(Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).
Стандарты зубчатых передач США
- Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
- Р = z/d = z/(z • m/25,4) =25,4/m
- Для перевода стандарта США в европейский стандарт служит зависимость:
- m = 25,4 мм / P
- Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
- CP = (25,4 мм / P) π.
- Табл. Стандарты зубчатых передач
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
- Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
- Обозначение (пример): Р 5 /7
- Р = 7 для расчета головки зуба,
- Р = 5 для расчета других параметров.
Система обозначений и преобразований
- Диаметр окружности выступов: OD = da.
- Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
- Диаметр окружности впадин: RD = df
- Начальный диаметр:
- LD =(N+2x) / P (в дюймах)
- или
- LD= (N+2x)·m (в мм).
- LD ≈ dw,
- где dw — диаметральный модуль.
Расчет наибольшего допустимого давления зубчатых передач
Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.
Величины и единицы измерения для расчета наибольшего допустимого давления
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1.
В случае зубчатого зацепления с z1 Читайте также: Какие диаметры металлических труб бывают
При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.
Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч
Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.
- При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
- В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.
Коэффициент срока службы ф
- Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1).
Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.
Расчет зубчатого зацепления на изгиб и разрушение зуба
Коэффициент профиля зуба YFa
Скоростной фактор fv
[1] Оценка действительна для А = 6 (средний уровень точности).
В следующей статье я расскажу об электрических свойствах материалов.
Примерный расчет элементов зубчатого колеса
Длина всякой окружности равна ΠD; следовательно, длина начальной окружности зубчатого колеса будет выражена формулой Πd,.
Шагом t зацепления называется длина дуги начальной окружности между обращенными в одну сторону (левыми или правыми) профилями двух смежных зубьев см 517, б.
Если размер этой дуги взять столько раз, сколько имеется зубьев у колеса, т. е. z раз, то также получим длину начальной окружности; следовательно,
Отношение шага t зацепления к числу Π называется модулем зацепления, который обозначают буквой m, т. е.
Модуль выражается в миллиметрах. Подставив это обозначение в формулу для d, получим.
Следовательно, модуль можно назвать длиной, приходящейся по диаметру начальной окружности на один зуб колеса. Диаметр выступов равен диаметру начальной окружности плюс две высоты головки зуба (фиг. 517, б) т.е.
Высоту h’ головки зуба принимают равной модулю, т. е. h’ = m. Выразим через модуль правую часть формулы:
- De = mz + 2m = m (z + 2) следовательно
- m = De : (z +2)
Из фиг. 517,б видно также, что диаметр окружности впадин равен диаметру начальной окружности минус две высоты ножки зуба, т. е.
- Di = d — 2h»
- Высоту h» ножки зуба для цилиндрических зубчатых колес принимают равной 1,25 модуля: h’ = 1,25m. Выразив через модуль правую часть формулы для Di получим
- Di = mz — 2 × 1,25m = mz — 2,5m или
- Di = m (z — 2,5m)
- Вся высота зуба h = h’ + h» т.е
- h = 1m + 1,25m = 2,25m
- Следовательно, высота головки зуба относится к высоте ножки зуба как 1 : 1,25 или как 4 : 5.
Толщину зуба s для необработанных литых зубьев принимают приблизительно равной 1,53m, а для обработанных на станках зубьев (например, фрезерованных) — равной приблизительно половине шага t зацепления, т. е. 1,57m.
Зная, что шаг t зацепления равен толщине s зуба плюс ширина sв впадины (t = s + sв) (Величину шага t определяем по формуле t/Π = m или t = Πm ), заключаем, что ширина впадины для колес с литыми необработанными зубьями.
- sв = 3,14m — 1,53m = 1,61m A для колес с обработанными зубьями.
- sв = 3,14m — 1,57m = 1,57m
Конструктивное оформление остальной части колеса зависит от усилий, которые испытывает колесо во время работы, от формы деталей, соприкасающихся с данным колесом, и др. Подробные расчеты размеров всех элементов зубчатого колеса даются в курсе «Детали машин». Для выполнения графического изображения зубчатых колес можно принять следующие приблизительные соотношения между их элементами:
Толщина обода e = t/2
Диаметр отверстия для вала Dв ≈ 1/в De Диаметр ступицы Dcm = 2Dв Длина зуба (т. е. толщина зубчатого венца колеса) b = (2 ÷ 3) t Толщина диска К = 1/3b Длина ступицы L = 1,5Dв : 2,5Dв
Размеры t1 и b шпоночного паза берутся из таблицы №26. После определения числовых величин модуля зацепления и диаметра отверстия для вала необходимо полученные размеры согласовать с ГОСТ 9563-60 (см таблицу №42) на модули и на нормальные линейные размеры по ГОСТ 6636-60 (таблица №43).
Модули (согласно ГОСТ 9563-60) Таблица №42.

Нормальные линейные размеры. Таблица №43. (Выдержка из ГОСТ 6636-60)

Если они отличаются от табличных значений, надо взять ближайшие большие табличные значения и пересчитать все величины, зависящие от вновь выбранного модуля или диаметра отверстия.
Вычерчивание контура зуба
Определение основных геометрических параметров зубчатых колес
- Лабораторная работа 10
- Цель работы — ознакомиться с практическими методами определения основных параметров зубчатых колес.
- Краткие теоретические сведения
Основными параметрами зубчатого колеса с эвольвентным профилем зубьев являются: модуль т, число зубьев z, угол зацепления а, величина смещения инструментальной рейки при нарезании зубчатого колеса.
Число зубьев, диаметры окружностей вершин и впадин зубьев можно измерить непосредственно, остальные параметры вычисляют в результате расчета.
Подсчитав число зубьев z, нетрудно определить модуль зацепления, используя свойство эвольвенты: нормаль в любой точке эвольвенты является касательной к основной окружности. Поэтому при охвате нескольких зубьев колеса губками штангенциркуля (размер АВ, рис. 2.5.1) линия АВ будет касательной к основной окружности и нормальной профилям зубьев.
Если отрезок АВ катить по основной окружности, то по свойству эвольвенты точка А придет в точку А0, точка В — в точку В0 и точка D — в точку D0. Тогда
Таким образом, измерив вначале длину общей нормали Wzn (мм), соответствующей числу зубьев z„, а затем размер Wzn+ь охватив губками штангенциркуля на один зуб больше, рь
шаг по основной окружности — определим как разность двух измерений:
Это выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профиля зуба.
Рис. 2.5.1. Схема замера
Чтобы не возникло кромочного контакта, необходимо правильно выбрать zn (табл. 2.5.1).
| Число зубьев колеса | 12-18 | 19-27 | 28-36 | 37-45 | 46-54 | 55-63 | 64-72 | 73-81 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Модуль зацепления определим по формуле
Полученное значение модуля сопоставим со стандартным значением (табл. 2.5.2) и примем его ближайшее значение.
| т, мм | 2,00 | 2,25 | 2,50 | 2,75 | 3,00 | 3,25 |
| Рь, мм | 5,904 | 6,642 | 7,380 | 8,818 | 8,856 | 9,954 |
| т, мм | 3,50 | 3,75 | 4,00 | 4,50 | 5,00 | 5,50 |
| Рь, мм | 10,33 | 11,07 | 11,808 | 13,28 | 14,76 | 16,84 |
По уточненному значению модуля рассчитаем шаги зацепления по делительной и основной окружностям.
Для определения величины смещения при нарезании зубчатого колеса инструментальной рейкой необходимо измерить толщину зуба по основной окружности, сопоставить результат с расчетным значением той же толщины зуба для колеса, нарезанного без смещения, и найти коэффициент смещения инструментальной рейки:
где sb = Wzn+l — znpb — толщина зуба по основной окружности данного колеса; sb = mcosa(^ + zinva) — толщина зуба по основной окружности зубчатого колеса, нарезанного при х = 0; a = 20°; inv 20° = 0,0149.
При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов da и впадин df.
Если число зубьев шестерни z четное, то оба диаметра могут быть непосредственно измерены штангенциркулем (рис. 2.5.2, а) При нечетном числе зубьев измерение проводится по схеме, изображенной на рис. 2.5.2, б.
Рис. 2.5.2. Определение диаметров при четном (а) и нечетном (б) числе зубьев
Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни ((/0Тв) и размер//’. Тогда диаметр окружности выступов
Аналогично измеряется диаметр окружности впадин:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измерительный инструмент — штангенциркуль.
Порядок выполнения работы
- 1. Подсчитать число зубьев колеса z.
- 2. По табл. 2.5.1 определить число зубьев z„, которые следует охватить штангенциркулем.
- 3. Измерить штангенциркулем Wzn и Wzn+ (рис. 2.5.1). Для большей точности обмерять нужно трижды на разных участках зубчатого венца. Окончательные значения Wzn и Wzn+ есть среднеарифметическое трех обмеров. По формуле (2.5.1) определить величину шага рь по основной окружности.
- 4. По формуле (2.5.2) найти модуль зацепления в миллиметрах, округлив его величину до ближайшего стандартного значения согласно табл. 2.5.2. В формуле 2.5.2 угол исходного контура а = 20°.
- 5. Учитывая, что есть колеса с углом а = 15°, выполнить проверочный расчет модуля по выражению
измерив диаметр da окружности вершин.
6. Измерить d/диаметр окружности впадин.
Примечание: da и df при четном числе z измерить штангенциркулем (рис. 2.5.2, а), при нечетном числе — найти в соответствии с рис. 2.5.2, б по формулам:
- 7. Определить:
- а) шаг по делительной окружности
б) диаметр делительной окружности
в) диаметр основной окружности
г) делительную высоту головки зуба
д) делительную высоту ножки зуба
е) коэффициент высоты головки зуба
ж) толщину зуба по основной окружности
- 8. По формуле (2.5.3) рассчитать коэффициент смещения х исходного контура, с которым нарезалось данное колесо.
- 9. Определить толщину зуба по основной окружности:
Контрольные вопросы и задания
- 1. Что такое модуль зубчатого колеса?
- 2. Как определить шаг зубчатого колеса?
- 3. Дайте понятие основной и делительной окружностей.
- 4. Какова зависимость между числом зубьев и диаметром зубчатого колеса?
- 5. Что называется коэффициентом смещения исходного контура?
- 6. Как изменяются основные параметры зубчатого колеса при смещении исходного контура?
- 1. Число зубьев z = …
- 2. Определение шага и модуля зацепления:
| Номер измерения | Wz,,+ь мм | Wzn, мм |
| Среднее |
* число zn выбирается по табл. 2.5.1.
Шаг зацепления по основной окружности pb = WZfJ+1 — Wzn = … мм.
Модуль т = ——— = … мм.
Модуль, уточненный по табл. 2.5.2, т = … мм.
Шаг зацепления по делительной окружностир = пт = … мм.
Шаг по основной окружности (уточненный)рь=р cos а= … мм.
- 3. Диаметр делительной окружности d = mz= … мм.
- 4. Диаметр основной окружности db = d cos а= … мм.
- 5. Определение действительной толщины зуба по основной окружности sb = Wzn +1 -znpb = … мм.
- 6. Расчет толщины зуба по основной окружности нулевого колеса:
7. Определение коэффициента смещения:
9. Определение диаметров окружностей вершин da и впадин df колеса:
| Номер измерения | doiB | Н’ | da | Н» | df | Расчётные формулы при нечётном числе z |
| Среднее |
10. Учитывая, что есть колеса с углом зацепления а = 15°, в и. 2 выполнить проверочный расчет модуля по выражению (для нормального колеса)
11. Определение коэффициента высоты головки зуба колеса, зубья которого нарезаны без смещения:
Модуль зуба – Модуль шестерни. Формулы расчёта
Шаг зубьев ρ так же, как и длина окружности, включает в себя трансцендентное число π, а потому шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число ρ/π, которое называют модулем зубьев т и измеряют в миллиметрах:
Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб. Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колес и унификации зуборезного инструмента значения m регламентированы стандартом (табл. 8.1).
Высота головки и ножки зуба. Делительная окружность рассекает зуб по высоте на головку ha и ножку hf. Для создания радиального зазора с (см. рис. 8.19)
Для нормального (некорригированного) зацепления ha = m. Длина активной линии зацепления. При вращении зубчатых колес точка зацепления S (см. рис. 8.9) пары зубьев перемещается по линии зацепления NN.
Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S” пересечения линии зацепления с окружностью вершин шестерни. Отрезок S’S” линии зацепления называется длиной активной линии зацепления и обозначается ga.
Длину ga легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S” и замеряют ga.
Коэффициент торцового перекрытия. Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность передачи.
Как определить модуль шестерни с прямым и косым зубом
Часто мне задают вопрос: Как определить модуль косозубой шестерни. Один из самых простых вариантов — обкатать фрезой, то есть методом подбора, вставить в шестерню фрезу и посмотреть совпадает ли шаг! Этот вариант подходит для шестернь малого модуля, для более больших шестернь требуются формулы расчёта.
Давайте определим модуль косозубой шестерни. В качестве примера я возьму небольшую шестерню. Данный метод идентичен и для более больших шестернь и больших модулей.
- Есть вот такая шестерня:
- Допустим что фрезы обкатать у нас на данный момент нет и вообще хочется просто посчитать по формуле!
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
- Можно использовать и другой вариант — высота зуба делится на 2,25.
- Я обычно или обкатываю фрезой или считаю по формуле — модуль = De/Z+2.
- Таким образом можно определить модуль как косозубой шестерни, так и шестерни с прямым зубом.
- Поделится, добавить в закладки!
- zuborez.info
Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?
Модуль зубчатого колеса геометрический параметр зубчатых колёс.
Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/π.
Для косозубых цилиндрических колёс различают: окружной модуль ms = dд/z = ts/π, нормальный модуль mn = tn/π, осевой модуль ma = tа/π, где ts, tn и ta— соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к.
стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Модуль высокоэластический
- Модуль расстояния
Смотреть что такое “Модуль зубчатого колеса” в других словарях:
- МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
- модуль зубчатого колеса — отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально… … Энциклопедический словарь
- нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
- нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
- окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
- расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
- Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
- Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Модуль зуба что такое
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня».
За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки.
Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
- Для расчета этого параметра применяют следующие формулы:
- m=t/π,
- где t — шаг.
- Параметры зубчатых колес
- Модуль зубчатого колеса можно рассчитать и следующим образом:
- m=h/2,25,
- где h — высота зубца.
- И, наконец,
- m=De/(z+2),
- где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
- Расчет модуля зубчатого колеса
- Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
- π×D=t×z,
- проведя преобразование, получим:
- D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
- t/π=m,
- размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
- В=m×z;
- выполнив преобразование, находим:
- m=D / z.
- Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
- De=d+2× h’,
- где h’- высота головки.
- Высоту головки приравнивают к m:
- h’=m.
- Проведя математические преобразования с подстановкой, получим:
- De=m×z+2m = m(z+2),
- откуда вытекает:
- m=De/(z+2).
- Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
- Di=D-2h“,
- где h“- высота ножки зубца.
- Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
- h’ = 1,25m.
- Устройство зубчатого колеса
- Выполнив подстановку в правой части равенства, имеем:
- Di = m×z-2×1,25m = m×z-2,5m;
- что соответствует формуле:
- Di = m(z-2,5m).
- Полная высота:
- h = h’+h“,
- и если выполнить подстановку, то получим:
- h = 1m+1,25m=2,25m.
- Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
- Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
- Для более крупных потребуются измерения и вычисления.
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Расчёт модулей зубчатых колёс
Перейти к загрузке файла
Ориентировочное минимально допустимое значение модуля m, мм. определим по формуле: где km — вспомогательный коэффициент; М1 — крутящий момент на шестерне, Н•м; z1 — число зубьев шестерни; kFв — коэффициент учитывающий неравномерность распределения нагрузки по ширине венца; шbd — отношение ширины венца к начальному диаметру шестерни; yF1 — коэффициент учитывающий форму зуба. Допустимое напряжение зубьев по изгибу уFP определяют по формуле у’FP — допускаемое напряжение зубьев по изгибу, МПа, соответствующее базовому числу циклов перемены напряжений; kFL — коэффициент долговечности. Ориентировочное минимально допустимое значение модуля: Рассчитанный по формуле модуль округляется до стандартного значения m=2. Характеристики зубчатых колёс сведём в таблицу:
| № зубчатого колеса | Число зубьев | Модуль, мм | Диаметр делительной окружности, мм | Ширина зубчатого венца, мм |
| 1 | 18 | 2 | 36 | 52 |
| 2 | 36 | 2 | 72 | 52 |
| 3 | 20 | 2 | 40 | 52 |
| 4 | 50 | 2 | 100 | 52 |
| 5 | 35 | 2 | 70 | 52 |
| 6 | 35 | 2 | 70 | 52 |
| 7 | 20 | 2 | 40 | 65 |
| 8 | 64 | 2 | 128 | 65 |
| 9 | 56 | 2 | 112 | 65 |
| 10 | 28 | 2 | 56 | 65 |
Расчёт на контактную выносливость рабочих поверхностей зубьев
Действующие в передаче контактные напряжения определяют по формуле
где ун — контактные напряжения, МПа; zН — коэффициент, зависящий от угла наклона зубьев, для x=0 применяем zН=1,76; zМ — коэффициент, учитывающий механические свойства материалов сопряжённых колёс, для стальных колёс zМ=275; zе — коэффициент, учитывающий суммарную длину контактных линий:
Коэффициент торцевого перекрытия:
где z1 и z2 — числа зубьев шестерни и колеса, знак «+» принимают для наружного зацепления.
Удельную расчётную окружную силу щHt определяют по формуле
где Pt — исходная окружная сила, Н:
где щHV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм.
Допускаемое контактное напряжение [ун] определяем по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kHL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kHL=1.
- Для стали 45 с улучшением =750 МПа.
- 532,25 МПа ? 750 МПа
- Условие контактной выносливости выполняется.
- Расчёт на изгибную выносливость зубьев
- Действующее в передаче напряжение изгиба сравнивается с допустимыми, с учётом коэффициента долговечности.
- Действующее напряжение изгиба:
Коэффициент yе — учитывает перекрытие зубьев. Для прямозубых колёс применяют yе=1. Коэффициент yв учитывает наклон зуба. Для прямозубых применяют yв=1.
Удельную расчётную окружную силу щFt определяем по формуле
где Pt — расчётная окружная сила в зубчатом зацеплении, Н; bщ — рабочая ширина венца, мм
Окружная сила Pt=2•103•M1/d1, где M1 — крутящий момент, Н•м; d1 — диаметр делительной окружности, мм.
Коэффициент kFa учитывает распределение нагрузки между зубьями. Для прямозубых передач приметаем kFa=1. Коэффициент kFв учитывает распределение нагрузки по ширине венца, можно принять kFв=1.1.
Коэффициент kFv учитывает динамическую нагрузку, возникающую в зацеплении.
где щFV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм; для прямозубых передач д=0.016; коэффициент g =47, учитывает влияние разности шагов зацепления.
Допускаемое изгибное напряжении [уF] определяется по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kFL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kFL=1.
Для стали Для стали 45 с улучшением у‘F=450 МПа, условие изгибной выносливости выполняется.
265.49 МПа ? 450 МПа
Условие на изгибную выносливость выполняется.
[spoiler title=”источники:”]
http://nzmetallspb.ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
[/spoiler]

Рисунок 3. Параметры эвольвентного зубчатого колеса.
К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.
Виды модулей: делительный, основной, начальный.
Для косозубых колес дополнительно различают: нормальный, торцевой и осевой.
Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.
Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.
m =p /π
Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения
d = Z · m
Делительная окружность делит зуб на головку и ножку.
Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.
Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.
Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.
Сумма высот головки ha и ножки hf соответствует высоте зубьев h:
h = ha + hf
Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.
da=d+2(h*a + x – Δy)m
Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.
df = d – 2(h*a – C* – x) · m
Согласно ГОСТ 13755-81 α = 20°, С* = 0,25.
Коэффициент уравнительного смещения Δу:
Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.
p = m·π
Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу
Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев
pb = p · cos α
Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба
S = 0,5 · ρ + 2 · х · m · tg α
Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев
е = p – S
Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.
Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.
Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра
1.1. Пример расчета прямозубого внешнего эвольвентного зубчатого зацепления.
1.2. Вычерчивание элементов зубчатого зацепления
![]()
 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки

 Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:- d = m × z,
- где z – число зубьев;
- m – модуль.
- Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
- m = t / π,
- где t – шаг зацепления.
- Высота зуба:
- h = ha + hf,
- где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
- Диаметр окружности выступов зубьев:
- da = d + 2ha = m(z + 2).
- Диаметр окружности впадин:
- df = d – 2hf = m(z – 2,5).

- Служит для передачи вращения при параллельных осях валов.


- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.

- Служит для преобразования вращательного движения в возвратно-поступательное.


- ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращательного движения между валами со скрещивающимися осями.
- ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
- Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
- Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращения при пересекающихся осях валов.
- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Источник: http://dgng.pstu.ru/sprav/8.htm
Зубчатые передачи
 Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев
 Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
Коррегирование зубчатого зацепления
 Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач

Степени точности зубчатых передач (DIN 3961…..3964)
Зубчатые передачи стартера
Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.
Модули зубчатых передач стартеров
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением.
Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х.
(Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).
Стандарты зубчатых передач США
- Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
- Р = z/d = z/(z • m/25,4) =25,4/m
- Для перевода стандарта США в европейский стандарт служит зависимость:
- m = 25,4 мм / P
- Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
- CP = (25,4 мм / P) π.
- Табл. Стандарты зубчатых передач
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
- Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
- Обозначение (пример): Р 5 /7
- Р = 7 для расчета головки зуба,
- Р = 5 для расчета других параметров.
Система обозначений и преобразований
- Диаметр окружности выступов: OD = da.
- Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
- Диаметр окружности впадин: RD = df
- Начальный диаметр:
- LD =(N+2x) / P (в дюймах)
- или
- LD= (N+2x)·m (в мм).
- LD ≈ dw,
- где dw — диаметральный модуль.
Расчет наибольшего допустимого давления зубчатых передач
Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.
Величины и единицы измерения для расчета наибольшего допустимого давления
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1.
В случае зубчатого зацепления с z1< 20 следует принимать Sw ⩾ 1,2…1,5 из-за более высоких контактных напряжений в точке однопарного зацепления.
Поскольку контактные давления равны по величине для обоих колес, значение kperm для зубчатого колеса 2 следует принимать такими же, как и для колеса 1 при частоте вращения n2, пользуясь помещаемой ниже таблицей.
Формулы для расчета наибольшего допустимого давления
Содержащиеся в таблице значения коэффициента &Perm применимы, когда оба колеса изготовлены из стали. Для пар зубчатых колес из чугуна и стали или бронзы и стали этот коэффициент следует увеличить в 1,5 раза. В случае зубчатых пар из чугуна по чугуну или бронзы по бронзе коэффициент kperm следует увеличить примерно в 1,8 раза.
Для зубчатого зацепления лишь с одним поверхностно упрочненным колесом, коэффициент kperm для незакаленного колеса необходимо увеличить на 20%. Все приведенные в таблице значения этого коэффициента рассчитаны на срок службы Lh = 5000 ч.
При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.
Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч
Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.
- При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
- В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.
Коэффициент срока службы ф
- Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
- Рекомендации по выбору расчетного срока службы зубчатых передач: при постоянной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной нагрузке — от 50 до 5000 ч.
Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1).
Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.
Расчет зубчатого зацепления на изгиб и разрушение зуба
Коэффициент профиля зуба YFa
Скоростной фактор fv
[1] Оценка действительна для А = 6 (средний уровень точности).
В следующей статье я расскажу об электрических свойствах материалов.
Источник: http://press.ocenin.ru/zubchatye-peredachi/
Примерный расчет элементов зубчатого колеса
Длина всякой окружности равна ΠD; следовательно, длина начальной окружности зубчатого колеса будет выражена формулой Πd,.
Шагом t зацепления называется длина дуги начальной окружности между обращенными в одну сторону (левыми или правыми) профилями двух смежных зубьев см 517, б.
Если размер этой дуги взять столько раз, сколько имеется зубьев у колеса, т. е. z раз, то также получим длину начальной окружности; следовательно,
- Πd = tz отсюда
- d = (t / Π) z
Отношение шага t зацепления к числу Π называется модулем зацепления, который обозначают буквой m, т. е.
t / Π = m
Модуль выражается в миллиметрах. Подставив это обозначение в формулу для d, получим.
- d = mz откуда
- m = d / z
Следовательно, модуль можно назвать длиной, приходящейся по диаметру начальной окружности на один зуб колеса. Диаметр выступов равен диаметру начальной окружности плюс две высоты головки зуба (фиг. 517, б) т.е.
De = d + 2h’
Высоту h’ головки зуба принимают равной модулю, т. е. h’ = m. Выразим через модуль правую часть формулы:
- De = mz + 2m = m (z + 2) следовательно
- m = De : (z +2)
Из фиг. 517,б видно также, что диаметр окружности впадин равен диаметру начальной окружности минус две высоты ножки зуба, т. е.
- Di = d — 2h»
- Высоту h» ножки зуба для цилиндрических зубчатых колес принимают равной 1,25 модуля: h’ = 1,25m. Выразив через модуль правую часть формулы для Di получим
- Di = mz — 2 × 1,25m = mz — 2,5m или
- Di = m (z — 2,5m)
- Вся высота зуба h = h’ + h» т.е
- h = 1m + 1,25m = 2,25m
- Следовательно, высота головки зуба относится к высоте ножки зуба как 1 : 1,25 или как 4 : 5.
Толщину зуба s для необработанных литых зубьев принимают приблизительно равной 1,53m, а для обработанных на станках зубьев (например, фрезерованных) — равной приблизительно половине шага t зацепления, т. е. 1,57m.
Зная, что шаг t зацепления равен толщине s зуба плюс ширина sв впадины (t = s + sв) (Величину шага t определяем по формуле t/Π = m или t = Πm ), заключаем, что ширина впадины для колес с литыми необработанными зубьями.
- sв = 3,14m — 1,53m = 1,61m A для колес с обработанными зубьями.
- sв = 3,14m — 1,57m = 1,57m
Конструктивное оформление остальной части колеса зависит от усилий, которые испытывает колесо во время работы, от формы деталей, соприкасающихся с данным колесом, и др. Подробные расчеты размеров всех элементов зубчатого колеса даются в курсе «Детали машин». Для выполнения графического изображения зубчатых колес можно принять следующие приблизительные соотношения между их элементами:
Толщина обода e = t/2
Диаметр отверстия для вала Dв ≈ 1/в De Диаметр ступицы Dcm = 2Dв Длина зуба (т. е. толщина зубчатого венца колеса) b = (2 ÷ 3) t Толщина диска К = 1/3b Длина ступицы L = 1,5Dв : 2,5Dв
Размеры t1 и b шпоночного паза берутся из таблицы №26. После определения числовых величин модуля зацепления и диаметра отверстия для вала необходимо полученные размеры согласовать с ГОСТ 9563-60 (см таблицу №42) на модули и на нормальные линейные размеры по ГОСТ 6636-60 (таблица №43).
Модули (согласно ГОСТ 9563-60) Таблица №42.

Нормальные линейные размеры. Таблица №43. (Выдержка из ГОСТ 6636-60)

Если они отличаются от табличных значений, надо взять ближайшие большие табличные значения и пересчитать все величины, зависящие от вновь выбранного модуля или диаметра отверстия.
Вычерчивание контура зуба
Источник: http://www.ViktoriaStar.ru/primerni-raschet-elementov-zubchatogo-kolesa.html
Определение основных геометрических параметров зубчатых колес
- Лабораторная работа 10
- Цель работы — ознакомиться с практическими методами определения основных параметров зубчатых колес.
- Краткие теоретические сведения
Основными параметрами зубчатого колеса с эвольвентным профилем зубьев являются: модуль т, число зубьев z, угол зацепления а, величина смещения инструментальной рейки при нарезании зубчатого колеса.
Число зубьев, диаметры окружностей вершин и впадин зубьев можно измерить непосредственно, остальные параметры вычисляют в результате расчета.
Подсчитав число зубьев z, нетрудно определить модуль зацепления, используя свойство эвольвенты: нормаль в любой точке эвольвенты является касательной к основной окружности. Поэтому при охвате нескольких зубьев колеса губками штангенциркуля (размер АВ, рис. 2.5.1) линия АВ будет касательной к основной окружности и нормальной профилям зубьев.
Если отрезок АВ катить по основной окружности, то по свойству эвольвенты точка А придет в точку А0, точка В — в точку В0 и точка D — в точку D0. Тогда
Таким образом, измерив вначале длину общей нормали Wzn (мм), соответствующей числу зубьев z„, а затем размер Wzn+ь охватив губками штангенциркуля на один зуб больше, рь ~ шаг по основной окружности — определим как разность двух измерений:
Это выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профиля зуба.
Рис. 2.5.1. Схема замера
Чтобы не возникло кромочного контакта, необходимо правильно выбрать zn (табл. 2.5.1).
Таблица 2.5.1
| Число зубьев колеса | 12-18 | 19-27 | 28-36 | 37-45 | 46-54 | 55-63 | 64-72 | 73-81 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Модуль зацепления определим по формуле
Полученное значение модуля сопоставим со стандартным значением (табл. 2.5.2) и примем его ближайшее значение.
Таблица 2.5.2
| т, мм | 2,00 | 2,25 | 2,50 | 2,75 | 3,00 | 3,25 |
| Рь, мм | 5,904 | 6,642 | 7,380 | 8,818 | 8,856 | 9,954 |
| т, мм | 3,50 | 3,75 | 4,00 | 4,50 | 5,00 | 5,50 |
| Рь, мм | 10,33 | 11,07 | 11,808 | 13,28 | 14,76 | 16,84 |
По уточненному значению модуля рассчитаем шаги зацепления по делительной и основной окружностям.
Для определения величины смещения при нарезании зубчатого колеса инструментальной рейкой необходимо измерить толщину зуба по основной окружности, сопоставить результат с расчетным значением той же толщины зуба для колеса, нарезанного без смещения, и найти коэффициент смещения инструментальной рейки:
где sb = Wzn+l — znpb — толщина зуба по основной окружности данного колеса; sb = mcosa(^ + zinva) — толщина зуба по основной окружности зубчатого колеса, нарезанного при х = 0; a = 20°; inv 20° = 0,0149.
При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов da и впадин df.
Если число зубьев шестерни z четное, то оба диаметра могут быть непосредственно измерены штангенциркулем (рис. 2.5.2, а) При нечетном числе зубьев измерение проводится по схеме, изображенной на рис. 2.5.2, б.
Рис. 2.5.2. Определение диаметров при четном (а) и нечетном (б) числе зубьев
Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни ((/0Тв) и размер//’. Тогда диаметр окружности выступов
Аналогично измеряется диаметр окружности впадин:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измерительный инструмент — штангенциркуль.
Порядок выполнения работы
- 1. Подсчитать число зубьев колеса z.
- 2. По табл. 2.5.1 определить число зубьев z„, которые следует охватить штангенциркулем.
- 3. Измерить штангенциркулем Wzn и Wzn+ (рис. 2.5.1). Для большей точности обмерять нужно трижды на разных участках зубчатого венца. Окончательные значения Wzn и Wzn+ есть среднеарифметическое трех обмеров. По формуле (2.5.1) определить величину шага рь по основной окружности.
- 4. По формуле (2.5.2) найти модуль зацепления в миллиметрах, округлив его величину до ближайшего стандартного значения согласно табл. 2.5.2. В формуле 2.5.2 угол исходного контура а = 20°.
- 5. Учитывая, что есть колеса с углом а = 15°, выполнить проверочный расчет модуля по выражению
измерив диаметр da окружности вершин.
6. Измерить d/диаметр окружности впадин.
Примечание: da и df при четном числе z измерить штангенциркулем (рис. 2.5.2, а), при нечетном числе — найти в соответствии с рис. 2.5.2, б по формулам:
- 7. Определить:
- а) шаг по делительной окружности
б) диаметр делительной окружности
в) диаметр основной окружности
г) делительную высоту головки зуба
д) делительную высоту ножки зуба
е) коэффициент высоты головки зуба
ж) толщину зуба по основной окружности
- 8. По формуле (2.5.3) рассчитать коэффициент смещения х исходного контура, с которым нарезалось данное колесо.
- 9. Определить толщину зуба по основной окружности:
Контрольные вопросы и задания
- 1. Что такое модуль зубчатого колеса?
- 2. Как определить шаг зубчатого колеса?
- 3. Дайте понятие основной и делительной окружностей.
- 4. Какова зависимость между числом зубьев и диаметром зубчатого колеса?
- 5. Что называется коэффициентом смещения исходного контура?
- 6. Как изменяются основные параметры зубчатого колеса при смещении исходного контура?
Содержание отчёта
- 1. Число зубьев z = …
- 2. Определение шага и модуля зацепления:
| Номер измерения | Wz,,+ь мм | Wzn, мм |
| Среднее |
* число zn выбирается по табл. 2.5.1.
Шаг зацепления по основной окружности pb = WZfJ+1 — Wzn = … мм.
Модуль т = ——— = … мм.
Ttcosoc
Модуль, уточненный по табл. 2.5.2, т = … мм.
Шаг зацепления по делительной окружностир = пт = … мм.
Шаг по основной окружности (уточненный)рь=р cos а= … мм.
- 3. Диаметр делительной окружности d = mz= … мм.
- 4. Диаметр основной окружности db = d cos а= … мм.
- 5. Определение действительной толщины зуба по основной окружности sb = Wzn +1 -znpb = … мм.
- 6. Расчет толщины зуба по основной окружности нулевого колеса:
7. Определение коэффициента смещения:
9. Определение диаметров окружностей вершин da и впадин df колеса:
| Номер измерения | doiB | Н’ | da | Н» | df | Расчётные формулы при нечётном числе z |
| Среднее |
10. Учитывая, что есть колеса с углом зацепления а = 15°, в и. 2 выполнить проверочный расчет модуля по выражению (для нормального колеса)
11. Определение коэффициента высоты головки зуба колеса, зубья которого нарезаны без смещения:
12. Вывод.
Источник: https://studref.com/529843/tehnika/opredelenie_osnovnyh_geometricheskih_parametrov_zubchatyh_koles
Модуль зуба – Модуль шестерни. Формулы расчёта
Шаг зубьев ρ так же, как и длина окружности, включает в себя трансцендентное число π, а потому шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число ρ/π, которое называют модулем зубьев т и измеряют в миллиметрах:
Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб. Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колес и унификации зуборезного инструмента значения m регламентированы стандартом (табл. 8.1).
Высота головки и ножки зуба. Делительная окружность рассекает зуб по высоте на головку ha и ножку hf. Для создания радиального зазора с (см. рис. 8.19)
Для нормального (некорригированного) зацепления ha = m. Длина активной линии зацепления. При вращении зубчатых колес точка зацепления S (см. рис. 8.9) пары зубьев перемещается по линии зацепления NN.
Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S” пересечения линии зацепления с окружностью вершин шестерни. Отрезок S’S” линии зацепления называется длиной активной линии зацепления и обозначается ga.
Длину ga легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S” и замеряют ga.
Коэффициент торцового перекрытия. Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность передачи.
reductory.ru
Как определить модуль шестерни с прямым и косым зубом
Часто мне задают вопрос: Как определить модуль косозубой шестерни. Один из самых простых вариантов — обкатать фрезой, то есть методом подбора, вставить в шестерню фрезу и посмотреть совпадает ли шаг! Этот вариант подходит для шестернь малого модуля, для более больших шестернь требуются формулы расчёта.
Давайте определим модуль косозубой шестерни. В качестве примера я возьму небольшую шестерню. Данный метод идентичен и для более больших шестернь и больших модулей.
- Есть вот такая шестерня:
- Допустим что фрезы обкатать у нас на данный момент нет и вообще хочется просто посчитать по формуле!
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
- Можно использовать и другой вариант — высота зуба делится на 2,25.
- Я обычно или обкатываю фрезой или считаю по формуле — модуль = De/Z+2.
- Таким образом можно определить модуль как косозубой шестерни, так и шестерни с прямым зубом.
- Поделится, добавить в закладки!
- zuborez.info
Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?
Модуль зубчатого колеса геометрический параметр зубчатых колёс.
Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/π.
Для косозубых цилиндрических колёс различают: окружной модуль ms = dд/z = ts/π, нормальный модуль mn = tn/π, осевой модуль ma = tа/π, где ts, tn и ta— соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к.
стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Модуль высокоэластический
- Модуль расстояния
Смотреть что такое “Модуль зубчатого колеса” в других словарях:
- МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
- модуль зубчатого колеса — отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально… … Энциклопедический словарь
- нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
- нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
- окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
- расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
- Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
- Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
Модуль зуба что такое
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня».
За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки.
Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Зубчатое колесо
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
- Для расчета этого параметра применяют следующие формулы:
- m=t/π,
- где t — шаг.
- Параметры зубчатых колес
- Модуль зубчатого колеса можно рассчитать и следующим образом:
- m=h/2,25,
- где h — высота зубца.
- И, наконец,
- m=De/(z+2),
- где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
- Расчет модуля зубчатого колеса
- Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
- π×D=t×z,
- проведя преобразование, получим:
- D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
- t/π=m,
- размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
- В=m×z;
- выполнив преобразование, находим:
- m=D / z.
- Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
- De=d+2× h’,
- где h’- высота головки.
- Высоту головки приравнивают к m:
- h’=m.
- Проведя математические преобразования с подстановкой, получим:
- De=m×z+2m = m(z+2),
- откуда вытекает:
- m=De/(z+2).
- Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
- Di=D-2h“,
- где h“- высота ножки зубца.
- Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
- h’ = 1,25m.
- Устройство зубчатого колеса
- Выполнив подстановку в правой части равенства, имеем:
- Di = m×z-2×1,25m = m×z-2,5m;
- что соответствует формуле:
- Di = m(z-2,5m).
- Полная высота:
- h = h’+h“,
- и если выполнить подстановку, то получим:
- h = 1m+1,25m=2,25m.
- Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
- Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
- Для более крупных потребуются измерения и вычисления.
- Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
- m=De/(z+2)
- Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Источник: https://stankotec.ru/raznoe/modul-zuba-modul-shesterni-formuly-raschyota.html
Расчёт модулей зубчатых колёс
|
< Предыдущая СОДЕРЖАНИЕ Следующая >
Перейти к загрузке файла |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ориентировочное минимально допустимое значение модуля m, мм. определим по формуле: где km — вспомогательный коэффициент; М1 — крутящий момент на шестерне, Н•м; z1 — число зубьев шестерни; kFв — коэффициент учитывающий неравномерность распределения нагрузки по ширине венца; шbd — отношение ширины венца к начальному диаметру шестерни; yF1 — коэффициент учитывающий форму зуба. Допустимое напряжение зубьев по изгибу уFP определяют по формуле у’FP — допускаемое напряжение зубьев по изгибу, МПа, соответствующее базовому числу циклов перемены напряжений; kFL — коэффициент долговечности. Ориентировочное минимально допустимое значение модуля: Рассчитанный по формуле модуль округляется до стандартного значения m=2. Характеристики зубчатых колёс сведём в таблицу:
|
Расчёт на контактную выносливость рабочих поверхностей зубьев
Действующие в передаче контактные напряжения определяют по формуле
где ун — контактные напряжения, МПа; zН — коэффициент, зависящий от угла наклона зубьев, для x=0 применяем zН=1,76; zМ — коэффициент, учитывающий механические свойства материалов сопряжённых колёс, для стальных колёс zМ=275; zе — коэффициент, учитывающий суммарную длину контактных линий:
Коэффициент торцевого перекрытия:
где z1 и z2 — числа зубьев шестерни и колеса, знак «+» принимают для наружного зацепления.
Удельную расчётную окружную силу щHt определяют по формуле
где Pt — исходная окружная сила, Н:
где щHV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм.
Допускаемое контактное напряжение [ун] определяем по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kHL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kHL=1.
- Для стали 45 с улучшением =750 МПа.
- 532,25 МПа ? 750 МПа
- Условие контактной выносливости выполняется.
- Расчёт на изгибную выносливость зубьев
- Действующее в передаче напряжение изгиба сравнивается с допустимыми, с учётом коэффициента долговечности.
- Действующее напряжение изгиба:
Коэффициент yе — учитывает перекрытие зубьев. Для прямозубых колёс применяют yе=1. Коэффициент yв учитывает наклон зуба. Для прямозубых применяют yв=1.
Удельную расчётную окружную силу щFt определяем по формуле
где Pt — расчётная окружная сила в зубчатом зацеплении, Н; bщ — рабочая ширина венца, мм
Окружная сила Pt=2•103•M1/d1, где M1 — крутящий момент, Н•м; d1 — диаметр делительной окружности, мм.
Коэффициент kFa учитывает распределение нагрузки между зубьями. Для прямозубых передач приметаем kFa=1. Коэффициент kFв учитывает распределение нагрузки по ширине венца, можно принять kFв=1.1.
Коэффициент kFv учитывает динамическую нагрузку, возникающую в зацеплении.
где щFV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм; для прямозубых передач д=0.016; коэффициент g=47, учитывает влияние разности шагов зацепления.
Допускаемое изгибное напряжении [уF] определяется по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kFL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kFL=1.
Для стали Для стали 45 с улучшением у‘F=450 МПа, условие изгибной выносливости выполняется.
265.49 МПа ? 450 МПа
Условие на изгибную выносливость выполняется.
Источник: https://studbooks.net/2523612/tovarovedenie/raschyot_moduley_zubchatyh_kolyos
На рис. 231 изображено два положения инструмента при нарезании зубьев первое (/), когда делительная плоскость рейки (ДП) совпадает с начальной плоскостью (НП) — это нарезание 6ej смещения, и второе II, когда инструмент смещен от оси нарезаемого колеса — это положительное смещение. При этом диаметры основной и делительной окружностей не изменились, но изменилась форма зуба. Толщина зуба у основания увеличилась, а следовательно, повысилась прочность зуба, но одновременно с этим заострилась головка зуба. Величина смещения характеризуется коэффициентом смещения х. Если рейка смещается в сторону оси нарезаемого колеса, то это отрицательное смещение. Применяют два типа передач со смещением. [c.252]
Окружность выступов (диаметр De) вычерчивается сплошной основной линией (рис. 285. а), проходящей по кромкам выступов зубьев, такой же толщины, как и толщина линий видимого контура окружность впадин (диаметр Di) вычерчивается штриховой линией, проходящей по основанию зубьев, такой же толщины, как и толщина линий невидимого контура начальная делительная окружность (диаметр — штрих-пунктирной линией, типа осевых и центровых линий). [c.229]
Делительный диаметр d, мм Основной диаметр мм Диаметр впадин df, мм Высота зуба /г, мм Диаметр вершин d , мм Начальный диаметр d , мм Окружная делительная толщина зуба s, мм [c.37]
Основные геометрические размеры (см. рис. 3.81 и 3.31) определяют в зависимости от модуля т и числа зубьев 2. Диаметры делительный и начальный [c.344]
В процессе нарезания по методу обкатывания рейка, как часть обода колеса бесконечно большого радиуса, движется поступательно вдоль самой себя (рис. 9.5, а) со скоростью Ор, а заготовка вращается с угловой скоростью (О. На некоторой окружности диаметра окружная скорость заготовки V = сйс/д/2 = Нр. Поэтому шаг зубьев на этой окружности равен шагу зубьев рейки р(. Очевидно, эта окружность есть начальная окружность или центроида колеса в его движении относительно рейки. Шаг р/ должен укладываться на длине указанной окружности ровно г раз, если 2 — число зубьев колеса. Эта окружность, называемая делительной, является основным геометрическим элементом, неизменным для каждого данного колеса. Таким образом. [c.240]
Поскольку для получения шага 1 приходится длину делительной окружности делить на число зубьев г, то шаг t, рассчитанный по формуле (10), носит название окружного или торцевого шага зубчатого колеса. В дальнейшем мы познакомимся с другими шагами цилиндрических колес — шагом по нормали, основным, а при наличии винтовых зубьев — еще и с нормальным и осевым шагами. Так как модуль получается делением начального диаметра колеса на число зубьев, то его можно назвать диаметральным шагом. Значение модулей в машиностроении и приборостроении стандартизировано подобно стандартизации диаметров винтовых резьб Поэтому модули, полученные по формулам при расчете зацепления на прочность, должны быть округлены до стандартных их значений. [c.411]
Диаметры начальных окружностей червяка и червячного колеса Диаметр делительной окружности червяка Коэфициент высоты зуба основной рейки Высота витка червяка и высота зуба червячного колеса [c.342]
Окружность, диаметр которой равен произведению числа зубьев на модуль, называется делительной. Следовательно, при зацеплении зубчатого колеса с рейкой, имеющей больше одного зуба (и, в частности, с основной рейкой), радиусы начальной и делительной окружностей равны друг другу. [c.445]
Начальная окружность делит высоту зуба на головку и ножку. При делении диаметра делительной окружности (мм) на число зубьев колеса получается основной параметр колеса, который называется модулем. Модуль является величиной стандартной, и ГОСТ 9563-60 устанавливает два ряда его чисел, выраженных в миллиметрах (табл. 85). При выборе числа модуля первый ряд предпочитается второму. [c.217]
Диаметры окружностей выступов червяка и червячного колеса Диаметры окружностей впадин червяка и червячного колеса Диаметры начальных окружностей червяка и червячного колеса Диаметр делительной окружности червяка Коэфициент высоты зуба основной рейки Высота витка червяка и высота зуба червячного колеса [c.680]
Если одно из колес заменить стандартной зубчатой-рейкой (рис. 33.6), то для другого колеса будет лишь одна окружность, катящаяся по начальной прямой рейки без скольжения эта окружность зубчатого колеса называется делительной. Для определения основных параметров зубчатой передачи принята именно делительная окружность диаметр ее обозначают й,-,. Если межосевое расстояние передачи точно равно сумме радиусов делительных [c.410]
Определим основные размеры зубчатых колес, у которых делительные окружности совпадают с начальными такие колеса будем называть коромысловыми. Эти размеры могут быть всегда выражены в функциях модуля по делительной окружности и числа зубьев. Согласно формуле (20.8) диаметры 1>1 и Ог начальных окружностей могут быть представлены в следующем виде [c.424]
На профиле зуба выделяют точки пересечения с разными окружностями, обозначение которых используют в качестве индексов в обозначениях параметров зубчатых колес и передачи (рис. 6.8). Например, диаметры окружности вершины зубьев Дг, окружности ПрИТуПЛеННЫХ кромок 4 окружности модификации головок зубьев начальной окружности с1 , делительной окружности й, окружности точек активных профилей р, окружности граничных точек dl, окружности впадин df, основной окружности dь. [c.243]
Обозначения основных А Ье Ь В Ое. О, величин, относящихся к геометрическому расчету Межцентровое расстояние Конусная дистанция (образующая делительного конуса) Рабочая ширина зубчатого колеса Ширина червячного колеса Диаметры начальной и делительной окружностей зубчатых колес Диаметры окружностей вершин и впадин зубчатых колес [c.472]
Составьте условные обозначения и приведите определения для следующих групп параметров зубчатых колес а) диаметры окружности основной, начальный, делительный, вершин и впадин б) шаг основной торцовой окружной, нормальный, осевой по делитель1гой и начальной окружностям, а также угловой шаг б) модуль торцовый, окружной, нормальный по делительной и начальной окружностям г) боковая поверхность и профиль зуба, контактная линия и пятно контакта зубьев д) шестерня, колесо межосевое расстояние, измерительное межосевое расстояние е) профильная модификация зуба и ее виды [c.176]
Смещение инструмента при нарезании зубьев и его влияние на юрму и прочность зубьев. На рис. 8.22 изображено два положения инструмента (рейки) при нарезании зубьев / — делительная плоскость рейки (ДП) совпадает с начальной плоскостью (НП) — нарезание без смеш,ения 2—инструменту дано положительное смещение хт. При этом основной и делительный d диаметры колеса не изменяются, так как не изменяется г. Как видно из чертежа, смеш,ениеин-сгрумеита вызвало значительное изменение формы зуба. Толщина зуба у основания увеличилась, увеличилась и прочность зуба по на-[фяжениям изгиба. Одновременно с этим заострилась головка зуба. Заострение является одной из причин, ограничивающих значение смещения инструмента. Отрицательное смещение инструмента сопровождается явлениями обратного характера. [c.122]
В сеченни II —II все размеры долбяка соответствуют размерам зубчатого колеса. В этом сечении шаг по делительной окружгюсти долбяка раней шагу обрабатываемого зубчатого колеса, т. е. t = юп. Диаметр основной окружности эвольвенты Dq = D, os Ид, где D, — диаметр начальной (делительной) окружности долбяка Ид — угол зацепления долбяка (равен углу зацепления колеса). [c.307]
Геометрические характеристики зубчатого венца. Геометрию зубчатого венца характеризуют концентрическими окружностями с центром на оси зубчатого колеса, лежащими Б торцовом сечении. Различают делительную, основную, вершин зубьев, впадин и другие концентрические окружности зубчатого колеса, принадлежащие соответственно поверхностям делительной, основной, вершин зубьев, впадин и другим соосным поверхнсстям зубчатого колеса. Им соответствуют диаметры концентрических окружностей делительный й, основной с/, вершин зубьев (1 , впадин df и др. (рис. 4,13). Кроме перечисленных окружностей отдельно рассмотрим понятие начальной окружности, диаметр которой обозначается dw. [c.73]
Диаметр основной окружности копира равен диаметру делительной (начальной) окружности шлифуемого долбяка. При расположении направляющих салазок вместе с производящей прялюй под углом к оси шлифовального шпинделя центр. основной окружности будет перемещаться по наклонной прямой О Ог, а профиль долбяка будет перемещаться по кольцевой поверхности круга от точки Мх к точке М , занимая последовательно положение —а а . [c.171]
Шаг зацепления Диаметр начальной окружности Диаметр делительной окружности Диаметр основной окружности Высота головки зуба Высота ножки зуба Высо13 зуба Радиальный зазор [c.203]
В третьей части таблицы помещают я справочные данные делительный диаметр d, число зубьев сектоэа, основной диаметр йь, радиус кривизны активного профиля зуба в нижней точке р/, радиу кривизны в граничной точке профиля зу ба р , начальный диаметр daiy высота зуба /г, шаг зацепления ра, основной угол наклона Рь, осевой шаг рх, ход зуба pz, параметрь модиф икации, обозначение чертежа сопряженного зубчатого колес . [c.272]
Начальный диаметр чер-вяка dyjj. Делительный угол подъема v Начальный угол подъема Основной угол подъема = ( + 2ж) m = = (10,2. 0,897) 6,3 v-f-4-о.г OS V(, = OS OS у = = OS 20° os 11°19 = 0,9214 Определяется для червяка Z1 74,30 мм V – 11П9 7 = 9 37 V , = 22052 [c.391]
Шестеренные клети и редукторы. Для разделения крутящего момента главного электродвигателя на два, три и четыре приводных валка служат шестеренные клети. Основным узлом шестеренных клетей является узел шестеренных валков. Шестеренный валок (шестерня) состоит из тех же элементов, что и прокатный валок — бочки, двух шеек и приводных концов. На цилиндрической поверхности шестеренного валка выполняют (дол-бяком, пальцевой фрезой и т. д.) шевронные зубья. Угол наклона шевронных зубьев на делительном цилиндре шестерни равен 30° профильный угол эвольвенты в торцовом сечении а=20° число зубьев 2=18—29. Диаметр начальной окружности шестерни (do) шестерной клети принимается для большинства прокатных станов равным среднему арифметическому значению диаметра новых и переточенных валков. Ширина шестеренных валков зависит от максимального крутящего момента, передаваемого шестеренной клетью. По отношению ширины бочки валков Ь к диаметру начальной окружности do различают три группы шестеренных клетей узкие /do=l- l,25 средние /do= 1,6- 2,0 широкие bldo= = 2,0-2.5. [c.288]
Коэффициент смещения червяка х Делительный диаметр червяка rfi колеса Номинальный диаметр червяка doai Угол подъема- делительный у начальный Vm основной Y [c.209]
Диаметр делительной окружности С1д Диаметр окружности, на которой шаг и угол зацепления в торцевом сечении соответртвенно равны теоретическому шагу и углу зацепления основной рейки, т. е. производственной (при нарезании зубьев рейкой) начальной окружности [c.7]
Основные параметры и кинематика конических передач. Основными параметрами конических передач являются trite — внешний окружной модуль, мм, определяемый на внешнем делительном (начальном) диаметре d/, величину Ши обычно округляют до стандартного значения (см. табл. 6.8) для конических колес с прямыми и тангенциальными зубьями, выполненными по форме I (нормально понижаюш,иеся зубья, вершины начального и внутреннего конуса совпадают) — ширина зубчатого венца, мм Re = mteZil 2 sin 61) — внешнее конусное расстояние, мм 1 и Zj — соответственно число зубьев шестерни и колеса 61 и 62 — углы делительных конусов шестерни и колеса, град К е = = = 0,25…0,3 — коэффициент ширины зубчатого венца (меньшие значения при и > 3, большие при и 3)-, и = = = tg 81 = tg 62 — передаточное число. [c.62]
Определяем основные геометрические размеры шестерни и колеса
Определяем
делительные диаметры
Шестерни:
d1 = z1 x m = 2 x 20 = 40 мм
Колеса:
d2 = z2 x m = 80 x 2 = 160 мм
Определяем
диаметры вершин зубьев
Шестерни:
dа1 = d1 + 2 x m = 40 + 2 x 2 = 44 мм
Колеса:
dа2 = d2 + 2 x m = 160 + 2 x 2 = 164 мм
Определяем
диаметры впадин
Для
прямозубых цилиндрических передач:
Шестерня:
df1 = d1 – 2,5 x m = 40 – 2,5 x 2 = 35 мм
Колесо:
df2 = d2 – 2,5 x m = 160 – 2,5 x 2 = 155 мм
Определяем
высоту зуба
h = 2,25 x m = 2,25 x 2= 4,5 мм
Определяем
ширину венца шестерни и колеса
Рабочая
ширина венца b2 = 0,4
x
100 = 40 мм
b1 = (2…5)
+ b2 = 45 мм.
Проверяем
величину межосевого расстояния
aw = 0,5 (d1 + d2) = 0,5 (40 + 160) =100 мм
Проверочный
расчет закрытой передачи.
Проверка контактной
выносливости рабочих поверхностей
зубьев колес.
Расчетом должна быть проверена
справедливость соблюдения неравенства:
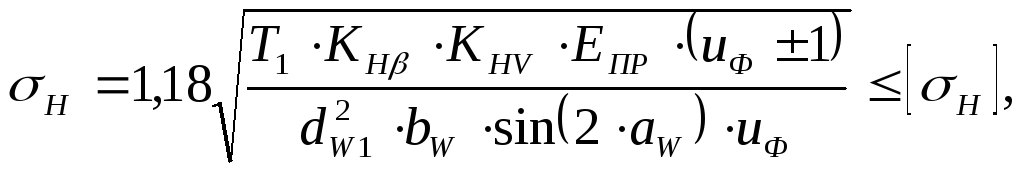
Т1
– вращающий момент на шестерне, Н
мм;
 КН
КН
– коэффициент неравномерности распределения
нагрузки по длине контакта;
КНV
– коэффициент внутренней динамической
нагрузки;
ЕПР
– приведенный модуль упругости, МПа;
uФ
– фактическое передаточное число;
dW
– начальный диаметр колеса, мм;
bW
– рабочая ширина зубчатого венца колеса,
мм;
aW
– фактическое межосевое расстояние,
мм 1.
bW
=ba
aW
=0.4×100
= 40мм
Величину вращающего
момента Т1
на шестерне определяем по формуле:
![]()
где
– КПД передачи, принимаем
= 0,96 1.
![]()
Коэффициент
неравномерности нагрузки по длине
контакта КН
выбирают в соответствии с расположением
колес относительно опор и твердостью
рабочих поверхностей зубьев колес по
графику, приведенному в 1:
КН
= 1,1.
Для определения
коэффициента внутренней динамической
нагрузки КНV
необходимо рассчитать окружную скорость
в зацеплении V,
м/с:
![]()
В зависимости от
значения V по таблице, приведенной в
1,
назначаем степень точности передачи –
8. Затем определяем коэффициент внутренней
динамической нагрузки КНV
= 1,1.
Подставив численные
значения в формулу (1.31) получим:

 Допускаемое
Допускаемое
контактное напряжение
![]() ,
,
т. е. неравенство не соблюдается:Н
> Н.
В результате
проверки выявилась существенная
недогрузка
10 %, то с целью более полного использования
возможностей материалов зубчатых колес
возможна корректировка рабочей ширины
зубчатого венца по формуле:
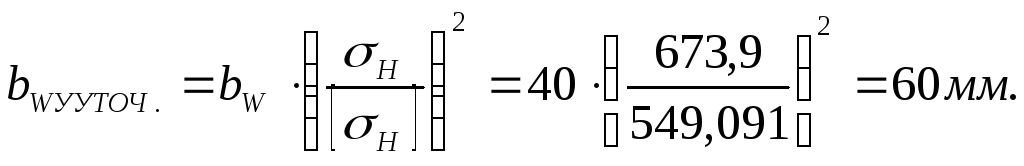
σH
нов =550≤549,09МПа
Проверка прочности
зубьев по напряжениям изгиба.
Проверяют справедливость соотношения
расчетных напряжений изгиба F
и допускаемых напряжений F
:
![]()
Ft
– окружное усилие в зацеплении колес,
Н;
КF
– коэффициент неравномерности распределения
нагрузки по длине контакта;
КFV
– коэффициент внутренней динамической
нагрузки;
YF1,2
– коэффициент формы зуба 1.
Окружное усилие
в зацеплении колес Ft
определяем по формуле:

![]()
Коэффициент
неравномерности нагрузки по длине
контакта КF
выбирают в соответствии с расположением
колес относительно опор и твердостью
рабочих поверхностей зубьев колес по
графику, приведенному в 1:
КF
= 1,05.
В зависимости от
значения окружной скорости V по таблице,
приведенной в 1,
назначаем степень точности передачи –
8. Затем определяем коэффициент внутренней
динамической нагрузки КFV
= 1,1.
YF1,2
– коэффициент формы зуба определяем
по графику 8.20 [2]
YF1=4,14;
YF2=3,72.
Подставив численные
значения в формулу найдем значения
расчетных напряжений изгиба F:
![]()
![]()
Допускаемые
напряжения изгиба: F1
= 193,8 МПа; F2
= 212,148 МПа, неравенство соблюдается.
Соседние файлы в папке Курсовой проект
- #
- #
02.05.201461.68 Кб152мое колесо.bak
- #
02.05.201463.65 Кб162мое колесо.cdw
- #
02.05.2014144.99 Кб154Мой чертеж!.bak
- #
02.05.2014144.99 Кб188Мой чертеж!.cdw
- #
- #
02.05.201487.65 Кб160редуктор.bak
- #
02.05.201487.32 Кб211редуктор.cdw
- #
- #
02.05.201461.19 Кб151Чертеж.bak
- #
02.05.201485.2 Кб179Чертеж.cdw




