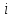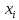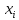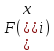Метод Риддера (Ridder’s method) является итерационным численным методом решения нелинейного уравнения ![]() непрерывной функции. Данный метод относится к методам интервалов локализации корня.
непрерывной функции. Данный метод относится к методам интервалов локализации корня.
В соответствии с методом задача поиска корня в уравнении ![]() сводится к задаче:
сводится к задаче:
– создание уникальной экспоненциальной функции ![]() вида
вида ![]() ;
;
– поиска корня уравнения экспоненциальной функции ![]() , который будет являться приближением корня функции
, который будет являться приближением корня функции ![]() .
.
Параметр ![]() выбирается из условия, чтобы экспоненциальная функция
выбирается из условия, чтобы экспоненциальная функция ![]() проходила через точки
проходила через точки ![]() ,
, ![]() и
и ![]() таким образом, чтобы значения функции
таким образом, чтобы значения функции ![]() в данных точках лежали на прямой линии. Следует отметить, что точки
в данных точках лежали на прямой линии. Следует отметить, что точки ![]() и
и ![]() – это левая и правая граница интервала локализации корня функции
– это левая и правая граница интервала локализации корня функции ![]() , а точка
, а точка ![]() – это середина интервала локализации корня, которая определяется по формуле
– это середина интервала локализации корня, которая определяется по формуле ![]() .
.
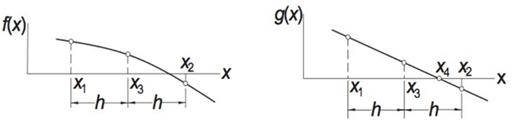
Рис.1. Метод Риддера.
Значение функции ![]() в трех точках определяется в следующем виде:
в трех точках определяется в следующем виде:
› В точке ![]() значение функции определяется
значение функции определяется ![]() ;
;
› В точке ![]() значение функции определяется
значение функции определяется ![]() ;
;
› В точке ![]() значение функции определяется
значение функции определяется ![]() .
.
В представленных формулах используется параметр h, который определяется по формуле ![]() .
.
В связи с тем, что значение функции ![]() в рассматриваемых трех точках лежат на прямой линии, то значение функции в средней точки может быть определено по формуле:
в рассматриваемых трех точках лежат на прямой линии, то значение функции в средней точки может быть определено по формуле:
![]()
![]()
![]()
Задача поиска корня уравнения f(x) сводится к поиску значения корней квадратного уравнения относительно переменной ![]() . Корень квадратного уравнения определяется по формуле:
. Корень квадратного уравнения определяется по формуле:
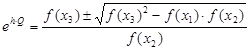
Используя математические преобразования данное уравнение можно привести к виду:
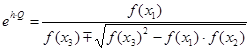
Рассматриваемая экспоненциальная прямая пересекает ось абсцисс в точке, которая находится границах рассматриваемого отрезка (основные положения по получению следующей формулы можно посмотреть в методе хорд):
![]()
![]()
В результате подстановки переменной ![]() в данное уравнение получим формулу для определения точки пересечения функции
в данное уравнение получим формулу для определения точки пересечения функции ![]() с осью абсцисс.
с осью абсцисс.
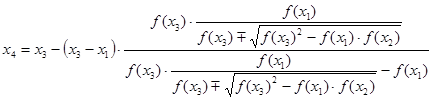
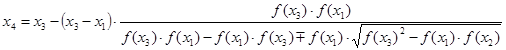
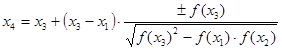
В дальнейших расчетах вместо используемого знака «±» применяется математическое выражение ![]() . В результате приближенное значение корня функции
. В результате приближенное значение корня функции ![]() определяется следующим выражением:
определяется следующим выражением:
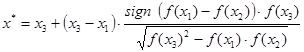 ,
,
где функция ![]() определена следующим образом:
определена следующим образом:
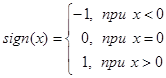 .
.
В качестве нового интервала для прохождения итерационного процесса выбираем один из двух ![]() или
или ![]() , на концах которого функция
, на концах которого функция ![]() принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
![]() или
или ![]() .
.
Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.
![]() .
.
Данный метод решения нелинейного уравнения характеризуется определёнными свойствами:
– приближенное значение корня на любой итерации всегда оказывается внутри интервала локализации корня [a,b];
– метод обладает сверхлинейной сходимостью с порядком сходимости √2. Вычисленная на основании него последовательность приближений сходится довольно быстро. Каждое последующее приближение будет в среднем на две значимые цифры более точным по сравнению с предыдущем значением.
Алгоритм нахождения корня нелинейного уравнения по методу Риддера
1. Найти начальный интервал неопределенности ![]() одним из методов отделения корней, задать малое положительное число
одним из методов отделения корней, задать малое положительное число ![]() . Положить
. Положить ![]() .
.
2. Определить среднюю точку в рассматриваемом интервале и найти значения функции в трех точках: по краям рассматриваемого интервала ![]() ,
, ![]() и в середине интервала
и в середине интервала![]() .
.
3. Выполнить расчет приближенного значения корня функции в соответствии с формулой:
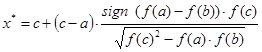
4. Определяем новый интервал неопределенности на котором находится искомых корень уравнения. При выборе данного интервала исходим из того, что функция ![]() на концах интервала должна принимать значение разных знаков. В соответствии с данным методом нахождения корня уравнения получается два возможных интервала неопределенности:
на концах интервала должна принимать значение разных знаков. В соответствии с данным методом нахождения корня уравнения получается два возможных интервала неопределенности:
1 интервал: если ![]() , то новый интервал
, то новый интервал ![]()
2 интервал: если ![]() , то новый интервал
, то новый интервал ![]()
5. Проверяем значение корня на предмет заданной точности, в случае:
– если разность двух последовательных приближений станет меньше заданной точности ![]() , то итерационный процесс заканчивается.
, то итерационный процесс заканчивается.
– если разность двух последовательных приближений не достигает необходимой точности ![]() , то необходимо продолжить итерационный процесс
, то необходимо продолжить итерационный процесс ![]() и перейти к п.2 рассматриваемого алгоритма.
и перейти к п.2 рассматриваемого алгоритма.
Пример решения уравнений методом Риддера
В качестве примера, рассмотрим решение нелинейного уравнения ![]() методом Риддера. Корень необходимо найти в рассматриваемом диапазоне
методом Риддера. Корень необходимо найти в рассматриваемом диапазоне ![]() с точностью
с точностью ![]() .
.
Вариант решения нелинейного уравнения в программном комплексе MathCAD.

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.2).
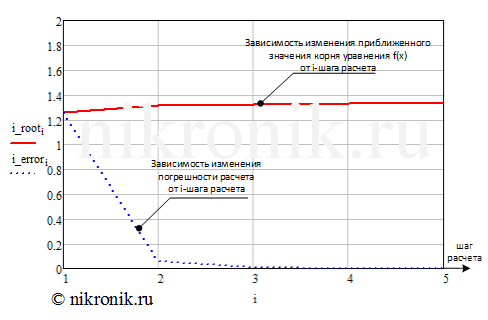
Рис.2. Результаты расчета по методу Риддера
Для обеспечения заданной точности ![]() при поиске уравнения в диапазоне
при поиске уравнения в диапазоне ![]() необходимо выполнить 5 итерации. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением:
необходимо выполнить 5 итерации. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: ![]() .
.
Алгоритм
Шаг 1.
Положить
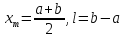 .
.
Вычислить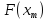 .
.
Шаг 2.
Положить
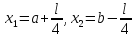 .
.
Заметим, что точки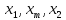 делят интервал
делят интервал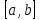 на
на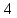 равные части. Вычислить значения
равные части. Вычислить значения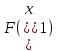 и
и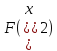 .
.
Шаг 3.
Сравнить
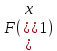 и
и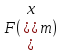 .
.
Если
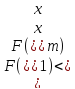 ,
,
исключить интервал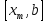 ,
,
положив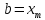 .
.
При этом средней точкой нового интервала
поиска становится точка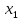 ,
,
следовательно, необходимо положить,
что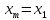 .
.
Перейти к шагу 5.
Если
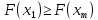 ,
,
перейти к шагу 4.
Шаг 4.
Сравнить
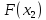 и
и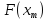 .
.
Если
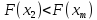 ,
,
исключить интервал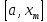 ,
,
положив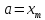 .
.
Т.к. в середине нового интервала
оказывается ,
,
положить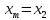 .
.
Перейти к шагу 5.
Если
 ,
,
исключить интервалы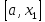 и
и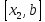 ,
,
положив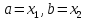 .
.
Заметим, что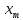 продолжает оставаться средней точкой
продолжает оставаться средней точкой
нового интервала. Перейти к шагу 5.
Шаг 5.
Вычислить
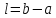 .
.
Если величина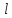 меньше заданной точности
меньше заданной точности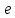 ,
,
закончить поиск. В противном случае
перейти к шагу 2.
Пример
Пусть
 определена на отрезке
определена на отрезке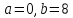 .
.
Найти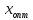 с точностью
с точностью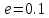 .
.
Итерация 1.
Шаг 1.
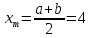
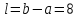
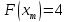
Шаг 2.
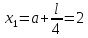

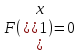
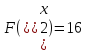
Шаг 3.
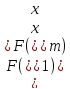 следовательно, исключается интервал
следовательно, исключается интервал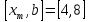 ,
,
поэтому
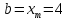
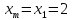
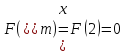
Переходим
к шагу 5.
Шаг 5.
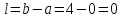
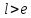 следовательно, поиск надо продолжать,
следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком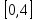 ,
,
при этом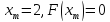 .
.
Итерация 2.
Шаг 2.
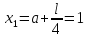
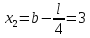
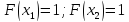
Шаг 3.
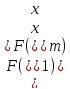 следовательно, переходим к шагу 4.
следовательно, переходим к шагу 4.
Шаг 4.
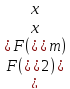 следовательно, исключаются интервалы
следовательно, исключаются интервалы ,
,
поэтому новое значение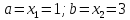 ,
,
старые значения сохраняются для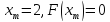 .
.
Переходим к шагу 5.
Шаг 5.
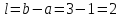
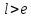 следовательно, поиск надо продолжать,
следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком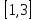 ,
,
при этом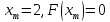 .
.
Итерация 3.
Шаг 2.
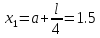
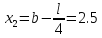
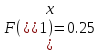
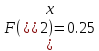
Шаг 3.
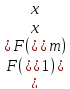 следовательно, переходим к шагу 4.
следовательно, переходим к шагу 4.
Шаг 4.
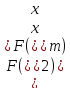 следовательно, исключаются интервалы
следовательно, исключаются интервалы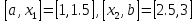 ,
,
поэтому новое значение ,
,
старые значения сохраняются для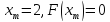 .
.
Переходим к шагу 5.
Шаг 5.
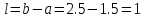
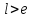 следовательно, поиск надо продолжать,
следовательно, поиск надо продолжать,
т.е. перейти к следующей итерации на
шаге 2 с отрезком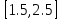 .
.
Последующие
итерации аналогичны проделанным и далее
не рассматриваются. Окончание процедуры
происходит при выполнении условия
 на шаге 5.
на шаге 5.
Выводы
В нашем
примере за 3 итерации (т.е. при шести
вычислениях функции
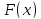 )
)
исходный интервал поиска сузился с 8 до
1. Как видите, метод дихотомии позволяет
довольно быстро попасть в область
экстремума. Так для определения положения
экстремума с точность в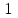 от длины начального интервала надо
от длины начального интервала надо
сделать всего 14 измерений показателя
качества (это 7 итераций дихотомии), т.к.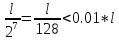 .
.
Это намного лучше, чем метод сканирования,
который требует 101 измерение.
Алгоритм получения границ начального интервала неопределённости
Если
начальный интервал, содержащий точку
мининмума, неизвестен, его можно получить.
Поиск граничных точек начального
интервала производится обычно с помощью
эвристических методов. Рассмотрим один
из них.
Алгоритм
полученияначального интервала состоит
из двух этапов:
-
Выбор
«удачного» направления -
Движение
в этом направлении до получения точки
минимума
Исходными
данными являются начальная точка
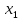 и величина шага
и величина шага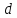 .
.
Рассмотрим шаги первого этапа алгоритма
получения начального интервала.
Шаг 1.
Вычислить
значение функции в начальной точке
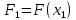
Шаг 2.
Вычислить
значения аргумента и функции после шага
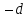 .
.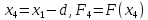 .
.
Шаг 3.
Вычислить
значения аргумента и функции после шага
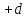 .
.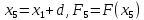
Шаг 4.
Шаг 4.1
Если
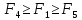 ,
,
то шаг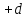 удачное направление. Оставляем его и
удачное направление. Оставляем его и
обозначим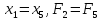 .
.
Шаг 4.2
Если
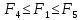 ,
,
то шаг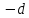 удачное направление. Оставляем его и
удачное направление. Оставляем его и
обозначим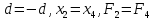 .
.
Шаг 4.3
Если
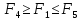 ,
,
то начальный интервал уже найден: точка
минимума лежит между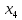 и
и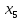 .
.
Шаг 4.1
Если
 ,
,
то функция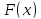 не является унимодальной и задачу надо
не является унимодальной и задачу надо
решать другим методом.
На втором
этапе – движения в выбранном направлении
до получения интервала, содержащего
точку минимума, -делается ряд шагов
увеличивающейся длины. Алгоритм второго
этапа для получения начального интервала
неопределённости.
Шаг 1.
Переприсвоение:
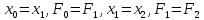 .
.
Шаг 2.
Расчёт
новой длины шага:
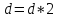 .
.
Шаг 3.
Расчёт
аргумента и функции в третьей точке:
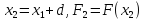 .
.
Шаг 4.
Сравнение
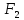 и
и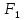 :
:
-
если
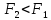 ,
,
перейти к шагу 1 -
если
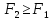 ,
,
окончание поиска: интервал неопределённости
равен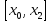
Эффективность
поиска граничных точек непосредственно
зависит от величины шага. Если шаг велик,
то получаем грубые оценки координат
граничных точек, и построенный интервал
оказывается весьма широким. С другой
стороны, если шаг мал, то для определения
граничных точек может потребоваться
достаточно большой объём вычислений.
Несомненным достоинством методов такого
рода является то, что они основаны лишь
на вычислении значений функции. При
этом не требуется, чтобы исследуемые
функции были дифференцируемы. Более
того, допустимы случаи, когда целевую
функцию нельзя даже записать в
аналитическом виде.
Единственным
требование является возможность
определения значений
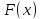 в заданных точках
в заданных точках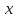 с помощью прямых расчётов или имитационных
с помощью прямых расчётов или имитационных
экспериментов.
Пример
Решим вместе
с вами задачу на установление границ
начального интервала. Найти начальный
интервал неопределённости для функции
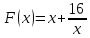 с начальной точкой
с начальной точкой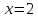 и величиной шага
и величиной шага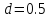 .
.
Выполним
шаги первого этапа алгоритма.
Шаг 1.
Вычислим
значение функции в начальной точке:
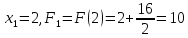 .
.
Шаг 2.
Вычислим
значение аргумента и функции слева от
начальной точки:
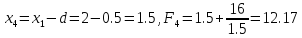 .
.
Шаг 3.
Вычислим
значения аргумента и функции справа от
начальной точки:
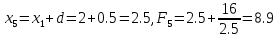 .
.
Шаг 4.
Сравним
значения функции в трёх точках:
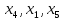 .
.
Получим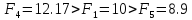 .
.
Т.е. функция убывает в направлении шага ,
,
а значит, это правильное направление и
нам надо двигаться в право по оси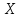 .
.
Принимаем: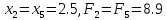 .
.
Выполним
второй этап алгоритма – движение в
выбранном направлении до получения
отрезка, содержащего точку минимума.
Итерация 1
Шаг 1.
Выполняем
присвоение:
 .
.
Шаг 2.
Расcчитываем
новую длину шага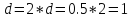 .
.
Шаг 3.
Находим в
третьей точке:
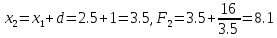 .
.
Шаг 4.
Сравниваем
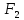 и
и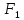 .
.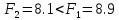 следовательно, надо вновь идти на шаг
следовательно, надо вновь идти на шаг
1 и делать вторую итерацию.
Итерация 2
Шаг 1.
Выполняем
присвоение:
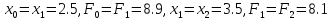 .
.
Шаг 2.
Расcчитываем
новую длину шага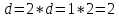 .
.
Шаг 3.
Находим в
третьей точке:
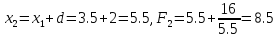 .
.
Шаг 4.
Сравниваем
 и
и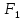 .
.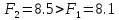 .
.
Поскольку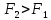 ,
,
процедуру поиска начального интервала
заканчиваем. Начальный интервал: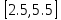 .
.
Метод сканирования
Метод
сканирования – это численный метод
оптимизации, в котором не требуется
знание априорной информации об исследуемой
функции. Будем считать, что с аналитическими
методами решения задач одномерной
оптимизации вы знакомы из курса
математического анализа. Мы же остановимся
именно на численных методах. Для
определённости будем рассматривать
задачу минимизации, поскольку известно,
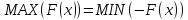 .
.
Существует
множество численных методов одномерной
оптимизации. Среди них есть более простые
и более сложные. Сложность метода зависит
от априорной информации о показателе
качества
 .
.
Если о функции известно только то, что она имеет
известно только то, что она имеет
экстремальный характер, и никакой другой
априорной информации нет, то при отыскании
экстремума единственным разумным
действием в такой ситуации будет
последовательное нахождение значения
критерия при всех допустимых значениях .
.
Поскольку
таких значений на отрезке
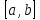 бесконечное множество, то практически
бесконечное множество, то практически
перед решением задачи задаются точностью
определения оптимального значения
переменной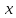 .
.
Обозначим данную точность через .
.
Тогда для отыскания экстремума следует
определить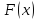 в
в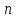 равноотстоящих друг от друга на величину
равноотстоящих друг от друга на величину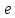 точках где целое число
точках где целое число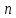 задаётся округлением значения
задаётся округлением значения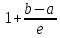 до ближайшего большего целого значения.
до ближайшего большего целого значения.
При этом значение реализуемой точности
решения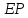 определяется как:
определяется как: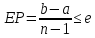 .
.
Значения
аргумента в
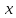 точках расчёт определяется по следующей
точках расчёт определяется по следующей
формуле: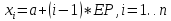 .
.
Крайние точки отрезка получаются при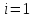 и
и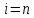 .
.
Из полученных значений функции выбирается
наименьшее значение. Номер наименьшего
значения и определяет оценку положения
экстремума с точностью не хуже, чем
заданная величина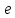 .
.
Пример
Пусть
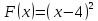 определена на отрезке
определена на отрезке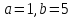 .
.
Найти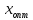 с точностью
с точностью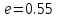 .
.
Рассчитаем необходимое число точек,
для этого вычислим выражение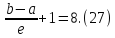 .
.
Округлив до ближайшего целого получаем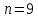 .
.
Реализуемая точность равна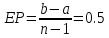 ,
,
что лучше заданной точности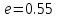 .
.
Рассчитаем
значение аргумента в 9 точках по формуле:
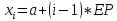 .
.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
Рассчитаем
значения функции в каждой точке:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
|
|
9 |
6.25 |
4 |
2.25 |
1 |
0.25 |
0 |
0.25 |
1 |
Сравнивая
значения функции в 9 точках, находим:
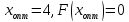 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Слайд 1
2.2.5. Метод деления интервала пополам
Метод относится к последовательным

стратегиям и
позволяет исключить из дальнейшего рассмотрения на
каждой итерации
в точности половину текущего
интервала.
Задается начальный интервал
неопределенности
и требуемая точность поиска
Реализация метода основана на выборе трех пробных
точек, равномерно распределенных на текущем
интервале ( делящем его на четыре равные части).
Слайд 2
Пусть

длина интервала
Разделим
интервал точками
и на четыре равные части
Вычисляются значения целевой функции
Сравниваются полученные значения и находится новый
интервал неопределенности следующим образом:
Слайд 6
Затем снова вычисляются координаты и
и

продолжают поиск до выполнения условия
За минимальное значение принимают
Слайд 8
2.2.6. Метод золотого сечения
Метод относится к последовательным стратегиям.
Задается

начальный интервал неопределенности
и требуемая точность поиска
В качестве точек
вычисления целевой функции
выбираются точки золотого сечения. Тогда с учетом
свойств золотого сечения на каждой итерации, кроме
первой, требуется только одно новое вычисление
целевой функции.
Слайд 9
Рассмотрим способ размещения точек золотого
сечения на интервале

Пусть длина интервала равна а точка
делит его на
две части и
Слайд 10
Термин золотое сечение ввел Леонардо да Винчи.
Точка называется

золотым сечением отрезка
если имеет место соотношение
Отсюда
Слайд 11
Так как нас интересует только положительное
решение, то

Слайд 13
Поскольку заранее неизвестно, в какой
последовательности (

или
) делить
интервал неопределенности, то рассматривают
внутренние
точки, соответствующие двум этим
способам деления
Слайд 14
Точки деления и

с учетом полученных
значений
Новый уменьшенный
интервал неопределенности
выбирается следующим образом.
Слайд 15
а) если
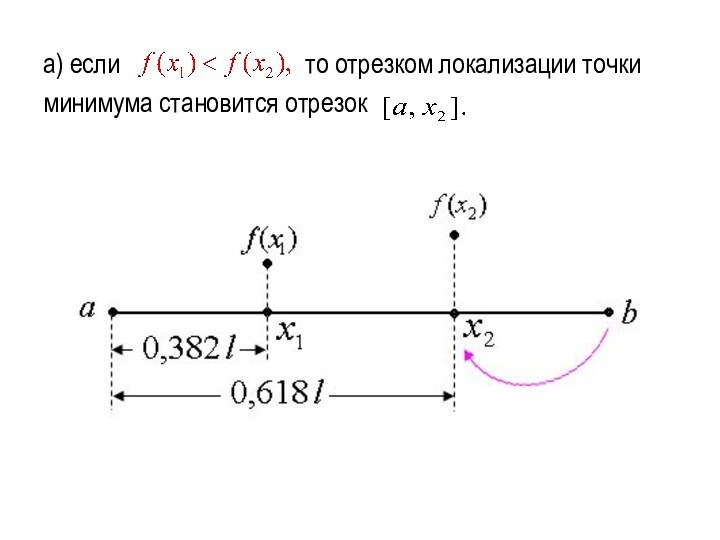
то
отрезком локализации точки
минимума становится отрезок
Слайд 16
Определим положение точки

на интервале
Вычислим отношение
Следовательно точка
является второй точкой
золотого сечения отрезка
Положим
Слайд 17
б) если
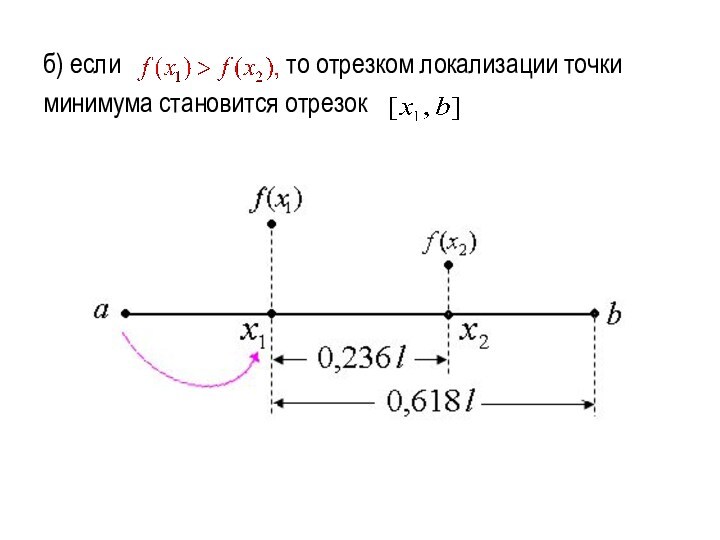
то отрезком локализации
точки
минимума становится отрезок
Слайд 18
Определим положение точки

на интервале
Вычислим отношение
Следовательно точка
первая точка
золотого сечения отрезка
Положим
Слайд 19
Процесс оптимизации заканчивается при выполнении
условия
В качестве минимального

значения берется середина
последнего интервала
Слайд 21
При эффективность

метода золотого сечения
выше, чем у метода дихотомии, так
как при каждом
последующем вычислении целевой функции интервал
неопределенности уменьшается
в раза.
За итераций длина интервала будет равна
Точность на шаге вычислений можно оценить
неравенством
Отсюда следует, что для достижения требуемой точности
требуется
итераций.
Слайд 22
2.2.7. Метод Фибоначчи
Метод Фибоначчи относится к последовательным
стратегиям

и обеспечивает максимальное
сокращение интервала неопределенности при
заданном количестве
вычислений целевой функции.
Алгоритм поиска по методу Фибоначчи
определяется тем же
правилом симметрии, что и
алгоритм по методу золотого сечения: на первой
итерации выбираются две точки, расположенные
симметрично внутри интервала неопределенности ;
на каждой последующей итерации точка очередного
вычисления выбирается симметрично оставшейся
точки. Разница заключается в выборе точек.
Слайд 23
Для простоты изложения алгоритма
рассмотрим интервал неопределенности

Обозначим
через – длину
интервала
Слайд 25
Предположим, что на расстоянии от

одного из концов интервала неопределенности
помещена точка Вторая точка
располагается симметрично
относительно
середины отрезка
Слайд 26
Определим величину Для этого

рассмотрим – ю итерацию.
Для того, чтобы
получить наибольшее
уменьшение интервала неопределенности,
расположим точки
и на расстоянии
по обе стороны от середины отрезка (см.
рисунок).
Слайд 28
Интервал неопределенности будет иметь
длину следовательно
На

предыдущем этапе точки и
должны быть помещены
симметрично
внутри интервала Следовательно
Аналогично
Слайд 30
Общее выражение для произвольного интервала
неопределенности имеет вид
где

коэффициенты называются числами Фибоначчи
и
определяются следующим образом
Последовательность чисел Фибоначчи имеет вид
Слайд 31
Пусть начальный интервал неопределенности имеет
длину

Через числа Фибоначчи
выражение для определения можно получить из
выражения (2.2), полагая
Из последнего выражения найдем длину
интервала неопределенности на -й итерации
Далее, используя выражение (2.2), находим положение
первой точки которая помещается на расстоянии
от одного из концов начального интервала.
Слайд 33
Используемое значение определяется
из

условия
После того как найдено положение первой
точки, числа Фибоначчи
больше не
используются.
Приведем дальнейшую схему вычисления
интервала неопределенности.
Вычислим
Слайд 40
Заметим, что при достаточно больших

значение
стремится к 0.618, так что методы Фибоначчи и
золотого сечения
становятся асимптотически
эквивалентными
Слайд 41
Сравнение методов уменьшения интервала неопределенности
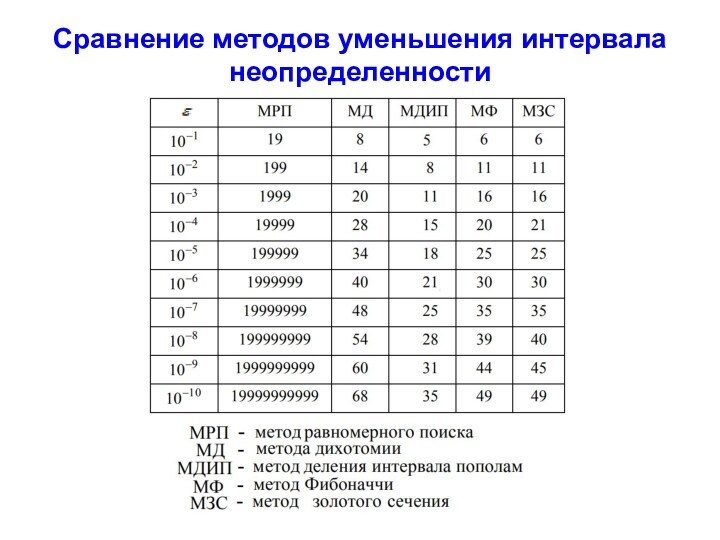
Слайд 42
2.2.8. Метод квадратичной аппроксимации
Основная идея метода связана с

возможностью
аппроксимации гладкой функции полиномом и
последующего использования аппроксимирующего
полинома для оценивания координат точки минимума.
Пусть известны значения целевой функции
в
трех различных точках равные
соответственно
Запишем интерполяционный многочлен в форме
Лагранжа
Слайд 43
Вычислим значения

в каждой из трех точек
При
при
при
Слайд 44
Разрешая последнее уравнение относительно
получим
Из уравнения (2.2)

Слайд 45
находим точку
Поскольку аппроксимирующий квадратичный полином
является унимодальной

функцией, то коэффициент
при старшем члене
будет положителен.
Следовательно, в точке
полином
имеет локальный минимум.
Слайд 46
Рассмотрим алгоритм квадратичной интерполяции, называемый методом Пауэлла.
Пусть

начальная точка,
– величина шага
по оси
и числа, характеризующие точность
поиска.
Вычислить точку
Вычислить значения целевой функции в точках
Сравнить значения и найти точку
так, чтобы точки были как можно ближе к
искомой точке минимума.
Слайд 48
Вычислить
Найти
По трем точкам

вычислить
используя
формулу (2.6) и величину
Если знаменатель в формуле (2.6) на некоторой
итерации обращается в нуль, то результатом
интерполяции будет прямая. В этом случае
рекомендуется обозначить и перейти
к пункту 1.
Слайд 49
Проверить условие окончания процесса вычислений
Если оба условия выполнены,

то поиск закончен и
В противном случае выбрать наилучшую
точку ( или ) и две точки по обе стороны от нее. Обозначить их в естественном порядке и перейти к пункту 5.
Слайд 50
Выбор двух точек слева и справа от наилучшей
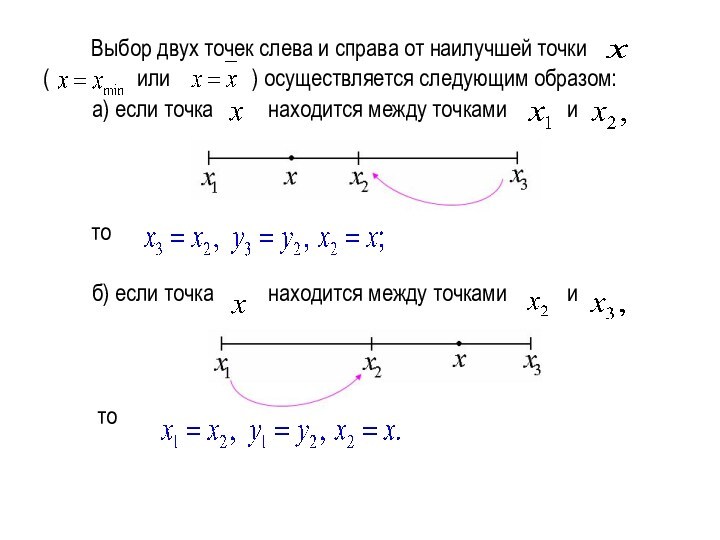
точки
( или
) осуществляется следующим
образом:
а) если точка находится между точками и
то
б) если точка находится между точками и
то
Слайд 54
Пример 2.3. Минимизировать функцию
методом

Пауэлла с точностью
Решение. Зададим начальную точку
и величину шага
Итерация
1. Вычислим и
Так как то положим
Вычислим
Найдем
По формулам (2.4) и (2.5) найдем
По формуле (2.6) вычислим точку интерполяционного полинома
и величину целевой функции
Слайд 55
Проверим условие окончания поиска

(не выполняется),
следовательно продолжаем поиск. Учитывая, что
выбираем как наилучшую точку. Слева от нее
а справа
Обозначим их в естественном порядке
Этим точкам соответствуют значения целевой функции
Итерация 2.
Слайд 56
По формулам (2.4) и (2.5) найдем
По формуле

(2.6) вычислим точку интерполяционного полинома
и величину целевой функции
Проверим
условие окончания поиска
– условие не выполняется.
Выбираем как наилучшую точку. Слева от нее
а справа
Обозначим их в естественном порядке
Этим точкам соответствуют значения целевой функции
Слайд 57
Итерация 3.
По формулам (2.4) и (2.5) найдем
По

формуле (2.6) вычислим точку интерполяционного полинома
и величину целевой
функции
Проверим условие окончания поиска
Следовательно, поиск закончен. Решение
Слайд 58
Найдем аналитически координату точки минимума
Проверим выполнение достаточного условия

экстремума
В точке
выполняется условие
– следовательно целевая функция
в данной точке имеет минимум.
2. Метод Фибоначчи. Метод “золотого сечения”
Одним из методов однопараметрической
оптимизации является метод Фибоначчи.
Предположим, что нужно определить минимум как можно точнее,
т.е. с наименьшим возможным интервалом
неопределенности, но при
этом можно выполнить только n вычислений функции.
Как следует выбрать n точек, в которых вычисляется функция?
С первого взгляда кажется ясным, что не следует искать решение
для всех точек, получаемых в результате эксперимента. Напротив,
надо попытаться сделать так, чтобы значения функции, полученные
в предыдущих экспериментах, определяли положение последующих
точек. Действительно, зная значения функции, мы тем самым имеем
информацию о самой функции и положении ее минимума и используем
эту информацию в дальнейшем поиске.
Предположим, что имеется интервал неопределенности (x1,x3) и известно значение
функции f(x2) внутри этого интервала
(см. рис. 9.3). Если можно
вычислить функцию всего один раз в точке х4,
то где следует поместить точку х4, для
того чтобы получить наименьший возможный интервал неопределенности?

Рис.
9.3.
Положим х2–х1=L и х3–х2=R, причем L > R, как показано на
рис. 9.3, и эти значения будут
фиксированы, если известны x1, x2 и х3.
Если х4 находится в интервале (х1; х2), то:
- если f(x4) < f(x2),
то новым интервалом неопределенности будет (x1,x2) длиной х2–х1=L ; - если f(х4)>f(x2),
то новым интервалом неопределенности будет (х4,х3) длиной х3–х4.
Поскольку не известно, какая из этих ситуаций будет иметь
место, выберем х4 таким образом, чтобы
минимизировать наибольшую из длин х3-х4 и х2-х1. Достигнуть этого
можно, сделав длины х3 – х4 и х2 – х1 равными т.е.
поместив х4 внутри интервала симметрично
относительно точки х2, уже лежащей
внутри интервала. Любое другое положение точки х4 может привести к тому, что полученный
интервал будет больше L. Помещая х4 симметрично относительно х2, мы ничем не рискуем в любом случае.
Если окажется, что можно выполнить еще одно вычисление функции,
то следует применить описанную процедуру к интервалу (х1, х2), в котором уже есть
значение функции, вычисленное в точке х4,
или к интервалу (х4,х3), в
котором уже есть значение функции, вычисленное в точке х2.
Следовательно, стратегия ясна с самого начала. Нужно поместить
следующую точку внутри интервала неопределенности симметрично
относительно уже находящейся там точке. Парадоксально, но, чтобы
понять, как следует начинать вычисления, необходимо разобраться в
том, как его следует кончать.
На n -м вычислении n -ю точку следует
поместить симметрично по отношению к (n — 1) -й точке.
Положение этой последней точки в принципе зависит от нас. Для
того чтобы получить наибольшее уменьшение интервала на данном
этапе, следует разделить пополам предыдущий интервал. Тогда точка х будет совпадать с точкой хn-1. Однако при этом мы не получаем
никакой новой информации. Обычно точки хn-1 и хn отстоят
друг от друга на достаточном расстоянии, чтобы определить, в какой
половине, левой или правой, находится интервал неопределенности.
Они помещаются на расстоянии е/2 по обе стороны от
середины отрезка Ln-1 ; можно самим задать
величину е или выбрать эту величину равной минимально
возможному расстоянию между двумя точками.
Интервал неопределенности будет иметь длину Ln, следовательно, Ln-1 = 2Ln – е
(рис.9.4, нижняя часть). На
предыдущем этапе точки хn-1 и хn-2 должны быть помещены симметрично
внутри интервала Ln-2 на расстоянии Ln-2 от концов этого интервала.
Следовательно, Ln-2 = Ln-1+Ln
(pис.9.4, средняя часть).
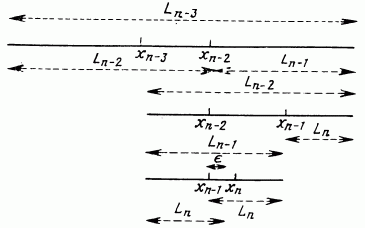
Рис.
9.4.
Замечание. Из рисунка ясно, что на предпоследнем
этапе хn-2 остается в качестве
внутренней точки.
Аналогично Ln-3=Ln-2+Ln-1
(pис. 9.4, верхняя часть)
В общем случае Lj-1=Lj + Lj+1
при 1<j<n.
Таким образом,
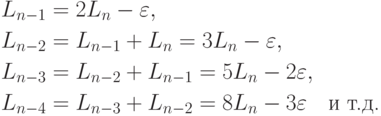
Если определить последовательность чисел Фибоначчи
следующим образом: F0=1, F1=l, и Fk=Fk-1+Fk-2 для k = 2, 3,..., то
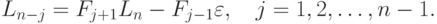 |
( 2.2) |
Если начальный интервал (a;b) имеет длину L = (b-а), то
 |
( 2.3) |
Следовательно, произведя n вычислений функции,
мы уменьшим начальный интервал неопределенности в l/Fn раз по сравнению с его начальной
длиной (пренебрегая е), и это – наилучший результат.
Если поиск начат, то его несложно продолжить, используя
описанное выше правило симметрии. Следовательно, необходимо
найти положение первой точки, которая помещается на расстоянии L2 от одного из концов начального
интервала, причем не важно, от какого конца, поскольку вторая
точкa помещается согласно правилу симметрии на расстоянии L2 от второго конца интервала:
 |
( 2.4) |
После того как найдено положение первой точки, числа Фибоначчи
больше не нужны. Используемое значение е
может определяться из практических соображений. Оно должно быть
меньше L1Fn+x, в противном
случае мы будем напрасно тратить время на вычисление функции.
Таким образом, поиск методом
Фибоначчи, названный так ввиду
появления при поиске чисел Фибоначчи, является итерационной
процедурой. В процессе поиска интервала (x1; x2) с точкой х2, уже
лежащей в этом интервале, следующая точка х2 всегда выбирается такой, что х3–х4 = х2–х1
или х4-х1 = х3-x2,
т.е. x4=х1-х2+х3.
Если f(x2) = f2 и f(x4) = f4,
то можно рассмотреть четыре случая
(рис. 9.5).

Рис.
9.5.
Следующий из методов одномерной оптимизаци называется методом “золотого сечения”.
Не всегда можно заранее определить, сколько раз придется
вычислять функцию. В методе Фибоначчи это нужно знать для
определения L2, т.е. положения
начальной точки (см. уравнение 2.4).
Метод “золотого сечения”
почти столь же эффективен,
как и метод Фибоначчи, однако при этом не требуется знать n – количество вычислений функции, определяемое
вначале. После того как выполнено j вычислений,
исходя из тех же соображений, что и ранее (см. уравнение 2.1),
записываем
 |
( 2.6) |
Однако если n не известно, то мы не можем
использовать условие Ln-1 = Ln – е.
Если отношение последующих интервалов будет постоянным, т.е.
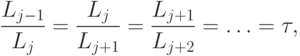 |
( 2.7) |
то

т.е. 
Таким образом, 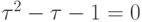 , откуда
, откуда 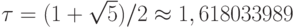 .
.
Тогда

Следовательно,  , т.е.
, т.е.
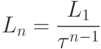 |
( 2.8) |
В результате анализа двух рассмотренных значений функции будет
определен тот интервал, который должен исследоваться в дальнейшем.
Этот интервал будет содержать одну из предыдущих точек и
следующую точку, помещаемую симметрично ей. Первая точка находится
на расстоянии L1/t от одного конца
интервала, вторая – на таком же расстоянии от другого. Поскольку
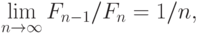
то из уравнения (2.4) видно, что поиск методом “золотого
сечения” является предельной формой поиска методом Фибоначчи.
Название “золотое сечение” произошло от названия
отношения в уравнении (2.7). Видно, что Lj-1
делится на две части так, что отношение целого к большей части равно
отношению большей части к меньшей, т.е. равно так называемому
“золотому отношению”.
Таким образом, если ищется интервал (х0, х3) и имеются два значения
функции f1 и f2 в точках x1 и x2, то следует
рассмотреть два случая (рис. 9.6).

Рис.
9.6.
Метод гарантирует нахождение минимума в самых неблагоприятных
условиях, однако он обладает медленной сходимостью.
Схема алгоритма метода “золотого сечения” представлена
на рис 9.7
Здесь c – константа,
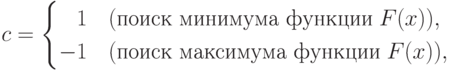
При выводе x – координата точки, в которой функция F(x) имеет минимум (или максимум), FM – значение функции F(x) в этой точке.