Как найти начальный момент инерции - Сайт, где вы сможете решить свои вопросы

Момент инерции
${displaystyle J=int limits _{(m)}r^{2}mathrm {d} m}$
Размерность	L²M
Единицы измерения
СИ	кг·м²
СГС	г·см²

Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции[править | править код]

Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси^[1]:

${displaystyle J_{a}=sum _{i=1}^{n}m_{i}r_{i}^{2},}$

где:

m_i — масса i-й точки,
r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

${displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}$

где:

dm = ρ dV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

${displaystyle J_{a}=rho int limits _{(V)}r^{2}dV.}$

Теорема Гюйгенса — Штейнера[править | править код]

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями^[1]:

${displaystyle J=J_{c}+md^{2},}$

где m — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

${displaystyle J=J_{c}+md^{2}={frac {1}{12}}ml^{2}+mleft({frac {l}{2}}right)^{2}={frac {1}{3}}ml^{2}.}$

Осевые моменты инерции некоторых тел[править | править код]

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Описание	Положение оси a	Момент инерции J_a
Материальная точка массы m	На расстоянии r от точки, неподвижная	$mr^{2}$
Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра	$mr^{2}$
Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра	${frac {1}{2}}mr^{2}$
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁	Ось цилиндра	$m{frac {r_{2}^{2}+r_{1}^{2}}{2}}$ ^{[Комм 1]}
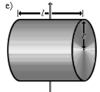
Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна образующей цилиндра и проходит через его центр масс	${1 over 4}mcdot r^{2}+{1 over 12}mcdot l^{2}$
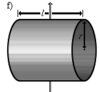
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс	${1 over 2}mcdot r^{2}+{1 over 12}mcdot l^{2}$
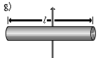
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс	${frac {1}{12}}ml^{2}$
Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец	${frac {1}{3}}ml^{2}$
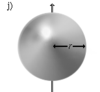
Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы	${frac {2}{3}}mr^{2}$
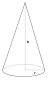
Шар радиуса r и массы m	Ось проходит через центр шара	${frac {2}{5}}mr^{2}$
Конус радиуса r и массы m	Ось конуса	${frac {3}{10}}mr^{2}$
Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину (при высоте)	${frac {1}{24}}m(a^{2}+12h^{2})$
Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс	${frac {1}{12}}ma^{2}$
Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс	${frac {1}{6}}ma^{2}$
Прямоугольник со сторонами a и b и массой m	Ось перпендикулярна плоскости прямоугольника и проходит через центр масс	${frac {1}{12}}m(a^{2}+b^{2})$
Правильный n-угольник радиуса r и массой m	Ось перпендикулярна плоскости и проходит через центр масс	${displaystyle {frac {mr^{2}}{6}}left[1+2cos(pi /n)^{2}right]}$
Тор (полый) с радиусом направляющей окружности R, радиусом образующей окружности r и массой m	Ось перпендикулярна плоскости направляющей окружности тора и проходит через центр масс	${displaystyle I=mleft({frac {3}{4}},r^{2}+R^{2}right)}$

Вывод формул[править | править код]

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

${displaystyle J=sum dJ_{i}=sum R_{i}^{2}dm.qquad (1).}$

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

$J=sum R^{2}dm=R^{2}sum dm=mR^{2}.$

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

$dm=rho dV=rho cdot 2pi rhdr;qquad dJ=r^{2}dm=2pi rho hr^{3}dr.$

Момент инерции толстого кольца найдём как интеграл

$J=int _{R_{1}}^{R}dJ=2pi rho hint _{R_{1}}^{R}r^{3}dr=$

${displaystyle =2pi rho hleft.{frac {r^{4}}{4}}right|_{R_{1}}^{R}={frac {1}{2}}pi rho hleft(R^{4}-R_{1}^{4}right)={frac {1}{2}}pi rho hleft(R^{2}-R_{1}^{2}right)left(R^{2}+R_{1}^{2}right).}$

Поскольку объём и масса кольца равны

$V=pi left(R^{2}-R_{1}^{2}right)h;qquad m=rho V=pi rho left(R^{2}-R_{1}^{2}right)h,$

получаем окончательную формулу для момента инерции кольца

$J={frac {1}{2}}mleft(R^{2}+R_{1}^{2}right).$

Однородный диск (сплошной цилиндр)

Вывод формулы

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

$J={frac {1}{2}}mR^{2}.$

Сплошной конус

Вывод формулы

Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен

$r={frac {Rh}{H}},$

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят

$dm=rho dV=rho cdot pi r^{2}dh;$

$dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left({frac {Rh}{H}}right)^{4}dh;$

Интегрируя, получим

${begin{aligned}J=int _{0}^{H}dJ={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}int _{0}^{H}h^{4}dh={frac {1}{2}}pi rho left({frac {R}{H}}right)^{4}left.{frac {h^{5}}{5}}right|_{0}^{H}=={frac {1}{10}}pi rho R^{4}H=left(rho cdot {frac {1}{3}}pi R^{2}Hright){frac {3}{10}}R^{2}={frac {3}{10}}mR^{2}.end{aligned}}$

Сплошной однородный шар

Вывод формулы

Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

$r={sqrt {R^{2}-h^{2}}}.$

Масса и момент инерции такого диска составят

$dm=rho dV=rho cdot pi r^{2}dh;$

$dJ={frac {1}{2}}r^{2}dm={frac {1}{2}}pi rho r^{4}dh={frac {1}{2}}pi rho left(R^{2}-h^{2}right)^{2}dh={frac {1}{2}}pi rho left(R^{4}-2R^{2}h^{2}+h^{4}right)dh.$

Момент инерции шара найдём интегрированием:

${begin{aligned}J&=int _{-R}^{R}dJ=2int _{0}^{R}dJ=pi rho int _{0}^{R}left(R^{4}-2R^{2}h^{2}+h^{4}right)dh=\&=pi rho left.left(R^{4}h-{frac {2}{3}}R^{2}h^{3}+{frac {1}{5}}h^{5}right)right|_{0}^{R}=pi rho left(R^{5}-{frac {2}{3}}R^{5}+{frac {1}{5}}R^{5}right)={frac {8}{15}}pi rho R^{5}=\&=left({frac {4}{3}}pi R^{3}rho right)cdot {frac {2}{5}}R^{2}={frac {2}{5}}mR^{2}.end{aligned}}$

Тонкостенная сфера

Вывод формулы

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

$J_{0}={frac {2}{5}}MR^{2}={frac {8}{15}}pi rho R^{5}.$

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

${displaystyle {begin{aligned}J&={frac {dJ_{0}}{dR}}dR={frac {d}{dR}}left({frac {8}{15}}pi rho R^{5}right)dR=\&={frac {8}{3}}pi rho R^{4}dR=left(rho cdot 4pi R^{2}dRright){frac {2}{3}}R^{2}={frac {2}{3}}mR^{2}.end{aligned}}}$

Тонкий стержень (ось проходит через центр)

Вывод формулы

Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

$dm={frac {mdr}{l}};qquad dJ=r^{2}dm={frac {mr^{2}dr}{l}}.$

Интегрируя, получим

$J=int _{-l/2}^{l/2}dJ=2int _{0}^{l/2}dJ={frac {2m}{l}}int _{0}^{l/2}r^{2}dr={frac {2m}{l}}left.{frac {r^{3}}{3}}right|_{0}^{l/2}={frac {2m}{l}}{frac {l^{3}}{24}}={frac {1}{12}}ml^{2}.$

Тонкий стержень (ось проходит через конец)

Вывод формулы

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние ^l⁄₂. По теореме Штейнера новый момент инерции будет равен

$J=J_{0}+mr^{2}=J_{0}+mleft({frac {l}{2}}right)^{2}={frac {1}{12}}ml^{2}+{frac {1}{4}}ml^{2}={frac {1}{3}}ml^{2}.$

Безразмерные моменты инерции планет и их спутников^[2]^[3]^[4]

Безразмерные моменты инерции планет и спутников[править | править код]

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра^[5]^[6].

Центробежный момент инерции[править | править код]

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины^[1]^[7]:

${displaystyle J_{xy}=int limits _{(m)}xydm=int limits _{(V)}xyrho dV,}$

${displaystyle J_{xz}=int limits _{(m)}xzdm=int limits _{(V)}xzrho dV,}$

${displaystyle J_{yz}=int limits _{(m)}yzdm=int limits _{(V)}yzrho dV,}$

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела^[7].

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции^[7].

Геометрические моменты инерции[править | править код]

Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

${displaystyle J_{Va}=int limits _{(V)}r^{2}dV,}$

где, как и ранее r — расстояние от элемента dV до оси a.

Размерность J_Va — длина в пятой степени ( $mathrm {dim} J_{Va}=mathrm {L^{5}}$ ), соответственно единица измерения СИ — м⁵.

Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

${displaystyle J_{Sa}=int limits _{(S)}r^{2}dS,}$

где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.

Размерность J_Sa — длина в четвёртой степени ( $mathrm {dim} J_{Sa}=mathrm {L^{4}}$ ), соответственно единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см⁴.

Через геометрический момент инерции площади выражается момент сопротивления сечения:

${displaystyle W={frac {J_{Sa}}{r_{max}}}.}$

Здесь r_max — максимальное расстояние от поверхности до оси.

Геометрические моменты инерции площади некоторых фигур
Прямоугольника высотой и шириной :	$J_{y}={frac {bh^{3}}{12}}$ $J_{z}={frac {hb^{3}}{12}}$
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно	$J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})$ $J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})$
Круга диаметром	$J_{y}=J_{z}={frac {pi d^{4}}{64}}$

Геометрические моменты инерции площади некоторых фигур

Прямоугольника высотой

и шириной

$J_{y}={frac {bh^{3}}{12}}$

$J_{z}={frac {hb^{3}}{12}}$

Прямоугольного коробчатого сечения высотой и шириной по внешним контурам

, а по внутренним

соответственно

$J_{z}={frac {BH^{3}}{12}}-{frac {bh^{3}}{12}}={frac {1}{12}}(BH^{3}-bh^{3})$

$J_{y}={frac {HB^{3}}{12}}-{frac {hb^{3}}{12}}={frac {1}{12}}(HB^{3}-hb^{3})$

Круга диаметром

$J_{y}=J_{z}={frac {pi d^{4}}{64}}$

Момент инерции относительно плоскости[править | править код]

Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости^[9].

Если через произвольную точку провести координатные оси x,y,z , то моменты инерции относительно координатных плоскостей xOy , yOz и zOx будут выражаться формулами:

${displaystyle J_{xOy}=sum _{i=1}^{n}m_{i}z_{i}^{2} ,}$

${displaystyle J_{yOz}=sum _{i=1}^{n}m_{i}x_{i}^{2} ,}$

${displaystyle J_{zOx}=sum _{i=1}^{n}m_{i}y_{i}^{2} .}$

В случае сплошного тела суммирование заменяется интегрированием.

Центральный момент инерции[править | править код]

Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) ${displaystyle J_{O}}$ — это величина, определяемая выражением^[9]:

${displaystyle J_{a}=int limits _{(m)}r^{2}dm=int limits _{(V)}rho r^{2}dV,}$

где:

Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей^[9]:

${displaystyle J_{O}={frac {1}{2}}left(J_{x}+J_{y}+J_{z}right),}$

${displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}$

Тензор инерции и эллипсоид инерции[править | править код]

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором ${displaystyle {vec {s}}=leftVert s_{x},s_{y},s_{z}rightVert ^{T},leftvert {vec {s}}rightvert =1}$ , можно представить в виде квадратичной (билинейной) формы:

${displaystyle I_{s}={vec {s}}^{T}cdot {hat {J}}cdot {vec {s}},qquad }$

(1)

где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:

${displaystyle {hat {J}}=leftVert {begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\-J_{yx}&J_{yy}&-J_{yz}\-J_{zx}&-J_{zy}&J_{zz}end{array}}rightVert ,}$

${displaystyle J_{xy}=J_{yx},quad J_{xz}=J_{zx},quad J_{zy}=J_{yz},quad }$

${displaystyle J_{xx}=int limits _{(m)}(y^{2}+z^{2})dm,quad J_{yy}=int limits _{(m)}(x^{2}+z^{2})dm,quad J_{zz}=int limits _{(m)}(x^{2}+y^{2})dm.}$

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :

${displaystyle {hat {J}}_{d}={hat {Q}}^{T}cdot {hat {J}}cdot {hat {Q}},}$

${displaystyle {hat {J}}_{d}=leftVert {begin{array}{ccc}J_{X}&0&0\0&J_{Y}&0\0&0&J_{Z}end{array}}rightVert ,}$

где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины ${displaystyle J_{X},J_{Y},J_{Z}}$ — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

${displaystyle I_{s}=J_{X}cdot s_{x}^{2}+J_{Y}cdot s_{y}^{2}+J_{Z}cdot s_{z}^{2},}$

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на ${displaystyle I_{s}}$

${displaystyle left({s_{x} over {sqrt {I_{s}}}}right)^{2}cdot J_{X}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}cdot J_{Y}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}cdot J_{Z}=1}$

и произведя замены:

${displaystyle xi ={s_{x} over {sqrt {I_{s}}}},eta ={s_{y} over {sqrt {I_{s}}}},zeta ={s_{z} over {sqrt {I_{s}}}},}$

получаем канонический вид уравнения эллипсоида в координатах :

${displaystyle xi ^{2}cdot J_{X}+eta ^{2}cdot J_{Y}+zeta ^{2}cdot J_{Z}=1.}$

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

${displaystyle r^{2}=xi ^{2}+eta ^{2}+zeta ^{2}=left({s_{x} over {sqrt {I_{s}}}}right)^{2}+left({s_{y} over {sqrt {I_{s}}}}right)^{2}+left({s_{z} over {sqrt {I_{s}}}}right)^{2}={1 over I_{s}}.}$

См. также[править | править код]

Кинематика твёрдого тела
Метод главных компонент
Сопротивление материалов
Теорема Штейнера
Теорема Кёнига (механика)
Механические приложения тройного интеграла
Механические приложения двойного интеграла
Полярный момент инерции
Список моментов инерции
Момент силы
Момент импульса

Комментарии[править | править код]

↑ При получении этой формулы путём вычитания момента инерции сплошного цилиндра радиусом r₁ из цилиндра радиусом r₂ необходимо обратить внимание, что их массы при этом не будут одинаковыми или равны m. При этом должно выполняться условие ${displaystyle m_{2}-m_{1}=m}$ . Из формулы для массы соответствующего цилиндра можно определить, что в этом случае ${displaystyle m_{1}=m{frac {r_{1}^{2}}{r_{2}^{2}-r_{1}^{2}}}}$ и ${displaystyle m_{2}=m{frac {r_{2}^{2}}{r_{2}^{2}-r_{1}^{2}}}}$ . В правильности использования знака «+» в этой формуле также можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r₁ к r₂ формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».

Примечания[править | править код]

↑ ¹ ² ³ Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Planetary Fact Sheet. Дата обращения: 31 августа 2010. Архивировано 14 марта 2016 года.
↑ Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — doi:10.1126/science.286.5437.77. — PMID 10506564.
↑ Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.) (рус. : journal. — 2012. — Vol. 117. — doi:10.1029/2012JE004161.
↑ Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты. Дата обращения: 31 августа 2010. Архивировано 3 октября 2013 года.
↑ ¹ ² ³ Тарг С. М. Краткий курс теоретической механики. — М.: «Высшая школа», 1995. — С. 269—271. — 416 с. — ISBN 5-06-003117-9.
↑ ¹ ² Бухгольц Н. Н. Основной курс теоретической механики. — 4-е изд. — М.: «Наука», 1966. — Т. 2. — С. 131.
↑ ¹ ² ³ Яблонский А. А. Динамика // Курс теоретической механики. — 3-е изд. — М.: «Высшая школа», 1966. — Т. II. — С. 102—103. — 411 с.

Литература[править | править код]

Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Архивная копия от 7 января 2014 на Wayback Machine Издательство Физического факультета МГУ, 1997.
Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки[править | править код]

Определение момента инерции тел простой формы.

Источник

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

фото из интернета

В нашем обиходе довольно часто встречаются выражения « он совершенно инертный» или «его инертность заставляет задуматься». Их применяют в отношении человека, который не обладает инициативой и не привык двигаться. Существуют другие понятия такого лица, но думаю, что они больше относятся к медицине. В общем понимании это человек не любящий принимать собственных решений. Или возьмем пример из цирка, где силач под аплодисменты зрителей выдерживает валун огромной массы. Данный объект лежит совершенно спокойно и не совершает никаких движений. Напарник бьет по камню и атлету совершенно не больно. Вся причина кроется в том, что объект инертен по отношению к цирковому артисту. Если бы на месте огромного валуна был маленький камушек, был бы тот же эффект.

Также можем применить пример из жизни, когда пешеход стоит на проезжей части и наблюдает за несущимся автомобильным потоком. Тяжелогруженная машина, если решила совершить остановку начинает тормозить раньше, чем легковая и совершает движение по инерции под влиянием груза. Естественно, что грузовик продвинется гораздо дальше по сравнению с легковушкой.

Момент инерции простыми словами: определение, формулы, примеры решения задач

Что такое инерция

В научном понимании это свойство тел находится в состоянии покоя, при этом внешние силы никакого воздействия не осуществляют. Понятие момента инерции вызывает определенный вопрос. Не каждому обывателю понятно это выражение, поэтому разберем его подробнее. Инерция, это свойство отдельного тела, лежать в спокойном состоянии при отсутствии на него внешних действий различной силы. Также объект может воспрепятствовать изменчивости скоростных показателей. Из жизни мы можем привести такой пример, когда машина находится на льду и начинает тормозить, то она не сразу останавливается, а совершает поступательное движение благодаря льду. Весь тормозной путь будет считаться инерцией. Или размешивая чай в стакане после того, как перестанем мешать, жидкость продолжает совершать вращательное движение. Это будет считаться инерцией.

Определение момента инерции

Еще со школьной скамьи нам было известно, что масса, это масса инертности тела. Если к примеру, мы совершим толчок двух вагонов у которых разный вес, то совершенно понятно, что остановить труднее будет тот вагон, у которого масса тяжелее. Одним словом, чем больше вес, тем нужно большее усилие для совершения движения. В данной ситуации мы рассматриваем поступательное движение, когда вагон совершает движение прямо.

Понятие момента инерции, включает в себя меру инертности тела при вращении вокруг своей оси. Момент инертности является физическим значением и обозначается буквой J. Измеряемость данной величины кг умноженный на метр в квадрате.

Высчитывают момент инертности при помощи следующей формулы.

Применяется она обычно в научной физике, при вычислении момента инерции тела. Если представить объект, разбившийся на несколько кусков, то момент инерции будет равняться сумме этих кусков, умноженный на квадрат расстояния к оси вращения. Так определяют момент инерции в физике. Если брать реальность, то определение происходит в результате расчетов, произведенных по формуле Штейнера.

Теорема Штейнера

Прежде всего, нам нужно понять, отчего зависит момент инерции. Ответ достаточно прост: от веса, оси вращения, формы и габаритов объекта. Теорема Штейнера имеет важное значение и студенты часто ее используют для решения различных задач. Что же она обозначает? Она имеет следующую формулировку. Момент инерции объекта относительно оси равен сумме момента инерции тела относительно оси, которая проходит через центр параллельно оси и произведения массы тела на квадрат расстояния между осями.

Немного мудреное понятие, но именно так объясняется теорема. В физике существуют разнообразные виды инерции: например, центральный или геометрический. Момент инерции является единицей измерения для тела, которое совершает вращательное движение вокруг своей оси.

Пример решения задачи

Вашему вниманию представим 2 варианта. В первом случае мы попытаемся найти момент инерции, а во втором, применим знания полученные при изучении теоремы Штейнера.

Упражнение 1. Установить момент инерции диска весом М и радиусом Р. Ось вращения соответственно расположена по центру объекта.

Оптимальное решение:

Диск делится на маленькие колечки, радиус которых изменяется от 0 до Р. Разберем более подробно отдельное кольцо. Обозначим, что его вес равен значение м, а радиус показателю р. Тогда получим момент инерции равный: DJ= DMR в квадрате.

Массу кольца можно представить в виде:

Упражнение 2. Установить момент инерции диска с массой М и радиусом Р.

Оптимальное решение:

Используя формулу Штейнера решаем упражнение, J = Jc+ мd в квадрате. Подставляем полученные данные в формулу и получаем решение.

Момент инерции неотъемлемо имеет связь с другими популярными физическими законами. Например, со вторым законом Ньютона. В данном случае момент инерции принимает значение массы.

Остались вопросы или нужна помощь, есть замечания по данной статье пишите в комментариях будем рады подискутировать, так же подписывайтесь на наш канал или другие соц сети:

ПОДПИСАТЬСЯ НА КАНАЛ I Сайт Антиплагиату НЕТ I ВКОНТАКТЕ

Источник

Определение момента инерции

Момент
инерции J (кгм2) – параметр, аналогичный
по физическому смыслу массе при
поступательном движении. Он характеризует
меру инерции тел, вращающихся относительно
фиксированной оси вращения. Момент
инерции материальной точки с массой m
равен произведению массы на квадрат
расстояния от точки до оси вращения:
.

Момент
инерции тела есть сумма моментов инерции
материальных точек, составляющих это
тело. Он может быть выражен через массу
тела и его размеры[1].

Моменты
инерции однородных тел простых форм
приведены в табл. 2.1.

Таблица
2.1

Моменты
инерции некоторых однородных тел

Диск или цилиндр вращающийся вокруг центральной оси
Момент инерции стержня при вращении относительно оси, проходящей через его конец
Момент инерции стержня при вращении относительно оси, проходящей через его центр
Момент инерции шара при вращении относительно оси, проходящей через его центр

Момент
инерции тела, если известно распределение
массы тела относительно оси вращения
mi (R), может быть определён как

.
(2.11)

Детали
электропривода, например ротор
электрической машины, представляют
собой конструкции, состоящие из деталей
сложных форм и изготовленные из материалов
различной плотности. Следовательно,
расчёт момента инерции связан со
значительными трудностями.

В
случаях, когда расчёт момента инерции
не возможен либо затруднён, используют
следующие методы экспериментального
определения момента инерции.

Метод
свободного выбега (самоторможения)[2].
Сущность этого метода состоит в следующем.
Исследуемый агрегат, включающий в себя
электродвигатель и механически
соединённые с ним элементы, разгоняется
до некоторой установившейся частоты
вращения в режиме х.х..
После этого электродвигатель отключают
от сети и наступает процесс самопроизвольного
торможения, т.е. торможения исключительно
за счёт внутренних сил трения в подшипниках
электродвигателя и сочленённых с ним
вращающих частей о воздух. На преодоление
этих сил трения затрачивается кинетическая
энергия (Дж), запасенная во вращающихся
частях агрегата:

.
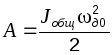
(2.12)

С
другой стороны, эта энергия может быть
определена как произведение мощности,
затраченной на приведение во вращение
агрегата в режиме х.х.
на
время:

.
(2.13)

Приравняв
(9.1) к (9.2), получим выражение общего
момента инерции, кг·м2:

.
(2.14)

Значения
иопределяют
экспериментально, выполнив опыт х.х. и
опыт свободного выбега, по кривой выбега:.

Метод
вспомогательного маятника. Этот метод
применяют в тех случаях, когда метод
свободного выбега не может быть
использован, в частности для электрических
машин большой мощности – до 1000 кВт.

Для
реализации этого метода вращающуюся
часть машины устанавливают на подшипниках
балансировочного станка. Если вращающаяся
часть машины имеет собственные подшипники,
то могут быть использованы и они.
Испытания проводят на собственной
машине. У коллекторных машин или
асинхронных двигателей с фазным ротором
при определении момента инерции следует
поднять щётки.

При
использовании метода вспомогательного
маятника к валу исследуемой вращающейся
части прикрепляют дополнительную массу
mдоп центр тяжести которой находится
на расстоянии а от центра вала.

Вращающуюся
часть вместе со вспомогательным маятником
следует привести в колебательное
движение. При этом одностороннее угловое
отклонение не должно превышать 15о.
Период колебаний принимают как средний
из нескольких колебаний. Для точности
рекомендуется производить измерения
периода колебаний в момент нахождения
маятника через положение статического
равновесия.

Момент
инерции испытуемой вращающейся части
определяется по формуле

.
(2.15)

Для
повышения точности измерения момента
инерции рекомендуется проводить
измерения несколько раз с разными
значениями дополнительной массы
вспомогательного маятника mдоп или
расстояния а.[3]

10.Приведення
моментів інерції і сил опору.

Приведення
моментів опору і моментів інерції при

обертальному
русі

Зазвичай
двигун приводить в дію робочий механізм
через систему передач (рисунок 2.1).

Приведення
моментів опору до вісі обертання
електродвигуна виконується на основі
енергетичного балансу всієї системи.
При цьому статичний момент опору,
приведений до валу двигуна

де – статичний момент опору робочого
механізму;

– швидкість обертання валу робочого
механізму;

– швидкість обертання валу двигуна;

– коефіцієнт корисної дії передачі
(редуктора).

Приведення
моментів інерції до однієї вісі обертання
спирається на те, що величина сумарного
запасу кінетичної енергії частин
приводу, що рухаються, віднесена до
однієї вісі, залишається незмінною. При
наявності обертових частин, що мають
моменти інерції
і кутові швидкості,
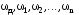
можна замінити їх динамічну дію дією
одного моменту інерції, приведеного до
швидкості обертання валу двигуна, тобто

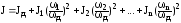
Зазвичай
в робочих механізмах використовуються
редуктори, в яких частини, що рухаються,
мають форму порожнього циліндру,
зрізаного конусу і прямолінійного
тонкого стрижня (вал). Моменти інерції
цих тіл визначаються наступними виразами.

Для
довгого тонкого валу відносно його вісі
обертання

де m –
маса валу;

l –
довжина валу.

Для
порожнього циліндра відносно його вісі
обертання

де R1,
R2 – зовнішній і внутрішній радіуси
циліндру.

Для
зрізаного прямого конусу відносно його
вісі обертання

де R1,
R2 – радіуси основ конусу.

Для
суцільного циліндру

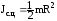
Приведення
сили і маси при поступальному русі до
моменту при обертальному русі

Необхідність
приведення поступального руху до
обертального виникає, наприклад, у
підйомниках, кранах, стругальних
верстатах і т.п.

Приведений
до швидкості обертання валу двигуна
підйомника (рисунок 2.2) момент опору

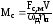
де Fс.м
– сила опору робочого механізму,
обумовлена силою ваги вантажу G, який
рухається поступально;

V –
швидкість поступального руху вантажу.

Момент
інерції, приведений до валу двигуна,

Якщо
механізм має елементи, які рухаються
обертально і поступально, то сумарний
приведений до валу двигуна момент
інерції

11.Система
рівнянь двигуна незалежного збудження
(ДНЗ) для природного ввімкнення.

Для
получения простейшей модели электропривода
постоянного тока, описывающей
установившиеся (статические) режимы и
позволяющей получить основные
характеристики, воспользуемся схемой
на рис. 1.

Будем
полагать, что якорная цепь питается от
независимого источника с напряжением
U* , сопротивление цепи якоря R постоянно,
магнитный поток Ф определяется лишь
током возбуждения и не зависит от
нагрузки (реакция якоря не проявляется),
индуктивные параметры цепей пока не
учитываются, поскольку рассматриваются
лишь установившиеся (статические)
режимы.

Рис.
1. Схема электропривода с двигателем
постоянного тока

Взаимодействие
тока I в обмотке якоря с магнитным потоком
Ф, создаваемым обмотками, расположенными
на полюсах машины, приводит в соответствии
с законом Ампера и возникновению
электромагнитных сил, действующих на
активные проводники обмотки и,
следовательно, электромагнитного
момента М:

М
= kФI
(1)

где
k- конструктивный параметр машины.

В
движущихся с угловой скоростью
в
магнитном поле под действием момента
М проводниках обмотки якоря в соответствии
с законом Фарадея наводится ЭДС вращения
Е:

E
= kФw ,
(2)

направленная
в рассматриваемом случае встречно по
отношению к вызвавшей движение причине
– ЭДС источника питания U.

В
соответствие со вторым законом Кирхгоффа
для якорной цепи машины справедливо
уравнение:

U-E
= IR.
(3)

Уравнения
(1)-(3) – простейшая, но достаточная для
понимания главных процессов в
электроприводе постоянного тока модель.
Для решения практических задач они
должны быть дополнены уравнением
движения с моментом потерь
,
входящим в Мс,

и
уравнениями цепи возбуждения для
конкретной схемы электропривода.

Разумеется,
в условиях каждой задачи должно быть
строго оговорено, что задано и известно,
а что нужно искать.

Рассмотрим
подробнее роль, которую играет ЭДС Е в
процессе преобразования энергии,
осуществляемом электрической машиной.
Если существовал некоторый установившийся
режим М1 = Мс1, а затем Мс изменился,
например, возрос до величины Мс2, то для
получения нового установившегося режима
необходимо иметь средство, которое
изменило бы М, приведя его в соответствие
с новым значением Мс. В двигателе
внутреннего сгорания эту роль выполнит
оператор, увеличив подачу топлива; в
паровой турбине – специальный регулятор,
который увеличит подачу пара. В
электрической машине эту роль выполнит
ЭДС. Действительно, при возрастании Мс
скорость двигателя начнет снижаться,
значит уменьшится в соответствии с (2)
и ЭДС (полагаем для простоты, что Ф, а
также U и R – постоянные). Из (3) следует,
что

следовательно,
ток вырастет, обусловив тем самым рост
момента в соответствии с (1). Двигатель
автоматически, без каких-либо внешних
воздействий перейдет в новое установившееся
состояние. Эти процессы будут иметь
место при любых величинах и знаках Мс,
то есть ЭДС будет выполнять функцию
регулятора как в двигательном, так и в
тормозных режимах работы машины.

12.Природні
механічні характеристики ДНЗ.

Двигатели
независимого и параллельного возбуждения.

Схема включения двигателя независимого
возбуждения показана на рис.
5.19.

Рис.
5.19.

В
цепь якоря может быть включено добавочное
сопротивление Rд, например пусковой
реостат. Для регулирования тока
возбуждения в цепь обмотки возбуждения
может быть включен регулировочный
реостат Rр. У двигателя параллельного
возбуждения обмотки якоря и возбуждения
подключены к одному источнику питания,
и напряжение на них одинаковое.
Следовательно, двигатель параллельного
возбуждения можно рассматривать как
двигатель независимого возбуждения
при Uя= Uв.

Механические
характеристики.
Механические
характеристики двигателей принято
подразделять на естественные и
искусственные. Естественная характеристика
соответствует номинальному напряжению
питания и отсутствию добавочных
сопротивлений в цепях обмоток двигателя.
Если хотя бы одно из перечисленных
условий не выполняется, характеристика
называется искусственной.
Уравнения
электромеханической ω=f(I я) и механической
ω=f(M эм.) характеристик могут быть найдены
из уравнения равновесия ЭДС и напряжений
для якорной цепи двигателя, записанного
на основании второго закона Кирхгофа:

U
я=E я+I я)(R я+R д), (5.35)

где
R я – активное сопротивление
якоря.
Преобразуя (5.35) с
учетом (5.6), получим уравнение
электромеханической характеристики

ω=(U
я-I я(R я+R д))/kФ. (5.36)

В
соответствии с (5.10) ток якоря I я=M эм./kФ
и выражение (5.36) преобразуется в уравнение
механической характеристики:

ω=Uя/
kФ – ( R я+ R д)/( kФ) 2)Mэм. . (5.37)

Это
уравнение можно представить в виде ω=
ω о.ид.- Δ ω, где

ω
о.ид.=Uя/kФ (5.38)

ω
о.ид – угловая скорость идеального
холостого хода ( при Iя=0 и, соответственно,
Мэм.=0 ); Δ ω= Мэм. [(Rя+Rд)/(kФ)2]– уменьшение
угловой скорости, обусловленное нагрузкой
на валу двигателя и пропорциональное
сопротивлению якорной цепи.
Семейство
механических характеристик при
номинальном напряжении на якоре и потоке
возбуждения и различных добавочных
сопротивлениях в цепи якоря изображено
на рис.
5.20,а.

Рис.5.20

Механические
характеристики двигателей принято
оценивать по трем показателям:
устойчивости, жесткости и
линейности.
Естественная
механическая характеристика,
соответствующая (5.37) при Rд=0, изображена
прямой линией 1. Механическая характеристика
линейная; отклонение от линейного закона
может быть вызвано реакцией якоря,
приводящей к изменению потока Ф. Эта
характеристика жесткая, так как при
изменении момента нагрузки и соответственно
скорости поток возбуждения не изменяется.
Жесткость характеристики уменьшается
при введении добавочного сопротивления
в цепь якоря (прямые линии 2 и 3 –
искусственные реостатные характеристики).
Характеристики устойчивые, так как
dω/dMэм.<0, и обеспечивают саморегулирование
двигателя, т.е. он автоматически
приспосабливается к изменяющейся
нагрузке. Увеличение статического
момента сопротивления на валу двигателя
приводит к уменьшению угловой скорости
и ЭДС якоря. Ток якоря, выражение для
которого можно записать на основании
(5.35),

Iя=
(Uя-Eя)/(R я+ R д)=(Uя -kωФ;)/( R я R д ),
(5.39)

возрастает.
Соответственно растет электромагнитный
момент вплоть до нового значения момента
сопротивления (переход из точки А в
точку В на механической характеристике).
По
аналогии на основании (5.37) может быть
построено семейство искусственных
характеристик при различных значениях
Uя или Ф. Анализ таких характеристик
будет проделан в разделе исполнительных
двигателей постоянного тока (§ 5.7).

13.Штучні
характеристики ДНЗ.

Механические
характеристики двигателей принято
подразделять на естественные и
искусственные.Механическая характеристика
двигателя это зависимость электромагнитного
момента, развиваемого двигателем, от
угловой скорости ротора. Механические
характеристики двигателей принято
подразделять на естественные и
искусственные. Естественная характеристика
соответствует номинальному напряжению
питания и отсутствию добавочных
сопротивлений в цепях обмоток двигателя.
Если хотя бы одно из перечисленных
условий не выполняется, характеристика
называется искусственной.

14.Статичні
режими роботи ДНЗ.

15.Переваги
ДНЗ перед двигунами послідовного
збудження.

16.Переваги
асинхронних (АД) двигунів перед
колекторними.

Преимущество
асинхронных двигателей перед коллекторными
— они не имеют коллектора, следовательно,
в асинхронном двигателе меньше потерь
на трение.

17.Схема
заміщення (АД)

Асинхронними
двигунами називаються такі двигуни
змінного струму, в яких швидкість
обертання ротора n при даній частоті
струму в мережі змінюється зі зміненням
навантаження.

Асинхронні
двигуни бувають трифазні, двофазні та
однофазні. Найбільш широке застосування
в РЛС та АСУ одержали трифазні та двофазні
асинхронні двигуни. Вони застосовуються
для обертання антени, вентиляторів, у
системах слідкування тощо.

Асинхронні
двигуни, як і інші електромашини,
зворотні, тобто можуть працювати в
режимі генератора. Але асинхронні
генератори застосовуються порівняно
рідко, оскільки вони значно поступаються
синхронним генераторам за своїми
“характеристиками”.

СХЕМА
ЗАМІЩЕННЯ АСИНХРОННОГО ДВИГУНА

Рис.
3. Схема замещения фазы асинхронного
двигателя

Принцип
действия асинхронной машины в самом
общем виде состоит в следующем: один из
элементов машины – статор используется
для создания движущегося с определенной
скоростью магнитного поля, а в замкнутых
проводящих пассивных контурах другого
элемента – ротора наводятся ЭДС, вызывающие
протекание токов и образование сил
(моментов) при их взаимодействии с
магнитным полем. Все эти явления имеют
место при несинхронном – асинхронном
движении ротора относительно поля, что
и дало машинам такого типа название –
асинхронные.

Статор
обычно выполнен в виде нескольких
расположенных в пазах катушек, а ротор
– в виде “беличьей клетки” (короткозамкнутый
ротор) или в виде нескольких катушек
(фазный ротор), которые соединены между
собой, выведены на кольца, расположенные
на валу, и с помощью скользящих по ним
щеток могут быть замкнуты на внешние
резисторы.

Несмотря
на простоту физических явлений и
материализующих их конструктивов полное
математическое описание процессов в
асинхронной машине весьма сложно:

во-первых,
все напряжения, токи, потокосцепления
– переменные, т.е. характеризуются
частотой, амплитудой, фазой или
соответствующими векторными величинами;

во-вторых,
взаимодействуют движущиеся контуры,
взаимное расположение которых изменяется
в пространстве;

в-третьих,
магнитный поток нелинейно связан с
намагничивающим током (проявляется
насыщение магнитной цепи), активные
сопротивления роторной цепи зависят
от частоты (эффект вытеснения тока),
сопротивления всех цепей зависят от
температуры и т.п.

Рассмотрим
самую простую модель асинхронной машины,
пригодную для объяснения основных
явлений в асинхронном электроприводе.

Принцип
получения движущегося магнитного
поля

Пусть
на статоре расположен виток (катушка)
А-Х (рис. 1,а,б), по которому протекает
переменный ток iA = Imsinw t; w = 2p f1. МДС FА,
созданная этим током, будет пульсировать
по оси витка

FА
= Fmsinw t

а)

б)

в)

г)

Рис.
1. К образованию
вращающегося
магнитного поля в машине

(горизонтальные
штриховые стрелки на рис. 1,в). Если
добавить виток (катушку) В-Y, расположенный
под углом 900 к А-Х, и пропускать по нему
ток iB = Imcosw t, то МДС FВ будет пульсировать
по оси этого витка
(вертикальные
стрелки):

FВ
= Fmcosw t.

Вектор
результирующей
МДС имеет модуль

Его
фаза a определится из условия

Таким
образом, вектор результирующей МДС при
принятых условиях, т.е. при сдвиге двух
витков в пространстве в
и
при сдвиге токов во времени на,
вращается с угловой скоростью,
где f1 – частота токов в витках.

В
общем случае для машины, имеющей р пар
полюсов (р=1,2,3…), синхронная угловая
скорость
,
рад/с, т.е. скорость поля, определится
как

;

(1)

для
частоты вращения n0, об/мин, будем иметь:

,

(2)

т.е.
при питании от сети f1=50Гц синхронная
частота вращения может быть 3000, 1500, 1000,
750, 600… об/мин в зависимости от конструкции
машины.

Выражения
(1) и (2) имеют принципиальный характер:
они показывают, что для данной машины
имеется лишь одна возможность изменять
скорость поля – изменять частоту источника
питания f1.

Процессы
при w = w 0

Пусть
ротор вращается со скоростью w 0, т.е. его
обмотки не пересекают силовых линий
магнитного поля и он не оказывает
существенного влияния на процессы.

В
весьма грубом, но иногда полезном
приближении можно представить обмотку
фазы статора как некоторую идеальную
катушку, к которой приложено переменное
напряжение
.
Мы будем дальше либо обозначать его и
другие синусоидально изменяющиеся
переменные соответствующими заглавными
буквами, если интерес представляют лишь
их действующие значения, либо будем
добавлять точку вверху, показывая тем
самым, что речь идет о временнo м векторе,
имеющем амплитудуи
фазу j .

Очевидно,
что приложенное напряжение
уравновесится
ЭДС самоиндукции(рис.
2,а,б)

,
(3)

где
w – число витков обмотки; kоб – коэффициент,
зависящий от конкретного выполнения
обмотки.

а)
б) в)

Рис.
2. Идеализированная модель асинхронной
машины при w = w 0 (а), векторная диаграмма
(б) и кривая намагничивания (в)

Можно
приближённо считать, что магнитный
поток определяется приложенным
напряжением, частотой и параметрами
обмотки:

.
(4)

Ток
в обмотке (фазе) статора – ток намагничивания
определится при этом лишь магнитным
потоком и характеристикой намагничивания
машины (рис. 2,в):

В
серийных машинах при U1=U1н и f1=f1н, т.е. при
номинальном магнитном потоке ток
холостого хода I10 составляет обычно 30%
– 40% от номинального тока статора I1н.

Процессы
под нагрузкой

При
нагружении вала
;
отличие скоростей w и w 0 принято
характеризовать скольжением

.

(5)

Теперь
в роторной цепи появится ЭДС,
наведенная по закону электромагнитной
индукции и равная

=E1ў
s;
(6)

штрихом
здесь и далее отмечены приведенные
величины, учитывающие неодинаковость
обмоток статора и ротора. Частота
наведенной ЭДС составляет

f2=f1s

(7)

Ток
I2ў в роторной цепи, обладающей
сопротивлением R2ў и индуктивностью L2ў
, определится как

или
после простых преобразований

,
(8)

где
Х2ў – индуктивное сопротивление рассеяния
вторичной цепи при частоте f1.

Мы
получили уравнение, соответствующее
традиционной схеме замещения фазы
асинхронного двигателя – рис. 3, в которой
учтены и параметры статора R1 и Х1. Эта
простая модель пригодна для анализа
установившихся режимов при симметричном
двигателе с симметричным питанием.

Рис.
3. Схема замещения фазы асинхронного
двигателя

18.
Механічна характеристика АД.(есть в
Чиликине -74стр.)

Асинхронные
двигатели в силу ряда достоинств
(относительная дешевизна, высокие
энергетические показатели, простота
обслуживания) являются наиболее
распространенными среди всех электрических
машин. В количественном отношении
они составляют около 90 % всего парка
машин в народном хозяйстве, а по
установленной мощности – около 55 %.[1]

В
настоящее время самым распространённым
двигателем промышленных электроприводов
является трёхфазный асинхронный
двигатель с короткозамкнутым ротором.
Про него можно сказать, что он является
самым простым, самым надёжным и самым
дешёвым электродвигателем в широком
диапазоне частоты вращения и мощности.
Самым эффективным и самым распространённым
среди глубокорегулируемых асинхронных
электроприводов является частотно-регулируемый
электропривод на основе преобразователя
частоты с промежуточным звеном постоянного
тока.

Применение
частотно-регулируемого асинхронного
электропривода в механизмах
подъемно-транспортного оборудования
является эффективным методом повышения
технологичности производства.
Использование таких приводов позволяет:

1)
значительно (до 40 %) снизить энергопотребление
крана, что особенно актуально при
постоянно растущих тарифах на
энергоносители;

2)
осуществить разгон и торможение двигателя
плавно, по линейному закону от времени,
при варьировании временем разгона и
временем торможения от долей секунды
до 50 мин;

3)
повысить комфортные показатели при
движении крана и долговечность
механического оборудования благодаря
плавности переходных процессов;

4)
защитить двигатель от перегрузок по
току, перегрева, утечек на землю и от
обрывов в цепях питания двигателей;

5)
снизить эксплуатационные расходы на
капитальный ремонт оборудования за
счет значительного снижения динамических
нагрузок в элементах кинематической
цепи;

6)
изменять скорости и ускорения движения
механизмов крана применительно к
конкретным технологическим задачам.

Эффективность
и экономичность таких электроприводов
в значительной степени зависит от
правильности выбора номинальных
параметров их основных элементов, т.е.
двигателя и преобразователя частоты[2].

Принцип
действия асинхронной машины в самом
общем виде состоит в следующем: один из
элементов машины – статор используется
для создания движущегося с определенной
скоростью магнитного поля, а в замкнутых
проводящих пассивных контурах другого
элемента – ротора наводятся ЭДС,
вызывающие протекание токов и образование
сил (моменты) при их взаимодействии с
магнитным полем. Все эти явления имеют
место при несинхронном (асинхронном)
движении ротора относительно поля, что
и дало машинам такого типа название –
асинхронные[3][10].

Статор
обычно выполнен в виде нескольких,
расположенных в пазах, катушек, а ротор
– в виде «беличьей клетки» (короткозамкнутый
ротор) или в виде нескольких катушек
(фазный ротор), которые соединены между
собой, выведены на кольца, расположенные
на валу, и, с помощью скользящих по ним
щеток, могут быть замкнуты на внешние
резисторы.

Несмотря
на простоту физических явлений и
материализующих их конструктивов полное
математическое описание процессов в
асинхронной машине весьма сложно.

В
общем случае для машины, имеющей р пар
полюсов (р = 1,2,3…), синхронная угловая
скорость 0, рад/с, т.е. скорость поля,
определится как

;

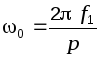
                    (4.11)

для
частоты вращения n0, об/мин, будем иметь:

,
(4.12)

т.е.
при питании от сети f1 = 50 Гц синхронная
частота вращения может быть 3000, 1500, 1000,
750, 600… об/мин в зависимости от конструкции
машины (числа пар полюсов р).

Выражения
(4.11) и (4.12) имеют принципиальный характер:
они показывают, что для данной машины
имеется лишь одна возможность изменять
скорость поля – изменять частоту
источника питания f1.

При
нагружении вала   0 отличие скоростей
 и 0 принято характеризовать
скольжением:

,
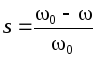
(4.13)

Асинхронный
электропривод, как и электропривод
постоянного тока, может работать в
двигательном и трёх тормозных режимах
с таким же, как в электроприводе
постоянного тока, распределением потоков
энергии (рис. 4.7).

Рис.
4.7. Механическая характеристика
асинхронной машины

Как
следует из рис. 4.7, по мере увеличении
момента сопротивления увеличивается
скольжение машины и развиваемый момент.
При некотором критическом значении
скольжения sКР, момент двигателя достигает
максимального (или критического) значения
– МКР. Жёсткость механической
характеристики асинхронных двигателей
переменна: на рабочем участке s = 0…sКР:
b < 0, а при ½s½>½sКР½ – положительна:
b < 0.

Специфическим
является режим динамического торможения,
которое представляет собою генераторный
режим отключенного от сети переменного
тока асинхронного двигателя, к статору
которого подведен постоянный ток Iп.
Этот режим применяется в ряде случаев,
когда после отключения двигателя от
сети требуется его быстрая остановка
без реверса.

Постоянный
ток, подводимый к обмотке статора,
образует неподвижное в пространстве
поле. При вращении ротора в его обмотке
наводится переменная эдс, под действием
которой протекает переменный ток. Этот
ток создает также неподвижное поле.

Складываясь,
поля статора и ротора образуют
результирующее поле, которое при
взаимодействии с током ротора создает
тормозной момент. Энергия, поступающая
с вала двигателя, рассеивается при этом
в сопротивлениях роторной цепи.

На
шильдике или в паспорте асинхронного
двигателя обычно указаны номинальные
линейные напряжения при соединении
обмоток в «звезду» и «треугольник»:
;
токи;
частота f1н; мощность на валу Рн; частота
вращения при номинальном моменте ωн
(nн); кпд – hн, cos jн.

Для
двигателей с короткозамкнутым ротором
в каталоге приводятся кратности пускового
тока:
;
пускового момента:;
критического момента:.
Следует иметь в виду, что данных,
приводимых в каталоге, недостаточно,
чтобы определить по ним параметры схемы
замещения и пользоваться ей при всех
расчетах, однако по каталожным данным
можно построить естественную
электромеханическую и механическую
характеристики, воспользовавшись
уравнением приближённой механической
характеристики[4].

Приближенное
уравнение механической характеристики
асинхронного двигателя (формула Клосса)
удовлетворительно воспроизводит
механическую характеристику в области
малых скольжений (от s = 0 до s = sкр)[5].

.
(4.14)

Необходимо
помнить, что на время разгона существенно
влияет вид механической характеристики
в области больших скольжений от s = 1 до
s = sкр, поэтому для определения моментов
при значениях скольжения, которое больше
критического, следует пользоваться
выражением

,
(4.15)

где
b – коэффициент, определяемый следующим
образом. Для пускового момента (s = l)
соотношение (4.14) приобретает следующий
вид:

Критическое
скольжение можно определить по
выражению:

откуда
.

(4.16)

.
(4.17)

Значение
пускового момента Мп можно вычислить
через кратность пускового момента
относительно номинального Мп / Мн,

которая приводится в справочниках
[4].

Используя
выражения (4.14)–(4.16) и паспортные данные
машины можно построить приближённую
механическую характеристику, которая
с достаточной точностью соответствует
реальной характеристике, приведённой
на рис. 4.8.[6]

Пример
построения механической характеристики
асинхронного электродвигателя обычного
исполнения с использованием соотношений
(4.14)–(4.17) приведен в подразд. 5.2 и прил.
1.

Двигатели
с повышенным скольжением предназначены
для привода механизмов с высоким
коэффициентом инерции, механизмов с
неравномерной пульсирующей нагрузкой
и механизмов с частыми пусками.
Двигатели отличаются от базовых
обмоткой короткозамкнутого ротора,
которая выполняется из сплава
повышенного сопротивления. Механическая
характеристика имеет вид, показанный
на рис. 4.9.[7]

Технические
данные двигателей с повышенным
скольжением приведены в [4]. Уровень
шума двигателей не превышает значений,
установленных для базовых двигателей
соответствующего габарита и частоты
вращения[8].

Электромеханическую
характеристику асинхронного
электродвигателя можно построить,
воспользовавшись несколькими опорными
точками (рис. 4.10).

При
номинальном моменте и, соответственно,
номинальной частоте вращения машина
потребляет из сети номинальный ток:

.
(4.18)

В
серийных машинах при U = Uн и f1 = fн, т.е.
при номинальном магнитном потоке, ток
холостого хода I10 составляет обычно
30…40 % от номинального тока статора
Iн:

.
(4.19)

Ток,
потребляемый машиной при критическом
скольжении:

.
(4.20)

Ток
при заторможенном роторе (в начальный
момент пуска) определяется по паспортной
характеристике – кратности пускового
тока:

.
(4.21)

19.Регулювання
швидкості обертання АД.

Частота
вращения асинхронного двигателя

n
= n1 (1 – s) = (60f1/p) (1-s) (85)

Из
этого выражения видно, что ее можно
регулировать, изменяя частоту f1 питающего
напряжения, число пар полюсов р и

Рис.
266. Схема переключения катушек обмотки
статора (одной фазы) для изменения числа
полюсов: а — при четырех полюсах; б —
при двух полюсах

скольжение
s. Последнее при заданных значениях
момента на валу Мвн и частоты f1 можно
изменять путем включения в цепь обмотки
ротора реостата.

Регулирование
путем изменения частоты питающего
напряжения. Этот способ требует наличия
преобразователя частоты, к которому
должен быть подключен асинхронный
двигатель. На основе управляемых
полупроводниковых вентилей (тиристоров)
созданы статические преобразователи
частоты и построен ряд опытных электровозов
и тепловозов с асинхронными двигателями,
частота вращения которых регулируется
путем изменения частоты питающего
напряжения. Такой способ регулирования
частоты вращения ротора асинхронного
двигателя является весьма перспективным.

Регулирование
путем изменения числа пар полюсов.
Этот способ позволяет получить ступенчатое
изменение частоты вращения. Для этой
цели отдельные катушки 1, 2 и 3, 4, составляющие
одну фазу (рис. 266), переключаются так,
чтобы изменялось соответствующим
образом направление тока в них (например,
с последовательного согласного соединения
на встречное). При согласном включении
катушек (рис. 266, а) число полюсов равно
четырем, при встречном включении (рис.
266, б) — двум. Катушки двух других фаз,
сдвинутые в пространстве на 120°,
соединяются таким же образом. Такое же
уменьшение числа полюсов можно осуществить
при переключении катушек с последовательного
на параллельное соединение. При изменении
числа полюсов изменяется частота
вращения n₁
магнитного поля двигателя, а следовательно,
и частота вращения n его ротора. Если
нужно иметь три или четыре частоты
вращения n₁,
то на статоре располагают еще одну
обмотку, при переключении которой можно
получить еще две частоты. Существуют
двигатели, которые обеспечивают изменение
частоты вращения n₁
при постоянном наибольшем моменте или
при приблизительно постоянной мощности
(рис. 267).

В
асинхронном двигателе число полюсов
ротора должно быть равно числу полюсов
статора. В короткозамкнутом роторе это
условие выполняется автоматически и
при переключении обмотки статора никаких
изменений в обмотке ротора выполнять
не требуется.

Рис.
267. Механические характеристики
двухскоростных асинхронных двигателей
с постоянным наибольшим моментом (а) и
постоянной мощностью (б)

Рис.
268. Механические характеристики
асинхронного двигателя при регулировании
частоты вращения путем включения
реостата в цепь обмотки ротора

Рис.
269. Схемы подключения асинхронного
двигателя к сети при изменении направления
его вращения

В
двигателе же с фазным ротором в этом
случае надо было бы изменять число
полюсов обмотки ротора, что сильно
усложнило бы его конструкцию, поэтому
такой способ регулирования частоты
вращения используется только в двигателях
с коротко-замкнутым ротором. Такие
двигатели имеют большие габаритные
размеры и массу по сравнению с двигателями
общего применения, а следовательно, и
большую стоимость. Кроме того, регулирование
осуществляется большими ступенями; при
частоте f₁
= 50 Гц частота вращения поля n₁
при переключениях изменяется в отношении
3000:1500:1000:750.

Регулирование
путем включения в цепь ротора реостата.
При включении в цепь обмотки ротора
реостата с различным сопротивлением
(R_п4,
R_пЗ,
R_п2
и т. д.) получаем ряд реостатных механических
характеристик 4, 3 и 2 двигателя. При этом
некоторому нагрузочному моменту М_ном
(рис. 268) будут соответствовать меньшие
частоты вращения n₄,
n₃,
n₂
и т. д., чем частота n_е
при работе двигателя на естественной
характеристике 1 (при R_п
= 0). Это способ регулирования может быть
использован только для двигателей с
фазным ротором. Он позволяет плавно
изменять частоту вращения в широких
пределах. Недостатками его являются
большие потери энергии в регулировочном
реостате, поэтому его используют только
при кратковременных режимах работы
двигателя (при пуске и пр.).

Изменение
направления вращения. Для
изменения направления вращения двигателя
нужно изменить направление вращения
магнитного поля, создаваемого обмотками
статора. Это достигается изменением
порядка чередования тока в фазах обмотки
статора. Например, если максимумы токов
поступают в фазы обмотки статора 1 (рис.
269, а) в следующем порядке: фаза А — фаза
В — фаза С, то ротор 2 двигателя будет
вращаться по часовой стрелке. Если же
подавать их в такой последовательности:
фаза В — фаза А — фаза С, то ротор начнет
вращаться против часовой стрелки. Для
этой цели необходимо изменить схему
соединения обмоток статора с сетью,
переключив две любые фазы (провода).
Например, зажим А обмотки статора,
который ранее был соединен с линейным
проводом Л1, нужно переключить на провод
Л2, а зажим В этой обмотки, соединенный
ранее с Л2, переключить на провод Л1 (рис.
269,б). Такое переключение можно осуществить
обычным переключателем.

ИЛИ
ВОТ ЭТОТ ВАРИАНТ

Регулирование
скорости асинхронного двигателя

Наиболее
распространены следующие способы
регулирования скорости асинхронного
двигателя: изменение
дополнительного сопротивления цепи
ротора, изменение напряжения, подводимого
к обмотке статора, двигателя изменение
частоты питающего напряжения, а также
переключение числа пар полюсов.

Регулирование
частоты вращения асинхронного двигателя
путем введения резисторов в цепь
ротора

Введение
резисторов
в цепь ротора приводит к увеличению
потерь мощности и снижению частоты
вращения ротора двигателя за счет
увеличения скольжения, поскольку n =
nо (1 – s).

Из
рис. 1 следует, что при увеличении
сопротивления в цепи ротора при том
же моменте частота вращения вала
двигателя уменьшается.

Жесткость
механических
характеристик значительно
снижается с уменьшением частоты
вращения, что ограничивает диапазон
регулирования до (2 – 3) : 1. Недостатком
этого способа являются значительные
потери энергии, которые пропорциональны
скольжению. Такое регулирование
возможно только для двигателя
с фазным ротором.

Регулирование
частоты вращения асинхронного двигателя
изменением напряжения на статоре

Изменение
напряжения, подводимого к обмотке
статора асинхронного двигателя,
позволяет регулировать скорость с
помощью относительно простых технических
средств и схем управления. Для этого
между сетью переменного тока со
стандартным напряжением U1ном
и статором электродвигателя включается
регулятор напряжения.

При
регулировании частоты вращения
асинхронного
двигателя изменением
напряжения, подводимого к обмотке
статора, критический момент Мкр
асинхронного двигателя изменяется
пропорционально квадрату подводимого
к двигателю напряжения Uрет
(рис. 3), а скольжение от Uрег
не зависит.

Рис.
1. Механические характеристики
асинхронного двигателя с фазным
ротором при различных сопротивлениях
резисторов, включенных в цепь ротора

Рис.
2. Схема регулирования скорости
асинхронного двигателя путем изменения
напряжения на статоре

Рис.
3. Механические характеристики
асинхронного двигателя при изменении
напряжения подводимого к обмоткам
статора

Если
момент сопротивления рабочей машины
больше пускового момента электродвигателя
(Мс > Мпуск), то двигатель не будет
вращаться, поэтому необходимо запустить
его при номинальном напряжении 17ном
или на холостом ходу.

Регулировать
частоту вращения короткозамкнутых
асинхронных двигателей таким способом
можно только при вентиляторном
характере нагрузки. Кроме того, должны
использоваться специальные
электродвигатели с повышенным
скольжением. Диапазон регулирования
небольшой, до nкр.

Для
изменения напряжения применяют
трехфазные
автотрансформаторы и
тиристорные регуляторы напряжения.

Рис.
4. Схема замкнутой системы регулирования
скорости тиристорный регулятор
напряжения – асинхронный двигатель
(ТРН – АД)

Замкнутая
схема управления асинхронным двигателем,
выполненным по схеме тиристорный
регулятор напряжения – электродвигатель
позволяет регулировать скорость
асинхронного двигателя с повышенным
скольжением (такие двигатели применяются
в вентиляционных установках).

Регулирование
частоты вращения асинхронного двигателя
изменением частоты питающего напряжения

Так
как частота вращения магнитного поля
статора nо
= 60f/р,
то регулирование частоты вращения
асинхронного двигателя можно производить
изменением частоты питающего напряжения.

Принцип
частотного метода
регулирования скорости асинхронного
двигателя заключается
в том, что, изменяя частоту питающего
напряжения, можно в соответствии с
выражением при неизменном числе пар
полюсов р изменять угловую скорость
nо
магнитного поля статора.

Этот
способ обеспечивает плавное регулирование
скорости в широком диапазоне, а
механические характеристики обладают
высокой жесткостью.

Для
получения высоких энергетических
показателей асинхронных двигателей
(коэффициентов мощности, полезного
действия, перегрузочной способности)
необходимо одновременно с частотой
изменять и подводимое напряжение.
Закон изменения напряжения зависит
от характера момента нагрузки Мс. При
постоянном моменте нагрузки напряжение
на статоре должно регулироваться
пропорционально частоте.

Схема
частотного электропривода приведена
на рис. 5, а механические характеристики
АД при частотном регулировании — на
рис. 6.

Рис.
5. Схема частотного электропривода

Рис.
6. Механические характеристики
асинхронного двигателя при частотном
регулировании

С
уменьшением частоты f критический
момент несколько уменьшается в области
малых частот вращения. Это объясняется
возрастанием влияния активного
сопротивления обмотки статора при
одновременном снижении частоты и
напряжения.

Частотное
регулирование скорости асинхронного
двигателя позволяет изменять частоту
вращения в диапазоне (20 – 30) : 1. Частотный
способ является наиболее перспективным
для регулирования асинхронного
двигателя с короткозамкнутым ротором.
Потери мощности при таком регулировании
невелики, поскольку минимальны потери
скольжения.

Большинство
современных преобразователей
частоты построено по
схеме двойного преобразования. Они
состоят из следующих основных частей:
звена постоянного тока (неуправляемого
выпрямителя), силового импульсного
инвертора и системы управления.

Звено
постоянного тока состоит из неуправляемого
выпрямителя и фильтра. Переменное
напряжение питающей сети преобразуется
в нем в напряжение постоянного тока.

Силовой
трехфазный импульсный инвертор
содержит шесть транзисторных ключей.
Каждая обмотка электродвигателя
подключается через соответствующий
ключ к положительному и отрицательному
выводам выпрямителя. Инвертор
осуществляет преобразование
выпрямленного напряжения в трехфазное
переменное напряжение нужной частоты
и амплитуды, которое прикладывается
к обмоткам статора электродвигателя.

В
выходных каскадах инвертора в качестве
ключей используются силовые
IGBT-транзисторы.
По сравнению с тиристорами они имеют
более высокую частоту переключения,
что позволяет вырабатывать выходной
сигнал синусоидальной формы с
минимальными искажениями. Регулирование
выходной частоты Iвых
и выходного напряжения осуществляется
за счет высокочастотной широтно-импульсной
модуляции.

Регулирование
частоты вращения асинхронного двигателя
переключение числа пар полюсов

Ступенчатое
регулирование скорости можно
осуществить, используя специальные
многоскоростные
асинхронные двигатели с короткозамкнутым
ротором.

Из
выражения nо
= 60f/р
следует, что при изменении числа пар
полюсов р получаются механические
характеристики с разной частотой
вращения nо
магнитного поля статора. Так как
значение р определяется целыми числами,
то переход от одной характеристики к
другой в процессе регулирования носит
ступенчатый характер.

Существует
два способа изменения числа пар
полюсов. В первом случае в пазы статора
укладывают две обмотки с разным числом
полюсов. При изменении скорости к сети
подключается одна из обмоток. Во втором
случае обмотку каждой фазы составляют
из двух частей, которые соединяют
параллельно или последовательно. При
этом число пар полюсов изменяется в
два раза.

Рис.
7. Схемы переключения обмоток асинхронного
двигателя: а – с одинарной звезды на
двойную; б – с треугольника на двойную
звезду

Регулирование
скорости путем изменения числа пар
полюсов экономично, а механические
характеристики сохраняют жесткость.
Недостатком этого способа является
ступенчатый характер изменения частоты
вращения асинхронного двигателя с
короткозамкнутым ротором. Выпускаются
двухскоростные двигатели с числом
полюсов 4/2, 8/4, 12/6. Четырехскоростной
электродвигатель с полюсами 12/8/6/4
имеет две переключаемые обмотки.

Использованы
материалы книги Дайнеко В.А., Ковалинский
А.И. Электрооборудование сельскохозяйственных
предприятий.

20.Механічні

характеристики
АД в гальмівних режимах.(Есть в
Чиликине-82стр.)

Асинхронный
двигатель может работать в следующих
тормозных режимах: в режиме рекуперативного
торможения, противовключения и
динамическом.

Рекуперативное
торможение асинхронного двигателя

Режим
рекуперативного торможения осуществляется
в том случае, когда скорость ротора
асинхронного двигателя превышает
синхронную.

Режим
рекуперативного торможения практически
применяется для двигателей с переключением
полюсов и в приводах грузоподъемных
машин (подъемники, экскаваторы и т.п.).

При
переходе в генераторный режим вследствие
изменения знака момента меняет знак
активная составляющая тока ротора. В
этом случае асинхронный
двигатель отдает активную
мощность (энергию) в сеть и потребляет
из сети реактивную мощность (энергию),
необходимую для возбуждения. Такой
режим возникает, например, при торможении
(переходе) двухскоростного двигателя
с высокой на низкую скорость, как показано
на рис. 1 а.

Рис.
1. Торможение асинхронного двигателя в
основной схеме включения: а) с рекуперацией
энергии в сеть; б) противовключением

Предположим,
что в исходном положении двигатель
работал на характеристике 1 и в точке
а, вращаясь со скоростью ωуст1. При
увеличении числа пар полюсов двигатель
переходит на характеристику 2, участок
бс которой соответствует торможению с
рекуперацией энергии в сеть.

Этот
же вид торможения может быть реализован
в системе преобразователь
частоты – двигатель при
останове асинхронного двигателя или
при переходе с характеристики на
характеристику. Для этого осуществляется
уменьшение частоты выходного напряжения,
а тем самым синхронной скорости ωо = 2πf
/ p.

В
силу механической инерции текущая
скорость двигателя ω будет изменяться
медленнее чем синхронная скорость ωо,
и будет постоянно превышать скорость
магнитного поля. За счет этого и возникает
режим торможения с
отдачей энергии в сеть.

Рекуперативное
торможение также может быть реализовано
в электроприводе
грузоподъемных машин при
спуске грузов. Для этого двигатель
включается в направлении спуска груза
(характеристика 2 рис. 1 б).

После
окончания торможения он будет работать
в точке со скоростью –ωуст2. При этом
осуществляется процесс спуска груза с
отдачей энергии в сеть.

Рекуперативное
торможение является наиболее экономичным
видом торможения.

Торможение
асинхронного электродвигателя
противовключением

Перевод
асинхронного двигателя в режим торможения
противовключением может быть выполнен
двумя путями. Один из них связан с
изменением чередования двух фаз питающего
электродвигатель напряжения.

Допустим,
что двигатель работает на характеристике
1 (рис. 1 б) при чередовании фаз напряжения
АВС. Тогда при переключении двух фаз
(например, В и С) он переходит на
характеристику 2, участок аб которой
соответствует торможению противовключением.

Обратим
внимание на то обстоятельство, что при
противовключении скольжение
асинхронного двигателя
изменяется от S = 2 до S = 1.

Ротор
при этом вращается против направления
движения поля и постоянно замедляется.
Когда скорость спадает до нуля, двигатель
должен быть отключен от сети, иначе он
может перейти в двигательный режим,
причем ротор его будет вращаться в
направлении, обратном предыдущему.

При
торможении противовключением токи в
обмотке двигателя могут в 7–8 раз
превышать соответствующие номинальные
токи. Заметно уменьшается коэффициент
мощности двигателя. О КПД в данном случае
говорить не приходится, т.к. и преобразуемая
в электрическую механическая энергия
и энергия, потребляемая из сети,
рассеиваются в активном сопротивлении
ротора, и полезно используемой энергии
в данном случае нет.

Короткозамкнутые
двигатели кратковременно перегружаются
по току. Правда, у них при (S > 1) вследствие
явления вытеснения тока заметно
возрастает активное сопротивление
ротора. Это приводит к уменьшению и
увеличению момента.

С
целью увеличения эффективности торможения
двигателей с фазным ротором в цепи их
роторов вводят добавочные сопротивления,
что позволяет ограничить токи в обмотках
и увеличить момент.

Другой
путь торможения противовключением
может быть использован при активном
характере момента нагрузки, который
создается, например, на валу двигателя
грузоподъемного механизма.

Допустим,
что требуется осуществить спуск груза,
обеспечивая его торможение с помощью
асинхронного двигателя. Для этого
двигатель путем включения в цепь ротора
добавочного резистора (сопротивления)
переводится на искусственную характеристику
(прямая 3 на рис. 1).

Вследствие
превышения моментом нагрузки Мс пускового
момента Мп двигателя и его активного
характера груз может опускаться с
установившейся скоростью –ωуст2. В этом
режиме торможение скольжения асинхронного
двигателя может изменяться от S = 1 до S
= 2.

Динамическое
торможение асинхронного двигателя

Для
динамического торможения обмотки
статора двигатель отключают от сети
переменного тока и подключают к источнику
постоянного тока, как это показано на
рис. 2. Обмотка ротора при этом может
быть закорочена, или в ее цепь включаются
добавочные резисторы с сопротивлением
R2д.

Рис.
2. Схема динамического торможения
асинхронного двигателя (а) и схема
включения обмоток статора (б)

Постоянный
ток Iп, значение которого может
регулироваться резистором 2, протекает
по обмоткам статора и создает относительно
статора неподвижное магнитное поле.
При вращении ротора в нем наводится
ЭДС, частота которой пропорциональна
скорости. Эта ЭДС, в свою очередь, вызывает
появление тока в замкнутом контуре
обмотки ротора, который создает магнитный
поток, также неподвижный относительно
статора.

Взаимодействие
тока ротора с результирующим магнитным
полем асинхронного двигателя создает
тормозной момент, за счет которого
достигается эффект торможения. Двигатель
в этом случае работает в режиме генератора
независимо от сети переменного тока,
преобразовывая кинетическую энергию
движущихся частей электропривода и
рабочей машины в электрическую, которая
рассеивается в виде тепла в цепи ротора.

На
рисунке 2 б показана наиболее
распространенная схема включения
обмоток статора при динамическом
торможении. Система возбуждения двигателя
в этом режиме является несимметричной.

Для
проведения анализа работы асинхронного
двигателя в режиме динамического
торможения несимметричную систему
возбуждения заменяют симметричной. С
этой целью принимается допущение, что
статор питается не постоянным током
Iп, а некоторым эквивалентным трехфазным
переменным током, создающим такую же
МДС (магнитодвижущую силу), что и
постоянный ток.

Электромеханическая
и механические характеристики представлены
на рис. 3.

Рис.
3. Электромеханическая и механические
характеристики асинхронного двигателя

Характеристика
расположена на рисунке в первом квадранте
I, где s
= ω
/ ωo
– скольжение асинхронного двигателя
в режиме динамического торможения.
Механические характеристики двигателя
расположены во втором квадранте II.

Различные
искусственные характеристики асинхронного
двигателя в режиме динамического
торможения можно получить, изменяя
сопротивление R2д
добавочных резисторов 3 (рис. 2) в цепи
ротора или постоянный ток Iп,
подаваемый в обмотки статора.

Варьируя
значения R2д
и Iп,
можно получить желаемый вид механических
характеристик асинхронного двигателя
в режиме динамического торможения и,
тем самым, соответствующую интенсивность
торможения асинхронного электропривода.

21.Класифікація
засобів живлення електричною енергією.

Источник

В прошлый раз мы поговорили о такой величине, как статические моменты. Теперь можем двигаться дальше: сегодня на повестке моменты инерции.

Внимательный читатель уже может возмутиться:
“И зачем мы изучаем эти моменты? Какой в этом прок?
Причём же тут инерция, если сопромат — по сути статика?»

На первый вопрос у меня есть два ответа — краткий и не очень. Пока ограничусь кратким:

Статические моменты и моменты инерции широко используются для определения нормальных и касательных напряжений, определении прогибов и деформаций конструкций. Читая о том, как все это вычислить, вы будете сталкиваться с геометрическими характеристиками постоянно. Поэтому лучше сразу понимать, о чем идёт речь, а, при необходимости, подсматривать тут.

В изгибаемом элементе от момента сил возникают напряжения, для определения которых нам и нужен момент инерции (хотя и опосредованно. Впрочем, если вы читали статью про моменты, то это уже знаете). При этом сам элемент деформируется, и величина этих деформаций (прогибов) также определяется с помощью момента инерции.

Для ответа на второй вопрос перейдем уже к моментам инерции.

Что такое момент инерции

Рисунок 1. Поперечное сечение стержня. Где-то я его уже видел…

Суть и смысл моментов инерции в общем случае походит на статические моменты, однако корни нужно искать в описании вращения тела. Для вращательного движения одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Рассмотрим вращающееся тело, как совокупность точек с предельно малыми размером и массой, которые находятся на расстояниях Ri (от нуля до R):

Где:
T — кинетическая энергия;
J — момент инерции;
m — масса;
v — скорость;
w — угловая скорость;
R — радиус;

Тут видно, что также, как в формуле кинетической энергии при линейном движении мера инертности — масса, при вращательном движении мера инертности — момент инерции. Впрочем, я немного забегаю вперёд.

Угловая скорость вращающегося тела — угол поворота, пройденный за единицу времени

Тут начальный угол поворота φ₀ может быть равен нулю, если мы рассматриваем начало движения.

Линейная скорость тела:

где r — расстояние от рассматриваемой точки до оси вращения

Ускорение вращающегося тела (а нас интересует нормальное) тогда:

Я не буду затрагивать динамику вращающегося тела, и расскажу только о жизненно необходимом.

Сила (которая по второму закону Ньютона — произведение массы на ускорение):

и момент:

И вот тут вспомним уже третий закон Ньютона — действию всегда есть равное и противоположное противодействие, а значит действию найденного нами момента будет сопротивляться — момент инерции.

Вспомним также, что, как и со статическими моментами, на разные точки тела, удаленные от оси вращения на разные расстояния будет действовать разный момент, а общий момент можно получить их просуммировав:

При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. Но, как я уже показал, рассказывая про статические моменты, массу точек для изотропных (в данном случае имеющих одинаковую плотность) объектов можно выносить за скобки и рассматривать исключительно геометрию. Формула момента инерции примет следующий вид:

Почему I_р? Потому что мы с вами оперировали радиусом и углом поворота (в формуле угловой скорости) — т.е. использовали полярную систему отсчета (что и демонстрирует индекс p).

Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.

Как найти момент инерции

Чтобы немного упростить себе операции со всеми этими величинами перейдем к родной и понятной системе отсчета: перпендикулярным осям X и Y. Возьмем случайное сечение стержня и рассмотрим интегралы, как мы уже делали со статическими моментами:

Первые два интеграла называются осевыми моментами инерции относительно осей x и y, а третий — центробежным моментом инерции сечения относительно осей x, y. Теперь рассмотрим случай параллельного переноса осей , не вдаваясь глубоко в вычисление интегралов.

Для осей x₁=x+a, y₁=y+b моменты инерции будут равны:

Если вы, как и часть прочитавших эту статью перед публикацией, не имеете черного пояса и седьмого дана в интегральных преобразованиях, то:

т.к.

Тут первый интеграл — Ix1, второй интеграл — Sx1, а третий раскрывается в площадь при нулевом свободном члене.

Надеюсь, понятно, что при параллельном переносе по y изменяется только ось (буква).

В последнем случае мы рассматриваем перенос по обеим осям сразу.

Где:
Ix — очевидно, момент инерции относительно оси x
Sx — статический момент сечения относительно оси y
F — площадь сечения

А теперь предположим, что некие оси x₁ и y₁ являются центральными, тогда и выражения упрощаются и принимают вид:

Немного проясню обозначение осей:

Центральными называются оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.

Главными называются оси, в которых центробежный момент инерции (I_xy) равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

И теперь можно уже коснуться практики: речь о моментах инерции простых сечений.

Момент инерции прямоугольника

Определим осевые моменты инерции прямоугольника со сторонами b и h относительно осей x и y, проходящих через его центр тяжести. В качестве элементарной площадки dA возьмем полоску шириной b и высотой . Тогда будем иметь:

Не прибегая к вычислениям, замечу, что для момента инерции относительно оси Y изменится только положение сторон b и h. Следовательно:

Момент инерции квадрата

Прямоугольник со сторонами b=h=a. Следовательно:

Момент инерции круга

Тут воспользуемся полярным моментом инерции относительно центра круга. Определим его, как сумму колец с толщиной dp:

Момент инерции кольца

А здесь – явная аналогия с моментом инерции круга:

Как мы видим, момент инерции кольца это разность моментов инерции большего и меньшего кругов.

Пример нахождения момента инерции тавра

Найдём осевые моменты инерции тавра (рисунок 5), приведенного на рисунке, относительно центральных осей x_c и y_c.

Рисунок 8. Тавр, положение осей

Так как оси x₁ и x₂ являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси x_c воспользуемся формулой.

Момент инерции относительно оси y_c получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось y_c является общей центральной осью для простых фигур и для всей фигуры.

Центробежный момент инерции относительно осей x_c и y_c равен нулю, так как ось инерции y_c является главной осью (осью симметрии фигуры).

Обобщение и подведение итогов

Момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении. В статике момент инерции применяется в определении прогибов, расчетах конструкций на касательные и нормальные напряжения. Момент инерции также, как и статические моменты, характеризует положение осей относительно сечения элемента. Так у нас появляются:

Центральные оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.

Главные оси, в которых центробежный момент инерции (I_xy) равен нулю, а осевые моменты инерции — максимальны. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

При этом главные и центральные оси могут совпадать!

Список использованных источников

Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3

Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников

5 372

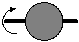
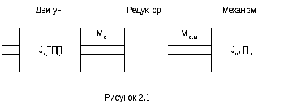
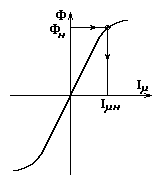
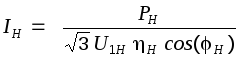Источник

Осевой момент инерции[править | править код]

Теорема Гюйгенса — Штейнера[править | править код]

Осевые моменты инерции некоторых тел[править | править код]

Вывод формул[править | править код]

Безразмерные моменты инерции планет и спутников[править | править код]

Центробежный момент инерции[править | править код]

Геометрические моменты инерции[править | править код]

Момент инерции относительно плоскости[править | править код]

Центральный момент инерции[править | править код]

Тензор инерции и эллипсоид инерции[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Что такое инерция

Определение момента инерции

Теорема Штейнера

Пример решения задачи на нахождение момента инерции

Что такое инерция

Определение момента инерции

Теорема Штейнера

Пример решения задачи

Определение момента инерции

Что такое момент инерции

Как найти момент инерции

Момент инерции прямоугольника

Момент инерции квадрата

Момент инерции круга

Пример нахождения момента инерции тавра

Обобщение и подведение итогов

Вам также может понравиться

Как составить акт при протечке крыши образец

Как найти детские куклы

Как найти произведение в ворде

Добавить комментарий Отменить ответ