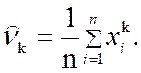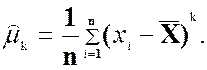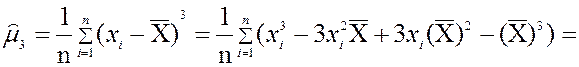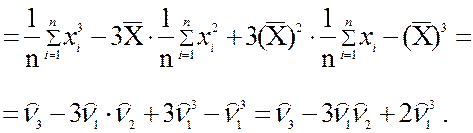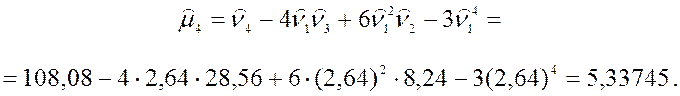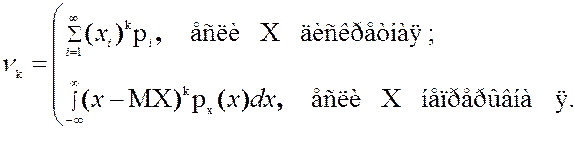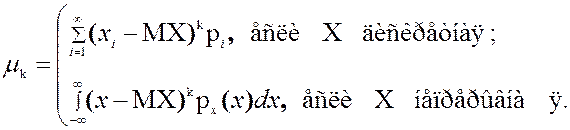Как найти начальный момент второго порядка

Рассмотрим
дискретную случайную величину Х,
заданную законом распределения

Найдем математическое
ожидание Х:

.

Найдем математическое
ожидание случайной величины Х
²:

.

Видим, что

значительно больше
.
Это объясняется тем, что после возведения
в квадрат возможное значение величины
Х
²,
соответствующее значению

величины Х,
стало равным 10 000, т. е. значительно
увеличилось; вероятность же этого
значения мала – 0,01.

Таким образом,
переход от

к

позволил лучше учесть влияние на
математическое ожидание того возможного
значения, которое велико и имеет малую
вероятность. Разумеется, если бы величина
Х
имела несколько больших и маловероятных
значений, то переход к величине Х
², а тем
более к величинам

и т. д., позволил бы еще больше усилить
роль этих больших, но маловероятных
возможных значений. Вот почему оказывается
целесообразным рассматривать
математическое ожидание целой
положительной степени случайной величины
(не только дискретной, но и непрерывной).

Начальным
моментом v_k
порядка k
случайной величины Х назы-вается
математическое ожидание k-ой
ее степени:

.

Если дискретная
случайная величина принимает конечное
множество значений, то по определению

.

Если дискретная
случайная величина принимает счетное
множество значений, то

,

когда этот ряд
сходится абсолютно. (В этой и предыдущей
формуле
).

Начальный момент
порядка k
непрерывной случайной величины с
плотностью распределения

определяется формулой

,

если интеграл
сходится абсолютно.

Центральным
моментом k-го
порядка случайной величины Х называется
математическое ожидание k-ой
степени отклонения этой величины от ее
математического ожидания. Обозначив
центральный момент k-го
порядка через _k
и положив
,
по определению получим:

.

Для дискретной
случайной величины

или
.

Для непрерывной
случайной величины с плотностью
распределения

центральный момент k-го
порядка определяется по формуле

если интеграл
сходится абсолютно.

Легко выводятся
соотношения, связывающие начальные и
центральные моменты:

,

,

.

Моменты более
высоких порядков применяются редко.

Пример
3.1.
Дискретная случайная величина задана
законом распределения

Найти центральные
моменты первого, второго и третьего
порядков.

Находим сначала
начальные моменты:

,

тогда

.

Пример
3.2.
Найти
начальный момент второго порядка
случайной величины с плотностью
вероятностей

.

Нетрудно показать,
что начальный момент нулевого порядка
равен единице, начальный момент первого
порядка равен ее математическому
ожиданию, центральные моменты нулевого,
первого и второго порядка равны
соответственно единице, нулю и дисперсии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Очевидно, что начальный выборочный момент  нулевого порядка всегда равен 1, а
начальный выборочный момент первого порядка 

    Определение
2.19  Центральным моментом   k–го порядка выборки  x₁, x₂, …, x_n  называется среднее  k-тых
степеней отклонений данных выборочных значений от среднего  ,  то есть

Из данного определения следует, что центральный выборочный
момент   нулевого порядка равен 1. При  k = 1 
получается, что

, а
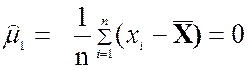
при  k=
2  имеем

.

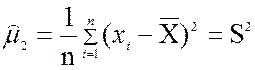
Следовательно, выборочная дисперсия  является центральным выборочным моментом
второго порядка. Для вычисления центрального выборочного момента третьего
порядка используем стандартные алгебраические преобразования:

В результате получилось выражение центрального момента
третьего порядка через начальные моменты. Таким же способом находятся выражения
для центральных моментов более высоких порядков. Приведем ряд формул, которые
на практике используются чаще других:

При вычислении начальных и
центральных выборочных моментов используются приемы и таблицы, аналогичные тем,
которые применялись ранее для вычисления среднего  и
дисперсии  .

Пример 2.28   В
ходе социологического исследования собраны ответы 25 рядовых сотрудников
учреждения о количестве стрессовых ситуаций, возникавших на работе в течение
недели. Данные опроса приведены в следующей таблице. Найдем начальные и
центральные выборочные моменты первого, второго, третьего и четвертого
порядков.

Таблица 2.20 
– Данные исследования стрессовых ситуаций

Необходимые промежуточные расчеты будем фиксировать              в
следующей таблице.

Таблица 2.21 – Вычисления начальных и
центральных моментов

Объем выборки  n = 25. 
Вычислим начальные выборочные          моменты:

;            ;

    ;        .

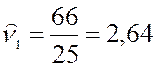
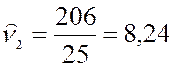
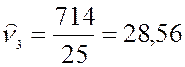
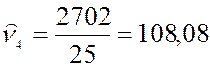
Используя соответствующие формулы, вычислим центральные
выборочные моменты:

;  ;

;

Округлим полученные значения центральных моментов:

;           ;            
;             

■

Начальные и центральные выборочные моменты являются аналогами
соответствующих понятий теоретических моментов всей генеральной совокупности
значений исследуемой случайной        величины.

Определение 2.20    Начальным моментом  k-го
порядка случайной величины  Х  называется число  , 
равное математическому ожиданию  k-й 
степени величины  Х:

.

Для вычисления начального момента  k-го
порядка используются следующие формулы:

Говорят, что момент   существует, если он конечен, в противном
случае считается, что момент не существует.

Определение 2.21  Центральным моментом  k-го 
порядка случайной величины  Х  называется число  ,  равное математическому
ожиданию величины

.

Для вычисления центрального момента  k–го
порядка используются   формулы:

Заметим,
что формулы, выражающие центральные моменты  через начальные, аналогичны
соответствующим формулам для выборочных моментов. В частности, имеют место
соотношения:

;

;

;

.

Очевидно, что математическое ожидание случайной
величины является начальным моментом первого порядка, а дисперсия – центральным
моментом второго порядка. Как теоретические, так и выборочные моменты
используются при исследовании закона распределения случайной величины. Все
центральные моменты четных порядков, как и дисперсия, характеризуют рассеяние
значений случайной величины вокруг математического ожидания. Центральные
моменты нечетных порядков выявляют асимметрию распределения относительно
центра. В частности, если значения случайной величины распределены симметрично
относительно математического ожидания, то все ее существующие моменты нечетных
порядков равны нулю. С другой стороны, существование отличного от нуля
центрального момента нечетного порядка показывает наличие асимметрии
распределения.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.