Как найти начальный объем газа

Как найти начальный объем газа

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,655
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,944
  • разное
    16,904

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

Как вычислить объем газа

Газ, как и вещества, находящиеся в других агрегатных состояниях, имеет ряд параметров, в число которых входит и объем. Объем газа находится на основании других его характеристик, которые приведены в условии задачи. Любой газ, независимо от вида и состава, имеет объем, который и требуется найти во многих задачах.

Как вычислить объем газа

Инструкция

Газ, независимо от его состава, имеет три основных параметра: массу, объем и плотность. В большинстве задач оперируют так называемым идеальным газом, поэтому опираться в них необходимо лишь на приведенные в условии значения массы, давления, температуры. Например, в условии задачи может быть указан газ азот N2 с температурой в 60 градусов, давлением в 30 кПа и массой в 0,05 г. Зная эти три параметра и состав газа, по уравнению Менделеева-Клапейрона можно найти его объем. Для этого необходимо переделать данное уравнение следующим образом:

pV=mRT/M.

Осуществив дальнейшее преобразование формулы, найдите объем азота:

V =mRT/pM.

При этом молярную массу M можно найти по таблице Д.И. Менделеева. У азота она равна 12 г/моль. Тогда:

V=0,05*12*8,31*333/30*12≈4,61.

Если известны объем при нормальных условиях, а объем при других условиях является искомым, примените законы Бойля-Мариотта и Гей-Люссака:

pV/T=pнVн/Tн.

В таком случае преобразуйте формулу следующим образом:

pV*Tн=pнVн*T.

Отсюда объем V равен:

V=pнVн*T/p*Tн.

Индекс н означает величину того или иного параметра при нормальных условиях.

Если рассматривать объем газа с точки зрения термодинамики, можно заметить, что на газы могут действовать силы, за счет которых меняется объем. При этом давление газа постоянно, что характерно для изобарных процессов. В ходе таких процессов объем изменяется с одной величины на другую. Их можно обозначить как V1 и V2. В условиях ряда задач описывается некоторый газ, находящийся под поршнем в сосуде. При расширении этого газа поршень передвигается на некоторое расстояние dl, в результате чего осуществляется работа:

A=pdV=p(V2 -V1).

Эта формула связывает изменение объема газа и работу. Как известно, если дан конечный объем V2, то можно найти начальный объем V1:

V1=pV2-A/p.

Наконец, наиболее просто найти объем газа, исходя из двух других физических параметров – массы и плотности. Если в условиях задан газ с некоторой плотностью и массой, то его объем следует вычислять по формуле:

V=m/ρ.

У каждого газа имеется определенная плотность, как и у любого твердого или жидкого вещества. Поэтому, находя объем газа, в первую очередь необходимо учитывать именно этот параметр.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Первый закон термодинамики

  • Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

  • Работа газа в изобарном процессе

  • Работа газа в произвольном процессе

  • Работа, совершаемая над газом

  • Применение первого закона термодинамики к изопроцессам

  • Адиабатный процесс

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой F=pS, где p — давление газа, S — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

к оглавлению ▴

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении p. Тогда сила F, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние Delta x (рис. 1).

Рис. 1. A = p Delta V

Работа газа равна:

A = F Delta x=pS Delta x.

Но S Delta x= Delta V — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

A = p Delta V. (1)

Если V_1 и V_2 — начальный и конечный объём газа, то для работы газа имеем: A = p(V2-V1). Изобразив данный процесс на pV-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма V_1 до объёма V_2. С помощью аналогичных рассуждений приходим к формуле:

A = -p(V_1 -V_2).

Но -(V_1-V_2) = V_2 -V_1 = Delta V, и снова получается формула (1).

Работа газа опять-таки будет равна площади под графиком процесса на pV-диаграмме, но теперь со знаком минус.

Итак, формула A=p Delta V выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

к оглавлению ▴

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на pV-диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение dV объёма газа — настолько малое, что давление p будет оставаться приблизительно постоянным. Газ совершит малую работу dA=p dV. Тогда работа A газа во всём процессе найдётся суммированием этих малых работ:

A=int_{V_1}^{V_2}p dV.

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):

Рис. 3. Работа газа как площадь

к оглавлению ▴

Работа, совершаемая над газом

Наряду с работой A, которую совершает газ по передвижению поршня, рассматривают также работу {A}, которую поршень совершает над газом.

Если газ действует на поршень с силой vec{F}, то по третьему закону Ньютона поршень действует на газ с силой {vec{F}}, равной силе vec{F} по модулю и противоположной по направлению: {vec{F}} (рис. 4).

Рис. 4. Внешняя сила {vec{F}}, действующая на газ

Следовательно, работа поршня {A} равна по модулю и противоположна по знаку работе газа:

{A}

Так, в процессе расширения газ совершает положительную работу left ( A> 0 right ); при этом работа, совершаемая над газом, отрицательна left ( {A}. Наоборот, при сжатии работа газа отрицательна left ( A < 0 right ), а работа, совершаемая поршнем над газом, положительна 0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа {A}.

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты Q, и если в то же время над телом совершена работа {A}, то изменение внутренней энергии тела будет равно:

Delta U = Q + {A} (2)

Нас больше всего интересует случай, когда тело является газом. Тогда {A} (где A, как всегда, есть работа самого газа). Формула (2) принимает вид: Delta U = Q-A, или

Q = Delta U + A. (3)

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина Q может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

к оглавлению ▴

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, T = const.
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: Delta U = 0. Тогда формула (3) даёт:

Q = A.

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, V = const.
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: A = 0. Тогда первый закон термодинамики даёт:

Q = Delta U.

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, p = const.
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:

Q = Delta U + p Delta V.

к оглавлению ▴

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе Q=0. Из первого закона термодинамики получаем: A+ Delta U = 0, или A = - Delta U.

В процессе адиабатного расширения газ совершает положительную работу, поэтому Delta U < 0 (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет A < 0, поэтому Delta U > 0: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

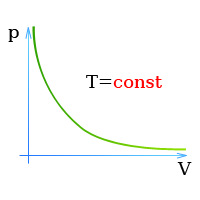
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на pV-диаграмме (рис. 5).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Закон Бойля-Мариотта — один из фундаментальных законов физики и химии, который связывает изменения давления и объема газообразных веществ. При помощи нашего калькулятора легко решить простые задачи по физике или химии.

Закон Бойля-Мариотта

Изотермический газовый закон был открыт ирландским ученым Робертом Бойлем, который проводил опыты над газами под давлением. При помощи U-образной трубки и обычной ртути Бойль установил простую закономерность, что в каждый момент времени произведение давления на объем газа неизменно. Если говорить сухим математическим языком, то закон Бойля-Мариотта гласит, что при неизменной температуре произведение давления и объема постоянно:

P×V = const.

Для сохранения постоянного соотношения величины должны изменяться в разные стороны: во сколько раз уменьшится одна величина, во столько же раз увеличится другая. Следовательно, давление и объем газа обратно пропорциональны и закон можно переписать в следующем виде:

P1×V1 = P2×V2,

где P1 и V1 — начальные значения давления и объема соответственно, а P2 и V2 — конечные значения.

Применение закона Бойля-Мариотта

Наилучшей иллюстрацией проявления открытого Бойлем закона является погружение пластиковой бутылки под воду. Известно, что если газ помещен в баллон, то давление на вещество будет определяться только стенками баллона. Другое дело, когда это пластичная бутылка, которая легко изменяет свою форму. На поверхности воды (давление 1 атмосфера) закрытая бутылка будет сохранять свою форму, однако при погружении на глубину 10 м на стенки сосуда будет действовать давление в 2 атмосферы, бутылка начнет сжиматься, а объем воздуха уменьшится в 2 раза. Чем глубже будет погружаться пластиковая тара, тем меньший объем будет занимать воздух внутри нее.

Это простая демонстрация действия газового закона иллюстрирует важный вывод для многих дайверов. Если на поверхности воды баллон с воздухом имеет емкость 20 л, то при погружении на глубину 30 м, воздух внутри сожмется в три раза, следовательно, воздуха для дыхания на такой глубине будет в три раза меньше, чем на поверхности.

Помимо дайверской темы, закон Бойля-Мариотта в действии можно наблюдать в процессе сжатия воздуха в компрессоре или в расширении газов при использовании насоса.

Наша программа представляет собой онлайн-инструмент, при помощи которого легко рассчитать пропорцию для любого газового изотермического процесса. Для использования инструмента вам требуется знать три любые величины, а калькулятор автоматически рассчитает искомую.

Примеры работы калькулятора

Школьная задача

Рассмотрим простую школьную задачку, в которой требуется найти первоначальный объем газа, если давление изменилось с 1 до 3 атмосфер, а объем уменьшился до 10 л. Итак, у нас есть все данные для расчета, которые требуется ввести в соответствующие ячейки калькулятора. В итоге получаем, что первоначальный объем газа составлял 30 литров.

Еще о дайвинге

Вспомним пластиковую бутыль. Представим, что мы погрузили бутыль, наполненную 19 л воздуха на глубину 40 м. Как изменится объем воздуха на поверхности? Это более сложная задачка, но только потому, что нам требуется перевести глубину в давление. Мы знаем, что на поверхности воды атмосферное давление составляет 1 бар, а при погружении в воду давление увеличивается на 1 бар каждые 10 м. Это означает, что на глубине 40 м бутыль будет под давлением приблизительно 5 атмосфер. У нас есть все данные для расчета, и в результате мы увидим, что объем воздуха на поверхности увеличится до 95 литров.

Заключение

Закон Бойля-Мариотта встречается в нашей жизни довольно часто, поэтому вам несомненно пригодится калькулятор, который автоматизирует расчеты по этой простой пропорции.

Источник

Закон Бойля — Мариотта (Давление и объем газа)

Давление газа при постоянной температуре пропорционально числу молекул газа,
находящихся в данном объеме, т.е. массе газа.
Состояние газов описывается законом Бойля — Мариотта:

При постоянной температуре объем находящегося в замкнутом
сосуде газа обратно пропорционален давлению,

Закон Бойля - Мариотта (Давление и объем газа)

Закон Бойля — Мариотта (Давление и объем газа)

или

При постоянной температуре произведение давления газа, находящегося в замкнутом сосуде,
на его объем есть постоянная величина,

или

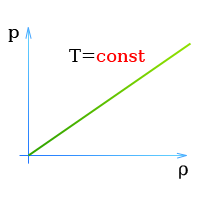
При постоянной температуре давление и плотность находящегося в замкнутом сосуде газа пропорциональны друг другу

Закон Бойля - Мариотта (Давление и объем газа)

Закон Бойля — Мариотта (Давление и объем газа)

Если

p1 начальное давление газа, Па
p2 конечное давление газа, Па
V1 начальный объем газа, м3
V2 конечный объем газа, м3

то

[ frac{p_1}{p_2} = frac{V_2}{V_1} ]

или

[ pV = const ]

Закон Бойля – Мариотта (Давление и объем газа)

 стр. 507
Источник

Добавить комментарий