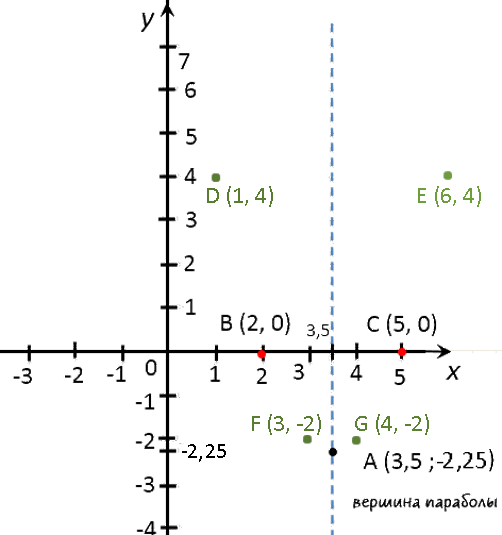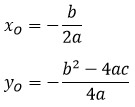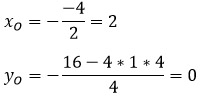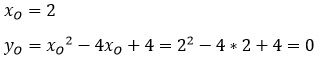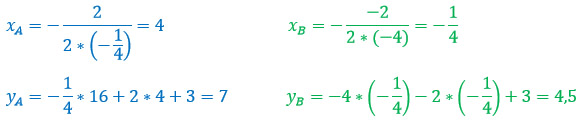В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 

В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с – свободный член.
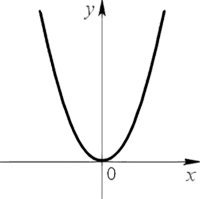
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Обратите внимание на точки, обозначенные зелеными кружками – это, так называемые “базовые точки”. Чтобы найти координаты этих точек для функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: 
И здесь возможны три случая:
1. Если 



2. Если 



3. Если 



Если 
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 
2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:

3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2. Уравнение квадратичной функции имеет вид 

или в уравнении квадратичной функции 

Построим для примера график функции 
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 
- сначала построить график функции
,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции 

Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: 
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
– ширины графика функции от значения коэффициента
,
– сдвига графика функции вдоль оси
от значения
,
– сдвига графика функции вдоль оси
от значения
– направления ветвей параболы от знака коэффициента
– координат вершины параболы от значений
и
:
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
|
y = 3x2 − 1
|
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
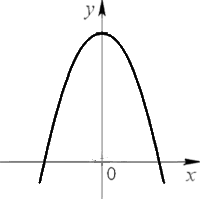
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a < 0», то ветви направлены вниз.
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy». - Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!
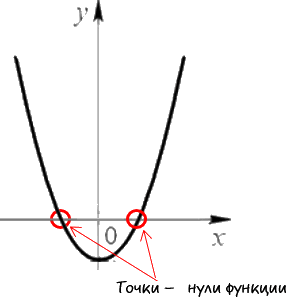
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график.
На забудьте после построения подписать график функции. - y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции
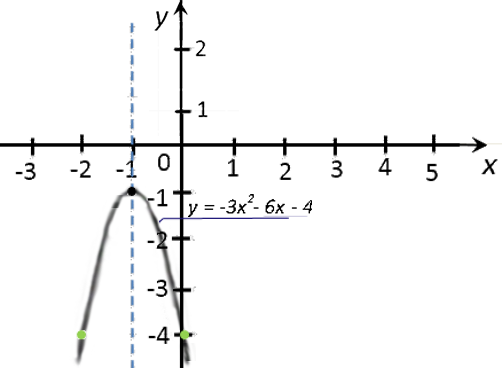
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
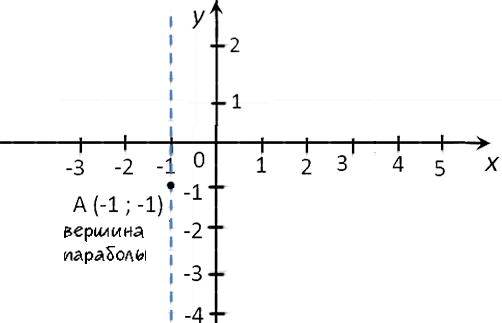
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
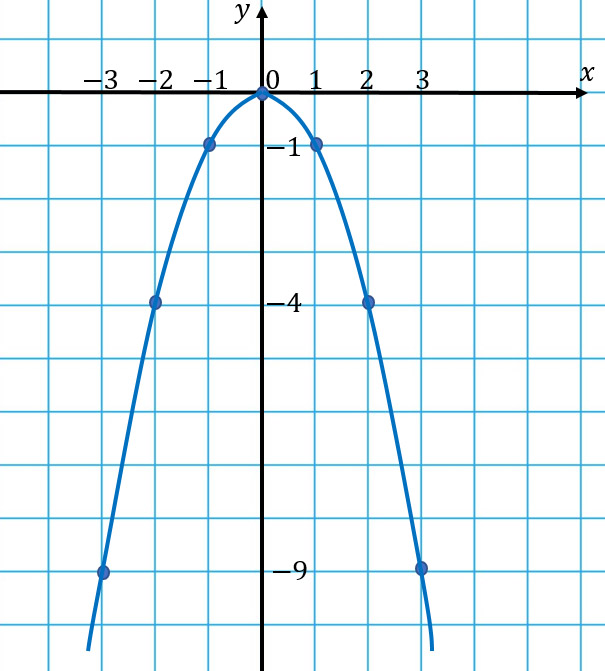
На координатной плоскости отмечаем эти точки и чертим параболу.
Вершина этой параболы находится в точке (0; 0). И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).
Еще одна стандартная парабола задается функцией y = –x2 (в этом случае а = -1). Для этого графика я тоже напишу табличку:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Сразу напрашивается вывод: если перед х2 стоит положительное число, то ветви параболы направлены вверх, если отрицательное – то вниз.
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя “на ура”.
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x2 + bx + c (обязательно коэффициент перед х2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Пример 1.
Дана функция y = x2 – 4x + 4. Найдите вершину параболы и постройте график.
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
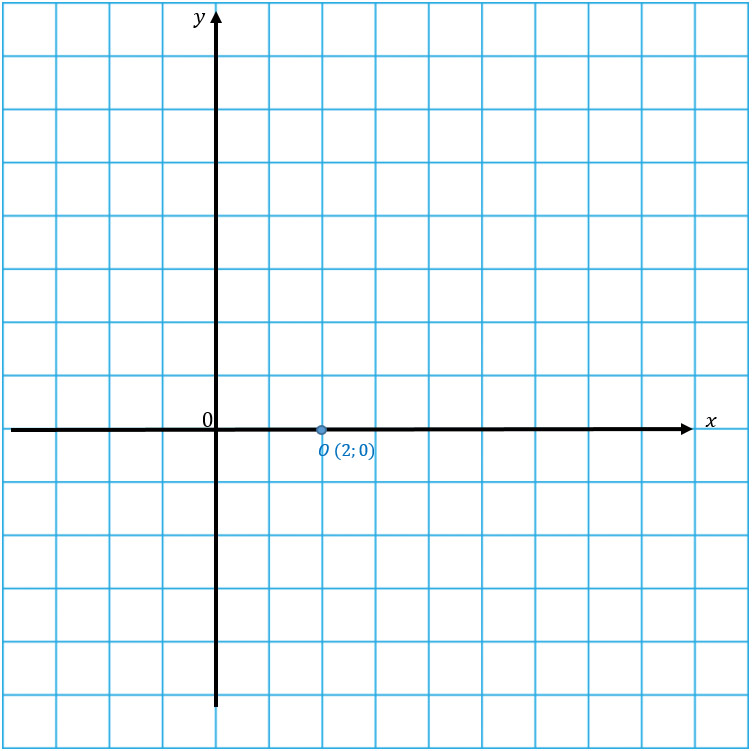
Итак, получили, что О(2; 0) – вершина параболы. Отмечаем ее на координатной плоскости.
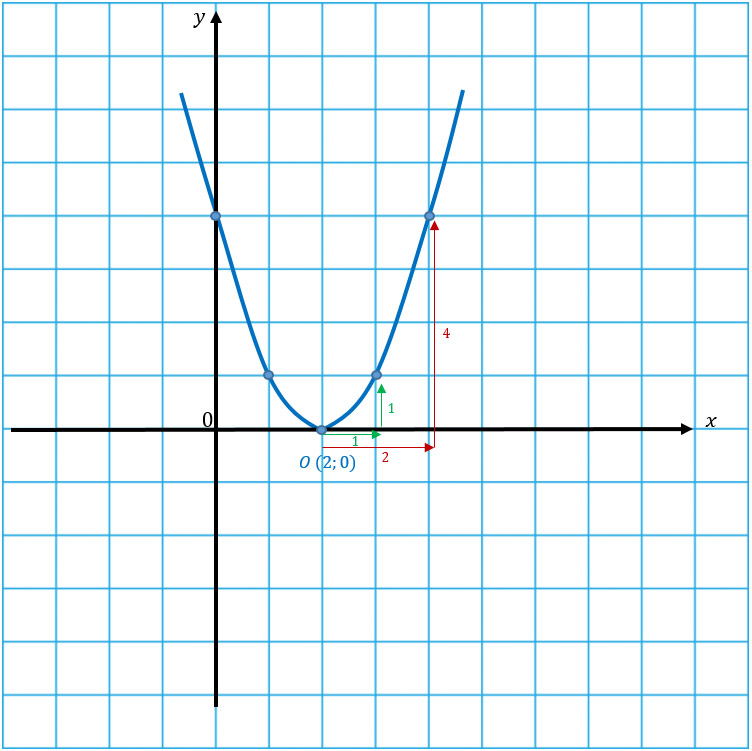
Перед х2 стоит положительное число, значит ветви параболы направлены вверх. Наша задача: нарисовать стандартную параболу, представив, что точка О – начало координат. Если тебе это сложно сделать, то необходимо начертить таблицу значений и уже по ней рисовать параболу.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.
А если числовой коэффициент лежит в промежутке (-∞; -1) ∪ (1; +∞), то парабола будет прижиматься к оси Оу и занимать меньше места на плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Пусть вершиной первой параболы будет точка А(хА; уА), а вершиной второй параболы – точка B(хB; уB). Вершины буду находить по второму способу (см. выше).
Переходим к таблицам значений.
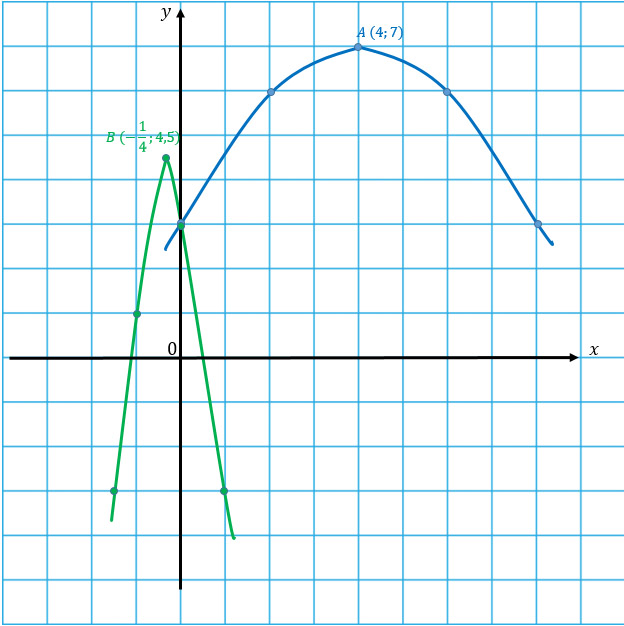
Голубая парабола.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
Зеленая парабола.
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
А ты заметил, что свободный член в уравнении функции – это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
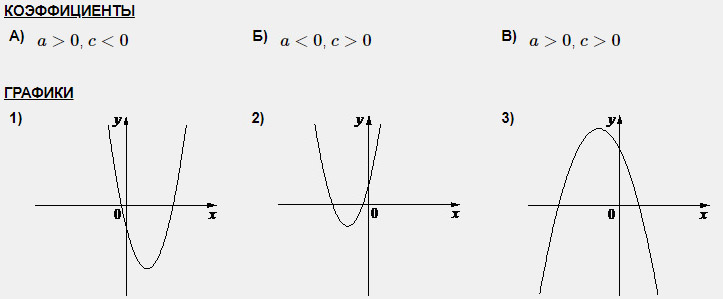
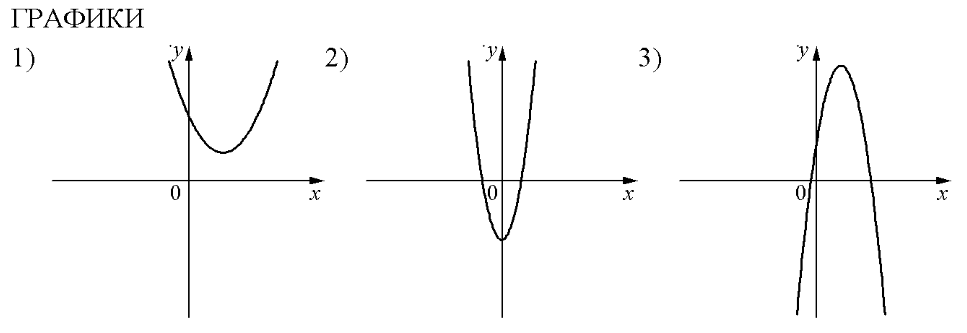
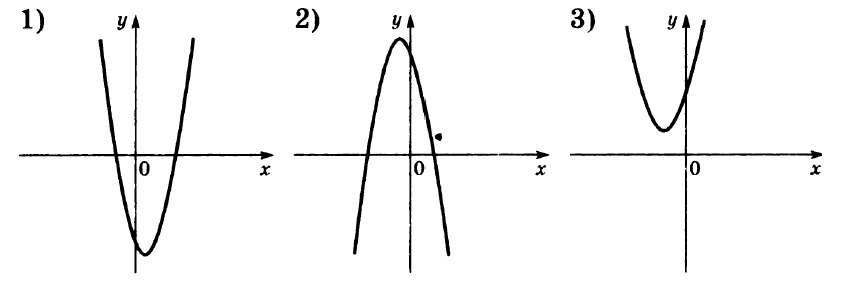
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
Решение. Коэффициент а, стоящий перед х2, отвечает за направление ветвей параболы, а свободный член с – за пересечение графика с осью Оу.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.
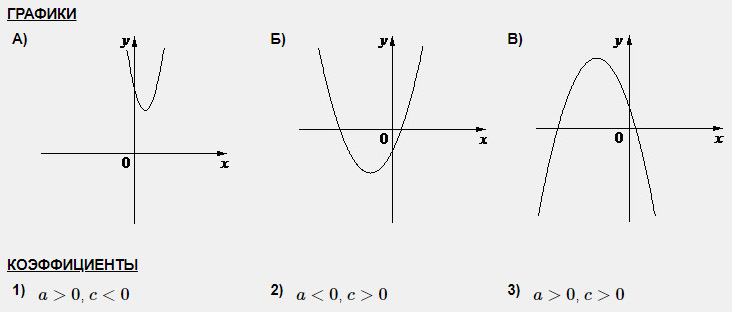
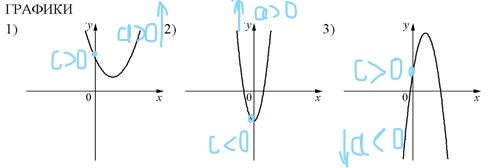
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.
В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.
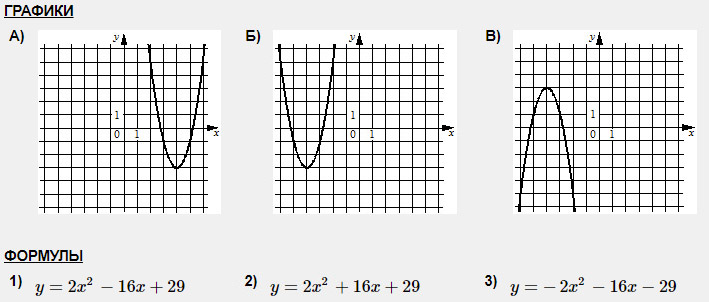
Задание 3. Установите соответствие между графиками и их функциями.
График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х2 – он отрицательный. Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)
Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.
Подставляем в первую функцию: -3 = 2 · 42 – 16 · 4 + 29; -3 = -3 – верно. Значит, А-1.
И остается Б-2.
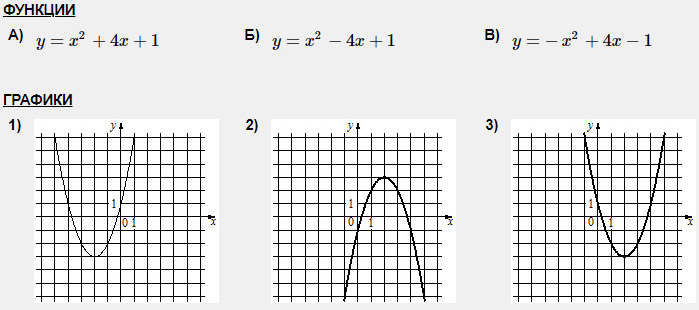
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
Очевидно, что В-2.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Подставляем в функцию А: 1 = (-4)2 + 4 · (-4) + 1; 1 = 1 – верно. Значит, А-1.
Соответственно, Б-3.
Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, – напиши мне в VK)
Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.6k
График квадратичной функции
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция.
Проверь себя, ответь на эти вопросы:
- Как выглядит квадратичная функция в общем виде (формула)?
- Как называется график квадратичной функции?
- Как влияет старший коэффициент на график квадратичной функции?
Если ты сходу смог ответить, продолжай читать.
Если хоть один вопрос вызвал затруднения, повтори тему «Квадратичная функция».
А мы начинаем!
График квадратичной функции — коротко о главном
Определение
Квадратичная функция – функция вида ( y=a{{x}^{2}}+bx+c), где ( ane 0), ( b) и ( c) – любые числа (коэффициенты), ( c) – свободный член.
График квадратичной функции – парабола.
Если коэффициент ( displaystyle a<0), ветви параболы направлены вниз, если ( displaystyle a>0) – ветви параболы направлены вверх.
Чем больше значение ( displaystyle a) (по модулю), тем у́же становится парабола (ветви становятся более крутыми). И наоборот, чем меньше ( displaystyle a), тем парабола шире.
Вершина параболы
( displaystyle {{x}_{в}}=frac{-b}{2a}), т.е. чем больше ( displaystyle b), тем левее смещается вершина параболы.
Подставляем ( displaystyle {{x}_{в}}) в функцию ( y=a{{x}^{2}}+bx+c), и получаем:
( displaystyle {{y}_{в}}=-frac{{{b}^{2}}-4ac}{4a^2}), т.е. чем ( displaystyle b) больше по модулю, тем выше будет вершина параболы
Свободный член ( displaystyle c) – это координата пересечения параболы с осью ординат.
Квадратичная функция и её коэффициенты
Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: ( y=a{{x}^{2}}+bx+c).
Давай вкратце вспомним, что делают коэффициенты.
- Старший коэффициент ( displaystyle a) отвечает за «крутизну» параболы, или, по-другому, за ее ширину: чем больше ( displaystyle a), тем парабола у́же (круче), а чем ( displaystyle a) меньше, тем парабола шире (более пологая).
- Свободный член ( displaystyle c) – это координата пересечения параболы с осью ординат.
- А коэффициент ( displaystyle b) каким-то образом отвечает за смещение параболы от центра координат. Вот об этом сейчас подробнее.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина. А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
( {{x}_{в}}=frac{-b}{2a}).
Вот так: чем больше ( displaystyle b), тем левее смещается вершина параболы.
Ординату вершины можно найти, подставив ( {{x}_{в}}) в функцию:
( {{y}_{в}}=a{{x}_{в}}^{2}+b{{x}_{в}}+c).
Подставь сам и посчитай. Что получилось?
Если сделать все правильно и максимально упростить полученное выражение, получится:
( {{y}_{в}}=-frac{{{b}^{2}}-4ac}{4a}).
Получается, что чем ( displaystyle b) больше по модулю, тем выше будет вершина параболы.
Перейдем, наконец, к построению графика.
Самый простой способ – строить параболу, начиная с вершины.
Пример №1
Построить график функции ( y=frac{1}{2}{{x}^{2}}+2{x}-1).
Решение:
Для начала определим коэффициенты: ( a=frac{1}{2};text{ }b=2;text{ }c=-1).
Теперь вычислим координаты вершины:
( {{x}_{в}}=frac{-b}{2a}=frac{-2}{2cdot frac{1}{2}}=-2)
( {{y}_{в}}=-frac{{{b}^{2}}-4ac}{4a}=-frac{4+2}{2}=-3)
А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково.
Значит, если мы построим параболу ( y=frac{1}{2}{{x}^{2}}) и переместим ее вершиной в точку ( left( -2;-3 right)), получится нужный нам график:
Просто, правда?
Остается только один вопрос. Как быстро рисовать параболу?
Как быстро рисовать график квадратичной функции — параболу?
Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить. Но с трафаретом везде ходить не получится, да и на экзамен его взять не разрешат. Значит, не будем пользоваться посторонними предметами, а будем искать закономерность.
Рассмотрим простейшую параболу ( y={{x}^{2}}). Построим ее по ( displaystyle 7) точкам:
Закономерность здесь такая.
Если из вершины сместиться вправо (вдоль оси ( displaystyle Ox)) на ( displaystyle 1), и вверх (вдоль оси ( displaystyle Oy)) на ( displaystyle 1), то попадем в точку параболы.
Дальше: если из этой точки сместиться вправо на ( displaystyle 1) и вверх на ( displaystyle 3), снова попадем в точку параболы.
Дальше: вправо на ( displaystyle 1) и вверх на ( displaystyle 5). Дальше что?
Вправо на ( displaystyle 1) и вверх на ( displaystyle 7).
И так далее: смещаемся на ( displaystyle 1) вправо, и на следующее нечетное число вверх.
То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным ( displaystyle 1).
Пример построения параболы быстрым способом
Например, нам стало известно, что вершина параболы находится в точке ( displaystyle left( 1;-2 right)). Построй (самостоятельно, на бумаге) эту параболу.
Построил?
Должно получиться так:
Теперь соединяем полученные точки:
Вот и все.
ОК, ну что же, теперь строить только параболы с ( displaystyle a=1)?
Конечно, нет. Сейчас разберемся, что с ними делать, если ( displaystyle ane 1).
Три типичных случая построения параболы
Cлучай 1. ( a=-1).
То есть функция выглядит как ( y=-{{x}^{2}}). Ну что же здесь сложного? Просто переворачиваем параболу рогами вниз, и все. То есть, теперь будем двигаться так:
- ( 1) вправо – ( 1) вниз
- ( 1) вправо – ( 3) вниз
- ( 1) вправо – ( 5) вниз и т. д.
И то же самое, только влево.
Случай 2. ( a>1).
Что делать, если, например, ( a=2)?
Все просто: начинаем так же: ( 1) вправо, но когда дело доходит до «вверх», любое число увеличиваем в ( 2) раза:
- ( 1) вправо – ( 2) вверх
- ( 1) вправо – ( 6) вверх
- ( 1) вправо – ( 10) вверх и т. д.
Аналогично в случае ( a<-1):
- ( 1) вправо – ( 2) вниз
- ( 1) вправо – ( 6) вниз
- ( 1) вправо – ( 10) вниз и т. д.
В общем случае так:
- ( 1) вправо – ( a) вверх
- ( 1) вправо – ( 3a) вверх
- ( 1) вправо – ( 5a) вверх и т. д.
Если ( a<0), то вместо «вверх» делаем «вниз».
Случай 3. А если ( -1<a<1)?
Принцип тот же: каждый шаг вправо или влево сопровождается шагом вверх или вниз, равным какому-то нечетному числу, умноженному на ( a).
Но отмерять нецелые (дробные) отрезки всегда лень. Поэтому иногда удобнее сделать по-другому: шаг вправо или влево делать не ( 1), а ( frac{1}{a}).
Тогда вверх/вниз придется смещаться на целые ( frac{1}{a}), ( frac{3}{a}), ( frac{5}{a}), ( frac{7}{a}), … клеток.
Например: построим график ( y=-frac{1}{3}{{x}^{2}}). Будем откладывать:
- вправо ( 3) – вниз ( 3)
- вправо ( 3) – вниз ( 9)
- вправо ( 3) – вниз ( 15) и т. д.
и затем то же самое влево.
Отлично, параболу рисовать научились, давай теперь потренируемся на настоящих функциях.
4 задачи на построение графика функции
Нарисуй 4 графика следующих функций:
- ( y={{x}^{2}}-2{x}+3)
- ( y=-2{{x}^{2}}+12{x}-20)
- ( y=frac{{{x}^{2}}}{2}-2{x}-2)
- ( y={{x}^{2}}+5{x}+3)
Ответы:
1. ( {{x}_{в}}=frac{-b}{2a}=1;text{ }{{y}_{в}}=-frac{{{b}^{2}}-4ac}{4a}=2):
2. ( {{x}_{в}}=3;text{ }{{y}_{в}}=-2)
3. Вершина: ( {{x}_{в}}=2;text{ }{{y}_{в}}=-4).
Помнишь, что делать, если старший коэффициент меньше ( displaystyle 1)?
Смотрим на знаменатель дроби: он равен ( displaystyle 2). Значит, будем двигаться так:
4. Вершина: ( {{x}_{в}}=-2,5;text{ }{{y}_{в}}=-3,25).
Ой, а что с этим делать? Как отмерять клетки, если вершина где-то между линиями?..
А мы схитрим.
Рассмотрим еще один способ записи квадратичной функции: выделение полного квадрата. Этот способ был подробно описан в теме «Квадратные уравнения».
Выделение полного квадрата
Напомню, что мы можем представить функцию ( y=a{{x}^{2}}+bx+c) в таком виде:
( y=a{{left( x-p right)}^{2}}+q).
Например: ( y={{x}^{2}}-6x+5={{left( x-3 right)}^{2}}-4).
Или: ( 2{{x}^{2}}+6x+1=2{{left( x+1,5 right)}^{2}}-3,5).
Что это нам дает?
Дело в том, что число, которое вычитается из ( displaystyle x) в скобках (( displaystyle p)) – это абсцисса вершины параболы, а слагаемое за скобками (( displaystyle q)) – ордината вершины.
Это значит, что, построив параболу ( y=a{{x}^{2}}), нужно будет просто сместить ось ( displaystyle Oy) на ( displaystyle p) влево и ось ( displaystyle Ox) на ( q) вниз.
Пример: построим график функции ( y=0,5{{x}^{2}}+2x+1).
Выделим полный квадрат:
( y=0,5left( {{x}^{2}}+4x right)+1=0,5left( {{x}^{2}}+4x+4-4 right)+1=0,5left( {{x}^{2}}+4x+4 right)-2+1=0,5{{left( x+2 right)}^{2}}-1)
Какое число вычитается из ( displaystyle x) в скобках? Это ( displaystyle -2) (а не ( displaystyle 2), как можно решить, не подумав).
Итак, строим параболу ( y=0,5{{x}^{2}}):
Теперь смещаем ось ( displaystyle Ox) на ( displaystyle -1) вниз, то есть на ( displaystyle 1) вверх:
А теперь – ( displaystyle Oy) на ( displaystyle -2) влево, то есть на ( displaystyle 2) вправо:
Вот и все. Это то же самое, как переместить параболу ( y=0,5{{x}^{2}}) вершиной из начала координат в точку ( displaystyle (-2;-1)), только прямые оси двигать намного легче, чем кривую параболу.
Теперь, как обычно, сам.
Еще два примера на самостоятельную работу
- ( y=2{{x}^{2}}-8x+3)
- ( y=-{{x}^{2}}-4x+2)
И не забывай стирать ластиком старые оси!
Я в качестве ответов для проверки напишу тебе ординаты вершин этих парабол:
- ( displaystyle -5)
- ( displaystyle 6)
Все сошлось?
Если да, то ты молодец! Уметь обращаться с параболой – очень важно и полезно, и здесь мы выяснили, что это совсем не трудно.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
Выделение полного квадрата
Посмотри это видео и ты научишься выделять полный квадрат на автомате!
Этот навык помимо построения параболы, поможет вам решать квадратные уравнения, раскладывать выражение на множители, разобраться с с уравнением окружности в задаче с параметром (18-я задача), которая дает целых 4 первичных балла.
В общем, метод выделения полного квадрата — бесценный навык.
Берите тетрадку, ручку и смотрите видео. Алексей разберет 8 примеров! Слушайте условие, ставьте на паузу, решайте и потом сравнивайте с тем, как решил Алексей.
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».