Функция вида y=ax2+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Рисунок №1.
Вершина параболы. Формула.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
х0=−b2a
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax2+bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0=−b2a=82∙2=84=2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2∙22 – 8∙2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Ответ: (2; –3).
Нули параболы
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
х2 +4х – 5=0
а=1, b=4, с= –5
D=b2 – 4ac=42 – 4∙1∙(−5)=36
x=−b±√D2a
x=−4±√362; х1=–5; х2=1
Значит, нули функции равны –5 и 1
Ответ: –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:
Ответ: 231
Пример №4
Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0. 
Итак, найдем х0 для формулы «Б»:
х0=−b2a=−42∙2=−44=−1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
Ответ: 231
Задание 11OM21R
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.
КОЭФФИЦИЕНТЫ
А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0
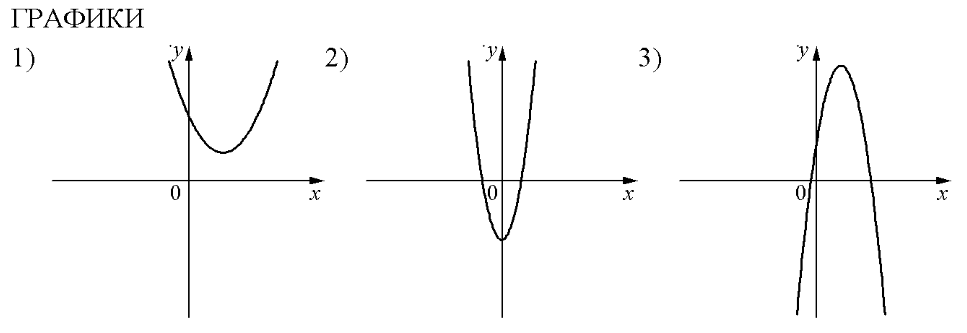
В таблице под каждой буквой укажите соответствующий номер.
Ответ:
Решение
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).
Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.
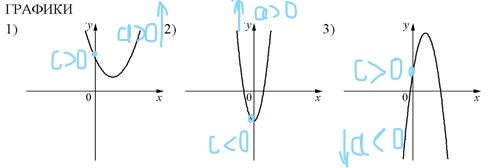
Теперь расставим в соответствии с указанными коэффициентами:
А) a>0, с >0 – это график №1
Б) а<0; с>0 – это график №3
В) а>0, с<0 – это график №2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1105o
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) у=–х2–4х–3 Б) у=–х2+4х–3 В) у=х2+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.
Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x0 отрицателен, значит, А-1, а Б-2.
Ответ: 123
pазбирался: Даниил Романович | обсудить разбор
Задание OM1101o
На рисунках изображены графики функций вида
y = ax² + bx + c
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Коэффициенты:
А) a > 0, c > 0
Б) a < 0, c > 0
В) a > 0, c < 0
Графики:
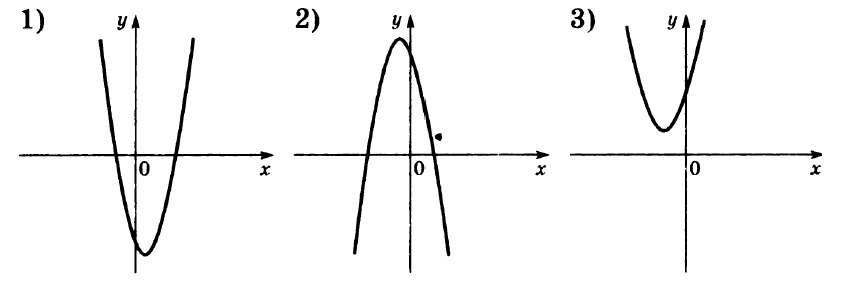
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
y = ax² + bx + c
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.
Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.
У первой и третьей ветви направлены вверх, то есть a > 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
если c < 0, то вершина параболы расположена ниже оси x
Так, у первой параболы c < 0, у второй и третьей c > 0.
Из всего вышеперечисленного можно найти ответ:
А) 3
Б) 2
В) 1
Ответ: 321
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 10.5k
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
![]()
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
|
y = −3x2 + 2x
|
|
Как построить график квадратичной функции
Запомните!
![]()
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
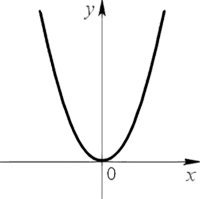
Также парабола может быть перевернутой.
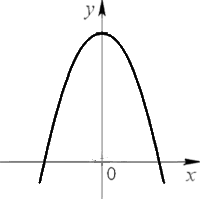
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.

- Координаты вершины параболы
Запомните!

Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».
- Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!

Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
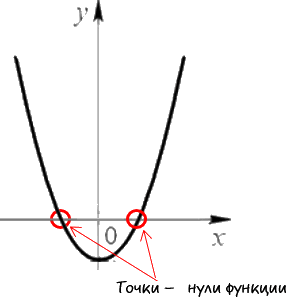
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.

- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
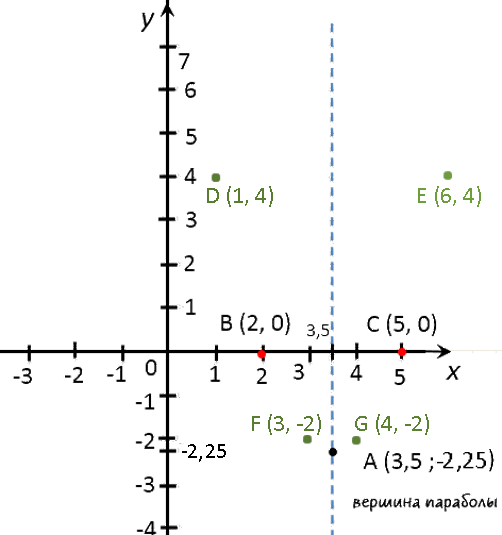
Теперь мы готовы построить график.
На забудьте после построения подписать график функции.
- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
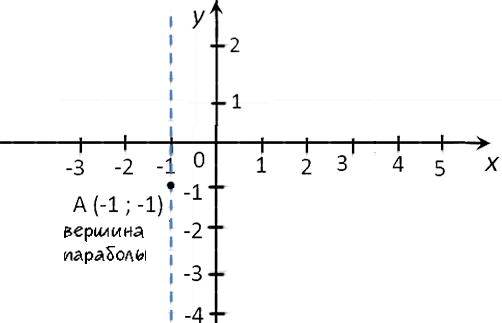
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
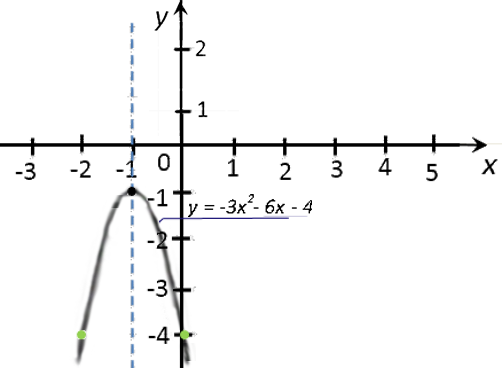
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Как найти функцию графика
Еще в школьные годы подробно изучаются функции и строятся их графики. Но, к сожалению, читать график функции и находить ее тип по представленному чертежу практически не учат. В действительности это довольно просто, если помнить основные виды функций.

Инструкция
Если представленным графиком является прямая линия, которая проходит через начало координат и образует с осью ОX угол α (который является углом наклона прямой к положительной полуоси), то функция, описывающая такую прямую, будет представлена как y = kx. При этом коэффициент пропорциональности k равен тангенсу угла α.
Если заданная прямая проходит через вторую и четвертую координатные четверти, то k равен 0, и функция возрастает. Пусть представленный график является прямой линией, располагающейся любым образом относительно осей координат. Тогда функцией такого графика будет линейная, которая представлена видом y = kx + b, где переменные y и х стоят в первой степени, а b и k могут принимать как отрицательные, так и положительные значения или нулевое значение.
Если прямая параллельна прямой с графиком y = kx и отсекает на оси ординат b единиц, тогда уравнение имеет вид x = const, если график параллелен оси абсцисс, то k = 0.
Кривая линия, которая состоит из двух ветвей, симметричных относительно начала координат и располагающихся в разных четвертях, называется гиперболой. Такой график показывает обратную зависимость переменной y от переменной x и описывается уравнением вида y = k/x, где k не должен быть равен нулю, так как является коэффициентом обратной пропорциональности. При этом, если значение k больше нуля, функция убывает; если же k меньше нуля – возрастает.
Если предложенным графиком является парабола, проходящая через начало координат, ее функция при выполнении условия, что b = с = 0, будет иметь вид y = ax2. Это самый простой случай квадратичной функции. График функции вида y = ax2 + bx + с будет иметь такой же вид, что и простейший случай, однако вершина параболы (точка, где график пересекается с осью ординат) будет находиться не в начале координат. В квадратичной функции, представленной видом y = ax2 + bx + с, значения величин a, b и c – постоянные, при этом a не равно нулю.
Параболой также может являться график степенной функции, выраженной уравнением вида y = xⁿ, только если n является любым четным числом. Если же значение n – нечетное число, такой график степенной функции будет представлен кубической параболой. В случае, если переменная n является любым отрицательным числом, уравнение функции приобретает вид гиперболы.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Начало декартовой системы координат на плоскости
Начало координат (начало отсчёта) в евклидовом пространстве — особая точка, обычно обозначаемая буквой О, которая используется как точка отсчёта для всех остальных точек. В евклидовой геометрии начало координат может быть выбрано произвольно в любой удобной точке.
Вектор, проведённый из начала координат в другую точку, называется радиус-вектором.
Декартова система координат[править | править код]
В декартовой системе координат, начало координат — это точка, в которой пересекаются все оси координат. Это означает, что все координаты этой точки равны нулю. Например, на плоскости она имеет координаты (0,0), а в трёхмерном пространстве — (0,0,0).
Начало координат делит каждую из осей на два луча — положительную полуось и отрицательную полуось.
В частности, начало координат можно ввести на числовой оси. В этом смысле можно говорить о начале координат для разных экстенсивных величин (времени, температуры и пр.)
Полярные системы координат[править | править код]
В полярной (на плоскости) и цилиндрической и сферической системах координат (в пространстве), начало координат имеет особое название — «полюс». Полюс является точкой сингулярности таких систем координат, поскольку в такой точке одна или несколько координат не определены. Обычно такой координатой является угол (например, в полярной системе координат, в точке О угол может принимать любое значение — положение точки, определяемой координатами 

Симметрия[править | править код]
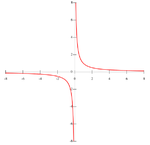
Этот график симметричен относительно начала координат
Если график функции симметричен относительно начала координат (то есть выглядит так же, если его повернуть на 180° относительно этой точки), то такая функция называется нечётной.
См. также[править | править код]
- Нулевой километр
- Нулевой меридиан
- Остров Ноль
Ссылки[править | править код]
Вершина параболы
Содержание:
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Что такое вершина параболы
Определение
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.
Чтобы найти ВП, необходимо применить формулу:
(lbrackfrac{-b}{2a};-frac{b^2-4ac}{4a}rbrack)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Исходя из координат, можно узнать расположение вершины параболы и построить ее.
Вывод формулы координат вершины параболы
Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:
(y;=;ax^2;+;bx;+;c)
Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y.
Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:
(y;=;f(x;+;l);+;m)
Делают это с помощью метода выделения полного квадрата, то есть (left(a+bright)^2) преобразуют в (a^2+2ab+b^2.)
Функции вида (y;=;f(x;+;l);+;m) отличаются от (y;=;f(x)) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:
(frac{-b}{2a}, а frac{left(4ac-b^2right)}{4a})
Получается, что l и m — это координаты x0 и y0.
Приведем доказательство:
- Соединяем первые два члена многочлена: (y;=;(ax^2;+;bx);+;c.)
- Выносим коэффициент a за скобку, b при этом делим на a: (y=aleft(x^2+frac baxright)+c.)
- Представляем, что у нас есть квадрат суммы, в котором x является слагаемым, а из выражения в скобках необходимо рассчитать его полный квадрат суммы. Одночлен (frac bax) умножаем на два и делим на два одновременно. Далее прибавляем и вычитаем квадрат второго слагаемого квадрата суммы. Получаем: (y=aleft(x^2+2frac b{2a}x+frac{b^2}{4a^2}-frac{b^2}{4a^2}right)+c.)
- Выделяем квадрат суммы: (y=aleft(left(x+frac b{2a}right)^2-frac{b^2}{4a}right)+c.)
- Умножаем на a: (y=aleft(x+frac b{2a}right)^2-frac{b^2}{4a}+c.)
- Приводим свободные члены к общему знаменателю: (y=aleft(x+frac b{2a}right)^2-frac{b^2+4ac}{4a}.)
- Меняем знак: (y=aleft(x+frac b{2a}right)^2+frac{b^2-4ac}{4a}.)
Мы привели функцию (y;=;ax^2;+;bx;+;c) к виду (y;=;a{(x;+;l)}^2;+;m,) что соответствует (y;=;f(x;+;l);+;m,) где (f(x);=;ax^2. )
Как найти координаты, основные способы
Существует несколько способов нахождения координат ВП:
- (x_0=frac{-b}{2a}) — подходит в том случае, если дискриминант квадратного уравнения равен нулю.
- (y_0=-frac{b^2-4ac}{4a}) — это формула дискриминанта, поделенная на 4а.
- (x_0=frac{x_1+x_2}2) — среднее арифметическое между нулями функции. Можно использовать, если в выражении есть нули.
- Если функция имеет вид (y=aleft(x-x_0right)^2+y_0), то в ее вершиной совпадают координаты (left(x_0;y_0right).)
Примеры решения задач
Задача №1
Найти вершину параболы для уравнения: (y=x^2-5x+7.)
Решение: В выражение (x=-frac b{2a}) подставляем известные числа и получаем (x=frac52=2,5). Теперь подставляем x в исходное уравнение: (2,5^2-5times2,5+7=0,75.)
Ответ: (2,5; 0,75).
Задача №2
Найти ВП для уравнения: y=5(x-1)(x+7).
Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.
Подставляем и получаем: (x_0=frac{x_1+x_2}2=frac{1+left(-7right)}2=-3.)
Второе: (y_0=5timesleft(-3-1right)left(-3+7right)=-80.)
Ответ: (-3; -80).
Задача №3
Найти вершину параболы для уравнения: (y=x^2-7x+3 ).
Решение: (х_0=-frac b{2a}=-frac{left(-7right)}{2times1}=3,5.)
Второе: (y_0=3,5^2-7times3,5+3=-9,25.)
Ответ: (3,5; -9,25).
Насколько полезной была для вас статья?
Рейтинг: 2.50 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
