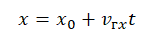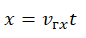Определение координаты движущегося тела

Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Где:
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Следовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
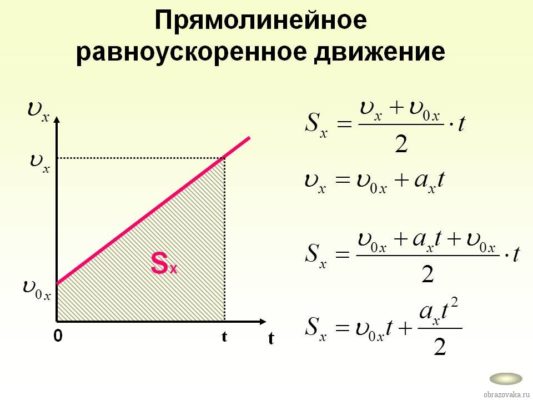
Как найти путь при равноускоренном движении?
Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
А какая ваша оценка?
На
прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним,
что путь — это скалярная величина, равная длине траектории, которую
описывает тело за некоторый промежуток времени.
А
перемещением называется направленный отрезок прямой, соединяющий
начальное и конечное положения тела.
Так
как перемещение — это векторная величина, то есть имеет модуль и направление,
то складывать и вычитать перемещения необходимо по правилам сложения и
вычитания векторов. Однако при решении большинства задач, используется понятие
не вектора, а проекции вектора на ось координат.
—
А что такое проекция вектора и каковы её свойства?
На
это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с
понятия проекция точки на ось. Проекция точки — это основание
перпендикуляра, опущенного из данной точки на ось.
На
представленном рисунке точка А1 — это проекция точки А
на ось Ox,
а точка B1 —
проекция точки B
на
ось Oy.
Теперь
разберёмся с проекцией вектора на ось. Согласно определению, проекция
вектора на ось — это длина отрезка между проекциями начала и конца вектора на
эту ось, взятая со знаком «плюс» или «минус».
Знак
«плюс» берут, если угол между вектором и осью острый, а «минус» — если угол
тупой.
Обозначать
проекцию вектора будем той же буквой, что и вектор, но с индексом внизу
(например, ax
— это проекция вектора a
на ось Ox).
—
А если вектор перпендикулярен оси?
Тогда
проекция этого вектора равна нулю.
Проекцию
вектора можно выразить через его модуль и угол между вектором и осью. Итак,
пусть у нас есть вектор a
направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на
ось.
У
нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине
вектора a,
а катет AB1
— это проекция вектора a
на
ось Ox.
Тогда,
на основании определения косинуса острого угла, мы можем записать, что проекция
вектора на ось равна модулю вектора, умноженному на косинус угла между вектором
и осью:
Это
правило справедливо при любых значениях угла φ. Например,
для углов, больше 90о, косинус угла φ отрицательный. Тогда по
формуле получается, что проекция вектора на ось также отрицательна, как и
должно быть по определению проекции.
—
А можно ли найти модуль и направление вектора по его проекциям на координатные
оси?
Чтобы
ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy.
Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси
координат.
Обратим
внимание на важное свойство проекций: проекция суммы векторов на ось равна
сумме их проекций на эту ось.
Но
вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что
положение тела, которое совершило некоторое перемещение, можно найти
графически. Для этого достаточно отложить вектор перемещения от начального
положения этого тела. Однако в большинстве случаев необходимо уметь вычислять
положение тела, то есть уметь определять его координаты. Давайте на примере
решения задачи посмотрим, как можно определить координату движущегося тела,
зная координату его начального положения и вектор перемещения.
Итак,
два поезда идут по параллельным путям в противоположных направлениях и
встречаются в шестидесяти километрах к востоку от железнодорожного вокзала.
Продолжив движение через некоторое время t первый поезд удалился от места
встречи на 50 километров в восточном направлении, а второй — на 80 километров в
западном. Определите координаты каждого поезда относительно вокзала и
расстояние между ними через промежуток времени t.
Введение
Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Определить положение движущегося тела в любой момент времени – это и есть основная задача кинематики.
Система отсчета
Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).
Рис. 1. Определение местоположения машины
Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).
Рис. 2. Положение телефона на столе
Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.
Координаты – это набор данных, по которому определяется положение того или иного объекта, его адрес.
Примеры упорядоченных и неупорядоченных имен
Координата тела – это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).
Рис. 3. Зал кинотеатра
Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).
Рис. 4. Положение фигуры на доске
Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).
Рис. 5. Поиск дома
Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).
Рис. 6. Неупорядоченные имена
Эти номера, идущие подряд, – это лишь совпадение, не означающее соседства.
Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).
Рис. 7. Долгота и широта местности
Можно выбрать любую точку в городе и считать, сколько километров нужно проехать на юг и сколько на восток, чтобы найти автомобиль (см. рис. 8).
Рис. 8. Местоположение относительно точки
Причем если мы выберем разные такие точки, то получим разные координаты, хотя они будут задавать положение одного и того же автомобиля.
Итак, положение тела относительно разных тел в разных системах координат будет разным. А что такое движение? Движение – это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.
Например, как движется стакан с чаем на столе в поезде, если сам поезд едет? Смотря относительно чего. Относительно стола или пассажира, сидящего рядом на сидении, стакан покоится (см. рис. 9).
Рис. 9. Движение стакана относительно пассажира
Относительно дерева около железной дороги стакан движется вместе с поездом (см. рис. 10).
Рис. 10. Движение стакана вместе с поездом относительно дерева
Относительно земной оси стакан и поезд вместе со всеми точками земной поверхности будут еще и двигаться по окружности (см. рис. 11).
Рис. 11. Движение стакана с вращением Земли относительно земной оси
Поэтому нет смысла говорить о движении вообще, движение рассматривается в привязке к системе отсчета.
Наблюдение и вычисление
Всё, что мы знаем о движении тела, можно разделить на наблюдаемое и вычисляемое. Вспомним пример с мячом, который мы бросили. Наблюдаемое – это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).
Рис. 12. Наблюдение
Это момент времени, когда мы его бросили; время, которое прошло после броска. Пусть на мяче нет спидометра, который показал бы скорость мяча, но ее модуль, как и направление, тоже можно узнать, используя, например, замедленную съемку.
С помощью наблюдаемых данных мы можем предсказать, например, что мяч через 5 секунд упадет за 20 м от места броска или через 3 секунды попадет в верхушку дерева. Положение мяча в любой момент времени – это в нашем случае вычисляемые данные.
Что определяет каждое новое положение движущегося тела? Его определяет перемещение, потому что перемещение – это вектор, характеризующий изменение положения. Если начало вектора совместить с начальным положением тела, то конец вектора укажет на новое положение переместившегося тела (см. рис. 13).
Рис. 13. Вектор перемещения
Нахождение координаты тела по перемещению
Рассмотрим несколько примеров на определение координаты движущегося тела по его перемещению.
Пусть тело двигалось прямолинейно из точки 1 в точку 2. Построим вектор перемещения и обозначим его (см. рис. 14).
Рис. 14. Перемещение тела
Тело двигалось вдоль одной прямой, значит, нам будет достаточно одной оси координат, направленной вдоль перемещения тела. Допустим, мы наблюдаем за движением со стороны, совместим начало отсчета с наблюдателем.
Перемещение – вектор, удобнее работать с проекциями векторов на оси координат (у нас она одна). – проекция вектора
(см. рис. 15).
Рис. 15. Проекция вектора
Как определить координату начальной точки, точки 1? Опускаем перпендикуляр из точки 1 на ось координат. Этот перпендикуляр пересечет ось и отметит на оси координату точки 1. Так же определяем координату точки 2 (см. рис. 16).
Рис. 16. Опускаем перпендикуляры на ось ОХ
Проекция перемещения равна:
При таком направлении оси и перемещения будет по модулю равна самому перемещению
.
Зная начальную координату и перемещение, найти конечную координату тела – дело математики:
Уравнение
Уравнение – это равенство, содержащее неизвестный член. В чем его смысл?
Любая задача заключается в том, что что-то нам известно, а что-то – нет, и неизвестное нужно найти. Например, тело из некоторой точки переместилось на 6 м в направлении оси координат и оказалось в точке с координатой 9 (см. рис. 17).
Рис. 17. Начальное положение точки
Как найти, из какой точки тело начало движение?
У нас есть закономерность: проекция перемещения – это разность конечной и начальной координат:
Смысл уравнения будет в том, что перемещение и конечную координату мы знаем () и можем подставить эти значения, а начальную координату не знаем, она будет неизвестным в этом уравнении:
И уже решая уравнение, мы получим ответ: начальная координата .
Перемещение и направление оси не совпадают по направлению
Рассмотрим другой случай: перемещение направлено в сторону, противоположную направлению оси координат.
Координаты начальной и конечной точек определяются так же, как и раньше, – опускаются перпендикуляры на ось (см. рис. 18).
Рис. 18. Ось направлена в другую сторону
Проекция перемещения (ничего не меняется) равна:
Обратите внимание, что больше, чем
, и проекция перемещения
, когда она направлена против оси координат, будет отрицательной.
Конечная координата тела из уравнения для проекции перемещения равна:
Как видим, ничего не меняется: в проекции на ось координат конечное положение равно начальному положению плюс проекция перемещения. В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
Перемещение и ось координат находятся под углом друг к другу
Рассмотрим случай, когда перемещение и ось координат направлены под углом друг к другу. Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).
Рис. 19. Ось направлена в другую сторону
Теперь перемещение будет иметь ненулевую проекцию на каждую ось координат. Эти проекции перемещения будут определяться, как и раньше:
Заметьте, модуль каждой из проекций в этом случае меньше модуля перемещения. Модуль перемещения можем легко найти, используя теорему Пифагора. Видно, что если построить прямоугольный треугольник (см. рис. 20), то его катеты будут равны и
, а гипотенуза равна модулю перемещения
или, как часто записывают, просто
.
Рис. 20. Треугольник Пифагора
Тогда по теореме Пифагора запишем:
Задача
Автомобиль находится в 4 км к востоку от гаража. Воспользуйтесь одной осью координат, направленной на восток, с началом отсчета в гараже. Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
В задаче ничего не сказано о том, что автомобиль поворачивал или изменял скорость, поэтому считаем движение равномерным прямолинейным.
Изобразим систему координат: начало координат у гаража, ось х направлена на восток (см. рис. 21).
Рис. 21. Направление оси Ох
Автомобиль изначально был в точке и двигался по условию задачи на запад (см. рис. 22).
Рис. 22. Движение автомобиля на запад
Проекция перемещения, как мы неоднократно писали, равна:
Мы знаем, что автомобиль проезжал по 0,5 км каждую минуту, значит, чтобы найти суммарное перемещение, нужно скорость умножить на количество минут
:
На этом физика закончилась, осталось математически выразить искомую координату. Выразим ее из первого уравнения:
Подставим перемещение:
Осталось подставить числа и получить ответ. Не забывайте, что автомобиль двигался на запад против направления оси х, это значит, что проекция скорости отрицательна: .
Задача решена.
Итоги
Главное, чем мы сегодня пользовались для определения координаты, – выражение для проекции перемещения:
И из него мы уже выражали координату:
При этом сама проекция перемещения может быть задана, может вычисляться как , как в было в задаче о равномерном прямолинейном движении, может вычисляться сложнее, что нам еще предстоит изучить, но в любом случае координату движущегося тела (где тело оказалось) можно определить по начальной координате (где тело было) и по проекции перемещения (куда переместилось).
На этом наш урок окончен, до свидания!
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М. Физика: 9 класс. Учебник для общеобразовательных учреждений. – 14-е изд. – М.: Дрофа, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «Class-fizika.narod.ru» (Источник)
- Интернет-портал «Av-physics.narod.ru» (Источник)
- Интернет-портал «Class-fizika.narod.ru» (Источник)
Домашнее задание
- Что такое перемещение, путь, траектория?
- Как можно определить координаты тела?
- Запишите формулу для определения проекции перемещения.
- Как будет определяться модуль перемещения, если перемещение имеет проекции на две оси координат?
Уравнение координаты при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Уравнение координаты — зависимость координаты тела от времени:
Уравнение координаты при равноускоренном прямолинейном движении:
x0 — координата тела в начальный момент времени, v0x —проекция начальной скорости на ось ОХ, ax —проекция ускорения на ось ОХ, x — координата тела в момент времени t
Зная уравнение координаты, можно определить координату тела в любой момент времени.
Пример №1. Движение автомобиля задано уравнением:
Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.
Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x0 = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v0 = 0 м/с.
В момент времени t = 10 c координата автомобиля равна:
Совместное движение двух тел
Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.
Аналитический способ решения задачи на совместное движение тел
Чтобы найти место встречи двух тел, нужно:
- Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
- Построить уравнение вида x1 = x2.
- Найти время встречи двух тел tвстр.
- Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату xвстрч.
Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.
Составим уравнения для движения каждого из тел:
Приравняем правые части этих уравнений и найдем время t:
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:
x = 3t = 3∙6 = 18 (м).
Графический способ решения задачи на совместное движение тел
Существует графический способ решения данной задачи. Для этого нужно:
- Построить графики x1(t) и x2(t).
- Найти точку пересечения графиков.
- Пустить перпендикуляр из этой точки к оси ОХ.
- Значение точки пересечения — координата места пересечения двух тел.
Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.
Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!
Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием tзапазд, то его уравнение координаты принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.
Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).
В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:
Приравняем правые части уравнений и вычислим t:
В результате получаем два
Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.
В момент времени t=0 проекции её скорости υx и ускорения ax на ось Ох удовлетворяют соотношениям:
а)
б)
в)
г)
Алгоритм решения
- Определить характер движения материальной точки.
- Записать уравнение координаты материальной точки.
- С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.
Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 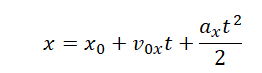
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Записать исходные данные.
- Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
- Выразить скорость грузовика из уравнения его движения.
- Записать уравнение движения мотоциклиста.
- Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
- Подставить время в формулу скорости грузовика и вычислить ее.
Решение
- Координата встречи грузовика и мотоциклиста: x = 150 м.
- Время запаздывания мотоциклиста: tзапазд = 5 с.
- Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .
Запишем уравнение движения грузовика:
Так как начальная координата равна нулю, это уравнение примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Отсюда скорость движения грузовика равна:
Запишем уравнение движения мотоциклиста:
Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:
Найдем время, через которое грузовик и мотоциклист встретились:
Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Механическое движение
О чем эта статья:
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
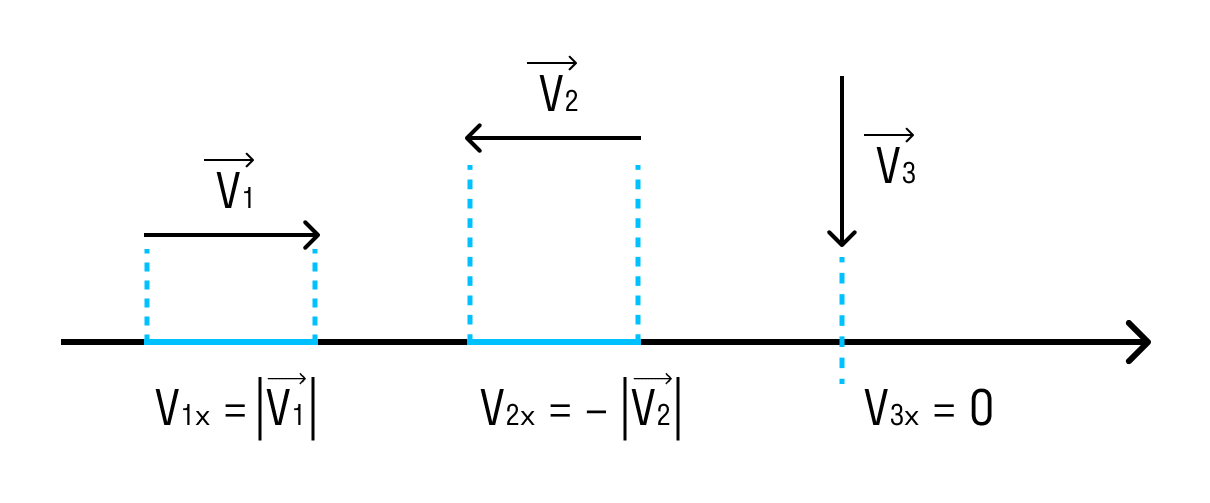
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Уравнение движения при движении против оси
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
Уравнение движения для равноускоренного движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с 2 ]
Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:
Формула конечной скорости
— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места, . Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt 2 /2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки:
км
Ответ: через полчаса координата автобуса будет равна 150 км.
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Формула координаты тела при равномерном прямолинейном движении
Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.
Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:
Формула координаты тела при прямолинейном равномерном движении
x0 — координата тела в начальный момент времени,
x — координата тела в текущий момент времени,
t — время движения,
V — скорость тела
Таким образом, необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат:
[spoiler title=”источники:”]
http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie
http://mnogoformul.ru/formula-koordinaty-tela-pri-ravnomernom-dvigenii
[/spoiler]
Содержание:
- калькулятор координаты тела при равномерном прямолинейном движении
- формула координаты тела при равномерном прямолинейном движении
Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.
Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:
Формула координаты тела при равномерном прямолинейном движении
x=x_0+ V cdot t
x0 – начальная координата тела
V – скорость тела
t – время движения
x – координата тела в текущий момент времени (в момент времени t)
Таким образом, для того, чтобы найти координату тела при равномерном прямолинейном движении необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат.