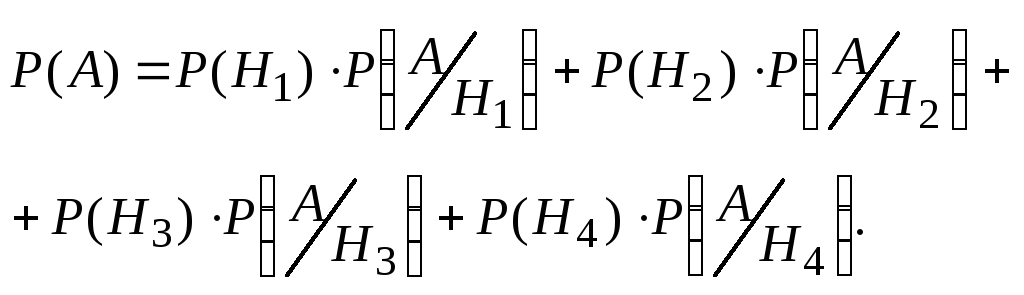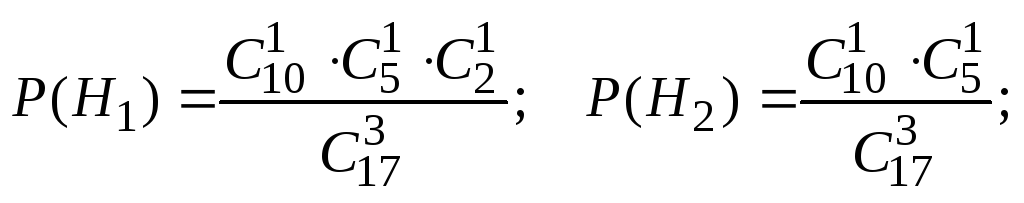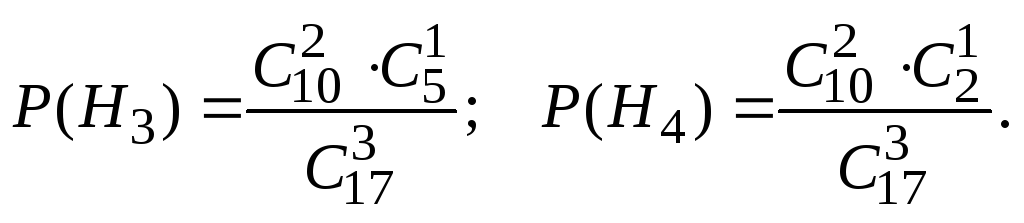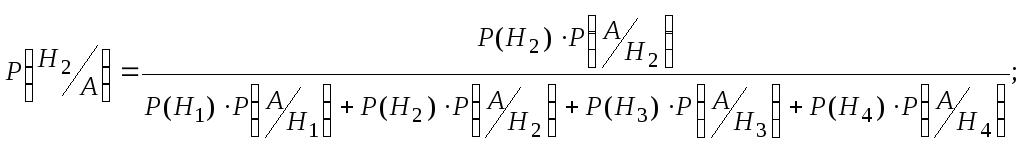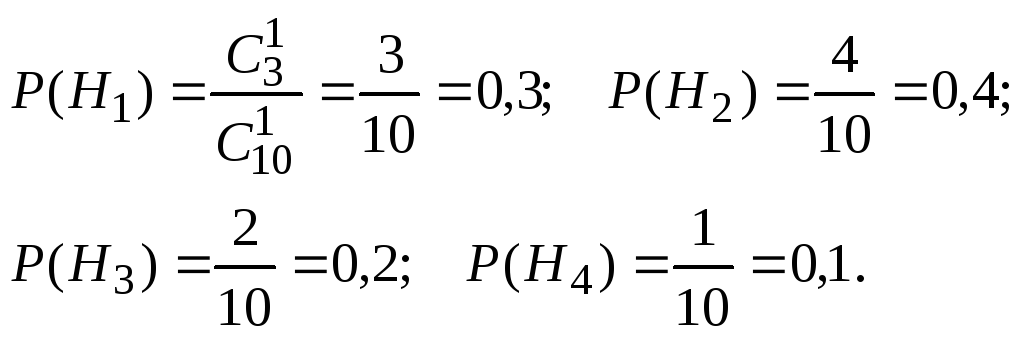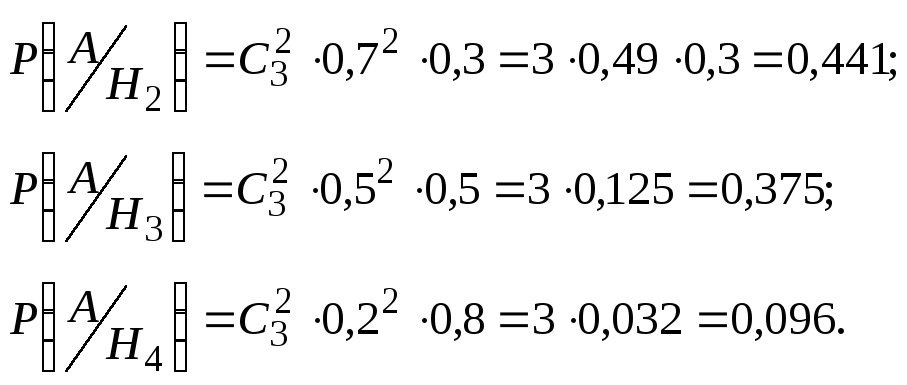Как решать задачи о прохождении тока через электрические схемы
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.
В этой статье мы рассмотрим задачи вида
“задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)”.
Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.
Далее:
- Базовые события, обозначения и формулы
- Последовательно или параллельно?
- Усложняем схему цепи
- Примеры решений
- На закуску: схема с мостиком
- Полезные ссылки
- Решебник
Спасибо за ваши закладки и рекомендации
Базовые события, обозначения и формулы
Самое первое, с чего мы начнем – формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:
$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:
$overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).
$A_i$ = (Элемент i работает, пропускает ток) и $overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,…,n$.
Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline{A_i})=q_i=1-p_i$, $i=1,2,…,n$.
Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.
Для независимых в совокупности событий (а отказы/работа элементов цепи – именно такие):
$$
P(A cdot B) = P(A) cdot P(B); quad(1)
$$
$$
P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2)
$$
$$
P(A_1+A_2+…+A_n)=1-P(overline{A_1})cdot P(overline{A_2})cdot … cdot P(overline{A_n}). quad(3)
$$
Последовательно или параллельно?
Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.
Последовательное соединение
Элементы цепи “нанизаны” на провод один за другим (следуют один за другим, отсюда и “последовательно”). Если откажет один любой – ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна
$$
P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3.
$$
Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:
$$
P(X) = p_1 cdot p_2 cdot …cdot p_n; qquad P(overline{X})=1-p_1 cdot p_2 cdot …cdot p_n. quad(4)
$$
Параллельное соединение
Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.
В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.
Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей – это сумма событий: $X=A_1+A_2+A_3$.
Используем формулу (3) чтобы записать вероятность работы такой цепи:
$$
P(A_1+A_2+A_3)=1-P(overline{A_1})cdot P(overline{A_2}) cdot P(overline{A_3})=1-q_1 cdot q_2 cdot q_3.
$$
И обобщим на случай $n$ параллельных элементов в цепи:
$$
P(X) = 1-q_1 cdot q_2 cdot …cdot q_n; qquad P(overline{X})=q_1 cdot q_2 cdot …cdot q_n. quad(5)
$$
Важно запомнить правило
Последовательному соединению соответствует произведение событий,
параллельному соединению – сумма событий.
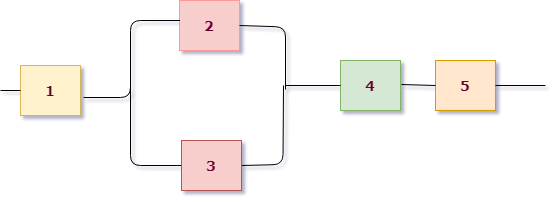
Усложняем схему цепи
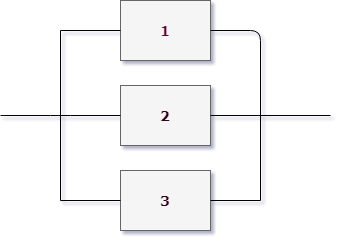
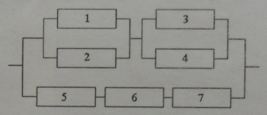
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с “тремя лампочками подряд” вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.
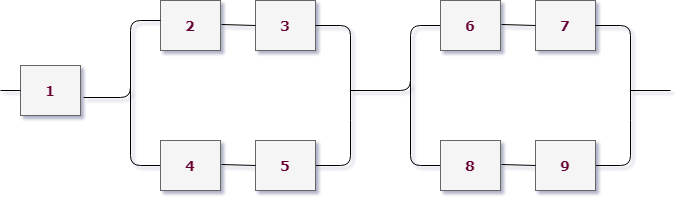
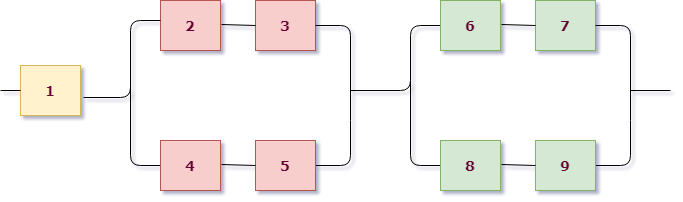
Возьмем для примера левую верхнюю схему:
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:
То есть тип схемы на первом уровне – последовательный:
Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть
$$
X=X_1 cdot X_2 cdot X_3,
$$
$X_1$ – работает первая группа элементов,
$X_2$ – работает вторая группа элементов,
$X_3$ – работает третья группа элементов.
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.
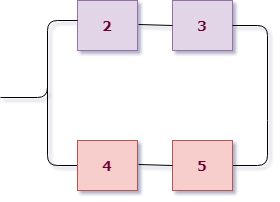
А вот дальше интереснее. Рассмотрим поближе вторую группу:
В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они “висят” на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает – $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает – $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.
Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$
Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):
$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$
Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
$$
X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right).
$$
Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
$$
P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\
= P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) =
$$
Для множителей с суммой событий внутри используем формулу (2):
$$
= P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) – P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) – P(A_6 cdot A_7 cdot A_8 cdot A_9)right] =
$$
И снова раскрываем вероятности произведений:
$$
= P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) – P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) – P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right].
$$
Перейдем к более компактной записи, положив $p_i=P(A_i)$:
$$
P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 – p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 – p_6 cdot p_7 cdot p_8 cdot p_9right].
$$
Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.
Алгоритм разбора схемы
- Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
- Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
- Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
- Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
- Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
- Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
- Если необходимо, находим вероятность отказа цепи $1-P$.
Примеры решений
Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.
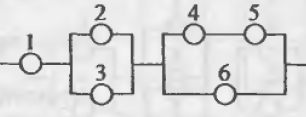
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.
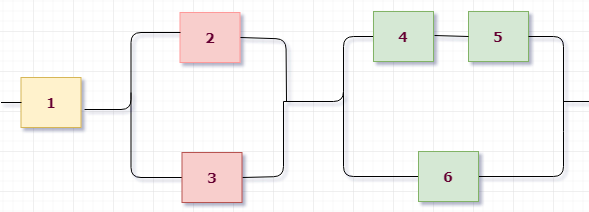
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:
Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ – работает $i$-aя группа элементов.
Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.
Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.
Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.
Подставляем все и получаем выражение для события $B$
$$
B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6).
$$
Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:
$$
P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) =
$$
Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:
$$= P(A_1) cdot left(1 – P(overline{A_2}) cdot P(overline{A_3}) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) – P(A_4) cdot P(A_5) cdot P(A_6) right).$$
Подставляем $P(A_i)=p$ и получим:
$$
p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right).
$$
Осталось только найти значение при $p=0,6$:
$$
p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375.
$$
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.
Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:
$$
X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5.
$$
Найдем вероятность этого события (работы цепи):
$$
P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \
= P(A_1) cdot left( 1- P(overline{A_2}) cdot P(overline{A_3}) right) cdot P(A_4) cdot P(A_5).
$$
Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов – 0,8, поэтому
$$
P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492.
$$
Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:
$$
P(overline{X}) = 1- P(X) = 1-0,492 = 0,508.
$$
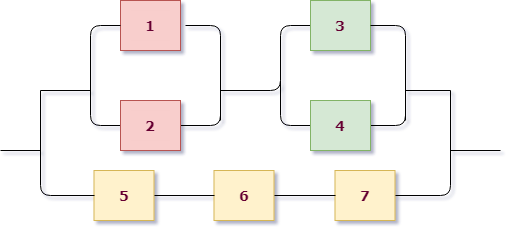
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.
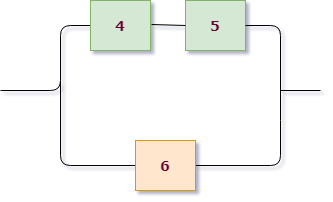
Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ – работает розово-зеленая линия, $X_2$ – работает желтая.
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.
Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.
Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:
$$
X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7.
$$
Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.
В данном случае слагаемых всего два, поэтому возьмем формулу (2):
$$
P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \
= P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) – P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right)
$$
Раскрываем все произведения по формуле (1):
$$
= P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) – P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) =
$$
По формуле (3) расписываем $P(A_1+A_2)=1-P(overline{A_1}) cdot P(overline{A_2}) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline{A_3}) cdot P(overline{A_4})= 1-q_3cdot q_4$.
Итого:
$$
P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 – \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7.
$$
Подставляем значения надежности элементов:
$$
P(X)= (1-0,2^2)^2 + 0,9^3 – (1-0,2^2)^2 cdot 0,9^3 approx 0,9788.
$$
Еще: другие уроки о решении задач по вероятности
На закуску: схема с мостиком
Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне – параллельную или последовательную, и весь алгоритм решения рушится.
Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:
Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) “портит” тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток – последовательную (конкретные схемы изобразим ниже).
Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)
Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).
То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.
Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:
Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность
$$
P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) – P(A_1cdot A_3 cdot A_2cdot A_4)=\
=p_1 cdot p_3 + p_2 cdot p_4 – p_1 cdot p_2 cdot p_3 cdot p_4.
$$
Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:
$$
X|H_2 = (A_1+A_2)cdot (A_3+A_4),\
P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline{A_1}) cdot P(overline{A_2})) cdot (1-P(overline{A_3}) cdot P(overline{A_4})) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Тогда по формуле полной вероятности, надежность схемы равна:
$$
P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \
= q_5 (p_1 cdot p_3 + p_2 cdot p_4 – p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).
Спасибо за ваши закладки и рекомендации
Полезные ссылки по ТВ
|
|
Решебник по вероятности
А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):
Решение типовых задач Случайные события
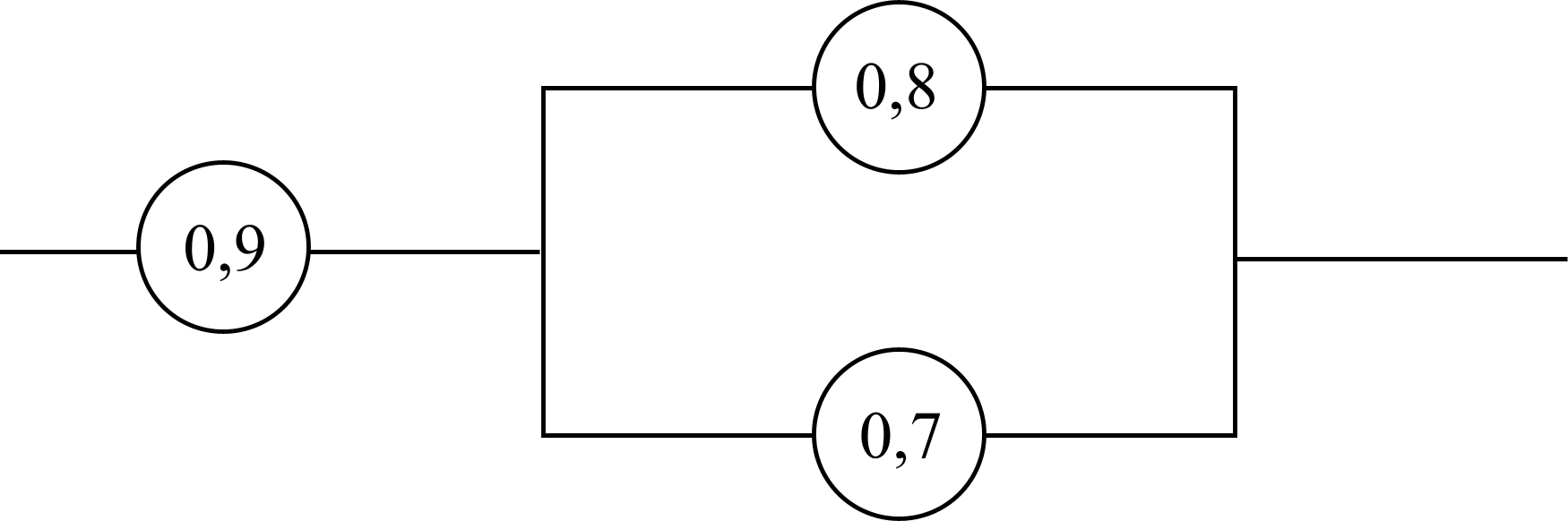
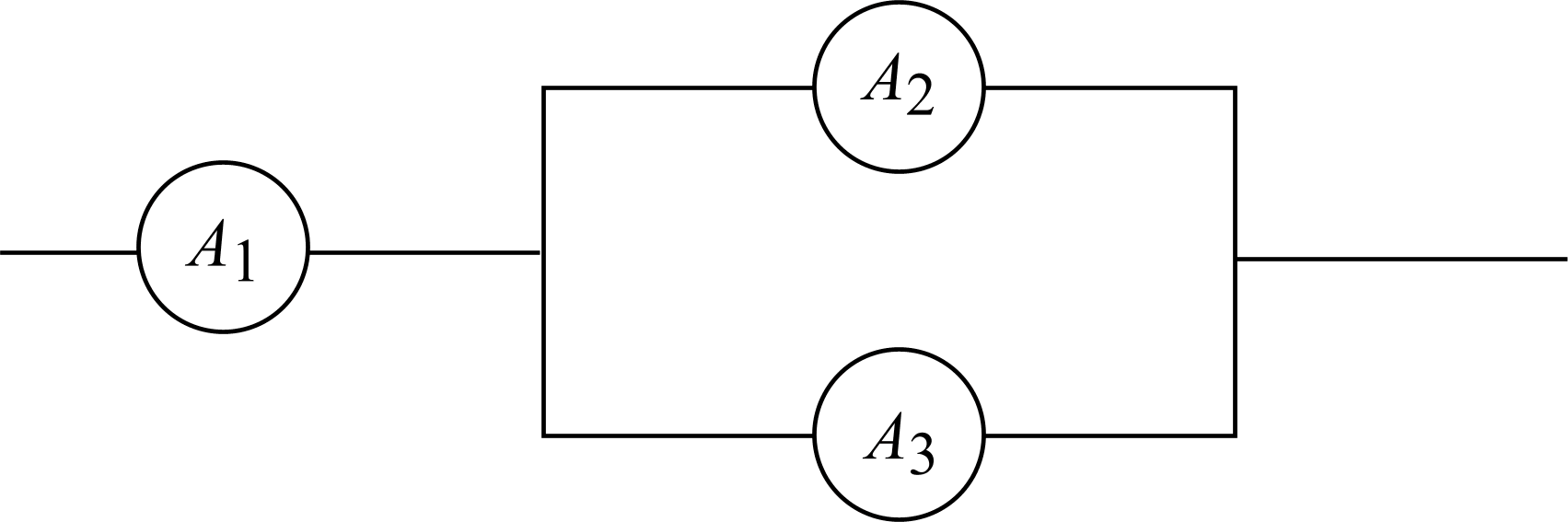
Пример
1.Найти надежность цепи, если надежности
элементов указаны на схеме (рис. 6, 7).
Рис. 6
Пусть
событие Аналичие тока в цепи, гдеА1,А2,А3–
исправность элементов.
Рис. 7
Последовательному
соединению отвечает произведение
событий, а параллельному – сумма
событий (сравните пример 10), поэтому
имеем:
А=А1(А2+А3).
Предполагается,
что элементы работают независимо,
следовательно, вероятность произведения
событий равна произведению их вероятностей:
P(A)
=P(A1) P(A2+A3).
События
A2,A3
совместны, следовательно,
P(A2 + A3) = P(A2) + P(A3) –
P(A2
A3)
= 0,8 + 0,7 – 0,8
0,7 = 0,94.
Этот
результат можно получить иначе:
P(A2 + A3) =
1 – = 1 –
=
= 1 – (1 – 0,8)(1 – 0,7) = 1 – 0,2 0,3
= 1 – 0,06 = 0,94.
Таким
образом удобно находить вероятность
суммы более чем двух совместных событий.
Окончательно
P(A) = 0,90,94 = 0,846.
Пример 2. В группе студентов 2
отличника, 5 хорошо успевающих и 10
занимающихся слабо. Отличники на экзамене
могут получить только отличные отметки;
хорошие студенты с равной вероятностью
хорошие и отличные; слабые студенты с
равной вероятностью хорошие,
удовлетворительные и неудовлетворительные
оценки. Вызываются наугад три студента.
Найти вероятность того, что они получат
отлично, хорошо и удовлетворительно.
Событие
А– получение отличной, хорошей,
удовлетворительной оценок, что возможно
при одном из следующих условий (гипотез):
H1 –
вызваны 1 слабый, 1 хороший, 1 отличный
студенты;
H2 –
вызваны 1 слабый и 2 хороших студентов;
H3 –
вызваны 2 слабых и 1 хороший студенты;
H4 –
вызваны 2 слабых и 1 отличный студенты.
Заметим,
что гипотезы H1,H2,H3,H4не составляют полную группу, но при
других условиях событиеА невозможно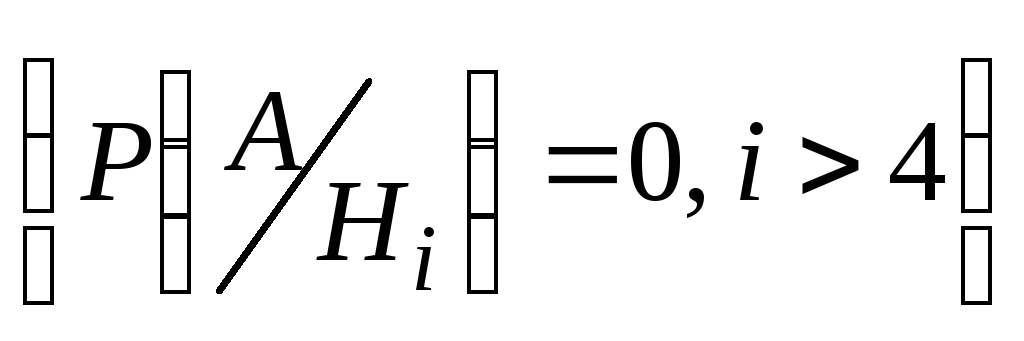
В тех
случаях, когда наступление события Азависит от некоторых условий (гипотез),
применяется формула полной вероятности:
Найдем
вероятности гипотез. Опыт состоит в
выборе 3 студентов из группы 17 человек,
следовательно, число всех исходов опыта:
В случае
гипотезы H1–
это 1 студент из 10 слабых, 1 студент из 5
хороших и 1 из 2 отличных, значит,
благоприятное число исходов
В случае
H2аналогично
Для H3имеемдляH4имеем
Окончательно,
по формуле
имеем:
Найдем
условные вероятности события при каждой
гипотезе.
Событие
–
слабый студент получил удовлетворительную
оценку (с вероятностью),
хороший студент получил хорошую оценку
(с вероятностью)
и отличник получил отличную оценку (с
вероятностью 1)
Событие
–
слабый студент получил удовлетворительную
оценку (с вероятностью),
хороший студент получил отличную, а
другой – хорошую оценку (событиеD).
Найдем вероятность последнего события.
Пусть
В1–
отличную оценку получил первый хороший
студент,
В2–
второй;
С1–
хорошую оценку получил первый хороший
студент,
С2–
второй студент.
Тогда
D = В1С2+В2С1.
События
В1С2иВ2С1несовместны, поэтомуP(D) = P(В1С2) + P(В2С1).
События
В1,В2,С1,С2независимы, окончательно:
P(D)
=P(В1)P(C2)
+P(В2)P(C1);
Событие
–
один слабый получил удовлетворительную,
другой хорошую и хороший студент получил
отличную оценки.
Аналогично
предыдущему:
Событие
–
один слабый получил удовлетворительную,
другой – хорошую, а отличник –
отличную оценки.
Напомним,
что
0! = 1;
Вычислим:
Пример 3.В группе из 10 студентов,
пришедших на экзамен, 3 подготовлены
отлично, 4 – хорошо, 2 – посредственно,
1 – плохо. В билете 3 вопроса. Вероятность
того, что отличник ответит на любой
вопрос программы 0,9; для хорошего студента
0,7; посредственного 0,5; плохого – 0,2.
Вызванный наугад студент ответил на 2
вопроса билета. Найти вероятность того,
что он подготовлен хорошо.
Событие
А– студент ответил на 2 из 3
вопросов билета; отвечавший мог быть
отличником – гипотезаH1,
хорошим студентом –H2,
посредственным –H3,
плохим – H4.
В отличие
от предыдущего примера, событие Ауже произошло и надо найти вероятность
того, что реализовалась вторая гипотеза,
т. е. что отвечал хороший студент.
Для
этого служит формула Байеса.
В
нашем случае она имеет вид:
События H1,H2,H3,H4составляют полную группу.
Событие
–
студент ответил на 2 вопроса из 3, если
вероятность ответить на любой вопросp= 0,9, а не ответитьq= 0,1.
Для нахождения
используем формулу Бернулли:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение типового варианта контрольной работы. Теория вероятностей, математическая статистика и случайные процессы.
Задача 1. Бросается 4 монеты. Какова вероятность того, что три раза выпадет «решка»?
Решение. Подбрасывание монеты будем считать одним опытом. По условию задачи производится 4 одинаковых испытания. Вероятность успеха (выпадение «решки») в каждом испытании равна . Требуется найти, что среди проведенных испытаний будет
успешных. Для решения задачи воспользуемся формулой биномиального закона распределения дискретной случайной величины.
. В условиях нашей задачи
.
Ответ: 0.25.
Задача 2. В квадрат со стороной 2 вписан квадрат, вершины которого лежат на серединах сторон большего квадрата. Найти вероятность того, что наудачу брошенная в больший квадрат точка попадет в маленький квадрат.
Решение. Воспользуемся понятием геометрической вероятности. Будем искать вероятность попадания в меньший квадрат как отношение площади меньшего квадрата к площади большего квадрата. .
Ответ: .
Задача 3. Определить надежность схемы, если Pi – надежность i – го элемента
Решение. Разобьем цепь на три последовательно соединенных блока. И вычислим надежность каждого блока отдельно. Первый блок пропускает электрический ток в трех случаях: если исправен первый элемент и неисправен второй; если исправен второй элемент и неисправен первый; и если оба элемента исправны. Таким образом, надежность этого блока может быть представлена суммой: . Однако проще надежность этого элемента вычислить через вероятность противоположного события. Вычислим вероятность того, что блок не пропускает ток и надежность найдем по формуле вероятности противоположного события. Блок не исправен только в случае когда и первый и второй элементы неисправны:
, следовательно, надежность блока может быть вычислена как разность:
. Аналогично вычисляется надежность второго блока:
. Теперь, зная надежности трех последовательно соединенных блоков, вычислим надежность цепи в целом. Схема пропускает ток только если все три блока исправны, то есть надежность схемы:
.
Ответ: .
Задача 4. Дан ряд распределения дискретной случайной величины Y. Определить значение x и вычислить математическое ожидание дискретной случайной величины Y.
|
Y |
5 |
6 |
7 |
10 |
|
P |
0,1 |
0,1 |
X |
0,3 |
Решение. Найдем значение x из условия .
Зная X, становится возможным вычисление математического ожидания.
Ответ:
Задача 5. Найти доверительный интервал для оценки математического ожидания M нормального закона с надежностью 0.95; зная выборочную среднюю .
Решение. Построить доверительный интервал с доверительной вероятностью для математического ожидания M Произвольной случайной величины можно следующим образом:
При надежности =0,95 найдем табличное значение
и запишем выражение, подставив значения из условия задачи:
,
.
Ответ: .
Задача 6. Задана матрица вероятностей перехода для цепи Маркова за один шаг. Найти матрицу перехода данной цепи за три шага
Решение. Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:
В каждой строке матрицы помещены вероятности событий (перехода из состояния I в состояние J), которые образуют полную группу, поэтому сумма вероятностей этих событий равна единице:
Обозначим через вероятность того, что в результате N шагов (испытаний) система перейдет из состояния I в состояние J. Например
– вероятность перехода из второго состояния в пятое за десять шагов. Отметим, что при N=1 получаем переходные вероятности
.
Перед нами поставлена задача: зная переходные вероятности , найти вероятности
перехода системы из состояния I в состояние J за N шагов. Для этого введем промежуточное (между I и J) состояние R. Другими словами, будем считать, что из первоначального состояния I за M шагов система перейдет в промежуточное состояние R с вероятностью
, после чего, за оставшиеся N–M шагов из промежуточного состояния R она перейдет в конечное состояние J с вероятностью
. По формуле полной вероятности получаем:
.
Эту формулу называют равенством Маркова. С помощью этой формулы можно найти все вероятности , а, следовательно, и саму матрицу
. Так как матричное исчисление ведет к цели быстрее, запишем вытекающее из полученной формулы матричное соотношение в общем виде
.
Вычислим матрицу перехода цепи Маркова за три шага, используя полученную формулу:
Ответ: 
Задача 7. DX = 3. Используя свойства дисперсии, найдите D(4X-2).
Решение.
.
Ответ: 48.
Задача 8. В вычислительный центр коллективного пользования с тремя компьютерами поступают заказы от предприятий на вычислительные работы. Если заняты все три компьютера, то вновь поступающий заказ не принимается и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0.25 (з/час). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.
Решение. В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов – так называемый Процесс гибели и размножения. Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т. е. из состояния
возможны переходы только либо в состояние
, либо в состояние
. В предположении, что все потоки событий, переводящие систему из одного состояние в следующее простейшие с соответствующими интенсивностями
или
, для отыскания предельных вероятностей, можно использовать систему уравнений Колмогорова для стационарных процессов. Правило для составления уравнений Колмогорова звучит следующим образом: слева в уравнениях стоит предельная вероятность данного состояния
, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа – сумма произведений интенсивностей всех потоков, входящих в I-ое состояние на вероятности тех состояний, из которых эти потоки выходят. Поток заявок характеризуется интенсивностью
(заявок/час), поток обслуживания – интенсивностью
(заявок/час). Согласно условию задачи
(заявок/час),
(заявок/час). В нашей задаче система массового обслуживания может находиться в одном из четырех состояний:
– когда все три компьютера свободны;
– когда загружен работой только один компьютер;
– когда заняты два компьютера;
– когда все компьютеры заняты. В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид:

К этой системе добавляется нормировочное уравнение .

Решая эту систему уравнений, получим:
.
То есть в стационарном режиме работы вычислительного центра в среднем 47,6% времени нет ни одной заявки, 35,7% – имеется одна заявка, 13,4% – две заявки и 3,3% времени – три заявки (заняты все вычислительные мощности).
Вероятность отказа в обслуживании (когда заняты все три компьютера), таким образом .
Относительная пропускная способность центра , то есть в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.
Абсолютная пропускная способность , то есть в один час в среднем обслуживается 0,242 заявки.
Среднее число занятых компьютеров есть математическое ожидание числа занятых каналов , то есть каждый компьютер будет занят обслуживанием заявок в среднем лишь на
%.
При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоя дорогостоящих компьютеров и выбрать компромиссное решение.
| < Предыдущая | Следующая > |
|---|
Закажите у меня новую работу, просто написав мне в чат!
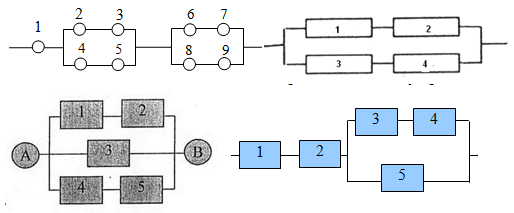
Рассчитать надежность цепи (указаны вероятности работы элементов).
Обозначим события 𝐴1 − элемент номер 1 работает безотказно; 𝐴2 − элемент номер 2 работает безотказно; 𝐴3 − элемент номер 3 работает безотказно; 𝐴4 − элемент номер 4 работает безотказно; 𝐴5 − элемент номер 5 работает безотказно; 𝐴6 − элемент номер 6 работает безотказно; 𝐴1 ̅̅̅ − элемент номер 1 вышел из строя; 𝐴2 ̅̅̅ − элемент номер 2 вышел из строя; 𝐴3 ̅̅̅ − элемент номер 3 вышел из строя; 𝐴4 ̅̅̅ − элемент номер 4 вышел из строя; 𝐴5 ̅̅̅ − элемент номер 5 вышел из строя; 𝐴6 ̅̅̅ − элемент номер 6 вышел из строя. Найдем вероятность события 𝐴 − цепь работает безотказно. Часть схемы из двух последовательных элементов 1 и 2 исправна только тогда, когда исправны оба этих элемента: Часть схемы из двух параллельных элементов 1 и 2 исправна во всех случаях, кроме одновременной поломки всех элементов: Вероятность безотказной работы части схемы с элементами 1 и 2 равна: Вероятность безотказной работы части схемы с элементами 3 и 4 равна: Вероятность безотказной работы части схемы с элементами 1 – 4 равна: