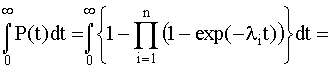Как найти надежность устройства

Целевое назначение и классификация
методов расчета

Расчеты надежности– расчеты,
предназначенные для определения
количественных показателей надежности.
Они проводятся на различных этапах
разработки, создания и эксплуатации
объектов.

На этапе проектирования расчет надежности
производится с целью прогнозирования
(предсказания) ожидаемой надежности
проектируемой системы. Такое прогнозирование
необходимо для обоснования предполагаемого
проекта, а также для решения
организационно-технических вопросов:

– выбора оптимального варианта структуры;

– способа резервирования;

– глубины и методов контроля;

– количества запасных элементов;

– периодичности профилактики.

На этапе испытаний и эксплуатации
расчеты надежности проводятся для
оценки количественных показателей
надежности. Такие расчеты носят, как
правило, характер констатации. Результаты
расчетов в этом случае показывают, какой
надежностью обладали объекты, прошедшие
испытания или используемые в некоторых
условиях эксплуатации. На основании
этих расчетов разрабатываются меры по
повышению надежности, определяются
слабые места объекта, даются оценки его
надежности и влияния на нее отдельных
факторов.

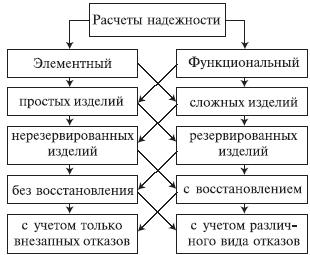
Многочисленные цели расчетов привели
к большому их разнообразию. На рис. 4.5.1
изображены основные виды расчетов.

Элементный расчет– определение
показателей надежности объекта,
обусловленных надежностью его
комплектующих частей (элементов). В
результате такого расчета оценивается
техническое состояние объекта (вероятность
того, что объект будет находиться в
работоспособном состоянии, средняя
наработка на отказ и т.п.).

Рис. 4.5.1. Классификация расчетов
надежности

Расчет функциональной надежности –
определение показателей надежности
выполнения заданных функций (например,
вероятность того, что система очистки
газа будет работать заданное время, в
заданных режимах эксплуатации с
сохранением всех необходимых параметров
по показателям очистки). Поскольку такие
показатели зависят от ряда действующих
факторов, то, как правило, расчет
функциональной надежности более сложен,
чем элементный расчет.

Выбирая на рис 4.5.1 варианты перемещений
по пути, указанному стрелками, каждый
раз получаем новый вид (случай) расчета.

Самый простой расчет– расчет,
характеристики которого представлены
на рис. 4.5.1 слева: элементный расчет
аппаратурной надежности простых изделий,
нерезервированных, без учета восстановлений
работоспособности при условии, что
время работы до отказа подчинено
экспоненциальному распределению.

Самый сложный расчет– расчет,
характеристики которого представлены
на рис. 4.5.1 справа: функциональной
надежности сложных резервированных
систем с учетом восстановления их
работоспособности и различных законов
распределения времени работы и времени
восстановления.

Выбор того или иного вида расчета
надежности определяется заданием на
расчет надежности. На основании задания
и последующего изучения работы устройства
(по его техническому описанию) составляется
алгоритм расчета надежности, т.е.
последовательность этапов расчета и
расчетные формулы.

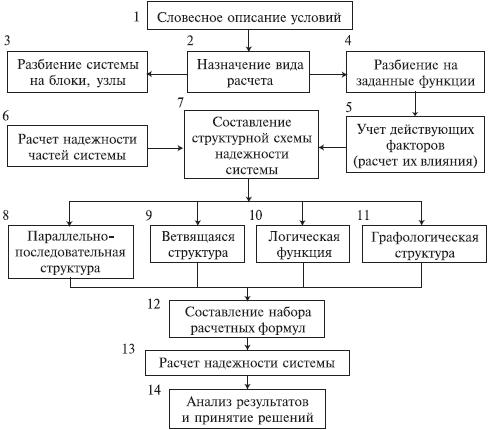
Последовательность расчета систем

Последовательность расчета системы
представлена на рис. 4.5.2. Рассмотрим
основные ее этапы.

Рис. 4.5.2. Алгоритм расчета надежности

Прежде всего четко следует сформулировать
задание на расчет надежности. В нем
должны быть указаны: 1) назначение системы
ее состав и основные сведения о
функционировании; 2) показатели надежности
и признаки отказов, целевое назначение
расчетов; 3) условия, в которых работает
(или будет работать) система; 4) требования
к точности и достоверности расчетов, к
полноте учета действующих факторов.

На основании изучения задания делается
вывод о характере предстоящих расчетов.
В случае расчета функциональной
надежности осуществляется переход к
этапам 4-5-7, в случае расчета элементов
(аппаратурной надежности) – к этапам
3-6-7.

Под структурной схемой надежности
понимается наглядное представление
(графическое или в виде логических
выражений) условий, при которых работает
или не работает исследуемый объект
(система, устройство, технический
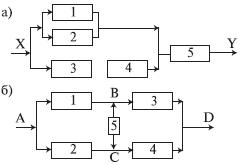
комплекс и т.д.). Типовые структурные
схемы представлены на рис. 4.5.3.

Рис. 4.5.3. Типовые структуры расчета
надежности

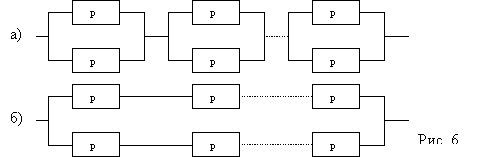
Простейшей формой структурной схемы
надежности является параллельно-последовательная
структура. На ней параллельно соединяются
элементы, совместный отказ которых
приводит к отказу.

В последовательную цепочку соединяются
такие элементы, отказ любого из которых
приводит к отказу объекта.

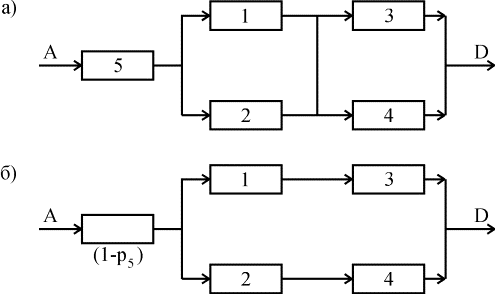
На рис. 4.5.3,а представлен вариант
параллельно-последовательной структуры.
По этой структуре можно сделать следующее
заключение. Объект состоит из пяти
частей. Отказ объекта наступает тогда,
когда откажет или элемент 5, или узел,
состоящий из элементов 1-4. Узел может
отказать тогда, когда одновременно
откажет цепочка, состоящая из элементов
3,4 и узел, состоящий из элементов 1,2. Цепь
3-4 отказывает, если откажет хотя бы один
из составляющих ее элементов, а узел
1,2 – если откажут оба элемента, т.е.
элементы 1,2. Расчет надежности при
наличии таких структур отличается
наибольшей простотой и наглядностью.
Однако не всегда удается условие
работоспособности представить в виде
простой параллельно-последовательной
структуры. В таких случаях используют
или логические функции, или графы и
ветвящиеся структуры, по которым
оставляются системы уравнений
работоспособности.

На основе структурной схемы надежности
составляется набор расчетных формул.
Для типовых случаев расчета используются
формулы, приведенные в справочниках по
расчетам надежности, стандартах и
методических указаниях. Прежде чем
применять эти формулы, необходимо
предварительно внимательно изучить их
существо и области использования.

Расчет надежности, основанный на
использовании параллельно-последовательных
структур

Пусть некоторая техническая система D
составлена из n элементов (узлов).
Допустим, надежности элементов нам
известны. Возникает вопрос об определении
надежности системы. Она зависит от того,
каким образом элементы объединены в
систему, какова функция каждого из них
и в какой мере исправная работа каждого
элемента необходима для работы системы
в целом.

Параллельно-последовательная структура
надежности сложного изделия дает
представление о связи между надежностью
изделия и надежностью его элементов.
Расчет надежности ведется последовательно
– начиная от расчета элементарных узлов
структуры к ее все более сложным узлам.
Например, в структуре рис. 5.3,а узел,
состоящий из элементов 1-2 – элементарный
узел, состоящий из элементов 1-2-3-4,
сложный. Эта структура может быть сведена
к эквивалентной, состоящей из элементов
1-2-3-4 и элемента 5, соединенных
последовательно. Расчет надежности в
данном случае сводится к расчету
отдельных участков схемы, состоящих из
параллельно и последовательно соединенных
элементов.

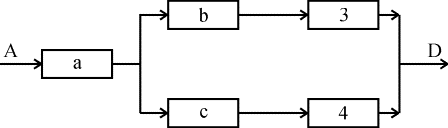
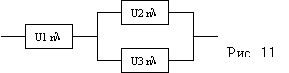
Система с последовательным соединением
элементов

Самым простым случаем в расчетном смысле
является последовательное соединение
элементов системы. В такой системе отказ
любого элемента равносилен отказу
системы в целом. По аналогии с цепочкой
последовательно соединенных проводников,
обрыв каждого из которых равносилен
размыканию всей цепи, мы и называем
такое соединение “последовательным”
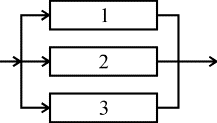
(рис. 4.5.4). Следует пояснить, что
“последовательным” такое соединение
элементов является только в смысле
надежности, физически они могут быть
соединены как угодно.

Рис. 4.5.4. Блок-схема
системы с последовательным соединением
элементов

С позиции надежности, такое соединение
означает, что отказ устройства, состоящего
из этих элементов, происходит при отказе
элемента 1 или элемента 2, или элемента
3, или элемента n. Условие работоспособности
можно сформулировать следующим образом:
устройство работоспособно, если
работоспособен элемент 1 и элемент 2, и
элемент 3, и элемент n.

Выразим надежность данной системы через
надежности ее элементов. Пусть имеется
некоторый промежуток времени (0,τ),
в течение которого требуется обеспечить
безотказную работу системы. Тогда, если
надежность системы характеризуется
законом надежности Р(t), нам важно знать
значение этой надежности при t=τ,
т.е. Р(τ). Это не функция,
а определенное число; отбросим аргументτи обозначим надежность
системы просто Р. Аналогично обозначим
надежности отдельных элементов P₁,
P₂, P₃, …, P_n.

Для безотказной работы простой системы
в течение времени τнужно,
чтобы безотказно работал каждый из ее
элементов. Обозначим S – событие, состоящее
в безотказной работе системы за времяτ; s₁, s₂, s₃,
…, s_n– события, состоящие в
безотказной работе соответствующих
элементов. Событие S есть произведение
(совмещение) событий s₁, s₂,
s₃, …, s_n:

S=s₁×s₂×s₃×…×s_n.

Предположим, что элементы s₁, s₂,
s₃, …, s_nотказывают независимо
друг от друга (или, как говорят применительно
к надежности, “независимы по отказам”,
а совсем кратко “независимы”). Тогда
по правилу умножения вероятностей для
независимых событий
Р(S)=P(s₁)×P(s₂)×P(s₃)×…×P(s_n)
или в других обозначениях,

Р = Р₁×Р₂×Р₃×…×Р_n., (4.5.1)

а короче P=
, (4.5.2)

т.е. надежность (вероятность работоспособного
состояния) простой системы, составленной
из независимых по отказам, последовательно
соединенных элементов, равна произведению
надежностей ее элементов.

В частном случае, когда все элементы
обладают одинаковой надежностью
P₁=P₂=P₃= … =P_n,
выражение (4.5.2) принимает вид

Р = Pⁿ. (4.5.3)

Пример 4.5.1. Система состоит из 10 независимых
элементов, надежность каждого из которых
равна Р=0,95. Определить надежность
системы.

По формуле (4.5.3) Р = 0,95¹⁰»0,6.

Из примера видно, как резко падает
надежность системы при увеличении в
ней числа элементов. Если число элементов
n велико, то для обеспечения хотя бы
приемлемой надежности Р системы каждый
элемент должен обладать очень высокой
надежностью.

Поставим вопрос: какой надежностью Р
должен обладать отдельный элемент для
того, чтобы система, составленная из n
таких элементов, обладала заданной
надежностью Р?

Из формулы (4.5.3) получим:

Р =
.

Пример 4.5.2. Простая система состоит из
1000 одинаково надежных, независимых
элементов. Какой надежностью должен
обладать каждый из них для того, чтобы
надежность системы была не меньше 0,9?

По формуле (4.5.4) Р =
;lgР =lg0,9^1/1000;
Р»0,9999.

Интенсивность отказов системы при
экспоненциальном законе распределения
времени до отказа легко определить из
выражения

λ_с=λ₁+λ₂+λ₃+ … +λ_n, (4.5.4)

т.е. как сумму интенсивностей отказов
независимых элементов. Это и естественно,
так как для системы, в которой элементы
соединены последовательно, отказ
элемента равносилен отказу системы,
значит все потоки отказов отдельных
элементов складываются в один поток
отказов системы с интенсивностью, равной
сумме интенсивностей отдельных потоков.

Формула (4.5.4) получается из выражения

Р = P₁P₂P₃…P_n= ехр{-(λ₁+λ₂+λ₃+ … +λ_n)}. (4.5.5)

Среднее время работы до отказа

Т₀= 1/λ_с. (4.5.6)

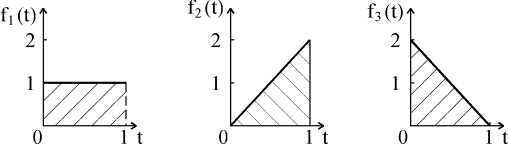
Пример 4.5.3. Простая система S состоит из
трех независимых элементов, плотности
распределения времени безотказной
работы которых заданы формулами:

при
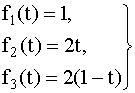
0 < t < 1 (рис. 4.5.5).

Рис. 4.5.5. Плотности
распределения времени безотказной
работы

Найти интенсивность отказов системы.

Решение. Определяем ненадежность каждого
элемента:

при 0 <t< 1.

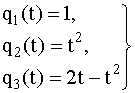
Отсюда надежности элементов:

при 0 <t< 1.

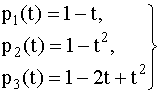
Интенсивности отказов элементов
(условная плотность вероятности отказов)
– отношение f(t) к р(t):

при 0 <t< 1.

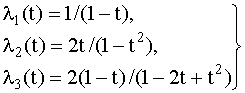
Складывая, имеем: λ_с=λ₁(t) +λ₂(t)
+λ₃(t).

Пример 4.5.4. Предположим, что для работы
системы с последовательным соединением
элементов при полной нагрузке необходимы
два разнотипных насоса, причем насосы
имеют постоянные интенсивности отказов,
равные соответственно λ₁=0,0001ч^-1иλ₂=0,0002ч^-1.
Требуется вычислить среднее время
безотказной работы данной системы и
вероятность ее безотказной работы в
течение 100ч. Предполагается, что оба
насоса начинают работать в момент
времениt=0.

С помощью формулы (4.5.5) находим вероятность
безотказной работы P_sзаданной системы в течение 100ч:

P_s(t)=

.

P_s(100)=е^{-(0,0001+0,0002)×100}=0,97045.

Используя формулу (4.5.6), получаем

ч.

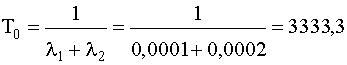
Система с
параллельным соединением элементов

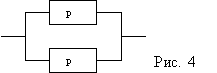
На рис. 4.5.6 представлено параллельное
соединение элементов 1, 2, 3. Это означает,
что устройство, состоящее из этих
элементов, переходит в состояние отказа
после отказа всех элементов при условии,
что все элементы системы находятся под
нагрузкой, а отказы элементов статистически
независимы.

Рис. 4.5.6. Блок-схема
системы с параллельным соединением
элементов

Условие
работоспособности устройства можно
сформулировать следующим образом:
устройство работоспособно, если
работоспособен элемент 1 или элемент
2, или элемент 3, или элементы 1 и 2, 1; и 3,
2; и 3, 1; и 2; и 3.

Вероятность безотказного состояния
устройства, состоящего из n параллельно
соединенных элементов определяется по
теореме сложения вероятностей совместных
случайных событий как

Р=(р₁+р₂+…р_n)-(р₁р₂+р₁р₃+…)-(р₁р₂р₃+р₁р₂р_n+…)-…±(р₁р₂р₃…р_n). (4.5.7)

Для приведенной блок-схемы (рис. 4.5.6),
состоящей из трех элементов, выражение
(4.5.7) можно записать:

Р=р₁+р₂+р₃-(р₁р₂+р₁р₃+р₂р₃)+р₁р₂р₃.

Применительно к проблемам надежности,
по правилу умножения вероятностей
независимых (в совокупности) событий,
надежность устройства из n элементов
вычисляется по формуле

Р = 1-
, (4.5.8)

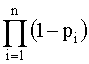
т.е. при параллельном соединении
независимых (в смысле надежности)
элементов их ненадежности (1-p_i=q_i)
перемножаются.

В частном случае, когда надежности всех
элементов одинаковы, формула (4.5.8)
принимает вид

Р = 1 – (1-р)ⁿ. (4.5.9)

Пример 4.5.5. Предохранительное устройство,
обеспечивающее безопасность работы
системы под давлением, состоит из трех
дублирующих друг друга клапанов.
Надежность каждого из них р=0,9. Клапаны
независимы в смысле надежности. Найти
надежность устройства.

Решение.
По формуле (4.5.9) Р=1-(1-0,9)³=0,999.

Интенсивность отказов устройства
состоящего из n параллельно соединенных
элементов, обладающих постоянной
интенсивностью отказов λ₀,
определяется как

. (4.5.10)

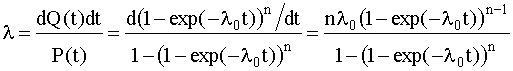
Из (4.5.10) видно, что интенсивность отказов
устройства при n>1 зависит от t: при t=0
она равна нулю, при увеличении t, монотонно
возрастает до λ₀.

Если интенсивности отказов элементов
постоянны и подчинены показательному
закону распределения, то выражение
(4.5.8) можно записать

Р(t)
=
. (4.5.11)

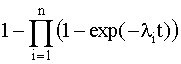
Среднее время безотказной работы системы
Т₀находим, интегрируя уравнение
(4.5.11) в интервале [0,¥]:

Т₀=

=(1/ λ ₁+1/λ
₂+…+1/λ _n)-(1/(λ ₁+λ
₂)+ 1/(λ ₁+λ
₃)+…)+ (4.5.12)

+(1/( λ ₁+ λ
₂+ λ ₃)+1/(
λ ₁+ λ ₂+
λ ₄)+…)+(-1)ⁿ⁺¹´

.

В случае, когда интенсивности отказов
всех элементов одинаковы, выражение
(4.5.12) принимает вид

Т₀=

. (4.5.13)

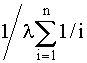
Среднее время работы до отказа также
можно получить, интегрируя уравнение
(4.5.7) в интервале [0,¥]

Пример 4.5.6. Предположим, что два одинаковых
вентилятора в системе очистки отходящих
газов работают параллельно, причем если
один из них выходит из строя, то другой
способен работать при полной системной
нагрузке без изменения своих надежностных
характеристик.

Требуется найти безотказность системы
в течение 400ч (продолжительность
выполнения задания) при условии, что
интенсивности отказов двигателей
вентиляторов постоянны и равны λ=0,0005ч^-1, отказы двигателей
статистически независимы и оба вентилятора
начинают работать в момент времени t=0.

Решение. В случае идентичных элементов
формула (4.5.11) принимает вид

Р(t) = 2еxp(-λt)
– еxp(-2λt).

Поскольку λ= 0,0005 ч^-1и t = 400 ч, то

Р₍₄₀₀₎= 2еxp(-0,0005´400)
– еxp(-2´0,0005´400)=0,9671.

Среднюю наработку на отказ находим,
используя (4.5.13):

Т₀= 1/λ(1/1 + 1/2) = 1/λ´3/2
= 1,5/0,0005 = 3000 ч.

Способы преобразования сложных
структур

Относительная простота расчетов
надежности, основанных на использовании
параллельно-последовательных структур,
делают их самыми распространенными в
инженерной практике. Однако не всегда
условие работоспособности можно
непосредственно представить
параллельно-последовательной структурой.
В этом случае можно сложную структуру
заменить ее эквивалентной
параллельно-последовательной структурой.
К таким преобразованиям относится:

– преобразование с эквивалентной заменой
треугольника на звезду и обратно;

– разложение сложной структуры по
базовому элементу.

Существо способа преобразования с
помощью эквивалентной замены треугольника
на звезду и обратно заключается в том,
что узел сложной конфигурации заменяется
на узел другой, более простой конфигурации,
но при этом подбираются такие характеристики
нового узла, что надежности преобразуемой
цепи сохранялись прежними.

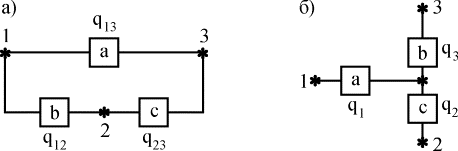
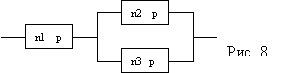
Пусть, например, требуется заменить
треугольник (рис. 4.5.7,а) звездой (рис.
4.5.7,б) при условии, что вероятность отказа
элемента aравна q₁₃, элементаbравна q₁₂, элементаc – q₂₃.
Переход к соединению звездой не должен
изменить надежность цепей 1-2, 1-3, 2-3.
Поэтому значение вероятностей отказов
элементов звезды q₁, q₂, q₃должны удовлетворять следующим
равенствам:
(4.5.14)

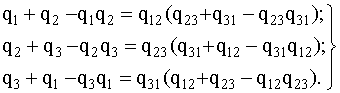
Рис. 4.5.7. Преобразование
“треугольник – звезда”

Если
пренебречь произведениями вида q_iq_j;
q_iq_jq_k,
то в результате решения системы уравнения
(4.5.14) можно записать:

q₁=q₁₂q₃₁;
q₂=q₂₃q₁₂;
q₃=q₃₁q₂₃. (4.5.15)

Для обратного
преобразования звезды в треугольник

q₁₂=

;
q₂₃=

;
q₃₁=

.  (4.5.16)

Пример 4.5.7. Определить
вероятность безотказной работы
устройства, структурная схема которого
изображена на рис. 4.5.3,б, если известно,
что вероятности безотказной работы
каждого из элементов схемы равны 0,9, а
вероятности отказов равны 0,1.

Решение.

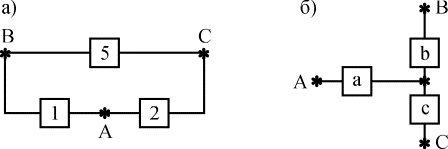
1. Преобразуем соединение элементов
1,2,5 в треугольник (рис. 4.5.8,а), в звезду
(рис. 4.5.8, б).

Рис. 4.5.8. К примеру
преобразования структуры

2.
Определим эквивалентные значения
вероятности отказов для новых элементов
a, b, c

q_a=q₁q₂=0,1´0,1
= 0,01;

q_b=q₁q₅=0,1´0,1
= 0,01;

q_с=q₂q₅=0,1´0,1
= 0,01.

3. Определим значения
вероятности безотказного состояния
элементов эквивалентной схемы (рис.
4.5.8,б)

p_a
= p_b
= p_c
= 0,99.

4. Определим
вероятность безотказной работы
эквивалентного устройства (рис. 4.5.9):

Р
= р_a(р_bр₃
+ р_cр₄
– р_bр₃р_cр₄)
=

=
0,99(0,99´0,9+0,99´0,9
– 0,99´0,9´0,99´0,9)
= 0,978.

Рис. 4.5.9. Преобразованная
структура

Способ
преобразования
с помощью разложения сложной структуры
по некоторому базовому элементу
основан на использовании теоремы о
сумме вероятностей несовместных событий.
В сложной структуре выбирают базовый
элемент (или группу базовых элементов)
и делаются следующие допущения:

– базовый элемент
находится в работоспособном состоянии;

– базовый элемент
находится в отказавшем состоянии.

Для этих случаев,
представляющих собой два несовместных
события, исходная структура преобразовывается
в две новые схемы. В первой из них вместо
базового элемента ставится “короткое
замыкание” цепи, а во второй – разрыв.
Вероятности безотказной работы каждой
из полученных простых структур вычисляются
и умножаются: первая – на вероятность
безотказного состояния базового
элемента, вторая – на вероятность отказа
базового элемента. Полученные произведения
складываются. Сумма равна искомой
вероятности безотказной работы сложной
структуры.

Пример 4.5.8. Решить предыдущий пример
методом разложения сложной структуры.

Решение.

1. В качестве базового элемента примем
элемент 5 (рис. 4.5.3,б).

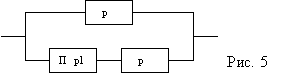
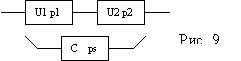
2. Закоротим базовый элемент, т.е. сделаем
допущение об абсолютной его проводимости.
Присоединим к полученной структуре
последовательно базовый элемент с
характеристикой его надежности р₅.
В результате вместо исходной структуры
получим новую структуру (рис. 4.5.10,а).

Рис. 4.5.10. Пример
разложения мостиковой структуры по
базовому элементу

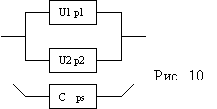
3. Произведем обрыв базового элемента,
т.е. сделаем предположение об его
абсолютной ненадежности (непроводимости).
К полученной структуре присоединим
последовательно базовый элемент с
характеристикой его ненадежности
(1-р₅). В результате получим структуру
(рис. 4.5.10,б).

4. Искомая вероятность равна сумме
вероятностей структур (рис. 4.5.10,а,б),
каждая из которых параллельно-последовательная.
Поэтому

Р
= р₅[(р₁+р₂-р₁р₂)(р₃+р₄-р₃р₄)]
+ (1-р₅)[р₁р₃+р₂р₄-р₁р₃р₂р₄]=

=
0,9[(0,9+0,9 – 0,9´0,9)
´
(0,9+0,9 – 0,9´0,9)]
+

+
(1-0,9) ´
[0,9´0,9
+ 0,9´0,9
– 0,9´0,9´0,9´0,9]»0,978.

Вероятность безотказной работы мостиковой
схемы, состоящей из пяти неодинаковых
и независимых элементов, можно определить
по формуле:

Р=2р₁р₂р₃р₄р₅-р₂р₃р₄р₅-р₁р₃р₄р₅-р₁р₂р₄р₅-р₁р₂р₃р₅–

-р₁р₂р₃р₄+р₁р₃р₅+р₂р₃р₄+р₁р₄+р₂р₅. (4.5.17)

В случае идентичных элементов эта
формула принимает вид

Р
= 2р⁵-5р⁴+2р³+2р². (4.5.18)

Подставляя соотношение (4.5.18) в формулу
(4.5.4), получаем, что в случае использования
элементов с постоянной интенсивностью
отказов (экспоненциальном законе
распределения отказов)

Р(t)
= 2ехр(-5λt)-5ехр(-4λt)+2ехр(-3λt)+2ехр(-2λt). (4.5.19)

Среднее время безотказной работы системы
Т₀находим, путем интегрирования
уравнения (5.19) в интервале [0,¥]:

Т₀
=

2ехр(-5λt)-5ехр(-4λt)+2ехр(-3λt)+2ехр(-2λt)dt=

=
(49/60)´(1/λ). (4.5.20)

Пример 4.5.9. Определить вероятность
безотказной работы устройства, структурная
схема которого изображена на рис.
4.5.3,б, если известно, что вероятности
безотказной работы каждого из элементов
схемы равны 0,9.

Решение.

Так как все элементы идентичны,
воспользуемся формулой (4.5.18); с ее помощью
получаем:

Р
= 2´0,9⁵
– 5´0,9⁴+2´0,9³
+ 2´0,9²»0,978.

Пример 4.5.10. Требуется определить
вероятность безотказной работы и среднюю
наработку на отказ системы, состоящей
из пяти независимых и одинаковых
элементов, соединенных по мостиковой
схеме (рис. 4.5.3,б); считается, что
λ=0,0005ч^-1, t=100ч и все
элементы начинают работать в момент
времени t=0.

Решение.

1. С помощью формулы (4.5.19) получаем

2. Р₍₁₀₀₎= 2е^-0,25-5е^-0,2+2е^-0,15+2е^-0,1
   = 0,9999.

3. 2. Подставляя полученное значение
   вероятности безотказной работы в
   формулу (4.5.20), находим среднюю наработку
   на отказ

4. Т₀= 49/(60´0,0005)
   = 1633,4 ч.

Расчёт надёжности — процедура определения значений показателей надёжности объекта с использованием методов, основанных на их вычислении по справочным данным о надежности элементов объекта, по данным о надёжности объектов-аналогов, данным о свойствах материалов и другой информации, имеющейся к моменту расчета.

В результате расчета определяются количественные значения показателей надёжности.

История[править | править код]

Необходимость расчёта надёжности технических устройств и систем существовала с момента начала использования их человеком. Например, в начале 1900-х годов существовала задача оценки среднего времени горения газовых фонарей, а в середине 1930-х, благодаря работам шведского ученого В. Вейбулла, получила известность задача описания среднего времени наработки электронной лампы до её выхода из строя (распределение Вейбулла).

Примером поиска методов расчёта надёжности является история создания ракетных комплексов Фау-1 и Фау-2 Вернером фон Брауном^[1]. В лаборатории Брауна тогда работал немецкий математик Эрик Пьеружка (Eric Pieruschka), который доказал, что надёжность ракеты равна произведению надёжности всех компонентов, а не надёжности самого ненадёжного элемента, как считал Браун. Позднее вместе с Брауном в середине 50-х годов в США работал немецкий инженер Роберт Луссер (англ.), который сформулировал основные теоретические положения будущей теории надёжности. Его формула для расчета надёжности системы с последовательным соединением элементов стала известна как «закон Луссера» (англ.).

К первым работам по расчёту надёжности в Советском Союзе можно отнести статью инженера Якуба Б. М. «Показатели и методы расчета надёжности в энергетическом хозяйстве», опубликованную в журнале «Электричество», № 18, 1934 г., и статью профессора Сифорова В. И. «О методах расчёта надёжности работы систем, содержащих большое число элементов» (Известия Академии наук СССР. Отделение технических наук. № 6, 1954 г.) Независимо от закрытых работ немецких ученых, в указанных статьях надёжность систем с последовательным соединением рассчитывалась как произведение надёжности элементов.

Первая в СССР монография по теории и расчёту надёжности — книга И. М. Маликова, А. М. Половко, Н. А. Романова, П. А. Чукреева «Основы теории и расчёта надёжности» (Ленинград, Судпромгиз, 1959 г.).

Цели расчета надёжности[править | править код]

Решение вопросов надёжности и безопасности современных структурно-сложных технических систем и объектов осуществляется на всех стадиях жизненного цикла, от проектирования и создания, производства, до эксплуатации, использования и утилизации. При этом могут преследоваться следующие цели^[2]:

• обоснование количественных требований к надёжности объекта или его составным частям;
• сравнительный анализ надёжности вариантов схемно-конструктивного построения объекта и обоснование выбора рационального варианта, в том числе по стоимостному критерию;
• определение достигнутого (ожидаемого) уровня надёжности объекта и/или его составных частей, в том числе расчетное определение показателей надёжности или параметров распределения характеристик надежности составных частей объекта в качестве исходных данных для расчета надёжности объекта в целом;
• обоснование и проверку эффективности предлагаемых (реализованных) мер по доработкам конструкции, технологии изготовления, системы технического обслуживания и ремонта объекта, направленных на повышение его надёжности;
• решение различных оптимизационных задач, в которых показатели надёжности выступают в роли целевых функций, управляемых параметров или граничных условий, в том числе таких, как оптимизация структуры объекта, распределение требований по надёжности между показателями отдельных составляющих надёжности (например, безотказности и ремонтопригодности), расчет комплектов ЗИП, оптимизация систем технического обслуживания и ремонта, обоснование гарантийных сроков и назначенных сроков службы (ресурса) объекта и др.;
• проверку соответствия ожидаемого (достигнутого) уровня надёжности объекта установленным требованиям (контроль надежности), если прямое экспериментальное подтверждение их уровня надёжности невозможно технически или нецелесообразно экономически.

На этапе проектирования технических систем выполняется проектный расчет надёжности.

Проектный расчет надёжности — процедура определения значений показателей надёжности объекта на этапе проектирования с использованием методов, основанных на их вычислении по справочным и другим данным о надёжности элементов объекта, имеющихся к моменту расчета.

Проектный расчет надёжности входит в состав обязательных работ по обеспечению надёжности любой автоматизированной системы и выполняется на основе требований нормативно-технической документации (ГОСТ 27.002-89, ГОСТ 27.301-95, ГОСТ 24.701-86).

На этапе испытаний и эксплуатации расчёт надёжности проводится для оценки количественных показателей надёжности спроектированной системы.

Методы расчёта надёжности[править | править код]

Структурные методы расчета надёжности[править | править код]

Структурные методы являются основными методами расчета показателей надёжности в процессе проектирования объектов, поддающихся разукрупнению на элементы, характеристики надёжности, которых в момент проведения расчетов известны или могут быть определены другими методами.
Расчет показателей надёжности структурными методами в общем случае включает:

• представление объекта в виде структурной схемы, описывающей логические соотношения между состояниями элементов и объекта в целом с учетом структурно-функциональных связей и взаимодействия элементов, принятой стратегии обслуживания, видов и способов резервирования и других факторов;
• описание построенной структурной схемы надёжности объекта адекватной математической моделью, позволяющей в рамках введенных предположений и допущений вычислить показатели надёжности объекта по данным о надёжности его элементов в рассматриваемых условиях применения.

В качестве структурных схем надёжности могут применяться:

• схемы функциональной целостности;
• структурные блок-схемы надёжности;
• деревья отказов;
• графы состояний и переходов.

Логико-вероятностный метод[править | править код]

В логико-вероятностных методах (ЛВМ) исходная постановка задачи и построение модели функционирования исследуемого системного объекта или процесса осуществляется структурными и аналитическими средствами математической логики, а расчет показателей свойств надёжности, живучести и безопасности выполняется средствами теории вероятностей.

ЛВМ являются методологией анализа структурно-сложных систем, решения системных задач организованной сложности, оценки и анализа надёжности, безопасности и риска технических систем. ЛВМ удобны для исходной формализованной постановки задач в форме структурного описания исследуемых свойств функционирования сложных и высокоразмерных систем. В ЛВМ разработаны процедуры преобразования исходных структурных моделей в искомые расчетные математические модели, что позволяет выполнить их алгоритмизацию и реализацию на ЭВМ.

Основоположником научно-технического аппарата ЛВМ и прикладных аспектов их применения, а также создателем и руководителем научной школы является профессор Рябинин И. А..

Общий логико-вероятностный метод[править | править код]

Необходимость распространения ЛВМ на немонотонные процессы привела к созданию общего логико-вероятностного метода (ОЛВМ). В ОЛВМ расчета надёжности аппарат математической логики используется для первичного графического и аналитического описания условий реализации функций отдельными и группами элементов в проектируемой системе, а методы теории вероятностей и комбинаторики применяются для количественной оценки безотказности и/или опасности функционирования проектируемой системы в целом. Для использования ОЛВМ должны задаваться специальные структурные схемы функциональной целостности исследуемых систем, логические критерии их функционирования, вероятностные и другие параметры элементов.

В основе постановки и решения всех задач моделирования и расчета надёжности систем с помощью ОЛВМ лежит так называемый событийно-логический подход. Этот подход предусматривает последовательное выполнение следующих четырёх основных этапов ОЛВМ:

• этап структурно-логической постановки задачи;
• этап логического моделирования;
• этап вероятностного моделирования;
• этап выполнения расчетов показателей надёжности.

Метод деревьев отказов[править | править код]

Метод Марковского моделирования^[3][править | править код]

Примеры расчета надёжности систем простой структуры[править | править код]

Последовательная система[править | править код]

В системе с последовательной структурой отказ любого компонента приводит к отказу системы в целом.

Система логических уравнений для приведенной выше последовательной системы:

Логическая функция работоспособности (решение системы логических уравнений):

Вероятность безотказной работы:

где  — вероятности безотказной работы компонентов.

В общем случае вероятность безотказной работы системы равна:

Параллельная система[править | править код]

В системе с параллельной структурой отказ системы в целом происходит только при отказе всех элементов.

Система логических уравнений для приведенной параллельной системы:

Логическая функция работоспособности (решение системы логических уравнений):

Вероятность безотказной работы:

В общем случае вероятность безотказной работы системы равна:

Система типа: «k из n»[править | править код]

Вероятность того, что в системе, состоящей из одинаковых (равнонадёжных) элементов, безотказно работают ровно элементов, может быть вычислена по формуле^[4]:

,

где

 — вероятность безотказной работы элемента системы;

 — биномиальный коэффициент из по .

Вероятность того, что в системе, состоящей из одинаковых и равнонадежных элементов, безотказно работают не менее элементов, может быть вычислена по формуле^[4]:

Вероятность того, что в системе, состоящей из одинаковых и равнонадёжных элементов, безотказно работают не менее элементов, может быть выражена через вероятности безотказной работы аналогичной системы меньшей размерности^[4]:

Некоторые программные пакеты для расчета надёжности[править | править код]

Программные средства, предназначенные для анализа и расчета надежности, готовности и ремонтопригодности (в алфавитном порядке)^{[5]
[6]
[7]
[8]}:

отечественные

• АРБИТР^[9]
• АРМ Надежности^[10]
• АСОНИКА-К^[11]
• AnyGraph^{[12][неавторитетный источник]}
• CRISS^[13]

зарубежные

• BlockSim^[14]
• ITEM Software^[15]
• RAM Commander от Advanced Logistics Development^[16]
• Reliability Workbench^[17]
• Windchill^[18]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Барлоу Р., Прошан Ф. Статистическая теория надёжности и испытания на безотказность. -М.: Наука, 1984. – 328 с.
• Барлоу Р., Прошан Ф. Математическая теория надёжности. -М.: Советское радио, 1969.- 485 с.
• Козлов Б. В., Ушаков И. А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. -М.:,Советское радио”, 1975.
• Маликов И. М., Половко А. М., Романов Н. А., Чукреев П. А. Основы теории и расчёта надёжности. — Л.:Судпромгиз, 1959.
• Маликов И. М., Половко А. М., Романов Н. А., Чукреев П. А. Основы теории и расчёта надёжности. Изд. 2-е, доп. — Л.:Судпромгиз, 1960. — 144с.
• Можаев А. С. Общий логико-вероятностный метод анализа надёжности сложных систем. Уч. пос. Л.: ВМА, 1988. — 68с.
• Половко А. М. Основы теории надёжности. — М.:Наука, 1964. — 446с.
• Половко А. М., Гуров С. В. Основы теории надёжности. — СПб.:БХВ-Петербург, 2006. — 702с.
• Половко А. М., Гуров С. В. Основы теории надёжности. Практикум. — СПб.:БХВ-Петербург, 2006. — 560с.
• Рябинин И. А. Надёжность и безопасность структурно-сложных систем. СПб.: Издательство Санкт-Петербургского университета, 2007 г., 278 с.
• Рябинин И. А. Основы теории и расчета надёжности судовых электроэнергетических систем. — Л.: Судостроение, 1967, 1971.
• Рябинин И. А., Черкесов Г. Н. Логико-вероятностные методы исследования надёжности структурно-сложных систем 1981. 264 с.
• Рябинин И. А. Reliability of Engineering Systems. Principles and Analysis. — M.: Mir, 1976.

Ссылки[править | править код]

• MIL-HDBK-217F-Notice2 — Американский военный стандарт расчета надёжности для электронных компонентов.
• Основные положения общего логико-вероятностного метода анализа систем.
• Левин В. И. Логическая теория надёжности сложных систем. М.: Энергоатомиздат, 1985.
• Расчет надёжности и безопасности автоматизированных систем управления — Методические рекомендации.
• Можаев А. С., Скворцов М. С., Струков А. В. «Применение автоматизированного структурно-логического моделирования для проектного расчета надёжности АСУ».
• Рябинин И. А. Надёжность и безопасность структурно-сложных систем.
• Рябинин И. А., Струков А. В.  — «Кратко аннотированный список публикаций зарубежный периодический изданий по вопросам оценивания надёжности структурно-сложных систем» в сборнике «Моделирование и Анализ Безопасности и Риска в Сложных Системах: Труды Международной научной школы МА БР — 2011».
• Ушаков И. А. Откуда есть пошла надёжность на Руси.

Онлайн калькулятор надёжности

Надёжность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования. Надёжность – одно из важнейших качеств любого объекта.

Внимание! Если вы открыли сайт со смартфона – сделайте горизонтальную ориентацию экрана. Сайт работает и офлайн. Если у вас неожиданно пропал интернет – расчёт можно вести в случае загруженной страницы. Перезагрузка страницы не требуется. Кроме того, вы можете сохранить калькулятор к себе на компьютер. Для этого в вашем браузере выполните команду – Файл – Сохранить как (или сохранить страницу как) – Веб страница, HTML.

Калькулятор спроектирован на основании ГОСТ 27.301-95 и ГОСТ Р МЭК 61078-2021.

---

Последовательное и параллельное соединение элементов

1. Расчет надежности системы при последовательном соединении элементов.

Пример построения структурной схемы надёжности для последовательного соединения элементов.

Для расчета вероятности безотказной работы всей системы воспользуемся формулой № 15 из ГОСТ Р МЭК 61078-2021 Надежность в технике. Структурная схема надежности

Исходными данными для нас будет ВБР (вероятность безотказной работы) каждого элемента нашей системы.

Пример для ввода данных: ВБР двигателя = 0.995. ВБР коробки передач = 0.996.

ВБР вводите с точкой, а не с запятой. 0,992 – неправильный формат. 0.992 – правильный.

Данный калькулятор позволяет сделать расчет надежности системы, если ваша структурная схема надёжности состоит из семи или менее последовательно соединённых элементов. Если у вас число элементов меньше семи, заполните ненужные ячейки единичками. Например, ваша структурная схема состоит из пяти элементов. Вводите ВБР пяти элементов, а для шестого и седьмого введите цифру 1.

ВБР – вероятность безотказной работы элемента, агрегата, системы. Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не произойдёт.

---

Расчёт надёжности системы для последовательного соединения элементов в случае, если известна интенсивность отказов элементов (failure rate) и время работы системы. Обратите внимание, интенсивность отказов, она же λ – лямбда как правило табличное значение, задаётся в размерности 10 в минус 6 степени. Например, интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность. Внимание! Если у вас в системе число элементов меньше пяти, ненужные ячейки можете не заполнять. Например, ваша структурная схема состоит из трёх элементов. Вводите ВБР трёх элементов, а четвёртый и пятый пропустите.

Табличные интенсивности отказов для многих агрегатов вы можете найти в этом справочнике.

Структурная схема надежности может выглядеть следующим образом:

Для расчёта воспользуемся следующей формулой:

---

2. Расчёт надёжности системы при параллельном соединении элементов

Пример для ввода данных: ВБР 1 двигателя = 0.995. ВБР 2 коробки передач = 0.996.

ВБР вводите с точкой, а не с запятой. 0,992 – неправильный формат. 0.992 – правильный.

Данный калькулятор позволяет сделать расчёт надёжности системы, если ваша структурная схема надёжности состоит из пяти параллельно соединённых элементов. Если у вас число элементов меньше пяти, ненужные ячейки можете не заполнять. Например, ваша структурная схема состоит из трёх элементов. Вводите ВБР трёх элементов, а четвёртый и пятый пропустите.

Расчёт надёжности системы для параллельного соединения элементов в случае, если известна интенсивность отказов резервируемых элементов (failure rate), количество этих элементов и время работы системы. Обратите внимание! В данном случае интенсивности отказов всех элементов системы одинаковые. Именно так и поступают на практике. Обратите внимание, интенсивность отказов, она же λ – лямбда как правило табличное значение, задаётся в размерности 10 в минус 6 степени. Например, интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность.

Табличные интенсивности отказов для многих агрегатов вы можете найти в этом справочнике.

---

3. Расчёт надёжности одного элемента в случае, если известна интенсивность отказов элемента (failure rate). Обратите внимание, интенсивность отказов, она же λ – лямбда как правило табличное значение, задаётся в размерности 10 в минус 6 степени. Например, интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность.

Табличные интенсивности отказов для многих агрегатов вы можете найти в этом справочнике.

---

Расчёт надёжности системы из k элементов, в которой может отказать один элемент.
Это очень ценный расчёт, который позволяет оценить, например, надёжность квадрокоптера, имеющего четыре несущих винта.

Предположим, что квадрик держится в воздухе и продолжает съёмку даже если отказал один винт из четырех. Тогда оценим надёжность всей системы. Введём общее количество элементов (четыре) и количество элементов, необходимых для работы системы (три). Так же можно оценить надёжность парашютной системы, где например из пяти парашютов может отказать один (но груз или люди опуститься безопасно). Или надёжность двигательной установки системы аварийного спасения, в которой из восьми двигателей может отказать один, но экипаж будет спасён. Или надёжность робота-спасателя, у которого может отказать один сервопривод из 25, но он спасёт человека из пожара.

Обратите внимание!
Пример для ввода данных: ВБР одного двигателя с винтом = 0.995.

ВБР вводите с точкой, а не с запятой. 0,995 – неправильный формат. 0.995 – правильный.

4. Расчёт среднего времени безотказной работы (MTBF – mean time between failures, наработка на отказ) в случае, если известна интенсивность отказов элемента. Обратите внимание, интенсивность отказов, она же лямбда – λ как правило табличное значение, в моём калькуляторе задаётся в размерности 10 в минус 6 степени. Например, интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность. Здесь результат получается в годах.

Табличные интенсивности отказов для многих агрегатов вы можете найти в этом справочнике.

---

5. Расчёт среднего времени безотказной работы (MTBF – mean time between failures, наработка на отказ) в случае, если известна интенсивность отказов элемента. Обратите внимание, интенсивность отказов, она же лямбда – λ как правило табличное значение, в моём калькуляторе задаётся в размерности 10 в минус 6 степени. Например, интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность. Здесь результат получается в часах.

Табличные интенсивности отказов для многих агрегатов вы можете найти в этом справочнике.

---

6. Иногда бывает необходимо и важно сделать обратный расчёт – вычислить интенсивность отказов (failure rate) в том случае если известна ВБР и время работы элемента. ВБР вводите с точкой, а не с запятой. 0,992 – неправильный формат. 0.992 – правильный.

---

7. В задачах реального мира порой важен следующий расчёт. У нас есть MTBF, выданная нам производителем оборудования, взятая из каталога продукции или справочника. Нам необходимо вычислить ВБР для заданного времени.

Комплексные показатели надёжности

---

8. Расчёт доступности (коэффициент готовности). Показывает вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Для расчёта необходимо знать значение среднего времени безотказной работы (MTBF) и среднее время восстановления (MTTR – mean time to repair).

---

9. Расчёт среднего времени простоя за год. Показывает время простоя объекта за год. Для расчёта необходимо знать коэффициент готовности.

---

Если вы хотите заказать у меня расчет надежности – нажмите на эту ссылку или на кнопку ниже.

Внимание! Если вас интересует корпоративное групповое обучение специалистов вашей компании, пожалуйста перейдите по ссылке ниже. Возможна адаптация учебной программы под ваши требования/пожелания/возможности как по объёму учёбы срокам обучения, формату обучения, так и по балансу теория/практика.

---

До встречи на обучении! С уважением, Алексей Глазачев. Инженер и преподаватель по надежности.

alexglazachev@me.com
+7(903)731-48-26 – WhatsApp, Telegram. Звоните, но лучше пишите.

---

В статье рассмотрены основные понятия, связанные с расчетом надежности. Приведен расчет наработки на отказ с наглядным примером.

Основные понятия

Надежность можно определить как вероятность того, что устройство будет корректно функционировать в течение указанного промежутка времени. Главная задача заключается в расчете срока службы, поскольку он должен быть указан в документации до того, как устройство перейдет в пользование. Определение срока службы экспериментальным путем затруднено, а иногда невозможно ввиду больших временных затрат. Как правило, срок службы устройства или системы составляет несколько лет.

Безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени.

Долговечность – свойство объекта сохранять работоспособное состояние при установленной системе технического обслуживания и ремонта.

Ремонтопригодность – свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта.

Сохраняемость – свойство объекта сохранять в заданных пределах значения параметров, характеризующих его способность выполнять требуемые функции во время хранения, а также при транспортировке и после нее.

Перечисленные важнейшие свойства надежности характеризуют определенные технические состояния объекта. Различают пять основных видов технического состояния объектов.

Исправное состояние – состояние объекта, при котором он соответствует всем требованиям нормативно-технической и проектной документации.

Неисправное состояние – состояние объекта, при котором он не соответствует хотя бы одному из требований нормативно-технической и проектной документации.

Работоспособное состояние – состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и проектной документации.

Неработоспособное состояние – состояние объекта, при котором значения хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям нормативно-технической и проектной документации.

Предельное состояние – состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно.

Согласно ГОСТ 27.002-89, для оценки надежности используется термин «наработка на отказ» – наработка с момента восстановления работоспособного состояния после отказа до возникновения следующего отказа. Это определение применимо к ремонтопригодной продукции, при эксплуатации которой допускаются многократно повторяющиеся отказы. В английской литературе данный параметр обозначается аббревиатурой MTBF (mean time between failures) – среднее время между отказами.

В случае не подлежащей ремонту продукции используется термин «наработка до отказа» – наработка от начала эксплуатации до возникновения первого отказа. Эквивалент в английской литературе – MTTF (mean time to failures). Наработка на отказ – это важный параметр для определения срока службы системы или устройства.

Зачастую производитель указывает гарантийный срок (lifetime warranty), в течение которого параметры изделия соответствуют тем, что значатся в документации. Средняя наработка на отказ определяется как отношение суммарной наработки восстанавливаемого устройства к количеству отказов, происшедших за суммарную наработку:

где t_i – наработка между i-1 и i-м отказами, ч; n(t) – суммарное количество отказов за время t.

Первые методики прогнозирования надежности появились в 50-х гг. Они закреплены в стандарте MIL-HDBK-217, который с тех пор обновлялся всего шесть раз (последняя редакция датируется 1995 г.). Недавние исследования показали, что имеющиеся методики не обеспечивают точного результата в силу нескольких причин, среди которых:

• справочные данные, на основе которых проводится расчет, быстро устаревают;
• приняты во внимание не все типы отказов;
• не учтены конструктивные особенности устройств.

В результате прогнозирования надежности получают коэффициент, описывающий сложную систему через степень интенсивности отказов. Прогнозирование целесообразно использовать для предварительной оценки надежности и эксплуатационных расходов, однако достоверных результатов оно не обеспечивает.

Табличные значения MILHDBK-217 не обновлялись с 1995 г. К тому же обновления, которые были произведены, не затронули разъемы. Таким образом, в стандарте предусмотрены только модели соединителей, которые были разработаны 35 лет назад. Кроме того, справочные данные были собраны из разных источников, в разные периоды и при разных условиях, о которых нет информации в этих справочниках. 

Ввиду перечисленных причин справочные данные отстают от технологических. Таким образом, зарождающиеся технологии не будут учтены даже после обновления данных.

Кривая отказов

При оценке надежности в MIL-HDBK-217 предполагается, что интенсивность отказов постоянна. Однако в реальности это не так, и она зависит от большого количества факторов, в частности от условий эксплуатации и оставшемуся сроку службы компонента.

На рисунке 1 представлен пример кривой интенсивности отказов для электронного устройства. По вертикальной оси отложена вероятность выхода устройства из строя. По горизонтальной оси – время без соблюдения масштаба. Левая кривая перед красной границей соответствует времени, в течение которого большая часть устройств выходит из строя при наличии брака. На этом этапе производится отсев бракованных устройств на заводе. Как правило, время выявления брака не превышает 50 ч, количество испытуемых устройств невелико.

Рис. 1. Интенсивность отказов
Early life period – начальный период работы; constant life period – период стабильного функционирования; wear out life period – период износа; burn in – нормализация параметров; hours – часы; years – годы; time – время

На втором горизонтальном участке вероятность отказа примерно постоянна. Длительность этого участка и есть наработка на отказ. Как правило, половина этого времени используется производителем в качестве ориентира для определения гарантийного срока. Далее кривая демонстрирует увеличение вероятности отказов. Имеются ввиду не только поломки, но и отклонение параметров работы изделия от заявленных. Это увеличение обусловлено тем, что ряд элементов в устройстве достигает жизненного предела из-за технологии изготовления, т.е. наступает технологический износ элементной базы. Таким образом, время наработки на отказ статистически определяет время работоспособной жизни устройства при заданных условиях эксплуатации.

Расчет надежности

Наиболее простым способом расчета надежности является вычисление отношения общего времени работы к общему количеству отказов. Этот способ применим для оценки массовых продуктов, а также для оценки надежности устройства на основе оценки работы аналогичных устройств предыдущего поколения. Чаще всего надежность определяется на первых стадиях спецификации.

Альтернативным способом определения надежности является вычисление отношения общего времени работы к общему количеству устройств. Отметим, что оба способа не обеспечивают абсолютной точности.

Производитель, как правило, определяет наработку на отказ на основании заявленной надежности используемых компонентов, результатов кратковременных интенсивных испытаний партии изделий и расчетов, учитывающих множество меняющихся во времени причин, влияющих на надежность изделия. При расчетах используются методики, применяемые для устройств военного назначения. Стандартом предусматривается, чтобы время наработки на отказ было приведено в часах, а не в годах.

Рассмотрим пример. В течение года тестировалось 1000 изделий. За время испытаний 10 изделий вышло из строя. Отсюда наработка на отказ составляет 1 год × (1000 шт/10 шт) = 100 лет = 876580 ч. Производитель округлит этот показатель до 900 тыс. ч, потому что продавец все равно предоставит гарантию 2–3 года. Итак, 900 тыс. ч – это срок, по истечении которого существует высокая вероятность того, что изделие конкретной серии выйдет из строя. В то же время опираться на одну величину, характеризующую надежность, не следует. Ниже рассмотрен пример, в котором надежность устройства зависит от условий установки и эксплуатации.

Одним из факторов, который не учитывается при расчете надежности, является виброперемещение печатной платы. Хотя компоненты на платах на рисунке 2 расположены одинаково, надежность у этих устройств очень разная. Причина очевидна: на одной плате имеются четыре винта, на другой – шесть.

Рис. 2. Сравнение профилей вибрации. (Слева плата закреплена 4 винтами, справа – шестью. Плата справа характеризуется более высокой надежностью)

На рисунке 3 рассматривается расположение резистора, установленного методом поверхностного монтажа. На первой плате резистор расположен в области, которая сильно вибрирует, а на второй плате резистор расположен на краю, и его срок службы увеличивается. Эти два примера позволяют обнаружить слабости методики MIL-HDBK-217.

Аппаратные отказы делятся на механические и электронные. Про­гно­зи­ро­вание должно быть проведено не только относительно электронных компонентов, но и относительно моделей, технологического процесса, износа, программной части и внешних факторов (обслуживающий персонал и т.д.).

Рис. 3. Варианты размещения резистора на плате. (Плата справа характеризуется более высокой надежностью)

Итак, при расчете надежности не учитываются такие факторы как способ установки устройства, собственная частота колебаний платы, расположение прогибов платы по отношению к компонентам, температурное распределение, влажность, вибрации, механические и температурные воздействия на компоненты в течение жизненного цикла устройства и т.д. Кроме того, предполагается, что рабочая температура и напряжение не меняются, хотя в некоторых проектах компоненты работают в нестандартных для них режимах. Это может приводить к непредвиденным отказам. Например, для силовых модулей и биполярных транзисторов с изолированным затвором двумя основными причинами отказов являются обрыв провода и отслоение кристалла. Эти процессы можно рассчитать аналитически и точно определить интенсивность и срок отказа.

Альтернатива

Для получения достоверной информации о надежности устройства необходимо обязать поставщика провести оценку надежности, которая будет состоять из двух этапов: анализ модели надежности (SRM – System Reliability Model) и An assessment of the contractor’s planned reliability Activities.

SRM – это графическое представление системы и анализ ее надежности (Reliability Block Diagram (блок-схема надежности), Fault Tree (дерево отказов), Event Tree (дерево событий)). Анализ позволит определить слабости проектируемой системы, которые могут привести к потере функциональности, безопасности и т.д., или обнаружить компоненты, отказ которых приводит к увеличению расходов.

Модель SRM описывает устройство в мельчайших деталях. Устройство разбивается на атомарные функциональные элементы и взаимосвязи между ними. Рассматривается как аппаратная, так и неаппаратные компоненты устройства, в т.ч. приобретенные готовые стандартные компоненты, арендованное оборудование, программное обеспечение, человеческие ресурсы, производственный процесс.

Когда спецификация системы закончена, приступают к предварительной оценке по стандартным критериям (интенсивность отказов, наработка на отказ и т.д.). Все допущения, источники данных и обоснования применяемых методов должны быть документально закреплены. Далее проводят оценку рисков и разрабатывают план действий, направленных на снижение риска элементов и повышение надежности системы. При проведении оценки рекомендуется использовать программный инструмент AMSAA Reliability Scorecard. Он представляет результаты анализа в наглядной форме, что позволяет быстро оценить наиболее уязвимые элементы и разработать стратегию повышения надежности устройства.

Заключение

Сложность определения надежности связана с необходимостью учета большого количества факторов, а также с невозможностью получить экспериментальные результаты. Время наработки на отказ не учитывает условий эксплуатации, поэтому к полученному значению следует относиться с осторожностью.

На основе анализа случаев возврата изделий производитель может определить доминирующие механизмы отказа, идентифицировать соответствующие модели и использовать их для оценки срока службы компонентов, которые будут применяться в конкретном приложении при известных условиях. С практической точки зрения целесообразно исследовать лишь один, наиболее уязвимый компонент системы, поскольку его выход из строя быстрее всего приведет к отказу.

Слабые места системы определяются при анализе дерева отказов или аналогичного исследования. Элементы дерева ошибок оцениваются по известным критериям, а потом выясняется, требуется ли дополнительное тестирование или доработка.

Литература

1. http://embedded-computing.com.
2. http://nomtbf.com/references.
3. www.hwp.ru.
4. http://nadegnost.narod.ru.

Читайте также:
Срок службы светодиодов и их надежность – ключ к успешной реализации светотехнических проектов
Новые MOSFET от IR: высокая эффективность и надежность
Знакомьтесь! PKC Group: устойчивый бизнес, надежность и качество
Повышение надежности и качества сложных печатных плат с помощью стандартов IPC
Методика достижения запланированного качества и надежности. Предупреждающие действия

Источник: журнал «Электронные компоненты»

Часть 1.

  
Введение
   Развитие современной аппаратуры характеризуется значительным увеличением ее сложности. Усложнение обуславливает повышение гарантии своевременности и правильности решения задач.
   Проблема надежности возникла в 50-х годах, когда начался процесс быстрого усложнения систем, и стали вводиться в действие новые объекты. В это время появились первые публикации, определяющие понятия и определения, относящиеся к надежности [ 1 ] и была создана методика оценки и расчета надежности устройств вероятностно-статистическими методами.
   Исследование поведения аппаратуры (объекта) во время эксплуатации и оценка ее качества определяет его надежность. Термин “эксплуатация” происходит от французского слова “exploitation”, что означает получение пользы или выгоды из чего-либо.
   Надежность – свойство объекта выполнять заданные функции, сохраняя во времени значения установленных эксплуатационных показателей в заданных пределах.
   Для количественного выражения надежности объекта и для планирования эксплуатации используются специальные характеристики – показатели надежности. Они позволяют оценивать надежность объекта или его элементов в различных условиях и на разных этапах эксплуатации.
   Более подробно с показателями надежности можно ознакомиться в ГОСТ 16503-70
– “Промышленные изделия. Номенклатура и характеристика основных показателей надежности.”, ГОСТ 18322-73
– “Системы технического обслуживания и ремонта техники. Термины и определения.”, ГОСТ 13377-75
– “Надежность в технике. Термины и определения”.

  
Определения
   Надежность – свойство [далее – (сво-во)] объекта [далее – (ОБ)] выполнять требуемые функции, сохраняя свои эксплуатационные показатели в течение заданного периода времени.
   Надежность представляет собой комплексное сво-во, сочетающее в себе понятие работоспособности, безотказности, долговечности, ремонтопригодности и сохранности.
   Работоспособность – представляет собой состояние ОБ, при котором он способен выполнять свои функции.
   Безотказность – сво-во ОБ сохранять свою работоспособность в течение определенного времени. Событие, нарушающее работоспособность ОБ, называется отказом. Самоустраняющийся отказ называется сбоем.
   Долговечность – сво-во ОБ сохранять свою работоспособность до предельного состояния, когда его эксплуатация становится невозможной по техническим, экономическим причинам, условиям техники безопасности или необходимости капитального ремонта.
   Ремонтопригодность – определяет приспособляемость ОБ к предупреждению и обнаружению неисправностей и отказов и устранению их путем проведения ремонтов и технического обслуживания.
   Сохраняемость – сво-во ОБ непрерывно поддерживать свою работоспособность в течение и после хранения и технического обслуживания.

  
Основные показатели надежности
   Основными качественными показателями надежности является вероятность безотказной работы, интенсивность отказов и средняя наработка до отказа.
   Вероятность безотказной работы
P(t) представляет собой вероятность того, что в пределах указанного периода времени
t, отказ ОБ не возникнет. Этот показатель определяется отношение числа элементов ОБ, безотказно проработавших до момента времени
t к общему числу элементов ОБ, работоспособных в начальный момент. 
   Интенсивность отказов l(t) – это число отказов n(t) элементов ОБ в единицу времени, отнесенное к среднему числу элементов
Nt ОБ, работоспособных к моменту времени
Dt:
   l(t)=n(t)/(Nt*Dt), где
Dt – заданный отрезок времени.
   Например: 1000 элементов ОБ работали 500 часов. За это время отказали 2 элемента. Отсюда,
l(t)=n(t)/(Nt*Dt)=2/(1000*500)=4*10^-6 1/ч, т.е. за 1 час может отказать 4-е элемента из миллиона.
   Показатели интенсивности отказов комплектующих берутся на основании справочных данных [ 1, 6, 8 ]. Для примера в
табл. 1 приведена интенсивность отказов
l(t) некоторых элементов.

Табл. 1.

№	Наименование элемента	Интенсивность отказов, *10-5, 1/ч
1	Резисторы	0,0001…1,5
2	Конденсаторы	0,001…16,4
3	Трансформаторы	0,002…6,4
4	Катушки индуктивности	0,002…4,4
5	Реле	0,05…101
6	Диоды	0,012…50
7	Триоды	0,01…90
8	Коммутационные устройства	0,0003…2,8
9	Разъемы	0,001…9,1
10	Соединения пайкой	0,01…1
11	Провода, кабели	0,01…1
12	Электродвигатели	100…600

 

Табл. 2.

№	Наименование элемента	Коэффициент надежности
1	Резисторы	1,0
2	Конденсаторы	0,25…0,83
3	Трансформаторы	1,3…3,0
4	Катушки индуктивности	1…2
5	Реле	1…10
6	Диоды	1,3…30,0
7	Триоды	1,3…75,0
8	Электродвигатели	10…40

   Надежность ОБ, как системы, характеризуется потоком отказов
L, численно равное сумме интенсивности отказов отдельных устройств:
   L=åli
   По формуле рассчитывается поток отказов и отдельных устройств ОБ, состоящих, в свою очередь, из различных узлов и элементов, характеризующихся своей интенсивностью отказов. Формула справедлива для расчета потока отказов системы из
n элементов в случае, когда отказ любого из них приводит к отказу всей системы в целом. Такое соединение элементов называется логически последовательным или основным. Кроме, того, существует логически параллельное соединение элементов, когда выход их строя одного из них не приводит к отказу системы в целом. Связь вероятности безотказной работы
P(t) и потока отказов L
определяется:
   P(t)=exp(-Dt), очевидно, что 0<P(t)<1 и
0<P(t)<1 и p(0)=1, а p(¥)=0
   Средняя наработка до отказа
To – это математическое ожидание наработки ОБ до первого отказа:
  
To=1/L=1/(åli), или, отсюда: L=1/To
   Время безотказной работы равно обратной величине интенсивности отказов.
   Например: технология элементов обеспечивает среднюю интенсивность отказов
li=1*10^-5 1/ч. При использовании в ОБ
N=1*10⁴ элементарных деталей суммарная интенсивность отказов
lо= N*li=10^-1 1/ч. Тогда среднее время безотказной работы ОБ
To=1/lо=10
ч. Если выполнить ОБ на основе 4-х больших интегральных схем (БИС), то среднее время безотказной работы ОБ увеличится в N/4=2500 раз и составит 25000 ч. или 34 месяца или около 3 лет.

  
Расчет надежности
   Формулы позволяют выполнить расчет надежности ОБ, если известны исходные данные – состав ОБ, режим и условия его работы, интенсивности отказов его компонент (элементов). Однако при практических расчетах надежности есть трудности из-за отсутствия достоверных данных о интенсивности отказов для номенклатуры элементов, узлов и устройств ОБ. Выход из этого положения дает применение коэффициентного метода.
Cущность коэффициентного метода состоит в том, что при расчете надежности ОБ используют не абсолютные значения интенсивности отказов
li, а коэффициент надежности ki, связывающий значения
li с интенсивностью отказов lb какого-либо базового элемента:
   ki=li/lb
   Коэффициент надежности ki практически не зависит от условий эксплуатации и для данного элемента является константой, а различие условий эксплуатации
ku учитывается соответствующими изменениями
lb. В качестве базового элемента в теории и практике выбран резистор. Показатели надежности комплектующих берутся на основании справочных данных [ 1, 6, 8 ]. Для примера в
табл. 2 приведен коэффициенты надежности
ki некоторых элементов. В табл. 3 приведены коэффициенты условий эксплуатации
ku работы для некоторых типов аппаратуры.
   Влияние на надежность элементов основных дестабилизирующих факторов – электрических нагрузок, температуры окружающей среды – учитывается введением в расчет поправочных коэффициентов
a. В табл. 4 приведены коэффициенты условий
a работы для некоторых типов элементов. Учет влияния других факторов – запыленности, влажности и т.д. – выполняется коррекцией интенсивности отказов базового элемента с помощью поправочных коэффициентов.
   Результирующий коэффициент надежности элементов ОБ с учетом поправочных коэффициентов:
   ki’=a1*a2*a3*a4*ki*ku, где

ku – номинальное значение коэффициента условий эксплуатации

ki – номинальное значение коэффициент надежности

a1 – коэффициент учитывающий влияние электрической нагрузки по U, I или P

a2 – коэффициент учитывающий влияние температуры среды

a3 – коэффициент снижения нагрузки от номинальной по U, I или P

a4 – коэффициент использования данного элемента, к работе ОБ в целом

Табл. 3.

№	Условия эксплуатации	Коэффициент условий
1	Лабораторные условия	1
2	Аппаратура стационарная:
	– в помещениях	2…8
	– вне помещений	10…15
3	Подвижная аппаратура:
	– корабельная	40…60
	– автомобильная	50…70
	– поездная	60…80

Табл. 4.

№	Наименование элемента и его параметры	Коэффициент нагрузки
1	Резисторы:
	– по напряжению	0,7…0,8
	– по мощности	0,3…0,7
2	Конденсаторы
	– по напряжению	0,7…0,8
	– по реактивной мощности	0,8…0,9
3	Диоды
	– по прямому току	0,7…0,8
	– по обратному напряжению	0,7…0,85
	– по температуре перехода	0,7…0,8
4	Триоды
	– по току коллектора	0,7…0,8
	– по напряж. коллектор-эмиттер	0,7…0,8
	– по рассеиваемой мощности	0,7…0,8

  
Порядок расчета состоит в следующем:

   1. Определяют количественные значения параметров, характеризующие нормальную работу ОБ.
   2. Составляют поэлементную принципиальную схему ОБ, определяющую соединение элементов при выполнении ими заданной функции. Вспомогательные элементы, использующиеся при выполнении функции ОБ, не учитываются.
   3. Определяются исходные данные для расчета надежности:

• тип, количество, номинальные данные элементов
• режим работы, температура среды и другие параметры
• коэффициент использования элементов
• коэффициент условий эксплуатации системы
• определяется базовый элемент lb и интенсивность отказов lb‘
• по формуле: ki‘=a1*a2*a3*a4*ki*ku
  определяется коэффициент надежности

   4. Определяются основные показатели надежности ОБ, при логически последовательном (основном) соединении элементов, узлов и устройств:

• вероятность безотказной работы:
  P(t)=exp{-lb*To*[n*å(Ni*ki’)]}, где
  Ni – число одинаковых элементов в ОБ
  n – общее число элементов в ОБ, имеющих основное соединение
• наработка на отказ:
  To=1/{lb*[n*å(Ni*ki’)]}

   Если в схеме ОБ есть участки с параллельным соединением элементов, то сначала
делается расчет показателей надежности отдельно для этих элементов, а затем для ОБ в целом.
   5. Найденные показатели надежности сравниваются с требуемыми. Если не соответствуют, то принимаются меры к повышению
надежности ОБ (см. часть 2).
   6. Средствами повышения надежности ОБ являются:
     – введение избыточности, которая бывает:

• внутриэлементная – применение более надежных элементов
• структурная – резервирование – общее или раздельное

  
Пример расчета:
   Рассчитаем основные показатели надежности для вентилятора на асинхронном электродвигателе. Схема приведена на
рис. 1. Для пуска М замыкают QF, а затем SB1. KM1 получает питание, срабатывает и своими контактами КМ2 подключает М к источнику питания, а вспомогательным контактом шунтирует SB1. Для отключения М служит SB2.

Рис.1.

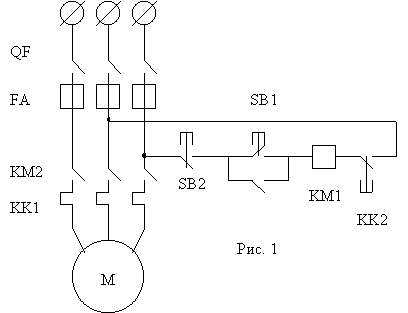
   В защите М используются FA и тепловое реле KK1 с КК2. Вентилятор работает в закрытом помещении при T=50 C в длительном режиме.
Для расчета применим коэффициентный метод, используя коэффициенты надежности компонент схемы. Принимаем интенсивность отказов базового элемента
lb=3*10^-8. На основании принципиальной схемы и ее анализа, составим основную схему для расчета надежности (см. рис.
2). В расчетную схему включены компоненты, отказ которых приводит к полному отказу устройства. Исходные данные сведем в
табл. 5.

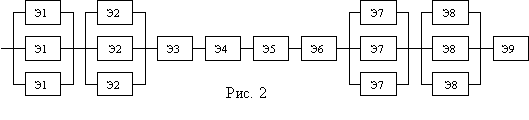
Табл. 5.

Базовый элемент, 1/ч	lб	3*10-8
Коэф. условий эксплуатации	ku	2,5
Интенсивность отказов	lб’	lб* ku=7,5*10-8
Время работы, ч	t	5000
Элемент принципиальной схемы		QF	FA	KK2	KM1	SB1	SB2	KM2	KK1	M
Элемент расчетной схемы		Э1	Э2	Э3	Э4	Э5	Э6	Э7	Э8	Э9
Число элементов	Ni	3	3	1	1	1	1	3	3	1
Коэф. надежности	ki	5	25	10	25	5	5	20	18	250
Коэф. нагрузки	Kn	0,6	0,6	0,6	0,6	0,6	0,8	0,6	0,6	0,85
Коэф. электрической нагрузки	a1	1	1	1	1	1	1	1	1	3,5
Коэф. температуры	a2	1	1	1	1	1	1	1	1	1
Коэф. нагрузки по мощности	a3	1	0,52	0,52	0,52	1	1	1	1	0,8
Коэф. использования	a4	4,4	4,2	1	1	4,2	0,3	4,4	4,2	4,4
Произведение коэф. a	*a	4,4	2,2	0,52	0,52	4,2	0,3	4,4	4,2	12,32
Коэф. надежности	ki’	2,2	55	5,2	13	21	1,5	88	75,6	3080
	Ni*ki’	6,6	165	5,2	13	21	1,5	264	226,8	3080
	S(Ni*ki’)	3783,9
Наработка до отказа, ч	To	1/[lб’*S(Ni*ki’)]=3523,7
Вероятность	p(t)	е[-lб’*To*S(Ni*ki’)]=0,24

   По результатам расчета можно сделать выводы:
1. Наработка до отказа устройства: To=3524 ч.
2. Вероятность безотказной работы: p(t)=0,24. Вероятность того, что в пределах заданного времени работы t в заданных условиях работы не возникнет отказа.

Часть
2.

  
Частные случай расчета надежности. 

P(A1)=P{X1>2}=1-P(X1<2)=1-P(X1=0)-P(X1=1)=1-(g1^m+m*g2^m-1*p1),
где
g1=1-p1

аналогично:
P(A2)=1-(g2ⁿ+n*g2^n-1*p2), где
g2=1-p2

Вероятность
безотказной работы ОБ:

R=P(A)=P(A1)*P(A2)=[1-(g1^m+m*g2^m-1*p1)]*[1-(g2ⁿ+n*g2^n-1*p2)],
где
g1=1-p1, g2=1-p2

11. ОБ состоит из 3-х узлов (см. рис.
11). В узле U1 n1 элементов с интенсивностью отказов l1. В узле U2 n2 элементов с интенсивностью отказов l2. В узле U3 n3 элементов с интенсивностью отказов l2, т.к. U2 и U3 дублируют друг друга. U1 выходит из строя если в нем отказало не менее 2-х элементов. U2 или U3, т.к. дублируются, выходят из строя если в них отказал хотя бы один элемент. ОБ выходит из строя если отказал U1 или U2 и U3 вместе. Вероятность безотказной работы каждого элемента p. Найти вероятность того, что за время t ОБ не выйдет из строя.


Решение: Вероятность выхода из строя одного элемента U1, U2 или U3 за t равны:

           
p1=1-e^–l1*t    
p2=p3=1-e^–l2*t    

           
Вероятность выхода из строя U1
за t
равна:

           
R1=1-(1-p1)ⁿ¹*n1*p1*(1-p1)^n1-1  

           
Вероятности выхода из строя U2
и U3
равны:

           
R2=1-(1-p2)ⁿ²    
R3=1-(1-p3)ⁿ³ 

Вероятности выхода из строя всего ОБ:
R=R1+(1-R1)*R2*R3

  
Литература:

• Малинский В.Д. и др. Испытания радиоаппаратуры, “Энергия”, 1965 г.
• ГОСТ 16503-70 – “Промышленные изделия. Номенклатура и характеристика основных показателей надежности”.
• Широков А.М. Надежность радиоэлектронных устройств, М, Высшая школа, 1972 г.
• ГОСТ 18322-73 – “Системы технического обслуживания и ремонта техники. Термины и определения”.
• ГОСТ 13377-75 – “Надежность в технике. Термины и определения”.
• Козлов Б.А., Ушаков И.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики, М, Сов. Радио, 1975 г.
• Перроте А.И., Сторчак М.А. Вопросы надежности РЭА, М, Сов. Радио, 1976 г.
• Левин Б.Р. Теория надежности радиотехнических систем, М, Сов. Радио, 1978 г.
• ГОСТ 16593-79 – “Электроприводы. Термины и определения”.

И. Брагин   08.2003 г.