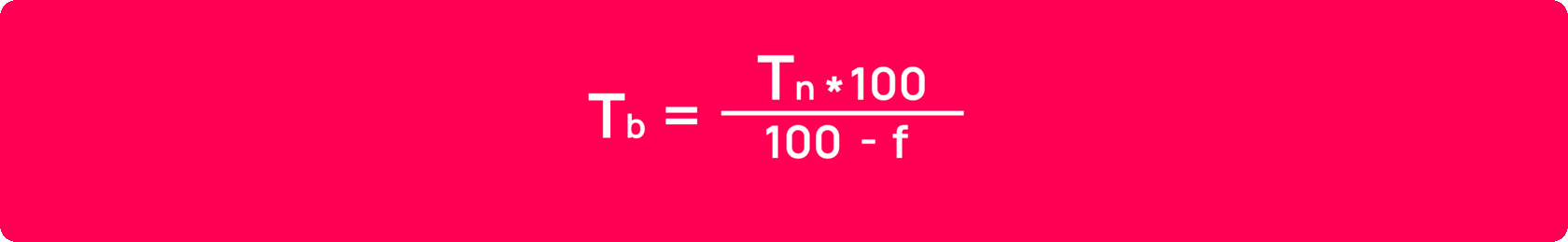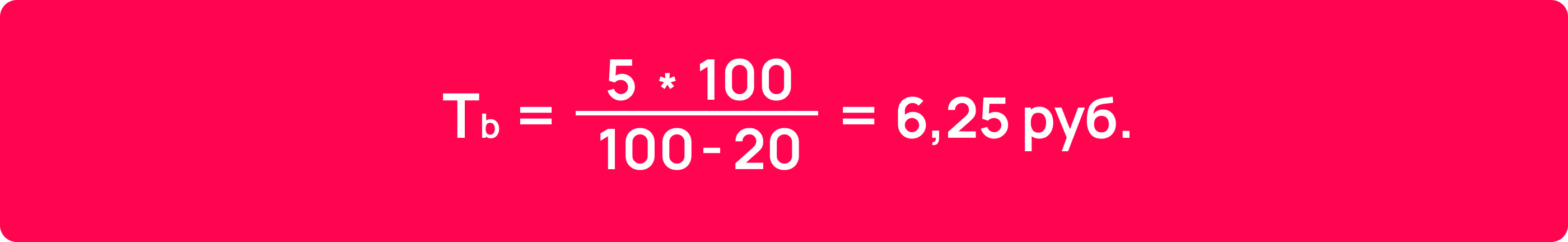Возможно, слова «нетто» и «брутто» ассоциируются у вас исключительно с торговлей или логистикой. Но в страховании тоже встречаются подобные термины. Mafin Media простыми словами рассказывает об одном из них — брутто-ставке.
Что это такое
Брутто-ставка (не путать с брутто-премией) — полный размер страхового взноса в пересчете на единицу страховой суммы. Этот показатель учитывает объем страхования, характер страхового риска и все возможные финансовые нагрузки, которые закладывает в оплату своих услуг страховая компания (СК).
Обычно при расчете брутто-ставки (также называемой тарифной ставкой или страховым тарифом) за единицу страховой суммы принимается 100 рублей. Чаще всего ставка выражается в процентах к этой сумме.
Пример
Андрей решил застраховать свой автомобиль по КАСКО в компании «Эпсилон Страхование» на 2 000 000 руб. Цена его полиса составила 100 000 руб. Это значит, что брутто-ставка по этому полису равна 5% — то есть на 100 руб. страховой суммы приходится 5 руб. страховой премии.
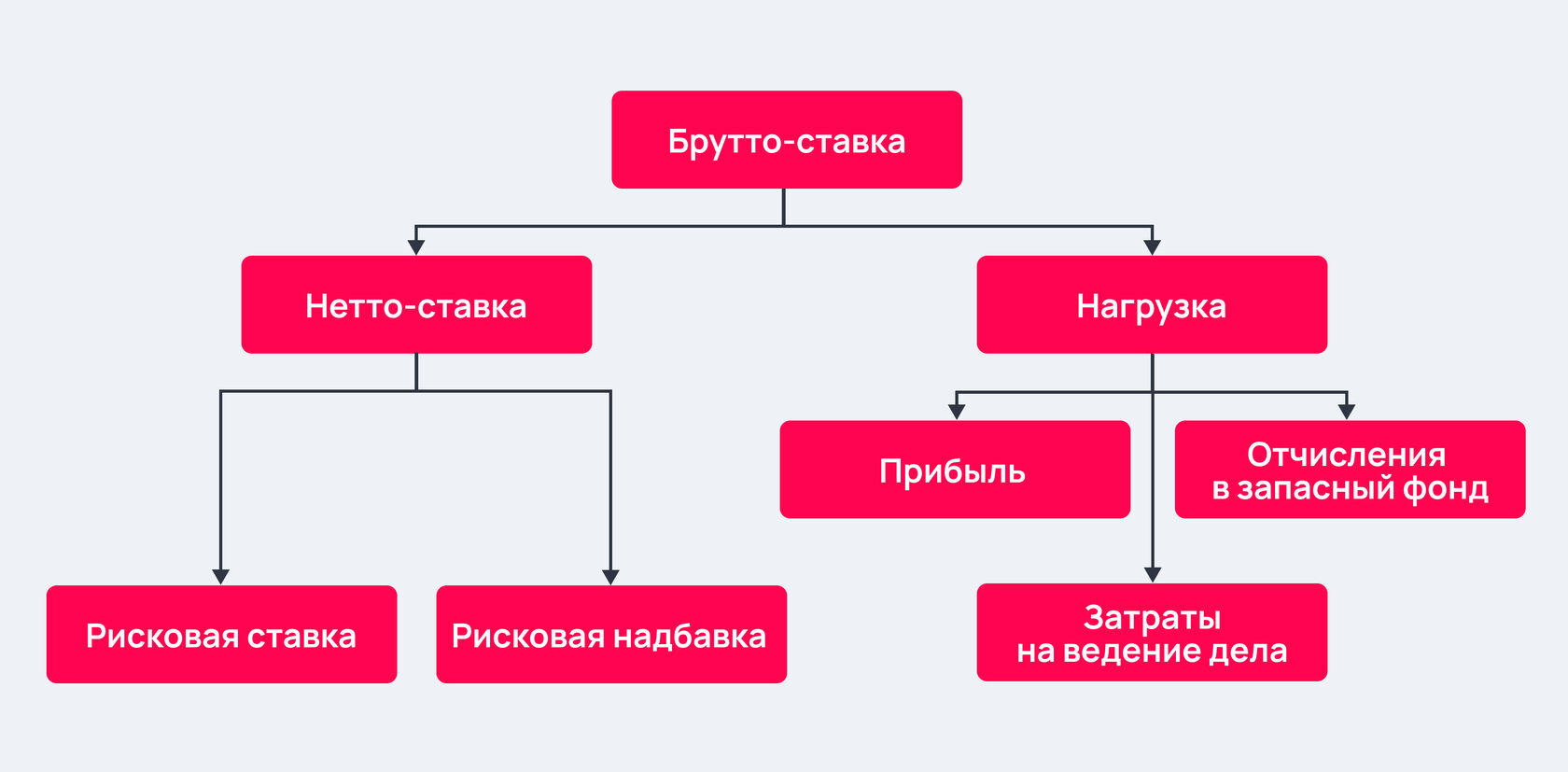
Страховой тариф определяется с помощью актуарных расчетов на основании двух ключевых компонентов:
- нетто-ставки — той части страхового сбора, которая будет использована для текущих страховых выплат и создания страховых резервов;
- страховой нагрузки — части, которая пойдет на покрытие аквизиционных и других расходов (в частности, на оплату услуг страховых агентов и брокеров).
Что учитывается при формировании страхового тарифа
При расчете брутто-ставки любого страхового продукта СК руководствуется несколькими ключевыми правилами:
Прибыльность. Доходы со страховых операций должны покрывать текущие и будущие расходы страховщика и формировать страховые резервы.
Соразмерность. Величина тарифа должна адекватно соответствовать вероятности ущерба.
Доступность. Размер ставки необходимо соотносить с покупательской способностью. Излишне высокие тарифы могут сделать полис невыгодным для страхователя.
Стабильность тарифов. Чем дольше страховщику удается сохранять ставку неизменной, тем больше доверия у страхователей вызывает такая компания.
Как выглядит формула брутто-ставки
Брутто-ставки в разных видах страхования могут рассчитываться по-разному. Вот один из обобщенных вариантов формулы для определения страхового тарифа:
В этой формуле:
Tb — брутто-ставка;
Tn — нетто-ставка;
f — страховая нагрузка, выраженная в процентном соотношении.
Пример
Нетто-ставка по одному из страховых продуктов компании «Консенсус» составляет 5 руб. При этом страховая нагрузка равна 20%. Значит, брутто-ставка по этому продукту составит:
Как это работает на практике
Размер страхового тарифа определяется не только расчетами страховой компании, но и тем, к добровольному или обязательному виду страхования он относится. Во втором случае брутто-ставку почти полностью регулирует государство. Наглядный пример этого — базовый тариф ОСАГО, который устанавливает Банк России и который напрямую влияет на финальную цену полиса.
Правда, стоит отметить, в случае со ставкой ОСАГО речь идет не про конкретное число, а про тарифный коридор ставок с минимальным и максимальным значением. Это необходимо для того, чтобы страховщики могли назначать более низкий тариф аккуратным водителям и высокий — систематическим нарушителям. Базовая ставка ОСАГО на 77% состоит из нетто-тарифа, 20% отводятся на аквизиционные расходы и всего 3% — на страховые резервы.
Подберите самые выгодные условия по КАСКО
Введите номер авто — данные заполнятся автоматически
или нажмите «Рассчитать», если еще не получили его
Утверждены
Распоряжением Федеральной службы
Российской Федерации по надзору
за страховой деятельностью
от 8 июля 1993 г. N 02-03-36
МЕТОДИКИ
РАСЧЕТА ТАРИФНЫХ СТАВОК ПО РИСКОВЫМ ВИДАМ СТРАХОВАНИЯ
Учитывая сложность оценки страховых рисков и расчета страховых тарифов для начинающих страховую деятельность страховых организаций, Федеральная служба России по надзору за страховой деятельностью рекомендует использовать предлагаемые методики расчета страховых тарифов по рисковым видам страхования.
Под рисковыми в настоящих методиках понимаются виды страхования, относящиеся к видам страховой деятельности иным, чем страхование жизни:
не предусматривающие обязательства страховщика по выплате страховой суммы при окончании срока действия договора страхования;
не связанные с накоплением страховой суммы в течение срока действия договора страхования.
Прилагаемые методики могут быть использованы при подготовке документов, представляемых страховыми организациями для получения государственных лицензий на проведение страховой деятельности, осуществления текущего контроля за обеспечением финансовой устойчивости страховых операций. Если страховая организация использует иные способы оценки страхового риска и размеров страховых тарифов, обоснованность применяемых методик должна быть подтверждена использованием математических методов, учитывающих специфику страховых операций.
Определение основных понятий,
использованных в методике
Страховой тариф (брутто – тариф) – ставка страхового взноса с единицы страховой суммы или объекта страхования. Страховой тариф состоит из нетто – ставки и нагрузки.
Нетто – ставка страхового тарифа – часть страхового тарифа, предназначенная для обеспечения текущих страховых выплат по договорам страхования.
Нагрузка – часть страхового тарифа, предназначенная для покрытия затрат на проведение страхования и создания резерва (фонда) предупредительных мероприятий. В составе нагрузки может быть предусмотрена прибыль от проведения страховых операций.
Методика (I) расчета тарифных ставок
по массовым рисковым видам страхования “*”
——————————–
“*” Под массовыми рисковыми видами страхования в настоящих методиках понимаются виды страхования, предположительно охватывающие значительное число субъектов страхования и страховых рисков, характеризующихся однородностью объектов страхования и незначительным разбросом в размерах страховых сумм.
Предлагаемая методика пригодна для расчета тарифных ставок для рисковых видов страхования и применима при следующих условиях:
1) существует статистика либо какая-то другая информация по рассматриваемому виду страхования, что позволяет оценить следующие величины:
q – вероятность наступления страхового случая по одному договору страхования,
S – среднюю страховую сумму по одному договору страхования,
Sв – среднее возмещение по одному договору страхования при наступлении страхового случая;
2) предполагается, что не будет опустошительных событий, когда одно событие влечет за собой несколько страховых случаев;
3) расчет тарифов проводится при заранее известном количестве договоров n, которые предполагается заключить со страхователями.
При наличии статистики по рассматриваемому виду страхования за величины q, S, Sв принимаются оценки их значений:
M
q = ---------, (1)
N
N
SUM Si
i=1
S = -----------, (2)
N
M
SUM Sвk
k=1
Sв = -----------, (3)
M
где N – общее количество договоров, заключенных за некоторый период времени в прошлом;
M – количество страховых случаев в N договорах;
Si – страховая сумма при заключении i-го договора,
i = 1, 2, …, N;
Sвk – страховое возмещение при k-м страховом случае,
k = 1, 2, …, M.
При страховании по новым видам рисков при отсутствии фактических данных о результатах проведения страховых операций, т.е. статистики по величинам q, S и Sв, эти величины могут оцениваться экспертным методом либо в качестве них могут использоваться значения показателей – аналогов. В этом случае должны быть представлены мнения экспертов либо пояснения по обоснованности выбора показателей – аналогов q, S, Sв, а отношение средней выплаты к средней страховой сумме (Sв / S) рекомендуется принимать не ниже:
0,3 – при страховании от несчастных случаев и болезней, в медицинском страховании;
0,4 – при страховании средств наземного транспорта;
0,6 – при страховании средств воздушного и водного транспорта;
0,5 – при страховании грузов и имущества, кроме средств транспорта;
0,7 – при страховании ответственности владельцев автотранспортных средств и других видов ответственности и страховании финансовых рисков.
Нетто – ставка Tn состоит из двух частей – основной части Tо и рисковой надбавки Tр:
Tn = Tо + Tр. (4)
Основная часть нетто – ставки (Tо) соответствует средним выплатам страховщика, зависящим от вероятности наступления страхового случая q, средней страховой суммы S и среднего возмещения Sв. Основная часть нетто – ставки со 100 руб. страховой суммы рассчитывается по формуле:
Sв
Tо = 100 x ------- x q (руб.). (5)
S
Рисковая надбавка Tр вводится для того, чтобы учесть вероятные превышения количества страховых случаев относительно их среднего значения. Кроме q, S и Sв, рисковая надбавка зависит еще от трех параметров: n – количества договоров, отнесенных к периоду времени, на который проводится страхование, среднего разброса возмещений Rв и гарантии гамма – требуемой вероятности, с которой собранных взносов должно хватить на выплату возмещения по страховым случаям.
Возможны два варианта расчета рисковой надбавки.
1. Рисковая надбавка может быть рассчитана для каждого риска. В этом случае
─────────────────────
┐ / 2
│ / 1 Rв
Tр = Tо x альфа (гамма) x │/ ----- [1 - q + (---) ], (6)
n x q Sв
где альфа (гамма) – коэффициент, который зависит от гарантии безопасности гамма. Его значение может быть взято из таблицы.
┌─────────┬──────────┬──────────┬───────────┬──────────┬─────────┐ │ гамма │ 0,84 │ 0,90 │ 0,95 │ 0,98 │ 0,9986 │ ├─────────┼──────────┼──────────┼───────────┼──────────┼─────────┤ │ альфа │ 1,0 │ 1,3 │ 1,645 │ 2,0 │ 3,0 │ └─────────┴──────────┴──────────┴───────────┴──────────┴─────────┘
Rв - среднеквадратическое отклонение возмещений при
наступлении страховых случаев. При наличии статистики выплат
2
страховых возмещений дисперсия выплат R оценивается следующим
в
образом:
2 1 M 2 1 M 2 M 2
R = ----- x SUM (S - S ) = ----- x SUM S - ----- x S , (7)
в M - 1 k=1 вk в M - 1 k=1 вk M - 1 в
где Sвk – страховое возмещение при k-м страховом случае,
k = 1, 2, …, M;
M – количество страховых случаев в N договорах;
Sв – среднее возмещение по одному договору страхования при наступлении страхового случая.
Если у страховой организации нет данных о величине Rв, допускается вычисление рисковой надбавки по формуле:
┐ ──────────
│ / 1 - q
Tр = 1,2 x Tо x альфа (гамма) x │ / ----------. (8)
│/ nq
2. В том случае, когда страховая организация проводит страхование по нескольким видам рисков (j = 1, 2, …, m), рисковая надбавка может быть рассчитана по всему страховому портфелю, что позволяет несколько уменьшить ее размер:
Tр = Tо x альфа (гамма) x мю, (9)
где мю – коэффициент вариации страхового возмещения, который соответствует отношению среднеквадратического отклонения к ожидаемым выплатам страхового возмещения. Если j-й риск
характеризуется вероятностью его наступления gj, средним возмещением Sвj и среднеквадратическим отклонением возмещений Rвj, то
┐ ───────────────────────────────────────────────
│ / m 2 2
│ / SUM [S x n x q x (1 - q ) + R x n x q ]
│/ j=1 вj j j j вj j j
мю = -----------------------------------------------------. (10)
m
SUM Sвj x nj x qj
j=1
При неизвестной величине Rвj среднеквадратического отклонения выплат при наступлении j-го риска соответствующее слагаемое в числителе формулы (10) допускается заменять величиной:
2
1,44 x S x n x q x (1 - q ). (11)
вj j j j
Если не известна ни одна из величин Rвj, то мю вычисляется по формуле:
┐ ───────────────────────────────
│ / m 2
│ / SUM x S x n x q x (1 - q )
│/ j=1 вj j j j
мю = 1,2 x -------------------------------------. (12)
m
SUM Sвj x nj x qj
j=1
Формулы (6), (9) и (10) для вычисления рисковой надбавки тем точнее, чем больше величины n x q и nj x qj. При n x q ” 10 и nj x qj ” 10 формулы (6), (9) и (10) носят приближенный характер.
Если о величинах q, S, Sв нет достоверной информации, например, в случае когда они оцениваются не по формулам (1) – (3) с использованием страховой статистики, а из других источников, то рекомендуется брать
альфа (гамма) = 3.
Брутто – ставка Tдельта рассчитывается по формуле:
Tn x 100
Tдельта = -------------, (13)
100 - f
где Tn – нетто – ставка;
f(%) – доля нагрузки в общей тарифной ставке.
Рассмотрим несколько примеров применения методики.
1. Допустим, что страховая компания заключает договоры имущественного страхования. Пусть вероятность наступления страхового случая q1 = 0,01, средняя страховая сумма составляет S1= 500 тыс. руб., среднее возмещение при наступлении страхового события Sв1 = 375 тыс. руб., количество договоров n1 = 10000, доля нагрузки в структуре тарифа f1 = 30%. Данных о разбросе возможных возмещений нет.
Тогда основная часть нетто – ставки со 100 руб. страховой суммы по формуле (5):
Sв1 375
Tо1 = 100 x ----- x q1 = 100 x --- x 0,01 = 0,75 (руб.).
S1 500
Рассчитаем рисковую надбавку. Пусть страховая компания с вероятностью гамма1 = 0,95 предполагает обеспечить непревышение возможных возмещений над собранными взносами, тогда из таблицы альфа = 1,645 рисковая надбавка по формуле (8):
(1 - q1)
Tр1 = 1,2 x Tо1 x альфа (гамма) x -------- = 1,2 x 0,75 x
n1 x q1
1 - 0,01
x 1,645 x ------------ = 0,15 (руб.).
10000 x 0,01
Нетто – ставка со 100 руб. страховой суммы по формуле (4):
Tn1 = Tо1 + Tр1 = 0,90 (руб.).
Брутто – ставка со 100 руб. страховой суммы по формуле (13):
Tn1 x 100 0,90 x 100
Tдельта1 = ------------ = ------------- = 1,29 (руб.).
100 - f1 100 - 30
2. Другая страховая компания проводит страхование граждан от несчастных случаев. При этом средняя страховая сумма S2 = 140 тыс. руб., среднее возмещение при наступлении страхового события Sв2 = 56 тыс. руб., вероятность наступления риска q2 = 0,04, количество договоров n2 = 3000, нагрузка f2 = 30%. Средний разброс возмещений Rв2 = 30 тыс. руб.
По формулам (5), (6), (4), (11) получаем:
Sв2 56
Tо2 = 100 x ----- x q2 = 100 x --- x 0,04 = 1,6 (руб.),
S2 140
───────────────────
┐ / 2
│ / Rв2
│ / 1 - q2 + (-----)
│ / Sв2
Tр2 = Tо2 x альфа (гамма) x │ / ------------------- =
│/ n2 x q2
┐ ────────────────────
│ / 2
│ / 30
│ / 1 - 0,04 + (----)
│ / 56
= 1,6 x 1,645 x │ / -------------------- = 0,27 (руб.),
│/ 3000 x 0,04
Tn2 = Tо2 + Tр2 = 1,6 + 0,27 = 1,87 (руб.),
Tn2 x 100 1,87 x 100
Tдельта2 = ----------- = ------------ = 2,67 (руб.).
100 - f2 100 - 30
3. Допустим, что страховая компания проводит виды страхования, описанные в предыдущих примерах, т.е. в ее портфеле есть разнородные риски. В этом случае основные части нетто – ставок будут такими же, как в примерах 1 и 2. Для расчета рисковых надбавок определяем коэффициент мю, используя формулу (10), учитывая, что средний разброс выплат по 1 риску неизвестен:
┐ ───────────────────────────────────────────────────────────────────────────
│ / 2 2 2
│ / 1,44 x S x n x q x (1 - q ) + S x n x q x (1 - q ) + R x n x q
│/ в1 1 1 1 в2 2 2 2 в2 2 2
мю = ------------------------------------------------------------------------------- =
Sв1 x n1 x q1 + Sв2 x n2 x q2
┐ ────────────────────────────────────────────────────────────────────────────────────────────
│ / 2 2 2
│/ 1,44 x 375 x 10000 x 0,01 x (1 - 0,01) + 56 x 3000 x 0,04 x (1 - 0,04) + 30 x 3000 x 0,04
= ------------------------------------------------------------------------------------------------ =
375 x 10000 x 0,01 + 56 x 3000 x 0,04
= 0,102.
Рисковая надбавка по формуле (9)
Tр = Tо x альфа (гамма) x мю = Tо x 1,645 x 0,102 = 0,17 x Tо,
нетто – ставка для любого вида страхования, составляющего страховой портфель,
Tn = Tо + 0,17 x Tо = 1,17 x Tо.
Нетто – ставка со 100 руб. страховой суммы:
при имущественном страховании
Tn1 = 1,17 x 0,75 = 0,88 (руб.),
при страховании граждан от несчастных случаев
Tn2 = 1,17 x 1,6 = 1,87 (руб.).
Соответствующие брутто – ставки со 100 руб. страховой суммы:
Tдельта1 = 1,26 руб.
Tдельта2 = 2,67 руб.
Методика (II) расчета тарифных ставок
по массовым рисковым видам страхования
Данную методику целесообразно использовать по массовым видам страхования на основе имеющейся страховой статистики за определенный период времени или при отсутствии таковой использовать статистическую информационную базу (демографическая статистика, смертность, инвалидность, производственный травматизм и т.д.).
Определение страхового тарифа на основе страховой статистики за несколько лет осуществляется с учетом прогнозируемого уровня убыточности страховой суммы на следующий год.
Предлагаемая методика применима при следующих условиях:
1) имеется информация о сумме страховых возмещений и совокупной страховой сумме по рискам, принятым на страхование, за ряд лет;
2) зависимость убыточности от времени близка к линейной.
Расчет нетто – ставки производится в следующей последовательности:
а) по каждому году рассчитывается фактическая убыточность страховой суммы (y) как отношение страхового возмещения к общей страховой сумме застрахованных рисков (Sв / S)
Таблица 1
┌─────────────┬────────────────┬───────────────┬─────────────────┐ │ Год │Общая страховая │ Страховое │ Фактическая │ │ │ сумма (S) │возмещение (Sв)│убыточность (yi) │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1988 │ 2278 │ 410 │ 0,18 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1989 │ 2942 │ 765 │ 0,26 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1990 │ 2755 │ 799 │ 0,29 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1991 │ 3094 │ 1114 │ 0,36 │ ├─────────────┼────────────────┼───────────────┼─────────────────┤ │ 1992 │ 3346 │ 1305 │ 0,39 │ └─────────────┴────────────────┴───────────────┴─────────────────┘
б) на основании полученного ряда исходных данных рассчитывается прогнозируемый уровень убыточности страховой суммы, для чего используется модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения:
*
y = a + a x i, (1)
i 0 1
*
где y - выравненный показатель убыточности страховой суммы,
i
a0, a1 - параметры линейного тренда,
i - порядковый номер соответствующего года.
Параметры линейного тренда можно определить методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными:
n n
a0 x n + a1 x SUM i = SUM yi,
i=1 i=1
(2)
n n 2 n
a x SUM i + a x SUM i = SUM y x i,
0 i=1 1 i=1 i=1 1
где n – число анализируемых лет.
Коэффициенты данной системы уравнений находятся с помощью таблицы 2:
Таблица 2
┌───────────┬──────────┬───────────────┬─────────────────────────┐ │ Год │ i │ Фактическая │ Расчетные показатели │ │ │ │ убыточность ├─────────────┬───────────┤ │ │ │ (yi) │ yi x i │ 2 │ │ │ │ │ │ i │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1988 │ 1 │ 0,18 │ 0,18 │ 1 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1989 │ 2 │ 0,26 │ 0,52 │ 4 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1990 │ 3 │ 0,29 │ 0,87 │ 9 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1991 │ 4 │ 0,36 │ 1,44 │ 16 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ 1992 │ 5 │ 0,39 │ 1,95 │ 25 │ ├───────────┼──────────┼───────────────┼─────────────┼───────────┤ │ │ 15 │ 1,48 │ 4,96 │ 55 │ └───────────┴──────────┴───────────────┴─────────────┴───────────┘
Подставив полученные в таблице 2 данные в систему уравнений (2), получим:
a0 x 5 + a1 x 15 = 1,48,
(3)
a0 x 15 + a1 x 55 = 4,96.
Решив систему уравнений (3), получаем следующие значения:
a0 = 0,14,
a1 = 0,052,
на основании которых можно определить выравненную убыточность по годам, подставляя необходимые данные в уравнение (1).
Таким образом, ожидаемая убыточность на 1993 год с учетом тренда исходных данных составит:
y6 = a0 + a1 x 6,
y6 = 0,14 + 0,052 x 6 = 0,452 руб. со 100 руб. страховой суммы, т.е. это и является основной частью нетто – ставки;
в) для определения рисковой надбавки необходимо по следующей формуле рассчитать среднее квадратическое отклонение фактических значений убыточности от выравненных значений:
┐ ──────────────────
│ / n * 2
│ / SUM x (y - y )
│ / i=1 i i (4)
сигма = │ / -----------------.
│/ n - 1
Используемые для определения рисковой надбавки показатели приведены в таблице 3:
Таблица 3
┌──────┬────┬───────────┬────────────┬──────────────┬────────────┐ │ Годы │ I │Фактическая│ Выравненная│ Отклонения │ Квадраты │ │ │ │убыточность│ убыточность│ выравненной │ отклонений │ │ │ │ (y ) │ * │ убыточности │ * 2 │ │ │ │ i │ (y ) │от фактической│ (y - y ) │ │ │ │ │ i │ * │ i i │ │ │ │ │ │ (y - y ) │ │ │ │ │ │ │ i i │ │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1988 │ 1 │ 0,18 │ 0,192 │ +0,012 │ 0,000144 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1989 │ 2 │ 0,26 │ 0,244 │ -0,016 │ 0,000256 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1990 │ 3 │ 0,29 │ 0,296 │ +0,006 │ 0,000036 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1991 │ 4 │ 0,36 │ 0,348 │ -0,012 │ 0,000144 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │ 1992 │ 5 │ 0,39 │ 0,400 │ +0,010 │ 0,000100 │ ├──────┼────┼───────────┼────────────┼──────────────┼────────────┤ │Сумма │ │ │ │ │ 0,000680 │ └──────┴────┴───────────┴────────────┴──────────────┴────────────┘
Подставив рассчитанные показатели в формулу (4), получим:
┐ ──────────
│ / 0,00068
сигма = │ / ---------- = 0,013;
│/ 5 - 1
г) нетто – ставка рассчитывается следующим образом:
Tn = y6 + бета (гамма; n) x сигма,
где бета (гамма; n) – коэффициент, используемый для исчисления размера рисковой надбавки. Величина бета (гамма; n) зависит от заданной гарантии безопасности гамма (той вероятности, с которой собранных взносов хватит на выплаты страховых возмещений) и n – числа анализируемых лет и может быть взята из таблицы 4.
Таблица 4
┌──────┬───────────┬──────────┬───────────┬───────────┬──────────┐ │гамма │ 0,8 │ 0,9 │ 0,95 │ 0,975 │ 0,99 │ │ n │ │ │ │ │ │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 3 │ 2,972 │ 6,649 │ 13,640 │ 27,448 │ 68,740 │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 4 │ 1,592 │ 2,829 │ 4,380 │ 6,455 │ 10,448 │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 5 │ 1,184 │ 1,984 │ 2,850 │ 3,854 │ 5,500 │ ├──────┼───────────┼──────────┼───────────┼───────────┼──────────┤ │ 6 │ 0,980 │ 1,596 │ 2,219 │ 2,889 │ 3,900 │ └──────┴───────────┴──────────┴───────────┴───────────┴──────────┘
Допустим, страховая компания считает необходимым с уровнем вероятности гамма = 0,9 быть уверена в том, что собранной суммы взносов будет достаточно для выплаты страховых возмещений. Тогда из таблицы 4 при гамма = 0,9 для n = 5, бета = 1,984.
Нетто – ставка со 100 руб. страховой суммы
Tn = 0,452 + 1,984 x 0,013 = 0,48 (руб.).
Брутто – ставка (Tдельта) определяется по следующей формуле:
Tn x 100
Tдельта = ----------,
100 - f
где Tn – нетто – ставка,
f(%) – доля нагрузки в общей тарифной ставке.
При условии, что нагрузка определена страховой организацией в размере 30% от брутто – ставки, рассчитывается брутто – ставка:
0,48 x 100
Tдельта = ------------ = 0,69 (руб.).
100 - 30
Брутто – ставка со 100 руб. страховой суммы равна 0,69 руб.
Страховой тариф представляет
собой ставку взноса с единицы страховой
суммы или объекта страхования. Обычно
за единицу страховой суммы принимается
100 рублей (реже 1 руб. или 1000 руб.). С помощью
тарифной ставки определяется величина
страховой премии, которую страхователь
должен заплатить при заключении договора
страхования. Для этого величина тарифной
ставки умножается на страховую сумму,
указанную в договоре.
По некоторым видам страхования
(страхованию пассажиров от несчастных
случаев, автомобилей, животных и некоторым
другим) тарифные ставки могут
устанавливаться с объекта страхования.
Таким образом, тарифная ставка является
базой для определения доли участия
каждого страхователя в формировании
денежного фонда. За счет этого фонда
должны быть осуществлены страховые
выплаты, покрыты прочие расходы
страховщика и получена прибыль.
Поэтому основная задача, которая ставится
при расчете тарифной ставки, связана
с определением вероятной суммы выплат
по страховым случаям и других расходов
страховщика, приходящихся на единицу
страховой суммы или один объект
страхования.
Если тарифные ставки рассчитаны
правильно, то страховщик за счет
полученных страховых взносов может в
полной мере выполнить взятые на себя
обязательства, покрыть свои издержки
по проведению страхования и получить
прибыль. Завышение тарифов по сравнению
с вероятностью имеющегося риска не
способствует заключению договоров
страхования с потенциальными
страхователями, снижает конкурентные
возможности страховщика на страховом
рынке.
Занижение тарифной ставки может привести
к тому, что у страховщика просто не
хватит средств для осуществления
страховых выплат, и в результате
понесенный страхователями или иными
участниками страхования ущерб не
будет возмещен. Последняя ситуация
крайне негативно отражается не только
на финансовом положении страховщика,
но и вызывает недоверие к страхованию
со стороны страхователей. Поэтому орган
страхового надзора в России
устанавливает контроль за обоснованностью
применяемого размера тарифной ставки
и может принимать строгие санкции за
снижение величины ставок страховщиками
без достаточных на то оснований.
Тарифная ставка, по которой страхователь
уплачивает страховую премию, называется
брутто-ставкой. Она состоит из двух
частей: нетто-ставки и нагрузки.
Нетто-ставка предназначена для
формирования страхового фонда, который
используется для страховых выплат
страхователям (страхового обеспечения
– при личном страховании и страхового
возмещения – при имущественном
страховании), то есть для выполнения
финансовых обязательств страховщика
по договорам страхования. Нагрузка
предназначена для компенсации расходов
страховщика: погашения накладных
расходов, формирования запасных,
резервных и других фондов. В нагрузку
включается также определенная плановая
прибыль от страховой деятельности.
Для компенсации возможных ценовых
отклонений к отдельным рисковым страховым
взносам делается (исчисляется) гарантийная
надбавка, которую принято называть
дельта-надбавка. Нетто-ставка складывается
из двух частей- убыточности страховой
суммы – это отношение суммы выплаченного
страхового возмещения к сумме
застрахованных объектов. Величина
рисковой премии зависит от степени
вероятности наступления страхового
случая. Рисковый взнос можно рассмотреть
как производную от вероятности
осуществления риска во времени и
пространстве.
При расчете брутто-ставки первоначально
находят нетто-ставку, к ней добавляется
нагрузка, и получается окончательная
ставка. Обычно нагрузка устанавливается
в процентах к брутто-ставке, и поэтому
последняя определяется по следующей
формуле:
где ^ БС – брутто-ставка;НС –
нетто-ставка;н – нагрузка в
процентах.
На размер нетто-ставки влияют два
фактора: вероятность наступления
страхового случая по данному договору;
ожидаемая тяжесть страхового случая,
которая определяется отношением
ожидаемой величины выплаты по страховому
случаю к страховой сумме по данному
договору.
По обязательным видам
страхования тарифы устанавливаются
законом или другими нормативными
документами. По добровольному
страхованию ставки рассчитываются
страховщиками самостоятельно. Расчет
тарифов с приложением использованной
методики по их определению и указанием
источника исходных данных представляется
в орган страхового надзора для одобрения.
Нагрузка (надбавка)составляет в
общем страховом тарифе существенно
меньшую часть от брутто-ставки (в
зависимости от формы и вида страхования
она колеблется от 9 до 40%). Нагрузка
включает в себя расходы на ведение дела.
последние в свою очередь подразделяется
на на адм-хоз расходы и оплату труда за
размещение страховых полисов. При
расчете брутто-ставки первоначально
определяется нетто-ставка, затем
добавляется нагрузка которая обычно
устанавливается в процентах к брутто
ставке.
Тб=Тн/100 – Н, где Н- нагрузка выраженная
в процентах.
Главным
достоинством рассмотренной структуры
(модели) страхового тарифа является
четкое разделение средств страхователя
и страховщика.
Здесь
следует отметить, что хотя структура
страхового тарифа Законом«О страховании»
не регламентирована, однако налогообложение
проводится по этой модели. Она же
применяется и при лицензировании
страховых организаций.
Страховой
тариф при добровольном страховании
определяется страховщиком на основе
ожидаемой совокупности объектов
страхования и используется для определения
страхового взноса как цены страховой
защиты (услуги).
Определение
(расчет) страхового тарифа производится
с помощью теории актуарных расчетов
(сочетание математических методов,
применяемых в статистике, теории
вероятностей и финансовых исчислений
с учетом социальных, демографических
и других факторов).
Экономическое
содержание страхового тарифа
можно определить как единицу измерения
взаимных обязательств страховщика и
страхователя(принцип эквивалентности).
Основой
деления брутто-ставки на нетто-ставку
и нагрузку является тезис, согласно
которому нетто-ставка предназначена
для погашения обязательств страховщика
перед страхователем, а нагрузка — на
финансирование деятельности страховой
организации.
Процесс
разработки и обоснования страхового
тарифа называется тарифной политикой,
под которой понимается целенаправленная
деятельность страховщика по установлению,
уточнению и упорядочению страховых
тарифов в интересах успешного и
безубыточного развития страхования.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Цена корпоративного страхования – один из факторов, который для большинства
страхователей остается приоритетным при выборе партнера. Как показывает
практика, покупатель страхового продукта обычно идет самым простым путем –
отдает предпочтение тому, кто предложит меньшую стоимость страховки. А вот
опыт урегулирования инцидентов демонстрирует, что такой подход не является
эффективным:
-
в 90% случаев низкий тариф страхования (ниже среднерыночного)
предлагают мелкие компании; -
на долю отказов по договорам малых организаций приходится более 30%
претензий.
Конечно, все это не может и не должно стимулировать страхователя страховать
риски бизнеса по самым высоким ставкам. Но разобраться, как должны
формироваться цены полиса, и что на них объективно влияет, полезно каждому,
кто заинтересован в работающем страховании (а не фиктивном, как это бывает
с дешевыми программами).
Для этого, прежде всего, необходимо понять, что такое страховой тариф в страховании имущественных
рисков корпоративного клиента, и как он формируется. Закон № 4015–1
рассматривает его в двух вариантах:
-
абсолютном выражении (принимается в заданном размере с единицы суммы
страхования); -
относительном выражении (процент, на который умножается сумма
страховки, чтобы получить размер премии – взноса страхователя).
Как формируется страховой тариф: научный подход
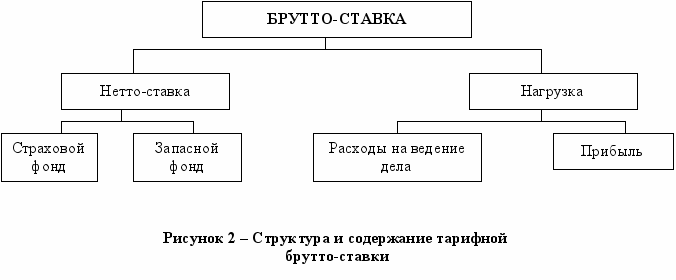
Структура тарифа (он называется брутто) включает два основных блока: ставку
нетто и нагрузку. Первая работает на пополнение страхового и запасного
фонда. Страховой фонд – размер накоплений, из которых берутся выплаты при
наступлении страховых событий. Его формирует рисковая ставка,
устанавливаемая страховщиком индивидуально.
Запасной фонд – резерв, покрывающий расходы страховщика при недостаточной
емкости страхового запаса. Он собирается из суммы рисковых надбавок,
которые входят в структуру ставки нетто.
Нагрузка – дополнительная часть страхового брутто-тарифа, которая
составляет доход страховщика и призвана покрывать его затраты на
обслуживание портфеля клиентов. У серьезных страховщиков в долю этого
компонента включен дополнительный процент на фонд предупредительных мер.
Что влияет на размер тарифа
Учитывая сложную структуру тарифной ставки по каждому виду страхования,
несложно предположить, что и показателей, которые ее формируют, много. На
каждую составляющую тарифа влияют свои показатели.
-
на рисковую ставку влияет выбор программы страхования и вероятность
наступления выбранного риска (если их несколько, то показатель
рассчитывается по каждому из них); -
рисковая надбавка определяется, согласно статистике убыточности по
конкретному продукту у страховщика, и заложенному (расчетному)
количеству вероятных страховых событий; -
нагрузку формируют «аппетиты» страховщика, размеры его постоянных и
переменных издержек, уровень организации бизнес-процессов и
автоматизации работы.
Формирование стоимости страхового продукта
Кроме того, страховой тариф (брутто) напрямую зависит от
финансовых показателей работы страховщика – размеров его портфеля,
управленческих затрат, дополнительных доходов (от инвестиционной
деятельности). На итоговую стоимость страхования будут влиять еще и
поправочные коэффициенты. Они умножаются на расчетный страховой тариф и в
зависимости от обстоятельств могут как увеличить конечную цену, так и
снизить ее.
В большинстве крупных страховых компаний тарифная таблица заполняется как
минимум двумя вариантами страхового тарифа – верхним уровнем ставки и
нижним. Первый, помимо перечисленных факторов, зависит еще и от действующей
депозитной ставки банка-партнера страховой компании.
Почему в страховании тоже «оптом дешевле»
При расчете ставок брутто и нетто в целях ценообразования применяются
громоздкие формулы. Но не всегда. При коллективном страховании используется
более простой расчет на основе усредненных показателей без учета
индивидуальной вероятности неблагоприятного развития событий. Что это дает:
-
сокращение расходов времени и технико-технологических ресурсов
страховщика; -
снижение суммарных расходов на аналитику и скорринг по коллективным
программам.
К этому добавляется по умолчанию более высокий объем сборов (за группу
застрахованных), что и определяет условия для оптимизации страхового тарифа
путем снижения надбавки.
Что страховой тариф расскажет о страховой компании
Чем более серьезный подход применяет страховая организация к расчету
страхового тарифа, тем выше финансовая устойчивость ее операций. Для
страхователя это значит, что грамотный расчет гарантирует его способность
погасить обязательства перед страхователем. Конечно, далеко не все
страховщики раскрывают подробности практики оценки продуктов.
Но здесь вы можете воспользоваться нашей помощью. СА «GALAXY страхование» проводит
комплексный анализ каждого партнера, чтобы гарантировать клиентам
эффективность каждого полиса. У нас на сайте можно оформить продукт только
от исполнительных надежных участников российского рынка. С возможностью
сравнить действующие ставки компаний и выбрать лучшую.