Наиболее вероятная, среднеквадратичная и средняя арифметическая скорости молекул газа
Рассмотрим, как изменяется с абсолютной
величиной скорости число частиц,
приходящихся на единичный интервал
скоростей, при единичной концентрации
частиц.
График функции распределения Максвелла
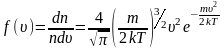
,
приведен
на рисунке 2.6.

Рис.
2.6
Из
графика видно, что при «малых» υ,
т.е. при
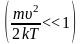
,
имеем

;
затем
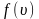
достигает максимума А
и далее экспоненциально спадает
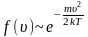
.
Величину
скорости, на которую приходится максимум
зависимости
,
называют
наиболее вероятной скоростью.
Найдем
эту скорость из условия равенства
производной
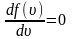
.
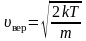
, (2.3.6)
– наиболее
вероятная скорость одной молекулы.
Для
одного моля газа:
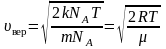
. (2.3.7)
Среднюю
квадратичную скорость
найдем, используя соотношение
:

– для одной молекулы. (2.3.8)
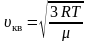
– для одного моля газа. (2.3.9)
Средняя
арифметическая скорость:
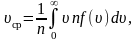
где
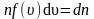
– число молекул со скоростью от υ
до
.
Если подставить сюда f(υ)
и вычислить, то получим:
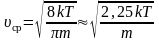
–
для одной молекулы. (2.3.10)
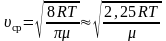
–
для одного моля газа. (2.3.11)
Все
три скорости незначительно отличаются
друг от друга множителем порядка единицы,
причем
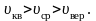
Формула Максвелла для относительных скоростей
Для
решения многих задач удобно использовать
формулу Максвелла, где скорость выражена
в относительных единицах.
Относительную
скорость обозначим через u:
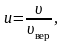
(2.3.13)
где
.
Тогда из (2.3.3), получим
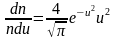
. (2.3.14)
Это
уравнение универсальное. В
таком виде функция
распределения
не зависит ни от рода газа, ни от
температуры.
На
рисунке 2.7 показано максвелловское
распределение частиц f(υ),
имеющих скорости от υ до
За единицу скорости здесь взята наиболее
вероятная скорость.
Полезно
знать, что
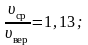
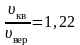
.
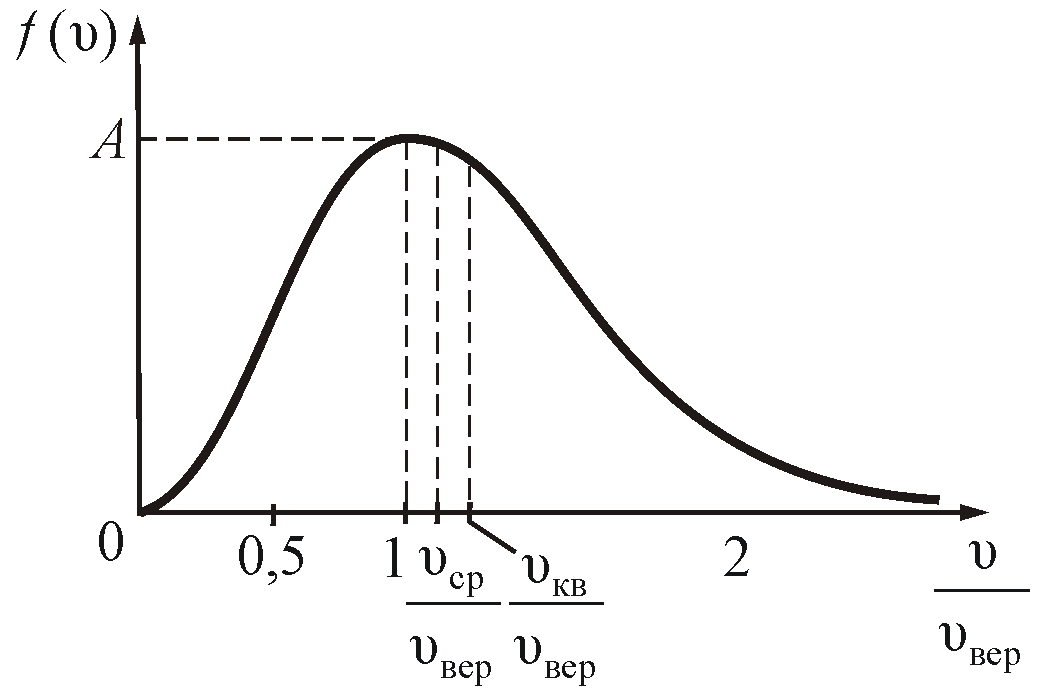
Рис.
2.7
Зависимость функции распределения Максвелла от массы молекул и температуры газа
На
рисунке 2.8 показана зависимость
при различных температурах и массах
молекул газа.
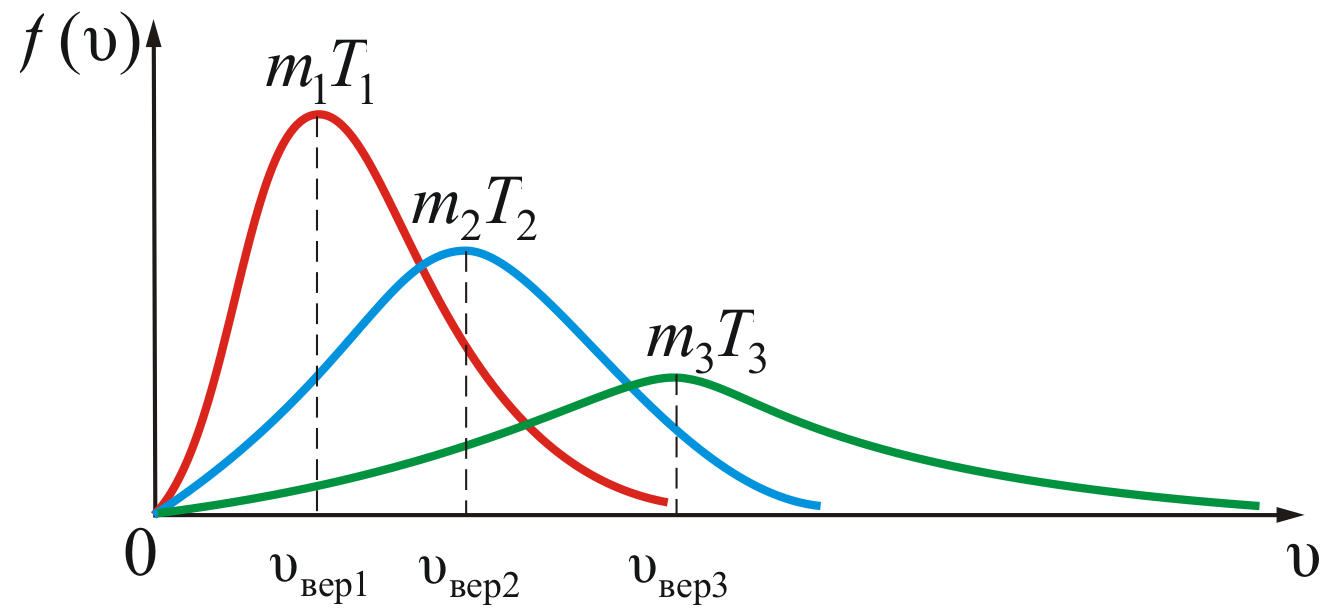
Рис.
2.8
Из
рисунка 2.8 можно проследить за изменением
при изменении m
и T.
В данном случае
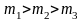
(при
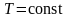
)
или
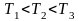
(при
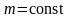
).
Площадь
под кривой величина постоянная,
равная единице (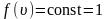
),
поэтому важно знать как будет изменяться
положение максимума кривой:
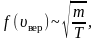
кроме
того

Максвелловский
закон распределения по скоростям и все
вытекающие следствия справедливы только
для газа в равновесной системе. Закон
статистический, и выполняется тем лучше,
чем больше число молекул.
Барометрическая формула
Рассмотрим
ещё один очень важный закон.
Атмосферное
давление на какой-либо высоте h
обусловлено весом слоёв газа, лежащих
выше. Пусть P
– давление на высоте h,
а
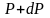
–
на высоте
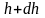
(рис. 2.9).
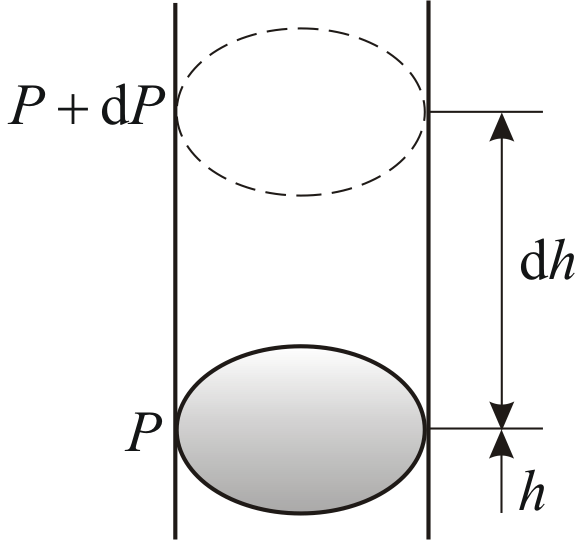
Рис.
2.9
Причём
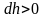
,
а dР
< 0, так как на большей высоте давление
меньше. Разность давления
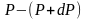
равна весу газа, заключённого в объёме
цилиндра с площадью основания равного
единице и высотой dh.
Т.к.
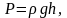
где

плотность газа на высоте h,
медленно убывающая с высотой, то можно
записать:

.
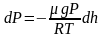
или
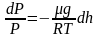
.
Проинтегрировав
это выражение, получим:
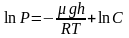
,
где
С
– произвольная постоянная.
В
силу произвольности, примем, что С
= Р0
– давление на высоте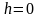
.
Отсюда, после потенцирования, получаем
барометрическую формулу:
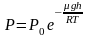
(2.4.1)
Из
формулы (2.4.1) следует, что P
убывает с высотой тем быстрее, чем
тяжелее газ (чем больше μ) и чем ниже
температура (например, на больших высотах
концентрация легких газов Не и Н2
гораздо больше, чем у поверхности Земли).
На
рисунке 2.10 изображены две кривые, которые
можно трактовать, либо как соответствующие
разным μ (при одинаковой Т),
либо как отвечающие разным Т,
при одинаковых μ.
Таким
образом, чем тяжелее
газ (больше μ) и чем ниже
температура, тем быстрее
убывает давление.
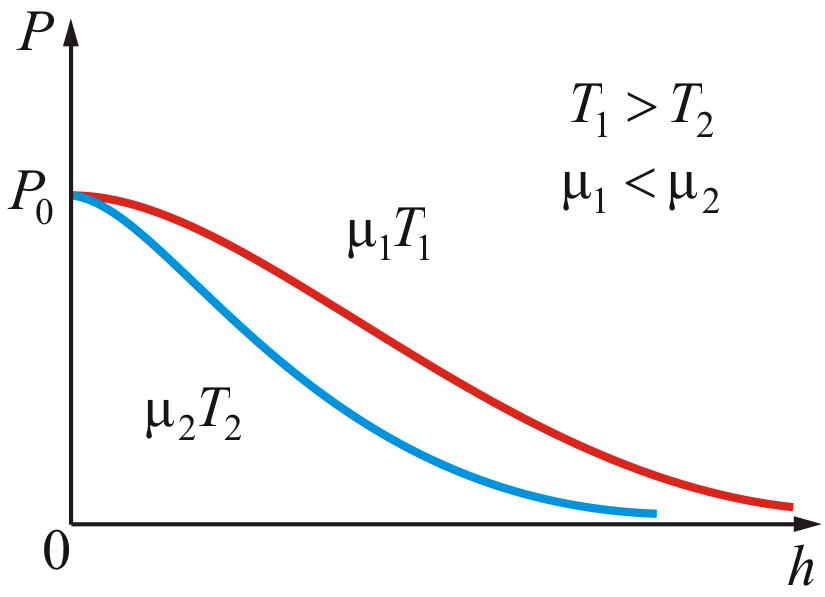
Рис.
2.10
Пусть идеальный газ находится в поле
консервативных сил в условиях теплового
равновесия. При этом концентрация газа
будет различной в точках с различной
потенциальной энергией, что необходимо
для соблюдения условий механического
равновесия. Так, число молекул в единичном
объеме n убывает с
удалением от поверхности Земли, и
давление, в силу соотношения
,
падает.
Если известно число молекул в единичном
объеме, то известно и давление, и наоборот.
Давление и плотность пропорциональны
друг другу, поскольку температура в
нашем случае постоянна. Давление с
уменьшением высоты должно возрастать,
потому что нижнему слою приходится
выдерживать вес всех расположенных
сверху атомов.
Исходя
из основного уравнения молекулярно-кинетической
теории:
,
заменим P
и P0
в барометрической формуле (2.4.1) на n
и n0
и получим распределение
Больцмана
для молярной массы газа:
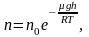
(2.5.1)
где
n0
и n
число молекул в единичном объёме на
высоте h
= 0 и h.
Так
как
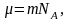
а
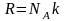
,
то (2.5.1) можно представить в виде
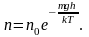
(2.5.2)
С
уменьшением температуры число молекул
на высотах, отличных от нуля, убывает.
При
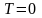
тепловое движение прекращается, все
молекулы расположились бы на земной
поверхности. При высоких температурах,
наоборот, молекулы оказываются
распределёнными по высоте почти
равномерно, а плотность молекул медленно
убывает с высотой. Так как
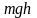
– это потенциальная энергия U,
то на разных высотах
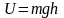
– различна. Следовательно, (2.5.2)
характеризует распределение частиц по
значениям потенциальной энергии:
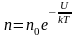
, (2.5.3)
– это
закон распределения частиц по потенциальным
энергиям – распределение Больцмана.
Здесь n0
– число молекул в единице объёма там,
где
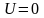
.
На
рисунке 2.11 показана зависимость
концентрации различных газов от высоты.
Видно, что число более тяжелых молекул
с высотой убывает быстрее, чем легких.
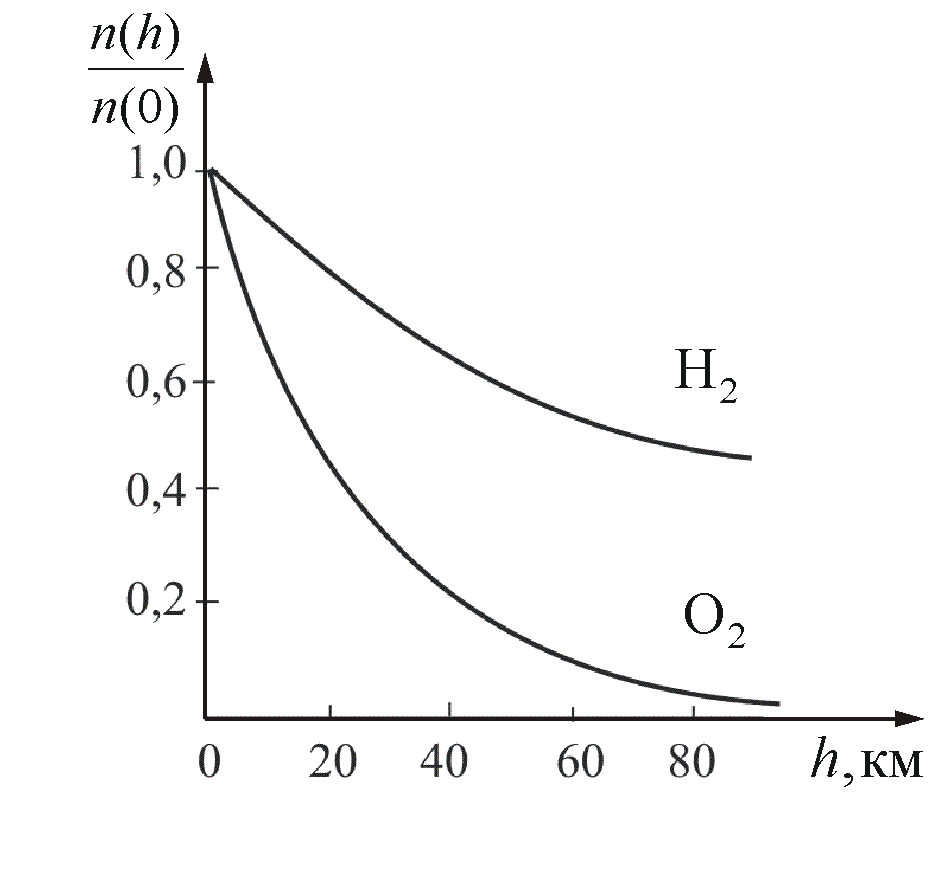
Рис.
2.11
Из
(2.5.3) можно получить, что отношение
концентраций молекул в точках с U1
и U2
равно:
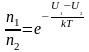
. (2.5.4)
Больцман
доказал, что соотношение (2.5.3) справедливо
не только в потенциальном поле сил
гравитации, но и в любом потенциальном
поле, для совокупности любых одинаковых
частиц, находящихся в состоянии
хаотического теплового движения.
В
п. 2.3 мы получили выражение для распределения
молекул по скоростям (распределение
Максвелла):
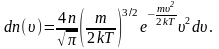
Из
этого выражения легко найти
распределение молекул газа по значениям
кинетической энергии
K.
Для этого перейдём от переменной υ
к переменной

:
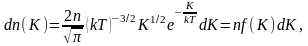
где
dn(K)
– число молекул, имеющих кинетическую
энергию поступательного движения,
заключённую в интервале от K
до
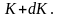
Отсюда получим функцию
распределения молекул по энергиям
теплового движения:
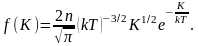
(2.6.1)
Средняя
кинетическая энергия
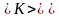
молекулы идеального газа:
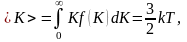
то
есть получаем результат, совпадающий
с прежним результатом, полученным в п.
1.3.
Итак,
закон Максвелла даёт распределение
частиц по значениям кинетической
энергии, а закон Больцмана – распределение
частиц по значениям потенциальной
энергии. Оба распределения можно
объединить в единый закон
Максвелла – Больцмана:
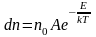
. (2.6.2)
Здесь
n0
– число молекул в единице объёма в той
точке, где
,
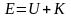
– полная энергия.
В
последнем выражении, потенциальная и
кинетическая энергии, а следовательно
и полная энергия Е,
могут принимать непрерывный ряд значений.
Если же энергия частицы может принимать
лишь дискретный ряд значений Е1,
Е2…,
(как это имеет место, например, для
внутренней энергии атома), то в этом
случае распределение Больцмана имеет
вид:
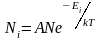
, (2.6.3)
где
Ni
– число частиц, находящихся в состоянии
с энергией Еi,
а А
– коэффициент пропорциональности,
который должен удовлетворять условию
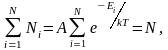
где
N
– полное число частиц в рассматриваемой
системе.
Тогда
окончательное выражение распределения
Максвелла – Больцмана для случая
дискретных значений энергий
будет иметь вид:
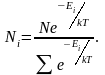
(2.6.4)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
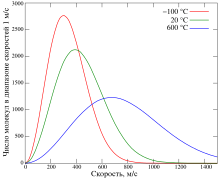
Функция плотности распределения для 106 молекул кислорода при −100, 20, 600 градусах Цельсия
Распределе́ние Ма́ксвелла — общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина: скорость частицы, проекция скорости, модуль скорости, энергия, импульс и т. д. — выступает в качестве непрерывной случайной величины. В ряде случаев распределение Максвелла может быть выражено как дискретное распределение по множеству уровней энергии.
Наиболее значимое распределение Максвелла записывается для модуля скорости частицы 
и
где 



Распределение Максвелла лежит в основе кинетической теории газов, объясняющей многие фундаментальные свойства газов, включая давление и диффузию. С его помощью вычисляются средние и наиболее вероятные скорости и энергии молекул газа. Оно также применимо для описания электронных процессов переноса и других явлений в физике и химии. Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Данное распределение является реализующимся с наивысшей вероятностью распределением изучаемого параметра.
Сфера применения распределения Максвелла[править | править код]
Требования к описываемой системе, примеры[править | править код]
Вопрос о применимости распределения Максвелла к конкретной системе равносилен вопросу о том, может ли эта система считаться идеальным газом с достаточной точностью. При этом система должна
- состоять из большого числа частиц и находиться в термодинамическом равновесии;
- являться изотропной;
- являться классической, то есть релятивистские и квантовые эффекты должны быть малы;
- быть столкновительно-доминируемой (взаимодействие частиц допускается лишь в случае, когда оно зависит только от относительного положения частиц, в частности, допускаются абсолютно упругие соударения).
Такой набор требований удовлетворяется в первую очередь в газах, например в воздухе, при обычных условиях. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. В первую очередь о нём обычно думают, как о распределении энергий молекул в газе, но оно может применяться к распределению скоростей и других параметров молекул. Чаще всего оно является непрерывным распределением по континууму изменения случайного параметра.
Во многих случаях, однако, условие доминирования упругих соударений над всеми другими процессами не выполняется даже приблизительно. Так, в физике ионосферы и космической плазмы, большое значение имеют процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы), в особенности для электронов. Использование распределения Максвелла в этом случае не только дало бы количественно неверные результаты, но и привело бы к качественно неправильной интерпретации соответствующих процессов.
Условия классического рассмотрения[править | править код]
В случаях, где квантовая дебройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, наблюдаются отклонения от распределения Максвелла из-за квантовых эффектов. Поэтому важен вопрос о границах применимости классического рассмотрения.
Соотношение неопределённостей (нередко упрощённо записываемое в форме 






где 

Учитывая, что 

(
— температура вырождения, а
— масса частицы).
При температурах ниже 
Распределение Максвелла по состояниям[править | править код]
Распределение Максвелла можно записать как дискретное распределение по множеству состояний молекулы, нумеруемых символом 
.
Через 







Разновидности непрерывного распределения Максвелла[править | править код]
Представленный в этом разделе вывод распределений Максвелла, естественный для современной учебно-методической литературы, отличается от вывода, предложенного самим Джеймсом Клерком Максвеллом и позже описанного с меньшим количеством предположений Людвигом Больцманом. Исторический вывод будет приведён в конце статьи.
Распределение по вектору импульса[править | править код]
В случае идеального газа из невзаимодействующих молекул вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы как:
,
где 
![{displaystyle mathbf {p} =[p_{x},p_{y},p_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/291bff54bd31331da418f06e8d7d69ce7de72e3a)
,
где 


Если уровни энергии расположены достаточно густо, факт дискретности становится непринципиальным и можно считать, что энергии распределены непрерывно. Тогда отношение 

.
Постоянная 



.
Таким образом, чтобы интеграл имел значение 1 необходимо, чтобы
.
Подставляя такое 


.
Распределение по вектору скорости[править | править код]
Учитывая, что плотность распределения по скоростям 
,
и используя 
,
что является распределением Максвелла по трём декартовым проекциям скоростей. Вероятность обнаружения частицы в бесконечно малом элементе 
![{displaystyle mathbf {v} =[v_{x},v_{y},v_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260191e6997e258925c22808a9e9d454e3af31c3)
.
Распределение по проекции скорости[править | править код]
Распределение Максвелла для вектора скорости ![{displaystyle [v_{x},v_{y},v_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61a890598143c1f2deb07aa3133a853eb24afcc7)
где распределение по одному направлению:
.
Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.
Распределение по модулю импульса[править | править код]
Интегрируя, мы можем найти распределение по абсолютной величине импульса:
Распределение по энергии[править | править код]
Наконец, используя соотношения 

Распределение по модулю скорости[править | править код]
Часто более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, 
,
он всегда неотрицателен. Так как все 


,
где 
.
Вид функции 

Характерные скорости молекул идеального газа[править | править код]
Уравнение для 
Наиболее вероятная скорость[править | править код]
Наиболее вероятная скорость, 



,
,
где 

Средняя скорость[править | править код]
.
Подставляя 
.
Среднеквадратичная скорость[править | править код]
.
Подставляя 
.
Исторический вывод распределения Максвелла[править | править код]
Получим теперь формулу распределения так, как это делал сам Максвелл[1][2].
Рассмотрим пространство скоростных точек (каждую скорость молекулы представляем как точку (скоростную точку) в системе координат 


Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента 


— фактически вероятность нахождения скоростной точки в объёме
.
Правая часть не зависит от 






Теперь нужно сделать принципиальный шаг — ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):
где 
Ввиду равноправия всех направлений:
Чтобы найти среднее значение 
Отсюда найдём 
Функция распределения плотности вероятности для 


Теперь рассмотрим распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скорости ![{displaystyle vsubset [v;v+dv]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65788bf47641e9a4bf64847343ef0f8e331c2317)



Таким образом, мы получили функцию плотности вероятности 
См. также[править | править код]
- Статистика Бозе — Эйнштейна
- Статистика Ферми — Дирака
- Статистика Максвелла — Больцмана
- Опыт Ламмерта
- Опыт Штерна
- Распределение Гиббса
- Распределение Бозе — Эйнштейна
- Распределение Ферми — Дирака
Примечания[править | править код]
- ↑ teach-in. Караваев В. А. – Молекулярная физика – Предельные случаи биномиального распределения (26 июля 2017). Дата обращения: 3 марта 2019.
- ↑ teach-in. Караваев В. А. – Молекулярная физика – Распределение Максвелла (26 июля 2017). Дата обращения: 3 марта 2019.
Ссылки[править | править код]
http://www.falstad.com/gas/
19 Июн
Наивероятнейшая, средняя и среднеквадратичная скорость молекул
Наиболее вероятная скорость молекул — это такая скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул.
Формула нахождения наиболее вероятной скорости молекул: ![]() ;
;
Средняя скорость молекулы — это сумма всех скоростей молекул деленная на их количество.
Формула нахождения средней скорости молекул: ![]() ;
;
Cреднеквадратичная скорость молекул — это среднее квадратическое значение модулей скоростей всех молекул.
Формула нахождения среднеквадратичной скорости молекул: ![]() ;
;
![]() — скорость молекул;
— скорость молекул;
![]() — универсальная газовая постоянная (8.31);
— универсальная газовая постоянная (8.31);
![]() — температура в кельвинах;
— температура в кельвинах;
![]() — молярная масса;
— молярная масса;
![]() — масса одной молекулы;
— масса одной молекулы;
![]() — постоянная Больцмана (
— постоянная Больцмана ( ![]() );
);
![]() — масса одной молекулы;
— масса одной молекулы;
Таким не хитрым образом мы разобрались с «наивероятнейшая, средняя и среднеквадратичная скорость молекул»!
Наиболее вероятная скорость молекул — это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул
![]()
Данная формула вытекает из распределения Максвелла. Наиболее вероятная скорость, как показал он, зависит от температуры газа и массы молекул
Что бы получить из первой формулы скорости молекулы вторую, надо сделать всего две замены, расписать универсальную газовую постоянную, как ![]() , и молярную массу
, и молярную массу ![]() , то у нас получится из этой формулы:
, то у нас получится из этой формулы:
![]()
Вот такая вот формула:
![]()
В Формуле мы использовали :
![]() — Наиболее вероятная скорость молекул
— Наиболее вероятная скорость молекул
![]() — Постоянная Больцмана
— Постоянная Больцмана
![]() — Температура
— Температура
![]() — Масса одной молекулы
— Масса одной молекулы
![]() — Универсальная газовая постоянная
— Универсальная газовая постоянная
![]() — Молярная масса
— Молярная масса
![]() — Количество вещества
— Количество вещества
![]() — Число Авогадро
— Число Авогадро
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Закон распределения молекул по скоростям
Закон распределения молекул по скоростям описывает распределение частиц макроскопической системы при условии, что эта система находится в состоянии термодинамического равновесия, распределение является стационарным и внешние силы на систему не действуют. Данное распределение выполняется как для газов, так и жидкостей, если в них можно использовать законы классической механики.
Определить, каким образом распределены молекулы по скоростям, — это значит ответить на вопрос: «сколько молекул имеет ту или иную скорость при заданной температуре в состоянии равновесия?» Для разъяснения вопроса введем понятие: «пространство скоростей» (рис.1). В таком пространстве на декартовых осях отложены не координаты, а проекции скоростей.
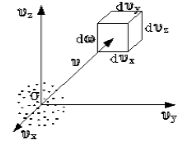
Рис. 1
В таком случае поставленный вопрос изменится на вопрос о том, как распределены молекулы в пространстве скоростей. Понятно, что молекулы распределены неравномерно.
Если в пространстве скоростей выделить параллелепипед объема $dw=dv_xdv_ydv_z$, тогда количество молекул, которые попадут в него $dN_v.$ Предположим, что N- количество молекул газа, $f(v)$- некоторая функция скорости. Тогда
Распределение Максвелла
Как было отмечено, газ находится в состоянии равновесия, все направления движения частиц равноправны, следовательно, распределение молекул в пространстве скоростей можно считать сферически симметричным (рис.2).
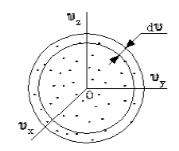
Рис. 2
Найдем число молекул в шаровом слое $dv$:
Разделим (2) на число частиц (N) и найдем вероятность$ (dW_v)$ того, что модуль скорости молекулы находится в пределах от $v до v+dv$:
«Закон распределения молекул по скоростям» 👇
где $Fleft(vright)$- функция распределения вероятности значения $v. $Эту функцию теоретически получил Д. Максвелл.
Таким образом, распределение молекул по скоростям (вернее их модулям) запишем как:
[dN_v=N4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2dv left(5right),]
при этом $v=sqrt{{v_x}^2+{v_y}^2+{v_z}^2}$, $m_0$- масса молекулы, k — постоянная Больцмана.
Можно записать распределение Максвелла по проекциям скоростей:
[dN=Nfleft(v_xright)fleft(v_yright)fleft(v_zright)dv_xdv_ydv_{z }left(6right),]
при этом
[fleft(v_iright)={left(frac{m_0}{2pi kT}right)}^{frac{1}{2}}expleft(-frac{m_0{v_i}^2}{2kT}right) left(i=x,y,zright)left(7right),]
где $v_x,v_y,v_{z }$ – проекции скорости молекулы на оси координат.
Еще один из вариантов написания распределения Максвелла по модулям скоростей представлен в виде:
[dN=Nfrac{4}{sqrt{pi }{v_{ver}}^3}{exp left(-{left[frac{v}{v_{ver}}right]}^2v^2right) }dvleft(8right),]
где $v_{ver}$ — вероятнейшая скорость молекулы.
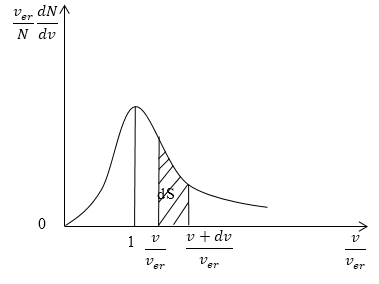
Рис. 3
На рисунке 3 изображена кривая закона распределения молекул по скоростям. Доля молекул газа, скорости которых лежат в интервале от $v до v+dv,$ пропорциональна заштрихованной площади dS под кривой.
Поскольку скорости всех молекул лежат в интервале от $0 до+infty $, то выполняется равенство:
[intnolimits^{infty }_0{fleft(vright)dv}=1 left(9right).]
Это так называемое условие нормировки функции распределения.
Таким образом, распределение Максвелла зависит от массы молекулы газа и его температуры. Давление и объем в распределение не входят.
Пример 1
Задание: Используя распределение Максвелла, найдите наиболее вероятную скорость молекул газа в равновесном состоянии газа при температуре T.
Решение:
За основу возьмем распределение молекул по модулям скоростей:
[dN_v=N4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2dv left(1.1right).]
Наиболее вероятной скорости соответствует максимум функции, то продифференцируем выражение (1.1) по скорости и приравняем к нулю, получим:
[frac{dN_v}{dv}=N4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}left[2v_{ver}expleft(-frac{m_0{v_{ver}}^2}{2kT}right)-{v_{ver}}^2frac{m_02v_{ver}}{2kT}expleft(-frac{m_0{v_{ver}}^2}{2kT}right)right]=0to ]
[2v_{ver}-{v_{ver}}^2frac{m_02v_{ver}}{2kT}=0to 1-{v_{ver}}^2frac{m_0}{2kT}=0to {v_{ver}}^2=frac{2kT}{m_0}]
[v_{ver}=sqrt{frac{2kT}{m_0}} (1.2)]
Ответ: Наиболее вероятная скорость молекул газа $v_{ver}=sqrt{frac{2kT}{m_0}}.$
Пример 2
Задание: Пусть $Т_1
Решение:
Из формулы для наиболее вероятной скорости молекул газа, полученной в предыдущем примере:
[v_{ver}=sqrt{frac{2kT}{m_0}} (2.1)]
очевидно, что с увеличением температуры скорость растет, то есть максимум кривой смещается в сторону больших скоростей. Площадь под кривой распределения величина постоянная, следовательно, кривые изобразим следующим образом (рис.4).
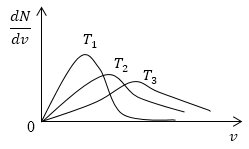
Рис. 4
Пример 3
Задание: На рис. 5 представлен график функции распределения молекул по проекциям скорости $v_x$. Сравнить числа молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$и от $v_{x1}$ до $v_{x2}$.
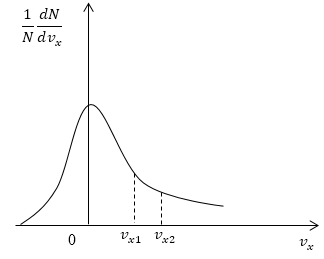
Рис. 5
Решение:
Как уже отмечалось в теоретической части, доля молекул газа, скорости которых лежат в интервале от $0 до v_{x1},$ пропорциональна площади $S_1$ фигуры, которая ограничена кривой распределения, вертикальной осью (0$ frac{1}{N}frac{dN}{dv_x})$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей проходящей через точку $v_{x1}$. Во втором случае доля молекул газа, скорости которых лежат в интервале от $v_{x1} до v_{x2},$ пропорциональна площади $S_2$ фигуры, которая ограничена кривой распределения, вертикальной прямой параллельной оси (0$ frac{1}{N}frac{dN}{dv_x}), проходящей через точку v_{x1}$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей, проходящей через точку $v_{x2}$. Очевидно, что $S_1>S_2. $ Следовательно, молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_{x1}$ до $v_{x2}$.
Ответ: Молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_{x1}$ до $v_{x2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме




![{displaystyle f_{p}=int _{theta =0}^{pi }int _{phi =0}^{2pi }~f_{mathbf {p} }p^{2}sin(theta ),dtheta ,dphi =4pi {sqrt {left({frac {1}{2pi mkT}}right)^{3}}}~p^{2}exp left[{frac {-p^{2}}{2mkT}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd762a9a868d0ed82d46e027da28f19a1206c847)
![{displaystyle f_{E}=f_{p}{frac {dp}{dE}}={frac {2pi }{sqrt {(pi kT)^{3}}}}{sqrt {E}}{}~exp left[{frac {-E}{kT}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77287b7265acc703d7d6a0c106faf9ec7a24aa20)















![{displaystyle qquad ={sqrt {frac {alpha }{2pi }}}left[-2,{frac {d}{dalpha }},int limits _{-infty }^{infty }e^{-{frac {alpha {v_{x}}^{2}}{2}}},dv_{x}right]=-2,{sqrt {frac {alpha }{2pi }}},{frac {delta }{delta alpha }}{sqrt {frac {2pi }{alpha }}}=-2{sqrt {alpha }}(-{frac {1}{2}}alpha ^{-{frac {3}{2}}})={frac {1}{alpha }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35149362a6c7de53078d7d2c77a9c3074223426b)





