Чтобы узнать наибольшую из этих десятичных дробей, нужно вначале найти дробь с наибольшей целой частью: у дробей 9,8 и 9,4 целые части – 9, у дробей 10,14 и 10,3 целые части – 10. Целая часть 10 больше целой части 9, значит дроби 9,8 и 9,4 можем больше не сравнивать – они в любом случае будут меньше двух оставшихся(10,14 и 10,3).
Теперь у нас осталось две дроби – 10,14 и 10,3. Целые части у них одинаковые, значит теперь нам нужно сравнивать дробные части. Начнём сравнение с десятых частей (10, 1 и 10, 3). У дроби 10,14 десятичная часть – 1, у дроби 10,3 десятичная часть – 3. Десятичная часть 1 в любом случае будет меньше десятичной части 3, значит можно даже не смотреть на сотую часть первой дроби(,14). Также есть способ полегче: 10,3 = 10,30(к концам десятичных дробей можно прибавлять сколько угодно нолей, они все равно не изменятся). Теперь у нас есть дроби 10,14 и 10,30. Как уже можно понять, сотая часть 14 меньше сотой части 30, а это значит, что десятичная дробь 10,14 меньше десятичной дроби 10,3.
Итак, можно составить тройное неравенство: 9,4 < 9,8 < 10,14 < 10,3. Из этого неравенства, да и из самих вычислений можно легко понять, что десятичная дробь 10,3 является наибольшей в данном списке.
Download Article
Download Article
Is your decimal homework giving you some trouble? Not to worry—with just a little practice, ordering decimals from least to greatest is an easy concept to get down. We’ve covered 2 simple ways to order any list of decimal problems so you can nail down your homework questions in no time. We’ve even included a quick place value review lesson to help you feel like a total decimal expert.
Things You Should Know
- Decimals are a combination of whole and fractional numbers. Whole numbers go to the left of the decimal point and fractional numbers go to the right.
- Transfer your decimals to a place value chart to compare their values and order them correctly.
- Draw your decimals on a number line to see which ones are the largest and smallest.
-

1
Compare the whole numbers in your list of decimals. Check out the number to the left of the decimal point—this is known as a whole number. If one decimal in the list has a higher whole number than the others, it’s automatically the greatest number. If a decimal in the list has a smaller whole number than the others on the list, it’s automatically the smallest number.
- Let’s say your homework asks you to order the decimals 12.45, 12.457, and 11.47. The whole number 11 is smaller than 12, so 11.47 is automatically going to be the smallest (least) number.
-

2
Set up a table for the remaining numbers. Create enough rows and columns for all of the digits and number spaces (including the decimal point). Going from left to right, label the columns as tens, ones, decimal, tenths, hundredths, and thousandths.[1]
- Let’s go back to our old example. Since we already figured out that 11.47 is the smallest decimal, we’re left with 12.45 and 12.457 to sort. Draw a table with 6 columns and 2 rows to fit both numbers.
- If you were asked to order a list of decimals like 0.3, 0.4, 0.01, 0.02, and 0.5, your chart would need to have 5 rows and 4 columns (including one column for the decimal point).
Advertisement
-

3
Transfer the decimals from your math problem into the table. Working from left to right, copy each decimal digit by digit into the table (don’t forget the decimal point column!). Fill in any empty portions of the table with 0 so all your decimals have the same number of digits.[2]
- Let’s take a look at the two decimals in our table. The number 12.45 only has 4 digits, so you’d add a 0 to the thousandths place (making it 12.450). This makes it a lot easier to compare with 12.457, right?
-

4
Compare the digits in the tenths column of the table. Take a peek at the tenths column—it’s immediately right of the decimal point column. Whichever decimal has a larger digit in the tenths column is automatically the larger number. If the numbers in the tenths column are identical, move on to the hundredths column instead.[3]
- In our chart, both 12.45 and 12.457 have a 4 in the tenths column. So, we’d move onto the hundredths column and make a new comparison.
- Let’s say you’re asked to compare 0.1 and 0.01. The decimal 0.1 has a 1 in the tenths column while 0.01 only has a 0. Therefore, 0.1 is the bigger number.
-

5
Compare the hundredths column (2 to the right of the decimal point). Is one number larger than the other, or are they both the same value? The number that has a larger digit in the hundredths column is the larger decimal overall. If both numbers are the same, move on to the thousandths column.[4]
- Let’s take another glance at our table—both 12.45 and 12.457 have a 5 in the hundredths place, so you’d shift over to the thousandths column for another comparison.
- Pretend you were asked to compare the decimals 4.04 and 4.02. The number 4.04 has a 4 in the hundredths place while 4.02 only has a 2, which makes 4.04 the bigger decimal.
Advertisement
-

6
Examine the digits in the thousandths column. Move on to the next column over, which is 3 spaces to the right of your decimal point column. Take a look at this column and see which digit is bigger—this decimal is the larger number.[5]
- Let’s take a final look at our table. The decimal 12.45 has a 0 in the thousandths place while 12.457 has a 7. With this in mind, 12.457 is a bigger decimal than 12.45.
-

7
Order the numbers from least to greatest. Jot down the smallest number first—in our example, that’s 11.47. Then, write out the next largest number, followed by the largest number. In our math problem, the final answer would be: 11.47, 12.45, and 12.457.
Advertisement
-

1
Write the decimals in a vertical list. Chances are, your assignment sheet listed the decimals horizontally, which makes them pretty tough to visualize. Grab a fresh sheet of paper (or use the margins of your homework sheet) to jot down the numbers in a vertical list instead.[6]
- If your assignment asks you to order the decimals 14.36, 13.458, and 14.369, you could write them like:
-
14.36
13.458
14.369
-
14.36
- If your assignment asks you to order the decimals 14.36, 13.458, and 14.369, you could write them like:
-

2
Compare the whole numbers before drawing out your number line. Examine the numbers to the left of the decimal point—these are “whole” numbers, and they’re the quickest way to compare and order your decimals right off the bat. If one whole number is bigger than the others, move it to the right side of the number line; if it’s smaller than the others, move it to the left.
- In our example, the number 13 is smaller than 14, so you’d automatically mark 13.458 as the smallest number.
-

3
Identify the first place value where the digits differ. Move from left to right and compare the digits in each place value. Examine each column until you find where the numbers don’t match up. Think of it like a game of spot the difference!
- Take 14.36 and 14.369, for instance—both decimals have a 3 in the tenths place and a 6 in the hundredths place. In the thousandths place, however, 14.36 has a 0 while 14.369 has a 9.
-

4
Set two different decimals as the lowest and highest points on your number line. Mark down the smallest decimal (in our case, 14.36) as the smallest number on the left side of your number line. Then, take the highest decimal (in our case, 14.369) and round it up to the nearest place value (making it 14.37). This rounded-up number acts as the highest decimal of your number line and goes on the far right side of the line.
-

5
Draw out your number line and divide it into tenths. Mark 10 notches that evenly separate your 2 decimals, which help you place your numbers more accurately on the number line. Then, label the notches with their corresponding decimal.[7]
In our example, the 10 notches represent 14.361, 14.362, 14.363, 14.364, 14.365, 14.366, 14.367, 14.368, 14.369, and 14.37. -

6
Plot the numbers you are comparing on the number line. Draw a big, obvious dot that represents each of the decimals from your list. [8]
In our example, you’d draw a dot on the first number of the number line to represent 14.36. Then, you’d draw a dot on the second-to-last number to represent 14.369. -

7
Compare the location of each number on the number line. On a number line, numbers get bigger as you go from left to right. So, the biggest number falls the furthest right on the number line, while the smallest number falls the furthest left.[9]
- In our example, 14.369 falls to the right of 14.36— that makes 14.369 the larger number.
-

8
Rewrite the numbers in order from least to greatest. Jot down the smallest number first and the largest number last. Then, list any other numbers between these 2 digits, keeping them in ascending (lowest to highest) order.[10]
- For our example problem, the final list would be: 13.458, 14.36, 14.369. You can also use the less than sign to show their relationship: 13.458 < 14.36 < 14,369.
Advertisement
-

1
A decimal point looks like a dot or period. It separates a number into its whole and fractional parts—the numbers to the left are whole numbers, while the numbers to the right are fractional. The numbers get bigger as you go to the left of the decimal point and get smaller as you go to the right.
- Let’s take a look at the decimal 12.38. For this number, the digits 1 and 2 are whole numbers, while 3 and 8 are fractional numbers.
- In Europe, people use a decimal comma instead of a decimal point.[11]
-

2
The place values for whole numbers go to the left of a decimal point. A whole number is a digit that has smaller parts attached—so, numbers like 13 and 270 are whole numbers, while 13.5 or 270.2 are not. From right to left, the place values of whole numbers are ones, tens, hundreds, thousands, ten-thousands, hundred-thousands, and millions.
- In the number 51 the 5 digit is in the tens place. It has a value of 5 tens. In the number 50,001, the digit 5 is in the ten-thousands place—this gives it a value 5 ten-thousands, or 50,000.
- The smallest place value for whole numbers is the ones place. Ten sets of 1 move the 1 into the tens place, while 10 sets of 10 move the number into the hundreds place. See the pattern? This pattern continues for the higher place values.
-

3
The place values for fractional numbers go to the right of the decimal point. Unlike whole numbers, fractional place values are ordered from left to right. Starting at the decimal point, the place values are tenths, hundredths, thousandths, ten-thousandths, hundred-thousandths, and millionths.[12]
- For example, in the number 1.5, the digit 5 is in the tenths place. It has the value of 5 tenths, or
. In the number 1.0005, however, the digit 5 has a value of 5 ten-thousandths, or
.
- The tenths place is the largest place value for fractional numbers. Ten hundredths make one-tenth, 10 thousandths make 1 hundredth, and 10 ten-thousandths create 1 thousandth.
- When comparing fractional numbers, it helps to convert decimals into fractions:
.
- To convert a fraction into a decimal, simply divide the numerator by the denominator.[13]
- For example, in the number 1.5, the digit 5 is in the tenths place. It has the value of 5 tenths, or
Advertisement
Add New Question
-
Question
Which is least: 0.52, 0.5, 0.54, 0.45

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor
Staff Answer
Of those numbers, 0.45 would be the smallest decimal and 0.54 would be the largest. From least to greatest, the order would be: 0.45, 0.5, 0.52, and 0.54.
-
Question
Which is least: 0.105, 0.501, 0.015, or 0.15?

All four numbers have nothing but a zero to the left of the decimal point, so the next thing to look at is the first place to the right of the decimal point. The numbers in that place are 1, 5, 0 and 1. So the number with the 0 in that place is the least: 0.015.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
About This Article
Thanks to all authors for creating a page that has been read 85,447 times.
Did this article help you?
Содержание
- Сравнение десятичных дробей
- Понятие десятичной дроби
- Свойства десятичных дробей
- Правило сравнения десятичных дробей
- Десятичные дроби
- Понятие десятичной дроби
- Свойства десятичных дробей
- Как записать десятичную дробь
- Как читать десятичную дробь
- Преобразование десятичных дробей
- Как перевести десятичную дробь в проценты
- Преобразование десятичных дробей
- Как перевести десятичную дробь в обыкновенную
- Действия с десятичными дробями
- Как разделить десятичную дробь на натуральное число
- Как разделить десятичную дробь на обыкновенную
- Как умножить десятичную дробь на обыкновенную
Сравнение десятичных дробей

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
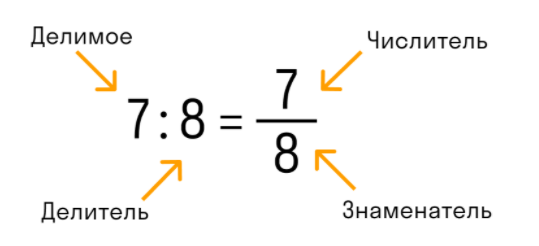
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,1
- 2,53
- 9,932
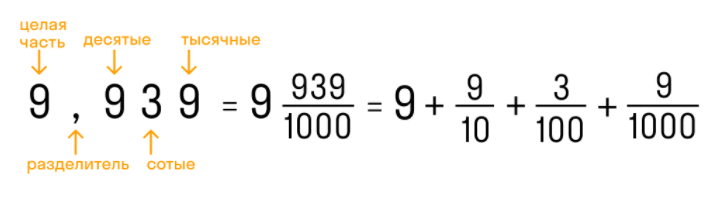
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Основные свойства
- Дробь не имеет значения, при условии, если делитель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
- Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
- Убедиться, что у обеих десятичных дробей одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописать (убрать) нужное количество нулей в одной из десятичных дробей.
- Сравнить десятичные дроби слева направо. Целую часть с целой, десятые с десятыми, сотые с сотыми и т. д.
- Когда одна из частей десятичной дроби окажется больше, чем другая, эту дробь можно назвать большей.
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
- Допишем в первой десятичной дроби нужное количество нулей, чтобы уравнять количество знаков справа от запятой: 15,700 и 15,719.
- Сравним десятичные дроби слева направо.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Сотые с сотыми: 0
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним 3,656 и 3,48.
- Уравниваем количество знаков справа после запятой: 3,656 и 3,480.
- Отбросим запятые: 3656 и 3480.
- Сравним полученные числа: 3656 > 3480.
Источник
Десятичные дроби

О чем эта статья:
5 класс, 6 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Пример 2. Перевести 37/1000 в десятичную дробь.
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Пример 1. Разделить 4,8 на 2.
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
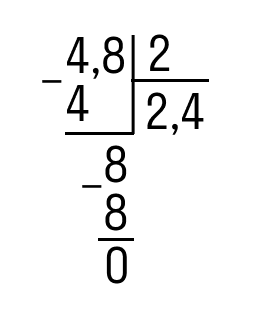
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
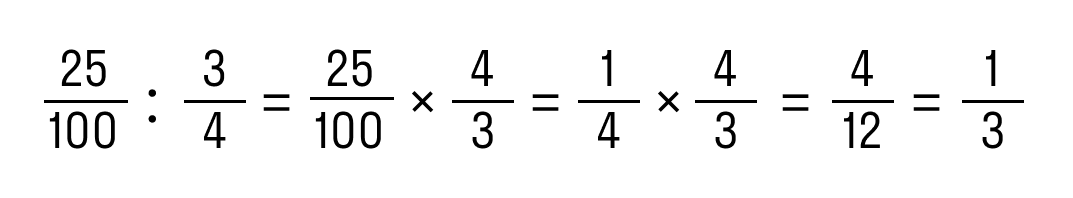
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
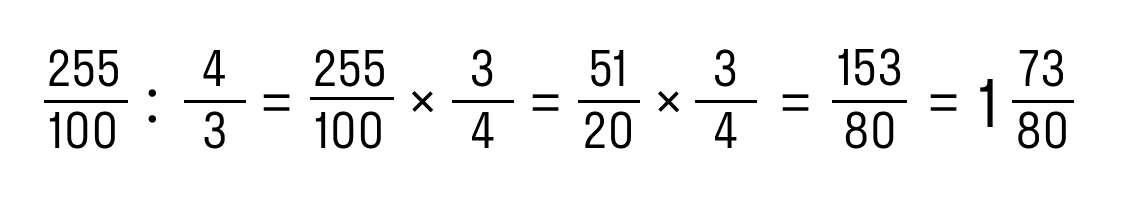
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Источник
Как найти наибольшую и наименьшую десятичную дробь?
На этой странице сайта, в категории Математика размещен ответ на вопрос
Как найти наибольшую и наименьшую десятичную дробь?. По уровню сложности вопрос рассчитан на учащихся
5 – 9 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Сравнение десятичных дробей
Поддержать сайт![]()
Запомните!
![]()
Удобно сравнивать десятичные дроби с одинаковым количеством цифр (знаков) справа от запятой.
Чтобы сравнить десятичные дроби нужно:
- Убедиться, что у обеих десятичных дробей
одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописываем (убираем) нужное количество
нулей в одной из десятичных дробей. - Сравниваем десятичные дроби слева направо.
Целую часть с целой, десятые с десятыми, сотые с сотыми и т.д. - Когда одна из частей десятичной дроби (целая часть, десятые, сотые и т.д.) окажется больше чем в другой дроби, эта дробь и больше.
Как сравнивать десятичные дроби
Пример. Сравним десятичные дроби:
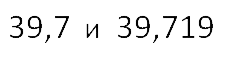
- Сперва дописываем в первой десятичной дроби нужное количество нулей,
чтобы уравнять количество знаков справа от запятой.39,700 и 39,719
- Начинаем сравнивать десятичные дроби слева направо.
Целую часть с целой частью:
39 = 39
Целые части
равны. Переходим к десятым.Десятые с десятыми:
7 = 7
Десятые также равны. Переходим к сотым.
Сотые с сотыми:
0 < 1
Так как сотые второй десятичной дроби оказались больше,
значит и сама дробь больше.39,700 < 39,719
39,7 < 39,719
Другой способ сравнения десятичных дробей
Так же как и в предыдущем методе сравнения
необходимо вначале уравнять количество знаков
справа от запятой в обеих десятичных дробях.
Затем, отбросив запятую в обеих дробях, сравнить
полученные результаты.
Пример:
3,656 и 3,48
Уравняем количество знаков справа у десятичных дробей.
3,656 и 3,480
Теперь отбросим запятые и сравним полученные числа.
3 656 > 3 480
3,656 > 3,48
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
4 мая 2023 в 17:15
Василина Перикова

Профиль
Благодарили: 0
Сообщений: 1

Василина Перикова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
