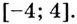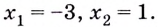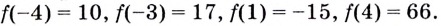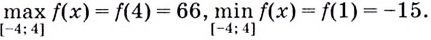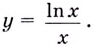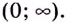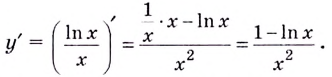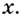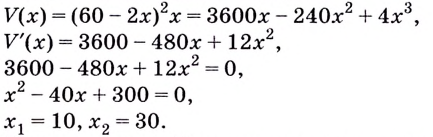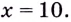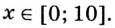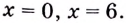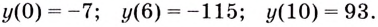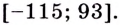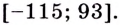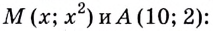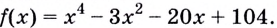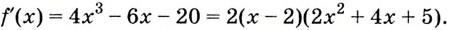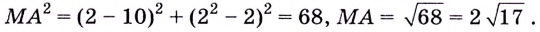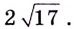Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно нами строится выражение этих значений в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x), чтобы вам не нужно было искать это самостоятельно онлайн.
Основные определения
Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.
Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Минимальное значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или то, что больше всего, значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы можем определить наибольшее или найти наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с интервалом, не имеющим конца. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения (мало и много). В этих случаях определить или найти наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
Как найти наибольшее и наименьшее значение функции на отрезке?
В этом пункте мы приведем последовательность действий, которую нужно выполнить, чтобы найти наибольшее значение функции на некотором отрезке или как найти наименьшее значение функции.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] – max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] – max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный (квадратичный) трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определяться с наименьшим значением функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Как найти наибольшее целое значение х, входящее в область определения функции??
Помогите, пожалуйста, хотя бы как примерно решается?
- область
- значение
- функция
- определение
Во многих сферах жизни можно столкнуться с тем, что потребуется что-то решить с помощью цифр, например, в экономике и бухгалтерии узнать минимум и максимум каких-то показателей можно только с помощью оптимизации заданных параметров. А это и есть не что иное, как нахождение наибольшего и наименьшего значений на заданном отрезке функции. Сейчас рассмотрим, как найти наибольшее значение функции.
Находим наибольшее значение: инструкция
- Выяснить, на каком отрезке функции требуется вычислить значение, обозначить его точками. Этот промежуток может быть открытым (когда функция равна отрезку), закрытым (когда функция находится на отрезке) и бесконечным (когда функция не заканчивается).
- Найти производную функцию.
- Найти на отрезке функции точки, где производная равна нулю, и все критические точки. Затем вычислить значения функции в данных точках, решить уравнение. Найти среди полученных значений наибольшее.
- Выявить значения функции на конечных точках, определить большее из них
- Сравнить данные с наибольшим значением, выбрать из них большее. Именно оно и будет являться наибольшим значением функции.
Как найти наибольшее целое значение функции? Требуется вычислить, является функция чётной или нечётной, а затем решить конкретный пример. Если число получилось с дробью, не учитывайте ее, результатом наибольшего целого значения функции будет только целое число.
Исследование такого объекта математического анализа как функция имеет большое значение
и в других областях науки. Например, в экономическом анализе постоянно требуется оценить поведение функции
прибыли, а именно определить ее наибольшее значение
и разработать стратегию его достижения.
Инструкция
Исследование поведения любой всегда следует начинать с поиска области определения. Обычно по условию конкретной задачи требуется определить наибольшее значение
функции
либо на всей этой области, либо на конкретном ее интервале с открытыми или закрытыми границами.
Исходя из , наибольшим является значение
функции
y(x0), при котором для любой точки области определения выполняется неравенство y(x0) ≥ y(x) (х ≠ x0). Графически эта точка будет наивысшей, если расположить значения аргумента по оси абсцисс, а саму функцию по оси ординат.
Чтобы определить наибольшее значение
функции
, следуйте алгоритму из трех этапов. Учтите, что вы должны уметь работать с односторонними и , а также вычислять производную. Итак, пусть задана некоторая функция y(x) и требуется найти ее наибольшее значение
на некотором интервале с граничными значениями А и В.
Выясните, входит ли этот интервал в область определения функции
. Для этого необходимо ее найти, рассмотрев все возможные ограничения: присутствие в выражении дроби, квадратного корня и т.д. Область определения – это множество значений аргумента, при которых функция имеет смысл. Определите, является ли данный интервал его подмножеством. Если да, то переходите к следующему этапу.
Найдите производную функции
и решите полученное уравнение, приравняв производную к нулю. Таким образом, вы получите значения так называемых стационарных точек. Оцените, принадлежит ли хоть одна из них интервалу А, В.
Рассмотрите на третьем этапе эти точки, подставьте их значения в функцию. В зависимости от типа интервала произведите следующие дополнительные действия. При наличии отрезка вида [А, В] граничные точки входят в интервал, об этом говорят скобки. Вычислите значения функции
при х = А и х = В. Если открытый интервал (А, В), граничные значения являются выколотыми, т.е. не входят в него. Решите односторонние пределы для х→А и х→В. Комбинированный интервал вида [А, В) или (А, В], одна из границ которого принадлежит ему, другая – нет. Найдите односторонний предел при х, стремящемся к выколотому значению, а другое подставьте в функцию. Бесконечный двусторонний интервал (-∞, +∞) или односторонние бесконечные промежутки вида: , (-∞, B). Для действительных пределов А и В действуйте согласно уже описанным принципам, а для бесконечных ищите пределы для х→-∞ и х→+∞ соответственно.
Задача на этом этапе
Методические
рекомендации для изучения темы «
Множество значений функции. Наибольшее
и наименьшее значения функции».
В
самой математике главные средства
достигнуть
истины – индукция и аналогия.
Дано:-
функция. Обозначим

область определения функции.
Множеством
(областью) значений функции называется
множество всех тех значений, которые
может принимать функция

это означает проекция графика функции
на ось

Если существует точка
такая, что для любого
из множества
имеет место неравенство

то говорят, что функция
на
множестве
принимает в точке
свое наименьшее значение
Если существует точка
такая,
что для любого
из множества
имеет место неравенство

то говорят, что функция
на
множестве
принимает в точке
свое наибольшее значение
.
Функция
называется ограниченной снизу
на
множестве
, если существует такое число

Геометрически это означает, что график
функции находится не ниже прямой

Функция
называется
ограниченной сверху
на множестве
,
если существует такое число

что для любого
из множества
справедливо неравенство

Геометрически это означает, что график
функции находится не выше прямой
Функция
называется ограниченной
на множестве
,
если она ограничена на этом множестве
снизу и сверху. Ограниченность функции
означает, что ее график находится внутри
некоторой горизонтальной полосы.
Неравенство
Коши о среднем арифметическом и среднем
геометрическом




Пример:
Наибольшее и
наименьшее значения функции на промежутке
(отрезок, интервал,
луч)
Свойства непрерывных на отрезке
функций.
1.Если
функция непрерывна на отрезке, то она
достигает на нем и своего наибольшего
и своего наименьшего значений.
2.Наибольшего
и наименьшего значений непрерывная
функция может достигать как на концах
отрезка, так и внутри него
3. Если
наибольшее (или наименьшее) значение
достигается внутри отрезка, то только
в стационарной или критической точке.
Алгоритм отыскания наибольшего и
наименьшего значений
непрерывной
функции
на
отрезке
1. Найти
производную

2. Найти
стационарные и критические точки,
лежащие внутри отрезка
.
3.Найти
значения функции
в
отобранных стационарных и критических
точках и на концах отрезка, т. е.


4.Среди
найденных значений выбрать наименьшее
(это будет

и наибольшее(это будет
Свойства непрерывных монотонных
на отрезке
функций:
Непрерывная возрастающая на отрезке
функция
достигает своего наибольшего значения
при

наименьшего – при

Непрерывная убывающая на отрезке
функция
достигает своего наибольшего значения
при
,
наименьшего – при
.
Если значение функции
неотрицательно на некотором промежутке,
то эта функция и функция

где n – натуральное число,
принимает наибольшее (наименьшее)
значение в одной и той же точке.
Отыскание наибольшего и наименьшего
значений непрерывной функции на интервале

на луче
(задачи на оптимизацию).
Если непрерывная функция имеет на
интервале или луче единственную точку
экстремума и этот экстремум максимум
или минимум, то в этой точке достигается
наибольшее или наименьшее значение
функции (
или
)
Применение свойства монотонности
функций.
1.Сложная
функция, составленная из двух возрастающих
функций, является возрастающей.
2.Если
функция
возрастает, а функция

то функция

убывающая.
3. Сумма
двух возрастающих (убывающих) функций,
функция возрастающая(убывающая).
4. Если
в уравнении

часть – возрастающая (или убывающая)
функция, то уравнение имеет не более
одного корня.
5.Если
функция
–
возрастающая (убывающая), а функция
–
убывающая (возрастающая), то уравнение
имеет не более одного решения.
6.
Уравнение
имеет хотя бы один корень в том и только
том случаи, когда
принадлежит
множеству значений


Применение свойства ограниченности
функций.
1. Если
левая часть уравнения (неравенства)
(
либо равна некоторого числа
(
а правая часть больше либо равна этому
числу (),
то имеет место система
решение которой и является решением
самого уравнения (неравенства).
Задания для
самоконтроля
Применение:
3. Найти все значения
,
при которых уравнение
имеет решение.
Домашнее задание
1.Найдите наибольшее значение функции:

если

2. Найдите наименьшее значение функции:

3. Найдите наибольшее целое значение
функции:

теми
, что соответствуют в наибольшей
. Идеал- …
Методические рекомендации для практических занятий Тема: Введение. Краткая история латинского языка. Алфавит. Фонетика
Методические рекомендации
Большой, верхний, малый, передний, наименьший
, наибольший
. 3) Переведите: A. Mm. palati et … значение
а) Streptocidum б) Barbamylum в) Corticotropinum г) Cholosasum д) Agovirin Факультет: МПД Модуль: латинского языка Методические
рекомендации
для
…
… . Наибольшие
и наименьшие
значения
функции
Наибольшее
и наименьшее
значения
2 14. Первообразная функции
Первообразная 2 15. Понятие о дифференциальных уравнениях Примеры использования производной для
…
Методические рекомендации для самостоятельной подготовки курсантов и слушателей по дисциплине «Физическая подготовка» Краснодар
Методические рекомендации
… Наибольшая
быстрота произвольного одиночного движения и наименьшая
… Имеется множество
рекомендаций
по… значение
имеет рациональное сочетание средств общего и локального действия. 4. Методические
рекомендации
для
самостоятельного изучения
… функций
. Они тем
…
Методические рекомендации по использованию учебных пособий «Алгебра и математический анализ, 10», «Алгебра и математический анализ, 11» (авторы: Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд) при узучении предмета на профильном уровне
Методические рекомендации
… , множество
значений
функции
, нули функции
, интервалы знакопостоянства функции
, четность, нечетность, периодичность. Монотонность функции
, интервалы монотонности, экстремумы функции
. Наибольшее
и наименьшее
значения
функции
…
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования… Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X
, который является или всей областью определения функции или частью области определения. Сам интервал X
может быть отрезком , открытым интервалом , бесконечным промежутком .
В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x)
.
Навигация по странице.
Наибольшее и наименьшее значение функции – определения, иллюстрации.
Кратко остановимся на основных определениях.
Наибольшим значением функции
, что для любого
справедливо неравенство .
Наименьшим значением функции
y=f(x)
на промежутке X
называют такое значение , что для любого
справедливо неравенство .
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .
Стационарные точки
– это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X
в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:”Всегда ли можно определить наибольшее (наименьшее) значение функции”? Нет, не всегда. Иногда границы промежутка X
совпадают с границами области определения функции или интервал X
бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На отрезке
На первом рисунке функция принимает наибольшее (max y
) и наименьшее (min y
) значения в стационарных точках, находящихся внутри отрезка [-6;6]
.
Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на
. В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее – в точке с абсциссой, соответствующей правой границе интервала.
На рисунке №3 граничные точки отрезка [-3;2]
являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
На четвертом рисунке функция принимает наибольшее (max y
) и наименьшее (min y
) значения в стационарных точках, находящихся внутри открытого интервала (-6;6)
.
На интервале
, о наибольшем значении никаких выводов сделать нельзя.
На бесконечности
В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y
) в стационарной точке с абсциссой x=1
, а наименьшее значение (min y
) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3
.
На интервале функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2
справа значения функции стремятся к минус бесконечности (прямая x=2
является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3
. Графическая иллюстрация этого примера приведена на рисунке №8.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке
.
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
- Находим область определения функции и проверяем, содержится ли в ней весь отрезок
. - Находим все точки, в которых не существует первая производная и которые содержатся в отрезке
(обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту. - Определяем все стационарные точки, попадающие в отрезок
. Для этого, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту. - Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a
и x=b
. - Из полученных значений функции выбираем наибольшее и наименьшее – они и будут искомыми наибольшим и наименьшим значениями функции соответственно.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Пример.
Найти наибольшее и наименьшее значение функции
- на отрезке
; - на отрезке [-4;-1]
.
Решение.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.
Находим производную функции по :
Очевидно, производная функции существует во всех точках отрезков
и [-4;-1]
.
Стационарные точки определим из уравнения . Единственным действительным корнем является x=2
. Эта стационарная точка попадает в первый отрезок
.
Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1
, x=2
и x=4
:
Следовательно, наибольшее значение функции достигается при x=1
, а наименьшее значение 
.
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1]
(так как он не содержит ни одной стационарной точки):
В этой статье я расскажу о том, как применять умение находить к исследованию функции: к нахождению ее наибольшего или наименьшего значения. А затем мы решим несколько задач из Задания В15 из Открытого банка заданий для .
Как обычно, сначала вспомним теорию.
В начале любого исследования функции находим ее
Чтобы найти наибольшее или наименьшее значение функции , нужно исследовать, на каких промежутках функция возрастает, и на каких убывает.
Для этого надо найти производную функции и исследовать ее промежутки знакопостоянства, то есть промежутки, на которых производная сохраняет знак.
Промежутки, на которых производная функции положительна, являются промежутками возрастания функции.
Промежутки, на которых производная функции отрицательна, являются промежутками убывания функции.
1
. Решим задание В15 (№ 245184)
Для его решения будем следовать такому алгоритму:
а) Найдем область определения функции
б) Найдем производную функции .
в) Приравняем ее к нулю.
г) Найдем промежутки знакопостоянства функции.
д) Найдем точку, в которой функция принимает наибольшее значение.
е) Найдем значение функции в этой точке.
Подробное решение этого задания я рассказываю в ВИДЕОУРОКЕ:
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр “Час ЕГЭ”, попробуйте скачать
Firefox
2
. Решим задание В15 (№282862)
Найдите наибольшее значение функции на отрезке
Очевидно, что наибольшее значение на отрезке функция принимает в точке максимума, при х=2. Найдем значение функции в этой точке:
Ответ: 5
3
. Решим задание В15 (№245180):
Найдите наибольшее значение функции
1. title=”ln5>0″>, , т.к. title=”5>1″>, поэтому это число не влияет на знак неравенства.
2. Т.к по область определения исходной функции title=”4-2x-x^2>0″>, следовательно знаменатель дроби всегда больще нуля и дробь меняет знак только в нуле числителя.
3. Числитель равен нулю при . Проверим, принадлежит ли ОДЗ функции. Для этого проверим, выполняется ли условие title=”4-2x-x^2>0″> при .
Title=”4-2(-1)-{(-1)}^2>0″>,
значит, точка принадлежит ОДЗ функции
Исследуем знак производной справа и слева от точки :
Мы видим, что наибольшее значение функция принимает в точке . Теперь найдем значение функции при :
Замечание 1. Заметим, что в этой задаче мы не находили область определения функции: мы только зафиксировали ограничения и проверили, принадлежит ли точка, в которой производная равна нулю области определения функции. В данной задаче этого оказалось достаточно. Однако, так бывает не всегда. Это зависит от задачи.
Замечание 2. При исследовании поведения сложной функции можно пользоваться таким правилом:
- если внешняя функция сложной функции возрастающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наибольшее значение. Это следует из определения возрастающей функции: функция возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
- если внешняя функция сложной функции убывающая, то функция принимает наибольшее значение в той же точке, в которой внутренняя функция принимает наименьшее значение. Это следует из определения убывающей функции: функция убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции
В нашем примере внешняя функция – возрастает на всей области определения. Под знаком логарифма стоит выражение – квадратный трехчлен, который при отрицательном старшем коэффициенте принимает наибольшее значение в точке . Далее подставляем это значение х в уравнение функции
и находим ее наибольшее значение.
Преподаватель который помогает студентам и школьникам в учёбе.
Наибольшее и наименьшее значения функции с примерами решения
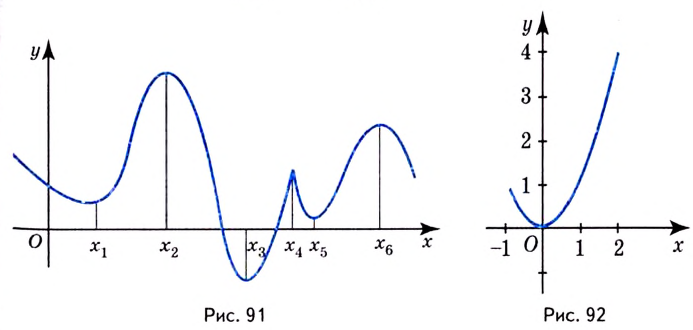
От максимумов и минимумов функции следует отличать её наибольшее и наименьшее значения на промежутке. Функция может иметь несколько максимумов (минимумов) на некотором промежутке (рис. 91), но не более одного наибольшего (наименьшего) значения. Функция может не иметь максимума (минимума) на промежутке, но иметь наибольшее (наименьшее) значение.
Например функция, график которой изображён на рисунке 91, наибольшее значение имеет в точке
Наибольшее и наименьшее значения функции тесно связаны с её областью значений. Если область значений непрерывной функции — промежуток 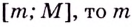
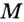
Поскольку непрерывная функция наибольшее и наименьшее значения может иметь только в точках экстремума или на концах отрезка, то для нахождения этих значений пользуются таким правилом.
Чтобы найти наибольшее и наименьшее значения непрерывной функции 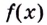
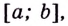
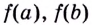
Записывают так:
Пример №1
Найдите наибольшее и наименьшее значения функции 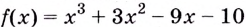
Решение:
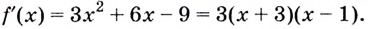
Из этих четырёх значений функции наименьшим является -15, а наибольшим — 66.
Ответ,
Пример №2
Найдите наибольшее и наименьшее значения функции
Решение:
Областью определения функции является промежуток
Если 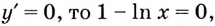
Если 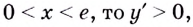
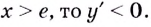

Поскольку на промежутке 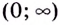
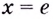
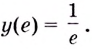
Ответ, 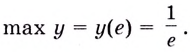
К нахождению наибольшего или наименьшего значений функции сводится решение многих прикладных задач.
Пример №3
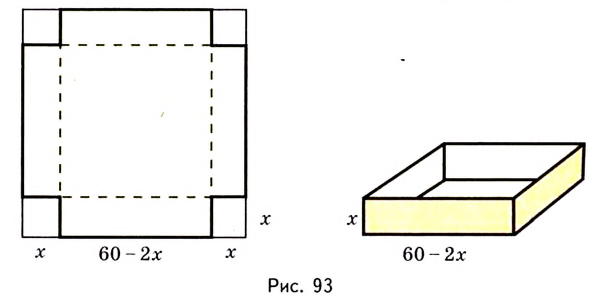
Есть квадратный лист жести со стороной 60 см. Найдите размеры квадратов, которые надо вырезать в углах данного листа, чтобы из полученной заготовки сделать коробку наибольшего объёма {рис. 93).
Решение:
Чтобы получить коробку (в форме прямоугольного параллелепипеда), надо вырезать равные квадраты в углах листа. Пусть 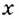
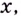
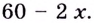
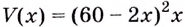
Надо исследовать математическую модель задачи: при каком значении 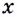
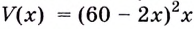
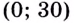
Значение 
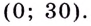
Поскольку при 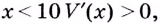
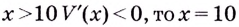
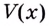
Ответ. Надо вырезать квадраты, стороны которых равны 10 см.
- Заказать решение задач по высшей математике
Пример №4
Найдите область значений функции 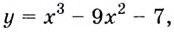
Решение:
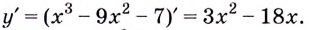
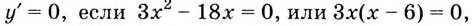
Найдём значение функции на концах промежутка 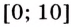
Заданная функция непрерывна, её наибольшее значение 93, а наименьшее -115, значит, область её значений — отрезок
Ответ.
Пример №5
Найдите кратчайшее расстояние от точки 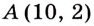
Решение:
Пусть ближайшая к 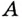
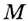
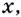
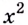
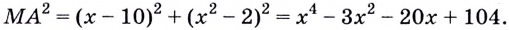
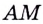
Уравнение 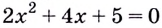
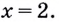
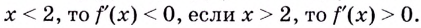
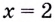
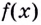
Наименьшее значение квадрата расстояния
Ответ.
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Рациональная дробь
- Функция в математике
- Правило Лопиталя
- Вычисления в Mathematica с примерами