Как найти наибольшее количество членов последовательности

Пусть a(n) = 2 ^ n + 5 ^ n. Какое наибольшее количество подряд идущих членов последовательности a(n) могут быть простыми числами? задан 29 Янв ’17 13:02 Doom 75●1●8 0% принятых При нечётном n число a(n) делится на 7. Если оно больше 7, то оно не простое. Если случая n=0 включать, то есть три простых числа подряд: 2, 7, 29. Если считать n>=1, то первое пропадает, и остаются только два. (29 Янв ’17 13:40) falcao а почему при нечётном n число a(n) делится на 7? (29 Янв ’17 17:57) Doom Если $%n -$% нечетное, то $$a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+…+b^{n-1})$$ @goldish09: это можно доказать при помощи тождества, которое указано в комментарии выше (оно часто используется в задачах), а можно при помощи свойств сравнений: 5=-2(mod 7), возводим в нечётную степень, знак “минус” остаётся, получается 5^n=-2^n(mod 7). Есть также стандартный тип задач доказательства факта делимости методом математической индукции. (29 Янв ’17 18:27) falcao

Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.

Присоединиться к ExamMe

Была ли эта статья полезной?

По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.

Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной. 

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность? 

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N. 

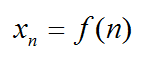
Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

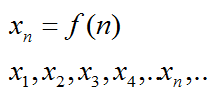
Какие бывают последовательности

Различают:

• постоянную, или монотонную последовательность: 1, 1, 1, 1, 1… 
• возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
• убывающую последовательность, в которой каждый следующий элемент меньше предыдущего

Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.

Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Посмотрим на числа:

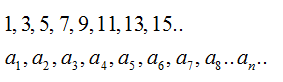
Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.

Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:

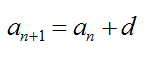
Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.

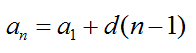
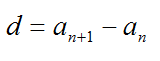
Сумма первых n членов прогрессии вычисляется по формуле:

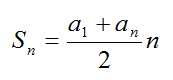
Также африфметическая прогрессия обладает характреристическим свойством:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:

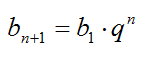
Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:

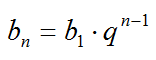
Сумма первых n членов прогрессии:

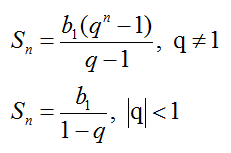
Характеристическое свойство геометрической прогрессии:

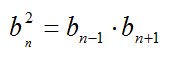
Способы задания последовательностей

Последовательность можно задать несколькими способами:

1. Аналитически или, проще говоря, формулой.
2. Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
3. Описательно, простым перечислением всех элементов последовательности.

Предел последовательности

Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.

Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.

Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.

Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел. 

Что нужно помнить, вычисляя пределы последовательностей

Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.

1. Последовательность может иметь только один предел.
2. Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
3. Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
4. Предел постоянной последовательности равен ее постоянному.
5. Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
6. Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
7. Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
8. Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей. 
9. Постоянный множитель можно выносить за знак предела.
10. Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором. 

Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.

Числовые последовательности в ОГЭ и ЕГЭ

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

ВВЕДЕНИЕ.

Задачи, связанные с последовательностями, в курсе алгебры рассматриваются фрагментарно. Немного больше времени уделяется частным видам последовательностей, а именно арифметической и геометрической прогрессиям. Однако для решения предлагаемых на Едином Государственном экзамене задач этих знаний недостаточно. В 2016 году задачу № 11 профильного уровня, согласно статистико-аналитическому отчёту о результатах ЕГЭ выполнили 32,2 % участников.

Цель исследования: изучить понятие числовой последовательности, виды числовых последовательностей и научиться решать задачи, связанные с числовыми последовательностями.

Для достижения цели поставлены следующие задачи:

1. изучение литературы по данной теме в печатном и электронном виде;

2. изучение видов последовательностей;

3. отработка полученных знаний в ходе решения задач;

4. ознакомление обучающихся 9 – 11 классов с решением задач из Единого Государственного экзамена, связанных с числовыми последовательностями.

Объект исследования: числовые последовательности

Предмет исследования: способы решения задач из ОГЭ и ЕГЭ, связанных с числовые последовательностями

Методы исследования:

изучение литературы;

2. выполнение практических заданий;

3. сравнение и обобщение полученных результатов.

Практическая значимость: использование материала при подготовке к Единому Государственному Экзамену.

Новизна проведённой исследовательской работы: изучение числовых последовательностей как темы, не входящей в школьную программу 7 класса. Задачи, связанные с числовыми последовательностями, также встречаются среди заданий под номером 19 Единого государственного экзамена, которые оцениваются максимальным количеством баллов.

Гипотеза:задачи, связанные с числовыми последовательностями, можно решить алгебраически, с помощью уравнений и преобразований выражений.

1. ОСНОВНАЯ ЧАСТЬ

1.1. Теоретическая часть

1.1.1.Определение числовой последовательности

Понятие числовой последовательности возникло задолго до создания учения о функциях. В нашей жизни многие события происходят последовательно: например, смена дня и ночи, смена дней недели, смена возраста живого существа с течением времени. Последовательно увеличивает свою скорость автомобиль, последовательно пронумерованы дома на улицах.

В математике мы впервые сталкиваемся с последовательностями в начальной школе, когда от нас требуется уловить закономерность и продолжить ряд чисел.

Определение. Если каждому натуральному числу 1, 2, 3….n,… поставлено в соответствие действительноечисло то множество действительных чисел , , ,….. , … называется числовой последовательностью.

Числа , , ,….. , … называются элементами (или членами) последовательности, а символ – общим членом последовательности.

Последовательность задают формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Элементами последовательности не обязательно должны быть различные числа. Так, если  a_n = 1, то последовательность имеет вид 1, 1, …, 1, …

Общий член     определяет знакочередующуюся последовательность вида 1, –1, 1, –1, …

Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член    последовательности и известно, что   , то есть  ) и так далее до нужного члена.

Самым известным примером рекуррентно заданной последовательности является знаменитая последовательность чисел Фибоначчи 1, 1, 2, 3 ,5 8, 13, 21, 34…., в которой каждое последующее число является суммой двух предыдущих чисел. Данную последовательность можно задать следующим рекуррентным соотношением:

= +, где = 1

Числовые последовательности бывают конечными и бесконечными. К бесконечным последовательностям можно отнести ряд натуральных чисел, множество нечётных чисел, к конечным последовательностям можно отнести, например, последовательность чётных двузначных чисел.

1.1.2.Виды числовых последовательностей

1) Возрастающая последовательность – последовательность, каждый член которой больше предыдущего > , где n N

Примером возрастающей последовательности служит ряд натуральных чисел 1,2,3,4,…

2) Убывающая последовательность – последовательность, каждый член которой каждый меньше предыдущего < , где nN

Примером убывающей последовательности служит гармонический ряд – ряд чисел, обратных членам натурального ряда 1, , , ,….

Существуют следующие способы задания последовательности

– Словесный – правило составления последовательности выражается словесным описанием, например: последовательность простых двузначных чисел, меньших 100

11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,53,59,61,67,71,73,79,83,89,97;

– Графический

Числа последовательности можно отмечать на координатной плоскости, причем по оси абсцисс откладывается номер члена последовательности, а по оси ординат соответствующий этому номеру член последовательности

Рис.1

На левом рисунке изображена возрастающая последовательность,на правом убывающая последовательность

– Аналитический.

указывается формула n-го члена последовательности а_п = 5n+17 а_п = или рекуррентное соотношение.

1.1.3. Арифметическая и геометрическая прогрессии

В курсе алгебры 9 класса изучаются такие виды последовательностей, как арифметическая и геометрическая прогрессии.

Определение. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

(а_п) – арифметическая прогрессия, если для любого п N выполняется условие

 а_п +1 = а_п + d, где d – некоторое число. Число d называется «разностью арифметической прогрессии», так как из определения следует, что а_{п + 1} – а_п = d. Если

d >0 , то прогрессия является возрастающей, в случае же, если d < 0,то прогрессия является убывающей.

Определение. Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число. Это число обозначается q и называется знаменателем геометрической прогрессии, поскольку q =b_п +1 : b_п.

В задании № 11 Основного Государственного экзамена и первой части Единого Государственного экзамена предложены задания, связанные с арифметической и геометрической прогрессиями. В задании № 19 ЕГЭ встречаются как арифметические и геометрические прогрессии, так и числовые последовательности.

Таблица 1. Основные формулы для арифметической и геометрической прогрессии

	Арифметическая прогрессия	Геометрическая прогрессия
Определение
Формула n-го члена	an=a1+(n-1)d,	bn=b1*qn-1,
Сумма n первых членов
Характеристическое свойство

1.2. ПРАКТИЧЕСКАЯ ЧАСТЬ

Решение задач, связанных с числовыми последовательностями.

Задача 1.(Открытый банк заданий ОГЭ, 1 часть, задача 11).

В первом ряду кинозала 20 мест, а в каждом следующем на 2 больше,чем в предыдущем. Сколько мест в 11 ряду?

Решение: в соответствии с условием последовательность мест в ряду 20, 22, 24,…- арифметическая прогрессия. Используем формулу для n-го члена арифметической прогрессии, получим 20 +2(11 – 1) =40.

Ответ:40 мест.

Задача 2(Открытый банк заданий ЕГЭ, задача 11)

Олегу надо решить 315 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Олег решил 11 задач. Определите, сколько задач решил Олег в последний день, если со всеми задачами он справился за 9 дней. 

Решение: в данной задаче мы имеем дело с арифметической прогрессией, поскольку решает на одно и то же количество задач больше по сравнению с предыдущим днем.

Известно, =11 n = 9 =315. Согласно формуле суммы первых членов арифметической прогрессии = · n решим уравнение 315 = (11 + )·9 : 2,откуда =70 – 11 = 59. Ответ: 59

Задача 3 (ЕГЭ, № 19)

Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 10 раз больше, либо в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 3024. 
а) Может ли последовательность состоять из двух членов? 
б) Может ли последовательность состоять из трёх членов? 
в) Какое наибольшее количество членов может быть в последовательности? 

Решение:  а) Предположим, что последовательность состоит из двух членов, a и 10 a  (в произвольном порядке).Тогда получим  a+10a=3024

Поскольку корень уравнения  11a=3024   не является целым числом, как это требуется в условии, делаем вывод:  последовательность не может состоять из двух членов.  

б) Составим уравнение: a + 10a + a =3024,откудаa=252

10a + a+ 10a = 3024 , откуда a=144

(Пример). Последовательность может состоять из трёх членов. Например: 252, 2520, 252 или 1440,144,1440

  в) Ближайшим к 3024 число, делящееся на 11 нацело, является 3014.

3014=11 174. Таким образом, в последовательности 174 пары вида (10; 1) и число 10.

Допустим, что в последовательности более чем 549 членов.   

Разобьём первые 550 членов последовательности на 275 пар соседних членов: первый и второй, третий и четвертый, пятый и шестой и т.д. 

Сумма двух членов в каждой паре делится на 11 и поэтому не меньше 11. 

Значит, сумма всех членов последовательности не меньше, чем  275*11 = 3025 > 3024 ,следовательно,  мы пришли к противоречию, а это значит, что наибольшее количество членов данной последовательности равно 549. 

 Ответ:  а) нет;   б) да;  в) 549.

Задача 4 (№19, тренировочный вариант ЕГЭ №52)

Можно ли из последовательности  1, , , , ….. выделить арифметическую прогрессию, содержащую 5 членов? Решение: Исходная последовательность (гармонический ряд) является убывающей. Значит, будем искать убывающую арифметическую прогрессию. Пусть это будет последовательность вида ; ; ; . Разность данной арифметической прогрессии равна Нам осталось подобрать число n таким образом, чтоб все числители сократились, а это возможно в том случае, когда это число будет наименьшим общим кратным числителей. В нашем случае это будет число 60. Значит, выделенная из гармонического ряда последовательность будет такой: ; ; ; Ответ: можно. Задача 5 (тренировочный вариант ЕГЭ 192, 2017г.). Дана последовательность ( ): = (n-1)n(n+1)+133 Найти два соседних члена этой последовательности, разность которых равна 29700 =(n -1)n(n+1)+133 = n(n+1)(n+2)+133 Согласно условию вычтем и после приведения подобных слагаемых получим 3n(n+1)=29700 Тогда получим квадратное уравнение относительно n n(n+1)=9900=99▪100, откуда n=99.(второй корень уравнения не удовлетворяет условиям задачи, поскольку номер члена последовательности является натуральным числом) Ответ : это 99 и 100 члены последовательности.

В приложении приведены задачи из открытого банка ОГЭ и ЕГЭ, связанные с числовыми последовательностями, первая из которых (№ 19 профильного ЕГЭ) – с решением.

ЗАКЛЮЧЕНИЕ

1.изучив литературу по теме, я ознакомилась с понятием числовой последовательности, с их видами, а также с их применением на практике.

2. рассмотрены основы ранее неизвестного мне раздела математики имеющего большую практическую пользу для решения задач из ЕГЭ и ОГЭ.

3. в ходе оформления работы я научилась работать с математическими формулами в редакторе Word.

Задания из ОГЭ и ЕГЭ 1 части, связанные с арифметической и геометрической прогрессиями, решаются достаточно быстро в соответствии с приведёнными формулами n-го члена последовательности, суммы первых n членов последовательности. Задания же № 19 требуют более деликатного подхода, однако алгебраический метод помогает справиться и с ними. Таким образом, выдвинутая гипотеза подтвердилась.

Можно сделать вывод, что изучение последовательностей полезно для каждого школьника, интересующегося математикой. Поскольку в будущем я собираюсь поступать в высшее учебное заведение и сдать Единый Государственный Экзамен на высокий балл, изучение данного материала было для меня очень полезным.

В будущем я планирую продолжить изучение последовательностей и их свойств.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1 М. М. Медынский. Полный курс элементарной математики в задачах и упражнениях. Книга 2: Числовые последовательности и прогрессии. М.: Эдитус, 2015.

2. Алгебра , 9 класс : учебник для общеобразовательных организаций (Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова) ; под редакцией С. А. Теляковского. М., «Просвещение»,2015.

3.Яковлев И.В. «Задача С6 на ЕГЭ по математике» (электронная версия книги на сайте http://mathus.ru/)

4. Ященко И.В. «ЕГЭ-2018. Типовые экзаменационные варианты». (М., «Экзамен», 2017)

5.Ященко И.В. « 3000 задач с ответами по математике. Все задания части 1 .- «Экзамен», МЦНМО,2014.

5. Сайт для подготовки к ЕГЭ по математике http://alexlarin.net/

6.Открытый банк заданий ОГЭ и ЕГЭ по математике

ПРИЛОЖЕНИЕ.

Задачи из открытого банка ОГЭ и ЕГЭ, связанные с числовыми последовательностями

Задача 6 (Единый Государственный Экзамен, № 19, 4 балла)

Дана последовательность натуральных чисел, причем каждый следующий ее член отличается от предыдущего либо на 10, либо в 6 раз. Сумма всех членов последовательности равна 257.

а) Какое наименьшее (минимальное) число членов может быть в данной последовательности?
б) Какое наибольшее (максимальное) количество членов может быть в этой последовательности?

Решение: а) Предположим, что последовательность состоит из двух чисел, одно из которых больше другого на 10. Если первое число нечетно, то второе число тоже нечетно. А сумма двух нечетных чисел есть число четное. Если же первое число четно, то второе число, которое больше первого на 10, тоже четно. А сумма двух четных чисел есть четное число. Получается, что нечетного числа 257 в сумме у нас не получится. 

Предположим теперь, что второе число в 6 раз больше первого. То есть первое число есть x тогда второе число есть 6x. Их сумма равна 7x  и равна 257. Однако 257 на 7 без остатка не делится. Значит, этот вариант также не удовлетворяет нашему условию. Исходя из вышеизложенного, делаем следующий вывод: двух чисел в этой последовательности быть не может. 

Рассмотрим следующий вариант. Предположим, что последовательность состоит из 3 чисел. Пусть каждое из них на 10 больше предыдущего. Тогда первое равно х, второе равно х+10, а третье х+20. Тогда их сумма равна 3х+30 и равна 257. То есть

 3х+30=257 ,откуда следует 3х=227. Но корень данного уравнения не является натуральным числом.

Рассмотрим такой вариант: пусть второе число в 6 раз больше первого, а третье на 10 больше второго. Тогда получим уравнение

х+6х+6х+10=257 , откуда 13х+10=257 , 13х=247, то есть х =19. 

Значит, минимальное количество чисел в нашей последовательности равно трем. Меньше уже не получается. К примеру, это может быть вот такая последовательность:  19,114,124. 

Б) Теперь нам нужно, чтобы в последовательности было как можно больше членов. Поэтому пара вида  (1; 6) должна встречалась в ней как можно чаще.

Сумма чисел этой пары равна 7. Если разделить 257 на 7, то получится 36 и 5 в остатке. Но эту 5 не получится представить, используя члены нашей последовательности. Поэтому возьмём пар вида (1; 6) в последовательности 35 штук, а оставшееся число 12 будетпредставлено в ней парой  (1;11). Теперь мы получили последовательность 1;11;1;6;1;6;1;.. (пар типа  (1;6) всего 35 штук) с максимально возможным числом членов. В этой последовательности   числа. То есть максимально возможное число членов последовательности равно 72.

Ответ: а)3 б) 72

ОГЭ по математике , № 11

1.Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −8,1, a₁ = 1,4. Най­ди­те a₆.

2. В ариф­ме­ти­че­ской про­грес­сии     известно, что   . Най­ди­те тре­тий член этой прогрессии.

3. Фи­гу­ра со­став­ля­ет­ся из квад­ра­тов так, как по­ка­за­но на ри­сун­ке: в каж­дой сле­ду­ю­щей стро­ке на 8 квад­ра­тов боль­ше, чем в преды­ду­щей. Сколь­ко квад­ра­тов в 16-й стро­ке?

4.В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 48, а сумма вто­ро­го и тре­тье­го чле­нов равна 144. Най­ди­те пер­вые три члена этой прогрессии.

5. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), для ко­то­рой a₅ = 71, a₁₁ = 149. Най­ди­те раз­ность прогрессии.

6. Какое наи­мень­шее число по­сле­до­ва­тель­ных на­ту­раль­ных чисел, на­чи­ная с 1, нужно сло­жить, чтобы по­лу­чив­ша­я­ся сумма была боль­ше 465?

7. Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: 5; −10; 20; … Най­ди­те сумму пер­вых пяти её членов.

8. В пер­вом ряду ки­но­за­ла 35 мест, а в каж­дом сле­ду­ю­щем на один больше, чем в предыдущем. Сколь­ко мест в вось­мом ряду?

ЕГЭ по математике, профильный уровень , № 11

1.Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.

2.Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено за девятый день, если вся работа была выполнена за 14 дней.

3.Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?

4.Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.

ЕГЭ по математике ,профильный уровень , № 19

1. Даны n различных натуральных чисел, составляющих арифметическую прогрессию 

а) Может ли сумма всех данных чисел быть равной 14?

б) Каково наибольшее значение n, если сумма всех данных чисел меньше 900?

в) Найдите все возможные значения n, если сумма всех данных чисел равна 123.

2.Возрастающие арифметические прогрессии   и   состоят из натуральных чисел.

а) Существуют ли такие прогрессии, для которых   и   — различные натуральные числа?

б) Существуют ли такие прогрессии, для которых   и   — различные натуральные числа?

в) Какое наименьшее значение может принимать дробь  , если известно, что   и   — различные натуральные числа.

3.Возрастающие арифметические прогрессии   и   состоят из натуральных числе.

а) Приведите пример таких прогрессий, для которых 

б) Существуют ли такие прогрессии, для которых  ?

в) Какое наибольшее значение может принимать произведение   если 

4.Последовательность   состоит из неотрицательных однозначных чисел. Пусть  — среднее арифметическое всех членов этой последовательности, кроме k-го. Известно, что 

а) Приведите пример такой последовательности, для которой 

б) Существует ли такая последовательность, для которой 

в) Найдите наименьшее возможное значение 

5. Все члены конечной последовательности являются натуральными числами. 
Каждый член этой последовательности, начиная со второго, либо в 5 раз больше, либо в 5 раз меньше предыдущего. 

Сумма всех членов последовательности равна 2013.
а). может ли эта последовательность состоять из трёх членов? 
б). может ли эта последовательность состоять из четырёх членов? 
в). может ли эта последовательность состоять из пяти членов?
г). какое наибольшее число членов может быть в этой последовательности?

Просмотров работы: 1295