|
2 |
4 |
5 |
|||||||||||||||
|
4 |
2 |
2 |
3 |
4 |
|||||||||||||
|
1 |
1 |
||||||||||||||||
|
5 |
|||||||||||||||||
|
1 |
3 |
5 |
3 |
||||||||||||||
|
Рис. 2.25 |
Рис. 2.26 |
Рис. 2.27 |
|||||||||||||||
|
1 |
|||||||||||||||||
|
1 |
3 |
2 |
4 |
5 |
4 |
2 |
3 |
||||||||||
|
Рис. 2.28 |
5 |
Рис. 2.29 |
|||||||||||||||
|
2 |
3 |
5


Рис. 2.30
Определение. Граф называется связным, если любые две несовпадающие вершины в нем соединены маршрутом.
Очевидно, для связности графа необходимо и достаточно, чтобы в нем для какой-либо фиксированной вершины и и каждой другой вершины v существовал (u, v)-путь.
Пусть задан граф G. Введем на множестве его вершин V(G) бинарное
|
отношение. Будем говорить, что vi |
~ v j , если существует путь из vi в |
|
v j . При этом будет считать, что vi |
~ vi , их соединяет путь нулевой |
длины. Введенное отношение является отношением эквивалентности. Следовательно, оно определяет разбиение множества вершин графа на

классы эквивалентности: V (G) =V1 V2 … Vk . Обозначим через Gi подграф графа G , порожденный множеством вершин Vi . При этом
V (G) =V (G1) V (G2 ) … V (Gk ) ,
E(G) = E(G1) E(G2 ) … E(Gk ) , G = G1 G2 … Gk .
Графы G1 , G2 , …, Gk называются компонентами связности графа G .
Теорема. Для любого графа либо он сам, либо его дополнение является связным.
Доказательство. Пусть G – несвязный граф. А – одна из его компонент связности. Положим В = VG VA. Возьмем произвольную вершину и графа А. Тогда для любой вершины v из из множества вершин В в
дополнительном графе G есть ребро uv. Следовательно, произвольная вершина из В соединена с и. Если и1 – отличная от и вершина графа А, то для любой вершины v из множества вершин В в дополнительном
графе G также найдется ребро u1v. Таким образом найдется путь из вершины и в вершину u1 (через вершину v). Следовательно, из вершины
и в графе G достижима любая вершина, а значит, граф G является связным. Утверждение доказано.
Утверждение. Пусть G – связный граф, e EG . Тогда:
1)если ребро е принадлежит какому-либо циклу графа G, то граф G e связен;
2)если ребро е не входит ни в какой цикл, то граф G e имеет
ровно две компоненты связности.
Доказательство. 1). Пусть ребро e = uv принадлежит циклу Z
графа G. Заменив в каждой (x, y) -цепи, содержащей е, ребро е на цепь
Z e , получим путь, соединяющий вершины х и у, не содержащий ребра е. Следовательно, для любых двух несовпадающих вершин в графе G найдется (x, y) -путь, не включающий ребро е. Но тогда и граф
G e связен.
2) Пусть ребро е не входит ни в какой цикл графа G. Тогда, очевидно, вершины и и v входят в разные компоненты связности графа G e . Обозначим их через Gu и Gv соответственно. Для произвольной
вершины x ≠ u в G найдется (x, u) -путь. Если ребро е в этот путь не входит, то x Gu . В противном случае x Gv . Утверждение доказано.
Обозначим через Р количество ребер графа, В – количество вершин, K – количество компонент связности.
Определение. Число ν(G) = P − B + K называется цикломатическим
числом графа.
Теорема. Для любого графа G выполняется неравенствоν(G) ≥ 0.
Доказательство проведем индукцией по числу вершин п. При п = 1 получаем граф, состоящий из одной вершины, соответственно без ребер: P = 0, B =1, K =1, ν(G) = 0 . Неравенствоν(G) ≥ 0 выполнено.
Предположим, что при любом количестве вершин, меньшем п, утверждение верно и докажем его для графа с п вершинами. Обозначим их v1, v2 , …, vn . Обозначим через G‘ подграф графа G , порожденный
вершинами v1, v2 , …, vn−1 . Тогда ν(G‘ ) ≥ 0 по предположению индукции. Пусть P, B, K – количество ребер, вершин, компонент связности графа G ; P‘, B‘, K ‘ – графа G‘ ; k – количество ребер графа G , не являющихся ребрами графа G‘ , т.е. степень вершины vn . Тогда P = P‘+k, B = B‘+1 . Возможны два случая.
а) k = 0 , следовательно, вершина vn – изолированная. При этом
P = P‘, B = B‘+1, K = K ‘+1 . Следовательно, P − B + K = P‘−B‘+K ‘ ,
ν(G‘ ) = ν(G) ≥ 0 .
б) k > 0 . Если при этом все k ребер, инцидентных вершине vn , соединяют ее с различными компонентами связности графа G‘ , то K = K ‘+1 − k , в остальных случаях K > K ‘+1 − k . Таким образом, K ≥ K ‘+1 − k . В итоге получаем
P − B + K ≥ P‘+k − B‘−1+ K ‘+1− k = P‘−B‘+K‘ , ν(G) ≥ν(G‘ ) ≥ 0 .
Теорема доказана.
Следствие. Для связного графа выполняется неравенство B ≤ P +1 .
Деревья
Определение. Связный граф без циклов называется деревом. Любой
граф без циклов называется
ациклическим (или лесом). Таким образом, компонентами связности леса являются деревья. На рис. 2.31
Рис.2.31
изображен лес, каждая компонента связности его является деревом. Теорема. Связный граф является деревом тогда и только тогда, когда число его вершин на единицу больше числа его ребер, т.е. B = P +1 . Доказательство. Необходимость. Заметим, что если граф G – дерево, то он имеет хотя бы одну вершину степени 1 (висячую вершину).
Действительно, предположим, что все вершины имеют степень, не меньшую 2. Возьмем произвольную вершину, обозначим ее v1 . Из нее
выходит по крайней мере два ребра. Найдется вершина v2 такая, что e1 = (v1, v2 ) EG . Так как степень вершиныv2 не меньше 2, то найдется вершина v3 , отличная от v1 , такая, что e2 = (v2 , v3) EG , и так далее.
Так как число вершин конечно, то в этой последовательности вершин найдутся совпадающие, и мы получим цикл, что противоречит определению дерева. Следовательно, висячая вершина существует. Далее доказательство проведем индукцией по числу вершин п. При п = 1 число ребер равно 0 и утверждение верно. Предположим оно верно при любом количестве вершин, меньшем п. Рассмотрим граф G с п вершинами. Среди них есть висячая. Рассмотрим подграф G‘, порожденный множеством остальных вершин. Для него по индукционному предположению P‘ = B‘−1 . Кроме того,
P = P‘+1, B = B‘+1 . Следовательно, P = B −1 . Необходимость доказана.
Достаточность. Пусть для связного графа G выполняется условие P = B −1 . Для того, чтобы доказать, что G является деревом, нужно показать лишь отсутствие циклов. Предположим, что циклы есть, тогда удаление одного ребра е из цикла не нарушает связности, граф
G‘ = G e
тоже связный. Следовательно, для него выполняется неравенство P‘ ≥ B‘−1. Но P‘ = P −1, B‘ = B , следовательно, P ≥ B и значит,
P > B −1 , что противоречит условию. Следовательно, G является связным графом без циклов, т.е. деревом. Теорема доказана.
Свойства деревьев.
1.Любые две вершины дерева можно соединить путем. Если это простой путь, то он единственный.
2. Если для некоторого дерева G V(G) ≥ 2, то оно имеет не менее двух висячих вершин.

Кодировка дерева
Существуют способы задания деревьев, более экономичные, чем с помощью матриц смежности и инцидентности, которые в компьютере
|
занимают много памяти. |
1 |
|
|
Первый способ кодирования. Пусть Т – дерево, |
||
|
n =| E(T ) |=|V (T ) | −1. Поставим в соответствие |
||
|
дереву Т с п ребрами слово, состоящее из 0 и 1 |
||
|
длиной 2п следующим образом. Выберем |
||
|
произвольно вершину и начнем обход дерева по |
||
|
произвольному ребру так, чтобы ребра все время |
||
|
оставались справа, поворачивая в висячих |
||
|
вершинах. Если ребро встретилось в первый раз, |
||
|
записываем 0, во второй – 1. Код дерева, |
Рис. 2.32 |
|
|
представленного на рис.2.32 – (010010101101) |
||
|
(обход начат с вершины 1). |
Заметим, что дереву с одним ребром сопоставляется код (01). Если
~
деревьям Т1 и Т2 (рис.2.33, а) сопоставлены коды α~ и β соответственно, то дереву С (рис. 2.33, б) сопоставляется код (0 α~ 1), а
C
|
T1 |
T2 |
C c |
D |
T1 |
T2 |
T2 |
T1 |
|
|
E |
||||||||
|
a |
b |
c |
c=a=b |
c=a=b |
||||
|
а) |
б) |
в) |
||||||
|
Рис. 2.33 |
||||||||
|
~ ~ |
~ ~ |
|||||||
|
деревьям D и E (рис. 2.33, в) – коды αβ |
и βα . |
Не всякая последовательность из п единиц и п нулей служит кодом дерева. Необходимым и достаточным условием для этого служит следующее: в любом начальном отрезке последовательности количество нулей не меньше количества единиц. Если это условие выполняется, дерево может быть построено по коду.
Построение дерева по коду
Для того чтобы восстановить дерево по коду, нужно разбить последовательность на пары из нулей и единиц, соответствующие одному и тому же дереву. Первая попавшаяся в коде единица образует пару с предшествующим нулем. Каждая следующая образует пару с ближайшим слева неиспользованным нулем. Пометим пары снизу дугами, которые соответствуют ребрам графа, занумеровав их. Например, если дан код (010010010111010011), поступим так (см. рис. 2.34а). Дерево, соответствующее этому коду, изображено на рис. 2.34б.
|
4 3 |
1 |
2 |
||||||||
|
(010010010111010011) |
1 |
|||||||||
|
5 |
4 |
1 2 |
8 |
6 |
5 |
|||||
|
3 |
7 |
|||||||||
|
9 |
8 |
6 |
||||||||
|
9 |
5 |
|||||||||
|
7 |
|
а) |
б) |
|
Рис. 2.34 |
Рис. 2.35 |
Второй способ кодирования
Перенумеруем вершины дерева произвольным образом (рис.2.35). Найдем висячую вершину с наименьшим номером. Запишем номер единственной смежной с ней вершины и удалим висячую вершину вместе с ребром. Для получившегося дерева снова найдем висячую вершину с наименьшим номером и т. д., пока не останется одно ребро. Длина кода при этом равна |E| – 1 = |V| – 2.
Пример. Построить код дерева, изображенного на рис. 2.35. Висячая вершина с наименьшим номером – 1, смежная с ней – 2.
Удаляем вершину 1 вместе с ребром и записываем в код 2. В оставшемся дереве висячая вершина с наименьшим номером – 5, смежная с ней – 4. Удаляем вершину 5 вместе с ребром и записываем в код 4. В оставшемся дереве висячая вершина с наименьшим номером – 6, смежная с ней – 4. Удаляем вершину 6 вместе с ребром и снова записываем в код 4. В оставшемся дереве висячая вершина с наименьшим номером – 7, смежная с ней – 4. Удаляем вершину 7 вместе с ребром и снова записываем в код 4. В оставшемся дереве
висячая вершина с наименьшим номером – 4, смежная с ней – 2. Удаляем вершину 4 вместе с ребром и записываем в код 2. В оставшемся дереве висячая вершина с наименьшим номером – 2, смежная с ней – 3. Удаляем вершину 2 вместе с ребром и записываем в код 3. Осталось одно ребро. Получили код дерева [244423].
Восстановление дерева по коду рассмотрим на примере кода
[2557389]. Вместо первого числа в коде пишем наименьшее, не встречающееся в коде: 1557389. Вместо второго числа в новой последовательности пишем наименьшее, не встречающееся в ней: 1257389 и т.д. Получаем последовательность 1245637. Расположив ее под кодом, получим список ребер: (2,1), (5, 2), (5, 4), (7, 5), (3,6), (8,3),
|
2 |
2 |
(9, 7). Строим |
сначала |
|||||||
|
5 |
7 |
7 |
граф по |
этому |
списку |
|||||
|
5 |
||||||||||
|
1 |
9 |
1 |
9 |
ребер |
(рис.2.36). |
В |
||||
|
4 |
4 |
последовательности |
||||||||
|
3 |
3 |
1245637 |
отсутствуют |
|||||||
|
6 |
8 |
|||||||||
|
6 |
8 |
числа 8 и 9. Соединяем |
||||||||
|
вершины 8 и 9 ребром и |
||||||||||
|
Рис. 2.36 |
Рис.2.37 |
|||||||||
|
получаем граф (рис. |
||||||||||
|
2.37). |
Можно показать, что между помеченными деревьями (т.е. деревьями с пронумерованными вершинами) и последовательностями
ε1, ε2 , …, εn−2 , где 1 ≤ εi ≤ n, существует взаимно однозначное
соответствие. Поэтому количество помеченных деревьев равно nn−2
(формула Кэли).
Эйлеровы пути. Эйлеровы циклы
Определение. В графе G путь из а в b называется эйлеровым путем, если он содержит все ребра графа, причем каждое по одному разу. Эйлеров цикл – путь из а в а, который содержит все ребра графа, каждое по одному разу. Гамильтонов путь – путь, обходящий все вершины графа по одному разу. Гамильтонов цикл – путь из а в а, обходящий все вершины графа, кроме а, по одному разу.
Теорема. Пусть дан связный граф. В нем существует эйлеров путь тогда и только тогда, когда две вершины графа имеют нечетную степень, а все остальные – четную. Эйлеров цикл существует тогда и только тогда, когда все вершины графа имеют четную степень.

Рис. 2.39
Доказательство. Доказательство обеих частей теоремы проведем одновременно.
Необходимость. Пусть в графе G существует эйлеров
путь из а в b. Тогда d(a) –
|
нечетное число. Действительно, |
||
|
из а выходит по крайней мере |
||
|
одно ребро, обозначим его е1 . |
||
|
Если путь возвращается в а по |
а) |
б) |
|
ребру е2, то он должен и |
Рис. 2.38 |
выходить из него по ребру е3, и так далее (рис. 2.38,а). Степень вершины а – нечетная. Аналогично для
вершины b. Если путь из а в а – эйлеров цикл, то первое и последнее ребро цикла инцидентны а. Если вершина а встречается внутри цикла, то вместе с ребром (vi , a) он содержит и ребро (a, vk ) . Степень
вершины а – четная. Остальные вершины являются внутренними и для эйлерова пути, и для эйлерова цикла, поэтому, если путь или цикл содержит ребро (vi , v j ) , то он содержит и ребро (v j , vk ) , если v j ≠ b .
Так как все ребра в пути и цикле встречаются ровно один раз, то степень вершины v j – четная (рис.2.38,б).
Достаточность. Доказательство проведем индукцией по количеству ребер. Пусть d(a) , d(b) – нечетные. Наименьшее
количество ребер равно 1. При этом граф G состоит из двух вершин а и b и соединяющего их ребра, который и будет
являться эйлеровым путем. Если степени всех вершин четные, то наименьшее количество ребер равно трем (при отсутствии кратных
ребер). Если степени всех вершин четные, возможен только граф, изображенный на рис.
2.39. Эйлеров цикл существует. Предположим, для графа с количеством ребер, меньшим п, утверждение истинно. Докажем утверждение
для графа с п ребрами. Удалим произвольное ребро, выходящее из а. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. Если удалено ребро (а, b), то степени всех вершин нового графа четны, граф связный, и по индукционному предположению, в нем существует эйлеров цикл. Его можно начинать из произвольной
вершины. Для нового графа рассмотрим эйлеров цикл из b в b. Присоединив к нему ребро (а, b) (если нужно, вместе с вершиной а), получим эйлеров путь из b в а в исходном графе.
Если произвольное ребро, выходящее из а, – это ребро (а, с),
c ≠ b , то, удалив его, получим, что степень вершины а стала четной, а степень вершины с – нечетной, число ребер уменьшилось на 1. Если удаление ребра нарушает связность, то удалим вместе с ребром и вершину а. В новом графе G’ также две вершины с четными степенями (b и с), остальные – с нечетными степенями. По предположению индукции в G’ существует эйлеров путь из с в b. Добавив к нему ребро (а, с), получим эйлеров путь из а в b.
Докажем теперь утверждение для эйлерова цикла с п ребрами. Пусть связный граф G имеет вершины только с четными степенями. Удалив из него одно ребро, например, (а, b) , получим граф G’, у которого степени двух вершин нечетны, остальные – четны. Предположим, что удаление ребра нарушило связность графа, т.е. у графа G’ две компоненты связности G1 и G2, при этом вершины с нечетными степенями а и b находятся в разных компонентах связности. Тогда сумма степеней вершин для каждого из графов G1 и G2 нечетна, чего не может быть. Следовательно, граф G’ – связный, и по индукционному предположению в нем существует эйлеров путь из а в b. Добавив к эйлерову пути ребро (а, b), получим эйлеров цикл. Теорема доказана.
Теорема о цикломатическом числе
Напомним, что цикломатическим числом графа G называется число ν(G) = P − B + K , где P – число ребер, B – число вершин, K – число
компонент связности графа G. Было доказано, что для любого графа ν(G) ≥ 0 , для дерева ν(G) = 0 .
Теорема. Если граф G состоит из нескольких компонент связности
G1, G2 , …, Gk , то ν(G) = ν(G1) + ν(G2 ) +… + ν(Gk ) .
Доказательство. Так как графы G1, G2 , …,Gk – связные графы, то
ν(G1) = P1 − B1 +1, ν(G2 ) = P2 − B2 +1 , …, ν(Gk ) = Pk − Bk +1.
Сложив почленно эти равенства, получим
k
∑ν(Gi ) = P − B + K = ν(G) . теорема доказана.
i=1
Введем определение суммы циклов произвольного графа. Пусть С1 и С2
– произвольные циклы графа G, содержащие общие участки пути, соединяющие вершины
|
vi и vi |
2 |
, vi |
3 |
и vi |
4 |
и так |
|||||
|
1 |
|||||||||||
|
далее. Тогда суммой |
|||||||||||
|
циклов С1 и С2 будем |
|||||||||||
|
называть граф, |
C1 |
||||||||||
|
вершинами которого |
|||||||||||
|
C1 |
C1+C2 |
||||||||||
|
являются все вершины |
|||||||||||
|
Рис. 2.40 |
|||||||||||
|
циклов С1 и С2, за |
исключением внутренних вершин их общих участков, а ребрами – все их ребра, за исключением ребер, составляющих их общие участки (рис. 2.40). Если циклы С1 и С2 не имеют общих участков, то их суммой
называется объединение циклов С1 + С2 = С1 С2. Вообще говоря, сумма двух циклов, даже и имеющих общие ребра, может не являться сама циклом, но является объединение простых циклов. Далее под циклом везде подразумевается либо простой цикл, либо объединение простых циклов.
Очевидно, что C +C = , C + = C . По сложению циклы образуют абелеву группу.
Если граф G имеет т ребер е1, е1, … ет, то любому циклу С графа G можно поставить в соответствие двоичный код длины т:
1, еслиei входит вC, C → (ε1ε2…εm ) , εi = 0, еслиei невходит вC.
Если циклу С1 соответствует код (ε1,ε2 ,…,εm ) , а циклу С2 – код (η1, η2 ,…, ηm ) , то циклу С1 + С2 соответствует код
(ε1 + η1, ε2 + η2 ,…, εm + ηm ) , где сложение производится по модулю 2. Таким образом, множество циклов графа G можно рассматривать, как
подгруппу группы Z2 × Z2 × Z2 × …× Z2 . Циклы образуют линейное
1444244443 m раз
пространство над полем Z2 .
Теорема. Пусть дан произвольный граф G (без петель, без кратных ребер, с конечным числом вершин) и ν(G) = k . Тогда:
1)Из графа G можно удалить k ребер так, что оставшийся граф будет без циклов и будет иметь столько же компонент связности, что и G.
2)Размерность пространства циклов графа G равна k.
Доказательство. 1° . Докажем, что ν(G) = 0 тогда только тогда, когда в графе G нет циклов. Действительно, если ν(G) = 0 , а
G1, G2 , …, Gs – компоненты связности графа G, то
ν(G) = ν(G1) + ν(G2 ) +… + ν(Gk ) = 0 . Так как
ν(G1) ≥ 0, ν(G2 ) ≥ 0, …, ν(Gs ) ≥ 0 , то ν(Gi ) = 0 при всяком i =1, 2, …, s .
Имеем ν(Gi ) = Pi − Bi +1 , следовательно, Gi – дерево, а значит, в Gi нет
циклов. Таким образом, в графе G тоже нет циклов. Докажем, что если в графе G нет циклов, то ν(G) = 0 .
Действительно, тогда G – лес, ν(G) = ν(G1) + ν(G2 ) +… + ν(Gk ) , где ν(G) = 0 , G1, G2 , …, Gs – компоненты связности графа G, т.е. деревья.
Так как для дерева ν(Gi ) = 0 , то ν(G) = 0 .
Таким образом, мы доказали, что если для графа G ν(G) = 0 , то в
нем нет циклов.
Пусть теперь ν(G) = k > 0 . Тогда в G есть циклы. Возьмем произвольно цикл С1, е1 – произвольное ребро этого цикла. Тогда граф G e1 имеет
то же количество компонент связности, что и G.
ν(G e1) = ν(G) −1 = k −1 . Если k −1 = 0 , то полученный граф будет без циклов. Если k −1 > 0 , то аналогично берем цикл С2 и ребро е2 и т.д. Этот процесс состоит ровно из k шагов. На каждом шаге количество компонент связности не меняется. Граф G {e1, e2 , …, ek } является
лесом, количество компонент связности у него такое же, как и у G. 2° . Занумеруем остальные ребра графа G:
E(G) ={e1, e2 , …, ek , ek +1, …, em} . Тогда циклам С1, С2, …, Сk
соответствуют коды
C1 → (1, , , . . ., ), C2 → (0, 1, , . . ., ),
…,
Ck → (0, 0, …, 0, 1, , . . ., ).
14243
k
Строки кодов линейно независимы. Осталось доказать, что любой цикл графа G можно линейно выразить через циклы С1, С2, …, Сk.. Возьмем произвольный цикл С с соответствующим ему кодом
C → (ε1, ε2 ,…, εk , εk +1, …, εm ) . Строки (1, , …, ),
(0, 1, , …, ),
…, (0, 0, …, 1)
линейно независимы, следовательно, образуют базис в пространстве размерности k. Поэтому
(ε1, ε2 ,…, εk ) = λ1(1, , …, ) + λ2 (0, 1, 0, …, ) +… + λk (0, 0, , …, 1)
при некоторых λ1, λ2 , …, λk {0,1} . Рассмотрим цикл
C‘ = C + λ1C1 + λ2C2 +… + λkCk .
Учитывая, что (ε1, ε2 ,…, εk ) + (ε1, ε2 ,…, εk ) = (0,0,…,0) , получаем C‘ = (ε1, ε2 ,…, εk , εk +1, …, εm ) +
+λ1(1, , …, ) + +λ2 (0, 1, 0, …, ) +… +
+λk (0, , 0, 1, , …, ) = (0, ,0, …0, , …, ).
Таким образом, C‘ – цикл в графе G {e1, e2 , …, ek } . Но по построению, G {e1, e2 , …, ek } – граф без циклов. Следовательно, C‘ = (0, 0, …, 0) и
C + λ1C1 + λ2C2 +… + λkCk = (0, 0, …, 0) , значит,
C = λ1C1 + λ2C2 +… + λkCk .
Теорема доказана.
Если G – связный граф и ν(G) = k , то по только что доказанной теореме
из G можно удалить некоторые k ребер так, чтобы получилось дерево Т. Назовем его остовным деревом графа G. Аналогично, если G – несвязный граф, то из G можно удалить некоторые k ребер так, чтобы
получился граф без циклов, т.е. лес, называемый остовным лесом графа G.
Решение типовых задач
|
1. Существует ли Эйлеров цикл у графа, |
1 |
2 |
|
|
изображенного на рис. 2.41? Если существует, |
|||
|
построить его. |
|||
|
Решение. Так как степени всех вершин четны, |
3 |
4 |
|
|
тот эйлеров цикл существует. Возьмем |
5 |
6 |
|
|
произвольный цикл, например, (1, 5, 3, 1). Этот |
|||
|
цикл не содержит все ребра графа. Рассмотрим |
Рис. 2.41 |
||
|
граф, полученный из исходного удалением этого |
цикла. Удаленный граф и оставшийся, в силу связности исходного графа всегда имеют общую вершину, в данном случае – 5. Рассмотрим теперь произвольный цикл нового графа, начинающийся в вершине 5, например, (5, 4, 6, 5). Присоединим его к первому циклу: (1, 5, 4, 6, 5, 3, 1). Остается единственный цикл (4, 1, 2, 4), присоединив который,
получим эйлеров цикл (1, 5, 4, 1, 2, 4, 6, 5, 3, 1).
2. Найти число компонент связности леса, который имеет 40 вершин и 23 ребра.
Решение. Так как для леса ν(G) = 0 , получаем P − B + K = 0 ,
K= B − P =17 .
3.Чему может равняться число ребер графа, имеющего 20 вершин и 4 компоненты связности?
Решение. Так как ν(G) ≥ 0 , имеем P − B + K ≥ 0 , следовательно,
P ≥16 . Покажем, что найдется граф, для которого P =16 , B = 20 ,
K = 4 . Пусть 3 компоненты связности – изолированные вершины, четвертая – простая цепь С17 с 16 ребрами. Таким образом, минимальное число ребер равно 16. Выясним, каким может быть максимальное число ребер.
Докажем, что наибольшее количество ребер у графа, три компоненты связности которого представляют собой изолированные вершины, четвертая – полны граф К17 с числом ребер, равным 136. Действительно, рассмотрим граф с 20 вершинами и 4 компонентами связности
G1, G2 ,G3 , G4 , из которых по крайней мере 2 содержат не менее двух вершин. Предположим, что V1 ≥V2 ≥1. Возьмем произвольно вершину из V2 , удалим все ребра, инцидентные ей, и соединим ее ребрами со
всеми вершинами из V1 . Новый граф будет иметь то же количество
вершин и компонент связности, но больше ребер. Таким образом, количество ребер может быть от 16 до 136.
4. Чему может равняться число компонент связности графа, имеющего 12 вершин и 27 ребер?
Решение. Так как простая цепь С12 имеет 11 ребер, а полный граф К12 – 66 ребер, то существует связный граф, имеющий 12 вершин и 27 ребер. Минимальное число компонент связности равно 1. Для того, чтобы определить максимально возможное число компонент связности, найдем наименьший полный граф, число ребер которого не меньше 27: n(n −1) / 2 ≥ 27, n = 8 . Рассмотрим граф, 4 компоненты связности
представляют собой изолированные вершины, а пятая имеет 8 вершин и 27 ребер. Докажем, что 6 компонент связности быть уже не может. Действительно, по предыдущей задаче, граф, имеющий 12 вершин и 6 компонент связности, может иметь не более 21 ребра. Таким образом Таким образом, количество компонент связности может быть от 1 до 5. 5. Для графа, изображенного на рис.2.42(а) найти цикломатическое число, укзать базис циклов,
|
построить остовное дерево. |
e2 |
e1 |
||||||
|
Для данного графа B = 9 , P =11 , |
e3 |
e4 |
||||||
|
K =1. Следовательно, ν(G) = 3 и из |
e5 |
|||||||
|
G надо удалить три ребра, чтобы |
||||||||
|
e6 |
e11 |
e7 |
||||||
|
получилось дерево. Базис циклов |
||||||||
|
также состоит из трех циклов. |
e9 |
|||||||
|
e10 |
||||||||
|
Выберем произвольно цикл, |
||||||||
|
например, C1 = {e2 , e4 , e5 , e3} . |
а) |
б) |
||||||
|
Удалим из графа ребро е2. В |
||||||||
|
получившемся графе возьмем цикл |
Рис 2 42 |
C2 ={e5 , e7 , e11, e6}. Удалим из
графа ребро е5. В получившемся графе возьмем цикл C3 ={e9 , e10 , e11} .
Удалим из графа ребро е10. Получим остовное дерево графа G , изображенное на рис. 2.42б). Циклы С1, С2, С3 образуют базис. Разложим какой-нибудь цикл, например, C4 = {e2 , e3, e6 , e9 , e10 , e7 , e4} , по этому базису. Запишем коды циклов:
C1 = (01111000000), C2 = (00001110001),
C3 = (00000000111), C4 = (01110110110).
Так как были удалены ребра е2, е5, е10, то в матрице, составленной из кодов циклов С1, С2, С3, С4, базисным будет минор, составленный из
|
1 |
0 |
0 |
|||||
|
0 |
1 |
1 |
|||||
|
столбцов под номерами 2, 5, 10: |
. |
||||||
|
0 |
0 |
1 |
|||||
|
1 |
0 |
1 |
|||||
Отсюда получаем C4 = C1 + C3 .
Задачи для самостоятельного решения
1.Сколько компонент связности имеет граф со следующим набором степеней вершин: 1, 1, 1, 2, 2, 2, 2, 3?
2.Изобразить граф G = Z3 ×C2 . Найти ν(G) , построить базис
циклов.
3. Изобразить граф G = Z3 ×C3 . Найти ν(G) , построить базис циклов.
4.Построить базис циклов графа K4 .
5.Построить базис циклов графа B3 .
6.Построить базис циклов графа B4 .
7.Построить базис циклов графа K3,3 .
8.Является ли деревом прямое произведение деревьев?
9.Найти число компонент связности леса, который имеет 76 вершин и 53 ребра.
10.Сколько ребер имеет лес с 10 вершинами, если он имеет 3 компоненты связности?
11.Чему может равняться число компонент связности графа, имеющего 15 вершин и 35 ребер?
12.Чему может равняться число компонент связности графа, имеющего 12 вершин и 20 ребер?
13.Чему может равняться число ребер графа, имеющего 10 вершин и 3 компоненты связности?
14.Доказать, что если граф имеет 10 вершин и 37 ребер, то он связен.
15.Доказать, что если граф имеет 8 вершин и 23 ребра, то он связен.
16.Связный граф имеет 12 вершин. Сколько он может иметь ребер?
17.Сколько ребер может быть у связного графа с п вершинами?
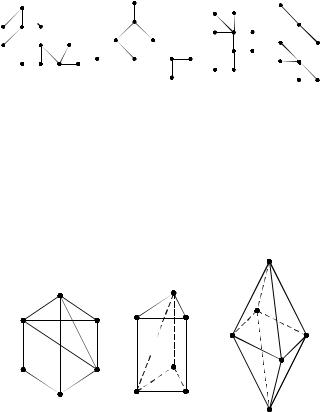
18.Сколько всего неизоморфных деревьев с пятью вершинами? Изобразить их.
19.Сколько всего графов с 12 вершинами и 65 ребрами? с 64 ребрами?
Рис. 2.43
20.Построить коды деревьев (два для каждого дерева), изображенных на рис.2.43.
21.Построить дерево по коду (00101001011101).
22.Построить дерево по коду (00101011001101).
23.Построить дерево по коду [5345566].
24.Построить дерево по коду [4445477].
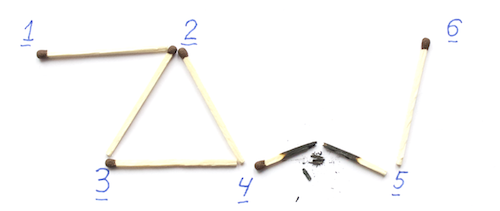
25.У каких из графов, изображенных на рис.2.44, существует эйлеров путь или эйлеров цикл? Если существует, то построить его.

Ответы
1. 1 или 2. Указание: рассмотреть, сколько вершин может быть в каждой компоненте связности. 2. См. рис. 2.45. ν(G) = 4 . Базис циклов:
(1, 2, 3), (1, 3, 6, 4), (3, 2, 5, 6), (1, 2, 5, 4). 3. ν(G) = 7 . 4. ν(G) = 3 .
|
5. |
ν(G) = 5 . |
|||||||||||
|
6. |
ν(G) =17 . |
|||||||||||
|
7. |
ν(G) = 4 . |
|||||||||||
|
8. |
Не |
является |
||||||||||
|
(см. рис. 2.12). |
||||||||||||
|
Рис. 2.45 |
Рис. 2.46 |
9. 23. |
10. 7. 11. |
|||||||||
|
От 1 |
до 7. 12. |
От 1 до 6. 13. От 7 до 28. 14. Указание. Доказать, что несвязный граф с 10 вершинами имеет не более 36 ребер. 15. Указание. Доказать, что несвязный граф с 8 вершинами имеет не более 21 ребра. 16. От 11 до 66. 17. От n −1 до n(n −1) / 2 . 18. 3 , см рис. 2.46. Указание. Рассмотреть
возможные наборы степеней вершин. 19. Один, два. 20. При нумерации,
указанной на рис. 2.47: а) (01000010110101101101), [114457557]; б) (0000101110010111); [2332477]; в) (0010100101011011), [ 4444666];
г) (00001010101111), [246666]. 21. См. рис. 2.48а . 22. См. рис. 2.48б. 23.
См. рис.2.48в 24. См. рис.2.48г. 25. а), в) – существует; б) нет.
|
1 |
1 |
1 |
2 |
1 |
||||||||||||||||||||
|
3 |
2 |
2 |
2 |
|||||||||||||||||||||
|
4 |
5 |
|||||||||||||||||||||||
|
8 |
3 |
4 |
3 |
3 |
||||||||||||||||||||
|
6 |
4 |
5 |
7 |
4 |
||||||||||||||||||||
|
7 |
8 |
6 |
||||||||||||||||||||||
|
9 |
5 |
6 |
9 |
5 |
6 |
|||||||||||||||||||
|
10 |
7 |
11 |
9 |
8 |
8 |
|||||||||||||||||||
|
7 |
||||||||||||||||||||||||
|
а) |
б) |
в) |
г) |
|||||||||||||||||||||
|
Рис. 2.47 |
||||||||||||||||||||||||
Компонентой связности неориентированного графа называется подмножество вершин, достижимых из какой-то заданной вершины. Как следствие неориентированности, все вершины компоненты связности достижимы друг из друга.
Дан неориентированный граф $G$ с $n$ вершинами и $m$ рёбрами. Требуется найти в нём все компоненты связности, то есть разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами путей не существует.
Для решения задачи модифицируем обход в глубину так, чтобы запустившись от вершины какой-то компоненты, от пометил все вершины этой компоненты — то есть все достижимые вершины — заданным номером этой компоненты. Для этого можно массив used заменить массивом номеров компонент для каждой вершины, изначально заполненный нулями:
const int maxn = 1e5;
int component[maxn]; // тут будут номера компонент
void dfs(int v, int num) {
component[v] = num;
for (int u : g[v])
if (!component[u]) // если номер не присвоен, то мы там ещё не были
dfs(u, num);
}
Теперь проведем серию обходов: сначала запустим обход из первой вершины, и все вершины, которые он при этом обошёл, образуют первую компоненту связности. Затем найдём первую из оставшихся вершин, которые ещё не были посещены, и запустим обход из неё, найдя тем самым вторую компоненту связности. И так далее, пока все вершины не станут помеченными.
Записывается это очень компактно:
int num = 0;
for (int v = 0; v < n; v++)
if (!component[v])
dfs(v, ++num);
После этого переменная num будет хранить число компонент связности, а массив component — номер компоненты для каждой вершины, который, например, можно использовать, чтобы быстро проверять, существует ли путь между заданной парой вершин.
Итоговая асимптотика составит $O(n + m)$, потому что такой алгоритм не будет запускаться от одной и той же вершины дважды, и каждое ребро будет просмотрено ровно два раза (с одного конца и с другого).
Рассмотрим базовую задачу.
Условие:
Дан неориентированный граф G, имеющий N вершин и M ребер. Чтобы все рассмотренные подходы имели практических смысл, ограничим N<=1000.
Необходимо найти количество компонент связности данного графа. Формат входных данных: В первой строке входного файла находятся N и M, разделенные пробелом. Далее идет M строк, содержащих пару вершин, между которыми находится ребро. Вершины нумеруются с 1.
Формат выходных данный: В единственной строке выдать количество компонент связности графа.
Пример: 
input.txt
15 11
1 2
2 3
2 11
10 11
11 12
11 15
4 12
12 13
8 14
7 14
5 6
output.txt
4
Компонента связности неориентированного графа является подграф, в котором для любой пары вершин v и u существует путь. Между двумя различными компонентами связности не существует пути.
Задача стара, как мир. Но тем не менее сегодня покажу несколько подходов по ее решению.
1. Поиск в глубину(DFS)
Самое классическое решение. Даже комментировать особо нечего.
- const int SIZE = 1e3 + 10;
- vector<int> adj[SIZE];
- bool usd[SIZE];
- ...
- void dfs(int cur) {
- usd[cur] = true;
- for (int i=0;i<adj[cur].size();++i) {
- int nxt = adj[cur][i];
- if (!usd[nxt])
- dfs(nxt);
- }
- }
- int connected_components_amount_dfs() {
- int cnt = 0;
- for (int i=1; i<=n; ++i) {
- if (!usd[i]) {
- dfs(i);
- ++cnt;
- }
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Граф храним в виде списка смежности(строка 2). Общая сложность решения $latex O(N + M)$.
Решение
2. DSU подобная структура(ленивый подход)
Будем делать конденсацию компоненты в одну вершину. Идея следующая: будем последовательно обрабатывать ребра. Каждая компонента связности будет представлена одной своей вершиной(титульная). При этом неважно какой. По ходу обработки ребер титульная вершина компонент может меняться.
В итоге для нахождения количества компонент связности нужно найти количество титульных вершин.
- const int SIZE = 1e3 + 10;
- int p[SIZE];
- bool usd[SIZE];
- ...
- int connected_components_amount_dsu() {
- scanf("%d %d", &n, &m);
- for (int i=1;i<=n;++i) {
- p[i] = i;
- }
- for (int i=0;i<m;++i) {
- scanf("%d %d", &f, &s);
- int par = p[f];
- for (int j=1;j<=n;++j) {
- if (p[j] == par)
- p[j] = p[s];
- }
- }
- for (int i=1;i<=n;++i)
- usd[p[i]] = true;
- int cnt = 0;
- for (int i=1;i<=n;++i) {
- if (usd[i]) ++cnt;
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Заметим, что сам граф непосредственно вообще никак не хранится. Общая сложность $latex O(M*N)$
Решение
3. Система непересекающихся множеств (DSU)
Реализацию, представленную выше можно существенно усовершенствовать. При добавлении нового ребра будем “мерджить меньшее подмножество к большему” + сжимать пути. У emaxx’а рассматривается доказательство того, что ассимптотика обработки одного ребра равна $latex O(alpha (N))$, где $latex alpha (N)$ – обратная функция Аккермана.
- const int SIZE = 1e3 + 10;
- int p[SIZE];
- int size[SIZE];
- int par(int x) {
- return p[x] == x ? x : p[x] = par(p[x]);
- }
- int connected_components_amount_dsu() {
- scanf("%d %d", &n, &m);
- for (int i=1;i<=n;++i) {
- p[i] = i;
- size[i] = 1;
- }
- for (int i=0;i<m;++i) {
- scanf("%d %d", &f, &s);
- f = par(f); s = par(s);
- if (f != s) {
- if (size[f] > size[s])
- swap(f,s);
- p[f] = s;
- size[s] += size[f];
- }
- }
- bool usd[SIZE];
- memset(usd, 0, sizeof(usd));
- for (int i=1;i<=n;++i)
- usd[par(i)] = true;
- int cnt = 0;
- for (int i=1;i<=n;++i) {
- if (usd[i]) ++cnt;
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Как и прежде сам граф не хранится в виде матрицы смежности. Общая сложность $latex O(M * alpha (N))$
4. Алгоритм Флойда.
Этот подход для самых ленивых, правда он требует хранить граф явно в виде матрицы смежности.
Запускаем алгоритм Флойда и строим матрицу достижимости для каждой пары вершин. В результате если первоначально adj[u][v] указывало на наличие ребра между u и v, то после работы алгоритма adj[u][v] будет указывать на наличие пути между u и v. После чего можно написать DFS двумя вложенными циклами.
- const int SIZE = 1e3 + 10;
- int adj[SIZE][SIZE];
- bool usd[SIZE];
- ...
- int connected_components_amount_floyd() {
- for (int k=1;k<=n;++k){
- for (int i=1;i<=n;++i){
- for (int j=1;j<=n;++j){
- if (adj[i][k] + adj[k][j] == 2)
- adj[i][j] = 1;
- }
- }
- }
- int cnt = 0;
- for (int i=1;i<=n;++i) {
- if (!usd[i]) {
- ++cnt;
- usd[i] = true;
- for (int j=1;j<=n;++j) {
- if (adj[i][j] && !usd[j])
- usd[j] = true;
- }
- }
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Алгоритм ужасно долгий, но зато пишется довольно просто. Общая сложность $latex O({ N }^{ 3 }) $
Решение
Собственно пока и все. Мы рассмотрели 3 принципиально разных подхода. На маленьких ограничениях можно выбрать тот из них, что больше по душе.
Помогаю со студенческими работами здесь
Посчитать количество компонент связности в неориентированном графе
В неориентированном графе посчитать количество компонент связности. В графе могут быть петли и…
На какое наибольшее количество частей может быть разбита плоскость двенадцатью квадратами с равными длинами сторон?
На какое наибольшее количество частей может быть разбита плоскость двенадцатью квадратами с равными…
Найти количество компонент связности в ориентированном графе, заданном матрицей смежности
Найти количество компонент связности в ориентированным графе, заданном с помощью матрицы смежности….

У Андрея есть палочки с целочисленными длинами и общей длиной 200. Ни из каких трёх нельзя…

В треугольник со сторонами 8, 12 и 14 вписана окружность. К окружности проведена касательная,…
Какое наибольшее число треугольников с нецелой площадью может быть среди них
На плоскости отметили 120 точек с целочисленными координатами. Какое наи-большее число…
Поиск компонент связности в ориентированом графе
Сабж. Само условие задачи тут.
Мое решение – модифицированый bfs, в булевом массиве head…
Искать еще темы с ответами
Или воспользуйтесь поиском по форуму:
Компоненты связности в динамическом графе за один проход
Время на прочтение
8 мин
Количество просмотров 18K
Люди встречаются, люди ссорятся, добавляются и удаляют друзей в социальных сетях. Этот пост о математике и алгоритмах, красивой теории, любви и ненависти в этом непостоянном мире. Этот пост о поиске компонент связности в динамических графах.
Большой мир генерирует большие данные. Вот и на нашу голову свалился большой граф. Настолько большой, что мы можем удержать в памяти его вершины, но не ребра. Кроме того, относительно графа приходят обновления – какое ребро добавить, какое удалить. Можно сказать, что каждое такое обновление мы видим в первый и последний раз. В таких условиях необходимо найти компоненты связности.
Поиск в глубину/ширину здесь не пройдут просто потому, что весь граф в памяти не удержать. Система непересекающихся множеств могла бы сильно помочь, если бы ребра в графе только добавлялись. Что же делать в общем случае?
Задача. Дан неориентированный граф на
вершинах. Изначально, граф – пустой. Алгоритму приходит последовательность обновлений
, которую можно прочитать в заданном порядке ровно один раз. Каждое обновление – это команда удалить или добавить ребро между парой вершин
и
. Гарантируется, что ни в какой момент времени между парой вершин не будет удалено ребер больше чем есть. По прочтении последовательности алгоритм должен вывести все компоненты связности с вероятностью успеха
. Разрешается использовать
памяти, где
– некоторая константа.
Решение задачи состоит из трех ингредиентов.
- Матрица инцидентности как представление.
- Метод стягивания как алгоритм.
-сэмплирование как оптимизация.
Реализацию можно посмотреть на гитхабе: link.
Матрица инцидентности как представление
Первая структура данных для хранения графа будет крайне неоптимальна. Мы возьмем матрицу инцидентности размера
, в которой преимущественно будут нули. Каждая строка в матрице соответствует вершине, а столбец – возможному ребру. Пусть
. Для пары вершин
, соединенных ребром, зададим
и
, в противном случае значения равны нулю.
Как пример, посмотрим на граф на картинке ниже.
Для него матрица инцидентности будет выглядеть так.
Невооруженным глазом видно, что у такого представления есть серьезный недостаток – размер . Мы его оптимизируем, но позже.
Есть и неявное преимущество. Если взять множество вершин и сложить все вектора-строки матрицы
, которые соответствуют
, то ребра между вершинами
сократятся и останутся только те, что соединяют
и
.
Например, если взять множество и сложить соответствующие вектора, мы получим
Ненулевые значения стоят у ребер ,
и
.
Стягивание графа как алгоритм
Поймем, что такое стягивание ребра. Вот есть у нас две вершины и
, между ними есть ребро. Из
и
могут исходить и другие ребра. Стягивание ребра
это процедура, когда мы сливаем вершины
и
в одну, скажем
, ребро
удаляем, а все оставшиеся ребра, инцидентные
и
, проводим в новую вершину
.
Интересная особенность: в терминах матрицы инцидентности, чтобы стянуть ребро , достаточно сложить соответствующие вектора-строки. Само ребро
сократится, останутся только те, что идут наружу.
Теперь алгоритм. Возьмем граф и для каждой неизолированной вершины выберем соседа.
Стянем соответствующие ребра.
Повторим итерацию раз.
Заметим, что после каждой итерации стягивания компоненты связности нового графа взаимно-однозначно сопоставляются компонентам старого. Мы можем даже помечать, какие вершины были слиты в результирующие, чтобы потом восстановить ответ.
Заметим также, что после каждой итерации, любая компонента связности хотя бы из двух вершин уменьшается как минимум в два раза. Это естественно, поскольку в каждую вершину новой компоненты было слито как минимум две вершины старой. Значит, после итераций в графе останутся только изолированный вершины.
Переберем все изолированный вершины и по истории слияний восстановим ответ.
 -сэмплирование как оптимизация
-сэмплирование как оптимизация
Все было бы замечательно, но приведенный алгоритм работает что по времени, что по памяти . Чтобы его оптимизировать, мы построим скетч – специальную структуру данных для компактного представления векторов-строк.
От скетча потребуется три свойства.
Во-первых, компактность. Если мы строим скетч для вектора размера
, то сам скетч
должен быть размера
.
Во-вторых, сэмплирование. На каждой итерации алгоритма, нам требуется выбирать соседа. Мы хотим способ получать индекс хотя бы одного ненулевого элемента, если такой есть.
В-третьих, линейность. Если мы построили для двух векторов и
скетчи
и
. Должен быть эффективный метод, получить скетч
. Это поможет стягивать ребра.
Мы воспользуемся решением задачи -сэмплирования.
Задача. Дан вектор нулевой вектор размерности
. Алгоритму приходит последовательность из
обновлений вида
: прибавить
к значению
.
может быть как положительным, так и отрицательным целым числом. Результирующий вектор на некоторых позициях может иметь ненулевые значения. Эти позиции обозначим через
. Требуется выдать любую позицию из
равновероятно. Все обновления нужно обработать за один проход, можно использовать
памяти. Гарантируется, что максимальное значение в
укладывается в
бит.
1-разреженные вектор
Для начала мы решим более простую задачу. Пусть у нас есть гарантия, что конечный вектор содержит ровно одну ненулевую позицию. Будем говорить, что такой вектор – 1-разреженный. Будем поддерживать две переменных и
. Поддерживать их просто: на каждом обновлении прибавляем к первой
, ко второй
.
Обозначим искомую позицию через . Если она только одна, то
и
. Чтобы найти позицию, считаем
.
Можно вероятностно проверить, является ли вектор 1-разреженным. Для этого возьмем простое число , случайное целое
и посчитаем переменную
. Вектор проходит тест на 1-разреженность, если
и
.
Очевидно, что если вектор действительно 1-разреженный, то
и тест он пройдет. В противном случае, вероятность пройти тест не более (на самом деле, максимум
).
Почему?
В терминах многочлена, вектор проходит тест, если значения полинома
в случайно выбронной точке равно нулю. Если вектор не является 1-разреженным, то
не является тождественно равным нулю. Если мы прошли тест, мы угадали корень. Максимальная степень полинома –
, значит, корней не более
, значит, вероятность их угадать не более
.
Если мы хотим повысить точность проверки до произвольной вероятности , то нужно посчитать значение
на
случайных
.
 -разреженный вектор
-разреженный вектор
Теперь попробуем решить задачу для -разреженного вектора, т.е. содержащего не более
ненулевых позиций. Нам потребуется хэширование и предыдущий метод. Общая идея – восстановить вектор целиком, а потом выбрать какой-нибудь элемент случайно.
Возьмем случайную 2-независимую хэш-функцию . Эта такая функция, которая два произвольных различных ключа распределяет равновероятно независимо.
Подробнее про хэш-функции
В алгоритмах есть два принципиально разных подхода к хэш-функциям. Первый основывается на том, что данные более менее случайные, и наша любимая хэш-функция размешает их правильно. Второй, на том, что данные может подбирать злой противник, и единственный шанс спасти алгоритм от лишних вычислений и прочих проблем – это выбирать хэш-функцию случайно. Да, иногда может работать плохо, но зато мы можем померять, насколько плохо. Здесь идет речь о втором подходе.
Хэш-функция выбирается из семества функций. Например, если мы хотим размешать все числа от до
, можно взять случайные
и
и определить хэш-функцию
Функции для всех возможнных задают семейство хэш-функций. Случайно выбрать хэщ-функцию – это по сути случайно выбрать те самые
и
. Выбираются они обычно равновероятно из множества
.
Замечательное свойство у приведенного примера, что два любых различных ключа распределяются случайно независимо. Формально, для любых различных и любых, возможно одинаковых,
вероятность
Такое свойство называется 2-независимостью. Иногда, вероятность может быть не , а
, где
какая-то разумно маленькая величина.
Есть обобщение 2-независимости — -независимость. Это когда функция распределяет не 2,
произвольных ключей независимо. Полиномиальные хэш-функции с
случайными коэффициентами обладают таким свойством.
У -независимости есть одно неприятное свойство. С ростом
функция занимает все больше памяти. Это свойство не зависит от какой-то конкретной реализации, а просто общее информационное свойство. Поэтому чем меньшей независимостью мы можем обойтись, тем легче на жить.
Возьмем хэш-таблицу размера . В каждой ячейке таблицы будет сидеть алгоритм для 1-разереженного вектора. Когда нам приходит обновление
, мы отправляем это обновление алгоритму в ячейке
.
Можно посчитать, что для отдельной ячейки, вероятность что там произойдет коллизия хотя бы по двум ненулевым координатам будет не более .
Почему?
Вероятность, что другой элемент не попадет в ячейку к нам . Вероятность, что все не попадут к нам:
. Вероятность, что хоть кто-нибудь попадет
. Можно заметить, что это функция монотонно возрастающая. Я здесь просто приведу картинку:
В пределе функция дает значение .
Пусть мы хотим восстановить все координаты с вероятностью успеха , или с вероятностью провала
. Возьмем не одну хэш-таблицу, а сразу
. Несложно понять, что вероятность провала в декодировании отдельной координаты будет
. Вероятность провала в декодировании хотя бы одной из
координат
. Если в сумме декодирование для 1-разреженных векторов работает с вероятностью провала
, то мы победили.
Итоговый алгоритм таков. Берем хэш-таблиц размера
. В каждой ячейке алгоритма будет находиться свой декодер для 1-разреженного вектора с вероятностью провала
.
Каждое обновление обрабатывается в каждой хэш-таблице отдельно алгоритмом в ячейке
.
По завершении, извлекаем из всех успешно отработавших 1-декодеров по координате и сливаем их в один список.
Максимум, в общей таблице будет затронутых 1-декодеров. Поэтому суммарная вероятность, что один из 1-декодеров отработает неверно не превысит
. Также вероятность, что хотя бы одна координата не будет восстановлена не превышает
. Итого, вероятность провала алгоритма
.
Еще одно хэширование для общего случая
Последний шаг в -сэмплировании, это понять, что делать с общим случаем. Мы снова воспользуемся хэшированием. Возьмем
-независимую хэш-функцию
для некоторого
.
Будем говорить, что обновление является
-интересным, если
. Иначе говоря, в бинарной записи
содержит
нулей в конце.
Запустим алгоритм для -разреженного вектора параллельно на
уровнях. На уровне
будем учитывать только
-интересные обновления. Несложно понять, что чем больше
, тем меньше шансов (а шансов
) у обновления быть учтенным.
Найдем первый уровень с наибольшим , где приходили хоть какие-то обновления, и попытаемся его восстановить. Если восстановление пройдет успешно, вернем случайно выбранную позицию.
Есть несколько моментов, на которые хочется вкратце обратить внимание.
Во-первых, как выбирать . В общем случае вектор может иметь более чем
ненулевых позиций, но с каждым увеличением
на единицу, мат. ожидание ненулевых позиций падает ровно в 2 раза. Можно выбрать такой уровень, при котором мат.ожидание будет между
и
. Тогда из оценок Чернова и
независимости хэш-функции, вероятность, что вектор будет нулевым или иметь более чем
ненулевых позиций, окажется экспоненциально мала.
Это определяет выбор , где
– допустимая вероятность провала.
Во-вторых, из -независимости хэш-функции следует, что для любой позиции вероятность пройти фильтр окажется равной. Поскольку
-разреженные вектора мы уже умеем восстанавливать, то получить равномерное распределение уже тривиально.
Итого, мы научились выбирать случайную ненулевую позицию согласно равномерному распределению.
Смешать, но не взбалтывать
Осталось понять, как все совместить. Нам известно, что в графе вершин. Для каждой вершины, точнее каждого вектора-строки в матрице инцидентности, заведем
скетчей
для
-сэмплирования. На
-ой итерации алгоритма стягивания будем использовать для сэмплирования
-ые скетчи.
При добавлении ребра добавим во все скетчи вершин
и
соответствующие +1 и -1 соответственно.
Когда ребра закончатся и нас спросят про компоненты, запустим алгоритм стягивания. На -ой итерации, через
-сэмплирование из скетча
найдем соседа каждой вершине. Чтобы стянуть ребро
, сложим все скетчи соответствующие
и
. У каждой новой вершины сохраним список вершин, которые были в нее слиты.
Все. В конце просто проходим по изолированным вершинам, по истории слияний восстанавливаем ответ.
Кто виноват и еще раз что делать
На самом деле тема этого поста возникла не просто так. В январе к нам, в Питер в CS Клуб, приезжал Илья Разенштейн (@ilyaraz), аспирант MIT, и рассказывал про алгоритмы для больших данных. Было много интересного (посмотрите описание курса). В частности Илья успел рассказать первую половину этого алгоритма. Я решил довести дело до конца и рассказать весь результат на Хабре.
В целом, если вам интересна математика, связанная с вычислительными процессами aka Theoretical Computer Science, приходите к нам в Академический Университет на направление Computer Science. Внутри научат сложности, алгоритмам и дискретной математике. С первого семестра начнется настоящая наука. Можно выбираться наружу и слушать курсы в CS Клубе и CS Центре. Если вы не из Питера, есть общежитие. Прекрасный шанс переехать в Северную Столицу.
Подавайте заявку, готовьтесь и поступайте к нам.
Источники
- «On Unifying the Space of l0-Sampling Algorithms», Graham Cormode, Donatella Firmani, 2013
- «Analyzing Graph Structure via Linear Measurements», Kook Jin Ahn, Sudipto Guha, Andrew McGregor, 2012