Алгебра и начала математического анализа, 11 класс
Урок №17. Наибольшее и наименьшее значения функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение наибольшего и наименьшего значения функции,
2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,
3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений
Глоссарий по теме
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти область определения функции D(f).
- Найти производную f‘ (x).
- Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).
- Среди полученных значений выбрать наибольшее и наименьшее.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Нахождение наибольшего и наименьшего значений функции на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.
- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее
Примеры и разбор решения заданий тренировочного модуля
№1.Найти наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3]
Решение. Действуем в соответствии с алгоритмом.
1) D(f) = (-∞; +∞).
2) f (x) = 6x2 – 18x + 12
(x) = 6x2 – 18x + 12
3) Стационарные точки: х = 1; х = 2.

4) f(0) = -2
f(3) = 7
f(1) = 3
f(2) = 2
5) fнаим.=f(0) = -2
fнаиб.=f(3) = 7.
Ответ: fнаим= -2
fнаиб.= 7.
№2.Найдите два положительных числа, сумма которых равна 16, а произведение наибольшее.
Решение.
Пусть первое число равно х, 
Тогда второе число – 
Следовательно, 
Произведение этих чисел равно х(16 – х).
Составим функцию:
f(x) = x(16 – x)

x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.
Следовательно, в этой точке функция F(x) = x(16 – x) принимает наибольшее значение.
Следовательно, два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.
Ответ: 8 и 8
Воскресенье, 18 декабря, 2011
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.
- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x3 – 18x2 + 81x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.
- Производная функции равна: y’ = 3x2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x2 – 36x + 81 = 0, значит x2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).
- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x3 – 18x2 + 81x + 23 = x(x-9)2+23:
- y(8) = 8 · (8-9)2+23 = 31;
- y(9) = 9 · (9-9)2+23 = 23;
- y(13) = 13 · (13-9)2+23 = 231.
Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции. Если точек минимума нет, то у функции нет наименьшего значения.
- Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции. Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции:
![]() .
.
Решение: действуем по алгоритму нахождения наибольшего значения функции:
- Область определения функции задается неравенством:
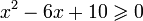 , которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R.
, которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R. - Производная функции равна:
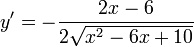 ,
,
область определения которой также не ограничена, поскольку по указанной выше причине x2 – 6x + 10 > 0, и знаменатель дроби нигде не обращается в ноль: D(y’) = R. - Нули производной: 2x — 6 = 0, откуда x = 3 (одна точка, подозрительная на экстремум).
- Отмечаем область определения функции и точки, подозрительные на экстремум, на числовой прямой, определяем знаки производной в получившихся промежутках:
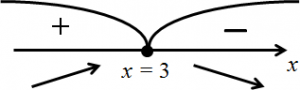 x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке. - Находим это значение:
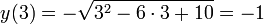 .
.
Итак, наибольшее значение функции равно -1. Ответ: -1.
Репетитор по математике
Сергей Валерьевич
Наибольшее и наименьшее значение функции
Как найти?
Постановка задачи
Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $
План решения
Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $
- Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
- Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
- Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
- Выбираем критические точки, принадлежащие отрезку $ [a,b] $
- Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $
Примеры решений
| Пример 1 |
| Найти наибольшее и наименьшее значение функции $ y = 2x^3 – 3x^2 – 4 $ на отрезке $ [0;2] $ |
| Решение |
|
Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 – 3x^2 – 4)’ = 6x^2 – 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 – 6x = 0 $$ $$ 6x(x – 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 – 3 cdot 0^2 – 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 – 3 cdot 1^2 – 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 – 3 cdot 2^2 – 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M = 0, m = -5 $$ |
| Пример 2 |
| Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $ |
| Решение |
|
Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $. |
| Ответ |
| $$ m = 0, M = 1 $$ |
Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции 
 , то функция
, то функция  возрастает на этом промежутке.
возрастает на этом промежутке.
Если на промежутке I производная функции 
 , то функция
, то функция  убывает на этом промежутке.
убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с “+” на “-“.
В точке минимума функции производная меняет знак с “-” на “+”.
6. Находим значение функции в концах отрезка,
- затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
- или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию  . График этой функции выглядит так:
. График этой функции выглядит так:
 В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;0}{]} {x}{in}delim{[}{-1;0}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_8d4ac2719ab1423f162f9779293da981.png)
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка:  , а наименьшее – в левом:
, а наименьшее – в левом:  .
.
2. Рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;1}{]} {x}{in}delim{[}{-1;1}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_fbae2bb0d6eaada0859d11280c8d6a23.png)
Очевидно, что наибольшее значение функция принимает в точке максимума  , а наименьшее – в одном из концов отрезка, то есть надо найти значения
, а наименьшее – в одном из концов отрезка, то есть надо найти значения  и
и  и выбрать из них наименьшее.
и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке ![{x}{in}delim{[}{-1;2}{]} {x}{in}delim{[}{-1;2}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_991.5_3bae536560f42bd0f0875793dd5a92e2.png) , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть
, то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть  и
и  .
.
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть  и
и  .
.
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции  – множество действительных чисел.
– множество действительных чисел.
2. 
3.  , если
, если  или
или 
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание – убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
1. Задание B15 (№ 26695)
Найдите наибольшее значение функции  на отрезке
на отрезке ![[-{pi}/2;0] [-{pi}/2;0]](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_9a7375f1961203c68e53ad122ab84a77.png) .
.
1. Функция  определена при всех действительных значениях х
определена при всех действительных значениях х
2. 
3. 
 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции  на отрезке [
на отрезке [ ].
].
1. ОДЗ функции 

2. 
Производная равна нулю при  , однако, в этих точках она не меняет знак:
, однако, в этих точках она не меняет знак:

 , следовательно,
, следовательно, 
 , значит,
, значит, 
 , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция
, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, при
возрастает и принимает наибольшее значение в правом конце промежутка, при  .
.
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

у(0)=5
Ответ: 5.
3. Задание B15 (№ 26708)
Найдите наименьшее значение функции  на отрезке [
на отрезке [ ].
].
1. ОДЗ функции  :
: 

2. 
3. 
 ,
, 
Расположим корни этого уравнения на тригонометрической окружности.

Промежутку ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png) принадлежат два числа:
принадлежат два числа:  и
и 
Расставим знаки. Для этого определим знак производной в точке х=0: 
 . При переходе через точки
. При переходе через точки  и
и  производная меняет знак.
производная меняет знак.

Изобразим смену знаков производной функции  на координатной прямой:
на координатной прямой:

Очевидно, что точка  является точкой минимума ( в ней производная меняет знак с “-” на “+”), и чтобы найти наименьшее значение функции
является точкой минимума ( в ней производная меняет знак с “-” на “+”), и чтобы найти наименьшее значение функции  на отрезке
на отрезке ![delim{[}{-{pi}/3;{pi}/3}{]} delim{[}{-{pi}/3;{pi}/3}{]}](https://ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_982_e5f186d35c95dd888150972e98bd371a.png) , нужно сравнить значения функции в точке минимума и в левом конце отрезка,
, нужно сравнить значения функции в точке минимума и в левом конце отрезка,  .
.
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а  таковым на является, следовательно подставим в уравнение функции
таковым на является, следовательно подставим в уравнение функции 

Ответ: -1
Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.



Образовательные задачи урока.
- повторить необходимые и достаточные условия
существования точек экстремума, понятия:
стационарные и критические точки; - ввести алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке - сформировать умение решать задачи на
нахождение наибольшего и наименьшего значения
степенной функции на отрезке с помощью
производной. - разобрать прототипы задач № 1 В14
экзаменационной работы в формате ЕГЭ. - Продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения писать
необходимом темпе.
Воспитательные задачи:
- cодействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - cодействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм; - cодействовать профилактике утомляемости
школьников, используя разнообразные виды работы
на уроке.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Актуализация знаний учащихся.
Повторить с учащимися основные понятия прошлых
уроков: точки экстремума, каково достаточное
условие точек экстремума, стационарные точки и
критические точки (учащихся отвечают с места)
Повторить таблицу производных основных
функций и основные правила нахождения
III. Изучение нового материала.
Алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке
(учащиеся записывают себе в тетрадь).
Пусть функция ![]() непрерывна и дифференцируема на
непрерывна и дифференцируема на
отрезке ![]() , то
, то
для нахождения наибольшего и наименьшего
значения функции на отрезке нужно:
- найти производную функции, найти стационарные
точки (решаем уравнение, приравнивая производную
к нулю) - среди полученных стационарных точек выбрать те,
которые принадлежат отрезку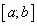
- найти значение в стационарных точках и в концах
отрезка, то есть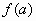 и
и 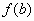 .
. - среди полученных значений выбрать наибольшее
или наименьшее.
Записать схему нахождения наибольшего и
наименьшего значения функции на отрезке в
тетради (учитель оформляет схему на доске):
Пусть![]()
непрерывна на ![]()
и дифференцируема. Тогда, для нахождения ![]() или
или ![]() :
:
- Находим
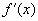
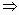
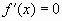
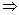 находим
находим 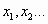
- Проверяем принадлежность
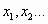 отрезку
отрезку 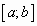
- Находим
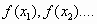 ,
, 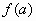 ,
, 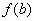 .
. - Среди полученных значений выбираем
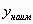 или
или 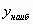 .
. - Записываем ответ (Акцентировать внимание, что в
ответе должно быть записано либо целое число,
либо конечная десятичная дробь).
Пример № 1. Найти наименьшее значение функции
![]() на отрезке
на отрезке ![]() . (Учитель
. (Учитель
совместно с учащимися записывает решение на
доске последовательно проговаривая каждый пункт
алгоритма).
Решение:
![]()
![]()
![]()
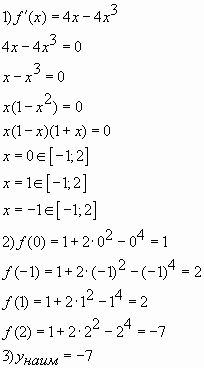
Ответ: ![]()
Пример № 2. Найти наибольшее значение
функции ![]() на
на
отрезке ![]()
Решение:
![]()
![]()
![]()
![]()
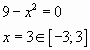
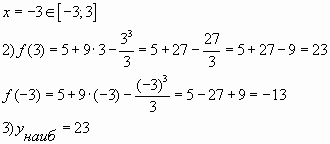
Ответ: 23
Пример № 3. Найдите наименьшее значение
функции ![]() на
на
отрезке ![]() .
.
Решение:
![]()
![]()
![]()
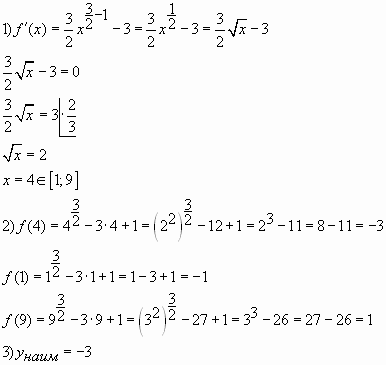
Ответ: -3
Пример № 4. Найдите наибольшее
значение функции ![]() на отрезке
на отрезке ![]() .
.
Решение:
Упростим функцию ![]()
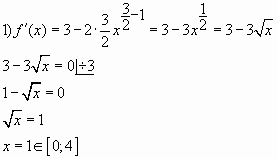
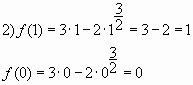
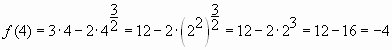
![]()
Ответ: 1
IV. Закрепление материала.
- Найдите наименьшее значение функции
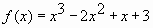 на отрезке
на отрезке 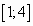
- Найдите наименьшее значение функции
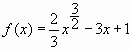 на отрезке
на отрезке 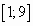
- Найдите наименьшее значение функции
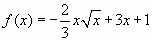 на отрезке
на отрезке 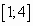
V. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Выставить отметки за урок.
VI. Домашнее задание:
- Найдите наименьшее значение функции
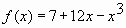 на отрезке
на отрезке 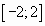
- Найдите наибольшее значение функции
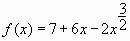 на отрезке
на отрезке 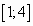
- Найдите наибольшее значение функции
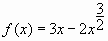 на отрезке
на отрезке 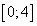
- Найдите наименьшее значение функции
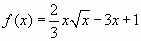 на отрезке
на отрезке 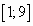
- Найти наибольшее значение функции
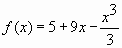 на отрезке
на отрезке 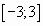
Урок № 2. “Нахождение наибольшего и
наименьшего значения функций ![]() и
и ![]() на отрезке
на отрезке ![]() .
.
Тип урока: комбинированный.
Образовательные задачи:
- обеспечить повторение в ходе урока алгоритма
нахождения наибольшего и наименьшего значения
функции на отрезке; - продолжить формирования навыка применения
этого алгоритма при решении второго типа задач
экзаменационных вариантов ЕГЭ; - продолжить формирование общеучебных умений и
навыков: навыков самоконтроля, умения в
необходимом темпе читать и писать, анализировать
условия задачи.
Воспитательные задачи:
- содействовать в ходе урока формированию
основных мировоззренческих идей (материальность
мира, познаваемость мира и его закономерностей,
обусловленность развития науки потребностям
производства); - содействовать воспитанию у учащихся таких
нравственных качеств, как коллективизм. умение
слушать товарищей; - содействовать профилактике утомляемости
школьников.
I. Организационный момент. Приветствие.
Проверка готовности класса к уроку. Выявление
отсутствующих.
II. Проверка домашнего задания. Фронтальная
проверка домашнего задания. Если у большинства
учащихся возникли вопросы, разобрать на доске
решение конкретного задания, если лишь у
некоторых, объяснить в индивидуальном порядке,
предварительно схематично обговорив решение у
доски.
III. Актуализация знаний. Повторить еще раз
алгоритм нахождения наибольшего и наименьшего
значения функции на отрезке с оформлением схемы
на доске.
Повторить следующие формулы для дальнейшего
изучения материала:
![]() ,
, ![]() ,
, ![]()
Решить на повторение примеры (1 учащийся пишет
решение на доске с комментариями по решению,
остальные записывают себе в тетради).
IV. Решение новых прототипов задач (разбирает
решение учитель)
Пример № 1. Найти наименьшее значение
функции ![]() на
на
отрезке ![]()
Решение
![]()
![]()
![]()
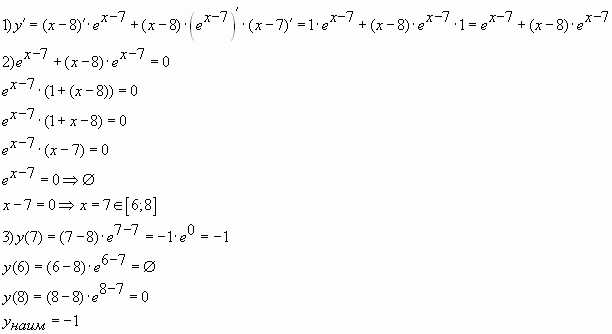
Ответ: –1
Пример № 2. Найти наименьшее значение
функции ![]() на
на
отрезке ![]()
Решение. Преобразуем и упростим функцию ![]() , используя
, используя
свойство логарифмов ![]()
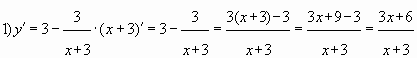
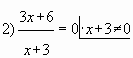
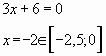
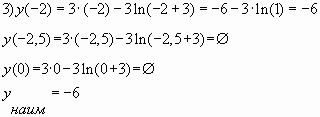
Ответ: -6
V. Закрепление материала (самостоятельное
решение задач учащимися у доски).
Пример № 3. Найти наибольшее значение функции
![]() на отрезке
на отрезке ![]()
Решение.
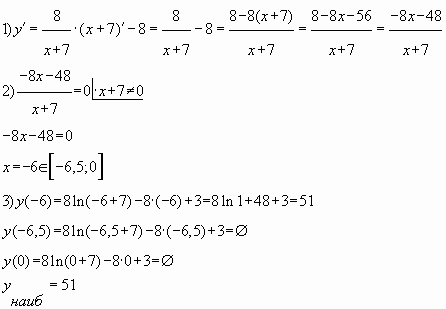
Ответ: 51
Пример № 4. Найти наименьшее значение функции
![]() на отрезке
на отрезке ![]()
Решение.
![]()
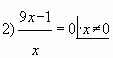
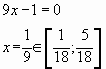
(![]() , так как
, так как ![]() )
)
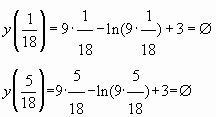
![]()
Ответ: 4
Пример № 5. Найти наименьшее значение функции
![]() на отрезке
на отрезке ![]()
Решение
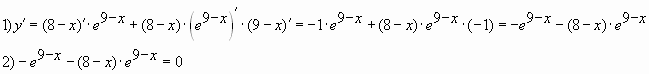
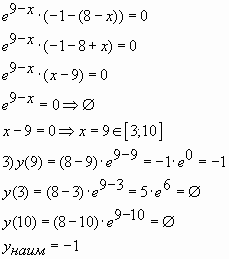
Ответ: -1
Пример № 6. Найти наибольшее значение функции
![]() на отрезке
на отрезке ![]()
Решение:
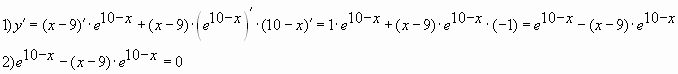
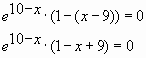
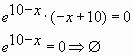
![]()
![]()
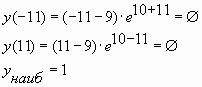
Ответ: 1
Пример № 7: Найдите наибольшее значение
функции ![]() на
на
отрезке ![]()
Решение
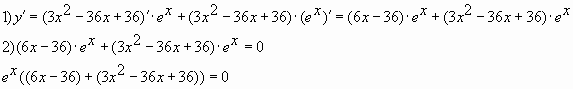
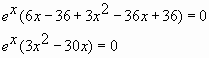
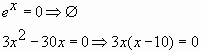
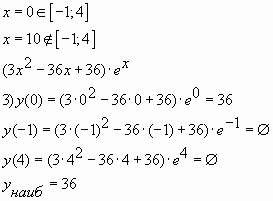
Ответ: 36
VI. Итоги урока.
- Повторить алгоритм нахождения наибольшего и
наименьшего значения функции на отрезке. - Проговорить основные алгоритмы решения тех
примеров, которые изучены на уроке.
VII. Домашнее задание по вариантам.
