Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.
Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.
Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].
Решение
Сначала вычисляем производную исходной функции:
y′=3×2−12xy’=3x^2-12x
Затем приравниваем ее к нулевому значению и решаем уравнение:
3×2−12x=03x^2-12x=0
x(3x−12)=0x(3x-12)=0
x1=0x_1=0
x2=4x_2=4
Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.
Находим значение функции в точке x1x_1:
f(0)=9f(0)=9
Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:
f(−1)=−1−6+9=2f(-1)=-1-6+9=2
f(2)=8−24+9=−7f(2)=8-24+9=-7
Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.
Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.
Решение
Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:
y′=6xy’=6x
Приравниваем производную к нулю:
6x=06x=0
x=0x=0
Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.
Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.
Тест по теме “Наибольшие и наименьшие значения функции”
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Исследование графика функции
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.
Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).
На нашем рисунке область определения функции — это отрезок
. Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок
— от самого нижнего до самого верхнего значения
.
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки
и
.
Значения функции положительны там, где . На нашем рисунке это промежутки
и
.
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от
до
.
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества
можно взять отрезок
, интервал
, объединение промежутков или всю числовую прямую.
Функция возрастает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Иными словами, чем больше , тем больше
, то есть график идет вправо и вверх.
Функция убывает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Для убывающей функции большему значению соответствует меньшее значение
. График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке
и убывает на промежутках
и
.
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и
на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и
.
А что делать, если нужно найти, например, минимум функции на отрезке
? В данном случае ответ:
. Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке
.
Можно сказать, что экстремумы функции равны и
.
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно
и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно
. Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Алгебра и начала математического анализа, 11 класс
Урок №17. Наибольшее и наименьшее значения функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение наибольшего и наименьшего значения функции,
2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,
3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений
Глоссарий по теме
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти область определения функции D(f).
- Найти производную f‘ (x).
- Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).
- Среди полученных значений выбрать наибольшее и наименьшее.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Нахождение наибольшего и наименьшего значений функции на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.
- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее
Примеры и разбор решения заданий тренировочного модуля
№1.Найти наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3]
Решение. Действуем в соответствии с алгоритмом.
1) D(f) = (-∞; +∞).
2) f (x) = 6x2 – 18x + 12
(x) = 6x2 – 18x + 12
3) Стационарные точки: х = 1; х = 2.

4) f(0) = -2
f(3) = 7
f(1) = 3
f(2) = 2
5) fнаим.=f(0) = -2
fнаиб.=f(3) = 7.
Ответ: fнаим= -2
fнаиб.= 7.
№2.Найдите два положительных числа, сумма которых равна 16, а произведение наибольшее.
Решение.
Пусть первое число равно х, 
Тогда второе число – 
Следовательно, 
Произведение этих чисел равно х(16 – х).
Составим функцию:
f(x) = x(16 – x)

x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.
Следовательно, в этой точке функция F(x) = x(16 – x) принимает наибольшее значение.
Следовательно, два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.
Ответ: 8 и 8
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^{n-1}, n∈N$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| ${1}/x{^n}, n∈N$ | $-{n}/{x^{n+1}}, n∈N$ |
| $√^n{x}, n∈N$ | ${1}/{n√^n{x^{n-1}}, n∈N$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | ${1}/{x}$ |
| $log_{a}x$ | ${1}/{xlna}$ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
$(f(x) ± g(x))′= f′(x)± g′(x)$
Пример:
Найти производную функции $f(x) = 3x^5 – cosx + {1}/{x}$
Производная суммы и разности равна производной каждого слагаемого
$f′(x)=(3x^5)′–(cosx)′+({1}/{x})’=15x^4+sinx-{1}/{x^2}$
2. Производная произведения.
$(f(x)∙g(x))′=f′(x)∙g(x)+f(x)∙g(x)′$
Пример:
Найти производную $f(x)=4x∙cosx$
$f′(x)=(4x)′∙cosx+4x∙(cosx)′=4∙cosx-4x∙sinx$
3. Производная частного
$({f(x)}/{g(x)})’={f^'(x)∙g(x)-f(x)∙g(x)’}/{g^2(x)}$
Пример:
Найти производную $f(x)={5x^5}/{e^x}$
$f'(x)={(5x^5)’∙e^x-5x^5∙(e^x)’}/{(e^x)^2}={25x^4∙e^x-5x^5∙e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= – sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ – это точка минимума.
Ответ: $-10,5$
Пример:
Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$
Решение:
1. Найдем производную функции $y′=30x^4-270x^2$
2. Приравняем производную к нулю и найдем стационарные точки
$30x^4-270x^2=0$
Вынесем общий множитель $30x^2$ за скобки
$30x^2(x^2-9)=0$
$30x^2(х-3)(х+3)=0$
Приравняем каждый множитель к нулю
$x^2=0 ; х-3=0; х+3=0$
$х=0;х=3;х=-3$
3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$
Нам подходят стационарные точки $х=0$ и $х=-3$
4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3
$y(-5)= 6∙(-5)^5-90∙(-5)^3-5=6∙(-3125)+90∙125-5= -18750+11250-5=-7505$
$y(-3)= 6∙(-3)^5-90∙(-3)^3-5=-1458+2430-5=967$
$y(0)= -5$
$y(1)= 6∙1^5-90∙1^3-5=6-90-5= -89$
Наибольшее значение равно $967$
Ответ: $967$
Преподаватель который помогает студентам и школьникам в учёбе.
Наибольшее и наименьшее значения функции с примерами решения
От максимумов и минимумов функции следует отличать её наибольшее и наименьшее значения на промежутке. Функция может иметь несколько максимумов (минимумов) на некотором промежутке (рис. 91), но не более одного наибольшего (наименьшего) значения. Функция может не иметь максимума (минимума) на промежутке, но иметь наибольшее (наименьшее) значение.
Например функция, график которой изображён на рисунке 91, наибольшее значение имеет в точке 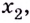
Наибольшее и наименьшее значения функции тесно связаны с её областью значений. Если область значений непрерывной функции — промежуток 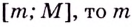 наименьшее значение данной функции,
наименьшее значение данной функции, 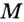 — наибольшее её значение.
— наибольшее её значение.
Поскольку непрерывная функция наибольшее и наименьшее значения может иметь только в точках экстремума или на концах отрезка, то для нахождения этих значений пользуются таким правилом.
Чтобы найти наибольшее и наименьшее значения непрерывной функции 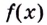 на промежутке
на промежутке 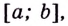 нужно вычислить её значения
нужно вычислить её значения 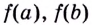 на концах данного промежутка и в критических точках, принадлежащих этому промежутку, а потом выбрать из них наибольшее и наименьшее.
на концах данного промежутка и в критических точках, принадлежащих этому промежутку, а потом выбрать из них наибольшее и наименьшее.
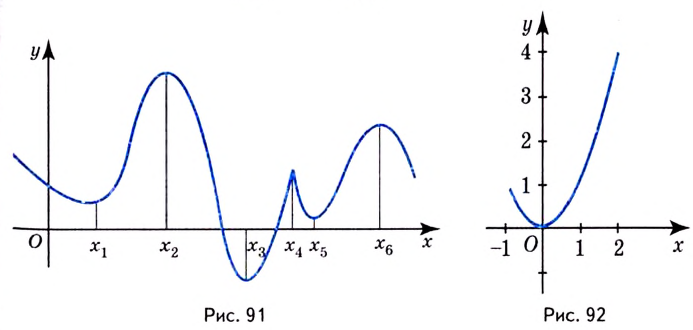
Записывают так: 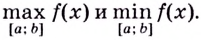
Пример №1
Найдите наибольшее и наименьшее значения функции 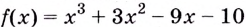 на промежутке
на промежутке 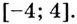
Решение:
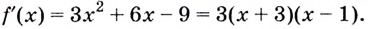 Критические точки:
Критические точки: 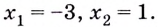
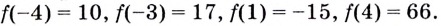
Из этих четырёх значений функции наименьшим является -15, а наибольшим — 66.
Ответ, 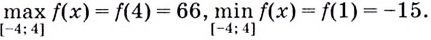
Пример №2
Найдите наибольшее и наименьшее значения функции 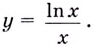
Решение:
Областью определения функции является промежуток 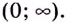
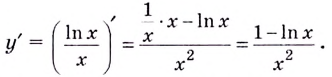
Если 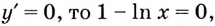 отсюда
отсюда 
Если 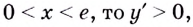 а если
а если 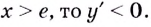 Следовательно,
Следовательно,  — точка максимума.
— точка максимума.
Поскольку на промежутке 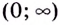 функция имеет только одну критическую точку
функция имеет только одну критическую точку 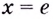 и эта точка является точкой максимума, то наибольшее значение функция принимает именно в этой точке и оно равно
и эта точка является точкой максимума, то наибольшее значение функция принимает именно в этой точке и оно равно 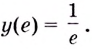 Наименьшего значения функция не имеет.
Наименьшего значения функция не имеет.
Ответ, 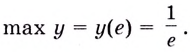 Наименьшего значения функция не имеет.
Наименьшего значения функция не имеет.
К нахождению наибольшего или наименьшего значений функции сводится решение многих прикладных задач.
Пример №3
Есть квадратный лист жести со стороной 60 см. Найдите размеры квадратов, которые надо вырезать в углах данного листа, чтобы из полученной заготовки сделать коробку наибольшего объёма {рис. 93).
Решение:
Чтобы получить коробку (в форме прямоугольного параллелепипеда), надо вырезать равные квадраты в углах листа. Пусть 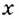 — длина стороны такого квадрата. Тогда высота коробки равна
— длина стороны такого квадрата. Тогда высота коробки равна 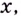 а сторона основания
а сторона основания 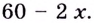 Объём коробки
Объём коробки 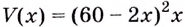 — функция от
— функция от 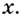
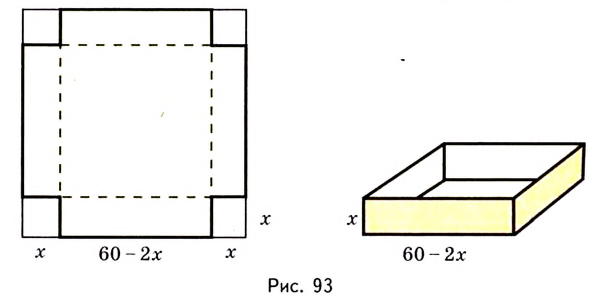
Надо исследовать математическую модель задачи: при каком значении 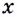 : функция
: функция 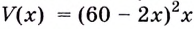 на промежутке
на промежутке 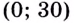 принимает наибольшее значение.
принимает наибольшее значение.
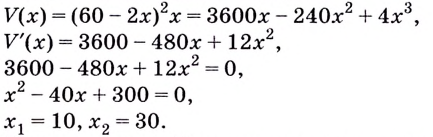
Значение  не принадлежит промежутку
не принадлежит промежутку 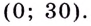 Поэтому
Поэтому 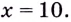
Поскольку при 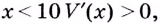 а при
а при 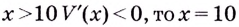 — точка максимума. Итак, в этой точке функция
— точка максимума. Итак, в этой точке функция 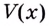 принимает наибольшее значение.
принимает наибольшее значение.
Ответ. Надо вырезать квадраты, стороны которых равны 10 см.
- Заказать решение задач по высшей математике
Пример №4
Найдите область значений функции 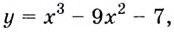 если
если 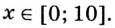
Решение:
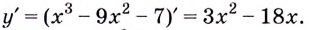 Найдём критические точки:
Найдём критические точки: 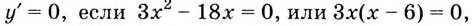 отсюда
отсюда 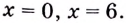
Найдём значение функции на концах промежутка 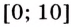 и в критических точках:
и в критических точках: 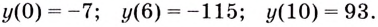
Заданная функция непрерывна, её наибольшее значение 93, а наименьшее -115, значит, область её значений — отрезок 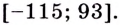
Ответ. 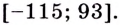
Пример №5
Найдите кратчайшее расстояние от точки 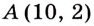 до графика функции
до графика функции 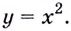
Решение:
Пусть ближайшая к 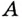 точка
точка 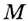 графика функции имеет абсциссу
графика функции имеет абсциссу 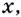 её ордината равна
её ордината равна 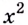 (рис. 94). Найдём квадрат расстояния между точками
(рис. 94). Найдём квадрат расстояния между точками 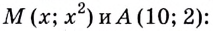
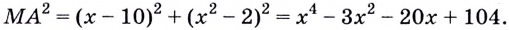 Длина расстояния
Длина расстояния  наименьшая, когда её квадрат наименьший. Итак, найдём наименьшее значение функции
наименьшая, когда её квадрат наименьший. Итак, найдём наименьшее значение функции 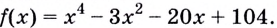
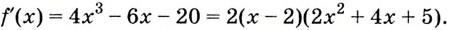
Уравнение 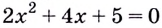 действительных корней не имеет, поэтому функция
действительных корней не имеет, поэтому функция 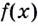 имеет одну критическую точку
имеет одну критическую точку 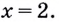 Если
Если 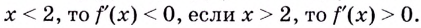 Следовательно,
Следовательно, 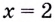 — точка минимума. В этой точке функция
— точка минимума. В этой точке функция 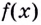 принимает наименьшее значение.
принимает наименьшее значение.
Наименьшее значение квадрата расстояния
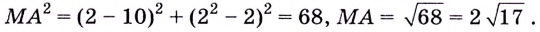
Ответ. 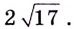
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Рациональная дробь
- Функция в математике
- Правило Лопиталя
- Вычисления в Mathematica с примерами

