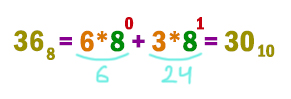
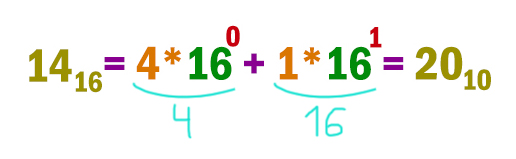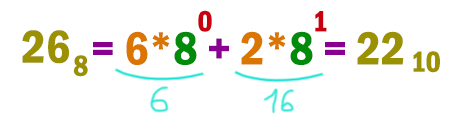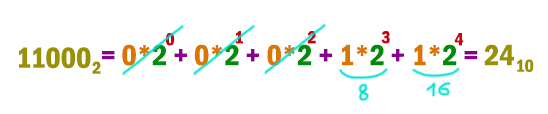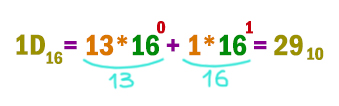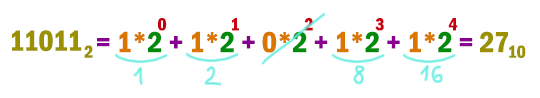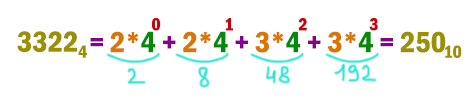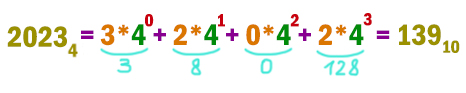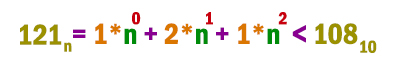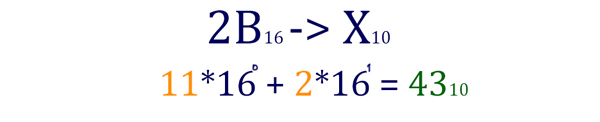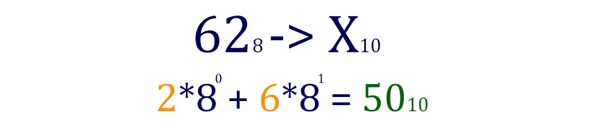Как найти наибольшее основание системы счисления - Сайт, где вы сможете решить свои вопросы

Формулировка задания: Запись числа в системе счисления с основанием N содержит 3 цифры и оканчивается на K. Чему равно максимально возможное основание системы счисления?

Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).

Рассмотрим, как решаются подобные задания на примере.

Пример задания:

Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?

Решение:

Пусть трехзначное число в системе счисления с основанием N выглядит так:

ab2_N, a < N, b < N

где a и b – цифры в системе счисления с основанием N.

Переведем число ab2_N в десятичную систему счисления:

ab2_N = a ⋅ N² + b ⋅ N + 2 = 338

aN² + bN = 336

Получается, что:

N² ≤ 336

Максимально возможное значение N равно 18, так как:

18² = 324 < 336

19² = 361 > 336

Подберем такое максимальное N ≤ 18, чтобы выполнялось:

N ⋅ (aN + b) = 336

То есть N должно быть делителем числа 336:

18:

336 / 18 = 18.666… – не является делителем

17:

336 / 17 = 19.764… – не является делителем

16:

336 / 16 = 21

16a + b = 21

a = 1, b = 5

338₁₀ = 152₁₆

Таким образом, максимально возможное основание системы счисления равно 16.

Ответ: 16

Источник

: May 16 2015, 21:18

Category:

Образование
Cancel

Подготовка к ЕГЭ: системы счисления

Задание 9
Укажите наибольшее основание системы счисления, в которой запись числа 15 имеет ровно 3 значащих разряда.
Решение:
Поскольку по условию задачи запись числа 15 в системе счисления с основанием р имеет три значащих разряда, то можно записать
100_p ≤ 15 < 1000_p следовательно, P² ≤ 15 < P³
Решаем первую часть неравенства: р²≤ 15. Получаем: р < 4. Поскольку имеем строгое неравенство, ответом не может быть р=4. Поэтому ответом будет р=3.
Проверяем вторую часть неравенства: Р³ > 15 3³>15 27>15 – что соответсвеут условию задачи.
Ответ: 3

Задание 10
Укажите наименьшее основание системы счисления, в которой запись числа 19 имеет ровно 3 значащих разряда. (3)

Задание 11
Укажите наименьшее основание системы счисления, в которой запись числа 65 имеет ровно 3 значащих разряда.
Ответ: 5

Задание 12
Укажите наименьшее основание системы счисления, в которой запись числа 130 имеет ровно 4 значащих разряда.
Ответ: 5

Задание 13
Укажите наименьшее основание системы счисления, в которой запись числа 65 имеет ровно 3 значащих разряда.
Ответ: 5
Задание 14
Укажите наименьшее основание системы счисления, в которой запись числа 97 имеет ровно 3 значащих разряда.
Ответ: 6

Источник

Привет! Сегодня исследуем 10 Задание из ОГЭ по информатике 2023.

Задание 9 из ОГЭ по информатике Вы можете научиться решать, прочитав статью по 13 заданию из ЕГЭ по информатике. Эту статью Вы можете найти здесь.

Десятое задание проверяет умение работать с различными системами счисления.

Задача (Классическая)

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

14₁₆, 26₈, 11000₂.

Решение:

Число 14 находится в шестнадцатеричной системе. Об этом говорит маленький индекс возле числа. Переведём его в нашу родную десятичную систему.

Берём поочередно цифры, начиная с младшего разряда. Первую правую цифру умножаем на 16 в нулевой степени, вторую цифру на 16 в первой степени и т.д. Умножаем на 16, потому что переводим из шестнадцатеричной системы. Степень потихоньку увеличивается на 1.

Необходимо помнить, что любое число в нулевой степени это единица!

Остаётся только посчитать полученный пример. Получается число 20 в десятичной системе.

Переведём число 26₈ из восьмеричной системы в нашу родную десятичную систему. Делаем аналогично предыдущему примеру.

Аналогично переведём число и из двоичной системы.

Наибольшее из трёх чисел это 24.

Ответ: 24

Задача (Классическая, закрепление)

1D₁₆, 36₈, 11011₂

Решение:

В шестнадцатеричной системе буквы при переводе в десятичную систему нужно превратить в числа.

A	B	C	D	E	F
10	11	12	13	14	15

Переведём первое число.

Переведём второе число.

Переведём третье число.

Наибольшее число получается 30.

Ответ: 30

Задача (Из десятичной в двоичную)

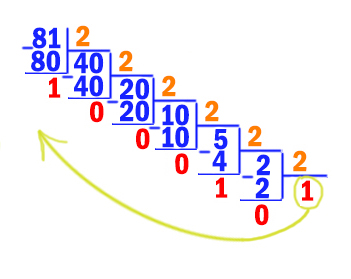
Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

59₁₀, 71₁₀, 81₁₀

Решение:

Нужно каждое число перевести в двоичную систему счисления.

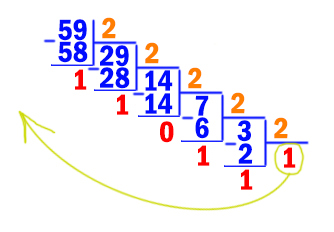
Переведём число 59₁₀ в двоичную систему.

Получается 59₁₀ = 111011₂. Здесь мы делим уголком на 2 (на основание системы, куда переводим) с остатком. Продолжаем делить, пока не получим 1. Затем остатки записываем задом наперёд. Получается число в двоичной системе счисления. Последнее число 1 (единицу) тоже берём.

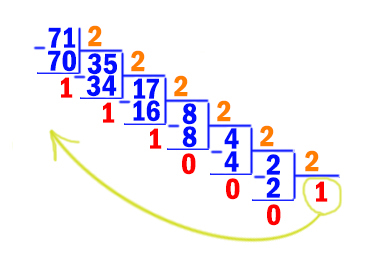
Переведём число 71₁₀ в двоичную систему.

Получается 71₁₀ = 1000111₂.

Переведём число 81₁₀ в двоичную систему.

Получается 81₁₀ = 1010001₂.

Найдём количество единиц для каждого числа, записанного в двоичной системе.

111011₂, Кол. ед.: 5
1000111₂, Кол ед.: 4
1010001₂, Кол ед.: 3

Ответ: 3

Задача (Из десятичной в восьмеричную)

Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, сумма цифр которого в восьмеричной записи наименьшая. В ответе запишите сумму цифр в восьмеричной записи этого числа.

86₁₀, 99₁₀, 105₁₀

Решение:

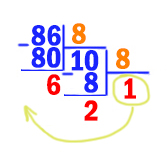
Переведём число 86₁₀ в восьмеричную систему.

Делаем аналогично тому, как мы переводили в двоичную систему, только теперь уголком делим на 8. Остатки могут получатся от 0 до 7.

Как только в результате деления получили число меньшее, чем 8, то завершаем процесс перевода.

Остатки опять записываем задом наперёд. Последнее число тоже участвует в формировании результата наравне с остатками.

Получается 86₁₀ = 126₈.

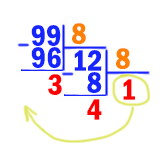
Переведём число 99₁₀ в восьмеричную систему.

Получается 99₁₀ = 143₈.

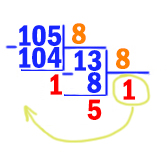
Переведём число 105₁₀ в восьмеричную систему.

Получается 105₁₀ = 151₈.

Найдём сумму цифр у полученных чисел.

126₈, Сумма цифр: 9
143₈, Сумма цифр: 8
151₈, Сумма цифр: 7

Наименьшая сумма цифр равна 7.

Ответ: 7

Разберём несколько нестандартных тренировочных задач для подготовки к 10 заданию ОГЭ по информатике.

Задача(Неожиданная)

Число 3322_n записано в системе счисления с основанием n (n > 1). Определите наименьшее возможное значение n. Для этого значения n в ответе запишите представление данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Наименьшее значение n в этой задаче может быть равно 4, потому что самая большая цифра – это тройка. Мы берём на 1 больше, т.к. в четверичной системе могут применяться только цифры: 0, 1, 2, 3. Тоже самое, как в нашей родной десятичной системе могут применяться 10 цифр: от нуля, до девяти. Самая большая цифра в нашей родной десятичной системе девятка.

Осталось перевести данное число из четверичной системы в десятичную.

Ответ: 250

Задача (Уже знаем)

Число 2023_n записано в системе счисления с основанием n (n > 1). Определите значение n, при котором данное число минимально. Для этого значения n в ответе запишите представление данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Здесь нужно, чтобы само число 2023_n было минимальным. Но это число будет минимальным, если мы выберем самое маленькое значение n при данных цифрах.

Самое маленькое основание системы может вновь 4. Переведём наше число 2023₄ из четверичной системы в десятичную.

Получается число 139.

Ответ: 139

Задача (Крепкий орешек)

Число 121_n записано в системе счисления с основанием n (n > 1). Определите наибольшее возможное значение n, для которого 121_n < 108₁₀. Для этого значения n в ответе запишите представления данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Мы не знаем в какой системе счисления записано число. Но всё равно начнём переводить его в десятичную систему, оставив переменную n в виде неизвестной.

Попробуем подобрать n.

При n=10

1*10⁰ + 2*10¹ + 1*10² = 121 > 108₁₀

Перебор. Ну это и так было понятно.

Значит, нужно уменьшать n. Возьмём n = 9.

1*9⁰ + 2*9¹ + 1*9² = 100 < 108₁₀

Как раз получилось число, которое меньше числа 108₁₀. Это и есть наибольшее n!

В ответе просили перевести исходное число в десятичную систему. Это и есть число 100, уже всё переведено.

Ответ: 100

Задача (Не все цифры одинаковые)

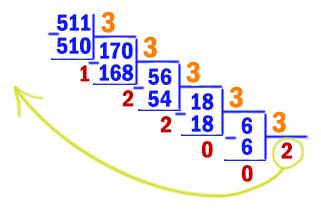
Десятичное число 511 записано в системе счисления с основанием n (n > 1). Определите минимальное значение n, при котором в полученной записи числа не все цифры одинаковые. В ответе запишите запись числа в системе счисления с найденным основанием n. Основание системы счисления указывать не нужно.

Решение:

Начнём перебирать основание системы n, начиная с наименьшего значения 2. Переведём число 511₁₀ в двоичную систему.

Можно переводить стандартно, через деление уголком на 2. Но в данном случае видно, что число 511 близко к 512. Число 512 = 2⁹.

Существует правило:

2⁴ = 10000₂
2⁶ = 1000000₂

Т.е. степень двойки показывает, сколько после единицы нулей у числа в двоичной системе.

Это касается любой системы счисления.

3² = 100₃
3³ = 1000₃

Наше число

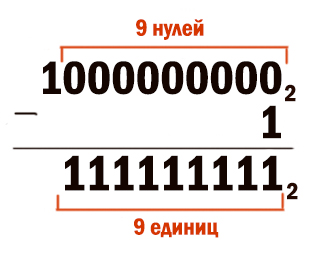
511₁₀ = 512₁₀ – 1 = 2⁹ – 1 = 1000000000₂ – 1

Сделаем вычитание столбиком.

Вычитание или суммирование столбиком в любой системе счисления выполняются так же, как и в нашей системе счисления. Здесь мы вычитаем единицу из нуля. Ноль идёт занимать у более старшего разряда и т.д. В итоге обращаемся к самой старшей единице. Эта единица превращается в младшем разряде в двойку, потому что работаем в двоичной системе. Как и в нашей системе, когда занимаем у старшего разряда единицу, она превращается в десяток. В итоге каждая двойка отдаёт единицу в младший разряд. В самом младшем разряде получается действие 2-1=1. А все разряды, т.к. отдали единицу в младший разряд превратятся в 1.

Получается 511₁₀ = 200221₃.

Видим, что не все цифры у числа одинаковые в троичной системе. И число n = 3 – это минимально возможное число.

Ответ: 200221

Задача(Диапазон чисел)

Сколько существует целых чисел x, для которых выполняется неравенство

2B₁₆ < x < 62₈?

В ответе укажите только количество чисел, сами числа писать не нужно.

Решение:

Нам нужно узнать сколько чисел находятся в диапазоне от 2B₁₆ до 62₈.
Переведём числа 2B₁₆ и 62₈ в нашу родную десятичную систему счисления. Затем, мы уже сможем сообразить, сколько чисел вмещается в этот диапазон.

Чтобы перевести число из любой системы счисления в нашу родную десятичную, необходимо воспользоваться методом “возведения в степень”.

Начинаем с младшего разряда. Цифра “B” превращается в 11. 2B₁₆ = 43₁₀. Теперь переведём число
62₈ в десятичную систему.

Таким образом, наше неравенство принимает вид 43 < x < 50. Кажется, что нужно сделать 50 – 43 = 7. Но если мы подставим небольшие числа 4 < x < 6, то мы увидим, что метод 6-4=2 неверен. Число будет только одно: 5 (пять). Поэтому и от нашего числа 7 мы тоже должны отнять единицу. 7 – 1 = 6. И ответ будет 6.

Если бы у нас было в одном месте знак “больше или равно”: 2B₁₆ ≤ x < 62₈, то мы бы оставили число 7. А если было бы два знака “больше или равно”, то даже прибавили единицу.

Ответ: 6

Источник

Автор – Лада Борисовна Есакова.

Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.

Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:

Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.

Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.

Например, $212_{3} = 2+1*3+2*3^{2} = 23_{10}$ . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 = $12_{3}$ ).

Вернемся опять к привычной десятичной системе. Число $10^{5}$ = 100000. Т.е. 10 в степени k– это единица и k нулей.

Аналогичное утверждение справедливо для любой системы счисления:

Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.

Например, $2^{4}=16_{10}=10000_{2}$ .

1. Поиск основания системы счисления

Пример 1.

В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда $27=30_{x}=0 cdot x^{0}+3 cdot x^{1}=3 cdot x$ .Т.е. x = 9.

Ответ: 9

Пример 2.

В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда $13 = 111_{x} = 1*x^{0} + 1*x^{1} +1*x^{2}$

$x^{2}+x+1 = 13$

$x^{2}+x-12 = 0$

Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.

Ответ: 3

Пример 3

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.

Решение:

Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,

Ответ: 6, 8, 12, 24

Пример 4

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Решение:

Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).

Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.

Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.

2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:

68:4 = 17; 17:4 = 4 (ост 1) – подходит

68:17 = 4; 4:17 = 0 (ост 4) – не подходит

68:34 = 2; 2:17 = 0 (ост 2) – не подходит

68:68 = 1; 1:68 = 0 (ост 1) – подходит

Ответ: 4, 68

2. Поиск чисел по условиям

Пример 5

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?

Решение:

Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.

$25_{10} = 121_{4}$ . Т.е. нам нужно найти все числа, не больше $121_{4}$ , запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа $11_{4}$ и $111_{4}$ . Переводим их в десятичную систему счисления:

$11_{4}=1*4^{0}+1*4^{1}=5_{10}$

$111_{4}=1*4^{0}+1*4^{1}+1*4^{2}=21_{10}$

Ответ: 5, 21

3. Решение уравнений

Пример 6

Решите уравнение: $121_{x}+1_{10}=101_{7}$

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Решение:

$121_{x}+1_{10}=10_{17}$ Переведем все числа в десятичную систему счисления:

$1*x^{0}+2*x^{1}+1*x^{2}+1=1*7^{0}+0*7^{1}+1*7^{2}$

$1 + 2*x + x^{2} + 1 = 1 + 49$

$x^{2} + 2*x- 48=0$

Квадратное уравнение имеет корни -8 и 6. $x=6_{10}$ (т.к. основание системы не может быть отрицательным). $x=6_{10}=20_{3}$ .

Ответ: 20

4. Подсчет количества единиц (нулей) в двоичной записи значения выражения

Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:

При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.

При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу. Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.

Пример 7

Сколько единиц содержится в двоичной записи значения выражения: $4^{2020} + 2^{2017} -15$ ?

Решение:

Представим все числа выражения, как степени двойки:

$4^{2020} + 2^{2017} -15=2^{4040}+2^{2017}-2^{4}+2^{0}$

В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя $4^{4040}$ и $2^{2017}$ , получим число, содержащее 2 единицы:

Теперь вычтем из получившегося числа 10000. По правилам вычитания занимаем у следующего разряда.

Теперь прибавляем к получившемуся числу 1:

Видим, что у результата 2013+1+1=2015 единиц.

Ответ: 2015.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки, арифметические действия в различных системах.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

14-е задание: «Операции в системах счисления»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 5 минут.

Проверяемые элементы содержания: Знание позиционных систем счисления

До ЕГЭ 2021 года — это было задание № 16 ЕГЭ

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Содержание:

Определите наибольшее/наименьшее значение x, y
Сколько цифр и сумма цифр
Найти основание системы счисления и уравнения

Определите наибольшее/наименьшее значение x, y

14_14:

Операнды арифметического выражения записаны в системе счисления с основанием 15.

82x19₁₅ – 6x073₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

Ответ: 7806

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
begin
  foreach var x in '0123456789abcde' do
  begin
    var a := dec('82'+ x +'19', 15);
    var b :=dec('6' + x +'073', 15);
    var sum := a - b;
    if sum mod 11 = 0 then
    begin
      print(sum / 11);
      break;
    end
  end;
end.

Python:

С++:

Сколько цифр и сумма цифр

14_12:

Значение арифметического выражения

43∙7¹⁰³ – 21∙7⁵⁷ + 98

записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.

Ответ: 276

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

begin
  var x,s: Biginteger;
  x := 43*Biginteger.Pow(7, 103) - 21*Biginteger.Pow(7, 57) + 98;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  s:=0;
  while x > 0 do
  begin
    s:=s+ x mod 7; // добавляем цифру правого разряда
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(s);
end.

PascalABC.net, Решение 2:

uses school;
 
begin
  var n: bigInteger;
  n := 43 * Biginteger.Pow(7, 103) - 21 * Biginteger.Pow(7, 57) + 98;
  print(n.ToString.ToBase(7).CountOf('1') +
    n.ToString.ToBase(7).CountOf('2') * 2 + 
    n.ToString.ToBase(7).CountOf('3') * 3 +
    n.ToString.ToBase(7).CountOf('4') * 4 +
    n.ToString.ToBase(7).CountOf('5') * 5 +
    n.ToString.ToBase(7).CountOf('6') * 6);
end.

Python:

x = 43*7**103 - 21*7**57 + 98
s = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    s+= x % 7 # добавляем цифру к сумматору
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( s )

С++:

14_1:

Значение арифметического выражения:
2¹⁰²⁴ + 4⁶⁴ — 64
записали в системе счисления с основанием 2.

Ответ: 123

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net, Решение 1:

begin
  var k := 0;
  var x: Biginteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  // в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
  while x > 0 do
  begin
    if x mod 2 = 1 then k += 1; // если цифра = 1, то считаем ее
    x := x div 2; // убираем разряд числа в 2-й системе сч.
  end;
  println(k);
end.

PascalABC.net, Решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(2, 1024) + Biginteger.Pow(4, 64) - 64;
  print(x.ToString.ToBase(2).CountOf('1'));
end.

Python:

x = 2**1024 + 4**64 - 64
k = 0
# в получившемся числе рассматриваем каждую цифру в 2-й системе сч.
while x: 
    if x % 2 == 1: # если цифра = 1, то считаем ее
        k += 1
    x //= 2 # убираем разряд числа в 2-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Существует правило:

2^N = 10..0₂(1 единица и N нулей)

Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:

2¹⁰²⁴ + (2²)⁶⁴ - 2⁶ = 2¹⁰²⁴ + 2¹²⁸ - 2⁶

При переводе в двоичную систему получим:

10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)

Обратим внимание, что разница между числами большая. Т.е. при выполнении сложения в столбик, единицы в одном и том же разряде быть не могут. Так:

 10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0

Из первого слагаемого 10…0 (1024 нуля) запомним одну единицу в старшем бите, остальные нули нас не интересуют, так как далее мы воспользуемся другим правилом — для разницы:

 10....00000  - 1024 нуля
+
       10..0  - 128 нулей
_________________________
 10....10..0  - запомним единицу

Существует также правило:

2^N — 2^K = 1…1 (N - K единиц)0…0(K нулей)

По формуле выполним вычитание 2¹²⁸ — 2⁶: получим 1..1 (122 единицы) 0..0(6 нулей):

 10..0000000  - 128 нулей
-
     1000000  
_________________________
 11..1000000  - 122 единицы и 6 нулей

Прибавим к 122 получившимся единицам еще одну из первого слагаемого (10…0 (1024 нуля)) и получим:

122 + 1 = 123 единицы

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

14 задание. Демоверсия ЕГЭ 2018 информатика:

Значение арифметического выражения:
49¹⁰ + 7³⁰ – 49
записали в системе счисления с основанием 7.

Сколько цифр «6» содержится в этой записи?

Типовые задания для тренировки

Ответ: 18

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net, решение 1:

begin
  var x: Biginteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  // в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
  var k:=0;
  while x > 0 do
  begin
    if x mod 7 = 6 then k+=1; // если цифра = 6, то считаем ее
    x := x div 7; // убираем разряд числа в 7-й системе сч.
  end;
  println(k);
end.

PascalABC.net, решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(49, 10) + Biginteger.Pow(7, 30) - 49;
  print(x.ToString.ToBase(7).CountOf('6'));
end.

Python:

x = 49**10 + 7**30 - 49
k = 0
# в получившемся числе рассматриваем каждую цифру в 7-й системе сч.
while x: 
    if x % 7 == 6: # если цифра = 6, то считаем ее
        k += 1
    x //= 7 # убираем разряд числа в 7-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Приведем все числа к степеням 7:

7²⁰ + 7³⁰ - 7²

Расставим операнды выражения в порядке убывания степеней:

7³⁰ + 7²⁰ - 7²

Вспомним две формулы для работы со системами счисления:

1.
aⁿ = 10..0_a
       ⁿ
2.
aⁿ - a^m = (a-1)..(a-1)0..0_a
              ^n-m       ^m

Переведем первое число согласно формуле 1:

7³⁰ = 10..0
        ³⁰

В данном числе нет цифры 6, как и в остальных числах.
Цифра 6 появляется при выполнении вычитания.
Подсчитаем все «6», используя формулу 2:

0 + (20 - 2) = 18

Получаем шестерок: 18

Результат: 18

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

14_2:

Значение арифметического выражения:
4⁵⁰⁰ + 3*4²⁵⁰⁰ + 16⁵⁰⁰ — 1024
записали в системе счисления с основанием 4.

Сколько цифр «3» содержится в этой записи?

Типовые задания для тренировки

Ответ: 496

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,500) + 3*Biginteger.Pow(4,2500) + Biginteger.Pow(16,500) - 1024;
  print(x.ToString.ToBase(4).CountOf('3'));
end.

Python:

x = 4**500 + 3*4**2500 + 16**500 - 1024
k = 0
# в получившемся числе рассматриваем каждую цифру в 4-й системе сч.
while x: 
    if x % 4 == 3: # если цифра = 3, то считаем ее
        k += 1
    x //= 4 # убираем разряд числа в 4-й системе сч.
print( k )

С++:

Результат: 496

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

14_5:

Значение арифметического выражения: 8¹⁰²⁴ + 8³² – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?

Типовые задания для тренировки

Ответ: 31

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(8,1024) + Biginteger.Pow(8,32) - 65;
  print(x.ToString.ToBase(8).CountOf('7'));
end.

Python:

x = 8**1024 + 8**32 - 65
k = 0
# в получившемся числе рассматриваем каждую цифру в 8-й системе сч.
while x: 
    if x % 8 == 7: # если цифра = 7, то считаем ее
        k += 1
    x //= 8 # убираем разряд числа в 8-й системе сч.
print( k )

С++:

✎ Решение теоретическое:

Приведем все числа к степеням восьмерки:

65 = 64 + 1 = 8² + 8⁰;

Получаем:

8¹⁰²⁴ + 8³² - (8² + 8⁰);
8¹⁰²⁴ + 8³² - 8² - 8⁰

Вспомним две формулы для работы с системами счисления:

1.
aⁿ = 10..0_a
       ⁿ
2.
aⁿ - a^m = (a-1)..(a-1)0..0_a
              ^n-m       ^m

Переведем первое число согласно формуле 1:

8¹⁰²⁴ = 10..0
        ¹⁰²⁴

В данном числе нет цифры 7, как и в остальных числах.
Цифра 7 появляется при выполнении вычитания. У нас два таких действия, идущих подряд. Это неудобно. Необходимо, чтобы действия чередовались (a + b — c + d — e…)
Вспомним еще одну формулу:

-2ⁿ = -2ⁿ⁺¹ + 2ⁿ

! Формула предназначена для чисел в двоичной системе счисления, но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать (для поиска единиц или нулей она не подходит!!!)

В нашем случае заменим часть выражения:

-8² = -8³ + 8²
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)


Получаем:

8¹⁰²⁴ + 8³² - 8³ + 8²- 8⁰

Получили чередование операций «+» и «-«.
Теперь посчитаем все «7», используя формулу 2:

0 + (32 - 3) + (2 - 0) = 31

Получаем семерок: 31

14_13:

Сколько значащих нулей в двоичной записи числа 4³⁵⁰ + 8³⁴⁰ – 2³²⁰ – 12?

Ответ: 324

Показать решение:

✎ Решение с использованием программирования:

PascalABC.net:

begin
  var b2 := biginteger(2);
  var numb := (2 * b2) ** 350 + (4 * b2) ** 340 - (1 * b2) ** 320 - 12;
  var digit: biginteger;
  var n := 0;
  while numb > 0 do
  begin
    digit := numb mod 2;
    if digit = 0 then n += 1;
    numb := numb div 2
  end;
  print(n)
 end.

PascalABC.net, решение 2:

uses school;
 
begin
  var x: bigInteger;
  x := Biginteger.Pow(4,350) + Biginteger.Pow(8,340) - Biginteger.Pow(2,320) - 12;
  print(x.ToString.ToBase(2).CountOf('0'));
end.

Python:

x = 4**350 + 8**340 - 2**320 - 12
print(x)
k = 0
while x:
  if x % 2 == 0: k += 1
  x //= 2
     print( k )

С++:

✎ Решение теоретическое:
4³⁵⁰ + 8³⁴⁰ – 2³²⁰ – 12

По возможности приведем каждое слагаемое к степеням 2. Получим:

(2²)³⁵⁰ + (2³)³⁴⁰ - 2³²⁰ - 3*2² =
(2²)³⁵⁰ + (2³)³⁴⁰ - 2³²⁰ - 12 =
2⁷⁰⁰ + 2¹⁰²⁰ - 2³²⁰ - (2³ + 2²)

Далее рассуждаем так: количество нулей можно найти, если из общего количества цифр в результирующем числе вычесть количество не нулей (любых других цифр).

Расположим операнды по убыванию:

2¹⁰²⁰ + 2⁷⁰⁰ - 2³²⁰ - 2³ - 2²

Наибольшее число 2¹⁰²⁰, в нем 1021 разряд в двоичной с.с. (одна единица и 1020 нулей). То есть всего 1021 знаков.

Для того, чтобы избежать два подряд идущих минуса, воспользуемся правилом -2ⁿ = -2ⁿ⁺¹+2ⁿ и преобразуем выражение:

2¹⁰²⁰ + 2⁷⁰⁰ - 2³²¹+ 2³²⁰- 2⁴ + 2³ - 2²

Посчитаем количество не нулей в каждом операнде:

2¹⁰²⁰ -> один не ноль
2⁷⁰⁰ - 2³²¹ -> 379 не нулей
2³²⁰- 2⁴ -> 316 не нулей 
2³ - 2² -> один не ноль
Итого: 1+ 379+316 +1 = 697

Получаем нулей:

1021 - 697 = 324

Результат: 324

Найти основание системы счисления и уравнения

14_7:

Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.

Типовые задания для тренировки

Ответ: 13

Показать решение:

Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:

1.
 13 | 3 
 12   4 | 3 
  1   3   1   
      1
131₀ = 111₃

2.
23 | 3 
21   7 | 3 
2    6   2
     1
23₁₀ = 212₃

Теперь добавим промежуточные числа в троичной системе счисления (прибавляя единицу к каждому очередному полученному числу), не забывая, что в троичной системе всего три цифры (0, 1 и 2):

111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

На всякий случай стоит посчитать количество полученных чисел и сравнить их с количеством чисел в исходной последовательности.
Теперь осталось посчитать количество цифр 2 в полученной последовательности. Их 13:

111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212

Ответ: 9

Показать решение:

Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):

204_N+1 = 204_N + 26₁₆
 1       2     3

Используем формулу разложения числа по степеням основания:

1. 
₂₁₀
204_N+1

По формуле получаем:
2*(N+1)² + 0*(N+1)¹ + 4*(N+1)⁰ =
= 2*(N² + 2N + 1) + 0 + 4 = 2N² + 4N + 6

Выполним то же самое для остальных двух частей:

2.
₂₁₀
204_N

По формуле получаем:
2*N² + 0*N¹ + 4*N⁰ =
= 2N2 + 4

3.
26₁₆ = 38₁₀

Подставим результаты всех частей в уравнение:

2N² + 4N + 6 = 2N² + 4 + 38;
4N = 36;
N = 9

Ответ: 7

Показать решение:

Вместо обозначения искомой системы счисления введем неизвестное x:

144_x + 24_x = 201_x

Запишем формулу перевода в десятичную систему счисления каждого из слагаемых и сумму исходного равенства:

144 + 24 = 201
1*x² + 4*x¹ + 4*x⁰ + 2*x¹ + 4*x⁰ = 2*x² + 0*x¹ + 1*x⁰

Упростим полученное уравнение:

x² - 6x - 7 = 0

Решим уравнение:

D = b² - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7

14_9:

В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.

Типовые задания для тренировки

Ответ: 13

Показать решение:

Вспомним правило:

Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X

Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:

94 / x = некоторое число и остаток 3
и
68 / x = некоторое число и остаток 3

Поскольку x должно быть целым числом, то следующее деление должно выполняться без остатка:

91/x 
65/x

Иными словами x — наибольший общий делитель чисел 91 и 65.
Найдем НОД, например, по алгоритму Евклида:

91 - 65 = 26
65 - 26 = 39
39 - 26 = 13
26 - 13 = 13

Получаем результат 13.

14_10:

Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:

X = *5₁₆ = *0*₈

Сколько чисел соответствуют условию задачи?

Типовые задания для тренировки

Ответ: 3

Показать решение:

Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:

1. *5₁₆
    *   |    5  ₁₆

* * * * | 0 1 0 1 ₂

2. *0*₈
  *  |  0  |  *  ₈
* * *|0 0 0|* * * ₂

Сопоставим известные и неизвестные биты в обеих получившихся масках:

* * 0 0 0 1 0 1

Неизвестными остались 7-й и 8-й бит. Они не могут быть одновременно нулями, так как для *0*₈ тогда исчезнет старший разряд. Поэтому оставшиеся варианты будут такими:

1. 01000101
2. 10000101
3. 11000101

Итого 3 варианта.

📹 Видео (аналитическое решение
📹 Видеорешение на RuTube здесь)

14_4:

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.

Типовые задания для тренировки

Ответ: 8,72

✍ Показать решение:

Так как 75 должно оканчиваться на 13, то имеем два общих случая:

1. 75₁₀ = 13_N 
2. 75₁₀ = ...13_N (число оканчивается на 13)

Рассмотрим подробно каждый случай.

1 случай:

Остаток должен быть равен 3 (последнее число в неизвестной системе), а частное должно равняться 1 (предпоследнее число в неизвестной системе):

 75|N 
  N|1  отсюда имеем => 75 - N = 3; т.е. N = 72
  3

Таким образом, мы получили одно из искомых оснований (72).

2 случай:

Искомое оканчивается на цифру 3, значит:

 75|N 
 72|y  отсюда имеем => 75 = Ny + 3, где N - целое, неотриц.
  3

и далее, частное от деления — 1 (предпоследнее число):

 75|N  
 72|  y |N   => y = Nz + 1, где z - целое, неотриц.
  3  y-1|z
       1

Получаем два равенства (систему уравнений):

75 = Ny + 3
y = Nz + 1

Подставим y из второго равенства в первое:

75 = N (Nz + 1) + 3;
75 = N²z + N + 3;
75 = N²z + N

Выразим z:

z = (72 - N)/N²

Учитывая то, что z — целое неотрицательное число, то 72 — N должно быть кратно N², т.е. в числителе не может быть простого числа.
Простое число 67 получается путем вычитания из 72 числа 5. Соответственно, 5 нам не подходит: N ≠ 5:

72 - 5 / 5² = 67 / 25  не делится, - не подходит!

Еще одно простое число — 71 получится при вычитании 72 — 1. Единица не подходит, так как при переводе в конце числа никак не останется 13: N ≠ 1.
Раз в знаменателе N², то отбросим все числа, квадрат которых больше 72: 9, 10, … и т.д. до бесконечности: N < 9
Раз в итоговом числе есть число 13, значит основание системы счисления больше 3 (т.е. цифра три присутствует в системах, начиная с 4-й): N >= 4
Проверим оставшиеся варианты — 4, 6, 7, 8:

 75 | 4 
 72 | 18| 4 
  3   16| 2
       2  => не подходит! должна быть единица

 75 | 6 
 72 | 12| 6 
  3   12| 1
       0  => не подходит! должна быть единица

 75 | 7 
 70 
  5 => не подходит! должна быть 3

 75 | 8 
 72 | 9| 8 
  3   8| 1
       1  => подходит!

📹 Видео (аналитический способ)
📹 Видеорешение на RuTube здесь

14_11:

Выражение 2⁵*3²⁵ записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.

Ответ: «0»=26, «1»=2, «2»=1

Показать решение:

Первый сомножитель:

2⁵ = 32

Переведем в троичную систему счисления (делением на 3, переписываем остатки).
Результат:
32₁₀= 1012₃

Для рассмотрения второго сомножителя будем использовать правило:

Получим:

3²⁵ = 10..0{25 нулей}₃

Выполним произведение, но для простоты счета, представим, что нулей не 25, а только 3:

В исходном числе было 3 нуля, стало 4. Значит если было 25 нулей, то станет 25 + 1 = 26.
Единиц = 2, двоек = 1.

📹 Видео (аналитическое решение)
📹 Видеорешение на RuTube здесь

Источник

Подготовка к ЕГЭ: системы счисления

Определите наибольшее/наименьшее значение x, y

Сколько цифр и сумма цифр

Найти основание системы счисления и уравнения

Вам также может понравиться

Потерялись документы как найти

Как найти подход к замкнутому человеку

Как найти сылка на свою игру

Добавить комментарий Отменить ответ