Среднеквадратичное (действующее, эффективное) значение
Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор). Для того, чтобы разобраться в этом, мы проведем простейший опыт.
Лампочка и постоянное напряжение
Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт
Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.
Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I — сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.
Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы
Подаем напряжение с блока питания на лампу и вуаля!
Замеряем напряжение на клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.
К этим же клеммах цепляем и наш осциллограф

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.
Замеряем силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.
Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку 😉
Лампочка и переменное напряжение
Теперь начинается самое интересное. Берем наш ЛАТР
Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.
Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.
Среднеквадратичное значение напряжения
Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение зажигали одну и ту же лампочку, которая кушала одну и ту же мощность. Значит эта осциллограмма


Среднеквадратичное значение напряжения — это такое значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении. То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном. То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.
Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала любой частоты равняется максимальной его амплитуде, поделенной на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то Umax = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉
Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение. Максимальная амплитуда этих 220 Вольт равняется 220х1,41=310 Вольт.
Где же среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот же они!

Vk — это и есть среднеквадратичное напряжение этого сигнала.
Ma — это и есть Umax.
Конечно, 16,6/1,41=11,8 Вольт, а он пишет 12,08 Вольт.
Источник
Как рассчитать падение напряжения на резисторах? Показываю на примерах
Простая электрическая цепь состоит из источника питания, проводников и сопротивлений. На практике же электроцепи редко бывают простыми и включают в себя несколько различных ответвлений и повторных соединений.
В больших масштабах в роли сопротивлений может выступать бытовая техника, осветительные приборы и другие потребители. Давайте разберемся, что происходит с током и напряжением на каждом таком потребителе или резисторе с точки зрения электротехники.
Основы электротехники
Закон Ома гласит, что напряжение равно силе тока умноженной на сопротивление. Это может относиться к цепи в целом, участку цепи или к конкретному резистору. Самая распространенная форма этого закона записывается:
Два типа схем в электротехнике
Последовательная цепь
Здесь ток протекает по одному проводнику. Независимо от того, какие сопротивления встречаются на его пути, просто суммируйте их, чтобы получить общее сопротивление цепи в целом:
Rобщй = R1 + R2 + … + RN (последовательная цепь)
Параллельная цепь
В этом случае проводник разветвляется на два или более других проводника, на каждом из которых имеется своё сопротивление. В этом случае полное сопротивление определяется как:
1/Rобщ = 1/R1 + 1/R2 + … + 1/R N (параллельная цепь)й
Если взглянуть на эту формулу, можно сделать вывод, что добавляя сопротивления одинаковой величины, вы уменьшаете сопротивление цепи в целом. Согласно закону Ома это фактически увеличивает ток!
Если это кажется нелогичным, представьте себе поток автомобилей, которые выезжают с парковки через один шлагбаум и тот же самый поток который выезжает со стоянки, которая имеет несколько выездов. Несколько выездов явно увеличит поток покидающих стоянку машин.
Падение напряжения в последовательной цепи
Если вы хотите найти падение напряжения на отдельных резисторах в цепи, выполните следующие действия:
- Рассчитайте общее сопротивление, сложив отдельные значения R.
- Рассчитайте ток в цепи, который одинаков для каждого резистора, поскольку в цепи только один проводник.
- Рассчитайте падение напряжения на каждом резисторе, используя закон Ома.
Пример : источник питания 24 В и три резистора подключены последовательно, где R1 = 4 Ом, R2 = 2 Ом и R3 = 6 Ом. Чему равно падение напряжения на каждом резисторе?
- Сначала рассчитаем общее сопротивление: 4 + 2 + 6 = 12 Ом.
- Далее рассчитываем ток: 24 В / 12 Ом = 2 А
- Теперь используем ток, чтобы вычислить падение напряжения на каждом резисторе. Используя Закон Ома (U = IR) для каждого резистора, получим значения R1, R2 и R3 равными 8 В, 4 В и 12 В соответственно.
Падение напряжения в параллельной цепи
Пример : источник питания 24 В и три резистора подключены параллельно, где R1 = 4 Ом, R2 = 2 Ом и R3 = 6 Ом, как и в предыдущей схеме. Чему будет равно падение напряжения на каждом резисторе?
В этом случае все проще: независимо от значения сопротивления, падение напряжения на каждом резисторе одинаково. Это означает, что падение напряжения на каждом из них — это просто общее напряжение цепи, деленное на количество резисторов в цепи, или 24 В / 3 = 8 В.
Применяя эти несложные правила вы сможете рассчитать падение напряжения даже в сложной цепи, достаточно лишь разделить её на простые участки.
Источник
Максимальный постоянный ток через полевой транзистор
На просторах интернета достаточно много информации о полевых транзисторах (далее ПТ) и их параметрах, но один из довольно простых, на первый взгляд, параметров, а именно – максимальный постоянный ток, который транзистор может через себя пропустить в ключевом режиме, и не сгореть – приводится в даташитах как-то размыто и неочевидно.
В статье будет рассмотрен пример расчёта максимального тока через MOSFET SQM50P03-07 (взял первый попавшийся из своей схемы), работающий в ключевом режиме, или на участке насыщения.
Сначала немного теории, чтобы понять в чём же вообще суть проблемы. Кому просто нужно посчитать ток – переходите сразу к практике.
Теория
Если кратко, то основным параметром, который ограничивает максимальный ток через ПТ, является температура, точнее её рост. Даже при работе в ключевом режиме, когда ток течёт через исток-сток, транзистор имеет некоторое сопротивление, для мощных MOSFET это значение может быть всего несколько мОм (не самое большое и не самое маленькое значение среди ПТ). При прохождении тока через такое сопротивление на нём рассеивается некоторая мощность (переходящая в тепло, транзистор нагревается). Рассеиваемая мощность прямо пропорциональна квадрату тока, проходящего через ПТ.
Проблема в том, что максимальный ток (DC), как и максимальную рассеиваемую мощность, зачастую не указывают в документации напрямую, вот, например, скрин из даташита на SQM50P03-07:
Continuous Drain Current указан 50 ампер, но со сноской, что это ограничение корпуса, т.е. ток, больше чем этот, физически не может пропустить через себя сам корпус без разрушения структуры.
Maximum Power Dissipation для разных температур 150 и 50 Вт, но со сноской, что это при пропускании тока импульсами, где за 1 период 98% времени транзистор «выключен», и остальные 2% он «включен» (напомню, нас интересует постоянный ток).
Так вот, для расчёта максимального тока через ПТ, важным параметром здесь является максимальная температура. Из даташита видно, что она 175 °C (Operating Junction and Storage Temperature Range), от неё и нужно отталкиваться в расчётах. Нужно определить какой ток нагреет полупроводниковый канал транзистора до 175 °C, но дальнейшее увеличение температуры не будет происходить за счёт передачи тепла в окружающую среду (охлаждения), это и будет значение тока, которое нам нужно.
Нагревание транзистора, как и любого другого тела, процесс сложный и зависит от многих параметров. Чтобы максимально упростить связанные с тепловыми расчётами действия, вводится параметр тепловое сопротивление, т.е. способность чего-либо, препятствовать распространению тепла. Чем тепловое сопротивление больше, тем медленнее будет охлаждаться ПТ, и тем быстрее вырастет до критической температура его кристалла. Так же, чем больше разница между максимально допустимой температурой на кристалле и окружающей средой, тем дольше ПТ будет нагреваться, и тем больший ток можно будет через него пропускать.
У каждого материала тепловое сопротивление своё, а транзистор, в свою очередь, состоит из подложки (тела), на которой формируется проводящий канал, изолятора, самого корпуса, который может тоже состоять из нескольких материалов, само собой они ещё и разной толщины, что тоже влияет на передачу тепла.
Кроме того, охлаждать транзистор тоже можно по-разному, на некоторых, есть большая контактная площадка, которая припаивается к плате или крепится к радиатору, в таких случаях тепловое сопротивление минимально. Некоторые транзисторы не имеют таких площадок и контактируют с окружающей средой только через пластиковый корпус, через который отдают тепло гораздо медленнее.
В итоге получается примерно следующая схема:
- T (Junction) – это температура проводящего канала внутри транзистора (который и нагревается при прохождении тока);
- T (Ambient) – это температура окружающей среды (куда отводится тепло);
- RT1-RT4 – это тепловые сопротивления материалов, которые преодолевает тепловая энергия.
С тепловыми сопротивлениями, как и в электротехнике, работает правило: «общее сопротивление равно сумме последовательных сопротивлений».
Как было отмечено ранее, ПТ можно охлаждать по-разному, и все возможные варианты в даташите предусмотреть просто невозможно, однако, обычно приводятся самые распространённые:
- ПТ установлен на плате без радиатора и без всяких теплоотводящих контактных площадок (сопротивление Junction-to-Ambient);
- даётся сопротивление до подложки, Junction-to-Case (или до определённой точки на корпусе, с которой отводится тепло), а дальше, в зависимости от применения, например, к подложке крепится радиатор, тогда надо его сопротивление добавлять в систему, и сопротивление прокладки между ним и корпусом ПТ (теплоотвод может быть очень большим и принимать на себя всё тепло с транзистора, в этом случае температурой окружающей среды будет считаться температура этого радиатора).
Не всегда тепловые сопротивления указываются прямо на странице с максимальными параметрами ПТ, вот, например, скрин из документации на Si4477DY:
Хотя там есть параметр Junction-to-Foot, допустим, нам интересно именно тепловое сопротивление Junction-to-Ambient, а оно приведено только для времени менее 10 секунд. В таком случае, можно порыться на сайте производителя и найти модели тепловых сопротивлений. В таких документах есть график зависимости разности температур Junction-Ambient от времени:
Из графика видно, что после 1000 секунд, значительный рост изменения температуры прекращается. В этом режиме разность температур численно равна тепловому сопротивлению. Следовательно, для постоянного тока можно ориентироваться на значение 80 °C/Вт – тепловое сопротивление Junction-to-Ambient.
(немного подробнее в комментарии)
Может не у всех фирм есть эта информация, но корпуса ПТ у всех в основном стандартные, достаточно найти данные по сопротивлениям для интересующего нас корпуса другой фирмы.
Когда разработчиком определено как именно будет охлаждаться ПТ, температура окружающей среды, в которой будет работать устройство, после этого, можно, наконец, приступить к расчёту.
Практика
Рассмотрим пример определения максимального постоянного тока через MOSFET SQM50P03-07 в ключевом режиме, который припаян к плате размером 300х300 мм (без радиатора). Плата будет работать в воздухе, при максимальной температуре 45 °C. Управлять ПТ будем, подавая на его затвор, напряжение в 5 вольт.
1. TJMAX
MOSFET греется в области сформированного проводящего канала (на подложке под изолятором и затвором), это и есть температура Tjunction (температура в месте соединения). Из даташита Operating Junction and Storage Temperature Range -55… +175, т.к. нас интересует максимальный ток, то и берём максимальную температуру, т.е. TJMAX=175°C (если не хочется, чтобы канал транзистора так грелся, то можно взять меньшее значение).
Температура окружающей среды. Берём максимально возможную температуру, в которую транзистору придётся отдавать тепло, по начальным условиям TA=45°C.
3. RΘJA
В даташите находим тепловое сопротивление проводящего канала транзистора к окружающей среде, притом ниже есть пометка, что это сопротивление актуально, если ПТ припаян к плате размерами больше 1 дюйма квадратного (в этом случае часть тепла уходит на плату, и при таких её размерах, с транзистора осуществляется необходимый теплоотвод):
Таким образом, RΘJA= 40 °C/Вт.
4. RDS(ON)
Максимальное сопротивление drain-source (сток-исток), при определённом управляющем напряжении на затворе. Информацию можно взять из таблицы, но там приводятся значения сопротивления канала только при напряжениях затвора в 10В и 4.5В, а у нас по плану 5 вольт. Разница, конечно, небольшая, можно взять и 4.5В:
Лучше всё-так найти в даташите график зависимости сопротивления канала от приложенного к затвору напряжения:
Нужно обратить внимание на то, что в случае с таблицей, данные приводятся для TC = 25 °C (температура подложки), а в случае с графиком есть 2 варианта: TJ = 25 °C и TJ = 150 °C (температура канала). В выбранном примере канал будет греться до 175°C (как было определено в первом пункте расчёта). Получается, что в данный момент лучше пользоваться не таблицей, а графиком, для определения сопротивления канала, т.к. данное в таблице значение при TC = 25 °C – это не то, что нам сейчас интересно.
Итак, 8 мОм (0,008 Ом) – это сопротивление канала при его температуре 25 °C. Чтобы определить сопротивление при температуре TJMAX=175°C ищем график зависимости нормализованного сопротивления канала от его температуры:
По горизонтальной оси здесь температура соединения, а по вертикальной коэффициент приращения к сопротивлению. Можно заметить, что при 25 °C он равен 1 (величина безразмерная), т.е. то значение, которое ранее было определено (8 мОм), находится на этом уровне. При температуре 175 °C, коэффициент равен примерно 1,69.
Чтобы найти сопротивление канала при TJ=175°C, нужно умножить сопротивление при 25 °C на коэффициент при 175°C. Получаем 0,008 * 1,69 = 13,52 мОм. RDS(ON)=13,52 мОм (0,01352 Ом).
5. IDMAX
Теперь можно по формуле ниже, определить максимальный ток (DC), который может пропустить транзистор:
Однако расчёты с использованием тепловых моделей, основанных на тепловых сопротивлениях, имеют погрешность, которая возникает вследствие упрощения тех самых моделей. Поэтому рекомендуется делать запас по току хотя бы 20 %. Делаем последний расчёт и получаем 12,403 ампера. Это и есть то значение тока, которое SQM50P03-07 может через себя пропустить в режиме насыщения и не сгореть, при заданных выше начальных условиях.
Обратите внимание, как значение в 12 А, отличается от того, что обозначено на первых страницах даташита (50 А, 150 А), такие цифры поначалу сбивают с толку, если не разобраться со всеми нюансами.
В заключении пару слов о Safe Operating Area, это диаграмма, показывающая зоны нормальной работы транзистора в разных режимах. Для того же SQM50P03-07 в даташите есть SOA, однако, как можно заметить, она приведена для температуры канала в 25 °C (не наш случай)
К тому же, далеко не во всех даташитах есть прямая, ограничивающая зону работы по DC, хотя, для грубой оценки, можно использовать и эти данные.
Источник
Одним из самых фундаментальных терминов в электротехнике является термин «электрическое напряжение». В этой статье мы объясним, что это такое и как его рассчитать.
Объяснение простыми словами
Электрическое напряжение U является той самой причиной, которая «заставляет» протекать электрический ток I. Электрическое напряжение всегда возникает, когда заряды разделены друг от друга, то есть все отрицательные заряды на одной стороне, а все положительные — на другой. Если соединить эти две стороны электропроводящим материалом, потечет электрический ток.
Общепринятое определение термина «электрическое напряжение».
Электрическое напряжение (или просто напряжение) — это разность потенциалов между двумя точками в электрическом поле. Это движущая сила для электрического заряда.
Потенциал в электрическом поле — это энергия заряженного тела, не зависящая от его электрического заряда. Для пояснения вы можете посмотреть на сравнение с водяным контуром чуть ниже в статье.
Есть другое определение (из учебника по физике 8 класса):
Напряжение — это физическая велuчuна, характеризующая электрическое поле. Электрическое напряжение между двумя точками электрического поля численно равно работе, совершенной при переносе между ними заряда 1 Кл силами электрического поля.
Сравнение с использованием модели протекания воды.
Хорошей аналогией, которая поможет вам представить себе электрическое напряжение и потенциал, является водяной контур. В этой схеме у вас есть два бассейна на разной высоте, которые соединены трубой. В этой трубе вода может перетекать из верхнего бассейна в нижний. Затем вода перекачивается обратно в верхний бассейн с помощью насоса, как показано на рисунке ниже.
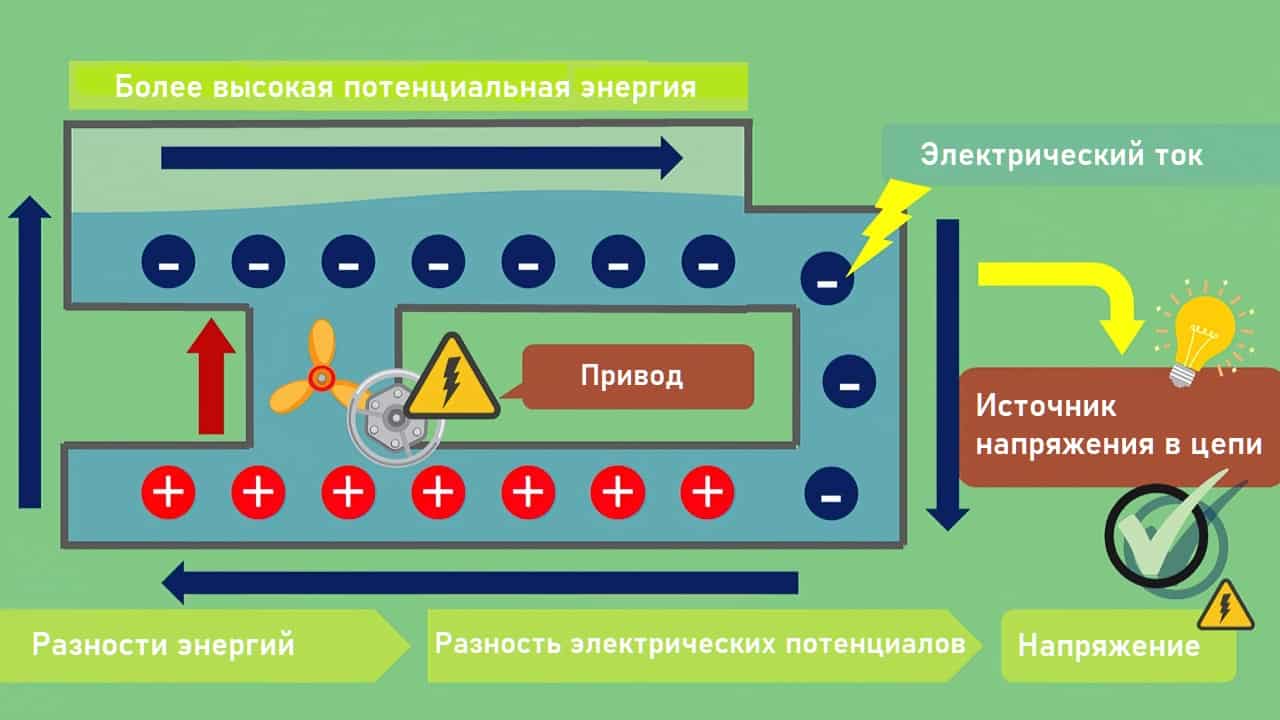
В своих размышлениях вы теперь легко можете сравнить насос с источником электрического напряжения. Кроме того, поток воды можно сравнить с электрическим током. Насос транспортирует воду из нижнего бассейна в верхний. Оттуда она самостоятельно течет обратно в нижний бассейн. В данном примере насос является приводом для потока. Чем больше разница в высоте, тем сильнее поток. Решающим фактором является потенциальная энергия верхнего бассейна. Вы можете сравнить разность энергий двух бассейнов с разностью электрических потенциалов. Проще говоря, большая разница в высоте соответствует большему электрическому напряжению.
Формула
Формула для электрического напряжения U, согласно закона Ома для участка цепи, имеет вид
U = R * I .
Как видно из этой формулы, если электрическое напряжение остается неизменным, то чем больше электрическое сопротивление (R), тем меньше сила тока (I).
Другая формула для расчета электрического напряжения такова:
U = P / I .
То есть электрическое напряжение U равно мощности деленной на силу тока I.
Единица измерения электрического напряжения
Единицей измерения электрического напряжения в СИ является Вольт, сокращенно В (в честь итальянского учёного А. Вольта).
1 вольт (1 В) — это напряжение между двумя точками электрического поля, при переносе между которыми заряда 1 Кл совершается работа 1 Дж.
[U] = 1 В
Теперь вы можете объяснить смысл надписи 4,5 В или 9 В на круглой или плоской батарейке. Смысл в том, что при переносе с одного полюса источника на другой (через спираль лампочки или другой проводник) заряда 1 Кл силами электрического поля может быть совершена работа соответственно 4,5 Дж или 9 Дж.
В электротехнике напряжение может варьироваться от микровольт (1 мкВ = 1 * 10-6 В) и миливольт (1 мВ = 10-3 В), до киловольт (1 кВ = 1 * 103 В) и мегавольт (1 МВ = 106 В)
Вы можете преобразовать отдельные единицы измерения следующим образом:
1 В = 1000 мВ, 1 мВ = 1000 мкВ, 1 МВ = 1000 кВ, 1 кВ = 1000 В.
Электрическое напряжение в цепи
Для источников напряжения в схемах обычно используется один из следующих символов.

Источник напряжения всегда имеет два соединения/полюса. Полюс «плюс» и полюс «минус». Само напряжение обозначено стрелкой напряжения (UQ). Для источников оно всегда отображается от плюса к минусу.
Электрическое напряжение, падающее на резисторе, также можно обозначить стрелкой напряжения (на схеме обозначена как красная стрелка UR ). Это указывает на техническое направление электрического тока.
Также часто можно услышать термин «напряжение холостого хода» или «напряжение источника». Это выходное напряжение ненагруженного источника, т.е. источника, к которому ничего не подключено. Если цепь замкнута с нагрузкой, то можно измерить только напряжение на полюсах источника.
Электрические напряжения при последовательном и параллельном соединении
У нас уже есть статья о последовательном и параллельном соединении проводников, в котором мы обсуждаем эту тему более подробно. Поэтому здесь мы рассмотрим лишь некоторые основы.
При последовательном соединении компоненты подключаются в ряд.

Здесь электрическое напряжение источника делится на резисторы. Этот момент также описывается вторым правилом Кирхгофа. Здесь применимо следующее:
UQ = U1 + U2 + U3
то есть напряжение источника равно сумме электрических напряжений на отдельных резисторах. Напряжение источника по-разному распределяется по разным резисторам.
В электрической цепи с параллельным соединением компоненты расположены, соответственно, параллельно друг относительно друга. Это можно увидеть на следующей схеме.

Здесь гораздо проще определить электрические напряжения на резисторах, так как при параллельном соединении:
UQ = U1 = U2 = U3
Поэтому электрическое напряжение на резисторах такое же высокое, как и электрическое напряжение источника.
Измерение электрического напряжения
Приборы для измерения напряжения, также называемые вольтметрами, всегда подключаются параллельно потребителю, на котором необходимо измерить электрическое напряжение.
Одним из наиболее часто используемых вольтметров является цифровой мультиметр (DMM), поэтому мы покажем вам процедуру измерения напряжения с помощью DMM. Сначала необходимо установить тип электрического напряжения (DC — постоянный ток или AC — переменный ток).
Для постоянного тока необходимо обратить внимание на правильную полярность, т.е. подключить плюс к положительному полюсу. На следующем этапе необходимо выбрать правильный диапазон измерения. Если вы не можете оценить, насколько велика измеряемая величина, установите наибольший возможный диапазон и двигайтесь от него вниз, пока не найдете нужный. Наконец, вам нужно только «считать» электрическое напряжение прибором.
Примеры типовых значений электрического напряжения
Для некоторых применений соответствующее электрическое напряжение можно найти в таблице ниже.
| Светодиод | 1,2 — 1,5 В |
| Зарядное устройство USB | 5 В |
| Напряжение автомобильного аккумулятора | 12, 4 — 12,8 В |
| Напряжение в розетке (среднеквадратичное или действующее значение) | 230 В |
| Высоковольтные линии электропередач (ЛЭП) | 60 кВ — 1 МВ |
Вы можете видеть, что на высоковольтных линиях присутствует напряжение до мегавольт. Такие большие электрические напряжения используются для того, чтобы уменьшить потери в длинных линиях.
Решающим фактором для потребителя является мощность P, которую можно рассчитать для постоянного напряжения с помощью формулы:
P = U * I
Это означает, что электрический ток I так же важен для потребителя, как и электрическое напряжение. Согласно закону Ома, зависимость между током и напряжением имеет вид:
U = R * I .
Если напряжение остается неизменным, сопротивление определяет величину тока. Чтобы проиллюстрировать это, представьте следующее. У вас есть три разных бассейна, которые заполнены одинаковым количеством воды. Каждый бассейн имеет слив, который различается по сечению, т.е. в одном бассейне сливная труба очень маленькая, а в другом — очень большая.
Постоянное электрическое напряжение можно определить по тому, что все емкости заполнены на одинаковую высоту. Если слив узкий в нижней части, он представляет собой большое сопротивление. Ток здесь может течь только медленно. Если сечение сливной трубы больше, то сопротивление меньше и, соответственно, может протекать больший ток.
Законы постоянного тока

Содержание
- Постоянный электрический ток. Сила тока
- Постоянный электрический ток. Напряжение
- Закон Ома для участка цепи
- Электрическое сопротивление. Удельное сопротивление вещества
- Электродвижущая сила. Внутреннее сопротивление источника тока
- Закон Ома для полной электрической цепи
- Параллельное и последовательное соединение проводников
- Смешанное соединение проводников
- Работа электрического тока. Закон Джоуля–Ленца
- Мощность электрического тока
- Носители свободных электрических зарядов в металлах, жидкостях и газах
- Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод
- Основные формулы раздела «Законы постоянного тока»
Постоянный электрический ток. Сила тока
Электрический ток – это упорядоченное движение заряженных частиц.
Условия существования электрического тока в проводнике:
- наличие свободных заряженных частиц;
- наличие электрического поля.
Напряженность электрического поля должна быть постоянной.
Цепь постоянного тока должна быть замкнутой.
Важно!
Тепловое движение заряженных частиц нельзя назвать электрическим током, так как оно беспорядочное.
Электрический ток можно обнаружить по его действиям:
- тепловому – при протекании тока проводник нагревается;
- химическому – изменяется состав вещества при прохождении электрического тока (электролиз);
- магнитному – электрический ток создает магнитное поле.
За направление тока принимают направление движения положительно заряженной частицы.
Сила тока – это скалярная физическая величина, равная отношению заряда, прошедшего через поперечное сечение проводника, ко времени, за которое этот заряд переносится.
Обозначение – ( I ), единица измерения в СИ – ампер (А) (является основной).
Вычисляется по формуле:
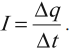
Если за одинаковые промежутки времени через поперечное сечение проводника проходит одинаковый заряд, то ток постоянный.
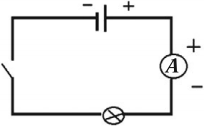
Для измерения силы тока используют амперметр.
Условное обозначение на схемах:

Амперметр – измерительный прибор для определения силы тока в электрической цепи.
При измерении силы тока амперметр включают в цепь последовательно с тем прибором, силу тока в котором измеряют, и с соблюдением полярности. Клемму амперметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока.
Для того чтобы включение амперметра не влияло на величину измеряемого тока, его сопротивление по сравнению с сопротивлением нагрузки должно быть как можно меньшим. Каждый амперметр рассчитывается на некоторое определенное максимальное значение измеряемой величины. Но возникают ситуации, когда необходимо выполнить измерение силы тока больше предельно допустимого значения силы тока.
Для этого параллельно амперметру присоединяют проводник (шунт), по которому проходит часть измеряемого тока. Значение сопротивления этого проводника рассчитывается так, чтобы сила тока, проходящего через амперметр, не превышала его максимально допустимого значения.
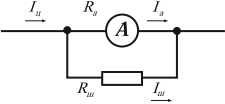
Сопротивление шунта рассчитывается по формуле:
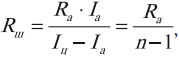
где ( I_ц ) – сила тока в цепи, ( I_а ) – максимально допустимая для данного амперметра сила тока, ( R_а ) – сопротивление амперметра, ( n=frac{I_ц}{I_а} ).
При этом цена деления прибора увеличивается в n раз, а точность измерений во столько же раз уменьшается.
Работающим с электрическими цепями надо знать, что для человеческого организма безопасной считается сила тока до 1 мА. Сила тока больше 100 мА приводит к серьезным поражениям организма.
Постоянный электрический ток. Напряжение
В проводнике, по которому протекает ток, заряды движутся под действием сил электростатического поля. Работу электростатических сил характеризуют разностью потенциалов или напряжением.
Электрическое напряжение – скалярная физическая величина, равная отношению работы по перемещению электрического заряда между двумя точками цепи к величине этого заряда.
Обозначение – ( U ), единица измерения в СИ – вольт (В).
Формула для вычисления:
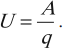
Напряжение равно разности потенциалов только в том случае, если рассматриваемый участок цепи не содержит источник тока (ЭДС = 0).
Измеряют напряжение вольтметром.
Изображение вольтметра на схеме:
При измерении напряжения вольтметр включают в цепь параллельно с тем прибором, напряжение на котором измеряют, и с соблюдением полярности. Клемму вольтметра со знаком «+» нужно обязательно соединять с проводом, идущим от положительного полюса источника тока. Для того чтобы включение вольтметра не влияло на измерение напряжения, его сопротивление должно быть большим.
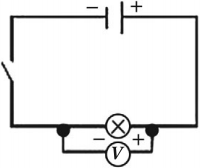
Для измерения напряжения больше, чем допустимое для данного вольтметра, используют добавочное сопротивление – резистор, включаемый последовательно с вольтметром.
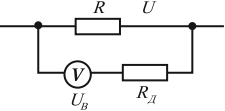
Величина добавочного сопротивления рассчитывается по формуле:
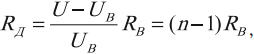
где ( U ) – напряжение, которое нужно измерить, ( U_В ) – напряжение, на которое рассчитан вольтметр, ( n=frac{U}{U_В} ), ( R_В ) – сопротивление вольтметра.
При этом цена деления прибора увеличивается в ( n ) раз, а точность измерений во столько же раз уменьшается.
Закон Ома для участка цепи
Взаимосвязь между силой тока, протекающей по проводнику, и напряжением на его концах была экспериментально установлена Г. Омом и носит название закона Ома для участка цепи.
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению:
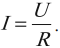
График зависимости силы тока от напряжения называется вольт-амперной характеристикой. Из закона Ома для участка цепи следует, что при постоянном сопротивлении сила тока прямо пропорциональна напряжению. Следовательно, вольт-амперная характеристика для металлического проводника представляет собой прямую линию, проходящую через начало координат.
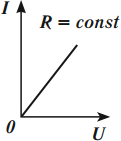
Проводник с такими свойствами называется резистором.
Угол наклона графика к оси напряжений зависит от сопротивления проводника. Тангенс угла наклона графика равен проводимости резистора.
Электрическое сопротивление. Удельное сопротивление вещества
Электрическое сопротивление – свойство материала проводника препятствовать прохождению через него электрического тока.
Обозначение – ( R ), единица измерения в СИ – Ом.
Объяснить наличие сопротивления можно на основе строения металлических проводников. Свободные электроны при движении по проводнику встречают на своем пути ионы кристаллической решетки и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Сопротивление различных проводников зависит от материала, из которого они изготовлены, их длины, геометрической формы и температуры. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 м2.
Обозначение – ( rho ), единица измерения в СИ – Ом·м.
Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 1,7·10-8 Ом·м, т. е. медный проводник длиной 1 м и сечением 1 м2 обладает сопротивлением 1,7·10-8 Ом. На практике часто используют единицу удельного сопротивления (Ом·мм2)/м.
Электрическое сопротивление проводника прямо пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника.
Формула для вычисления:
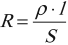
Сопротивление проводника увеличивается с ростом температуры. Удельное сопротивление зависит от температуры:
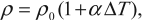
где ( rho_0 ) – удельное сопротивление при ( T_0 ) = 293 К (20°С), ( Delta T=T-T_0 ), ( alpha ) – температурный коэффициент сопротивления.
Единица измерения температурного коэффициента сопротивления – К-1.
При нагревании увеличивается интенсивность движения частиц вещества. Это создает трудности для направленного движения электронов. Увеличивается число столкновений свободных электронов с ионами кристаллической решетки.
Свойство изменения сопротивления при изменении температуры используется в термометрах сопротивления. Эти приборы могут измерять температуру, основываясь на зависимости сопротивления от температуры. У термометров сопротивления высокая точность измерений.
Электродвижущая сила. Внутреннее сопротивление источника тока
Для создания электрического поля в проводниках используют источник тока. Внутри источника тока происходит перераспределение зарядов, в результате которого на полюсах источника возникает избыток зарядов разных знаков.
Виды источников тока:
- электрофорная машина;
- термопара;
- фотоэлемент;
- аккумулятор;
- гальванический элемент.
Сторонними называются силы неэлектрической природы, действующие внутри источника тока.
Когда проводник соединяют с полюсами источника, то на внешнем участке цепи заряженные частицы движутся под действием электростатической силы. А внутри источника на заряды действуют сторонние и электростатические силы.
Под действием этих сил внутри источника происходит перемещение положительных зарядов от отрицательного полюса источника к положительному. Это перемещение происходит до тех пор, пока сторонние силы не станут равными электростатическим. При переносе заряда эти силы совершают работу. Работа сторонних сил по перемещению заряда компенсирует потери энергии заряженными частицами при их движении по цепи.
Электродвижущей силой (ЭДС) называется отношение работы сторонних сил по перемещению положительного заряда к величине этого заряда.
Обозначение – ( varepsilon ), единица измерения в СИ – вольт (В).
Формула для вычисления:
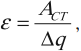
где ( Delta q ) – модуль перенесенного заряда.
Если электрическая цепь содержит несколько источников тока с ЭДС ( varepsilon_1,varepsilon_2,,…,varepsilon_T ), то суммарная ЭДС ( varepsilon=varepsilon_1+varepsilon_2+…,varepsilon_T ).
ЭДС считается положительной, если направление обхода цепи против часовой стрелки совпадает с переходом внутри источника тока от отрицательного полюса источника к положительному полюсу.
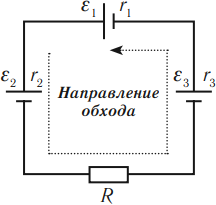
На рисунке: ( varepsilon_1>0,,varepsilon_2<0,,varepsilon_3>0. )
Суммарная ЭДС: ( varepsilon=varepsilon_1-varepsilon_2+varepsilon_3. )
При подключении проводника к полюсам источника тока происходит перераспределение заряда на поверхности проводника, а внутри проводника возникает постоянное электрическое поле. Заряды начинают перемещаться по замкнутой цепи, в которой устанавливается постоянная сила тока.
Сопротивление источника тока называется внутренним сопротивлением.
Обозначение внутреннего сопротивления – ( r ). Единица измерения в СИ – Ом.
Закон Ома для полной электрической цепи
Полная электрическая цепь состоит из источника тока и проводников, представляющих внешнее сопротивление.
Закон Ома для полной электрической цепи
Сила тока в полной цепи прямо пропорциональна ЭДС, действующей в цепи, и обратно пропорциональна полному сопротивлению цепи:
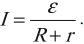
Полное сопротивление – это сумма внутреннего сопротивления источника и сопротивления внешней цепи. Во внешней цепи ток идет по направлению электрического поля, внутри источника тока – против поля.
Напряжение на внешней цепи (падение напряжения):
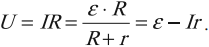
Если цепь разомкнута, то ток внутри источника не проходит и ( varepsilon=U ).
ЭДС численно равна напряжению на зажимах источника тока (разности потенциалов на полюсах источника).
Сопротивление внешней цепи больше внутреннего сопротивления источника.
Если сопротивление внешней цепи мало ( (R=0) ), то возможно короткое замыкание. Сила тока короткого замыкания: ( I_{кз}=frac{varepsilon}{r} )Возрастание силы тока приводит к резкому увеличению количества теплоты и может стать причиной пожара. Для предотвращения возгорания в электрическую цепь последовательно включают предохранители.
Соединение источников тока
Источники тока можно соединять между собой последовательно и параллельно.
При параллельном соединении положительные полюсы элементов соединяют между собой, отрицательные – между собой. Если ЭДС источников одинаковы, то общая ЭДС ( varepsilon=varepsilon_1 ) (( varepsilon_1 ) – ЭДС одного источника). Величина, обратная общему внутреннему сопротивлению, равна сумме величин, обратных внутренним сопротивлениям элементов: ( frac{1}{r}=frac{1}{r_1}+frac{1}{r_2}+… ) Если внутренние сопротивления источников одинаковы, то ( r_{общ}=frac{r_1}{n} ), ( r_1 ) – сопротивление одного источника, ( n ) – число источников. Сила тока: ( frac{varepsilon}{R+frac{r}{n}} ).
При последовательном соединении положительный полюс источника соединяется с отрицательным полюсом следующего. Общая ЭДС батареи ( varepsilon=varepsilon_1+varepsilon_2+… ), а общее внутреннее сопротивление равно сумме внутренних сопротивлений отдельных источников: ( r=r_1+r_2+… ) Если внутренние сопротивления источников одинаковы, то ( r_{общ}=nr_1 ). Сила тока: ( I=frac{nvarepsilon}{R+nr} ).
Параллельное и последовательное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
Последовательное соединение проводников
При последовательном соединении начало одного проводника соединяется с концом другого.
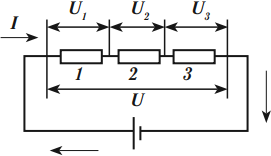
При последовательном соединении сила тока во всех проводниках одинакова:
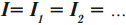
Общее напряжение ( U ) на проводниках равно сумме напряжений на отдельных проводниках:
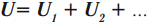
Напряжение на проводниках прямо пропорционально их сопротивлениям:
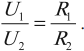
Общее сопротивление равно сумме сопротивлений проводников, образующих цепь:
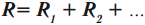
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:
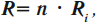
где ( n ) – число проводников, ( R_i ) – сопротивление проводника.
Параллельное соединение проводников
При параллельном соединении проводники подключаются между одной и той же парой точек. Если в этой точке соединяются три и более проводников, то она называется узлом электрической цепи.
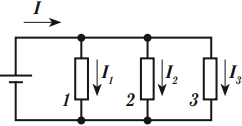
При параллельном соединении напряжение на всех проводниках одинаково:
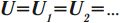
Сумма сил токов, протекающих по проводникам, равна силе тока в неразветвленной цепи:
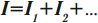
Это следствие того факта, что в точках разветвления цепи заряды не могут накапливаться.
Силы токов в разветвленных частях цепи обратно пропорциональны их сопротивлениям:
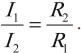
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников:
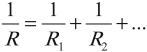
Если проводники имеют одинаковое сопротивление, то общее сопротивление находится по формуле:

где ( n ) – число проводников, ( R_1 ) – сопротивление проводника.
Если параллельно соединены два проводника, от общее сопротивление вычисляется по формуле:
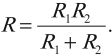
Смешанное соединение проводников
Смешанное соединение проводников – соединение, при котором часть проводников соединена последовательно, а часть – параллельно.
Важно!
Чтобы рассчитать общее сопротивление такого участка или найти силу тока и напряжение при таком соединении, нужно:
- разбить его на простые участки с последовательно или параллельно соединенными проводниками;
- найти общее (эквивалентное) сопротивление каждого из этих участков;
- составить эквивалентную схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений;
- рассчитать сопротивление полученной схемы.
Если в схеме не удается выделить участки с последовательным или параллельным соединением проводников, то можно использовать такое правило: точки с одинаковыми потенциалами можно соединять и разъединять, ток между такими точками не идет.
На рисунке, если ( R_1=R_2,R_4=R_5, ) то потенциалы точек 1 и 2 равны. Резистор ( R_3 ) можно убрать на эквивалентной схеме – ток по нему не идет.
Точки с одинаковыми потенциалами есть в схемах с осью или плоскостью симметрии относительно точек подключения источника тока.
Если схема симметрична относительно оси, проходящей через точки входа и выхода тока, то точки равного потенциала находятся на концах симметричных сопротивлений (по ним идут одинаковые токи).
Если схема симметрична относительно оси, перпендикулярной линии, на которой лежат точки входа и выхода тока, то точки равного потенциала находятся на пересечении этой оси с проводниками.
Если в схеме нет участков с известным видом соединения и нет точек с равным потенциалом, то для расчета таких цепей используют правила Кирхгофа.
Правила Кирхгофа:
- Алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
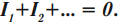
Положительными считают токи, входящие в узел, отрицательными – выходящие из узла.
- В любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, имеющихся в контуре:
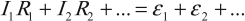
Порядок расчета цепи:
- выбрать направление токов во всей цепи;
- записать уравнения токов для узлов;
- записать уравнения для выделенных контуров. Произвольные замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок, не входящий в ранее рассмотренные контуры;
- решить полученную систему уравнений.
Алгоритм решения задач на определение силы тока, напряжения или сопротивления на участке цепи:
- начертить схему цепи и указать на ней все элементы;
- установить, какие элементы цепи включены последовательно, какие – параллельно;
- расставить токи и напряжения на каждом участке цепи и записать для каждой точки разветвления (если они есть) уравнения токов и уравнения, связывающие напряжения на участках цепи;
- используя закон Ома, установить связь между токами, напряжениями и ЭДС;
- если в схеме делают какие-либо переключения сопротивлений или источников, уравнения составить для каждого режима работы цепи;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Работа электрического тока. Закон Джоуля–Ленца
Работа тока – работа сил электрического поля, создающего электрический ток.
Работа тока на участке цепи вычисляется по формуле:
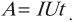
Используя формулу закона Ома для участка цепи, можно работу тока вычислить так:
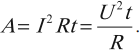
Работа тока в замкнутой цепи находится по формуле:
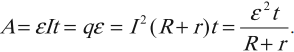
При протекании постоянного тока по металлическому проводнику электроны сталкиваются с положительными ионами, расположенными в узлах кристаллической решетки. При этом электроны передают им энергию. Это приводит к нагреванию проводника. Количество теплоты, выделяющееся в проводнике за время ( t ), равно:
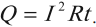
Эта формула выражает закон Джоуля–Ленца: количество теплоты, выделяющееся при прохождении тока по проводнику, прямо пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника.
Мощность электрического тока
Мощность электрического тока равна отношению работы тока ко времени, в течение которого она совершается.
Обозначение – ( P ), единица измерения в СИ – ватт (Вт).
Вычисляется по формуле:
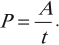
Можно записать еще несколько формул для вычисления мощности электрического тока на участке цепи:
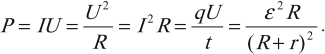
Полная мощность источника тока:
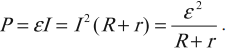
Коэффициент полезного действия источника тока:
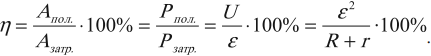
При решении задач на тепловое действие тока нужно учитывать следующее:
1. Если на участке есть источник тока, то необходимо использовать для решения формулу закона Джоуля–Ленца:
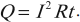
2. Если сила тока в цепи постоянна, то удобно использовать формулу закона Джоуля–Ленца:
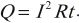
3. Если постоянно напряжение, то формулу:
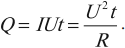
4. Количество теплоты можно находить, используя формулы термодинамики.
Носители свободных электрических зарядов в металлах, жидкостях и газах
Одним из условий существования электрического тока является наличие свободных заряженных частиц.
Носители электрического тока: в металлах – свободные электроны; в электролитах – положительные и отрицательные ионы; в газах – электроны и положительные ионы; в полупроводниках – электроны и дырки; в вакууме – любые заряженные частицы, но чаще всего это электроны.
Электрический ток в металлах
Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. При протекании тока по металлическому проводнику не происходит переноса вещества (опыт Рикке). Это значит, что ионы металла не принимают участия в переносе электрического заряда. Носителями заряда являются частицы одинаковые для всех металлов – электроны.
Сила тока в металлическом проводнике с площадью поперечного сечения ( S ):
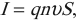
где ( q ) – элементарный электрический заряд (заряд электрона), ( n ) – концентрация электронов проводимости, ( v ) – средняя скорость упорядоченного движения электронов.
Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыты Мандельштама и Папалекси, Стюарта и Толмена). Катушка с большим числом витков проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному гальванометру. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона.
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема. Электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между положительными ионами, образующими кристаллическую решетку металла.
У некоторых металлов и сплавов обнаружено явление сверхпроводимости. Это явление открыто в 1911 г. Камерлинг-Оннесом. При температурах ниже критической сопротивление проводника становится равным нулю. Значения критической температуры для чистых металлов изменяются в диапазоне от долей кельвина до 30 К. В настоящее время получены вещества с критической температурой 125 К. Сверхпроводящие свойства наблюдаются у ртути, свинца, олова.
Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.
Явление сверхпроводимости используется для получения сильных магнитных полей
Электрический ток в жидкостях
Жидкости, проводящие электрический ток, называют электролитами. К электролитам относятся водные растворы неорганических кислот, солей и оснований, многие соединения металлов в расплавленном состоянии. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы.
В результате электролитической диссоциации (распада нейтральных молекул на ионы) образуются положительные и отрицательные ионы. При подключении электродов к источнику тока ионы под действием электрического поля начинают упорядоченное движение. Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду).
Электролиз – явление прохождения электрического тока через электролит, сопровождающееся выделением веществ на электродах.
Закон электролиза был экспериментально установлен английским физиком М. Фарадеем в 1833 году.
Масса ( m ) вещества, выделившегося на электроде, прямо пропорциональна заряду ( Q ), прошедшему через электролит:
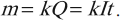
Величину ( k ) называют электрохимическим эквивалентом.
Электрохимический эквивалент ( k ) равен отношению массы ( m_0 ) иона данного вещества к его заряду ( q_0 ):
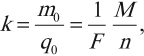
где ( M ) – молярная масса вещества, ( n ) – валентность вещества, ( F=eN_A ) – постоянная Фарадея. ( F ) = 96,5·103 Кл/моль.
Постоянная Фарадея численно равна заряду, который нужно пропустить через раствор любого электролита для получения одного моля одновалентного вещества.
Явление электролиза широко применяется в современном промышленном производстве: получение чистых металлов (меди, алюминия), нанесение металлических покрытий (гальваностегия), изготовление копий с матриц (гальванопластика).
Электрический ток в газах
В обычных условиях газы являются диэлектриками, но при определенных условиях газ может стать проводником. Процесс протекания электрического тока через газ называется газовым разрядом. Носители заряда в газе – свободные электроны и ионы. Проводимость в газах смешанная – электронно-ионная.
Свободные носители заряда в газах появляются в процессе ионизации. Ионизация – процесс вырывания электрона из атома. Наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация заряженных частиц.
Ионизацию вызывают нагревание газа, излучение (ультрафиолетовое, рентгеновское или гамма-излучение).
Выделяют два вида разрядов в газе: несамостоятельный и самостоятельный разряды.
Несамостоятельный разряд происходит под действием внешнего ионизатора и прекращается, как только ионизатор перестает действовать. Самостоятельный разряд происходит без действия внешнего ионизатора под действием электрического поля, существующего между электродами. С ростом напряженности электрического поля скорости свободных заряженных частиц растут. Достигая катода, такие частицы выбивают из него электроны (вторичная электронная эмиссия). Эти электроны, разгоняясь полем, вызывают ионизацию других молекул (ионизация электронным ударом). Число заряженных частиц нарастает лавинообразно, и внешний ионизатор не нужен для поддержания тока.
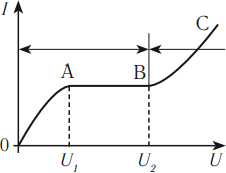
На рисунке участок ОАВ соответствует несамостоятельному разряду, участок ВС – самостоятельному разряду.
Виды самостоятельного разряда:
- тлеющий;
- дуговой;
- коронный;
- искровой.
Тлеющий разряд происходит в разреженном газе при низком давлении. Применяется в газосветных трубках, лампах дневного света, цифровых индикаторах, ртутных лампах низкого давления.
Дуговой разряд – разряд между электродами, нагретыми до высокой температуры при атмосферном или повышенном давлении. Применяется в ртутных лампах высокого давления, при сварке металлов, в электропечах, в источниках света (прожекторах).
Коронный разряд возникает при нормальном и повышенном давлении у заостренных электродов. У острия электрода напряженность электрического поля велика, и в этой области возникает ударная ионизация при атмосферном давлении. Коронный разряд может возникнуть в тонких проводах, находящихся под высоким напряжением. Это приводит к утечке электроэнергии. Применяется в электрофильтрах, громоотводах, счетчике Гейгера–Мюллера.
Искровой разряд – это прерывистый самостоятельный разряд при нормальном или повышенном атмосферном давлении газа в электрическом поле очень большой напряженности. Применяется при обработке металлов. Пример такого разряда в природе – молния.
Плазма – частично или полностью ионизированный газ, в котором плотности отрицательных и положительных зарядов одинаковы. При сильном нагревании любое вещество испаряется, превращается в газ. Если увеличивать температуру и далее, резко усиливается процесс термической ионизации. Молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
В состоянии плазмы находится подавляющая часть вещества Вселенной: звезды, галактические туманности и межзвездная среда. Около Земли плазма существует в виде солнечного ветра и ионосферы. Плазму можно наблюдать в рекламных газовых трубках, кварцевых лампах. За последние годы применение плазмы существенно расширилось. Высокотемпературная плазма (Т ∼ 106–108 К) из смеси дейтерия с тритием используется для осуществления управляемого термоядерного синтеза; низкотемпературная плазма (Т ≤ 105 К) – в различных газоразрядных приборах: газовых лазерах, ионных приборах.
Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод
В природе существует большая группа веществ, занимающих промежуточное положение между проводниками и диэлектриками по величине электропроводности.
Полупроводниками называют вещества, удельное сопротивление которых находится в интервале от 10-3 до 107 Ом·м. К типичным полупроводникам относятся германий и кремний, селен, теллур, мышьяк.
Удельное сопротивление полупроводника зависит от внешних факторов: температуры, освещенности, электрического поля. С ростом температуры удельное сопротивление полупроводника уменьшается. С ростом освещенности также происходит уменьшение сопротивления полупроводника.
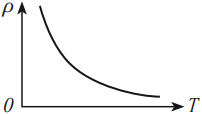
Такой ход зависимости удельного сопротивления от температуры ( rho(T) ) показывает, что у полупроводников концентрация свободных носителей заряда не остается постоянной, а увеличивается с ростом температуры. Объясним такую зависимость на примере германия.
Атомы германия на внешней оболочке имеют четыре валентных электрона. В кристаллической решетке каждый атом окружен четырьмя ближайшими соседями. Связь между атомами в кристалле германия является ковалентной, т. е. осуществляется парами валентных электронов. Каждый валентный электрон принадлежит двум разным атомам. Валентные электроны в кристалле германия связаны с атомами гораздо сильнее, чем в металлах, поэтому концентрация электронов проводимости при комнатной температуре в полупроводниках значительно меньше, чем у металлов. Вблизи абсолютного нуля температуры в кристалле германия все электроны заняты в образовании связей. Такой кристалл электрического тока не проводит.
При повышении температуры некоторая часть валентных электронов может получить энергию, достаточную для разрыва ковалентных связей. Тогда в кристалле возникнут свободные электроны (электроны проводимости). Одновременно в местах разрыва связей образуются вакансии, которые не заняты электронами. Эти вакансии получили название дырок. Вакантное место может быть занято валентным электроном из соседней пары, тогда дырка переместится на новое место в кристалле. При заданной температуре полупроводника в единицу времени образуется определенное количество электронно-дырочных пар. В то же время идет обратный процесс – при встрече свободного электрона с дыркой восстанавливается электронная связь между атомами германия. Этот процесс называется рекомбинацией. Электронно-дырочные пары могут появляться также при освещении полупроводника за счет энергии электромагнитного излучения. В отсутствие электрического поля электроны проводимости и дырки участвуют в хаотическом тепловом движении.
Если полупроводник поместить в электрическое поле, то в упорядоченном движении участвуют свободные электроны и дырки, которые ведут себя как положительно заряженные частицы. Поэтому ток ( I ) в полупроводнике складывается из электронного ( I_Э ) и дырочного ( I_Д ) токов:
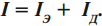
Концентрация электронов проводимости в полупроводнике равна концентрации дырок.
Электронно-дырочный механизм проводимости проявляется только у чистых (т. е. без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников.
Собственный полупроводник — полупроводник, не содержащий примесей, влияющих на его электропроводность.
При наличии примесей электрическая проводимость полупроводников сильно изменяется. Например, добавка в кристалл кремния примесей фосфора в количестве 0,001 атомного процента уменьшает удельное сопротивление более чем на пять порядков.
Важно!
Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.
Примесной проводимостью называют проводимость полупроводников при наличии примесей.
Различают два типа примесной проводимости – электронную и дырочную.
Электронная проводимость
Электронная проводимость возникает при введении в кристалл германия с четырехвалентными атомами пятивалентных атомов (например атомов мышьяка, ( As )).
Четыре валентных электрона атома мышьяка включены в образование ковалентных связей с четырьмя соседними атомами германия. Пятый валентный электрон оказывается лишним, он легко отрывается от атома мышьяка и становится свободным.
Атом, потерявший электрон, превращается в положительный ион, расположенный в узле кристаллической решетки. Примесь из атомов с валентностью, превышающей валентность основных атомов полупроводникового кристалла, называется донорной примесью. В результате ее введения в кристалле появляется значительное число свободных электронов. Это приводит к резкому уменьшению удельного сопротивления полупроводника.
Основными носителями заряда являются электроны. Концентрация свободных электронов намного больше концентрации дырок. Такая проводимость называется электронной, а полупроводник, обладающий электронной проводимостью, называется полупроводником ( n )-типа.
Дырочная проводимость
Дырочная проводимость возникает при введении в кристалл германия трехвалентных атомов (например атомов индия, ( In )). Атом индия с помощью своих валентных электронов создал ковалентные связи лишь с тремя соседними атомами германия. На образование связи с четвертым атомом германия у атома индия нет электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. В этом случае атом индия превращается в отрицательный ион, расположенный в узле кристаллической решетки, а в ковалентной связи соседних атомов образуется вакансия.
Примесь атомов, способных захватывать электроны, называется акцепторной примесью. В результате введения акцепторной примеси в кристалле разрывается множество ковалентных связей и образуются вакантные места – дырки. На эти места могут переходить электроны из соседних ковалентных связей, что приводит к движению дырок по кристаллу.
Наличие акцепторной примеси резко снижает удельное сопротивление полупроводника за счет появления большого числа свободных дырок. Концентрация дырок в полупроводнике с акцепторной примесью значительно превышает концентрацию электронов.
Проводимость такого типа называется дырочной проводимостью. Примесный полупроводник с дырочной проводимостью называется полупроводником p-типа. Основными носителями заряда в полупроводниках p-типа являются дырки.
p-n переход (электронно-дырочный переход) – это область контакта двух полупроводников с разными типами проводимости.
При контакте двух полупроводников n- и p-типов начинается процесс диффузии: дырки из p-области переходят в n-область, а электроны, наоборот, из n-области в p-область. В результате в n-области вблизи зоны контакта уменьшается концентрация электронов и возникает положительно заряженный слой. В p-области уменьшается концентрация дырок и возникает отрицательно заряженный слой. Таким образом, на границе полупроводников образуется двойной электрический слой, поле которого препятствует процессу диффузии электронов и дырок. Пограничная область раздела полупроводников с разными типами проводимости называется запирающим слоем. Объемные заряды этого слоя создают между p- и n-областями запирающее напряжение ( U_З ), приблизительно равное 0,35 В для германиевых n-p-переходов и 0,6 В для кремниевых.
p-n-переход обладает свойством односторонней проводимости. Если полупроводник с p-n-переходом подключен к источнику тока так, что положительный полюс источника соединен с n-областью, а отрицательный – с p-областью, то напряженность поля в запирающем слое возрастает. Дырки в p-области и электроны в n-области будут смещаться от p-n-перехода, увеличивая тем самым концентрации неосновных носителей в запирающем слое. Ток через p-n-переход практически не идет. Напряжение, поданное на p-n-переход, в этом случае называют обратным. Незначительный обратный ток обусловлен только собственной проводимостью полупроводниковых материалов.
Если p-n-переход соединить с источником так, чтобы положительный полюс источника был соединен с p-областью, а отрицательный с n-областью, то напряженность электрического поля в запирающем слое будет уменьшаться, что облегчает переход основных носителей через контактный слой. Дырки из p-области и электроны из n-области, двигаясь навстречу друг другу, будут пересекать p-n-переход, создавая ток в прямом направлении. Сила тока через p-n-переход в этом случае будет возрастать при увеличении напряжения источника.
Способность p-n-перехода пропускать ток практически только в одном направлении используется в приборах, которые называются полупроводниковыми диодами.
Обозначение на схемах полупроводникового диода:
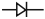
Полупроводниковые диоды изготавливают из кристаллов кремния или германия. Они используются в выпрямителях для преобразования переменного тока в постоянный. Вольт-амперная характеристика полупроводникового диода приведена на рисунке.
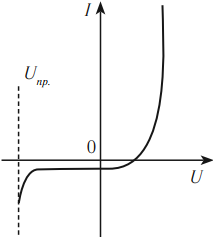
Полупроводниковые диоды имеют малые размеры, длительный срок службы, механическую прочность. Существенным недостатком полупроводниковых диодов является зависимость их параметров от температуры.
Основные формулы раздела «Законы постоянного тока»



Законы постоянного тока
3.3 (65%) 64 votes
Действующее напряжение и амплитудное напряжение — что это, и в чем отличие

Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.
Синусоида действующего и амплитудного напряжения
Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.
И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:
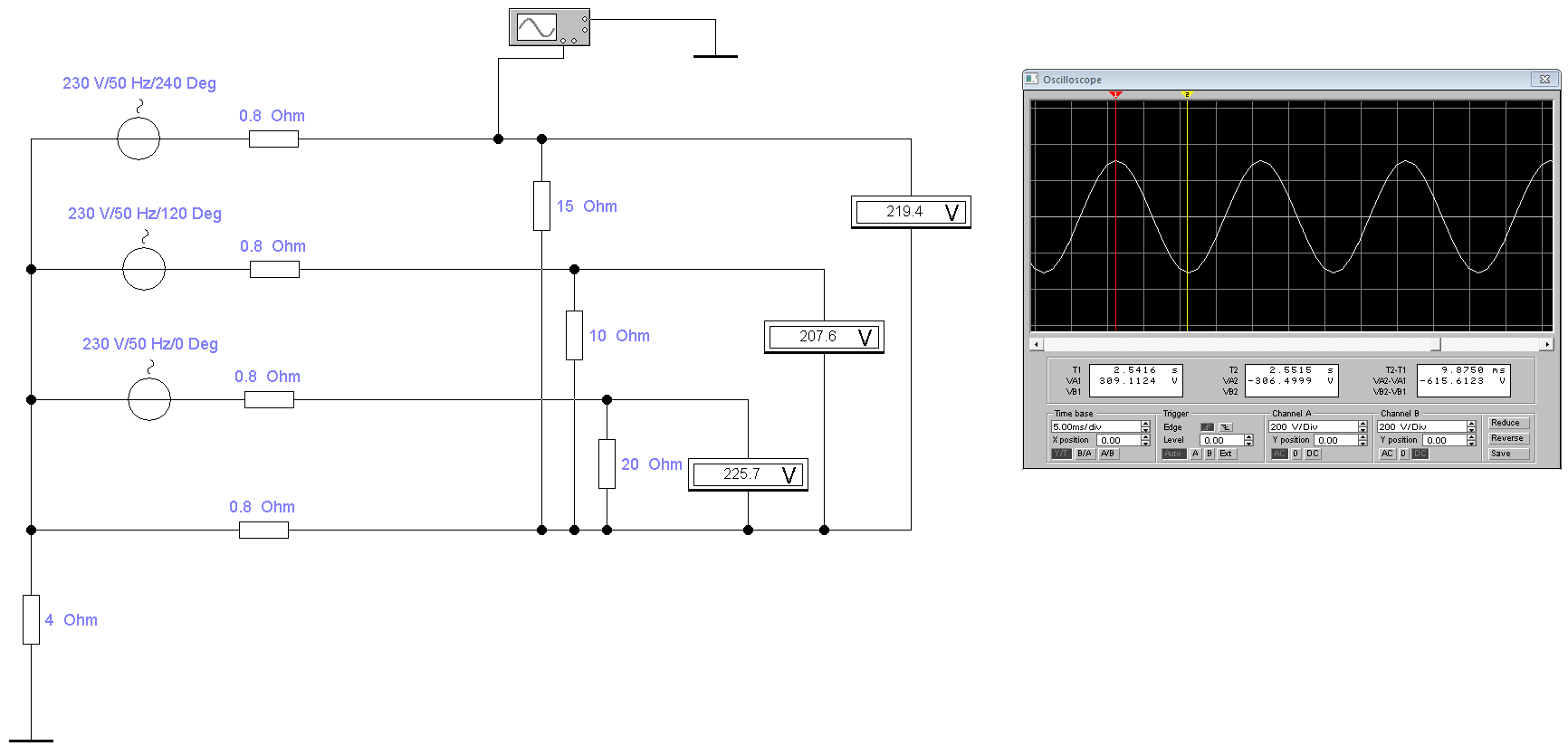
Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.
Начнем со схемы:
- Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
- Резистор 4 Ом — это заземление нейтрали трансформатора.
- Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
- Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
- К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.
Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.
Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.
Видео — действующее напряжение и амплитудное
С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:
Работа генератора трехфазного переменного тока
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:
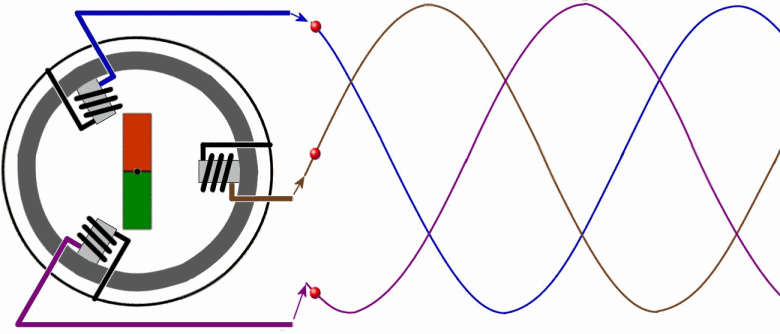
Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.
Определение действующего напряжения
Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.
Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.
Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
Общая формула расчета действующего напряжения произвольной формы следующая:
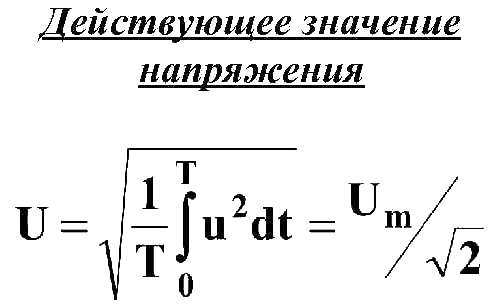
Объяснение действующего напряжения
Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.
Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.
Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.
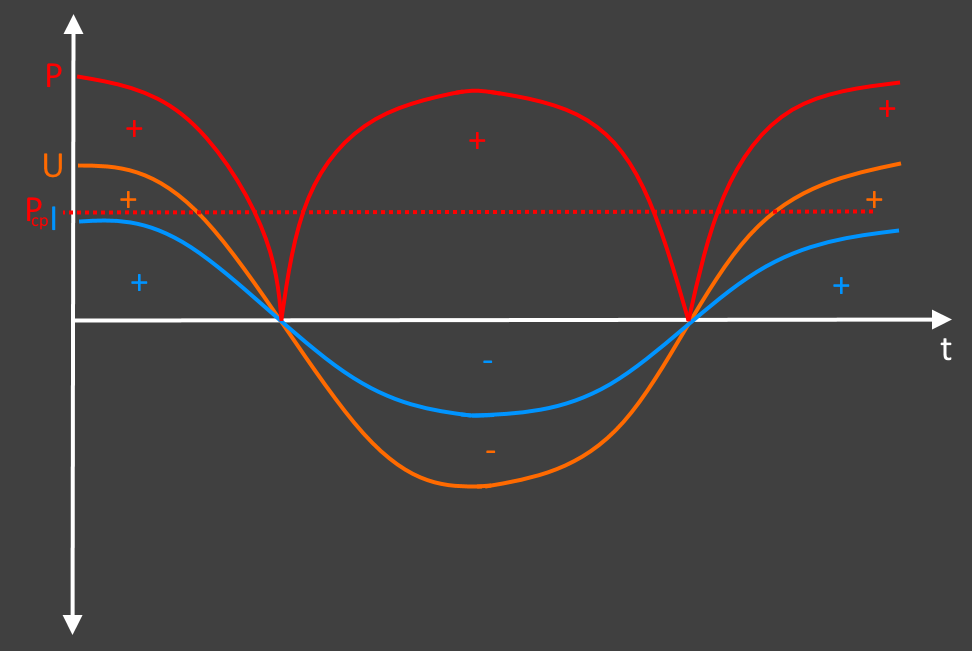
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».
Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:
Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.
Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).
Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.
И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
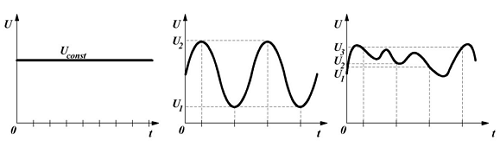
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
![]()
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
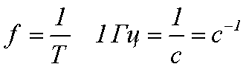
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
 Синусоидальное переменное напряжение.
Синусоидальное переменное напряжение.
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
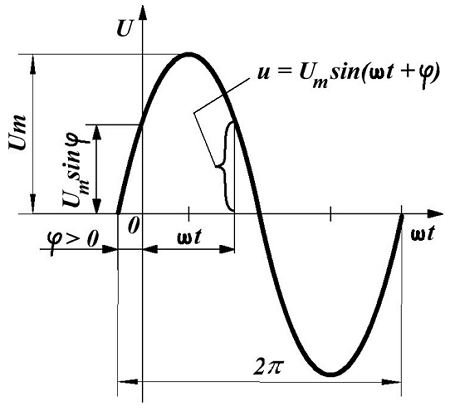
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
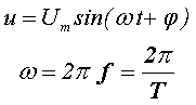
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
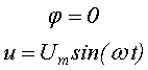
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
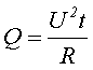
Для переменного напряжения мгновенное значение выделяемой энергии составит
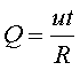
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
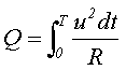
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
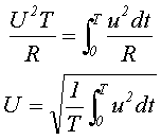
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
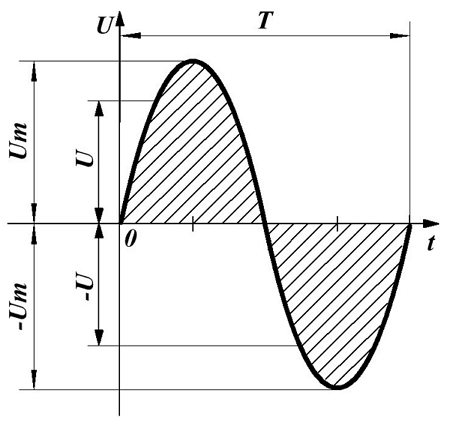
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
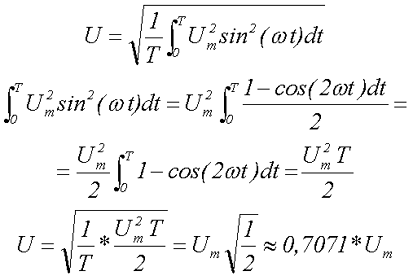
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
![]()
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
![]()
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
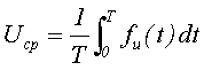
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
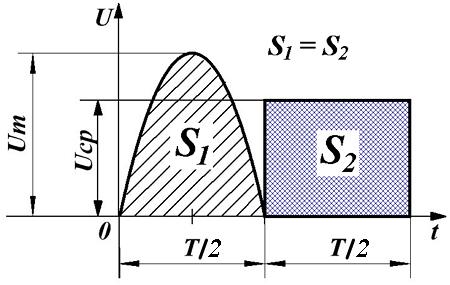
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
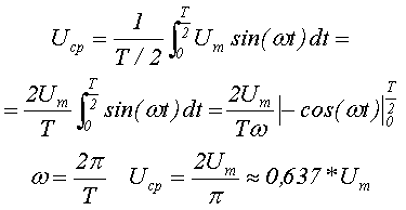
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
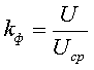
Так для синусоидального напряжения коэффициент формы составит
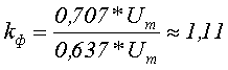
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
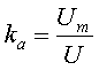
Так для синусоидального напряжения коэффициент амплитуды составит
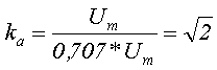
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.

