Укажите наибольшее решение неравенства:
x < (294 * 7500 − 3690460 : 5) : 4 − 359999.

reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 10 урок. Прикидка результатов арифметических действий. Номер №11
Решение
x < (294 * 7500 − 3690460 : 5) : 4 − 359999
x < (2205000 − 738092) : 4 − 359999
x < 1466908 : 4 − 359999
x < 366727 − 359999
x < 6728
Наибольшее решение неравенства x = 6727.
×
294
7500
¯
0
0
0
1470
00
2058
000
2205000
¯
0
¯
3690460
0
35
¯
0
0
¯
19
00
15
¯
00
0
¯
40
000
40
¯
0000
0
¯
4
00000
0
¯
0000
0
¯
46
00000
45
¯
00000
0
¯
10
000000
10
¯
0000000
0
5
738092
¯
–
2205000
738092
1466908
0
¯
1466908
0
12
¯
0
0
¯
26
00
24
¯
00
0
¯
26
000
24
¯
000
0
¯
29
0000
28
¯
0000
0
¯
10
000000
8
¯
00000
0
¯
28
000000
28
¯
0000000
0
4
366727
¯
–
366727
359999
6728


ГДЗ (готовое домашние задание из решебника) на 10 урок №13, Часть 2 по учебнику Математика. 4 класс. Часть 1, 2, 3. / Л.Г. Петерсон. – М. Ювента, 2013г.
Условие
Найди наибольшее натуральное решение неравенства:
а) k ≤ 568 + 80 * (205 * 906 − 124885) : 400;
б) n < (643 + 257) * (497 * 403 − 155956 : 307).
Решение 1

Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
 В этой статье вы сможете найти ответы к учебнику по математике автора Петерсон за 4 класс. (1 часть 2020 год) Надо заметить, что программа этого автора наиболее продвинутая в плане сложности примеров. В учебнике не размусоливается одно и то же, а приведены примеры достойной сложности для того уровня знаний, которыми должен обладать школьник.
В этой статье вы сможете найти ответы к учебнику по математике автора Петерсон за 4 класс. (1 часть 2020 год) Надо заметить, что программа этого автора наиболее продвинутая в плане сложности примеров. В учебнике не размусоливается одно и то же, а приведены примеры достойной сложности для того уровня знаний, которыми должен обладать школьник.
В целом, если ваши детки учатся по этой программе, то мы за вас рады! Ведь это значит что они шагают в ногу со знаниями, так как некоторый из учебников порой откровенно слабы в плане уровня сложности материала, что нам кажется излишними поблажками, способными привести к оболваниванию:)
Переходим к самим ответам.
3
Страница 3:
1. Прочитай текст в рамке. Найди в нём:
а) тему;
б) вводную часть;
в) главную мысль;
г) пример. Какими символами обозначены эти части текста? Cделай конспект (краткую запись содержания текста). Придумай свои примеры неравенств и их решений. Как ты думаешь, что понимается в тексте под «решением неравенства» – действие или число?
а) вводная часть − обозначена символом | (прямая горизонтальная)
Неравенство y < 9 верно при y = 5 и неверно при y = 16. Говорят, что число 5 удовлетворяет этому неравенству, а число 16 ему не удовлетворяет.
б) главная мысль обозначена символом VV (две галочки):
Решение неравенства − это значение переменной, которое при подстановке в неравенство превращает его в верное высказывание.
в) пример, иллюстрирующий эту главную мысль − обозначен символом (волнистая черта)
например, число 5 является решением неравенства y < 9, а число 16 не является решением этого неравенства.
Примеры x > 15 верно при x = 20 и неверно при x = 10.
t < 7 верно при t = 6 и неверно при t = 9.
Конспект:
1. Неравенство x < 25 верно при x = 20 и неверно при x = 30.
2. Значение переменной, удовлетворяющее неравенству, называют решением неравенства.
3. Пример, число 20 является решением неравенства x < 25, а число 30 не является решением данного неравенства.
Под термином решение неравенства понимается число.
2. Какие из чисел 24, 91, 318, 56, 7 удовлетворяют неравенству t > 56, а какие ему не удовлетворяют? Почему?
Решение:
Числа 91, 318 − удовлетворяют неравенству t > 56.
Числа 24, 56 и 7 − не удовлетворяют неравенству t > 56, потому что данные числа меньше или равны числу 56, а по условию должны быть больше числа 56.
3. Какие из чисел 75, 71, 70, 65, 9, 0 являются решениями неравенства 75 – x > 4? Докажи.
Решение:
Решением неравенства 75 – х > 4 являются числа: 70, 65, 9, 0, так как:
75-70>4, в итоге 5>4
75-65>4, в итоге 10 >4
75 – 9 > 4, в итоге 66 >4
75 – 0 > 4, в итоге 75 >4
4. Будет ли число 6 решением неравенства:
а)
15 + x > 40
15 + 6 > 40
21 > 40 – не будет
б)
2 + y < 96
2 + 6 < 96
8 < 96 – будет
в)
54 : t > 1
54 : 6 > 1
9 > 1 – будет
г)
48 – n < 39
48 – 6 < 39
42 < 39 – будет
д)
a + a < 20
6 + 6 < 20
12 < 20 – будет
е)
0 : b > 5
0 : 6 > 5
0 > 5 – не будет
4
Страница 4:
5. Имеются ли среди чисел 6, 9, 12, 30, 72 решения неравенства:
а) 8 • b – 7 > 90
Решение:
при b = 6,
8*b-7>90
8*6-7>90
48-7>90
41>90 нет решения
при b = 9,
8*b-7>90
8*9-7>90
72-7>90
65>90 нет решения
при b = 12,
8*b-7>90
8*12-7>90
96-7>90
89>90 нет решения
при b = 30,
8*b-7>90
8*30-7>90
240-7>90
233>90 есть решение
при b = 72,
8*b-7>90
8*72-7>90
576-7>90
569>90 есть решение
Ответ: 30 и 72
б) d : 3 + 9 < 12
Решение:
при b = 6
d : 3 + 9 < 12
d : 3 + 9 < 12
d : 3 + 9 < 12
при b = 9
d : 3 + 9 < 12
d : 3 + 9 < 12
d : 3 + 9 < 12
при b = 12
d : 3 + 9 < 12
d : 3 + 9 < 12
d : 3 + 9 < 12
при b = 30
d : 3 + 9 < 12
d : 3 + 9 < 12
d : 3 + 9 < 12
при b = 72
d : 3 + 9 < 12
d : 3 + 9 < 12
d : 3 + 9 < 12
Ответ:
6. Найди два решения неравенства:
а) n – 3 > 960
Решение а
n − 3 > 960
n > 960 + 3
n > 963
n = {964, 965, 966, …}, то есть неравенство будет верным при n > 963, например при:
n = 964, n = 1100.
б) 43 • m < 100
Решение б
43 * m < 100
m < 100 : 43
m < 2 (ост. 14)
m = {0, 1, 2}, то есть неравенство будет верным при m < 3, например при:
m = 0, m = 2.
в) 180 : y > 20
Решение в
180 : y > 20
y < 180 : 20
y < 9
y = {1, 2, 3, 4, 5, 6, 7, 8}, то есть неравенство будет верным при y < 9 и не равно 0, например
при:
y = 2, y = 7.
7. Перечисли все решения неравенства, которые ты сможешь найти:
а) 7 • c < 9
Решение а
7 * c < 9
c < 9 : 7
c < 1 (ост. 2)
неравенство будет верно при c = {0, 1}.
б) 12 : d > 3
Решение б
12 : d > 3
d < 12 : 3
d < 4
неравенство будет верно при d = {1, 2, 3}.
в) x • 7 < 21
Решение в
x * 7 < 21
x < 21 : 7
x < 3
неравенство будет верно при x = {0, 1, 2}.
г) y • 5 < 1
Решение г
y * 5 < 1
y < 1 : 5
y < 0 (ост. 1)
неравенство будет верно при y = {0}.
д) b + b < 4
Решение д
b + b < 4
2b < 4
b < 4 : 2
b < 2
неравенство будет верно при b = {0, 1}.
е) 3 – t > 2
Решение е
3 − t > 2
t < 3 − 2
t < 1
неравенство будет верно при t = {0}.
8. Заяц за 2 ч пробегает 14 км, а сокол за 3 ч пролетает 210 км. Во сколько раз сокол движется быстрее зайца? На сколько километров в час скорость зайца меньше скорости сокола? Перенеси в тетрадь и заполни таблицу*:
Ответь на вопросы и реши задачу: 1) Чему равна скорость зайца? 2) Чему равна скорость сокола? 3) Во сколько раз сокол движется быстрее зайца? 4) На сколько километров в час скорость зайца меньше скорости сокола?
| S | v | t | |
| Заяц | 14 | 7 | 2 |
| Сокол | 210 | 70 | 3 |
План решения:
1) Какова скорость зайца?
2) Какова скорость сокола?
3) Во сколько раз сокол движется быстрее зайца?
4) На сколько километров в час скорость зайца меньше скорости сокола?
Решение
1) 14 : 2 = 7 (км/ч) – скорость зайца.
2) 210 : 3 = 70 (км/ч) – скорость сокола.
3) 70 : 7 = в 10 (раз) – во столько скорость сокола, больше скорости зайца.
4) 70 − 7 = на 63 (км/ч) – на столько километров в час скорость зайца меньше скорости сокола.
Ответ: скорость зайца 7 км/ч, скорость сокола 70 км/ч, в 10 раз сокол движется быстрее зайца; на 63 км/ч скорость зайца меньше скорости сокола.
9. Туристы прошли 14 км и сделали привал. После привала они прошли на 6 км меньше, чем до привала, и остановились на ночлег. Им предстояло пройти ещё в 3 раза больше, чем они прошли. Какой длины путь был ими намечен?
Решение
1) 14 − 6 = 8 (км) – столько км прошли туристы после привала.
2) 14 + 8 = 22 (км) – всего они прошли.
3) 22 * 3 = 66 (км) – столько им предстояло пройти еще.
4) 22 + 66 = 88 (км) – такой длины путь был ими намечен.
Ответ: 88 км − путь, который намечен туристами.
10. Составь программу действий и вычисли:
1 3 6 2 4 7 5
а) (786 – 600) • 19 + (1007 – 965) • 14 – 48 • 16 = 3354
1) 786 – 600 = 186
2) 1007 – 965 = 42
3)
*186
19
+1674
186
3534
4)
*42
14
+168
42
588
5)
* 48
16
+ 288
48
768
6)
+3534
588
4122
7)
+ 4122
768
3354
1 3 5 6 4 2
б) (9867 + 76 535) • 105 – 96 + 78 • (1080 – 789) = 9094812
1)
+9867
76535
86402
2)
-1080
789
291
3)
*86402
105
+432010
86402
9072210
4)
*78
291
+78
702
156
22698
5)
-9072210
96
9072114
6)
+9072114
22698
9094812
11. Установи закономерность и заполни таблицу в тетради:
| 6 | 7 | 4 | 6 | 3 | 4 | 4 | 6 | 8 |
| 31 | 28 или 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 |
Решение
Числа в нижней строке похожи на количество дней в месяцах, в январе 31, в феврале 28 или 29 и т.д.
А числа в верхней строке могут говорить о количестве букв в названиях месяцев:
январь − 6 букв;
февраль − 7;
март − 4;
апрель − 6;
май − 3 буквы.
Продолжим закономерность и заполним таблицу:
5
Страница 5:
1. Найди в тексте, выделенном рамкой, вводную часть, главную мысль, примеры. Придумай свой пример неравенства, множество решений которого является: а) конечным; б) бесконечным; в) пустым. Сделай конспект.
Решение
1) Вводная часть − 1 абзац − выделяем знаком |.
2) Главная мысль − 2 абзац − знаком w.
3) Примеры − 3, 4 абзацы − знаком S.
Примеры неравенств:
а) x < 4 {0, 1, 2, 3};
б) x > 5 {6, 7, 8, …}.
в) x + 5 < 3 − не имеет ни одного решения ∅.
Конспект:
1) У неравенства может быть несколько решений. y < 4 {0, 1, 2, 3}.
2) Множество решений − полный список решений неравенства.
3) Примеры:
y + 10 < 5 − не имеет ни одного решения. Так как y > 5 {6, 7, 8, …}.
2. Запиши множество решений неравенства и отметь его на числовом луче. Существует ли в этом множестве наименьший элемент?
Образец: b < 5 Ответ: {0, 1, 2, 3, 4}
а) m > 4 Ответ: {4, 5, 6, …}
б) m < 4 Ответ: {0, 1, 2, 3}
в) c > 3 Ответ: {3, 4, 5, …}
г) c < 3 Ответ: {0, 1, 2}
6
Страница 6:
3. Запиши множество решений неравенства. Существует ли в этом множестве наибольший элемент?
а) k > 5 Ответ: {6, 7, 8, …}
б) k < 5 Ответ: {0, 1, 2, 3, 4}
в) y > 7 Ответ: {8, 9, 10…}
г) y < 7 Ответ: {0, 1, 2, 3, 4, 5, 6}
4. Реши неравенства. Что в них интересного?
x < 2 Ответ: {0, 1}
a < 2 Ответ: {0, 1}
2 > c Ответ: {0, 1}
В них имеется одна и тот же предел – до 2 не включительно.
5. Какое из множеств {0, 1, 2, 3}, {0, 1, 2}, {1, 2, 3}, {3, 4, 5, …}, {4, 5, 6, …}, служит множеством решений неравенства x < 3?
x < 3 Ответ: {0, 1, 2}
6. При решении неравенства получили ответ:
а) {0, 1, 2, 3, 4, 5, 6}; б) {5, 6, 7, …}. Какое неравенство могли решать?
Для случая а
b < 7
Для случая б
v > 4
7. Найди ошибки в записи и решении примеров. Запиши и реши их правильно.
*1790
204
+716
358
365160
-45540|9
45 |5060
– 54
54
0
8. Выполни действия:
372 • 814 = 302808
*372
814
+1488
372
2976
302808
7050 • 608 = 4286400
*7050
608
+5640
4230
4286400
63 280 : 7 = 9040
– 63280|7
63 |9040
-28
28
0
802 000 : 5 = 160 400
– 802000|5
80 |160400
-20
20
0
9. Реши задачу, используя формулу работы: «Оператор в первый день напечатал 48 страниц рукописи, а во второй день – на 12 страниц больше, чем в первый. На всю работу за два дня он затратил 9 часов. Сколько часов работал он в каждый из этих дней, если производительность его не менялась?»
1) 48 + 12=60 (стр.) – напечатано во второй день
2) 48 + 60 = 108 (стр.) – напечатано за два дня
3) 108 : 9 = 12 (стр.) – в час
4) 48 : 12 = 4 (ч) – потрачено в первый день
5) 60 : 12 = 5 (ч) – потрачено во второй день
Ответ: 4 и 5 часов.
10. Придумай и реши задачу, аналогичную задаче № 9:
а) на формулу пути;
«Турист в первый день прошел 20 км, а во второй день – на 2 км больше, чем в первый. На весь путь затратил 21 час. Сколько часов он шел каждый из этих дней, если его средняя скорость не менялась?»
1) 20 + 2 = 22 (км) – прошел во второй день
2) 20 + 22 = 42 (км) – прошел за два дня
3) 42 : 21 = 2 (км) – в час средняя скорость
4) 20 : 2 = 10 (ч) – шел в первый день
5) 22 : 2 = 11 (ч) – шел во второй день
Ответ: 4 и 5 часов.
б) на формулу стоимости.
«В магазине в первый день продали открыток на 48 рублей, а во второй день – на 12 рублей больше, чем в первый. Всего было продано 9 открыток. Сколько открыток продали в первый день и во второй?»
1) 48 + 12 = 60 (р.) – на эту сумму продали во второй день
2) 48 + 60 = 108 (р.) – на эту сумму продали за два дня
3) 108 : 9 = 12 (р.) – стоит открытка
4) 48 : 12 = 4 (от.) – продали в первый день
5) 60 : 12 = 5 (от.) – продали во второй день
Ответ: 4 и 5 открыток.
11. Реши уравнения с комментированием и сделай проверку:
а) 16 + 48 : z = 40
48 : z = 40 – 16
48 : z = 24
z = 48 : 24
z = 2
Проверка: 16 + 48 : 2 = 40
40 = 40
б) 320 : (52 – x) = 8
52 – x = 320 : 8
52 – x = 40
x = 52 – 40
x = 12
Проверка: 320 : (52 – 12) = 8
8 = 8
в) 50 • y – 72 = 78
50 • y = 78 + 72
50 • y = 150
у = 150 : 50
у = 3
Проверка: 50 • 3 – 72 = 78
78 = 78
12. Верны ли высказывания?
а) Число 0 меньше любого натурального числа. истинное
б) Число 8 удовлетворяет равенству x • x – x = 56. истинное
в) Два часа больше семи тысяч секунд. 2 *60 * 60 = 7200 с истинное
г) Пять гирь по 3 кг тяжелее трёх гирь по 5 кг. ложное
д) В двух квадратных дециметрах содержится 200 сантиметров. истинное
7
Страница 7:
1. Что общего и чем различаются примеры каждого столбика? Вычисли устно и объясни приём вычислений:
9 + 7
16 – 9
63 – 25
25 + 38
19 • 4
190 • 4000
72 : 6
72 000 : 600
45 : 15
48 : 15
Решение:
9 + 7 = 16
16 – 9 = 7
63 – 25 = 38
25 + 38 = 63
19 • 4 = 76
190 • 4000 = 760 000
72 : 6 = 12
72 000 : 600 = 12
45 : 15 = 3
48 : 15 = 3 (ост. 3)
2. Выполни действия:
30 007 – 5939
745 918 + 62
162 903 • 8000
54 600 • 207
Решение:
30 007 – 5939 = 24 068
745 918 + 62 162 = 808 080
903 • 8000 = 7 224 000
54 600 • 207 = 11 302 200
3. Найди неравенства, решением которых является число 6:
a > 5
b < 6
c · 3 > 12
10 – d : 2 < 3
Решение:
a > 5 – 6 является решением в том числе
c · 3 > 12 – 6 является решением в том числе
4. Запиши множество решений неравенства и отметь его на числовом луче:
а) x > 3
б) y < 8
в) z > 2
г) m < 5
Решение:
а) x > 3 {4, 5, 6, 7, …}.
б) y < 8 {0, 1, 2, 3, 4, 5, 6, 7}
в) z > 2 {3, 4, 5, 6, 7, …}.
г) m < 5 {0, 1, 2, 3, 4}
5. A, B и C – множества решений трёх неравенств. Напиши эти неравенства, если: А = {2, 3, 4, …}; В = {0, 1, 2, 3, 4, 5, 6, 7, 8}; С = {0, 1, 2, 3, 4}.
Решение:
А = {2, 3, 4, …}; с > 2
В = {0, 1, 2, 3, 4, 5, 6, 7, 8}; x < 9
С = {0, 1, 2, 3, 4}. f < 5
6. Реши задачу, используя формулу стоимости:
«Папа дал в кассу магазина 1500 р. в уплату за 3 рубашки по цене 360 р. каждая. Сколько сдачи он должен получить?» Придумай и реши задачи, которые решаются так же: а) на формулу пути; б) на формулу работы.
Решение:
1) 360 * 3 = 1080 (р.) стоили 3 рубашки
2) 1 500 – 1 080 = 420 (р.) сдача.
Ответ: 420 рублей.
Задачи на формулу пути
Поезд выехал от одной станции до другой, между которыми 200 км, и ехал со скоростью 60 км/ч в течение 3 часов. Сколько км ему осталось проехать?
1) 60 * 3 = 180 (км) проехал поезд за 3 часа
2) 200 – 180 = 20 (км) осталось проехать.
Ответ: 20 километров.
Задачи на формулу работы
Рабочий делает 20 деталей за час. За смену ему надо сделать 160 деталей. Он проработал 5 часов. Сколько деталей ему осталось сделать по плану за смену?
1) 20 * 5 = 100 (дет.) сделал рабочий за 5 часов.
2) 160 – 100 = 60 (дет.) осталось сделать.
Ответ: 60 деталей.
7.
а) В библиотеке на первой полке стоит 120 книг, на второй – в 2 раза больше, чем на первой, а на третьей – в 3 раза меньше, чем на второй. На сколько книг на третьей полке меньше, чем на первой?
б) На туристической базе летом проживало в палатках 200 человек и в доме 180 человек. К осени число людей в палатках уменьшилось в 8 раз, а в доме – в 2 раза. Сколько туристов было на базе осенью?
Решение:
а) В библиотеке на первой полке стоит 120 книг, на второй – в 2 раза больше, чем на первой, а на третьей – в 3 раза меньше, чем на второй. На сколько книг на третьей полке меньше, чем на первой?
1) 120 * 2 = 240 (кн.) книг на второй полке.
2) 240 : 3 = 80 (кн.) на третьей полке.
3) 120 – 80 = 40 (кн.) на третьей полке меньше, чем на первой.
Ответ: на 40 книг.
б) На туристической базе летом проживало в палатках 200 человек и в доме 180 человек. К осени число людей в палатках уменьшилось в 8 раз, а в доме – в 2 раза. Сколько туристов было на базе осенью?
1) 200 : 8 = 25 (чел.) стало жить в палатках.
2) 180 : 2 = 90 (чел.) стало жить в доме.
3) 25 + 90 = 115 (тур.) стало жить на базе осенью.
Ответ: 115 туристов.
8. Автомобиль за три дня проехал 980 км. В первые два дня он проехал 725 км. Сколько километров проезжал автомобиль в каждый из этих дней, если во второй день он проехал больше, чем в третий, на 123 км?
Решение:
1) 980 – 725 = 255 (км) проехала автомобиль в третий день
2) 255 + 123 = 378 (км) проехал во второй день.
3) 378 + 255 = 633 (км) проехал во второй день.
4) 980 – 633 = 347 (км) проехал в первый день.
Ответ: 347 км в первый день, 378 км во второй и 255 км в третий день.
8
Страница 8:
9. Ширина прямоугольного участка земли равна 25 м, а длина на 15 м больше. Как и на сколько изменится площадь участка, если его ширину увеличить на 7 м, а длину уменьшить на 5 м?
Решение:
1) 25 + 7 = 32 (м) станет ширина участка.
2) 15 – 5 = 10 (м) станет длина участка.
3) 25 * 15 = 375 (м2) площадь участка.
4) 32 * 10 = 320 (м2) станет площадь участка.
5) 375 – 320 = 55 (м2) на столько изменится площадь.
Ответ: на 55 м2
10. Запиши выражения и найди их значения.
а) Сумма числа 26 и произведения чисел 9 и 8.
б) Разность частного чисел 800 и 40 и числа 15.
в) Произведение суммы и разности чисел 14 и 6.
г) Частное произведения и разности чисел 12 и 4.
Ответ:
а) Сумма числа 26 и произведения чисел 9 и 8.
26 + 9*8 = 26 + 72 = 98
б) Разность частного чисел 800 и 40 и числа 15.
(800 : 40) – 15 = 20 – 15 = 5
в) Произведение суммы и разности чисел 14 и 6.
(14 + 6) * (14 – 6) = 20 * 8 = 160
г) Частное произведения и разности чисел 12 и 4.
(14 * 4) : (12 – 4) = 56 : 8 = 7
11. Составь программу действий и вычисли:
а) 4045 : 5 + 451 • 75 – (729 – 642)
б) 1027 – 428 + 307 • 280 – (60 005 – 5168) : 9
Решение:
2 4 3 5 1
а) 4045 : 5 + 451 • 75 – (729 – 642) = 34 547
1) 729 – 642 = 87
2) 4045 : 5 = 809
3) 451 * 75 = 33 825
* 451
75
+ 2255
3157
33825
4) 809 + 33 825 = 34 634
5) 34 634 – 87 = 34 547
4 5 2 6 1 3
б) 1027 – 428 + 307 • 280 – (60 005 – 5168) : 9 = 80 506
1) 60 005 – 5 168 = 54 837
2) 307 * 280 = 85 960
*307
280
+2456
614
85960
3) 54 837 : 9 = 6093
-54837|9
54 |6093
83
–81
-27
27
0
4) 1027 – 428 = 599
5) 599 + 85 960 = 86 559
6) 86 599 – 6093 = 80 506
12. Построй квадрат и треугольник, пересечением которых является пятиугольник.
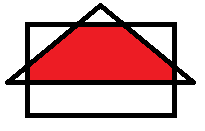
13. Вычисли. Расшифруй и отгадай загадку.
Ь (17 + 28) : 9 = 5
Н 60 – 32 : 4 = 52
И (80 – 50) : 15 = 2
К 27 • 3 – 34 = 47
Д 20 • 8 : 40 = 4
О 75 : 3 • 2 – 18 = 25 * 2 – 18 = 32
Л 800 : 100 • 9 : 3 = 72 : 3 = 24
Б 600 : 10 • 3 : 18 = 60 * 3 : 18 = 180 : 18 = 10
А (76 – 40) : 18 • 8 = 2 * 8 = 16
Т 650 : 5 • 3 : 10 = 130 * 3 : 10 = 39
Ч 280 • 2 : 80 · 12 = 7 * 12 = 84
Е 100 – 72 : 9 • 11 = 100 – 8 * 11 = 100 – 88 = 12
Ю 15 • (16 – 9) : 3 = 15 * 7 : 3 = 105 : 3 = 35
ТО ОН БЛИН ТО ОН КЛИН НОЧЬЮ НА НЕБЕ ОДИН
МЕСЯЦ
14. Чтобы открылись ворота при въезде в сказочный город Числоград, ребятам надо было на табло: зажечь числа в свободных клетках так, чтобы сумма чисел, стоящих в любых трёх соседних клетках, равнялась 20. Помоги ребятам попасть в этот город.
| 8 | 7 | 5 | 8 | 7 | 5 | 8 | 7 | 5 | 8 |
9
Страница 9:
1.
а) Маленький Артём заплакал. Чтобы его успокоить, Таня сказала: «Я дам тебе конфету или печенье». Саша сказал: «Я дам тебе конфету и печенье». Чем отличаются их высказывания?
б) Таня и Саша дали Артёму только по конфете. Кто из них выполнил своё обещание?
Решение:
а) Маленький Артём заплакал. Чтобы его успокоить, Таня сказала: «Я дам тебе конфету или печенье». Саша сказал: «Я дам тебе конфету и печенье». Чем отличаются их высказывания?
Таня сказала “ИЛИ” то есть один из элементов множества, а Саша “И”, то есть все элементы множества.
б) Таня и Саша дали Артёму только по конфете. Кто из них выполнил своё обещание?
Саша не выполнил обещания, так как не дал все элементы множества, хотя обещал и то и другое.
2. Прочитай неравенства. Из каких высказываний они состоят? Какие из них верны, а какие – нет?
5 ≤ 16
12 ≤ 12
29 ≤ 1
99 ≥ 100
180 ≥ 7
25 ≥ 25
94 ≥ 49
805 ≤ 508
Решение:
5 ≤ 16 – верное
12 ≤ 12 – верное
29 ≤ 1 – ложное
99 ≥ 100 – верное
180 ≥ 7 – верное
25 ≥ 25 – верное
94 ≥ 49 – верное
805 ≤ 508 – ложное
3. Запиши неравенства. Докажи, что они верны:
а) 15 меньше или равно 34
в) 17 меньше или равно 17
б) 72 больше или равно 27
г) 56 больше или равно 56
Решение:
а) 15 меньше или равно 34
15≤34 – верное, так как 15 меньше 34, при этом равно может не выполняться, так как по логике программирования если хотя бы одно из условий верное, то уже является истинным, то есть читается как одно условие “ИЛИ” второе.
в) 17 меньше или равно 17
17 ≤ 17 – верное, так как 17 = 17 (по логике программирования если хотя бы одно из условий верное, то уже является истинным, то есть читается как одно условие “ИЛИ” второе)
б) 72 больше или равно 27
72 ≥ 27 – верное, так 27 меньше 72 (по логике программирования если хотя бы одно из условий верное, то уже является истинным, то есть читается как одно условие “ИЛИ” второе)
г) 56 больше или равно 56
56 ≥ 56 – верное, так как 56 = 56 (по логике программирования если хотя бы одно из условий верное, то уже является истинным, то есть читается как одно условие “ИЛИ” второе)
10
Страница 10:
4. Запиши множество решений каждого неравенства и отметь его на числовом луче. Найди «похожие» неравенства. Что ты замечаешь?
а) х < 5
б) x ≤ 5
в) y > 2
г) y ≥ 2
Решение:
а) х < 5 Ответ: {0, 1, 2, 3, 4}

б) x ≤ 5 Ответ: {0, 1, 2, 3, 4, 5}

в) y > 2 Ответ: {3, 4, 5, …}

г) y ≥ 2 Ответ: {2, 3, 4}

5. Реши неравенства. Чем различаются множества их решений?
а) m ≤ 3 и m < 3
б) d > 4 и d ≥ 4
Решение:
а) m = 3 и m < 3 Ответ: {0, 1, 2, 3}
б) d > 4 и d = 4 Ответ: {4, 5, 6, …}
6. Реши неравенства. Что ты замечаешь?
z ≤ 6
n ≤ 6
6 ≥ k
Решение а
z ≤ 6 {0, 1, 2, 3, 4, 5, 6}
Решение б
n ≤ 6 {0, 1, 2, 3, 4, 5, 6}
Решение в
6 ≥ k {0, 1, 2, 3, 4, 5, 6}
7. Напиши множество решений неравенства y < 7. Какое неравенство со знаком ≤ имеет то же самое множество решений?
Решение:
y ≤ 6
8. Напиши множество решений неравенства t > 9. Какое неравенство со знаком ≥ имеет то же самое множество решений?
Решение:
t ≥ 8
9. Выполни действия. Проверь результаты с помощью калькулятора.
а) 33 330 • 440
б) 80 800 • 7070
в) 646 400 : 8
г) 45 004 500 : 50
Решение:
а) 33 330 • 440 = 14665200
*33330
440
+133320
133320
14665200
б) 80 800 • 7070
*7070
80800
+56560
56560
571256000
в) 646 400 : 8
– 646400|8
64 |80800
-64
64
0
г) 45 004 500 : 50
-45004500|50
45 |900090
-45
45
0
10. Выполни действия. Как быстрее найти все ответы? Прочитай их.
а)
382 • 87
3820 • 870
38 200 • 8700
382 000 • 87 000
б)
32 448 : 6
324 480 : 60
3 244 800 : 600
32 448 000 : 6000
Решение:
а)
382 • 87 = 33234
* 382
87
+2674
3056
33234
3820 • 870 = 3 323 400
38 200 • 8700 = 332 340 000
382 000 • 87 000 = 33 234 000 000
б)
32 448 : 6 = 5408
-32448|6
30 |5408
-24
24
-48
48
0
324 480 : 60 = 5408
3 244 800 : 600 = 5408
32 448 000 : 6000 = 5408
11.
а) Масса птички зарянки примерно 18 граммов, а масса её яйца 3 грамма. Во сколько раз масса зарянки больше массы её яйца?
б) Птенцы жаворонка сидят в гнезде до вылета 8 дней, а птенцы синицы – в 2 раза больше. Сколько времени сидят в гнезде до вылета птенцы синицы?
в) Масса яйца сороки примерно 7 граммов, что в 4 раза меньше массы яйца фазана. Чему равна масса яйца фазана? Чья масса больше – яйца сороки или яйца фазана, и на сколько граммов?
Решение:
а) 18 : 3 = 6 (раз) масса зарянки больше массы её яйца
Ответ: в 6 раз
б) 8 * 2 = 16 (дн.) сидят в гнезде до вылета птенцы синицы
Ответ: 16 дней.
в) 7 * 4 = 28 (гр.) масса яйца фазана
Ответ: 28 грамм
12. Перерисуй фигуры в тетрадь. Раздели их на две равные части ломаной линией, проходящей по сетке.

11
Страница 11:
1. Начерти числовой луч. Отметь на нём множество чисел, которые одновременно больше 3 и меньше 7. Запиши неравенство, множество решений которого составляют отмеченные числа. Сравни свою запись с общепринятой записью «двойных неравенств». Сделай вывод.

1) 3 < x < 7;
или
2) 4 ≤ x ≤ 6; * – будет то же множество чисел, но числовой луч будет другим.
12
Страница 12:
2. Прочитай неравенства:
7 < a < 12
18 ≤ c < 75
130 < m < 182
15 < b ≤ 96
21 ≤ d ≤ 49
274 < n ≤ 360
Решение:
7 < a < 12 – а больше 7 и меньше 12
18 ≤ c < 75 – с больше или равно 18 и меньше 75
130 < m < 182 – m больше 130 и меньше 182
15 < b ≤ 96 – b больше 15 и меньше или равно 96
21 ≤ d ≤ 49 – d больше или равно 21 и меньше или равно 49
274 < n ≤ 360 – n больше 274 и меньше или равно 360
3. Замени двойное неравенство двумя неравенствами:
а) 9 ≤ x < 18
б) 3 < y ≤ 11
в) 4 ≤ z ≤ 7
Решение:
а) 9 ≤ x < 18 9 ≤ x и x< 18
б) 3 < y ≤ 11 3 < y и у ≤ 11
в) 4 ≤ z ≤ 7 4 ≤ z и z ≤ 7
4. Запиши двойные неравенства:
а) t больше 4 и меньше 9
б) k больше или равно 5 и меньше 18
в) m больше 10 и меньше или равно 25
г) n больше или равно 6 и меньше или равно 15
Решение:
а) t больше 4 и меньше 9 4 < t < 9
б) k больше или равно 5 и меньше 18 5 ≤ k < 18
в) m больше 10 и меньше или равно 25 10 < m ≤ 25
г) n больше или равно 6 и меньше или равно 15 6 ≤ n ≤ 15
5. Отметь на числовом луче и запиши множество решений каждого неравенства. Что ты замечаешь?
3 < x < 8
4 ≤ x < 8
3 < x ≤ 7
4 ≤ x ≤ 7
Решение:
3 < x < 8

4 ≤ x < 8

3 < x ≤ 7

4 ≤ x ≤ 7

6. Напиши двойные неравенства, множество решений которых отмечено на числовом луче:
2 ≤ x ≤ 5 или 1 < x < 6
7. Можно ли заменить данные неравенства двойным неравенством? Если да, то запиши подходящее двойное неравенство.
а) y > 2 и y < 6
в) y > 2 и y > 6
б) y > 2 и z < 6
г) y < 2 и y > 6
Решение:
а) y > 2 и y < 6 – 2 < y < 6
в) y > 2 и y > 6 – не заменить
б) y > 2 и z < 6 – не заменить
г) y < 2 и y > 6 – не заменить
8. Верны ли высказывания?
1) Некоторые решения неравенства x ≤ 10 являются однозначными числами.
2) Все решения неравенства x ≤ 10 являются однозначными числами.
Решение:
1) Некоторые решения неравенства x ≤ 10 являются однозначными числами. неверное
2) Все решения неравенства x ≤ 10 являются однозначными числами. верное
9. Запиши формулы периметра и площади прямоугольника. Реши с их помощью задачи:
а) Ширина прямоугольника равна 6 см, а длина в 2 раза больше ширины. Чему равны периметр и площадь этого прямоугольника?
б) Длина прямоугольника равна 7 см, что на 4 см больше его ширины. Найди периметр и площадь этого прямоугольника.
в) Периметр квадрата равен 36 см. Чему равна площадь этого квадрата?
Решение:
P = (a + b) * 2 – периметр прямоугольника;
S =a * b – площадь прямоугольника.
а) Ширина прямоугольника равна 6 см, а длина в 2 раза больше ширины. Чему равны периметр и площадь этого прямоугольника?
1) (6 + 2) * 2 = 8 * 2 = 16 (см) периметр прямоугольника.
2) 6 * 2 = 12 (см2) площадь прямоугольника.
Ответ: 16 см периметр и 12 см2 площадь.
б) Длина прямоугольника равна 7 см, что на 4 см больше его ширины. Найди периметр и площадь этого прямоугольника.
1) 7 – 4 = 3 (см) ширина прямоугольника.
1) (7 + 3) * 2 = 10 * 2 = 20 (см) периметр прямоугольника.
2) 7 * 3 = 21 (см2) площадь прямоугольника.
Ответ: 20 см периметр и 21 см2 площадь.
в) Периметр квадрата равен 36 см. Чему равна площадь этого квадрата?
1) 36 : 4 = 9 (см) сторона квадрата.
2) 9 * 9 = 81 (см2) площадь квадрата.
Ответ: 81 см2 площадь квадрата.
13
Страница 13:
10. Реши уравнения с комментированием. Что ты замечаешь?
а) x + 389 = 2076
б) x – 1687 = 389
в) 2076 – x = 1687
Решение:
а) x + 389 = 2076
х+389=2076
х=2076-389
х=1687
б) x – 1687 = 389
х-1687=389
х=389+1687
х=2076
в) 2076 – x = 1687
2076-х=1687
х=2076-1687
х=389
11. Составь программу действий и вычисли:
а) 78 • 607 – 19 • 97 + 904 • (2081 – 1978)
б) 805 001 + 908 • 407 – 65 • (403 – 289) – 205 • 78
Решение:
2 5 3 6 4 1
а) 78 • 607 – 19 • 97 + 904 • (2081 – 1978) = 138 615
1) 2081 – 1978 = 103
-2081
1978
103
2) 78 • 607 = 47 346
*78
607
+546
468
47346
3) 19 • 97 = 1 843
*19
97
+133
171
1843
4) 904 * 103 = 93 112
*904
103
+2712
904
93112
5) 47 346 – 1 843 = 45 503
-47346
1843
45503
6) 45 503 + 93 112 = 138 615
+45503
93112
138615
5 2 6 3 1 7 4
б) 805 001 + 908 • 407 – 65 • (403 – 289) – 205 • 78 = 1 151 157
1) 403 – 289 = 114
-403
289
114
2) 908 • 407 = 369 556
*908
407
+ 6356
3632
369556
3) 65 * 114 = 7 410
*65
114
+260
65
65
7410
4) 205 • 78 = 15 990
*205
78
+1640
156
15990
5) 805 001 + 369 556 = 1 174 557
+805001
369556
1174557
6) 1 174 557 – 7 410 = 1 167 147
-1174557
7410
1167147
7) 1 167 147 – 15 990 = 1 151 157
-1167147
15990
1151157
12. БЛИЦтурнир*
а) Олегу a лет, а Света на 6 лет старше. Во сколько раз Олег младше Светы?
б) Маме b лет, а Ира в 4 раза младше мамы. На сколько лет мама старше Иры?
в) Мише c лет, а его сестре d лет. Во сколько раз Миша будет старше сестры через 3 года?
г) Кате, Даше и Наташе вместе x лет. Кате n лет, а Даша в 2 раза младше Кати. Сколько лет Наташе?
Решение:
а) Олегу a лет, а Света на 6 лет старше. Во сколько раз Олег младше Светы?
(a + 6) : a
б) Маме b лет, а Ира в 4 раза младше мамы. На сколько лет мама старше Иры?
b – b : 4
в) Мише c лет, а его сестре d лет. Во сколько раз Миша будет старше сестры через 3 года?
(c + 3) : (d + 3)
г) Кате, Даше и Наташе вместе x лет. Кате n лет, а Даша в 2 раза младше Кати. Сколько лет Наташе?
x – n – (n : 2)
13. Найди пропущенные цифры
*217
6320
+ 434
651
1302
1371440
37050
809
+3345
29640
29973450
-540180|6
54 |90030
-18
18
0
14. За день на фабрике изготовили 1240 м ситца, шерсти – в 4 раза меньше, чем ситца, вельвета – на 490 м больше, чем шерсти, а полотна столько, сколько шерсти и вельвета вместе. Сколько ткани изготовили на фабрике за этот день?
Решение:
1) 1240 : 4 = 310 (м) шерсти изготовили.
2) 310 + 490 = 800 (м) вельвета изготовили.
3) 310 + 800 = 1110 (м) полотна изготовили.
4) 1240 + 310 + 800 + 1110 = 3460 (м) ткани израсходовали.
Ответ: 3460 метров.
15. Сколько различных произведений, кратных 10, можно образовать из множителей 2, 3, 5, 7, 9? (Каждый множитель можно использовать только один раз, порядок множителей не принимается во внимание.)
Решение:
2 * 5 − кратно десяти.
В каждом следующем произведении указываем множители 2 и 5, что в результате даст число, оканчивающееся на 0, а все числа, которые заканчиваются нулем − кратны 10.
2 * 5;
2 * 5 * 3;
2 * 5 * 3 * 7;
2 * 5 * 3 * 7 * 9;
2 * 5 * 7;
2 * 5 * 7 * 9;
2 * 5 * 9.
Итого, можно образовать 7 различных произведений, кратных 10.
14
Страница 14:
1. Какое из множеств {0, 1, 2, 3, 4}, {4, 5, 6, …}, {5, 6, 7, 8, …} является множеством решений неравенства x > 4? Какое неравенство со знаком ≥ имеет такое же множество решений?
Решение:
множеством решений неравенства x > 4 является {5, 6, 7, 8, …}
неравенство со знаком ≥ имеет такое же множество решений {4, 5, 6, …}
2. Какие из чисел 3, 7, 8, 12, 40, 50, 60 являются решениями неравенства 7 < y ≤ 50?
Решение:
{8, 12, 40, 50, 60}
3. Отметь на числовом луче и запиши множество решений каждого неравенства. Что ты замечаешь?
1 < х < 5
2 ≤ х < 5
1 < х ≤ 4
2 ≤ х ≤ 4
Решение:
1 < х < 5
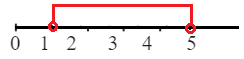
2 ≤ х < 5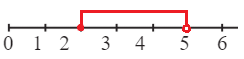
1 < х ≤ 4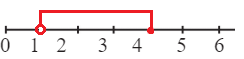
2 ≤ х ≤ 4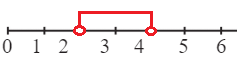
4. Запиши неравенство и укажи множество его решений: а) b меньше или равно 3 в) t больше 5 и меньше или равно 8б) k больше 9 г) m больше или равно 7 и меньше 12
Решение:
а) b меньше или равно 3 b ≤ 3
б) k больше 9 k ≥ 9
в) t больше 5 и меньше или равно 8 5 ≤ t ≤ 8
г) m больше или равно 7 и меньше 12 7 ≤ m ≤ 12
5. Составь выражения к задачам:
а) Длина прямоугольника равна y см, что в 2 раза больше его ширины. Чему равен периметр этого прямоугольника?
б) Ширина прямоугольника равна c дм, а его длина – на 4 дм больше ширины. Чему равна площадь этого прямоугольника?
Решение:
а) Длина прямоугольника равна y см, что в 2 раза больше его ширины. Чему равен периметр этого прямоугольника?
2 * (y + 2*y) = 2 * y + 4 * y = 6y (см)
б) Ширина прямоугольника равна c дм, а его длина – на 4 дм больше ширины. Чему равна площадь этого прямоугольника?
с * (с + 4)
6. Запиши формулу пути и найди пропущенные значения величин:
Решение:
S = v*t
| S | v | t |
| 210 км | 70 км/ч | 3 ч |
| 60 м | 5 м/с | 12 с |
| 720 м | 90 м/мин | 8 мин |
7. Используя формулу пути, реши задачу: «Велосипедист ехал 2 ч со скоростью 18 км/ч. После этого ему осталось ехать в 3 раза больше, чем он проехал. Чему равен весь путь этого велосипедиста?»
Решение:
S = v*t
1) 2 * 18 = 36 (км) проехал велосипедист.
2) 36 * 3 = 108 (км) осталось проехать.
3) 36 + 108 = 144 (км) путь велосипедиста.
Ответ: 144 км.
8. Придумай и реши задачу, имеющую такое же решение:
а) на формулу стоимости;
б) на формулу работы.
Решение:
а) на формулу стоимости;
В магазине продали 2 кг моркови по 18 рублей за кг, а затем картофеля на сумму в 3 раза больше. Сколько выручили за овощи при их продаже?
1) 2 * 18 = 36 (р.) стоили 2 кг моркови.
2) 36 * 3 = 108 (р.) стоил картофель.
3) 36 + 108 = 144 (р.) выручили за овощи.
Ответ: 144 рубля.
б) на формулу работы.
Ученик делал 18 деталей в час, в течение 2 часов, а мастер сделал потом еще в 3 раза больше деталей, чем ученик. Сколько деталей сделали мастер и ученик?
1) 2 * 18 = 36 (д.) сделал ученик.
2) 36 * 3 = 108 (д.) сделал мастер.
3) 36 + 108 = 144 (д.) сделали мастер и ученик.
Ответ: 144 деталей.
9. Сравни выражения с помощью знаков >, <, = *:
a + 85 75 + a
b – 49 b – 130
48 : k 72 : k
d • 16 21 • d
86 – c 68 – c
m : 56 m : 94
Решение:
a + 85 > 75 + a
b – 49 > b – 130
48 : k < 72 : k
d • 16 < 21 • d
86 – c > 68 – c
m : 56 > m : 94
15
Страница 15:
10. Прочитай задания. Определи, можно ли ответить на поставленные вопросы? Обоснуй свой ответ.
а) Папа принёс 12 яблок и раздал их поровну детям. Сколько досталось каждому?
б) Пешеход шёл со скоростью 6 км/ч. Сколько километров он прошёл?
в) Ученик купил тетради на 36 р. Сколько стоит одна тетрадь?
г) К празднику Нового года Гек вырезал 18 снежинок, а Чук – 27 снежинок. На сколько дольше Чук вырезал снежинки, чем Гек, если на изготовление одной снежинки они оба затрачивали одинаковое время?Какие данные нужны для ответа на вопросы? Подбери подходящие значения и реши полученные задачи.
Решение:
Какие данные нужны для ответа на вопросы? Подбери подходящие значения и реши полученные задачи.
а) Папа принёс 12 яблок и раздал их поровну детям. Сколько досталось каждому? нельзя ответить, так как не знаем количество детей
Скажем детей было 3, тогда 12 : 3 = 4 (яб.) досталось каждому ребенку.
б) Пешеход шёл со скоростью 6 км/ч. Сколько километров он прошёл? не можем ответить, так как не знаем сколько времени он шел
Скажем пешеход шел 2 часа, тогда 2 * 6 = 12 (км) прошел пешеход.
в) Ученик купил тетради на 36 р. Сколько стоит одна тетрадь? не можем ответить, так как не знаем количество тетрадей
Скажем он купил 2 тетради, тогда 36 : 2 = 18 (р.) стоит тетрадь.
г) К празднику Нового года Гек вырезал 18 снежинок, а Чук – 27 снежинок. На сколько дольше Чук вырезал снежинки, чем Гек, если на изготовление одной снежинки они оба затрачивали одинаковое время? невозможно ответить, так как не знаем производительность мальчиков.
Скажем они вырезали 1 снежинку в минуту. В итоге 1 * 18 = 18 (мин.) вырезал снежинки Гек, 1 * 27 = 27 (мин.) вырезал снежинки Чук. 27 – 18 = 9 (мин.) На минут дольше вырезал Чук.
11. Запиши множество многоугольников, изображённых на рисунке:
а) содержащих угол B;
б) не содержащих угол E;
в) одной из сторон которых является сторона AC.
Решение:
а) содержащих угол B;
АВС, ABCD, ABCDE
б) не содержащих угол E;
АВС, ACD, ABCD
в) одной из сторон которых является сторона AC.
АВС, ACD, ACDE
12. Реши уравнения с комментированием. Что ты замечаешь?
а) 504 560 : x = 8
б) x : 8 = 63 070
в) 8 • x = 504 560
Решение:
а) 504 560 : x = 8
8 * x = 504 560
x * 8 = 504 560
x = 504 560 : 8
x = 63 070
б) x : 8 = 63 070
x : 8 = 63 070
504560 : x = 8
x = 504560 : 8
x= 63070
в) 8 • x = 504 560
504 560 : x = 8
x : 8 = 63 070
8 * x = 504 560
x= 63070
13. Запиши сумму, разность, произведение и частное, значение которых равно 32. Прочитай их разными способами.
Решение:
Запиши сумму, разность, произведение и частное, значение которых равно 32. Прочитай их разными способами.
Сумма: 20+12=32 ; 16+16=32 ; 23+9=32
Разность: 33-1=32 ; 32-0=32 ; 42-10=32
Произведение: 16*2=32 ; 8*4=32 ; 32*1=32
Частное: 64:2=32 ; 96:3=32 ; 128:4=32
14. Найди значения выражений:
а) 81 308 – 308 • (8856 – 8649) + 54 600 : 6
б) (52 • 390 – 8765 – 4098) • (1228 : 4 – 207)
Решение:
4 2 1 5 3
а) 81 308 – 308 • (8856 – 8649) + 54 600 : 6 = 26 652
1) 8856 – 8649 = 207
2) 308 * 207 = 63 756
*308
207
+ 2149
616
63756
3) 54 600 : 6 = 9 100
4) 81 308 – 63 756 = 17 552
81308
– 63756
17552
5) 17 552 + 9 100 = 26 652
1 2 3 6 4 5
б) (52 • 390 – 8765 – 4098) • (1228 : 4 – 207) = 74 170
1) 52 • 390 = 20 280
*52
390
+468
156
20280
2) 20 280 – 8 765 = 11 515
20280
– 8765
11515
3) 11 515 – 4098 = 7 417
11515
– 4098
7417
4) 1228 : 4 = 307
5) 307 – 20 7 = 100
6) 7 417 * 100 = 74 170
15. Сколько ударов за сутки сделают часы, если они отбивают целое число часов от 1 до 12, да ещё одним ударом отмечают середину каждого часа?
Решение:
1) Сколько ударов отобьют часы за день, если будут отбивать целое число часов?
В сутках 24 часа, но на циферблате они обозначены как с 1 часу дня до 12 часов ночи, и с 1 часу ночи до 12 часов дня.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 3 + 7 + 11 + 15 + 19 + 23 = 10 + 26 + 19 + 23 = 36 + 42 = 78 (ударов) − с 1 часу дня и до 12 часов ночи.
2) Сколько ударов отобьют часы в сутки?
78 * 2 = 156 (ударов) − всего за сутки.
3) Сколько ударов отобью часы, если будут отмечать середину каждого часа?
24 часа в сутках, значит 24 удара.
4) Сколько всего ударов отобьют часы за сутки?
156 + 24 = 180 (ударов).
Ответ: 180 ударов за сутки сделают часы.
16
Страница 16:
1.
а) Как изменяется сумма, если слагаемые увеличиваются? А если уменьшаются?
б) Не выполняя вычислений, расставь суммы в порядке возрастания:14 + 15 2 + 3 14 + 39 2 + 15
Решение:
а) Как изменяется сумма, если слагаемые увеличиваются? А если уменьшаются?
Если увеличиваются, то сумма увеличивается. Если уменьшаются, то само собой уменьшаются.
б) Не выполняя вычислений, расставь суммы в порядке возрастания:
2 + 3
2 + 15
14 + 15
14 + 39
2. Найди границы, в которых заключены суммы:
а) 238 + 517
б) 561 + 829
в) 3123 + 5317
Решение:
а) 200 + 500 < 238 + 517 < 300 + 600
700 < 238 + 517 < 900
б) 500 + 800 < 561 + 829 < 600 + 900
1300 < 561 + 829 < 1 500
в) 3000 + 5000 < 3123 + 5317 < 4000 + 6000
8 000 < 3123 + 5317 < 10 000
3. Сделай оценку сумм. Проверь с помощью вычислений.
а) 784 + 519
б) 632 + 947
в) 7384 + 4608
г) 56 625 + 72 493
Решение:
700 + 500 < 784 + 519 < 800 + 600
1200 < 784 + 519 < 1400
1200 < 1303 < 1400
600 + 900 < 632 + 947 < 700 + 1000
1500 < 632 + 947 < 1700
1500 < 1579 < 1700
7300 + 4600 < 7384 + 4608 < 7400 + 4700
11900 < 7384 + 4608 < 12100
11900 < 11 992 < 12100
56600 + 72400 < 56625 + 72493 < 56700 + 72500
129000 < 56625 + 72493 < 129200
129000 < 129 118 < 129200
17
Страница 17:
4. От Москвы до Санкт-Петербурга 653 км, а от Москвы до Тбилиси 1965 км. Докажи, что от Санкт-Петербурга до Тбилиси через Москву больше, чем 2500 км, но меньше, чем 2700 км
Решение:
Поскольку Тбилиси находится на юг от Москвы, а Санкт-Петербург на север, то данные города являются противоположными по своему расположению. Для того, чтобы определить расстояние от Санкт-Петербурга до Тбилиси, нужно суммировать расстояние от Москвы до Петербурга и расстояние от Тбилиси до Москвы. В таком случае получим:
653 + 1965 = 2618 км. Полученное расстояние больше чем 2500 км, поскольку: 2618 – 2500 = 118 км.
Данное расстояние меньше чем 2700 км, поскольку: 2700 – 2618 = 82 км.
Ответ: 2500<2618<2700.
5. Найди множество значений выражения 7552 + a + 243 для всех значений переменной a из множества {24; 408; 5229}.
Решение 1
7552 + a + 243 = 7795 + a.
+7552
243
7795
при a = 24:
7795 + a = 7795 + 24 = 7819.
при a = 408:
7795 + a = 7795 + 408 = 8203.
+7795
408
8203
7795 + a = 7795 + 5229 = 13024.
+7795
5229
13024
Ответ: {7819, 8203, 13024}.
Решение 2
983 * b
при b = 37:
983 * b = 983 * 37 = 36371
× 983
37
6881
2949
36371
при b = 504:
983 * b = 983 * 504 = 495432
×983
37
6881
2949
36371
при b = 504:
983 * b = 983 * 80200 = 78836600
×983
80200
1966
7864
78836600
Ответ: {36371, 495432, 78836600}.
6. Найди множество решений неравенства 2 < y < 6. Запиши другие неравенства, имеющие то же самое множество решений. Сделай рисунки
Решение:
2 < y < 6 {3,4,5}
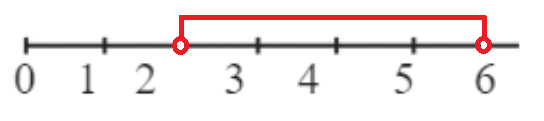
те же самые решения у неравенств:
2 < y ≤ 5 {3,4,5}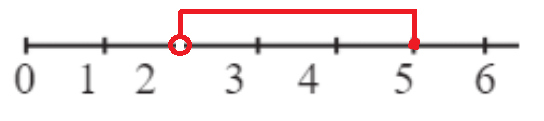
3 ≤ y < 6 {3,4,5}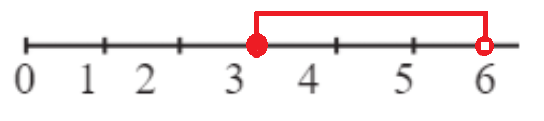
3 ≤ y ≤ 5 {3,4,5}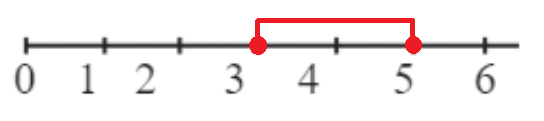
7. Прочитай и реши неравенства:
a > 13
b ≥ 11
1 < c < 4
6 ≤ d ≤ 10
8. Стриж кормит птенцов 20 раз в день и за один раз приносит примерно 370 мелких насекомых. Сколько примерно насекомых должен наловить стриж для птенцов, если период выкармливания длится 32 дня?
Решение:
1) 370 * 20 = 7 400 (н.) приносит стриж за день.
2) 7 400 * 32 = 236 800 (н.) должен наловить стриж.
Ответ: 236 800 насекомых.
9. Реши задачи и сравни их решения. Что ты замечаешь?
а) Купили 4 кг груш по цене 60 р., столько же яблок по цене 55 р. и 5 кг бананов. За всю покупку заплатили 710 р. Сколько рублей стоил 1 кг бананов?
б) Мотоциклист ехал в первый день 4 часа со скоростью 60 км/ч, во второй день – столько же времени со скоростью 55 км/ч. Всего ему надо проехать 710 км. С какой скоростью он должен ехать дальше, чтобы преодолеть оставшееся расстояние за 5 часов?
Решение:
а) Купили 4 кг груш по цене 60 р., столько же яблок по цене 55 р. и 5 кг бананов. За всю покупку заплатили 710 р. Сколько рублей стоил 1 кг бананов?
1) 4 * 60 = 240 (р.) стоили груши.
2) 4 * 55 = 220 (р.) стоили яблоки.
3) 220 + 240 = 460 (р.) стоили яблоки и груши.
4) 710 – 460 = 250 (р.) стоили 5 кг бананов.
5) 250 : 5 = 50 (р.) стоил 1 кг бананов.
Ответ: 50 рублей.
б) Мотоциклист ехал в первый день 4 часа со скоростью 60 км/ч, во второй день – столько же времени со скоростью 55 км/ч. Всего ему надо проехать 710 км. С какой скоростью он должен ехать дальше, чтобы преодолеть оставшееся расстояние за 5 часов?
1) 4 * 60 = 240 (км) проехал в первый день.
2) 4 * 55 = 220 (км) проехал во второй день.
3) 220 + 240 = 460 (км) проехал за 2 дня.
4) 710 – 460 = 250 (км) осталось проехать.
5) 250 : 5 = 50 (км/ч) с такой скоростью надо ехать мотоциклисту.
Ответ: 50 км/ч
10. Запиши сумму, разность, произведение и частное, значение которых равно 120. Прочитай их разными способами.
Решение:
сумма
100+20=120
разность
130-10=120
произведение
2*60=120
частное
240 : 2 = 120
11. Составь программу действий и вычисли:
а) 84 • 703 – 312 + 72 640 : (40 : 5) + 3009 • 240
б) 2980 • (423 + 168) – (57 • 17 – 209) • 6 : 3 + 533 700 : 9
Решение:
2 5 6 3 1 7 4
а) 84 • 703 – 312 + 72 640 : (40 : 5) + 3009 • 240 = 789 980
1) 40 : 5 = 8
2) 84 * 703 = 59 052
3) 72 640 : 8 = 9 080
4) 3009 * 240 = 722 160
5) 59 052 – 312 = 58 740
6) 58 740 + 9 080 = 67 820
7) 67 820 + 722 160 = 789 980
4 1 8 2 3 5 6 9 7
б) 2980 • (423 + 168) – (57 • 17 – 209) • 6 : 3 + 533 700 : 9 = 1818960
1) 423 + 168 = 591
2) 57 • 17 = 969
3) 969 – 209 = 760
4) 2980 * 591 = 1 761 180
5) 760 * 6 = 4 560
6) 4560 : 3 = 1 520
7) 533 700 : 9 = 59 300
8) 1 761 180 – 1520 = 1 759 660
9) 1 759 660 + 59 300 = 1 818 960
12. Запиши множество решений неравенства:
а) х > 0
б) х ≥ 0
в) х < 0
г) х ≤ 0
Решение для 0 и натуральных чисел, без отрицательных чисел:
а) {1, 2, 3, 4…}
б) {0, 1, 2, 3…}
в) ∅
г) {0}
18
Страница 18:
1.
а) Как изменяется разность при увеличении и уменьшении её компонентов?
б) Не вычисляя, расставь разности в порядке возрастания: 74 – 32 42 – 32 74 – 15 82 – 15
Решение:
а) Как изменяется разность при увеличении и уменьшении её компонентов?
При увеличении уменьшаемого разность увеличится на столько же единиц;
при уменьшении уменьшаемого разность уменьшится на столько же единиц;
при увеличении вычитаемого разность уменьшится на столько же единиц;
при уменьшении вычитаемого разность увеличится на столько же единиц.
б) Не вычисляя, расставь разности в порядке возрастания:
42 – 32
74 – 32
74 – 15
82 – 15
2. Найди границы, в которых заключены следующие разности:
а) 94 – 27
б) 975 – 639
в) 526 – 387
Решение:
Решение a
90 − 30 < 94 − 27 < 100 − 20
60 < 94 − 27 < 80
Решение б
900 − 700 < 975 − 639 < 1000 − 600
200 < 975 − 639 < 400
Решение в
500 − 400 < 526 – 387 < 600 − 300
100 < 526 – 387 < 300
19
Страница 19:
3. Сделай оценку разностей. Проверь с помощью вычислений.
а) 711 – 284
б) 856 – 397
в) 4611 – 1315
г) 9568 – 3419
Решение а
700 − 300 < 711 − 284 < 800 − 200
400 < 711 − 284 < 600
Решение б
800 − 400 < 856 − 397 < 900 − 300
400 < 856 − 397 < 600
Решение в
4600 − 1400 < 4611 − 1315 < 4700 − 1300
3200 < 4611 − 1315 < 3400
Решение г
9500 − 3500 < 9568 − 3419 < 9600 − 3400
6000 < 9568 − 3419 < 6200
4. От Москвы до Смоленска 378 км, а от Москвы до Бреста – 1037 км. Докажи, пользуясь рисунком, что расстояние от Смоленска до Бреста больше 600 км, но меньше 800 км.
Решение:
Расстояние от Смоленска до Бреста равно:
1037 − 378.
Докажем, что это расстояние меньше 800 км:
1000 − 400 < 1037 − 378 < 1100 − 300
600 < 1037 − 378 < 800
Следовательно, расстояние от Смоленска до Бреста больше 600 км, но меньше 800 км, что и требовалось доказать.
5. Контейнер с грузом весит 3219 кг, а пустой контейнер – 237 кг. Докажи, что груз весит больше 2900 кг, но меньше 3100 кг.
Решение:
3200 − 300 < 3219 – 237 < 3300 – 200
2900 < 3219 – 237 < 3100
6. Прочитай и реши неравенства:
а) 6 ≤ a < 9
б) 315 ≤ t ≤ 317
в) 16 < x < 20
г) 108 < n ≤ 112
7. Запиши все двойные неравенства, имеющие множество решений {8, 9, 10}.
8. Сделай оценку сумм:
а) 384 + 215 + 461
б) 730 + 947 + 519
9. Реши уравнения. Что ты замечаешь?
а) х + 6 = 84
г) х • 6 = 84
б) х – 7 = 63
д) х : 7 = 63
в) 54 – х = 27
е) 54 : х = 27
10. За 5 кг помидоров заплатили 400 р., а за 4 кг огурцов – в 2 раза меньше. На сколько рублей килограмм огурцов дешевле килограмма помидоров? Сколько надо заплатить за покупку из 3 кг помидоров и 2 кг огурцов?
11. Найди множество значений выражения 983 • b для всех значений переменной b из множества {37; 504; 80 200}.
12. Проведи две окружности радиусами 2 см и 3 см, которые: а) не имеют общих точек; б) имеют одну общую точку; в) пересекаются в двух точках.
13. Найди значения выражений:
а) (321 – 18) • 304 • (27 609 – 7609) : 4000
б) 63 000 • (627 + 163) • (937 – 637) : 90 000
Решение:
а) (321 – 18) • 304 • (27 609 – 7609) : 4000
1)
2)
3)
4)
5)
6)
б) 63 000 • (627 + 163) • (937 – 637) : 90 000
1)
2)
3)
4)
5)
6)
14. Из спичек составлено 4 квадрата. Переложи 3 спички так, чтобы получилось 3 таких же квадрата.
20
Страница 20:
1. Сделай оценку сумм и разностей:
а) 458 + 197
в) 1218 + 6372
д) 5207 – 3684
б) 964 – 583
г) 4459 + 8023
е) 7081 – 2936
2. Найди значение выражения:
а) 345 600 : b, если b = 6, 10, 900
б) 7 224 000 : с, если с = 4, 800, 1000
3.
а) Путь от дома Марины до школы равен 1 км 200 м, а от её дома до парка – 400 м. Путь до парка занимает у неё на 10 мин меньше времени, чем до школы. Сколько времени идёт Марина до школы и сколько – до парка, если скорость её не меняется?
б) Первый моток тесьмы стоит 600 р., а второй моток такой же тесьмы – 840 р. В первом мотке на 2 м тесьмы меньше, чем во втором. Сколько метров тесьмы в каждом мотке?
4. У Кати 98 р. Что из представленного на рисунке она может купить на эти деньги?
5. Какие из чисел 30, 32, 45, 99, 102 являются решениями неравенства 30 x – 2 < 100? Найди ещё два решения этого неравенства. Сколько всего натуральных чисел являются его решениями?
6. Какое из множеств {0, 1, 2, 3}; {1, 2, 3, 4}; {0, 1, 3, 4}; {0, 1, 2, 3, 4}; {0, 1, 2, 3, 4, 5} является множеством решений неравенства n < 5?
7. Найди пересечение и объединение множеств решений неравенств: 2 х < 6 и 4 < x 8.
8. Реши уравнения с комментированием и сделай проверку:
а) 6 + m • 4 = 70
б) k : 5 + 8 = 27
21
Страница 21:
9. Какие фигуры ты видишь на чертеже? Запиши их обозначения. Есть ли среди них пересекающиеся фигуры?
10. Игра «Головоломки Стивенса» Жители острова Рокфор любили решать головоломки Стивенса – мудрейшего жителя этого острова. Попробуй и ты решить две его головоломки.
11. Найди значения выражений:
а) 635 400 : 9 : 100 + 9004 • 50 – (52 360 – 57 • 65)
б) 603 • (1812 : 2) • 30 – (790 • 970 – 92 142 : 6)
Решение:
1)
2)
3)
4)
5)
6)
12. Собрался Иван Царевич на бой со Змеем Горынычем, трёхглавым и трёххвостым. «Вот тебе меч-кладенец, – говорит ему Баба-Яга. – Одним ударом ты можешь срубить Змею либо 1 голову, либо 2 головы, либо 1 хвост, либо 2 хвоста. Запомни: срубишь голову – новая вырастет, срубишь хвост – 2 новых вырастут, срубишь 2 хвоста – голова вырастет, срубишь 2 головы – ничего не вырастет». Сможет ли Иван-царевич срубить Змею все головы и все хвосты за 9 ударов? Обоснуй свой ответ.
Решение:
1 удар − 1 хвост − остается 4 хвоста и 3 головы.
2 удар − 1 хвост − остается 5 хвостов и 3 головы.
3 удар − 1 хвост − остается 6 хвостов и 3 головы.
4 удар − 2 хвоста − остается 4 хвоста и 4 головы.
5 удар − 2 хвоста − остается 2 хвоста и 5 голов.
6 удар − 2 хвоста − остается 0 хвостов и 6 голов.
7 удар − 2 головы − остается 0 хвостов и 4 головы.
8 удар − 2 головы − остается 0 хвостов и 2 головы.
9 удар − 2 головы − остается 0 хвостов и 0 голов.
Ответ: Иван − царевич сможет за 9 ударов срубить змею все головы и все хвосты.
22
Страница 22:
1.
а) Как изменяется произведение при увеличении и уменьшении множителей?
б) Не вычисляя, расставь произведения в порядке возрастания: 52 • 63 312 • 147 85 • 147 85 • 63
2. Докажи, что:
а) 420 < 79 • 6 < 480
б) 2000 < 145 • 29 < 6000
3. Найди границы, в которых заключены произведения:
а) 54 • 9
б) 27 • 53
в) 871 • 25
г) 176 • 421
4. Сделай оценку произведений. Проверь с помощью вычислений.
а) 35 • 24
б) 78 • 36
в) 194 • 49
г) 552 • 896
23
Страница 23:
5. Запиши множества решений неравенств: 3 < x 7 и 5 x 9. Найди их пересечение и объединение.
6. Найди значения выражений:
а) 642 • x, если x = 407, 4070, 40 700б) y : 5, если y = 1030, 10 300, 103 000
7. БЛИЦтурнир
а) 3 одинаковых пакета молока стоят a р. Сколько стоят 5 таких пакетов?
б) 7 метров ткани стоят b р. Сколько такой ткани можно купить на c р.?
в) За 4 пары варежек, купленных по одной цене, заплатили x р., а за 2 пары одинаковых перчаток – y р. На сколько рублей пара перчаток в этой покупке дороже пары варежек?
г) У Гены было a р. Он купил 2 ручки по цене n р. и 6 карандашей по цене m р. Сколько денег у него осталось?
д) У Насти было c р. На мороженое она истратила d р., а на остальные деньги купила 5 одинаковых леденцов. Сколько стоит один такой леденец?
8. В поезде Москва – Тольятти 17 вагонов. Из них 6 вагонов плацкартные, а остальные – купейные. В каждом плацкартном вагоне 54 места, а в купейном – 36 мест. На этот поезд уже продано в плацкартные вагоны 87 билетов, а в купейные – в 3 раза больше билетов, чем в плацкартные. Поставь разумные вопросы к этому условию и ответь на них
9. Найди значения выражений:
а) (375 018 + 5678 • 924) : 7 – 15 192
б) 2002 • 96 + (437 140 – 42 • 1085) : 5 – 908 • 60
10. Запиши с помощью букв переместительное и сочетательное свойства сложения и умножения. Пользуясь ими, упрости выражения:23 + a + 67 42 + b + 34 + 128 15 • c • 4 2 • d • 7 • 5 • 5 • 2
24
Страница 24:
11. Викторина «В мире животных» В нашей стране водится много бобров. Бобр – крупный грызун, ведёт полуводный образ жизни, обитает по лесным рекам, сооружает из ила и ветвей домики, поперёк реки делает плотины длиной от 5 м до 6 м.
1) Узнай длину тела бобра (в сантиметрах), выполнив действия по программе: Вырази длину тела бобра в дециметрах, в метрах.
2) Узнай массу бобра (в килограммах): Назови геометрические фигуры, которые встречаются в этом задании.
3) Используя результаты вычислений, ответь на вопросы:
а) На сколько 120 больше 39?б) Во сколько раз 30 меньше 120?
в) На сколько надо умножить 39, чтобы получить 156?
г) Чему равно частное от деления 1656 на 8?
4) Бобр – отличный пловец и ныряльщик. Заполни таблицу в тетради. Узнай, сколько минут бобр может находиться под водой, выбрав наименьшее из полученных значений x
12. В семье четверо детей – Таня, Юра, Света и Лена, им 5, 8, 13 и 15 лет. Одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3. Сколько лет каждому из детей?
Решение:
Таня, Света и Лена – одна из них ходит в садик, тогда мальчик Юра старше 5 лет. Так как в садик ходит не мальчик, а Таня старше Юры, значит ей или 13 или 15 лет, приходим к выводу, что Юре 8 лет. Суммируем возраст Тани и Светы: 13 плюс 5 равно 18, делим на 3 получаем 6, сумма делится на 3, тогда Татьяне 13 лет. А значит Свете 5 лет. Остается неопределенным возраст Лены, получается что ей 15 лет.
Ответ: Свете 5 лет, Юре 8 лет, Тане 13 лет, Лене 15 лет.
25
Страница 25:
1. а) Как изменяется частное при увеличении и уменьшении делимого, делителя? б) Не выполняя вычислений, расставь частные в порядке возрастания:72 : 9 180 : 9 72 : 36 144 : 9
2. Определи, верно ли найдены границы частных:
а) 360 : 6 < 384 : 6 < 420 : 6 60 < 384 : 6 < 70
б) 40 000 : 80 < 40 592 : 86 < 45 000 : 90500 < 40 592 : 86 < 500
в) 24 000 : 60 < 27 612 : 59 < 30 000 : 50400 < 27 612 : 59 < 600
26
Страница 26:
3. В каких границах заключены частные:
а) 432 : 27 б) 2128 : 38 в) 42 849 : 529 г) 222 264 : 756
4. Сделай оценку частных. Проверь с помощью вычислений.
а) 423 : 9 б) 124 056 : 6 в) 22 848 : 56 г) 367 846 : 698
5. Реши уравнения с комментированием и сделай проверку:
а) 30 – 200 : n = 25 б) t • 20 – 36 = 144
6. Запиши сумму, разность, произведение и частное, значение которых равно 450. Прочитай их разными способами.
7. а) 4 280 185 + (89 040 • 705 – 478 760) : 8б) (5000 – 87 • 39) • (600 • 504 – 295 200) : 80 + 38 • 9520
8. Составь выражение и найди его значение. Придумай задачу с другими величинами, которая решается так же.
а) За 4 часа теплоход прошёл 136 км. Сколько километров он пройдёт за 8 часов, двигаясь с той же скоростью?
б) Путь между двумя станциями товарный поезд прошел за 9 часов, а пассажирский – за 6 часов. Чему равна скорость пассажирского поезда, если скорость товарного поезда равна 40 км/ч?
в) Геологи 3 часа летели на вертолёте со скоростью 95 км/ч, затем 2 часа ехали верхом со скоростью 12 км/ч. Чему равен путь, который проделали геологи за это время?
9. Вот задача не для робких! Вычитай, дели и множь, Плюсы ставь, а также скобки! Верим, к финишу придёшь!
27
Страница 27:
10. «Древнерусский календарь» Названия месяцев, которыми мы пользуемся, – январь, февраль, март и так далее – не русские. Они пришли к нашим предкам из Византии вместе с юлианским календарём. А как называли месяцы в Древней Руси? Реши примеры и расшифруй эти названия
28
Страница 28:
1. Докажи, что
:698 : 2 > 300 400 < 896 : 2 < 500 500 < 22 464 : 36 < 800785 : 5 < 200 30 < 1645 : 47 < 50 700 < 385 636 : 458 < 1000
2. Сделай оценку результатов умножения и деления:
а) 218 • 76
б) 539 • 421
в) 3592 : 57
г) 337 008 : 826
3. Найди два решения неравенства:1) а – 9 < 6 3) 2 • с – 7 52) 8 • b > 32 4) 16 – d : 3 8
4. БЛИЦтурнир
а) За 4 пакета кефира заплатили m р., а за 5 пакетов сока – k р. На сколько рублей пакет кефира дешевле пакета сока?
б) Воробей пролетел x м за 9 мин, а бабочка – y м за 2 мин. Во сколько раз скорость бабочки меньше скорости воробья?
в) Мастер сделал а деталей за 4 ч. Сколько таких деталей сделает он за 7 ч, если будет работать с той же производительностью?
г) Моторная лодка прошла b км за 2 ч. За сколько времени она пройдёт d км, если будет идти с той же скоростью?
5. Реши уравнения с комментированием и сделай проверку:
а) (32 – x) • 6 – 39 = 45
б) (275 + 80 : y) : 4 = 70
6. Нарисуй таблицу в тетради. Поставь букву B в те клетки, для которых неравенство верно, и букву H – в те, для которых оно неверно.
29
Страница 29:
7. Реши задачи. Что в них общего и чем они различаются?1) С двух ульев получено 100 кг мёда, с одного из них на 4 кг больше, чем с другого. Сколько мёда получено с каждого улья?
2) В двух мешках 100 кг картофеля, в одном из них на 4 кг меньше, чем в другом. Сколько картофеля в каждом мешке? Придумай задачу, которая решается так же.
8. Выполни действия. Расшифруй скороговорку.
9. Продолжи ряд на три числа, сохраняя закономерность:
а) 15, 16, 18, 21, 25, …
б) 4, 7, 13, 22, 34, …
10. Задача-шутка
Шёл Кондрат в Ленинград, А навстречу – двенадцать ребят, У каждого – по 3 лукошка, В каждом лукошке – кошка, У каждой кошки – 12 котят, У каждого котёнка в зубах по 4 мышонка. И задумался старый Кондрат: Сколько мышат и котят ребята несут в Ленинград?
Решение:
Глупый, глупый Кондрат!
Он один и шагал в Ленинград.
А ребята с лукошками,
С мышками и кошками
Шли навстречу ему – в Кострому.
30
Страница 30:
1. а) Вера умножила 248 на 702 и получила в ответе 17 856. Докажи, что она ошиблась.
б) Володя разделил 42 300 на 6 и получил в ответе 750. Докажи, что он не прав.
2. Сделай прикидку умножения и деления, а затем вычисли ответ:
а) 603 • 490
в) 9025 • 5090
д) 422 814 : 7
ж) 403 500 : 5
б) 708 • 8009
г) 7103 • 703
е) 163 680 : 8
з) 1 600 236 : 4
3. Составь выражение: «За a одинаковых мячей уплатили b рублей, а за c одинаковых кукол – d рублей. На сколько рублей кукла в этой покупке стоит дороже мяча?» Найди значение составленного выражения при a = 18, b = 900, c = 16, d = 1600.
31
Страница 31:
4. В роще 240 берёз, а клёнов на 93 меньше. Сосен в ней вдвое больше, чем клёнов, а елей – в 3 раза меньше, чем сосен и берёз вместе. Сколько всего деревьев в этой роще?
5. Из леса принесли 38 грибов: белых, подосиновиков и подберёзовиков. Подберёзовиков было в 4 раза больше, чем белых, а подберёзовиков и подосиновиков вместе было 34 гриба. Сколько грибов каждого вида принесли из леса?
6. Найди наибольшее решение неравенства:
x < (294 • 7500 – 3 690 460 : 5) : 4 – 359 999
7. Сравни выражения:
8. При делении на 96 получилось частное 325 и остаток 37. Какое число делили?
9. Реши уравнения с комментированием и сделай проверку:
а) (920 – x) : 20 + 25 = 63
б) (150 : y + 7) • 40 = 480
10. Найди множества решений двух неравенств. Что ты замечаешь?
а) a < 5 и a 5
б) 3 > b и с < 3
в) x > 7 и x 8
11. Отметь множество решений неравенства 3 x < 8 на числовом луче. Запиши его с помощью фигурных скобок. Найди все неравенства, которые имеют то же самое множество решений.
12. Игра «Проверь своё внимание!» Построй в тетради 4 квадрата со стороной 3 клетки. За 10 секунд запомни, как расположены точки в квадратах на рисунке. Затем по памяти точно так же расположи точки в своих квадратах.
32
Страница 32:
1.Сделай прикидку, а затем выполни действия:
а) 507 • 2800
в) 256 640 : 8
б) 30 960 • 70 400
г) 42 415 200 : 60
2. Реши уравнения с комментированием:
а) (х – 15) • 40 + 80 = 320
б) (580 – 20 • х) : 70 = 6
3. Укажи два решения неравенства. Имеет ли это неравенство наибольшее решение, наименьшее решение? Если да, то найди их.
а) а 6 б) b > 4 в) 2 • с + 9 23 г) d : 4 – 5 < 7
4. Начерти числовой луч и отметь на нём множество решений неравенства 3 < x 8. Запиши это множество с помощью фигурных скобок. Найди ещё три неравенства, которые имеют то же самое множество решений.
5. Выполни оценку результатов указанных действий:
а) 5716 + 2029
в) 628 • 407
б) 70 400 – 21 408
г) 2088 : 36
6. Лена разместила в своём альбоме 60 марок, а её брат Алёша – 96 марок. На каждой странице они размещали одинаковое число марок, при этом у Алёши оказалось заполнено на 3 страницы больше, чем у Лены. Сколько страниц заполнила марками Лена и сколько – Алёша?
7.
а) 57 яблок разложили на кучки по 6 яблок в каждой. Сколько получилось кучек и сколько яблок осталось?
б) Когда сливы разложили на 36 тарелок по 12 слив, осталось ещё 7 слив. Сколько было слив?
в) Было 120 конфет. После того как каждому ученику раздали по 4 конфеты, осталось 12 конфет. Сколько было учеников?
8. Заполни в тетради таблицу, пользуясь формулой a = b • c + r, где r < b.
33
Страница 33:
9. Игра «Головоломки Стивенса»
Известно, что среди данных примеров только один решён верно. Сумей отыскать его за 1 минуту.
10. Пешеход прошёл a км за b ч, а велосипедист проехал c км за d ч. На сколько километров в час скорость пешехода меньше скорости велосипедиста? Составь выражение и найди его значение при a = 20, b = 4, c = 48, d = 3
11. На луче указаны некоторые числа. Запиши неравенство так, чтобы отмеченные числа были его решениями.
Существуют ли другие неравенства, удовлетворяющие этому условию? Если да, то приведи примеры.
12. Построй диаграмму Эйлера–Венна множеств A, B, C и D, еслиA – множество животных,B – множество птиц,C – множество рыб,D – множество животных, занесённых в Красную книгу. Назови несколько элементов множества D.Приведи примеры подмножеств множества B.
13. Что больше – половина числа 10, треть числа 15 или четверть числа 20?
14. Замени буквы цифрами так, чтобы получилась верная запись. Найди два решения этой задачи.
34
Страница 34:
1. Как связаны между собой умножение и деление? Объясни запись: а : b = с с · b = aИспользуя связь умножения и деления, вычисли:70 : 14 156 : 52 608 : 304 8036 : 2009Как можно выполнить деление чисел с однозначным частным?
2. Сделай прикидку и подбери частное чисел:
а) 152 : 19
в) 175 : 35
д) 159 : 53
ж) 648 : 72
б) 104 : 26
г) 294 : 49
е) 427 : 61
з) 504 : 84
3. Сделай прикидку и выполни деление углом:
а) 954 : 318
б) 1376 : 172
в) 3575 : 715
г) 2180 : 436
35
Страница 35:
4. Реши задачи. Что ты замечаешь?
а) С 6 грядок первого огорода собрали 504 огурца, а с 8 грядок второго – 336 огурцов. С грядки какого из огородов огурцов собрали больше и на сколько? (На всех грядках каждого из огородов огурцов было поровну.)
б) Ширина первого прямоугольника равна 6 дм, а его площадь – 504 дм2. Ширина второго прямоугольника – 8 дм, а его площадь – 336 дм2. Длина какого из этих прямоугольников больше и на сколько?
в) Мастер за 6 часов сделал 504 одинаковые детали, а его ученик за 8 ч сделал 336 таких же деталей. У кого из них производительность больше и на сколько? Придумай задачу с другими величинами, которая решается так же.
5. Найди наименьшее решение неравенства:
а) y 4005 • 7030
б) z > (27 150 : 3 • 80 – 6 389 • 26) : 7 + 604 • 508
6. При делении некоторого числа на 15 получили частное 308 и остаток 12. Найди это число. Какой остаток получится при делении этого числа на 9?
7. Реши уравнения и сделай проверку:
а) (470 – x) : 3 + 65 = 172
б) (270 : y – 18) • 9 = 108
8. Прочитай число: 8 372 507. Что обозначает каждая из цифр 7 в записи этого числа? Какая цифра стоит в разряде сотен тысяч? Сколько всего сотен тысяч в этом числе? Представь его в виде суммы разрядных слагаемых.
9. Сколько углов ты видишь на чертеже? Есть ли среди этих углов острые углы, прямые углы, тупые углы? Назови их.
10. Найди число, если его треть равна четверти числа 12.
35
Страница 36:
1. Выполни деление 218 : 35. Что ты замечаешь? Какими способами можно записать решение этого примера?
2. Выполни деление с остатком:
а) 149 : 37
в) 567 : 99
д) 947 : 312
ж) 3728 : 408
б) 284 : 81
г) 601 : 64
е) 1367 : 225
з) 2801 : 674
3. Выполни деление с остатком и сделай проверку: а) 4527 : 539 б) 5006 : 714 в) 17 526 : 8422 г) 26 914 : 5130
37
Страница 37:
4. Какие из чисел 7, 25, 124, 0 являются решениями данных неравенств:
а) x > 65
в) 4 • b 100
д) 7 t < 25
б) 6 + y < 12
г) 15 – a 45
е) 25 k 120
5. На решение трёх задач Петя потратил a минут. Первую задачу он решал b минут, а вторую – на c минут дольше, чем первую. Сколько времени он решал третью задачу? Составь выражение и найди его значение при a = 25, b = 7, c = 5.
6. Прочитай число: 18 560 025. Что означает каждая из цифр 5 в записи этого числа? Какая цифра записана в разряде десятков тысяч? Сколько всего десятков тысяч в этом числе? Увеличь его на 9 единиц, в 9 раз. Уменьши на 9 единиц, в 9 раз.
7. Реши задачи. Что в них общего и различного?
а) Толя прочитал за 5 часов две книги. В первой книге было 126 страниц, а во второй – 84 страницы. Сколько времени он читал каждую книгу, если скорость его чтения не изменялась?
б) Мотоциклист проехал до озера 126 км, а затем еще 84 км с той же скоростью. На весь путь он затратил 5 часов. Сколько времени мотоциклист ехал до озера и сколько потом? Придумай задачи с другими величинами, которые решаются так же.
8. Имеются по одной гире в 1 кг, 2 кг, 4 кг, 8 кг, 16 кг. Докажи, что ими можно уравновесить любой груз массой m кг, где m < 32 и m N.
9. Вспомни и назови свойства действий с 0 и 1. Используя их, вычисли:
а) (418 : 418 – 0 • 75) • (62 – 62) + (89 • 1) : 89
б) (54 : 1 + 0 : 1) • 0 + (25 – 24) • (12 + 0 : 36)
Решение:
1)
2)
3)
4)
5)
6)
10. Перенеси в тетрадь и заполни таблицу. Как можно упростить вычисления?
11. Продолжи ряд на три числа, сохраняя закономерность:
а) 101, 1002, 10003, …
б) 4, 9, 6, 18, 8, 27, …
38
Страница 38:
1. Сделай прикидку и подбери частные. Проверь с помощью умножения.
а) 576 : 72
б) 1925 : 275
в) 2552 : 638
г) 20 395 : 4079
2. Выполни деление с остатком и сделай проверку:
а) 182 : 41 в) 1604 : 198б) 2956 : 916 г) 17 000 : 2094
3. БЛИЦтурнир
а) Самолёт летел 2 ч со скоростью х км/ч и 3 ч со скоростью у км/ч. Какое расстояние пролетел самолёт за всё это время?
б) Автомобиль проехал а км за 4 часа. Какое расстояние он проедет за 6 часов, двигаясь с той же скоростью?
в) Плот проплыл b км за 3 ч. Сколько времени ему потребуется для того, чтобы проплыть с км, если скорость его не изменится?г) Андрей пробежал с м за 8 минут. За сколько времени пробежит такое же расстояние Олег, если его скорость на 20 м/мин меньше?
4. Вырази в указанных единицах измерения:
а) 8 см 9 мм = … мм
б) 8 км 9 м = … м 8 дм 9 мм = … мм 8 км 9 м = … дм 8 дм 9 см = … мм 8 км 9 м = … см 8 м 9 мм = … мм 8 км 9 м = … мм 8 м 9 см = … см 8 км 9 см = … мм 8 м 9 дм = … см 8 км 9 дм = … мм
5. Вырази в указанных единицах измерения:
а) 8 см 9 мм = … мм
б) 8 км 9 м = … м 8 дм 9 мм = … мм 8 км 9 м = … дм 8 дм 9 см = … мм 8 км 9 м = … см 8 м 9 мм = … мм 8 км 9 м = … мм 8 м 9 см = … см 8 км 9 см = … мм 8 м 9 дм = … см 8 км 9 дм = … мм
6. На луче отмечены некоторые числа. Запиши такое двойное неравенство, чтобы:
а) каждое отмеченное число было его решением;
б) каждое отмеченное число, кроме наименьшего, было его решением;
в) каждое отмеченное число, кроме наибольшего, было его решением;
г) ни одно из отмеченных чисел не было его решением.
39
Страница 39:
7. Найди для каждого неравенства множество его решений:
а) x + x 2
б) 5 – y < 2
в) 12 + z 2
8. Составь и реши неравенство: «Летели галки и сели на палки. Палок было 5. Если галки сядут по одной на каждую палку, то некоторым галкам не хватит места, а если они сядут по две на каждую палку, то некоторые палки останутся свободными. Сколько было галок?»
9.
а) Тамара спросила Сашу: «Сколько тебе лет?» Саша ответил: «Если бы число моих лет увеличить в 3 раза, а потом уменьшить на 16, то мне было бы 17 лет». Сколько лет Саше?
б) Если число лет Кати увеличить сначала на 19, а потом в 2 раза, затем полученный результат уменьшить на 10 и разделить на 11, то будет 4. Сколько лет Кате?
10. У Дениса 15 орехов, а у Славика 33 ореха.
а) Сколько орехов должен съесть Денис, чтобы у них стало поровну орехов?
б) Сколько орехов должен сорвать с куста Славик, чтобы у них стало поровну орехов?
в) Сколько орехов должен отдать Денис Славику, чтобы у них стало поровну орехов?
11. Вычисли. Расшифруй фамилию детского писателя, расположив ответы в порядке возрастания. Узнай, какие книги он написал.
12. Запиши выражение в 2 действия, значение которого равно 96. Прочитай его разными способами.
13. Определи, где в записи 1 2 3 4 5 нужно поставить знаки действий и скобки так, чтобы получились верные равенства:1 2 3 4 5 = 120 1 2 3 4 5 = 100 1 2 3 4 5 = 301 2 3 4 5 = 50 1 2 3 4 5 = 12 1 2 3 4 5 = 270
14. Две трети бревна составляют 6 метров. Найди длину этого бревна.
40
Страница 40:
1. Объясни разные способы деления 732 : 4. Чем удобен каждый из них?
7 с : 4 = 1 с (ост. 3 с)33 д : 4 = 8 д (ост. 1 д) 12 е : 4 = 3 е
Итак, 732 : 4 = 183
Выполни деление 952 : 17 любым из этих способов. Сделай вывод.
41
Страница 41:
2. Вычисли, используя алгоритм деления на двузначное число:
а) 1428 : 42
б) 30 296 : 56
в) 136 576 : 64
г) 254 415 : 35
3. Выполни деление с остатком и сделай проверку:
а) 2938 : 68
б) 53 940 : 56
в) 710 278 : 91
4. Реши уравнения и сделай проверку:
93 • x = 6231
15 768 : y = 36
z : 407 = 814
5. БЛИЦтурнир
а) Пешеход шёл 4 ч со скоростью b км/ч. Всего ему надо пройти a км. Сколько километров ему осталось пройти?
б) Автобус ехал 2 ч со скоростью c км/ч и 3 ч со скоростью d км/ч. Какое расстояние проехал автобус за всё это время?
в) Самолёт пролетел за 2 ч y км. Какое расстояние он пролетит с той же скоростью за 5 ч?
г) Теплоход проплыл вниз по реке x км за 3 ч, а на обратный путь он затратил 4 ч. На сколько меньше была его скорость на обратном пути?
6. Запиши множество решений неравенства:
а) x > 15
б) k 0
в) 6 < y 10
г) 9 z 12
7. Построй прямоугольник со сторонами 8 см и 2 см 5 мм. Найди его периметр и площадь.
8. Найди значения выражений. Проверь результаты по действиям с помощью калькулятора.
а) 6003 • (24 396 : 76 – 319 + 26)
б) (34 217 – 25 329) • 902 – (58 508 + 498 115) : 69
9. Упрости выражения:
а) 17 + x + 39 б) y • 6 • 12 в) n + 24 + 16 г) 4 • m • 25
10. Найди сумму всех возможных двузначных чисел, все цифры которых нечётные.
42
Страница 42:
1. Докажи с помощью прикидки, что примеры решены неверно. Найди ошибки в их решении. Реши их в тетради правильно.
2. Выполни деление:
а) 31 496 : 62
в) 127 854 : 18
д) 235 300 : 26
ж) 16 340 : 53
б) 18 060 : 43
г) 280 560 : 35
е) 411 600 : 84
з) 85 282 : 79
3. Игра «Головоломки Стивенса» Среди данных примеров только один решён верно. Найди его за одну минуту.
4.
а) Для живого уголка в школе купили 50 рыбок. Из них 26 рыбок пустили в большой аквариум, а остальных – в маленькие аквариумы по 8 рыбок в каждый. Сколько было маленьких аквариумов?
б) Группа из 28 туристов отправилась в лодочный поход. Две лодки у них были 6-местные, а остальные – 4-местные. Сколько было 4-местных лодок?
5. Расстояние между двумя городами равно 384 км. Первые 2 часа поезд ехал со скоростью 72 км/ч. На оставшемся пути он увеличил скорость на 8 км/ч. За сколько времени поезд прошёл весь путь между этими городами?
6. Реши уравнения с комментированием и проверкой:
а) 8 • х – 6045 = 1963
б) 92 : (3 • у + 5) = 4
7. У Марины сегодня день рождения. Она младше своего родного брата, которому неделю назад исполнилось 8 лет. Сколько лет может быть Марине? Составь неравенство и укажи множество его решений.
43
Страница 43:
8. Александр Сергеевич Пушкин родился 6 июня 1799 года. Сколько лет и дней прошло со дня рождения Пушкина до сегодняшнего дня, включая его?
9. Вычисли значения х. Расшифруй имя замечательного русского поэта. Узнай, когда он жил.
10. Вычисли периметр и площадь многоугольника ABCDEF.
11. Составь программу действий и вычисли:
а) 213 213 : (403 • 36 – 5939 – 8530)
б) 2 010 201 – 415 498 : 83 + 616 528 : (21 851 – 21 763)
Решение:
1)
2)
3)
4)
5)
6)
12. Алиса считала ступеньки лестницы. Между пятым и первым этажами она насчитала 100 ступенек. Сколько ступенек между первым и вторым этажами, если их количество между всеми этажами одинаковое?
Решение:
1) 5 − 1 = 4 (этажа) – нашли, сколько этажей со ступеньками посчитала Алиса:
2) 100 : 4 = 25 (ступенек) – между первым и вторым этажом.
Ответ: 25 ступенек между первым и вторым этажом.
44
Страница 44:
1. Сравни частные. Чем они похожи и чем отличаются? 8208 : 27 8208 : 152Выполни деление в столбик и сделай вывод.
2. Вычисли, используя алгоритм деления (с. 40):
а) 9756 : 271
б) 16 514 : 718
в) 158 130 : 315
г) 371 960 : 547
3. Выполни деление с остатком и сделай проверку:
а) 4420 : 126
б) 15 830 : 293
в) 284 640 : 472
г) 153 000 : 805
4. Турист прошёл 27 км. Ранним утром он шёл 2 ч со скоростью 5 км/ч, а затем следующие 2 ч – со скоростью 4 км/ч. Остальной путь он прошёл с постоянной скоростью за 3 ч. Чему была равна его скорость на последнем участке пути?
5. За первые 14 рабочих дней месяца завод изготовил 560 одинаковых стиральных машин. Затем он стал изготавливать в день на 5 таких машин больше. Сколько машин выпустил завод за месяц (20 рабочих дней), если производительность его не менялась?
6. Найди значение выражения: (529 + 179) • (55 545 : 69) – (128 • 430 – 6912) : 16
7. Реши уравнения и сделай проверку:
а) 1475 – x : 12 = 275
б) (240 : x + 48) : 26 = 2
8.Выполни действия:
а) 7 ч 43 мин 12 с : 16
б) 15 ч 8 мин 42 с : 18
45
Страница 45:
9. Викторина «Хочу всё знать»
а) На земном шаре обитают птицы, которых в народе называют составителями прогноза на лето. Они строят гнёзда из песка. Замечено, что обычно высота гнезда зависит от того, каким будет лето – сухим или дождливым. Если лето ожидается дождливым, то гнёзда строятся высокими, а если засушливым – то более низкими. Выполни деление и расшифруй название этих птиц: 1554 : 37 4366 : 59 18 165 : 519 13 888 : 24820 826 : 89 52 972 : 76106 110 : 786 256 626 : 807
б) Самое крупное на суше животное – африканский слон. Узнай высоту и длину тела африканского слона (в сантиметрах) и его массу (в килограммах).
в) Масса новорождённого слонёнка в 60 раз меньше массы взрослого слона. Найди массу новорождённого слонёнка и определи, на сколько она меньше массы взрослого слона.
10. Задача очень непроста –Найти не каждый сможет: Чему равняются звезда, Велосипед и ёжик? (Фигуры обозначают цифры, отличные от указанных на рисунке. При этом разные фигуры обозначают разные цифры.)
46
Страница 46:
1.
1) Библиотеке нужно переплести 1800 книг. Первая мастерская может выполнить эту работу за 3 дня, а вторая – за 6 дней. За сколько дней переплетут все книги обе мастерские, если будут работать одновременно? (Считать, что на переплёт каждой книги расходуется одинаковое время.)
2) Требуется изготовить 1500 одинаковых деталей. Один станок может выполнить эту работу за 15 часов, а другой – за 10 часов. За сколько времени изготовят все детали оба станка, работая одновременно?
2. Докажи с помощью прикидки, что примеры решены неверно. Найди ошибки и выполни деление правильно.
3. Докажи с помощью прикидки, что примеры решены неверно. Найди ошибки и выполни деление правильно.
4. Составь программу действий и вычисли:
27 312 : 48 + (900 – 669) • (8 • 125) – 306 • 580
Решение:
1)
2)
3)
4)
5)
6)
5. Составь выражение и найди его значение при a = 685, b = 2, c = 56:«С первого поля собрали a мешков картошки, со второго поля – на b мешков больше, чем с первого, а с третьего – на c мешков меньше, чем с первого. Сколько всего мешков картошки собрали с этих трёх полей?»
6. Придумай задачи, решениями которых могут служить выражения:
a – b : 3
(a – b) : 3
a + b • 3
(a + b) • 3
47
Страница 47:
7. Определи, что общего и что различного в задачах. Реши их, пользуясь схемами.
а) В двух пачках 160 тетрадей, причём в одной из них на 20 тетрадей больше, чем в другой. Сколько тетрадей в каждой пачке?
б) В двух пачках 160 тетрадей, причём в одной из них в 3 раза больше тетрадей, чем в другой. Сколько тетрадей в каждой пачке?
8.
а) Картина с рамой стоит 13 200 р., причём картина в 10 раз дороже рамы. Сколько стоит картина и сколько стоит рама?
б) Стакан с подстаканником стоит 280 р., причём стакан в 6 раз дешевле подстаканника. Сколько стоит стакан и сколько подстаканник?
9. Найди значения выражений:
а) 7 м 6 см – 3 м 8 дм
в) 4 м2 5 дм2 : 3
б) 8 дм 4 мм + 6 см 7 мм
г) 1 дм3 25 см3 • 16
10. Фанерный ящик для посылки имеет форму прямо-угольного параллелепипеда с размерами 40 см, 25 см и 20 см. Его перевязывают шпагатом, как показано на рисунке. На узел и концы нужно оставить 50 см. Сколько сантиметров шпагата требуется для того, чтобы перевязать ящик?
11. Лёня продолжил стороны треугольника так, что образовалось три прямых. На каждой из них он отметил по 2 точки, а всего – 4 точки. Как он это сделал?
12. Математическое исследование. Запиши число 10 всеми возможными способами в виде суммы двух натуральных чисел. Затем для каждого способа найди произведение слагаемых. Какое из этих произведений самое большое? Проделай то же самое с числом 12. Сформулируй гипотезу. Проверь свою гипотезу для какого-нибудь другого числа.
Решение:
Решение
1) Представим число 10 в виде суммы двух чисел:
0 + 10 = 10;
1 + 9 = 10;
2 + 8 = 10;
3 + 7 = 10;
4 + 6 = 10;
5 + 5 = 10.
2) Найдем произведение данных слагаемых:
0 * 10 = 0;
1 * 9 = 9;
2 * 8 = 16;
3 * 7 = 21;
4 * 6 = 24;
5 * 5 = 25.
Самое большое из произведений 5 * 5 = 25.
1) Представим число 12 в виде суммы двух чисел:
0 + 12 = 12;
1 + 11 = 12;
2 + 10 = 12;
3 + 9 = 12;
4 + 8 = 12;
5 + 7 = 12;
6 + 6 = 12.
2) Найдем произведение данных слагаемых:
0 * 12 = 0;
1 * 11 = 11;
2 * 10 = 20;
3 * 9 = 27;
4 * 8 = 32;
5 * 7 = 35;
6 * 6 = 36.
Самое большое из произведений 6 * 6 = 36.
Гипотеза: Самое большое произведение получается при умножении одинаковых слагаемых.
Проверим на числе 14:
Представим число 14 в виде суммы двух чисел:
0 + 14 = 14;
1 + 13 = 14;
2 + 12 = 14;
3 + 11 = 14;
4 + 10 = 14;
5 + 9 = 14;
6 + 8 = 14;
7 + 7 = 14.
Найдем произведение данных слагаемых:
0 * 14 = 0;
1 * 13 = 13;
2 * 12 = 24;
3 * 11 = 33;
4 * 10 = 40;
5 * 9 = 45;
6 * 8 = 48;
7 * 7 = 49.
Самое большое из произведений 7 * 7 = 49.
48
Страница 48:
1. Докажи с помощью прикидки, что примеры решены неверно. Найди ошибки и выполни деление правильно.
2. Вычисли частное и сделай проверку умножением:
а) 318 424 : 53
б) 277 240 : 956
в) 3 332 300 : 47
3. Выполни деление с остатком. Что ты замечаешь? Сделай вывод.
а) 5408 : 10
б) 36 015 : 10
в) 900 202 : 10 5408 : 100 36 015 : 100 900 202 : 100 5408 : 1000 36 015 : 1000 900 202 : 1000
4. Вырази числа в десятках и единицах, сотнях и единицах, тысячах и единицах.
а) 5408
б) 36 015
в) 900 202
5. За 6 минут Наташа сделала 12 пельменей, а мама – 18 пельменей. За сколько времени, работая так же, они вместе сделают 100 пельменей?
6. Литературная викторина 1 Вычисли. Расположи частные в порядке убывания. Расшифруй, кто из поэтов написал о русском языке такие строки: Язык, великолепный наш язык. Речное и степное в нём раздолье, В нём клёкоты орла и волчий рык, Напев, и звон, и ладан богомолья. В нём воркованье голубя весной, Взлёт жаворонка к солнцу – выше, выше. Берёзовая роща. Свет сквозной. Небесный дождь, просыпанный по крыше.
49
Страница 49:
7. Литературная викторина 2Кто автор этих стихов? Когда не ладятся дела, Мне помогает похвала. Вот, например, такой пример: Я не сумел решить пример, Но вдруг сказал мне педагог: – А ты способный, ты бы мог… Нажал на ручку я слегка, И без особого труда
Чтоб лучше шли чернила, Я сладил с цифрами тогда. И за минуту до звонка Не может быть двух мнений: Меня вдруг осенило, Во мне проснулся гений! Чтобы проверить правильность ответа, найди множество решений каждого неравенства и запиши по порядку номера соответствующих столбцов. При правильном решении полученное число укажет автора стихов.
8. Практическая работа
а) Нарисуй на клетчатой бумаге прямоугольник со сторонами 10 см и 6 см. Измерь его площадь, выбрав в качестве единицы измерения е (мерки) квадрат со стороной 2 см.
б) Вырази площадь этого прямоугольника в квадратных сантиметрах, в клеточках. Установи, как изменяется значение площади при увеличении мерки, уменьшении мерки. Сделай вывод.
9. Продолжи ряд на три числа, сохраняя закономерность:
а) 0, 36, 72, 108, …
б) 5, 6, 8, 11, 15, 20, …
50
Страница 50:
1.
а) Сравни площади фигур А и В, M и N, E и F. Всегда ли это можно сделать с помощью наложения?
б) Как измеряют площадь фигур? Какие единицы измерения площади ты знаешь?
2. Практическая работа
а) Вырежи из клетчатой бумаги прямоугольник со сторонами 3 см и 4 см. Чему равна его площадь в квадратных сантиметрах, в клеточках?
б) Нарисуй на вырезанном прямоугольнике кривую замкнутую линию A. Можешь ли ты точно указать площадь фигуры A? Сделай оценку её площади (в клеточках) как можно точнее
51
Страница 51:
3. Сделай оценку площади фигур M, N, K:
4. Вычисли. Расшифруй слово. Что оно означает? Нужно ли это тебе, другим людям? Почему?
5. БЛИЦтурнир
а) В 4 одинаковых коробках лежат a карандашей. Сколько карандашей в 15 таких коробках?
б) За 8 ч экскаватор выкапывает b м канавы. За сколько часов он выкопает c метров, работая с той же производительностью?
в) За 6 кг яблок заплатили d р., а за 4 кг груш – n р. На сколько рублей 1 кг этих груш дороже, чем 1 кг яблок?
г) Черепаха ползла 3 мин со скоростью x м/мин, а затем ещё 2 мин со скоростью y м/мин. Сколько метров проползла черепаха за всё это время?
6. Реши уравнения с комментированием и сделай проверку:
а) 26 • (x + 427) = 15 756 б) 9024 : (y – 39) = 564
7. Составь программу действий и вычисли:25 • (34 • 206 + 3672 : 18) – (6867 – 2019) : 6 • 93
8. Продолжи ряд на три числа, сохраняя закономерность:
а) 15, 14, 16, 13, 17, 12, …
б) 1, 3, 7, 15, 31, 63, …
52
Страница 52:
1. Сделай оценку площади фигуры F. Найди число из найденного промежутка, которое наиболее точно выражает площадь этой фигуры. Обоснуй свой ответ.
2. Нарисуй на клетчатой бумаге какую-нибудь замкнутую линию. Найди приближённо площадь получившейся фигуры (в клеточках).
53
Страница 53:
3. На фигуры наложены палетки. Вычисли приближённо площади этих фигур, приняв е = 1 клетке.
4. Наложи кальку на клетчатую бумагу и сделай палетку (e = 1 см2). Начерти циркулем окружность радиусом 4 см и найди с помощью палетки приближённую площадь получившегося круга.
5. Токарь вытачивает 72 одинаковые детали за 3 ч. А его ученику на эту же работу требуется в 2 раза больше времени. За сколько часов они выточат все эти детали, работая вместе?
6. Найди значение выражения: 54 240 : 678 • 5009 + 830 • 671 – (125 • 96 – 73 836 : 9)
7. Викторина «Хочу всё знать»
а) На островах Тихого океана живут черепахи-гиганты. Они такой величины, что дети могут кататься, сидя у них на панцире. Расположи ответы примеров в порядке убывания и узнай название самой крупной в мире черепахи.
б) Черепаха-гигант прекрасно плавает, а её конечности превратились в ласты. Найди её массу в килограммах, сосчитав сумму корней двух уравнений:(x • 6 – 956) : 4 = 70 и 328 – (y + 6) : 4 = 228в) Вырази массу черепахи-гиганта в центнерах, в граммах. Какие ещё единицы массы ты знаешь?
8. Расшифруй запись * * + * * * = * * * *, если известно, что оба слагаемых и сумма не изменятся, если прочитать их справа налево.
54
Страница 54:
1. На фигуры наложены палетки с площадью клетки 1 см2. Сделай оценку площади этих фигур и найди её приближённое значение.
2. Запиши множество решений неравенства и укажи наименьшее решение:
а) х > 9 в) 7 m < 10б) y 24 г) 53 < n 56
3. БЛИЦтурнир
а) На 4 метра забора пошло k досок. Сколько досок пойдёт на 9 метров такого забора?
б) Из х мотков шерсти связали 3 одинаковые шапки. Сколько таких шапок можно связать из у мотков этой шерсти?
в) Аня вышила а крестиков за 5 мин, а её брат Пётр – столько же крестиков за 8 мин. У кого из них производительность больше и на сколько?
г) Крейсеру надо проплыть b км. Он уже проплыл d км. С какой скоростью ему надо плыть, чтобы преодолеть оставшееся расстояние за 4 часа?
д) С одной яблони собрали m кг яблок, а с другой – n кг. Все яблоки разложили поровну в 5 коробок. Сколько килограммов яблок было в каждой коробке?
4. Придумай задачу, которая решается так: a + a • 3 + (a – 5).
5.Реши уравнения с комментированием и сделай проверку:
а) 170 + 2160 : (х – 18) = 350
б) (3820 – у • 75) : 14 = 5
6. Найди наибольшее решение неравенства:
а) х < 90 412 – 128 • 84 : (6040 – 5848) • 370 + 53 878 • 0б) y 4800 • 74 – (506 – 399) • 301 + 30 075 : 15 • 42
55
Страница 55:
7.
а) Выполни деление:27 506 : 10 27 506 : 100 27 506 : 1000
б) Вырази в указанных единицах счёта и измерения: 27 506 = … дес. … ед. 27 506 мм = … см … мм27 506 = … сот. … ед. 27 506 мм = … дм … мм27 506 = … тыс. … ед. 27 506 мм = … м … мм
8. Один специалист переплёл 240 книг за 10 дней, а второй – столько же книг за 15 дней. За сколько дней выполнят эту работу оба переплётчика, работая вместе?
9. Автобус проехал 480 км за 8 ч. За сколько времени проедет этот путь автомобиль, скорость которого на 36 км/ч больше скорости автобуса? С какой скоростью надо ехать, чтобы преодолеть это расстояние за 4 часа?
10. Какие высказывания об элементах множества A истинны, а какие – ложны?
1. Все элементы множества A – фрукты.
2. Некоторые элементы множества A – фрукты.
3. Ни один из элементов множества A не является фруктом.
4. В множестве A нет фруктов.
5. В множестве A имеются фрукты.6. Каждый элемент множества A является фруктом.
7. В множестве A нет ни одного элемента, являющегося фруктом. В каких высказываниях говорится одно и то же? Придумай другие истинные и ложные высказывания об элементах множества A
11. Запиши ряд из 10 чисел, в котором первое число 1, второе – 2, а каждое следующее равно произведению двух предыдущих.
56
Страница 56:
1. Начерти отрезок АВ длиной 9 см. Измерь его с помощью мерки e, равной 2 см. Что ты замечаешь? Сделай оценку длины отрезка АВ в мерках е. Каким числом из полученного промежутка можно выразить длину этого отрезка?
57
Страница 57:
2. Докажи, что ответы следующих задач нельзя выразить натуральными числами.
а) Одну конфету разделили поровну между двумя детьми. Сколько конфет получил каждый?
б) Литр сока разлили поровну в 4 стакана. Сколько литров сока в каждом стакане?
в) 7 кг крупы рассыпали поровну в 3 пакета. Сколько килограммов крупы в каждом пакете?
Придумай свои примеры из жизни, когда невозможно выразить точное значение величин натуральными числами.
3. Нарисуй 2 квадрата со стороной 4 клетки. Раздели их по-разному на две равные части. Как можно назвать полученные части квадрата?
4. Практическая работа а) Вырежи из листа бумаги круг радиусом 3 см. Раздели его с помощью перегибания на 4 равные части и закрась одну часть красным карандашом. Какая это часть круга?
б) Какую часть круга составляет незакрашенная часть? Какая из частей круга больше – закрашенная или незакрашенная?
в) Сколько четвёртых частей содержит половина круга?
5. Начерти четыре отрезка длиной 12 клеток. Выдели на первом из них половину, на втором – треть, на третьем – шестую часть, на четвёртом – пять двенадцатых этого отрезка. Придумай свой способ обозначения этих частей с помощью чисел.
6. Реши уравнения с комментированием и сделай проверку:
а) 32 • x – 59 = 453
б) y : 23 + 312 = 390
в) 7035 : (120 – z) = 67
7. В школьном саду на клумбах посадили 900 цветов, причём 630 из них были тюльпаны, а остальные – розы. На одну клумбу сажали по35 тюльпанов или по 30 роз. Сколько всего получилось клумб?
8. Найди значения выражений:
а) 306 • 24 : 72 – (35 280 : 7 – 63 • 80) : 97
б) (2005 • 8 – 704 • 21 + 6400 : 800) : (702 • 860 – 603 704)
58
Страница 58:
9. Литературная викторина «В мире животных»
а) Расшифруй, как звали красивого и мужественного чёрного лиса из рассказа Э. Сетона-Томпсона?
б) Кто из писателей рассказал историю о лисичкином хлебе? Вычисли и проверь свой ответ, расположив ответы в порядке убывания. Узнай, какие ещё рассказы есть у этого писателя?
10. Сколько минут в одном часе? Сколько секунд в одной минуте? Вырази:
а) в часах и минутах: 142 мин, 256 мин, 1032 мин
б) в минутах и секундах: 68 с, 608 с, 6008 с
11. Перед мастером 5 звеньев цепи. Их надо соединить в одну цепь, не употребляя дополнительных колец. Какое наименьшее число колец надо мастеру для этого расковать, а потом опять заковать?
12. Что меньше – половина или треть? Что больше – две трети или три четверти?
59
Страница 59:
Из истории дробей
Потребность в более точных измерениях величин привела к тому, что единицы измерения стали делить на несколько равных частей: 2, 4, 8 и т. д. Каждая часть первоначальной мерки получала своё собственное название. Например, половину в Древней Руси называли ещё ПОЛТИНОЙ, о четвёртой части говорили – ЧЕТЬ, о восьмой части – ПОЛЧЕТЬ, о шестнадцатой части – ПОЛПОЛЧЕТЬ и т. д. Равные части целой мерки называли долями: четвёртые доли, восьмые, шестнадцатые и т. д. Несколько равных долей стали называть дробями. Интересная система дробей была принята в Древнем Риме. Она основывалась на делении древнеримской единицы массы, которая называлась АСС. Асс делили на 12 равных частей. Двенадцатую часть асса называли УНЦИЕЙ. Со временем унции стали применять для измерения других величин. Например, римлянин мог сказать, что он прошёл 7 унций пути. При этом речь, конечно, не шла о взвешивании пути. Имелось в виду, что пройдено семь «двенадцатых долей» пути. Так постепенно происходил переход от конкретных дробей к отвлечённым дробям, не связанным с какой-нибудь определённой мерой. Запись дробей и правила действий с ними в древности были так сложны, что учение о дробях считалось самым трудным разделом арифметики. Чтобы его освоить, приходилось заучивать огромное число правил действий с дробями. Например, в Древнем Риме в ходу было 18 различных дробей: СЕМИС – половина асса, СЕКCТАНC – шестая доля, СЕСКУНЦИЯ – восьмая, ТРИЕНС – треть асса, БЕС – две трети, и т. д. Правил работы с дробями было так много, что умение оперировать ими воспринималось как чудо. Поэтому всегда и везде знание дробей пользовалось особым почётом и уважением. Так, например, автор славянской рукописи XVI века пишет: «Несть сё дивно, что в целых, а то похвально, что в долях…»
60
Страница 60:
А вот как об этом писал в своей знаменитой «Арифметике» русский математик XVIII века Л. Ф. Магницкий: Но несть тот арифметик, Иже в целых ответчик, А в долях ничтоже Отвещате возможе. Тем же о ты радеяй, Буди в частях умеяй. В древности основные дроби, которые были в обиходе, обозначали специальными знаками. Остальные дроби получались из основных с помощью арифметических действий. Например, некоторые дроби в Древнем Египте записывали так: Старинные задачи с дробями?70 быков треть? четверть число 10половина – три четверти – треть – четверть – шестая часть – У древних римлян унция обозначалась чертой «—», половина асса, или 6 унций, – буквой S. А семь двенадцатых записывались так: «S—».Современная система записи дробей была создана в Индии, а затем усовершенствована арабами. Широкое распространение эта запись получила совсем недавно – начиная с XIII века.
Старинные задачи с дробями
1. Задача из «Папируса Ахмеса» (Египет, 1850 г. до н. э.)«Приходит пастух с 70 быками. Его спрашивают:– Сколько приводишь ты своего многочисленного стада? Пастух отвечает:– Я привожу две трети от трети скота. Сочти!»
2. Задача аль-Хорезми (Средняя Азия, IX век н. э.)«Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»
61
Страница 61:
1. Дыню разделили поровну между 4 детьми. Какую часть дыни получил каждый из детей? Узнай, как это записывают в математике.
2. Какую долю квадрата составляет закрашенная его часть?
62
Страница 62:
3. Можно ли назвать отрезок CD пятой долей отрезка АВ? Обоснуй свой ответ.
4. Прочитай записи: 17 отрезка, 14 пирога, 1100 килограмма, 112 суток, 13 дороги, 12 яблока, 18 арбуза. Что они означают?
5. Как называется:
а) одна тысячная доля тонны; б) одна десятая доля метра;
в) одна сотая доля центнера; г) одна тысячная доля килограмма?
6.
а) Вырази в метрах: 1 дм, 1 см, 1 мм.
б) Вырази в километрах: 1 м, 1 дм, 1 см.
в) Вырази в центнерах: 1 кг, 1 г.
г) Вырази в тоннах: 1 ц, 1 кг, 1 г.
7. БЛИЦтурнир
а) Первый пакет весит a кг, а второй – в 4 раза меньше. На сколько килограммов первый пакет тяжелее второго?
б) За 4 часа Вадим прополол b грядок, а Денис – только c грядок. Во сколько раз производительность Вадима больше, чем Дениса?
в) В трёх отрезах x м ткани. В первом отрезе y м, а во втором – на 8 м больше, чем в первом. Сколько метров ткани в третьем отрезе?
г) Корабль в первый день проплыл d км, во второй день – в 2 раза больше, чем в первый, а в третий – на 40 км меньше, чем во второй. Какой путь проплыл корабль за третий день?
8.Реши уравнения с комментированием и сделай проверку:
а) 42 172 – 5 • x = 7152
б) (y + 3698) : 507 = 630
9. Верно ли высказывание:
(38 175 : 75 + 1369 + 47 • 708 – 6560 : 82) : 38 > 923
10. Учитель задал на уроке замысловатую задачу. Число мальчиков, решивших эту задачу, оказалось равным числу девочек, её не решивших. Кого в классе больше – решивших задачу или девочек?
63
Страница 63:
1. Единица разделена на 5, 12, 21, 84, 916, 2586, 1 000 000 равных частей. Как назвать одну часть в каждом из этих случаев? Запиши полученные дроби в тетради.
2. Какую долю фигуры составляет закрашенная часть? Сделай записи.
3. Нарисуй квадрат со стороной 3 см и закрась 16 часть этого квадрата
4. Как называется:
а) одна шестидесятая доля часа;
б) одна двадцать четвёртая доля суток;
в) одна сотая доля квадратного метра;
г) одна миллионная доля кубического метра?
5.
а) Вырази в часах: 1 мин, 1 с.
б) Вырази в сутках: 1 ч, 1 мин.
в) Вырази в квадратных метрах: 1 см2, 1 мм2.
г) Вырази в кубических метрах: 1 дм3, 1 см3.
6. Какую долю шахматной доски составляет: а) один ряд клеток; б) два ряда клеток; в) четыре ряда клеток; г) одна клетка?
7. Верно ли высказывание: 16 > 16 48 48 315 < 315 752 752
8. Докажи, что высказывание верно:(1905 • 690 – 2006 • 607 + 39 872) : 402 – 284 56
9. БЛИЦтурнир
а) Из a м ситца сшили 7 одинаковых сарафанов. Сколько метров ситца потребуется, чтобы сшить 12 таких же сарафанов?
б) Из b м шерсти сшили 5 одинаковых юбок. Сколько таких юбок можно сшить из c м шерсти?
в) В куске было d м полотна. Из него взяли ткань на 6 одинаковых наволочек. Сколько полотна осталось в куске, если на одну наволочку идёт k м полотна?
г) В куске было x м шёлка. От него отрезали y м, а из остальной ткани сшили 9 одинаковых блузок. Сколько метров шёлка идёт на одну блузку?
64
Страница 64:
10.
а) Арбуз весит 8 кг. Сколько весит половина арбуза?
б) Яблоко весит 400 г. Сколько весит 15 этого яблока?
в) Площадь 14 садового участка составляет 200 м2. Чему равна площадь этого участка?
г) Седьмая часть учеников класса составляет 4 человека. Сколько всего учеников в классе?
11. Вычисли устно:
543 + 215 859 – 407 40 • 93 225 : 5732 + 48 300 – 179 128 • 300 384 : 32
12.
а) Из деревни Годуново в Москву выехал велосипедист со скоростью 15 км/ч. Расстояние от Годунова до Москвы равно 120 км. Используя схему, определи, на каком расстоянии от Годунова и от Москвы был велосипедист через 3 ч после выезда. Через сколько времени после выезда он прибыл в Москву?
б) Пусть s км – расстояние, пройденное велосипедистом, а d км – его расстояние до Москвы. Перенеси в тетрадь и заполни таблицу. Запиши формулы, выражающие зависимость величин s и d от времени t.
13. Что больше – треть трети или половина четверти?
14. Для каждой фигуры на рисунке объясни, почему она может быть лишней:
65
Страница 65:
1. Практическая работа
Вырежи из бумаги прямоугольник со сторонами 4 см и 16 см и согни его пополам. Затем раздели его с помощью перегибания на 4 равные части, на 8 равных частей. Как изменяется каждая часть, когда их число увеличивается?
2. Когда долька яблока будет больше – когда его разрежут на 2, 4, 10, 32 части? Сделай вывод.
3. Сравни доли:17 15 115 120 1480 1408 1601 1610
4. Для каких значений переменной x верно неравенство:
а) 17 1x б) 16 1x < 13
5. а) Расположи в порядке возрастания числа: 17, 15, 13, 112, 110, 115.б) Расположи в порядке убывания числа: 19, 116, 14, 18, 12, 125, 13.
6. а) Нарисуй числовой луч с единичным отрезком, равным 10 клеткам. Сколько клеток содержат доли 110, 15, 12? Отметь их на числовом луче в тетради.
б) На сколько равных частей надо разделить единичный отрезок, чтобы отметить на числовом луче доли 16, 13, 12? Сделай рисунок в тетради.
66
Страница 66:
7. Как называется:
а) одна шестидесятая доля минуты;
б) одна сотая доля дециметра;
в) одна десятая доля тонны;
г) одна сотая доля метра?
8.
а) Вырази в сантиметрах: 1 дм, 1 мм.
б) Вырази в метрах: 1 км, 1 см.
в) Вырази в центнерах: 1 т, 1 кг.
г) Вырази в минутах: 1 ч, 1 с.
д) Вырази в квадратных дециметрах: 1 м2, 1 см2.
9. Папа с Алёшей отправились на рыбалку. Они ехали поездом 2 ч со скоростью 80 км/ч, затем a ч шли пешком со скоростью 3 км/ч. После этого они 2 ч плыли по озеру со скоростью v км/ч. Какой путь они проделали от вокзала до места рыбалки? Составь выражение и найди его значение, если a = 3, v = 6.
10. Серёжа ехал на велосипеде 3 ч со скоростью 12 км/ч. С какой скоростью он должен был ехать, чтобы преодолеть это расстояние за 2 ч? Придумай задачу про другие величины, которая решается так же.
11. Пусть A – множество натуральных решений неравенства 4 x < 8, а B – множество натуральных решений неравенства 5 < x 9. Запиши множества A и B с помощью фигурных скобок. Найди объединение и пересечение множеств A и B.
12. Реши уравнения с комментированием и сделай проверку:
а) 160 + 2400 : (75 – х) = 200
б) 26 176 : (y • 56 – 45 856) = 409
13. Сделай прикидку результата и вычисли:
а) 186 438 : 46
б) 8090 • 2005
14. Определи, верно ли высказывание:
59 • (536 – 78 769 : 347) + 69 898 – 82 320 : 84 < 87 250
15. Составь слова. Какое из этих слов может быть лишним?
ВМЕДЬЕД ФЕЛЕТОН АБРЕЗ ГРИТ
67
Страница 67:
1. Дополни и прочитай предложения. Проверь себя по учебнику (стр. 61, 65).
а) Доля – это одна из … частей величины.
б) Целое обозначают числом …в) Чем больше долей, тем … каждая доля.
2. Сравни дроби с помощью знаков >, <, = : 115 15 127 172 1 19 139
3. Верно ли отмечены доли на числовом луче? Прочитай их сначала в порядке возрастания, а затем – в порядке убывания.
4. Назови пропущенные единицы измерения:11000 м – это … 110 т – это … 160 мин – это …1100 000 км – это … 1100 ц – это … 124 сут. – это …
5. Вырази в указанных единицах измерения:1 мм = … м 1 кг = … т 1 с = … ч1 м = … дм 1 г = … ц 1 мин = … сут.
6. Что общего и что различного в задачах? Реши их. Придумай и реши аналогичные задачи.а) У Тани 16 открыток. 14 часть этих открыток она подарила подругам к празднику. Сколько открыток она подарила?
б) На платье израсходовали 3 м ткани, что составляет 16 всей имеющейся ткани. Сколько всего было ткани?
68
Страница 68:
7. Мама купила 2 кг яблок по цене 45 р. за кило-грамм и в 3 раза больше помидоров по цене на 9 р. больше, чем цена яблок. Сколько сдачи она должна получить с 500 рублей? Придумай задачу с другими величинами, которая решается так же.
8. Объясни смысл равенств: (a + b) + c = a + (b + c) a – (b + c) = a – b – cНазови эти свойства сложения и вычитания. Используя их, вычисли наиболее простым способом:а) (54 + 72) + 28 в) 196 + 207 + 4 + 593 д) 504 – 79 – 21б) 39 + (1 + 26) г) 316 – 198 – 2 е) 164 – (64 + 15)
9. Найди значения выражений:
а) 50 010 – 854 б) 80 900 • 370
в) 18 084 080 : 602
10. Определи, верно ли высказывание:194 815 + 206 • (376 200 : 495 – 193) – 50 • (48 600 : 8) 7867
11. Найди объединение и пересечение множеств решений неравенств x 5 и 3 x < 7.
12. Староиндийская задача математика Сриддхары (XI век н. э.)Есть кадамба цветок, на один лепестокПчёлок пятая часть опустилась.Рядом тут же росла вся в цвету сименгда, И на ней третья часть поместилась. Разность их ты найди, её трижды сложи И тех пчёл на кутай посади, Только две не нашли себе место нигде, Всё летали то взад, то вперёд и вездеАроматом цветов наслаждались. Назови теперь мне, подсчитавши в уме, Сколько пчёлок всего здесь собралось?
69
Страница 69:
1.12 кг конфет разложили поровну в 3 пакета. Какая доля всех конфет в одном пакете? Чему равна масса одного пакета?
Как найти 13 долю числа? Как найти 1n долю числа? Сделай вывод.
2. Вырази в минутах: а) половину часа; б) треть часа; в) четверть часа; г) 16 долю часа; д) 15 долю часа; е) 110 долю часа; ж) 115 долю часа; з) 12 долю часа.
3. Нарисуй в тетради схему и ответь на вопрос задачи:
а) В классе 32 ученика. Из них 14 играют в хоккей. Сколько хоккеистов в этом классе?
б) В саду 120 деревьев. Из них 16 составляют вишни. Сколько вишнёвых деревьев в этом саду?
4. Как найти долю числа?
Найди:
а) 19 от 45 м
б) 17 от 84 кг
в) 15 от 70 ц
г) 18 от 96 км
70
Страница 70:
5. Купили кусок ткани длиной 2 м 50 см. Из 15 этого куска сшили платье для куклы. Сколько сантиметров ткани ушло на это платье? Сколько ткани ещё осталось?
6. Начерти числовой луч, выбрав единичный отрезок, равный 15 клеточкам. Отметь на нём 115, 15, 13 доли.
7. Составь выражение и найди его значение, если a = 20, b = 24:«Из a м шерсти сшили 4 одинаковых костюма, а из b м шёлка сшили 8 одинаковых платьев. На сколько метров больше пошло ткани на костюм, чем на платье?»
8. Найди значение выражения. Проверь результаты по действиям с помощью калькулятора.
650 • 906 – 161 990 : (152 228 : 76 – 108 • 17) – 92 596
9. Сравни, не вычисляя:
946 + 518 607 + 274 3902 – 652 3920 – 848206 – 479 6208 – 479 1000 – 325 592 – 380
10. По тропинке вдоль кустов Шло одиннадцать хвостов. Насчитать я также смог, Что шагало тридцать ног. Это вместе шли куда-то Индюки и жеребята. А теперь вопрос таков: Сколько было индюков? Спросим также у ребят: Сколько было жеребят?
11. В корзине лежат 30 грибов – рыжиков и груздей. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?
71
Страница 71:
1.
а) Что особенного в числах 10, 100, 1000 …? Какие свойства действий с этими числами ты знаешь?
б) Сравни дроби с помощью знаков >, <, = :110 1100 1100 11000 11000 110 1100 110 000
2. Найди 1 % от:
а) 500 г;
б) 8000 км;
в) 42 000 р.;
г) 7300 л;
д) 1 т;
е) 3 ц.
3.
а) Папа получил премию 12 000 рублей. 1 % этой премии он потратил на покупку торта. Сколько стоил торт?
б) В комнате у дедушки в полдень бьют часы. Продолжительность боя составляет один процент от одного часа. Сколько секунд продолжается бой часов?
4. Найди 1 % от чисел:
а) 600;
б) 8500;
в) 4000;
г) 90 000;
д) 720 000;
е) 1 000 000.
72
Страница 72:
5. Масса дыни равна 2 кг 400 г. Ване отрезали сначала 15 дыни, а потом – ещё 16 этой дыни. Чему равна масса каждого отрезанного куска? Сколько граммов дыни ещё осталось?
6. Сравни, не вычисляя:
376 • 85
420 • 58
6300 : 35
3780 : 355963 : 67 5963 : 89 2668 : 46 1792 : 56
7. Из деревни Берёзовки, находящейся на расстоянии 72 км от Москвы, выехал велосипедист. В каком направлении и с какой скоростью он едет? Покажи в тетради его движение по числовому лучу. Составь и заполни таблицу, где t ч – время движения, s км – пройденный путь и d км – его расстояние от Москвы. Запиши формулы зависимости величин s и d от времени движения t.
8. Выполни действия:
а) 9 876 543 210 – 123 456 789
б) 600 000 000 – 95 959 595
9. Реши уравнения с комментированием и сделай проверку:
а) х : 8 + 3970 = 6000
б) 38 007 : (5000 – у) = 9
10. Составь программу действий и вычисли:
(305 • 380 – 18 512 : 89) : 12 • 100 – 847 • 407
11. Торт разрезали на 4 равные части, а каждую из полученных частей – ещё на 3 равные части. Сколько весит каждый кусочек, если масса всего торта равна 1 кг 200 г?
73
Страница 73:
1. Прочитай предложения, вставляя пропущенные слова:
а) Чтобы найти 1n долю числа, можно …
б) 1 % – это одна … доля числа.
в) Целое содержит … %.Проверь себя по учебнику (стр. 69, 71).
2. Как найти часть числа, выраженную дробью? Найди:
а) 17 числа 56 б) 1 % числа 800
в) 130 от 120 м г) 1 % от 1 т
3.
а) Кате нужно почистить 48 картошек. Она уже почистила 14 всех картошек. Сколько картошек она уже почистила? Сколько картошек ей осталось почистить?
б) Максиму надо посадить 18 саженцев. Он уже посадил 13 всех саженцев. Сколько саженцев ему осталось посадить?
4. Сколько четырнадцатых долей единичного отрезка содержат 114, 17, 12 доли? Начерти числовой луч и отметь на нём эти доли.
5. Вычисли устно: 136 + 423 692 – 280 54 • 40 552 : 625 + 814 400 – 379 207 • 60 480 : 15
6. Верно ли высказывание:(492 345 – 264 174) : 57 + 26 • 693 – 88 592 : 98 20 984
7. Реши уравнения с комментированием и сделай проверку:
а) 3 • х – 7800 = 1200
б) (y + 2958) : 57 = 139
74
Страница 74:
8. Викторина «Хочу всё знать»
а) Однажды в английском графстве Камберленд разразилась гроза. Сильный ветер вырывал деревья с корнями, образуя воронки. В одной из таких воронок жители обнаружили вещество, обладающее удивительными свойствами. Реши уравнения и расшифруй его название.
Кусочками этого вещества пастухи стали метить овец, а торговцы делали надписи на корзинах. Используют ли это вещество в наши дни?б) В пустые клетки квадрата запиши такие числа, чтобы квадрат стал магическим (суммы чисел во всех его строках, столбцах и диагоналях равны). Затем найди сумму всех вписанных чисел, и ты узнаешь, в каком году случилось описанное событие. В каком веке это было?
9. Одна коробка имеет размеры 2 дм 8 см, 5 дм и 3 дм, а вторая – 4 дм, 3 дм 6 см и 2 дм 5 см. Объём какой коробки больше и на сколько?
10. Выполни действия:
а) 8 м 7 см + 14 дм 9 см 4 мм – 9 м 64 мм
б) 6 м2 3 дм2 – 35 дм2 + 23 200 см2
11. Петя готовил уроки 2 ч. На математику он потратил 13 этого времени, а на географию – 14 оставшегося времени. Сколько минут Петя готовил уроки по математике и сколько – по географии?
12. За 4 мин бревно распилили на полуметровые поленья. Каждый распил занимал 1 мин. Какой длины было бревно?
75
Страница 75:
1. Мешок муки разделили на 3 равные части. Масса каждой части 4 кг. Чему равна масса всей муки в мешке?
Как найти число, если известна его 13 доля? А если известна его 1n доля? Сделай вывод.
2. Найди весь пройденный путь, если 400 м составляют:
а) половину этого пути
б) 15 пути
в) 13 пути
г) 1 % пути.
3.
а) Сколько стоит книга, если 16 часть её цены составляет 14 р.?
б) Масса 18 пирога равна 150 г. Чему равна масса всего пирога?
в) Сколько болельщиков было на стадионе, если 1 % всех болельщиков составляет 7 человек?
4. Найди массу яблок, если известно, что:
а) 17 этой массы составляет 8 кг
в) 13 массы составляет 15 кг
б) 1 % массы составляет 2 кг
г) 1 % массы составляет 400 г
5. Расположи доли в порядке возрастания: 19, 15, 175, 1120, 1 %
76
Страница 76:
6. Мотоциклист за день проехал некоторое расстояние. 1 % пути он ехал по просёлочной дороге, что составило 3 км. Остальную часть пути он ехал по шоссе. Сколько километров ехал мотоциклист по шоссе?
7. Сколько двадцать четвёртых долей единичного отрезка содержат 124, 112, 18, 16, 14, 13, 12 доли? Начерти числовой луч и отметь на нём эти доли.
8. Прочитай неравенство и найди множество его натуральных решений:
а) 18 1x < 14
б) 112 < 1y 17
9. Реши уравнения с комментированием и проверкой:
а) х : 6 + 480 = 6000
б) 640 – 17 040 : у = 72
10. Выполни действия:
а) 5 ч 6 мин – 3 ч 48 мин
б) 8 мин 20 с • 24
11. Найди значение выражения. Проверь результаты по действиям с помощью калькулятора.
307 • (30 405 – 29 596) + 765 000 : (317 + 533) – 226 896 : 87
12. На одной планете живут 40 колиордов. 12 из них вечером пьют чай, 28 – смотрят телевизор, а 5 не делают ни того ни другого, так как рано ложатся спать. Сколько колиордов пьют по вечерам чай, смотря телевизор?
13. Одноклассники Саша, Оля, Катя и Жанна родились в один год. Их дни рождения: 20 февраля, 12 апреля, 12 мая и 25 мая. Дни рождения Жанны и Кати приходятся на одно число, а Оли и Жанны – в одном месяце. Когда у каждого из них день рождения? Кто самый старший?
77
Страница 77:
1. Вычисли устно. Проверь себя с помощью письменных вычислений.76 • 3 84 : 12 3628 : 490 • 80 720 : 18 14 049 : 7405 • 6 6300 : 90 56 781 : 9
2. Найди число, если:
а) 19 его равна 5000
в) 140 его равна 8 мб) 1 % его равен 600
г) 1 % его равен 4 кг
3. Дополни и прочитай предложение. Проверь себя по учебнику (стр. 75).«Чтобы найти неизвестное число, можно его 1n долю…»
4. Сравни две задачи. Чем они похожи и чем различаются? Реши их.
а) Туристы прошли 15 часть маршрута, что составило 28 км. Сколько километров составляет весь путь?
б) Туристы прошли 15 часть маршрута, что составило 28 км. Сколько километров им ещё осталось пройти?
5. Реши задачи. Сравни их. Как называют такие задачи?
а) В коробке было 18 пирожных. Съели 16 всех пирожных. Сколько пирожных осталось?
б) Съели 3 пирожных, что составляет 16 всех пирожных из коробки. Сколько пирожных осталось?
78
Страница 78:
6.
а) Зверёк землеройка за сутки съел 12 г пищи. Чему равна масса зверька, если она составляет 13 массы съеденной им за сутки пищи?
б) В доме 15 четырёхкомнатных квартир, что составляет 17 всех квартир этого дома. Сколько всего квартир в этом доме?
7. Тамара гуляла 1 ч 40 мин. 14 этого времени она играла с ребятами в прятки, а остальное время гуляла по парку. Сколько времени Тамара гуляла по парку?
8. Отметь на числовом луче дроби 118, 19, 16, 13, 12. Сколько клеточек должно быть в единичном отрезке, чтобы удобно было выполнить построение?
9. Прочитай число 32 075 206 000. Сколько единиц в разряде десятков миллионов этого числа? Сколько всего десятков миллионов в этом числе? Назови предыдущее и последующее числа.
10. Выполни действия:
а) 95 959 596 + 6 070 809
в) 18 500 • 3003
б) 222 222 221 – 98 765 432
г) 25 453 350 : 247
11. Велосипедист ехал t ч со скоростью 14 км/ч. Какое расстояние он проехал за это время? Составь таблицу значений полученного выражения, если множество значений переменной равно {1, 2, 3, 4, 5}. Запиши формулу зависимости расстояния s от времени t.
12. Составь программу действий и вычисли:
(50 225 – 49 817) • 506 – 275 184 : 39 + 182 400 : (216 + 84)
Решение:
1)
2)
3)
4)
5)
6)
13. Из целого вычли треть и остаток разделили на 4 равные части. Какая часть целого содержится в каждой из полученных частей?
14. Найди закономерность и вставь пропущенную букву и пропущенное число:
79
Страница 79:
1. Арбуз разрезали на 7 равных кусков и 2 куска дали Ире. Какая часть арбуза у Иры? Как это можно записать?
2. Какая часть фигур закрашена? Какая часть фигур осталась незакрашенной? Запиши эти дроби в виде mn.
80
Страница 80:
3. Нарисуй фигуры в тетради и закрась указанные части этих фигур:
4. Прочитай дроби. Назови числитель и знаменатель каждой дроби и объясни, что они обозначают: 29, 45, 710, 1124, 9542, 379000.
5. Какие части величин выражают дроби: 2100, 6100, 25100, 41100, 78100, 95100. Запиши их с помощью знака %
6. Запиши 8 %, 15 %, 43 %, 56 %, 72 % в виде дробей со знаменателем 100. Прочитай дроби и объясни их смысл.
7. Реши задачу. Придумай свою задачу, которая решается так же. «Рабочий сделал 16 одинаковых деталей, что составило 18 часть всего задания. Сколько деталей ему осталось сделать?»
8. Найди 2 значения переменной, при которых неравенство верно, и 2 значения, при которых оно неверно:
а) x < 206 • 504 – 208 • 401
б) y > 12 322 : 61 – 3328 : 32
9. Длина круговой дорожки для бега 400 м. За 6 мин 40 с Андрей пробежал 4 круга, а Николай – 5 кругов. На сколько метров в секунду скорость Николая больше скорости Андрея?
10. Составь слова. Какое из этих слов может быть лишним? Найди разные варианты ответа. АККЛУ ЯЧМ ИНСИАЦ ИДРАМАКИП
81
Страница 81:
1.
а) На числовом луче отмечены дроби. Что в них общего? Назови их в порядке возрастания, убывания. Сделай вывод.
б) Единичный отрезок разделён на 12 равных частей. Сколько таких частей содержат 112 и 16,512 и 56? Сравни дроби с одинаковыми числителями. Сделай вывод.
2. Сравни дроби с одинаковыми знаменателями:37 17 89 49 511 211 724 1324
3. Сравни дроби с одинаковыми числителями:25 23 34 310 617 69 412 415
4. Сравни дроби:58 38 710 79 916 1416 811 819
82
Страница 82:
5.
а) Отметь на числовом луче дроби 48, 24, 12. Что ты замечаешь? Почему эти дроби называют равными?
б) Отметь на числовом луче дроби 112, 16, 36, 212, 12, 912, 34. Найди среди них равные дроби. Придумай свои примеры равных дробей и сделай записи.
6.Найди число, если: а) 18 его равна 16 б) 1 % его равен 600 в) 15 его равна k
7. Пекарня за день выпекает 2400 пирожков. 13 всех пирожков с капустой, 14 – с мясом, 15 – с грибами, а остальные – с творогом. Сколько пирожков каждого вида выпекает пекарня за день?
8. Укажи наибольшее натуральное решение неравенства:
а) x < 767 520 : 4 : 15 : 123
б) y 319 488 : 96 : 16 • 505
9. Какие из высказываний верны, а какие – нет?
1) Число 0 – натуральное.
2) Через точку можно провести больше 100 прямых.
3) Все радиусы одной окружности равны между собой.
4) При делении числа на 5 может получиться остаток, равный 6.
10.
а) Какую часть метра составляет 1 дм? Вырази в метрах 1 дм, 4 дм, 7 дм, 9 дм.б) Какую часть часа составляет 1 мин? Вырази в часах 1 мин, 3 мин, 18 мин, 25 мин.
в) Какую часть года составляют 1 месяц, 4 месяца, 7 месяцев?
11. Какая картинка следующая?
12. Сумма уменьшаемого, вычитаемого и разности равна 100. Найди уменьшаемое.
83
Страница 83:
1. Какая часть фигуры закрашена?
2. Прочитай предложения, вставляя пропущенные слова: «Дробь 79 показывает, что целое разделили на … равных частей и взяли … таких частей». «15 % показывают, что целое разделили на … равных частей и взяли … таких частей». Проверь себя по учебнику (с. 79)
3. Запиши с помощью цифр дроби: а) пять восьмых; б) семнадцать двадцатых; в) двадцать три сорок пятых; г) девять сотых. Как иначе можно записать последнюю дробь с помощью знака %?
4. Сравни с помощью знаков >, <, = :69 49 511 516 1 27 6 % 625
5. БЛИЦтурнир
а) Космонавт был в полёте k дней. 14 времени полёта проходило исследование здоровья человека. Сколько дней длилось это исследование?
б) У Бори на грядке взошло b ростков, что составило 13 от всех посаженных им семян. Сколько всего семян посадил Боря?
в) В лотерее участвовали d человек. Выиграли в ней 1 % всех участников. Сколько человек выиграли в этой лотерее?
6. В магазине повесили объявление: «Цены увеличены на 1 %». Сколько надо теперь платить за товар, который стоил раньше 500 р., 2000 р., 40 000 р.?
84
Страница 84:
7. В магазине повесили объявление: «Цены снижены на 1 %». Сколько надо теперь платить за товар, который стоил раньше 500 р., 2000 р., 40 000 р.?
8. Найди значение выражения в левой части неравенства. Проверь с помощью калькулятора. Верно ли высказывание?
(16 250 : 130 – 86) • 9040 – 7008 • (25 094 – 24 786) : 704 349 494
9. Длина изгороди вокруг прямоугольного участка земли равна 46 м. Ширина участка 4 м. Чему равны его длина и площадь?
10. Запиши формулу стоимости и определи, какие числа пропущены:
11. У Алёши было 540 р. Он купил машинку, книгу и 3 диска с компьютерными играми. Машинка стоила 90 р., книга на 20 р. дороже машинки, а цена каждого диска в 2 раза меньше, чем цена машинки и книги, вместе взятых. На оставшиеся деньги Алёша решил купить мороженое по цене 20 р. Сколько порций мороженого он может купить?
12. Филя, Степашка и Каркуша тянули жребий (три палочки разной длины).
Филя сказал: «У меня средняя палочка!»
Степашка сказал: «У меня палочка короче, чем у Фили».
Каркуша сказала: «А у меня палочка короче, чем у Степашки!»
Кому досталась самая длинная палочка, если все сказали неправду?
85
Страница 85:
1. Длина дороги равна 20 км. Заасфальтировано 25 дороги. Сколько километров этой дороги заасфальтировано?
Проанализируй решение задачи. Как найти часть числа, выраженную дробью? Сделай вывод.
2. Найди:
а) 29 числа 18
б) 4 % числа 300
в) 712 от 600 м
г) 15 % от 2 м
3. Урок длится 45 минут. 35 урока ученики писали диктант. Сколько времени длился диктант?
86
Страница 86:
4. У Кати было 56 р. За завтрак она заплатила 37 имеющихся у неё денег. Сколько стоил завтрак? Сколько денег у неё осталось?
5. Вырази в минутах: 34 ч, 56 ч, 712 ч, 2930 ч.
6. Сравни дроби с помощью знаков >, <, = :
а) 78 48 519 1219 836 2436 a + 357 a57
б) 29 23 611 615 1728 1721 42b + 5 42b
7. Выбери удобный единичный отрезок, построй числовой луч и отметь на нём дроби 110, 210, 410, 810, 15, 25, 45, 12. Найди среди этих дробей равные дроби. Придумай свои примеры равных дробей.
8. Выполни действия (устно). Что общего в полученных числах? Какое число лишнее?
Расположи ответы в порядке возрастания и расшифруй слово. Что оно означает?
9. Найди множество значений выражения 16 995 + 32 040 : a, если a принимает значения из множества {1, 8, 10, 40}. Как изменяется значение этого выражения с увеличением a? Почему?
10. Что больше – 3 % от миллиона или 15000 от миллиарда?
87
Страница 87:
1. Целое разделено на 100 равных частей. Запиши в виде дроби 5, 17, 36, 54, 89 таких частей. Прочитай эти дроби и запиши их с помощью знака %.
2. Найди:
а) 45 числа 80
в) 89 от 54 кг
д) 34 числа а
ж) mn числа 24
б) 32 % числа 700
г) 5 % от 3 м
е) 2 % числа b
з) k % числа с
3.
а) На проект по введению в школе электронного дневника запланировано 40 дней. Прошло уже 38 этого времени. Через сколько дней в школе должен появиться электронный дневник?
б) На строительство было отправлено 24 000 целых кирпичей. По дороге разбилось 3 % отправленных кирпичей. Сколько кирпичей разбилось по дороге? Сколько было доставлено целых кирпичей?
4. Реши уравнения с комментированием и проверкой:
а) 800 – (90 • x + 17) = 423 б) 240 : (y : 15) – 18 = 42
5. Расшифруй названия театральных представлений, расположив дроби: а) в порядке возрастания:
88
Страница 88:
6. Расшифруй имена богинь – покровительниц комедии и трагедии в греческой мифологии, расположив дроби:
а) в порядке возрастания:
б) в порядке убывания:
7. Выполни действия и определи, верно ли высказывание:
30 303 – (76 • 507 + 68 400 : 450) : 76 + 2350 • (1050 – 441) 1 408 945
8. Найди периметр и площадь земельных участков по указанным размерам. Что ты замечаешь?
9.
а) В 1 см2 палетки, изображённой на рисунке, содержится 4 клетки. Вычисли с её помощью примерную площадь четырёхугольника ABCD в квадратных сантиметрах.
б) Вырежи четырёхугольник ABCD из клетчатой бумаги. Разрежь его на 4 равные части по диагоналям AC и BD. Сложи из полученных частей прямоугольник. Найди его площадь и сравни её с площадью четырёхугольника ABCD.Что ты замечаешь?
Сделай вывод
10. Расшифруй числовой ребус:
ABB + BAC = BDDD (Одинаковым буквам соответствуют одинаковые цифры, а разным – разные.)
89
Страница 89:
1. Чему равна длина дороги, если её 25 составляют 8 км?
Проанализируй решение задачи. Как найти число по его части, выраженной дробью? Сделай вывод.
2. Найди число, 415 которого составляют 8, 32, 60, 240.
3. Найди величину:
а) 56 которой составляют 25 см
в) 7 % которой составляют 56 л
б) 23 которой составляют 120 г
г) 4 % которой составляют 200 м
4. Запиши число:
а) 23 которого составляют х
б) 5 % которого составляют у
90
Страница 90:
5. Нарисуй в тетради схемы, заполни их и реши задачи:
а) Заяц живёт примерно 6 лет. Продолжительность жизни зайца составляет 25 продолжительности жизни волка. Сколько примерно лет живёт волк?
б) Масса бурого медведя равна примерно 200 кг, что составляет 40 % массы белого медведя. Чему равна масса белого медведя?
6. Велогонщики проехали в первый день соревнований 130 км, что составляет 26 % всего пути. Сколько километров им ещё осталось преодолеть?
7. Сравни с помощью знаков >, <, = :78 48 37 311 1417 817 5 % 6100613 68 431 1231 1542 1547 7 % 729
8. Выполни действия и найди наибольшее решение неравенства:
х 608 • (3076 + 5081) – 2 111 022 : (5960 – 5646)
9. Аня задумала число, прибавила его к числу 789 и полученную сумму разделила на 8. В результате у неё получилось 4005. Какое число задумала Аня?
10. Учитель принёс в класс билеты в театр и цирк. 15 учеников класса купили билеты в театр, а 18 – в цирк, причём 7 человек из них – на оба представления сразу. Сколько учеников класса купили билеты на эти представления?
91
Страница 91:
1.
а) Вырежи из бумаги прямоугольник ABCD со сторонами 4 см и 5 см. Разрежь его по диагонали AC на два треугольника. Докажи, что полученные треугольники равны.
б) Сравни площади треугольников ABC и ADC сначала между собой, а затем – с площадью прямоугольника ABCD. Сделай вывод.
в) Найди у треугольников ABC и ADC прямые углы. Как ты думаешь, почему такие треугольники называют прямоугольными?
2. Что общего у треугольников на рисунке? Назови катеты и гипотенузу каждого треугольника. Измерь их катеты и найди площадь.
3. Начерти в тетради прямоугольный треугольник. Измерь его стороны и найди площадь.
92
Страница 92:
4. Вычисли площади закрашенных фигур:
5. Как найти часть от числа, выраженную дробью? Как найти число по его части? Найди: а) 58 числа 16 в) число, 29 которого составляют 8 б) 7 % числа 900 г) число, 5 % которого составляют 35
6. Нарисуй в тетради схемы, заполни их и реши задачи:
а) В городе 18 000 детей, что составляет 24 % всех его жителей. Сколько всего жителей в этом городе?
б) В залах музея выставлено 240 экспонатов, что составляет 38 всех имеющихся в музее экспонатов. Сколько экспонатов этого музея не выставлено (хранится в запаснике)?
7. На базу в Антарктиду доставили 22 собаки. Для похода из 511 всех доставленных собак составили упряжку. Сколько собак не вошло в упряжку?
8. Найди значение выражения в левой части неравенства. Проверь с помощью калькулятора. Верно ли высказывание?
9008 • (416 + 334) : 563 – (600 000 – 4272) : 84 4908
93
Страница 93:
9. Сравни дроби с помощью знаков >, <, = :3265 4965 796 712 1423 1437 1819 1619
10. Максим задумал число и вычел его из числа 740. Затем полученную разность он умножил на 57. В результате у него получилось 40 185. Какое число задумал Максим?
11. БЛИЦтурнир
а) Масса дыни a кг, а масса арбуза на b кг больше. Во сколько раз арбуз тяжелее дыни?
б) Скорость автобуса c км/ч, а скорость грузовика d км/ч. На сколько большее расстояние пройдёт автобус за 6 ч, чем грузовик за 4 ч?
в) У Алёши x р., а у Кости y р. Они сложили свои деньги и купили 2 мороженых по n р. Сколько денег у них ещё осталось?
г) После уроков Алиса идёт домой из школы со скоростью v м/мин. Какое расстояние останется ей пройти через 5 мин после выхода, если между школой и её домом s метров?
д) За 3 часа рабочий сделал k одинаковых деталей. Сколько таких деталей он сделает за 8 часов, работая с той же производительностью?
12. Выбери из множества {8, 16, 24, 35, 40, 48, 54, 64} числа, которые: а) кратны 8; б) являются делителями 48.
13. Литературная викторина Найди значения буквенных выражений для всех значений переменной. В полном алфавите найди соответствующие им буквы. Из полученных букв составь в каждой задаче имя героя известной книги. Назови эту книгу и её автора.
1) 20 – a : 3, если a {57, 15, 48, 42}
2) 0 + 63 • 0 + b • 1, если b {10, 13, 15, 19, 30}
3) 94 + c : 1 – 94, если c {6, 16, 17, 18, 30}
4) 1 • d – 65 : 65 + 0 : 6, если d {27, 2, 17, 10, 22, 14, 13}
94
Страница 94:
1. Объясни по рисунку, как найти 37 от числа a? Как найти число, если37 его составляют b?
2. Объясни, как найти 4 % от числа a? Как найти число, если 4 % его составляют b?
3. Найди:
а) 511 числа 55
в) число, 47 которого составляют 24
б) 3 % числа 60 000
г) число, 18 % которого составляют 36
4.
а) Найди число, 635 которого равны произведению 18 • 705.
б) Найди число, 20 % которого равны частному 3 360 840 : 42.
5. Нарисуй в тетради схемы, заполни их и реши задачи:
а) В аквариум налили 6 л воды, заполнив 25 его объёма. Сколько литров воды вмещает аквариум?
б) Цена на кофту снизилась на 45 р., что составляет 15 % её первоначальной цены. Сколько рублей стала стоить эта кофта?
в) Самолёт пролетел 240 км, что составило 12 % всего намеченного пути. Сколько километров всего должен пролететь самолёт? Что ещё можно узнать?
95
Страница 95:
6. В куске было 96 м ткани. Для детского сада взяли 38 этого куска, а для детских яслей – 512 куска. Сколько материи ещё осталось в этом куске?
7. Запиши формулу работы. Используя её, найди пропущенные числа
8. Перенеси в тетрадь таблицу, заполни её и реши задачу:
Первый автомат в минуту закрывает 40 банок, а второй – на 5 банок больше первого. Сколько банок закроют эти автоматы за 34 часа при их одновременном включении? За сколько времени, работая вместе, они закроют 5780 банок?
9. Реши уравнения с комментированием и сделай проверку:
а) (a + 6882) : 28 = 2660
б) (14 289 – b) • 404 = 4 242 000
10. Выполни действия и найди наименьшее решение неравенства:
х > 2 045 639 : (6700 – 6279) + 783 • (66 161 – 65 752)
Решение:
1)
2)
3)
4)
5)
6)
11. Запиши множество натуральных решений неравенства:
а) 5y < 57
б) x6 < 46
12. У Кирилла 600 фантиков. Половина из них синие, треть – красные, а четверть остальных – зелёные. Сколько у него зелёных фантиков?
Математика 4 класс. Решение неравенства. Множество решений

Математика. “Решение неравенства” (по Петерсон Л.Г.).

МАТЕМАТИКА 4 КЛАСС . РЕШЕНИЕ НЕРАВЕНСТВА .МНОЖЕСТВО РЕШЕНИЙ / ПЕТЕРСОН . НАЧАЛЬНАЯ ШКОЛА
Мотивация
(самоопределение) к учебной деятельности
2.
Актуализация знаний
Выявление места затруднения
Проект коррекции затруднений (локализация затруднения)
Построение проекта выхода из затруднения
Реализация построенного проекта
Обобщение затруднений во внешней речи
Самостоятельная работа с самопроверкой в классе
Включение в систему знаний и повторение.
Рефлексия
3)
4.
5
6.
7.
.
9
Девиз урока
Бороться и искать, найти и не сдаваться.
– Прочитайте девиз, который нас сегодня встречает.- Как вы его понимаете? Попробуйте связать его с уроком математики.
– Назовите тему наших предыдущих уроков (неравенства)
– Все ли получалось у нас при решении неравенств, были ли ошибки?
– Чем же мы займемся на сегодняшнем уроке?
С чего предлагаете начать урок?
С какой целью будем повторять?
Математический диктант (ответьте устно на вопросы и запишите полученное множество чисел):-найдите сумму чисел 18 и 32; -найдите разность чисел 64 и 13; -увеличьте число 13 в 4 раза; -на сколько 100 больше, чем 47; -во сколько раз 2 меньше, чем 108.
-Что вы заметили?
-Запишите на листках одно какое-нибудь неравенство, которое имеет данное множество решений.
Чему вы научились, изучая тему «Неравенства»?
Назовите опорные конспекты на доске и расскажите алгоритмы действий.
Чем мы сейчас с вами занимались?
Что будем делать дальше?
С какой целью?
Предлагаю выполнить самостоятельную работу на использование этих алгоритмов.
Давайте отметим причины возможных ошибок на доске и на листках: – запись и чтение неравенств (строгого, нестрогого, двойного); – нахождение множества решений неравенства (строгого, нестрогого, двойного); – вычисления; – другая причина. Проверьте свою работу.
Если всё правильно поставьте знак «+», если нет, то «?».
Поднимите руку, у кого всё правильно, у кого есть ошибки?
У кого ошибки в 1 задании? Во 2 задании? В 3 задании?
Зафиксируем количество ошибок на доске. Что будем делать дальше?
С какой целью?
Дети, у кого нет ошибок, вы молодцы! Теперь поработайте над дополнительным заданием самостоятельно.
Вы подчеркнули место затруднения. Теперь определим причину ошибок. Поднимите руку, у кого ошибки в записи неравенств; в нахождении множества решений неравенства; в вычислениях.
Что будем делать дальше, после того, как нашли место и причину ошибки?
Что будем использовать для исправления ошибки?
Допущенные ошибки фиксируются на доске.
Кто смог исправить свою ошибку? Что вам в этом помогло? У кого остались затруднения? На что обратить внимание, чтобы не допускать ошибки в решении неравенств?
Чем займёмся дальше?
Зачем?
Выберите подобное задание в самостоятельной работе №2 и решите.
Те дети, которые работали над дополнительным заданием, проверяют свою работу по подробному образцу.
Дети, выполнившие самостоятельную работу №2 проверяют себя по подробному образцу. Поставьте «+», если всё правильно, если есть ошибки «?».
Поднимите руки, у кого нет ошибок. Молодцы!
У кого есть ошибки? На что нужно обратить внимание дома?
Решаем задачу №9 с.14. Что известно в задаче? Что надо узнать? Какую формулу используем? Что узнаем сначала? Что потом? Ответили на вопрос задачи? Запишем ответ.
Вспомните цель нашего урока.
Цель урока достигнута?
Объясните, почему вы так считаете.
Какие ошибки были допущены?
Как работали над ошибками?
В чём смогли потренироваться в творческом задании?
Помог ли вам наш девиз на уроке? Удалось справиться с трудностями?
Над чем ещё нужно поработать?
Оцените свою работу на уроке на «Лесенке успеха».
Если встречаются ошибки или трудности, не надо сдаваться, а надо бороться, искать ошибки, а когда найдешь их, исправить.
Потренируемся в решении неравенств.
С повторения.
Вспомнить и повторить изученные алгоритмы решения неравенств.
(50,51,52,53,54)
Числа идут по порядку.
49<х<55; 50≤ х ≤54; 49< х ≤54;
50≤ х <55.
Определять, является ли число решением неравенства или нет; читать и записывать неравенства – строгие, нестрогие, двойные, находить множество их решений.
Ответы детей.
Повторили опорные сигналы, вспомнили алгоритм действий.
Выполнять самостоятельную работу.
Чтобы проверить, какие у кого трудности.
Учащиеся выполняют работу.
Каждый учащийся проверяет свою работу по готовому образцу и фиксирует, где у него расхождение с образцом.
Проверять по подробному образцу.
Найти место ошибки в решении, определить причину.
Дети проверяют по подробному образцу и подчёркивают то место, где его допустили.
Дети поднимают руки и выявляют, в чём именно заключается ошибка.
Повторим алгоритм и попробуем исправить ошибки сами, потом проверим по подробному образцу.
Используем алгоритм исправления ошибки.
Дети исправляют ошибки на основе правильного применения указанных способов действий.
Дети исправляют ошибки самостоятельно, а потом проверяют по подробному образцу.
Дети обсуждают ошибки и проговаривают алгоритмы решения неравенств, вызвавшие затруднения (запись, вычисления, нахождение множества решений неравенств (строгого, нестрогого, двойного).
Выполним те задания в самостоятельной работе, где допустили ошибки.
Потренироваться в применении того алгоритма, в котором допустили ошибку в самостоятельной работе №1.
Дети выполняют самостоятельную работу №2.
Дети решают задачу фронтально.
Повторить и закрепить наши знания.
Да.
Дети, которые не допустили ошибок в самостоятельной работе выполняли творческое задание, а те, кто допустил ошибки, потренировались, чтобы больше ошибок не было.
Запись, вычисления, нахождение множества решений неравенств (строгого, нестрогого, двойного).
Вспомнили алгоритм нахождения множества решений неравенства.
Вычисления, порядок действий.
Да.

