Как найти наибольшее значение двузначного числа

Перейти к контенту

Когда человек только учился считать, ему хватало пальцев рук, чтобы определить, что два мамонта, гуляющие у пещеры, это меньше, чем то стадо за горой. Но как только он осознал, что такое позиционное счисление (когда число имеет конкретное место в длинном ряду), он стал задумываться: а что дальше, каково наибольшее число?

С тех пор лучшие умы стали искать, как можно вычислить такие величины, а самое главное, каким смыслом их наделить.

Многоточие в конце ряда

Когда школьников знакомят с первоначальным понятием натуральных чисел, по краям ряда чисел благоразумно ставят многоточие и объясняют, что наибольшее и наименьшее число – это категория бессмысленная. Всегда есть возможность к самому большому числу прибавить единицу, и оно уже не будет самым большим. Но прогресс не был бы возможен, если бы не было тех, кто захотел найти смысл там, где его быть не должно.

Бесконечность числового ряда, кроме пугающего и неопределенного философского значения, создавала и чисто технические трудности. Приходилось искать обозначения для очень больших чисел. Сначала это делалось отдельно для основных языковых групп, а с развитием глобализации появились слова, именующие наибольшее число, общепринятые во всем мире.

Десять, сто, тысяча

В каждом языке для чисел, имеющих практическое значение, найдено собственное название.

В русском прежде всего это ряд от нуля до десяти. До сотни дальнейшие числа называются или на их основе, с небольшим изменением корней – «двадцать» (два по десять), «тридцать» (три по десять) и т. д., или являются составными: «двадцать один», «пятьдесят четыре». Исключение – вместо «четыредцать» мы имеем более удобное «сорок».

Наибольшее двузначное число — «девяносто девять» – имеет составное название. Далее из собственных традиционных названий – «сто» и «тысяча», остальные образованы из нужных сочетаний. Похожая ситуация в других распространенных языках. Логично думать, что устоявшиеся имена давались числам и цифрам, с которыми имели дело большинство обычных людей. Даже что такое тысяча голов скота, мог представить и обычный крестьянин. С миллионом было сложнее, и началась путаница.

Миллион, квинтиллион, дециллиард

В середине XV века французом Николя Шуке для того, чтобы обозначить самое наибольшее число, была предложена система наименования на основе числительных из общепринятой среди ученых латыни. В русском языке они претерпели некоторую модификацию для удобства произношения:

• 1 – Unus – ун.
• 2 – Duo, Bi (двойной) – дуо, би.
• 3 – Tres – три.
• 4 – Quattuor – квадри.
• 5 – Quinque – квинти.
• 6 – Sex – сексти.
• 7 – Septem – септи.
• 8 – Octo – окти.
• 9 – Novem – нони.
• 10 – Decem – деци.

Основой названий должно было стать -иллион, от «миллион» – «большая тысяча» – т. е. 1 000 000 – 1000^2 – тысяча в квадрате. Это слово, чтобы упомянуть наибольшее число, впервые употребил знаменитый мореход и ученый Марко Поло. Так, тысяча в третьей степени стала триллионом, 1000^4 – квадриллионом. Другой француз – Пелетье – предложил для чисел, которые у Шюке назывались «тысяча миллионов» (10^9), «тысяча биллионов» (10^15) и т. д., использовать окончание «-иллиард». Получилось, что 1 000 000 000 – это миллиард, 10^15 – биллиард, единица с 21 нулём – триллиард и так далее.

Терминология французских математиков стала использоваться во многих странах. Но постепенно выяснилось, что 10^9 в некоторых трудах стали именовать не миллиардом, а биллионом. А в США приняли систему, по которой окончание -иллион получили степени не миллиона, как у французов, а тысячи. В результате сегодня в мире действуют две шкалы: «длинная» и «короткая». Чтобы понять, какое число имеется в виду под наименованием, например, квадриллион, лучше уточнить в какую степень возведено число 10. Если в 15-ю, – это «короткая» шкала, принятая в США, Канаде, Великобритании и ряде других стран, в том числе в России (правда, у нас 10^9– не биллион, а миллиард), если в 24 – это «длинная», принятая в большинстве регионов мира.

Тредециллион, вигинтиллиард и миллеиллион

Но эти построения интересны только ограниченному числу людей — они не используются в практике, да и сами эти величины не привязаны даже к теоретическим задачам или теоремам. Именно для сугубо теоретических построений предназначены числа-великаны, получавшие иногда очень звучные имена или называемые по фамилии автора.

Тьма, легион, асанкхейя

Вопрос огромных чисел волновал и «докомпьютерные» поколения. У славян существовали несколько систем счисления, в некоторых они добирались до огромных высот: наибольшее число — 10^50. Названия чисел с высоты нашего времени кажутся поэзией, а во всех ли в них был практический смысл, знают только историки и лингвисты: 10^4 – «тьма», 10^5 – «легион», 10^6 – «леодр», 10^7 – вран, ворон, 10^8 – «колода».

Не менее красивое по названию число asaṃkhyeya упоминается в буддийских текстах, в древнекитайских и древнеиндийских собраниях сутр.

Количественное значение числа асанкхейя исследователи приводят как 10^140. Для понимающих оно полно божественного смысла: именно столько космических циклов должна пройти душа, чтобы очиститься от всего телесного, накопленного за долгий путь перерождений, и достигнуть блаженного состояния нирваны.

Гугол, гуголплекс

Математик из Колумбийского университета (США) Edward Kasner с начала 1920 годов начал задумываться о больших числах. В частности, его интересовало звучное и выразительное название для красивого числа 10^100. Однажды он гулял с племянниками и рассказал им об этом числе. Девятилетний Милтон Сиротта предложил слово googol – гугол. Дядя получил от племянников и бонус – новое число, которое они объяснили так: единица и столько нулей, сколько можешь написать, пока совсем не устанешь. Имя этому числу было гуголплекс. Поразмыслив, Кашнер решил, что это будет число 10^googol.

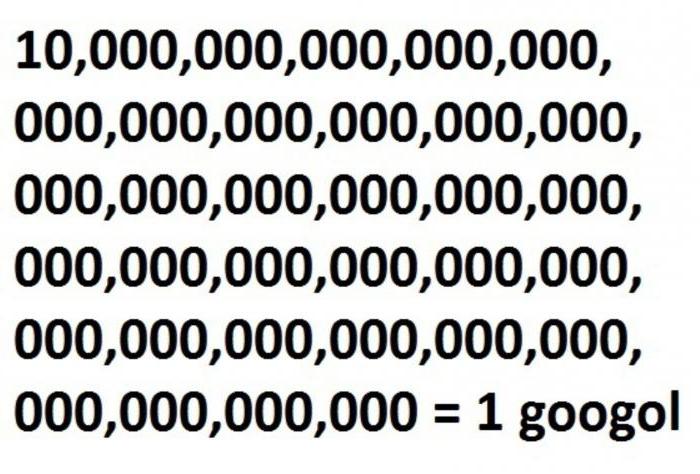
Смысл в таких числах Кашнер видел больше педагогический: наука тогда не знала чего-либо в таком количестве, а будущим математикам на их примере он объяснял, какое наибольшее число может сохранять отличие от бесконечности.

Шикарную идею маленьких гениев нейминга оценили основатели компании по продвижению нового поисковика. Домен googol оказался занят, и буква o выпала, зато появилось название, для которого эфемерное число может стать когда-нибудь реальным — столько будут стоить его акции.

Число Шеннона, число Скьюза, медзон, мегистон

В отличие от физиков, периодически натыкающихся на ограничения, налагаемые природой, математики продолжают путь в сторону бесконечности. Любитель шахматной игры Клод Шеннон (1916-2001) наполнил смыслом число 10^118 — именно столько вариантов позиций может возникнуть в течении 40 ходов.

Стенли Скьюз из Южной Африки занимался одной из семи задач, входящих в список «проблем тысячелетия» – гипотезой Римана. Она касается поиска закономерности в распределении простых чисел. В ходе рассуждений он использовал сначала число 10^10^10^34, обозначенное им Sk₁ , а затем 10^10^10^963 — второе число Скьюза — Sk₂.

Для оперирования такими числами не подходит даже привычная система записи. Гуго Штейнгауз (1887-1972) предложил использовать геометрические фигуры: n в треугольнике – это n в степени n, n в квадрате – n в n треугольниках, n в круге — это n в n квадратах. Он объяснял эту систему на примере чисел мега – 2 в круге, медзон – 3 в круге, мегистон – 10 в круге. Так трудно обозначить, например, наибольшее двузначное число, но оперировать колоссальными величинами стало проще.

Профессор Дональд Кнут предложил стрелочную нотацию, в которой повторное возведение в степень обозначалось стрелкой, заимствованной из практики программистов. Гугол в этом случае выглядит как 10↑10↑2, а гуголплекс — 10↑10↑10↑2.

Число Грэма

Рональд Грэм (р. 1935) американский математик, в ходе исследования теории Рамсея, связанной с гиперкубами — многомерными геометрическими телами – ввел особые числа G₁ – G₆₄ , с помощью которых он обозначил границы решения, где верхним пределом стало наибольшее кратное число, получившее его имя. Он вычислил даже 20 последних цифр, а исходными данными послужили следующие значения:

– G₁ = 3↑↑↑↑3 = 8,7 х 10^115.

– G₂= 3↑…↑3 (число стрелок сверхстепени = G₁).

– G₃= 3↑…↑3 (число стрелок сверхстепени = G₂).

…

– G₆₄= 3↑…↑3 (число стрелок сверхстепени = G₆₃ )

G₆₄, обозначаемое просто G, и является самым большим в мире числом, использованным в ходе математических вычислений. Оно занесено в книгу рекордов.

Представить его масштаб практически невозможно, учитывая, что весь объём известной человеку вселенной, выраженный в самой маленькой единице объёма (кубик с гранью планковской длины (10^-35 м)), выражается цифрой 10^185.