Как найти наибольшее значение функции корень

Сайты, меню, вход, новости

Как решать задачи B15 без производных

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Другими словами, для возрастающей функции Для убывающей функции все наоборот:

Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:

f ( x ) = log _a x ( a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

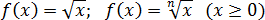
Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только

f ( x ) = a x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

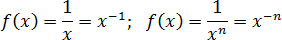
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

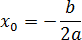
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы и найти ее вершину по формуле:
2. Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

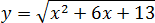
Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент

x ₀ = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.

Корень монотонно возрастает, значит точка минимума всей функции. Имеем:

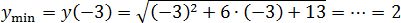
Задача. Найдите наименьшее значение функции:

Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,

x ₀ = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1

Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:

y _min = y (−1) = log ₂ ((−1) 2 + 2 · (−1) + 9) = . = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

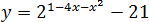
В показателе стоит квадратичная функция Перепишем ее в нормальном виде:

Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке

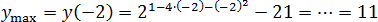
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

Аргумент логарифма должен быть положительным:

y = log _a f ( x ) ⇒ f ( x ) > 0

Арифметический квадратный корень существует только из неотрицательных чисел:

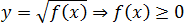
Знаменатель дроби не должен равняться нулю:

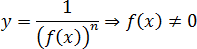
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

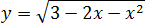
Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒

Теперь найдем вершину параболы:

Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:

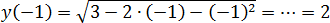
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x ₀ = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только

y _min = y (3) = log _0,5 (6 · 3 − 3 2 − 5) =

Наибольшее и наименьшее значение функции

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал ( a ; b ) , ( a ; b ] , [ a ; b ) , бесконечный интервал ( a ; b ) , ( a ; b ] , [ a ; b ) либо бесконечный промежуток – ∞ ; a , ( – ∞ ; a ] , [ a ; + ∞ ) , ( – ∞ ; + ∞ ) .

В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f ( x ) .

Основные определения

Начнем, как всегда, с формулировки основных определений.

Наибольшее значение функции y = f ( x ) на некотором промежутке x – это значение m a x y = f ( x 0 ) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f ( x ) ≤ f ( x 0 ) .

Наименьшее значение функции y = f ( x ) на некотором промежутке x – это значение m i n x ∈ X y = f ( x 0 ) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f ( x ) ≥ f ( x 0 ) .

Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .

Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .

Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.

Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения ( m a x y и m i n y ) в стационарных точках, расположенных на отрезке [ – 6 ; 6 ] .

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ – 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.

Наибольшее и наименьшее значение функции на открытом интервале

Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале ( – 6 ; 6 ) .

Если мы возьмем интервал [ 1 ; 6 ) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .

На графике 6 наименьшее значение данная функция приобретает в правой границе интервала ( – 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.

Наибольшее и наименьшее значение функции на бесконечности

На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .

Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.

1. Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
2. Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
3. Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
4. Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .
5. 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.

Посмотрим, как правильно применить этот алгоритм при решении задач.

Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ – 4 ; – 1 ] .

Решение:

Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D ( y ) : x ∈ ( – ∞ ; 0 ) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:

y ‘ = x 3 + 4 x 2 ‘ = x 3 + 4 ‘ · x 2 – x 3 + 4 · x 2 ‘ x 4 = = 3 x 2 · x 2 – ( x 3 – 4 ) · 2 x x 4 = x 3 – 8 x 3

Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ – 4 ; – 1 ] .

Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 – 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .

Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4 :

y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4

Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 – при x = 2 .

Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:

y ( – 1 ) = ( – 1 ) 3 + 4 ( – 1 ) 2 = 3

Значит, m a x y x ∈ [ – 4 ; – 1 ] = y ( – 1 ) = 3 , m i n y x ∈ [ – 4 ; – 1 ] = y ( – 4 ) = – 3 3 4 .

Ответ: Для отрезка [ 1 ; 4 ] – m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , для отрезка [ – 4 ; – 1 ] – m a x y x ∈ [ – 4 ; – 1 ] = y ( – 1 ) = 3 , m i n y x ∈ [ – 4 ; – 1 ] = y ( – 4 ) = – 3 3 4 .

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.

• Если интервал имеет вид [ a ; b ) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b – 0 f ( x ) .
• Если интервал имеет вид ( a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f ( x ) .
• Если интервал имеет вид ( a ; b ) , то нам надо вычислить односторонние пределы lim x → b – 0 f ( x ) , lim x → a + 0 f ( x ) .
• Если интервал имеет вид [ a ; + ∞ ) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f ( x ) .
• Если интервал выглядит как ( – ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → – ∞ f ( x ) .
• Если – ∞ ; b , то считаем односторонний предел lim x → b – 0 f ( x ) и предел на минус бесконечности lim x → – ∞ f ( x )
• Если же – ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f ( x ) , lim x → – ∞ f ( x ) .

1. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 – 8 в первой части материала.

Пример 2

Условие: дана функция y = 3 e 1 x 2 + x – 6 – 4 . Вычислите ее наибольшее и наименьшее значение в интервалах – ∞ ; – 4 , – ∞ ; – 3 , ( – 3 ; 1 ] , ( – 3 ; 2 ) , [ 1 ; 2 ) , 2 ; + ∞ , [ 4 ; + ∞ ) .

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :

x 2 + x – 6 = 0 D = 1 2 – 4 · 1 · ( – 6 ) = 25 x 1 = – 1 – 5 2 = – 3 x 2 = – 1 + 5 2 = 2 ⇒ D ( y ) : x ∈ ( – ∞ ; – 3 ) ∪ ( – 3 ; 2 ) ∪ ( 2 ; + ∞ )

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

y ‘ = 3 e 1 x 2 + x – 6 – 4 ‘ = 3 · e 1 x 2 + x – 6 ‘ = 3 · e 1 x 2 + x – 6 · 1 x 2 + x – 6 ‘ = = 3 · e 1 x 2 + x – 6 · 1 ‘ · x 2 + x – 6 – 1 · x 2 + x – 6 ‘ ( x 2 + x – 6 ) 2 = – 3 · ( 2 x + 1 ) · e 1 x 2 + x – 6 x 2 + x – 6 2

Следовательно, производные функции существуют на всей области ее определения.

Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = – 1 2 . Это стационарная точка, которая находится в интервалах ( – 3 ; 1 ] и ( – 3 ; 2 ) .

Вычислим значение функции при x = – 4 для промежутка ( – ∞ ; – 4 ] , а также предел на минус бесконечности:

y ( – 4 ) = 3 e 1 ( – 4 ) 2 + ( – 4 ) – 6 – 4 = 3 e 1 6 – 4 ≈ – 0 . 456 lim x → – ∞ 3 e 1 x 2 + x – 6 = 3 e 0 – 4 = – 1

Поскольку 3 e 1 6 – 4 > – 1 , значит, m a x y x ∈ ( – ∞ ; – 4 ] = y ( – 4 ) = 3 e 1 6 – 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение – 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.

Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к – 3 с левой стороны, мы получим только интервал значений:

lim x → – 3 – 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 – 0 3 e 1 ( x + 3 ) ( x – 3 ) – 4 = 3 e 1 ( – 3 – 0 + 3 ) ( – 3 – 0 – 2 ) – 4 = = 3 e 1 ( + 0 ) – 4 = 3 e + ∞ – 4 = + ∞ lim x → – ∞ 3 e 1 x 2 + x – 6 – 4 = 3 e 0 – 4 = – 1

Значит, значения функции будут расположены в интервале – 1 ; + ∞

Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = – 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к – 3 с правой стороны:

y – 1 2 = 3 e 1 – 1 2 2 + – 1 2 – 6 – 4 = 3 e 4 25 – 4 ≈ – 1 . 444 y ( 1 ) = 3 e 1 1 2 + 1 – 6 – 4 ≈ – 1 . 644 lim x → – 3 + 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 + 0 3 e 1 ( x + 3 ) ( x – 2 ) – 4 = 3 e 1 – 3 + 0 + 3 ( – 3 + 0 – 2 ) – 4 = = 3 e 1 ( – 0 ) – 4 = 3 e – ∞ – 4 = 3 · 0 – 4 = – 4

У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ ( 3 ; 1 ] = y – 1 2 = 3 e – 4 25 – 4 . Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до – 4 .

Для интервала ( – 3 ; 2 ) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:

y – 1 2 = 3 e 1 – 1 2 2 + – 1 2 – 6 – 4 = 3 e – 4 25 – 4 ≈ – 1 . 444 lim x → – 3 + 0 3 e 1 x 2 + x – 6 – 4 = – 4 lim x → 2 – 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 + 0 3 e 1 ( x + 3 ) ( x – 2 ) – 4 = 3 e 1 ( 2 – 0 + 3 ) ( 2 – 0 – 2 ) – 4 = = 3 e 1 – 0 – 4 = 3 e – ∞ – 4 = 3 · 0 – 4 = – 4

Значит, m a x y x ∈ ( – 3 ; 2 ) = y – 1 2 = 3 e – 4 25 – 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом – 4 .

Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2 ) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.

На промежутке ( 2 ; + ∞ ) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка – 1 ; + ∞ .

lim x → 2 + 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 + 0 3 e 1 ( x + 3 ) ( x – 2 ) – 4 = 3 e 1 ( 2 + 0 + 3 ) ( 2 + 0 – 2 ) – 4 = = 3 e 1 ( + 0 ) – 4 = 3 e + ∞ – 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x – 6 – 4 = 3 e 0 – 4 = – 1

Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞ ) = y ( 4 ) = 3 e 1 14 – 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = – 1 .

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Задание 11 Профильного ЕГЭ по математике

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции

Найдем производную функции.

Приравняем производную к нулю. Получим:

Исследуем знаки производной.

В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

Определим знаки производной.

В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции

Исследование сложных функций

3. Найдите точку максимума функции

Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.

при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при

4. Найдите абсциссу точки максимума функции

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции

Это вершина квадратичной параболы

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

Найдем знаки производной.

В точке производная равна нулю и меняет знак с “+” на “-“. Значит, x = – 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.

6. Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.

Найдем знаки производной.

Точка — точка минимума функции . Точка не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.

7. Найдите наименьшее значение функции на отрезке

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при

Если то Если , то

Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке

8. Найдите наибольшее значение функции на отрезке

Найдем производную функции

Приравняем производную к нулю:

Найдем знаки производной на отрезке

При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

9. Найдите наименьшее значение функции на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

Найдем производную функции

При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции

10. Найдите наибольшее значение функции на отрезке

Как всегда, возьмем производную функции и приравняем ее к нулю.

По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки

В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при

11.Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при

Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/funktsii/naibolshee-i-naimenshee-znachenie-funktsii/

http://ege-study.ru/zadanie-12-profilnogo-EGE-po-matematike

[/spoiler]

Дата публикации: 09 апреля 2017.

График функции квадратного корня

Ребята, с построением графиков функций мы с вами уже встречались, и не раз. Мы строили множества линейных функций и парабол. В общем виде любую функцию удобно записать, как $y=f(x)$. Это уравнение с двумя переменными – для каждого значения x мы получаем y. Выполнив некоторую заданную операцию f, мы отображаем множество всех возможных x на множество y. В качестве функции f мы можем записывать практически любую математическую операцию.

Обычно при построении графиков функций мы пользуемся таблицей, в которой записываем значения х и у. Например, для функции $y=5x^2$ удобно использовать следующую таблицу:

Отметим полученные точки на декартовой системе координат и аккуратно соединим их гладкой кривой. Наша функция не ограничена. Только этими точками мы можем подставить совершенно любое значение х из заданной области определения, то есть тех х, при которых выражение имеет смысл.

На одном из прошлых уроков мы изучили новую операцию извлечения корня квадратного. Возникает вопрос, а можем ли мы, используя эту операцию, задать какую-нибудь функцию и построить ее график? Воспользуемся общим видом функции $y=f(x)$. y и х оставим на своем месте, а вместо f введем операцию корня квадратного: $y=sqrt{x}$.
Зная математическую операцию, мы смогли задать функцию.

Построение графика функции квадратного корня

Давайте построим график этой функции. Исходя из определения корня квадратного, мы можем вычислять его только из неотрицательных чисел, то есть $x≥0$.
Составим таблицу:

Отметим наши точки на координатной плоскости.

Нам осталось аккуратно соединить полученные точки.

Ребята, обратите внимание: если график нашей функции повернуть на бок, то получится левая ветка параболы. На самом деле, если строчки в таблице значений поменять местами (верхнюю строчку с нижней), то у нас получаться значения, как раз для параболы.

Область определения функции $y=sqrt{x}$

Используя график функции, свойства описать довольно таки просто.
1. Область определения: $[0;+∞)$.
2. $у=0$ при $х=0$, $у>0$ при $х>0$.
3. Чем больше х, тем больше у. Значит наша функция возрастает, то есть мы движемся, как будто “в горку”. Функция возрастает на всей области определения.
4. Из графика хорошо видно, что наименьшее значение функции равно 0 при $х=0$. Наибольшего значения нет, функция постоянно растет.
5. Непрерывная функция. Мы не видим ни каких точек разрыва, везде проходит сплошная линия.

Принято выделять еще одно свойство.
Выпуклость. Принято считать, что функции выпуклы либо вверх, либо вниз. Посмотрев на наш график, заметно, что функция как бы выпячивается вверх.
6. Выпукла вверх.

Те значения, которые может принимать y называются “множеством значением функции”. Их также удобно находить по графику. Смотрим область изменения функции по оси ординат. Как изменяется функция: вверх или вниз?
7. Область значений: $[0;+∞)$.

Примеры решения функции квадратного корня

Пример 1.
Найти наибольшее и наименьшее значение функции корня квадратного на отрезке:
а) $[4;9]$.
б) $[2;11]$.

Решение.
Мы можем решить наш пример двумя способами. В каждой букве опишем разные способы.

а) Вернемся к графику функции, построенному выше, и отметим требуемые точки отрезка. Хорошо видно, что при $х=9$ функция больше всех остальных значений. Значит и наибольшее значение она достигает в этой точке. При $х=4$ значение функции ниже всех остальных точек, а значит, тут и есть наименьшее значение.

$y_{наиб}=sqrt{9}=3$, $y_{наим}=sqrt{4}=2$.

б) Мы знаем, что наша функция возрастающая. Значит, каждому большему значению аргумента соответствует большее значение функции. Наибольшее и наименьшее значение достигаются на концах отрезка:

$y_{наиб}=sqrt{11}$, $y_{наим}=sqrt{2}$.

Пример 2.
Решить уравнение:

$sqrt{x}=12-x$.

Решение.
Проще всего построить два графика функции и найти их точку пересечения.

На графике хорошо видна точка пересечения с координатами $(9;3)$. А значит, $х=9$ – решение нашего уравнения.
Ответ: $х=9$.

Ребята, а можем ли мы быть уверены, что больше решений у этого примера нет? Одна из функций возрастает, другая – убывает. В общем случае, они либо не имеют общих точек, либо пересекаются только в одной.

Пример 3.

Построить и прочитать график функции:

$begin {cases} -x, x<0, \ sqrt{x}, 0≤x≤9 \ 12-x, x>9. end {cases}$

Нам нужно построить три частных графика функции, каждый на своем промежутке.

Опишем свойства нашей функции:
1. Область определения: $(-∞;+∞)$.
2. $y=0$ при $х=0$ и $х=12$; $у>0$ при $хϵ(-∞;12)$; $y<0$ при $хϵ(12;+∞)$.
3. Функция убывает на отрезках $(-∞;0)U(9;+∞)$. Функция возрастает на отрезке $(0;9)$.
4. Функция непрерывна на всей области определения.
5. Наибольшего и наименьшего значения нет.
6. Область значений: $(-∞;+∞)$.

Задачи для самостоятельного решения

1. Найти наибольшее и наименьшее значение функции корня квадратного на отрезке:
а) $[25;64]$;
б) $[3;7]$.
2. Решить уравнение: $sqrt{x}=30-x$.
3. Построить и прочитать график функции: $begin {cases} 2-x, x<1, \ sqrt{x}, 1≤x≤4 \ 10-2x, x>4. end {cases}$
4. Построить и прочитать график функции: $y=sqrt{-x}$.

Комментарии преподавателя

На примере 1 рассмотрим, как найти наибольшее и наименьшее значения функции y=√x на отрезке. Возьмем отрезок от единицы до пяти [1; 5].

Решение: Построим график функции y=√x и выделим его часть на отрезке [1; 5].

Замечаем, что yнаим= 1 (при x = 1),

а yнаиб=√5 (при x = 5).

Обратите внимание, на всем отрезке [1;5] функция y=√x возрастает, а если функция возрастает, то при наименьшем (наибольшем) значении x будет достигаться наименьшее (наибольшее) значение функции y. Т.е. графическая иллюстрация была не обязательна при решении этого примера.

Источник конспекта: http://znaika.ru/catalog/8-klass/algebra/Funktsiya-y=√x,-ee-svoystva-i-grafik.

Источник видео: http://www.youtube.com/watch?v=x9tsGGEgKrc

Основные цели:

1) сформировать представление о
целесообразности обобщённого исследования
зависимостей реальных величин на примере
величин, связанных отношением у=

2) формировать способность к построению графика
у= и его
свойства;

3) повторить и закрепить приёмы устных и
письменных вычислений, возведение в квадрат,
извлечение квадратного корня.

Оборудование, демонстрационный материал: раздаточный
материал.

1. Алгоритм:

2. Образец для выполнения задания в группах:

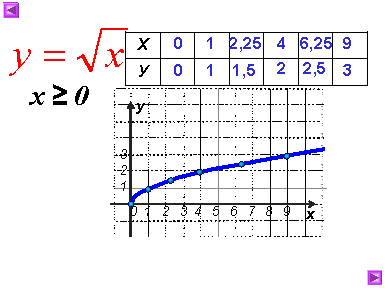
3. Образец для самопроверки самостоятельной
работы:

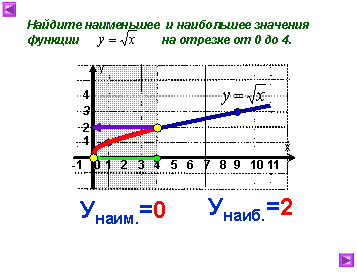
4. Карточка для этапа рефлексии:

1) Я понял, как построить график функции у=.

2) Я могу по графику перечислить его свойства.

3) Я не допустил ошибок в самостоятельной
работе.

4) Я допустил ошибки в самостоятельной работе
(перечислить эти ошибки и указать их причину).

Ход урока

1. Самоопределение к учебной деятельности

Цель этапа:

1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урока:
продолжаем работать с действительными числами.

Организация учебного процесса на этапе 1:

– Что мы изучали на прошлом уроке? (Мы изучали
множество действительных чисел, действия с ними,
построили алгоритм для описания свойств функции,
повторяли функции изученные в 7 классе).

– Сегодня мы продолжим работать с множеством
действительных чисел, функцией.

2. Актуализация знаний и фиксация затруднений в
деятельности

Цель этапа:

1) актуализировать учебное содержание,
необходимое и достаточное для восприятия нового
материала: функция, независимая переменная,
зависимая переменна, графики

y = kx + m, y = kx, y =c, y =x², y = – x² ,

2) актуализировать мыслительные операции,
необходимые и достаточные для восприятия нового
материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и
алгоритмы в виде схем и символов;

4) зафиксировать индивидуальное затруднение в
деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся
знаний.

Организация учебного процесса на этапе 2:

1. Давайте вспомним как можно задать
зависимости между величинами? (С помощью текста,
формулы, таблицы, графика)

2. Что называется функцией? (Зависимость между
двумя величинами, где каждому значению одной
переменной соответствует единственное значение
другой переменной y = f(x)).

Как называется х? (Независимая переменная –
аргумент)

Как называется у? (Зависимая переменная).

3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c,
y =x², y = – x² , ).

Индивидуальное задание:

Что является графиком функций y = kx + m, y =x², y
= ?

3. Выявление причин затруднений и постановка
цели деятельности

Цель этапа:

1) организовать коммуникативное
взаимодействие, в ходе которого выявляется и
фиксируется отличительное свойство задания,
вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

– Что особенного в этом задании? (Зависимость
задана формулой y = с которой мы еще не встречались).

– Какая цель урока? (Познакомиться с функцией y =
, ее
свойствами и графиком. Функцией в таблице
определять вид зависимости, строить формулу и
график.)

– Можно сформулировать тему урока? (Функция у=, ее свойства и
график).

– Запишите тему в тетради.

4. Построение проекта выхода из затруднения

Цель этапа:

1) организовать коммуникативное взаимодействие
для построения нового способа действия,
устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в
знаковой, вербальной форме и с помощью эталона.

Организация учебного процесса на этапе 4:

Работу на этапе можно организовать по группам,
предложив группам построить график y = , затем
проанализировать получившиеся результаты. Также
группам можно предложить по алгоритму описать
свойства данной функции.

5. Первичное закрепление во внешней речи

Цель этапа: зафиксировать изученное
учебное содержание во внешней речи.

Организация учебного процесса на этапе 5:

Постройте график у= – и опишите его свойства.

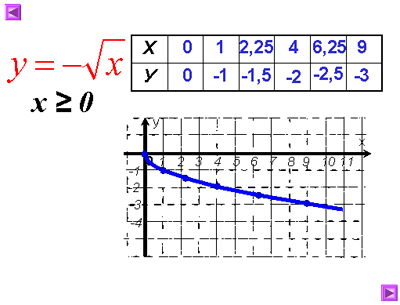
Свойства у= – .

1.Область определения функции.

D(y) =

2.Область значений функции.

E(y) =

3. y = 0, y> 0, y<0.

y =0, если x = 0.

y<0, если х(0;+)

4.Возрастания, убывания функции.

Функция убывает при х [0;+ )

5. Ограниченность функции.

Функция ограничена сверху, и не ограничена
снизу.

6.Наибольшее, наименьшее значения функции.

у _наиб. = нет у _наим. = 0.

7.Непрерывность функции.

Функция непрерывна на все области определения.

№13.2(в)

Используя график функции у=, найдите наименьшее и
наибольшее значения функции на отрезке [1; 9].

Построим график у=.

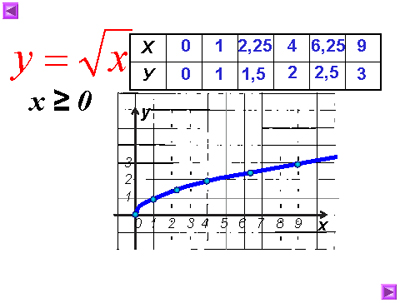
Выделим его часть на отрезке [1;9]. Заметим, что у _наим.
= 1 при х = 1, а у _наиб. =3 при х = 9.

Ответ: у _наим. = 1, у _наиб. =3

6. Самостоятельная работа с самопроверкой по
эталону

Цель этапа: проверить своё умение
применять новое учебное содержание в типовых
условиях на основе сопоставления своего решения
с эталоном для самопроверки.

Организация учебного процесса на этапе 6:

№ 13.1(в)

Учащиеся выполняют задание самостоятельно,
проводят самопроверку по эталону, анализируют,
исправляют ошибки.

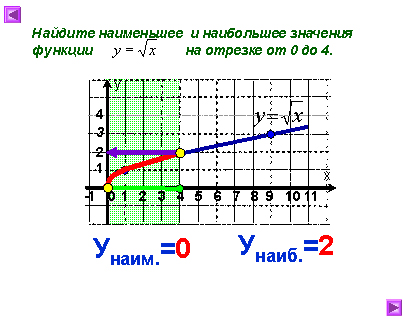
Построим график у=.

С помощью графика найдите наименьшее и
наибольшее значения функции на отрезке [0; 4].

7. Включение в систему знаний и повторение

Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.

Организация учебного процесса на этапе 7:

Решите графически уравнение: = х – 6.

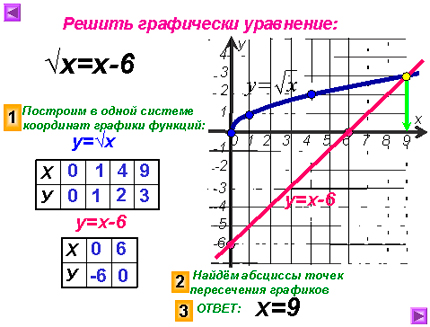
Ответ: 9.

Один ученик у доски остальные в тетрадях.

8. Рефлексия деятельности

Цель этапа:

1) зафиксировать новое содержание, изученное на
уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые
помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как
направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 8:

– Ребята, какая цель стояла сегодня перед нами?
(Изучить функцию у=, ее свойства и график).

– Какие знания нам помогли в достижении цели?
(Умение искать закономерности, умение читать
графики.)

– Проанализируйте свою деятельность на уроке.
(Карточки с рефлексией)

Домашнее задание

п. 13 (до примера 2) № 13.3, 13.4

Решите графически уравнение:

Постройте график функции и опишите его
свойства: