Найдите наименьшее и наибольшее значения линейной функции:
а) y = −2x на полуинтервале [−2;2);
б) y = −2x на луче [0;+∞);
в) y = −2x на отрезке (−∞;1];
г) y = −2x на отрезке (−1;0].
reshalka.com
ГДЗ учебник по алгебре 7 класс Мордкович. §9. Линейная функция y = kx. Номер №9.11.
Решение а
y = −2x на полуинтервале [−2;2).
y
m
i
n
− не существует.
y
m
a
x
=
−
2
∗
(
−
2
)
=
4
Решение б
y = −2x на луче [0;+∞).
y
m
i
n
− не существует.
y
m
a
x
=
−
2
∗
0
=
0
Решение в
y = −2x на отрезке (−∞;1].
y
m
i
n
=
−
2
∗
1
=
−
2
y
m
a
x
− не существует.
Решение г
y = −2x на отрезке (−1;0].
y
m
i
n
=
−
2
∗
0
=
0
y
m
a
x
− не существует.
наибольшее и наименьшее значение функции!?
Мастер
(1292),
закрыт
13 лет назад
Про_хвост
Искусственный Интеллект
(283844)
13 лет назад
А что тут сложного?
Функция ваша парабола, ветви направлены вниз.
Вершина в точке 0 0
Производная от нее будет -Х . Приравниваете 0 получаете 0.
с лева возрастает, с права убывает… значит максимум. функции вообще.
Вот вам и первая критическая точка ( и так видно без всяких производных, но если требуется) и она на полуинтервале (-2; 1] будет максимумом, считаете для -2, то есть находите х при у =-2, вот вам минимум на этом промежутке. Для второго минимум в + бесконечности маскимум снова в 0 0 и для третьего минус бесконечность и опять 0 0.
почитайте тут про экстримумы функции. . Не знаю, на каком уровне вам нужно. С границами сами смотрите. где открыто где что. Или вам нужно решение с оформлением?
Его можно получить алгебраически и геометрически. Точки экстримума, “исследование функции” Но решать ни за кого не решаю, подсказать могу.
12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.
(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).
(blacktriangleright) Основные формулы поиска производной ((f=f(x), g=g(x)) – функции):
1. Умножение функции на число: [(ccdot f)’=ccdot f’]
2. Сумма или разность двух функций: [(fpm g)’=f’pm
g’]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
15
#903
Уровень задания: Сложнее ЕГЭ
Найдите наибольшее на полуинтервале I значение суммы функций (f(x)) и (g(f(x))), если I (= (-4; 2]), (f(t) = t + 1), (g(z) = z^3 – 4z + 1).
(y = f(x) + g(f(x)) = x + 1 + g(x + 1) = x + 1 + (x + 1)^3 – 4(x + 1) + 1 = (x + 1)^3 – 3(x + 1) + 1).
1) (y’ = 3(x + 1)^2 – 3).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3(x + 1)^2 – 3 = 0qquadLeftrightarrowqquad x^2 + 2x = 0,] откуда (x_1 = 0), (x_2 = -2). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
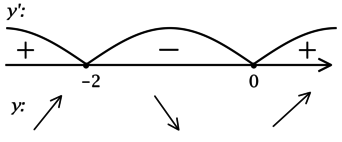
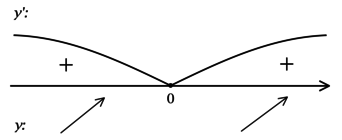
2) Найдём промежутки знакопостоянства (y’):
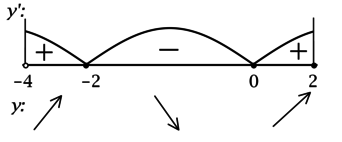
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом полуинтервале ((-4; 2]):
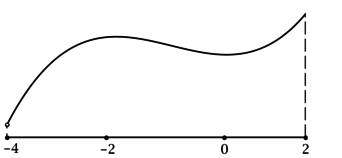
4) Эскиз графика на I:
Таким образом, (x = -2) – точка локального максимума функции (y) и наибольшее на I значение (y) достигает в ней или в (x = 2). Сравним эти значения:
(y(-2) = (-1)^3 – 3cdot(-1) + 1 = 3),
(y(2) = 3^3 – 3cdot 3 + 1 = 19).
Итого: наибольшее на I значение суммы (f(x)) и (g(f(x))) равно (19).
Ответ: 19
Задание
16
#2633
Уровень задания: Сложнее ЕГЭ
Найдите наименьшее значение функции (f(x)=2x^4-2x^3-x^2+2) на отрезке ([-1;1]).
Найдем производную: [y’=8x^3-6x^2-2x]Найдем критические точки: [y’=0 quadLeftrightarrowquad 8x^3-6x^2-2x=0
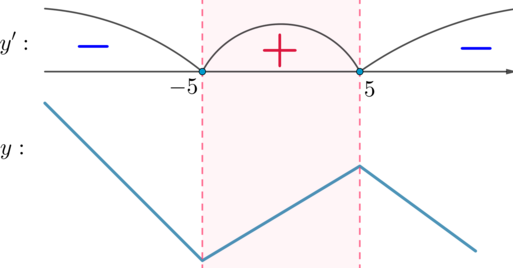
quadLeftrightarrowquad x_1=0, x_2=-frac14 text{и} x_3=1] Определим, какие из данных точек являются точками максимума/минимума, для этого найдем знаки производной на промежутках, образованных этими точками:
Таким образом, (x=0) – точка максимума, (x=-frac14) и (x=1) – точки минимума.
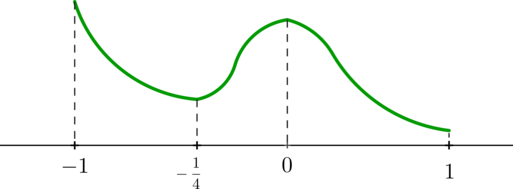
Следовательно, на отрезке ([-1;1]) функция схематично выглядит так:
Следовательно, наименьшее значение она принимает либо в точке (x=-frac14), либо в точке (x=1). Сравним: [begin{aligned}
& fleft(-frac14right)=1frac{125}{128}\[1ex]
&f(1)=1 end{aligned}] Таким образом, наименьшее значение функции на данном отрезке равно (1).
Ответ: 1
Задание
17
#902
Уровень задания: Сложнее ЕГЭ
Найдите наименьшее на отрезке I значение разности функций (f(x)) и (g(x)), если I (= [-5; 5]), (f(t) = t^3 + 12t), (g(z) = 12z – 2).
(y = f(x) – g(x) = (x^3 + 12x) – (12x – 2) = x^3 + 2)
1) (y’ = 3x^2).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 = 0qquadLeftrightarrowqquad x = 0.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
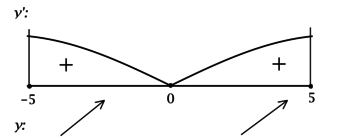
2) Найдём промежутки знакопостоянства (y’):
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-5; 5]):
4) Эскиз графика на отрезке ([-5; 5]):
Таким образом, у функции (y) на отрезке I нет точек экстремума и наименьшее значение на I функция достигает в (x = -5) (так как (y) возрастает на I).
(y(-5) = -125 + 2 = -123).
Итого: наименьшее значение разности (f(x)) и (g(x)) на I равно (-123).
Ответ: -123
Задание
18
#4026
Уровень задания: Легче ЕГЭ
Найдите наименьшее значение функции (y=13+75x-x^3) на отрезке ([-5;5]).
Для того, чтобы найти наименьшее значение функции на отрезке, нужно схематично изобразить график функции на этом отрезке.
1) Найдем производную. [y’=75-3x^2]
2) Найдем нули производной: [75-3x^2=0quadRightarrowquad x=pm 5]
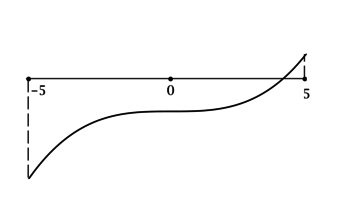
3) Найдем знаки производной на получившихся промежутках и изобразим схематично график функции:
Таким образом, мы видим, что на отрезке ([-5;5]) функция (y) возрастает, следовательно, наименьшее значение на этом отрезке она принимает в точке (x=-5). Тогда [y(-5)=13-5cdot 75+5^3=-237]
Ответ:
-237

УСТАЛ? Просто отдохни