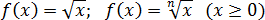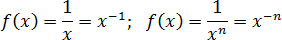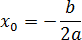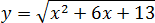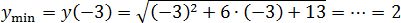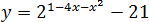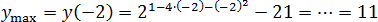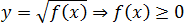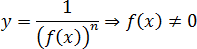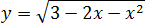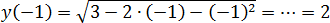Как найти наибольшее значение функции парабола

Была ли эта статья полезной?

Как решать задачи B15 без производных

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Другими словами, для возрастающей функции Для убывающей функции все наоборот:

Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:

f ( x ) = log _a x ( a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только

f ( x ) = a x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы и найти ее вершину по формуле:
2. Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент

x ₀ = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.

Корень монотонно возрастает, значит точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,

x ₀ = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1

Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:

y _min = y (−1) = log ₂ ((−1) 2 + 2 · (−1) + 9) = . = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

В показателе стоит квадратичная функция Перепишем ее в нормальном виде:

Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

Аргумент логарифма должен быть положительным:

y = log _a f ( x ) ⇒ f ( x ) > 0

Арифметический квадратный корень существует только из неотрицательных чисел:

Знаменатель дроби не должен равняться нулю:

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒

Теперь найдем вершину параболы:

Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:

Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x ₀ = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только

y _min = y (3) = log _0,5 (6 · 3 − 3 2 − 5) =

Наибольшее и наименьшее значение функции

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал ( a ; b ) , ( a ; b ] , [ a ; b ) , бесконечный интервал ( a ; b ) , ( a ; b ] , [ a ; b ) либо бесконечный промежуток – ∞ ; a , ( – ∞ ; a ] , [ a ; + ∞ ) , ( – ∞ ; + ∞ ) .

В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f ( x ) .

Основные определения

Начнем, как всегда, с формулировки основных определений.

Наибольшее значение функции y = f ( x ) на некотором промежутке x – это значение m a x y = f ( x 0 ) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f ( x ) ≤ f ( x 0 ) .

Наименьшее значение функции y = f ( x ) на некотором промежутке x – это значение m i n x ∈ X y = f ( x 0 ) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f ( x ) ≥ f ( x 0 ) .

Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .

Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .

Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.

Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения ( m a x y и m i n y ) в стационарных точках, расположенных на отрезке [ – 6 ; 6 ] .

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ – 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.

Наибольшее и наименьшее значение функции на открытом интервале

Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале ( – 6 ; 6 ) .

Если мы возьмем интервал [ 1 ; 6 ) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .

На графике 6 наименьшее значение данная функция приобретает в правой границе интервала ( – 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.

Наибольшее и наименьшее значение функции на бесконечности

На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .

Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.

1. Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
2. Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
3. Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
4. Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .
5. 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.

Посмотрим, как правильно применить этот алгоритм при решении задач.

Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ – 4 ; – 1 ] .

Решение:

Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D ( y ) : x ∈ ( – ∞ ; 0 ) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:

y ‘ = x 3 + 4 x 2 ‘ = x 3 + 4 ‘ · x 2 – x 3 + 4 · x 2 ‘ x 4 = = 3 x 2 · x 2 – ( x 3 – 4 ) · 2 x x 4 = x 3 – 8 x 3

Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ – 4 ; – 1 ] .

Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 – 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .

Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4 :

y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4

Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 – при x = 2 .

Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:

y ( – 1 ) = ( – 1 ) 3 + 4 ( – 1 ) 2 = 3

Значит, m a x y x ∈ [ – 4 ; – 1 ] = y ( – 1 ) = 3 , m i n y x ∈ [ – 4 ; – 1 ] = y ( – 4 ) = – 3 3 4 .

Ответ: Для отрезка [ 1 ; 4 ] – m a x y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , m i n y x ∈ [ 1 ; 4 ] = y ( 2 ) = 3 , для отрезка [ – 4 ; – 1 ] – m a x y x ∈ [ – 4 ; – 1 ] = y ( – 1 ) = 3 , m i n y x ∈ [ – 4 ; – 1 ] = y ( – 4 ) = – 3 3 4 .

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.

• Если интервал имеет вид [ a ; b ) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b – 0 f ( x ) .
• Если интервал имеет вид ( a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f ( x ) .
• Если интервал имеет вид ( a ; b ) , то нам надо вычислить односторонние пределы lim x → b – 0 f ( x ) , lim x → a + 0 f ( x ) .
• Если интервал имеет вид [ a ; + ∞ ) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f ( x ) .
• Если интервал выглядит как ( – ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → – ∞ f ( x ) .
• Если – ∞ ; b , то считаем односторонний предел lim x → b – 0 f ( x ) и предел на минус бесконечности lim x → – ∞ f ( x )
• Если же – ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f ( x ) , lim x → – ∞ f ( x ) .

1. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 – 8 в первой части материала.

Пример 2

Условие: дана функция y = 3 e 1 x 2 + x – 6 – 4 . Вычислите ее наибольшее и наименьшее значение в интервалах – ∞ ; – 4 , – ∞ ; – 3 , ( – 3 ; 1 ] , ( – 3 ; 2 ) , [ 1 ; 2 ) , 2 ; + ∞ , [ 4 ; + ∞ ) .

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :

x 2 + x – 6 = 0 D = 1 2 – 4 · 1 · ( – 6 ) = 25 x 1 = – 1 – 5 2 = – 3 x 2 = – 1 + 5 2 = 2 ⇒ D ( y ) : x ∈ ( – ∞ ; – 3 ) ∪ ( – 3 ; 2 ) ∪ ( 2 ; + ∞ )

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

y ‘ = 3 e 1 x 2 + x – 6 – 4 ‘ = 3 · e 1 x 2 + x – 6 ‘ = 3 · e 1 x 2 + x – 6 · 1 x 2 + x – 6 ‘ = = 3 · e 1 x 2 + x – 6 · 1 ‘ · x 2 + x – 6 – 1 · x 2 + x – 6 ‘ ( x 2 + x – 6 ) 2 = – 3 · ( 2 x + 1 ) · e 1 x 2 + x – 6 x 2 + x – 6 2

Следовательно, производные функции существуют на всей области ее определения.

Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = – 1 2 . Это стационарная точка, которая находится в интервалах ( – 3 ; 1 ] и ( – 3 ; 2 ) .

Вычислим значение функции при x = – 4 для промежутка ( – ∞ ; – 4 ] , а также предел на минус бесконечности:

y ( – 4 ) = 3 e 1 ( – 4 ) 2 + ( – 4 ) – 6 – 4 = 3 e 1 6 – 4 ≈ – 0 . 456 lim x → – ∞ 3 e 1 x 2 + x – 6 = 3 e 0 – 4 = – 1

Поскольку 3 e 1 6 – 4 > – 1 , значит, m a x y x ∈ ( – ∞ ; – 4 ] = y ( – 4 ) = 3 e 1 6 – 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение – 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.

Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к – 3 с левой стороны, мы получим только интервал значений:

lim x → – 3 – 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 – 0 3 e 1 ( x + 3 ) ( x – 3 ) – 4 = 3 e 1 ( – 3 – 0 + 3 ) ( – 3 – 0 – 2 ) – 4 = = 3 e 1 ( + 0 ) – 4 = 3 e + ∞ – 4 = + ∞ lim x → – ∞ 3 e 1 x 2 + x – 6 – 4 = 3 e 0 – 4 = – 1

Значит, значения функции будут расположены в интервале – 1 ; + ∞

Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = – 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к – 3 с правой стороны:

y – 1 2 = 3 e 1 – 1 2 2 + – 1 2 – 6 – 4 = 3 e 4 25 – 4 ≈ – 1 . 444 y ( 1 ) = 3 e 1 1 2 + 1 – 6 – 4 ≈ – 1 . 644 lim x → – 3 + 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 + 0 3 e 1 ( x + 3 ) ( x – 2 ) – 4 = 3 e 1 – 3 + 0 + 3 ( – 3 + 0 – 2 ) – 4 = = 3 e 1 ( – 0 ) – 4 = 3 e – ∞ – 4 = 3 · 0 – 4 = – 4

У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ ( 3 ; 1 ] = y – 1 2 = 3 e – 4 25 – 4 . Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до – 4 .

Для интервала ( – 3 ; 2 ) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:

y – 1 2 = 3 e 1 – 1 2 2 + – 1 2 – 6 – 4 = 3 e – 4 25 – 4 ≈ – 1 . 444 lim x → – 3 + 0 3 e 1 x 2 + x – 6 – 4 = – 4 lim x → 2 – 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 + 0 3 e 1 ( x + 3 ) ( x – 2 ) – 4 = 3 e 1 ( 2 – 0 + 3 ) ( 2 – 0 – 2 ) – 4 = = 3 e 1 – 0 – 4 = 3 e – ∞ – 4 = 3 · 0 – 4 = – 4

Значит, m a x y x ∈ ( – 3 ; 2 ) = y – 1 2 = 3 e – 4 25 – 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом – 4 .

Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2 ) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.

На промежутке ( 2 ; + ∞ ) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка – 1 ; + ∞ .

lim x → 2 + 0 3 e 1 x 2 + x – 6 – 4 = lim x → – 3 + 0 3 e 1 ( x + 3 ) ( x – 2 ) – 4 = 3 e 1 ( 2 + 0 + 3 ) ( 2 + 0 – 2 ) – 4 = = 3 e 1 ( + 0 ) – 4 = 3 e + ∞ – 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x – 6 – 4 = 3 e 0 – 4 = – 1

Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞ ) = y ( 4 ) = 3 e 1 14 – 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = – 1 .

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции (f'(x)).
2. Найдите корни уравнения (f'(x)=0).
3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
4. Определите знак производной в каждом промежутке (методом интервалов).
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   – если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
   – если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
   – если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/funktsii/naibolshee-i-naimenshee-znachenie-funktsii/

http://cos-cos.ru/math/327/

[/spoiler]

Решение задач на нахождение наибольших и наименьших значений

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Квадратичная функция

Часто квадратичную функцию применяют при решении различных задач, которые сводятся к нахождению тех или иных наибольших или наименьших значений. Но перед рассмотрением таких задач стоит напомнить, какая функция является квадратичной и как найти наибольшее/наименьшее значение.

Определение 1

Функция, имеющая вид $y=ax^2+bx+c$, где $a$ не равняется нулю, называется квадратичной функцией.

График такой функции принято называть параболой. Отметим, что если $a >0$ то ее ветви будут направлены вверх и ее вершина будет принимать минимальное значение, а если $a

Наибольшее и наименьшее значение

Определение 2

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x’in X$, если выполняется

[fleft(xright)le f(x’)]

Определение 3

Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x’in X$, если выполняется

[fleft(xright)ge f(x’)]

Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:

1. Найти $f'(x)$;
2. Найти точки, в которых $f’left(xright)=0$;
3. Найти точки, в которых $f'(x)$ не будет существовать;
4. Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
5. Вычислить значения в оставшихся точках и на концах $[a,b]$;
6. Выбрать из этих значений наибольшее и наименьшее.

Приведем пример на нахождение наибольшего и наименьшего значения функции.

Пример 1

Найти наибольшее и наименьшее значения на [0,6]:$fleft(xright)=x^3-3x^2-45x+225$

Решение.

1. $f’left(xright)=3x^2-6x-45$;

2. $f’left(xright)=0$;

   [3x^2-6x-45=0] [x^2-2x-15=0] [x=5, x=-3]

3. $f'(x)$ существует на всей $D(f)$;

4. $5in left[0,6right]$;

5. Значения:

   [fleft(0right)=225] [fleft(5right)=50] [fleft(6right)=63]

6. Наибольшее значение равняется $225$, наименьшее равняется $50.$

Ответ: $max=225, min=50$.

«Решение задач на нахождение наибольших и наименьших значений» 👇

Рассмотрим далее задачи на использование наибольшего и наименьшего значений квадратичной функции.

Примеры задач

Пример 2

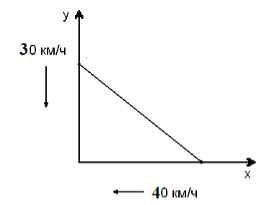
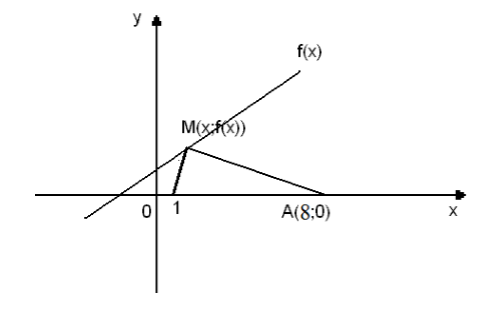
По перекрестным дорогам движутся два автомобиля в сторону перекрестка. Каждому автомобилю до перекрестка ехать по $50$ км. Автомобили движутся со скоростями $30$ и $40$ км/ч, соответственно. Найти, когда автомобили будут друг от друга на наименьшем расстоянии и на каком.

Решение.

Изобразим ситуацию на рисунке (рис. 1).

Рисунок 1.

Пусть наименьшее расстояние между автомобилями будет в момент времени $t$.

В это время одному автомобилю до перекрестка остается ехать

[50-30t км]

А второму

[50-40t км]

Расстояние между ними, по теореме Пифагора, будет равняться

[Sleft(tright)={(50-30t)}^2+{(50-40t)}^2=2500-3000t+{900t}^2+2500-4000t+{1600t}^2={2500t}^2-7000t+5000]

Найдем наименьшее значение такой функции

[t=-frac{b}{2a}=-frac{-7000}{5000}=frac{7}{5}=1,4] [Sleft(tright)=2500cdot frac{49}{25}-7000cdot frac{7}{5}+5000=4900-9800+5000=100]

Ответ: $1$ ч $24$ мин, $100$ км.

Пример 3

Найти на графике функции $y=x+2$ точку, которая дает наименьшую сумму квадратов расстояний от него до точки $(8,0)$ и $(1,0)$.

Решение.

Рассмотрим рисунок:

Рисунок 2.

Обозначим абсциссу искомой точки через $x$. Точка искомая точка имеет вид $(x,x+1)$.

Найдем расстояние до точки $(8,0)$: $sqrt{{(8-x)}^2+{(x+1)}^2}$

Найдем расстояние до точки $(1,0)$: $sqrt{{(1-x)}^2+{(x+1)}^2}$

Получаем, сумма равна

[Sleft(xright)={(8-x)}^2+{(x+1)}^2+{(1-x)}^2+{(x+1)}^2=64-16x+x^2+1+2x+x^2+1-2x+x^2+1+2x+x^2=4x^2+18x+67]

Наименьшее значение

[x=-frac{18}{8}=-frac{9}{4}=-2,25] [y=frac{81}{4}-frac{162}{4}+frac{268}{4}=frac{187}{4}=46,75]

Ответ: $(-2,25;46,75)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 13.07.2022