Как найти наибольшее значение интеграла

Нахождение наибольших и наименьших значений.

Пусть функция u
= f (x₁
, x₂ ,…,
x_n)
определена и непрерывна в некотором
ограниченном и замкнутом множестве D
и имеет на этом множестве конечные
частные производные (за исключением,
быть может, отдельных точек). Тогда эта
функция достигает на D
своего наибольшего и наименьшего
значения (см. свойства непрерывных
функций). Если это значение достигается
во внутренней точке множества, то,
очевидно, эта точка должна быть
стационарной; кроме того, наибольшее и
наименьшее значение может достигаться
на границе множества D.
Поэтому для определения наибольшего и
наименьшего значений функции на множестве
D требуется:

1. найти стационарные точки функции,
   принадлежащие D, и
   вычислить значения функции в этих
   точках;

2. найти наибольшее и наименьшее значение,
   принимаемое функцией на границе
   множества D;

3. выбрать наименьшее и наибольшее из
   полученных чисел, которые и будут
   являться наименьшим и наибольшим
   значениями функции на всем множестве
   D.

Примеры.

1. Найдем наибольшее значение функции
   z = sin
   x + sin
   y – sin
   (x + y)
   в треугольнике со сторонами х = 0,
   у = 0, х + у = 2π. Стационарные точки
   определяются из решения системы,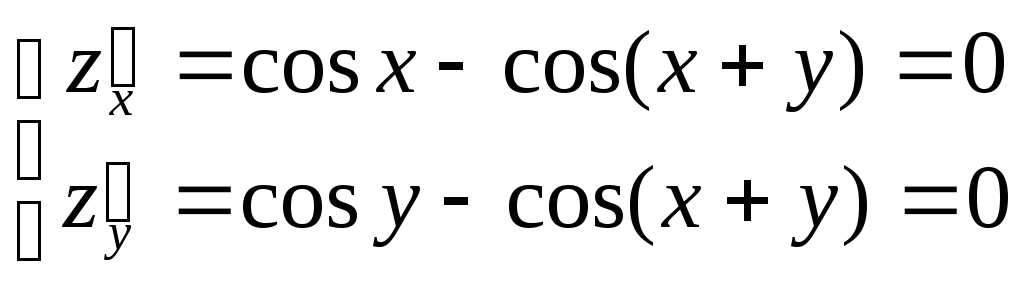
   откуда
   .
   Единственной внутренней точкой данного
   треугольника, являющейся решением
   полученной системы, будет
   ,
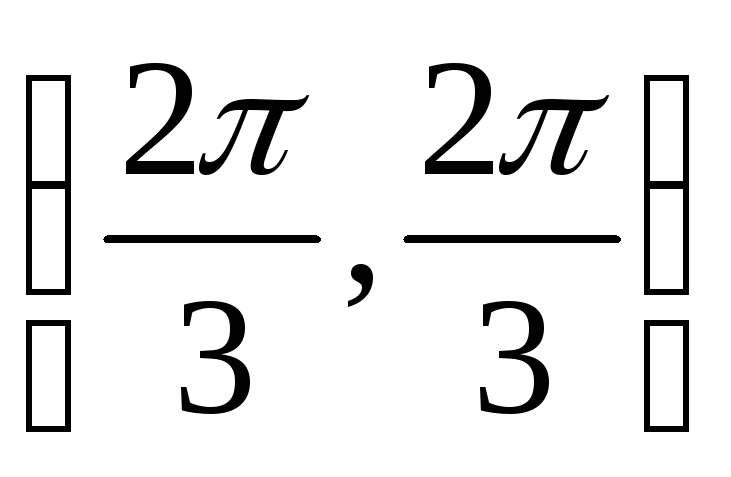   в которой
   .
   Это значение оказывается наибольшим
   и на всем рассматриваемом множестве,
   так как на его границе z
   = 0.

2. Найдем наибольшее и наименьшее значения
   функции z = x²
   + y² – 12x
   + 16y в области x²
   + y² ≤ 25.
   ,
   откуда х =6, у = -8 – точка, не
   лежащая в заданном круге. Следовательно,
   наибольшее и наименьшее значения
   данная функция принимает на границе
   области, то есть на окружности x²
   + y² = 25. Составим
   функцию Лагранжа
   L (x,
   y ) = x²
   + y² – 12x
   + 16y + λ (x²
   + y² – 25). Ее стационарные
   точки найдем из системы.
   Получим
   ,
   откуда λ₁ =1, λ₂
   = -3. Следовательно, стационарными
   точками являются (3, -4) и (-3, 4). В первой
   из них z = -75, во
   второй z = 125. Эти
   числа являются наименьшим и наибольшим
   значениями z в заданной
   области.

Лекция 6.

Первообразная. Неопределенный интеграл и его свойства. Табличные интегралы. Замена переменной и интегрирование по частям в неопределенном интеграле.

Определение 6.1. Функция F(x)
называется первообразной (для)
функции f(x)
на некотором множестве значений х,
если F΄(x)
= f(x)
на этом множестве.

Теорема 6.1. Если функции F(x)
и G(x)
являются первообразными одной и той же
функции f(x)
на некотором множестве, то необходимым
и достаточным условием этого является
то, что G(x)
= F(x)
+ C, где С – любая
постоянная.

Доказательство.

1. Пусть F(x)
   – первообразная f(x),
   то есть F΄(x)
   = f(x).
   Тогда для любого числа C
   (F(x)
   + C)΄=
   F΄(x)
   + C΄= F΄(x)
   + 0 = f(x),
   то есть F(x)
   + C – первообразная
   f(x).

2. Пусть F(x)
   и G(x)
   – две различные первообразные одной
   и той же функции f(x).
   Тогда (F(x)
   – G(x))΄=
   F΄(x)
   – G΄(x)
   = f(x)
   – f(x)
   = 0, следовательно, F(x)
   – G(x)
   = C (по следствию из
   теоремы Лагранжа). Теорема доказана.

Таким образом, если функция на данном
множестве имеет одну первообразную, то
она имеет их бесконечно много, причем
все они отличаются друг от друга
постоянными слагаемыми.

Определение 5.2. Совокупность всех
первообразных функции f(x)
на некотором множестве называется ее
неопределенным интегралом.

Обозначение:

.

f(x)
при этом называется подынтегральной
функцией, а f(x)dx
– подынтегральным выражением.

Свойства неопределенного интеграла.

1.

2.

3.

Действительно,

а
.
Но, поскольку С₁+С₂
– произвольная постоянная, выражения
в левой и правой частях равны.

4.

Замечание. Все перечисленные свойства
формулировались и доказывались в
предположении, что на некотором множестве
существуют первообразные функций f(x)
и g(x),
равные соответственно F(x)
и G(x).

Табличные интегралы.

Из определения первообразной и
неопределенного интеграла следует, что
таблицу основных интегралов можно
получить из таблицы основных производных
(см. лекцию 18 первой части курса), считая
производные табличных функций
подынтегральными функциями, а сами
функции – их первообразными.

1.

2.

3.

3΄)

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

Можно добавить к этой таблице еще
несколько формул, не следующих
непосредственно из таблицы производных,
но удобных для вычисления многих
интегралов, а именно:

14.

15.

Доказательство справедливости этих
формул предлагается провести
самостоятельно.

Примеры.

1.

2.

Соседние файлы в папке Лекции

• #
• #

  13.06.20141.98 Mб40Курс лекций – Вычислительная математика.doc

• #
• #

Макеты страниц

     Оценка интеграла. Теорема о среднем. Среднее значение функции.

     1. Оценка интеграла. Укажем границы, между которыми наверняка заключено значение интеграла.

     Теорема об оценке опеределенного интеграла. Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е.

где (M) и (m) – соответственно наибольшее и наименьшее значения функции (f(x)) в интервале ([a,b]): $$mleq f(x)leq M.$$

     Доказательство. Возьмем две функции (M-f(x)) и (m-f(x)). Первая из них в интервале ([a,b]) неотрицательна, вторая неположительна. Значит по теореме о знаке интеграла

Применяя теоремы из пункта простейших свойств определенного интеграла и формулу (int_{a}^{b}{dx}=b-a), получим

что и требовалось доказать. Из доказательства теоремы о знаке интеграла следует, что знаки неравенств могут перейти в знаки равенств только в том случае, когда функция (f(x)) постоянна.

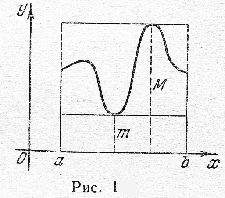
     Геометрический смысл доказанных неравенств таков: площадь криволинейной трапеции больше площади прямоугольника с основанием, равным основанию трапеции, и высотой, равной наименьшей ординате трапеции, и меньше площади прямоугольника с тем же основанием и высотой, равной наибольшей ординате трапеции (рис. 1).

     Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.

     Указанные в теореме об оценке определенного интеграла границы для интеграла тем более точны, чем короче интервал интегрирования и чем меньше линия (y=f(x)) отличается по положению от прямой, параллельной оси (Ox).

     Пример 1. Оценим интеграл $$int_{0}^{2}{frac{5-x}{9-x^{2}}dx}.$$

Известными методами дифференциального исчисления находим, что наибольшее и наименьшее значения подынтегральной функции в интервале ([0, 2]) равны соответственно (0,6) и (0,5). Значит, $$0,5(2-0)<int_{0}^{2}{frac{5-x}{9-x^{2}}dx}<0,6(2-0)$$

т.е. интеграл заключен между (1) и (1,2). Если считать, что он равен (1,1), то предельная абсолютная ошибка равна (0,1), а относительная (frac{0,1cdot 100}{1,1}approx 9%).

     Пример 2. Оценим интеграл $$int_{frac{pi }{4}}^{frac{pi }{2}}{frac{sin x}{x}dx}.$$

     Легко проверить, что подынтегральная функция в интервале ([frac{pi }{4}, frac{pi }{2}]) убывает и, следовательно, $$frac{sin frac{pi }{2}}{frac{pi }{2}}cdot frac{pi }{4}<int_{frac{pi }{4}}^{frac{pi }{2}}{frac{sin x}{x}dx}<frac{sin frac{pi }{4}}{frac{pi }{4}}cdot frac{pi }{4},$$

т.е. $$frac{1}{2}<int_{frac{pi }{4}}^{frac{pi }{2}}{frac{sin x}{x}dx}<frac{1}{2}sqrt{2}.$$

     Таким образом, интеграл заключен между (0,5) и (0,71), что дает нам право считать его равным (0,6) с точностью до (0,1). Более точные приемы показывают, что приближенно он равен (0,62).

     Оценка интеграла. Теорема о среднем. Среднее значение функции.
Продолжение здесь

2012-11-05 • Просмотров [ 62545 ]

5.
Оценка интеграла. Теорема о среднем
Укажем границы, между которыми наверняка заключено значение интеграла.
Теорема 7. (об
оценке
определенного
интеграла).
Значение
определенного
интеграла заключено между произведениями наименьшего и наибольшего значений
подынтегральной функции на длину интервала интегрирования, т. е.
Z b
m(b − a) ≤
f (x)dx ≤ M (b − a), a < b,
a
где m и M — соответственно наименьшее и наибольшее значения функции f (x) в
интервале [а,b]:
m ≤ f (x) ≤ M.
Доказательство. Возьмем две функции M − f (x) и m − f (x) . Первая из них в
интервале [a, b] неотрицательна, вторая неположительна. Значит, по теореме 6
Z b
Z b
[M − f (x)]dx ≥ 0,
[m − f ()]dx ≤ 0.
a
a
Применяя теоремы п. 3 и формулу
Rb
dx = b − a , получим
a
Z
Z
b
M (b − a) ≥
b
f (x)dx и m(b − a) ≤
a
f (x)dx.
a
что и требовалось доказать. Из доказательства теоремы 6 следует, что если только
функция f (x) не постоянная, то нестрогие неравенства можно заменить на строгие:
Z b
m(b − a) <
f (x)dx < M (b − a).
a
Находя границы для интеграла, мы, как говорят, производим его оценку. Может
случиться, что весьма трудно или даже невозможно найти точное значение интеграла,
а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода
оценками приходится довольно часто встречаться в математике.
Указанные в теореме 7 границы для интеграла тем более точны, чем короче интервал
интегрирования и чем меньше линия y = f (x) отличается по положению от прямой,
параллельной оси Ox .
Пример 1. Оценим интеграл
Z 2
5−x
dx.
2
0 9−x
Известными методами дифференциального исчисления находим, что наибольшее и
наименьшее значения подынтегральной функции в интервале [0,2] равны соответственно
y(2) = 0, 6 и y(2) = 0, 5 . Значит,
Z 2
5−x
dx < 0, 6(2 − 0),
0, 5(2 − 0) <
2
0 9−x
1
т. е. интеграл заключен между 1 и 1,2. Если считать, что он равен 1,1, то предельная
абсолютная ошибка равна 0,1, а относительная — 9%. Позже мы сумеем найти точное
значение приведенного интеграла. Оно равно 4/3 · ln 5 − ln 3 ≈ 1, 047 .
Пример 2. Оценим интеграл
Z π/2
sin x
dx.
x
π/4
Легко проверить, что подынтегральная функция в интервале [π/4, π/2] убывает и,
следовательно,
Z π/2
sin(π/2) π
sin x
sin(π/4) π
<
dx <
π/2 4
x
π/4 4
π/4
т. е.
√
Z π/2
1
sin x
2
<
dx <
.
2
x
2
π/4
Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его
равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он
равен 0,62.
Обобщение теоремы об оценке интеграла.
Интегрирование неравенств
Справедлива следующая более общая теорема, чем теорема 7.
Теорема 8. Если в каждой точке x интервала [a, b]
ψ(x) ≤ f (x) ≤ φ(x),
то
Z
Z
b
ψ(x)dx ≤
a
Z
b
b
f (x)dx ≤
a
φ(x)dx.
a
Это значит, что неравенство между функциями влечет неравенство того же
смысла между их определенными интегралами, или, говоря коротко, неравенства
можно интегрировать. Понятно хотя бы из простых геометрических соображений, что
дифференцирование неравенства может привести к нелепым результатам.
Доказательство теоремы немедленно следует из применения к неравенствам f (x) −
φ() ≤ 0 и f (x)−ψ(x) ≥ 0 теоремы 7 о знаке интеграла. Опять-таки знак равенства между
интегралами возможен только тогда, когда функции тождественно равны между собой.
В частном случае, когда φ(x) тождественно равно M , а ψ(x) тождественно равно
m , получаем теорему 7.
С помощью теоремы 8 легко получается важное неравенство, которым мы
воспользуемся в дальнейшем. При любом x
−|f (x)| ≤ f (x) ≤ |f (x)|.
(Если f (x) > 0 , то правая часть неравенства превращается в равенство, а левая часть
очевидна; если f (x) < 0 , то наоборот.) Тогда
Z b
Z b
Z b
−
|f (x)|dx ≤
f (x)dx ≤
|f (x)|dx,
a
a
a
2
или
Z
Z
b
|
b
f (x)dx| ≤
a
|f (x)|dx.
a
Модуль интеграла не превосходит интеграла от модуля функции. Предоставляем
читателю выяснить геометрический смысл этого неравенства. Напомним еще, что
аналогичное неравенство имеет место и для сумм: модуль суммы не превосходит суммы
модулей.
Теорема о среднем
Определенный интеграл обладает следующим важным свойством.
Теорема 9. (о среднем). Пусть функция f (x) непрерывна в замкнутом интервале [а,b].
Тогда внутри этого интервала существует хотя бы одно значение x = ξ , для которого
Rb
f (x)dx
a
= f (ξ).
(1)
b−a
Доказательство. Если функция f (x) постоянная, то формула (1) очевидна, причем
ξ — любая точка интервала [а,b]. Пусть теперь f (x) не постоянная, тогда в силу теоремы 7
имеем
Rb
f (x)dx
m< a
< M,
b−a
и, значит,
Rb
f (x)dx
a
= µ,
b−a
где µ — некоторое число, заключенное между наименьшим (m) и наибольшим (M )
значениями функции f (x) в интервале [a, b] .
В силу свойств непрерывных функций функция f (x) в каких-то двух точках
интервала [a, b] принимает значения m и и в какой-то точке, лежащей между ними,
принимает промежуточное значение µ . Значит, существует точка ξ ∈ (a, b) , в которой
f (ξ) = µ . Теорема доказана.
Из равенства (1) находим
Z
b
f (x)dx = f (ξ)(b − a), ξ ∈ (a, b).
a
Эта формула позволяет теорему о среднем сформулировать в такой форме:
Определенный интеграл от непрерывной функции равен произведению значения этой
функции в некоторой промежуточной точке интервала интегрирования на длину
интервала.
Среднее арифметическое значение функции
Определение 1. Средним арифметическим значением непрерывной функции y =
f (x) в интервале [а,b] называется отношение определенного интеграла от этой
функции к длине интервала:
Rb
f (x)dx
.
yc = a
b−a
3
На основании теоремы о среднем заключаем, что yc = f (ξ) , где ξ ∈ (a, b) . Среднее
значение непрерывной функции в замкнутом интервале всегда (если только функция не
постоянная) меньше некоторых ее значений, больше других ее значений и равно хотя бы
одному ее значению.
Понятие среднего значения функции очень употребительно в технике. Многие
величины часто характеризуются своими средними значениями, например: давление пара,
мощность переменного тока, скорость химической реакции и т. п.
4

Пусть на отрезке [a, b] задана непрерывная функция f(x).

y

M

m

0 a xi b x

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]

Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

X0 < x1 < x2 < … < xn

Тогда x1 – x0 = Dx1, x2 – x1 = Dx2, … ,xn – xn-1 = Dxn;

На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.

[x0, x1] ® m1, M1; [x1, x2] ® m2, M2; … [xn-1, xn] ® mn, Mn.

Составим суммы:

N = m1Dx1 + m2Dx2 + … +mnDxn =

N = M1Dx1 + M2Dx2 + … + MnDxn =

Сумма называется Нижней интегральной суммой, а сумма – Верхней интегральной суммой.

Т. к. mi £ Mi, то N £ N, а m(b – a) £ N £ N £ M(b – a)

Внутри каждого отрезка выберем некоторую точку e.

X0 < e1 < x1, x1 < e < x2, … , xn-1 < e < xn.

Найдем значения функции в этих точках и составим выражение, которое называется Интегральной суммой для функции f(x) на отрезке [a, b].

Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn =

Тогда можно записать: MiDXi £ F(EI)DXi £ MiDXi

Следовательно,

Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.

Обозначим MaxDXi – наибольший отрезок разбиения, а MinDXi – наименьший. Если MaxDXi® 0, То число отрезков разбиения отрезка [a, b] стремится к бесконечности.

Если , то

Определение: Если при любых разбиениях отрезка [a, b] таких, что MaxDXi® 0 и произвольном выборе точек ei интегральная сумма стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].

Обозначение :

А – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Определение: Если для функции f(x) существует предел то функция называется Интегрируемой на отрезке [a, b].

Также верны утверждения:

Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.