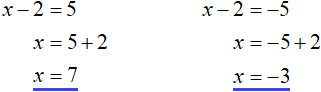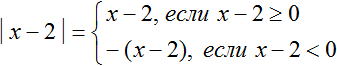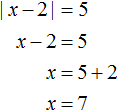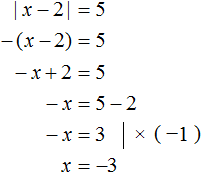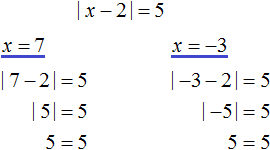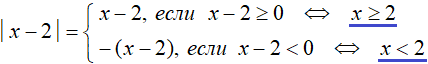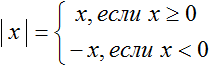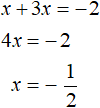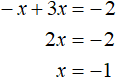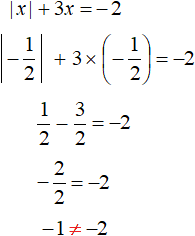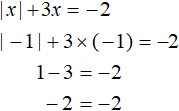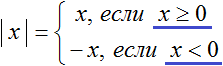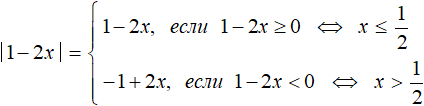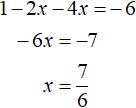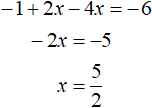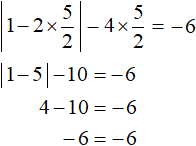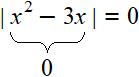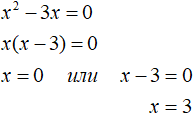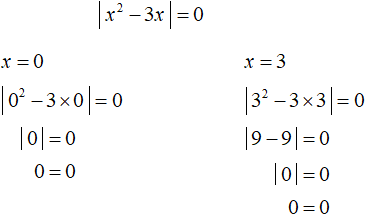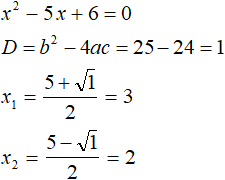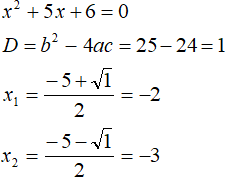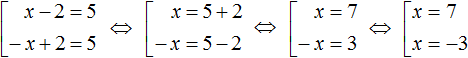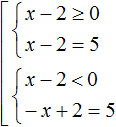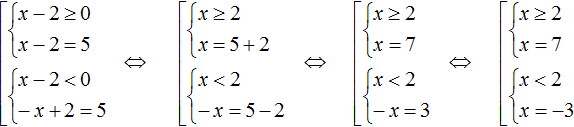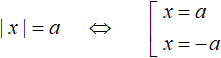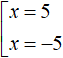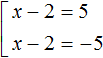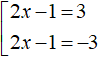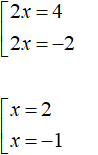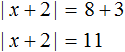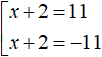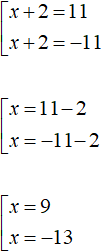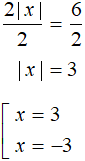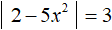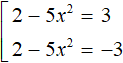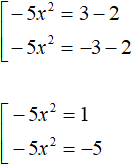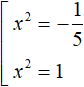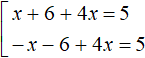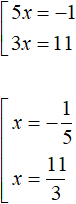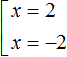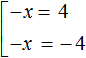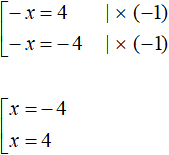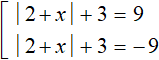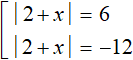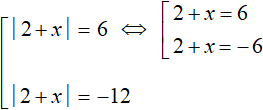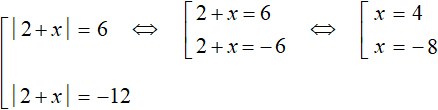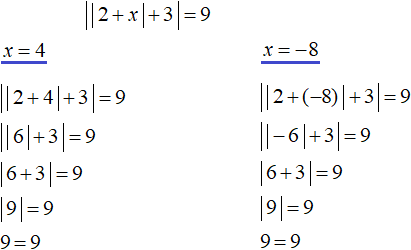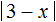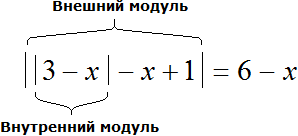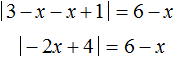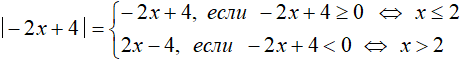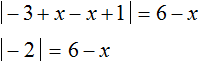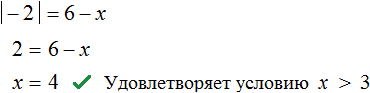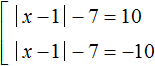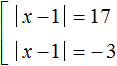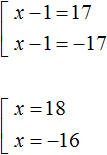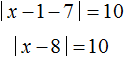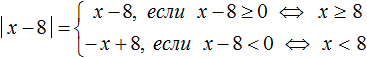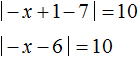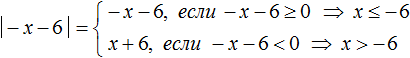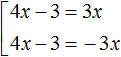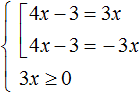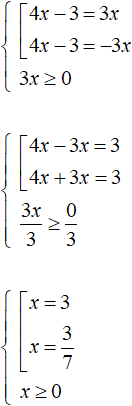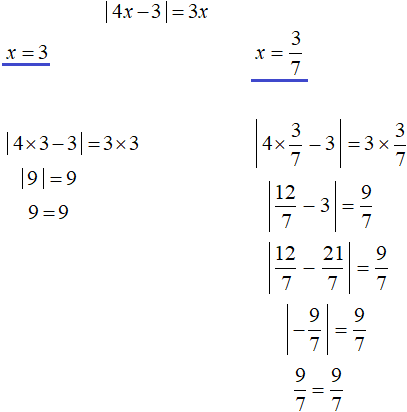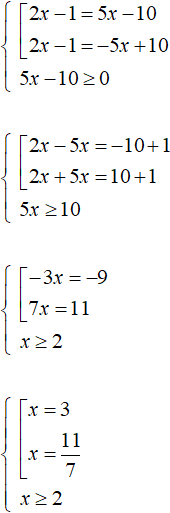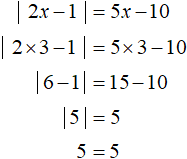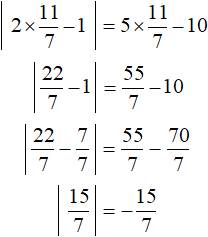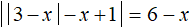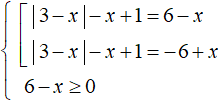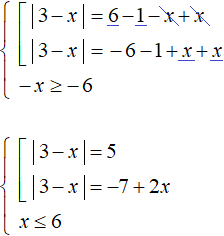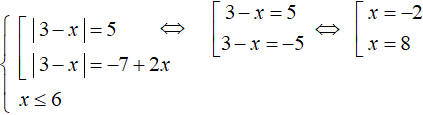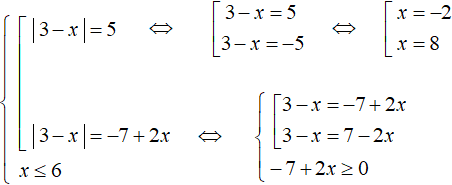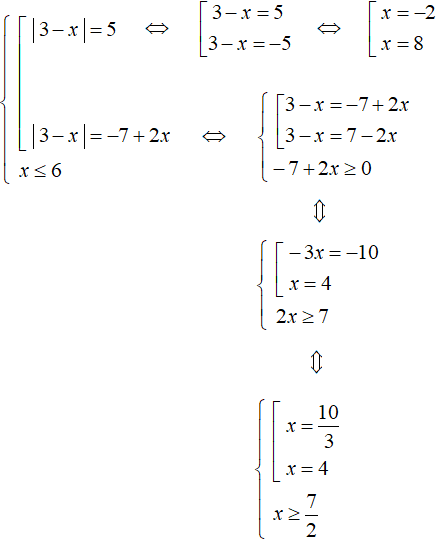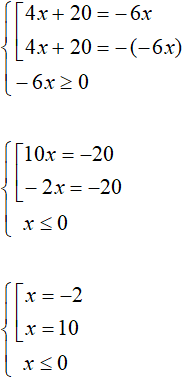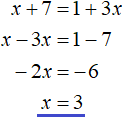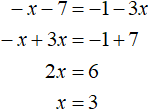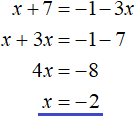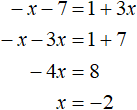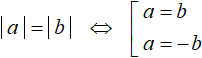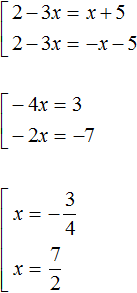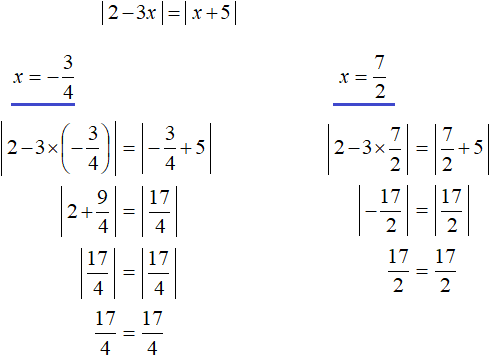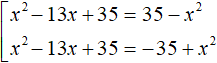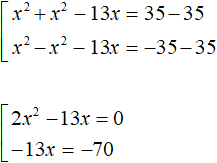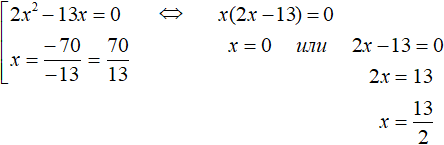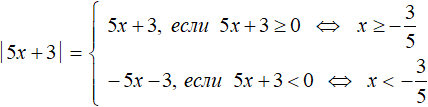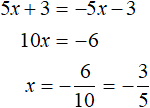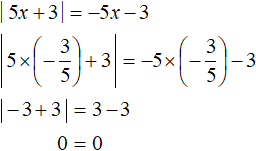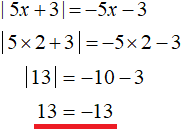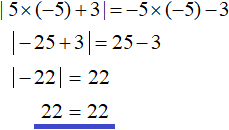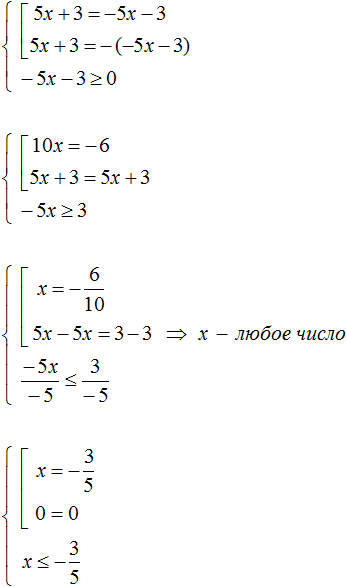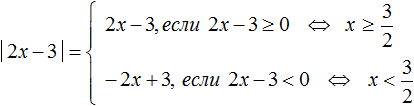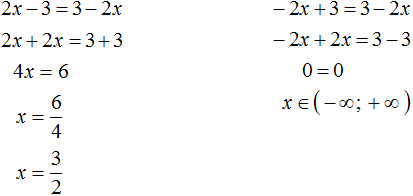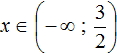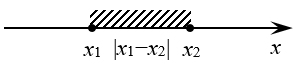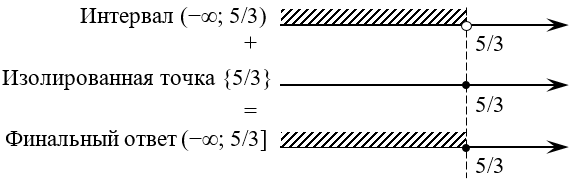Модули. Применение геометрического смысла модуля при решений уравнений и неравенств
Классы: 9 , 10 , 11
Ключевые слова: модуль числа , свойства модуля , геометрический смысл модуля
Цель: Актуализировать знания школьников о смысле понятия «модуль». Учить их применять эти знания при решении уравнении, неравенств и систем уравнении с модулями.
Для того, чтобы научиться решать уравнения и неравенства с модулем, необходимо хорошо разобраться с понятием модуля, его геометрическим смыслом и свойствами.
С рассмотрения этого материала мы и начнем наше занятие.
1. Определение: Модулем числа называется само число, если оно неотрицательно, или число противоположное данному, если оно отрицательно.
Следовательно, при любых значениях переменной |а| есть число неотрицательное.
2. Рассмотрим основные свойства модуля, которые используются при решении уравнений и неравенств, содержащих модуль.
Свойства модуля
— Модуль числа есть величина неотрицательная: |а|>0 или равно 0.
— Модули противоположенных чисел равны: |а|= |-а|
— Модуль произведения равен произведению модулей множителей: |а*в|= |а|*|в|.
— Модуль частного равен частному модулей числителя и знаменателя: |а/в|=|а|/|в|, где в не равен нулю.
— Квадрат модуля равен квадрату подмодульного выражения: |а| 2 =а 2 .
— Модуль суммы не больше суммы модулей ее слагаемых: |а+в|≤|а|+|в|.
При этом равенство |а+в|=|а|+|в| имеет место тогда и только тогда, когда слагаемые одного знака или одно из слагаемых равно нулю.
— Два числа, модули которых равны, либо равны между собой, либо отличаются только знаками, то есть являются противоположными: |а|=|в|, если, а=в или, а=–в.
Преобразование выражений, содержащих модули
При решении уравнении и неравенств с модулем, часто приходится преобразовывать их, раскрывая знак модуля.
Рассмотрим, по каким правилам раскрывается модуль.
Из определения модуля следует: чтобы раскрыть знак модуля, надо знать знак подмодульного выражения.
Составим схему раскрытия модуля:
а) если знак подмодульного выражения неотрицателен, то знак модуля опускается: |а| =а.
б) если знак подмодульного выражения отрицателен, то подмодульное выражение умножается на (-1), то есть заменяется противоположенным выражением: |а| =-1а.
Рассмотрим несколько примеров.
Пример 1.1
а) т.к. с 0, то -7х 5;
б) |3+х|, если х 5, то х-2 > 0, поэтому |х-2|=х-2;
в) т.к. х 0, |8-х|= 8 – х, х-6 (=) 2/3 3х – 2 >(=)0, следовательно, |3[ — 2|= 3х – 2.
4. Задания для самостоятельной работы
б) |- 3/7х|, если х 2 |, если а > 0;
г) |8 + х|, если х > -7;
д) |х — 5| — |х + 4|, если -3 13.
3. Решить неравенство самостоятельно:
4. Решить уравнение:
5. Решить уравнение:
6. Решить неравенство:
7. Найдите наибольшее натуральное значение параметра с при котором решение неравенства
- ||2х + 4| — 7| — 13 ≤ 2с 2 удовлетворяет условию х [-37; 35].
Это задание можно предложить сильным школьникам для домашней работы с последующей проверкой на уроке.
Решения и ответы:
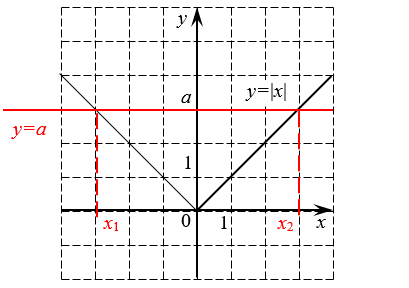
1. Для решения уравнении используем рисунок на доске и правило: «Модуль — это расстояние»:
2. Для решения неравенства сделаем ещё два рисунка.
Значение выражения, стоящего под модулем, не должно превышать 2, значит
Значение выражения, стоящего под модулем, должно быть больше, чем 48 единиц, значит:
18 – х ≥ 48 или 18 – х ≤ -48 => х ≤ -30 или х ≥66.
Уравнения с модулем
Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Решение первой системы: . У второй системы решений нет.
Ответ: 1.
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения
Стало быть, годятся лишь и .
Ответ:
Квадратные уравнения с заменой |x| = t
Поскольку , удобно сделать замену |x| = t. Получаем:
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Модуль в модуле
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.
Уравнение с модулем
Уравнение с модулем достаточно сложная тема для начинающих. Учитывая это обстоятельство, в данный урок войдут только элементарные уравнения.
Что такое уравнение с модулем и как его решить?
В уравнениях с модулем неизвестное значение содержится под знáком модуля. Например:
Уравнения с модулем бывают разными и решаются они различными методами. Нельзя сказать что какой-то метод наиболее рационален. Всё зависит от исходного уравнения.
Например, в каких-то уравнениях можно просто угадать корень, в то время как в других нужно логически мыслить, раскрывать модули, выполнять тождественные преобразования. Человек волен выбирать каким методом решения пользоваться.
К примеру, решим вышеприведённое уравнение |x − 2| = 5 . Допустим, что мы не знаем ни одного метода решения. Как бы мы его решили?
Прежде всего заметим, что правая часть данного уравнения равна числу 5. Слева же располагается модуль из выражения |x − 2| . Это означает что подмодульное выражение x − 2 должно равняться числу 5 или −5
Значит нужно выяснить при каких значениях переменной x подмодульное выражение x − 2 будет обращаться в число 5 или −5.
Искомые значения x найдутся если приравнять подмодульное выражение к числу 5 и −5, а затем поочерёдно решить каждое из уравнений:
Значит корнями уравнения |x − 2| = 5 являются числа 7 и −3.
Большинство элементарных уравнений с модулем можно решить используя правило раскрытия модуля. Для этого раскрывают модуль содержащийся в уравнении, затем получившееся выражение подставляют в исходное уравнение вместо выражения с модулем.
Раскрывать модуль нужно для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля.
Решим наше уравнение |x − 2| = 5 с помощью правила раскрытия модуля. Выпишем отдельно его модуль и раскроем его:
В этой конструкции говорится, что если подмодульное выражение x − 2 больше или равно нулю, то модуль раскроется как x − 2, и тогда исходное уравнение примет вид x − 2 = 5 , откуда x = 7
А если же подмодульное выражение x − 2 меньше нуля, то модуль раскроется как −(x − 2) . Тогда исходное уравнение примет вид −(x − 2) = 5 , откуда x = −3
Итак, уравнение |x − 2|= 5 имеет корни 7 и −3. Для проверки подстáвим числа 7 и −3 в исходное уравнение вместо x . Тогда получим верное равенство:
Подмодульное выражение как правило содержит такое x, которое может обращать всё подмодульное выражение как в положительное число, так и в отрицательное, либо вообще в ноль.
Поэтому модуль и раскрывается для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля. Каждый из случаев будет давать независимое уравнение со своим корнем.
Вернёмся теперь к моменту, где мы раскрывали модуль:
Условия x − 2 ≥ 0 и x − 2 являются неравенствами, которые можно решить, тем самым приведя их к простому виду:
Символ ⇔ означает равносильность. В данном случае указывается, что условие x − 2 ≥ 0 равносильно условию x ≥ 2 , а условие x − 2 равносильно условию x
Такой вид записи условий позволяет однозначно сказать при каких x модуль будет раскрываться с плюсом, а при каких с минусом.
В первом случае получилось условие x ≥ 2. Это значит что при всех x бóльших либо равных 2, модуль |x − 2| будет раскрываться с плюсом. Так, при x = 7, подмодульное выражение станет равно 5
А значит дальнейшее раскрытие будет с плюсом
Таким же образом модуль |x − 2| будет вести себя и с другими значениями x на промежутке x ≥ 2 . То есть, будет раскрываться с плюсом. Примеры:
При x = 3, |3 − 2|=|1| = 1
При x = 4, |4 − 2|=|2| = 2
При x = 2, |2 − 2|=|0| = 0
При x = 13, |13 − 2|=|11| = 11
А во втором случае получилось условие x . Это значит что при всех x мéньших 2, модуль будет раскрываться с минусом. Так, при x = −3, подмодульное выражение опять же станет равно 5. Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:
Модуль |x − 2| будет вести себя так же и с другими значениями x на промежутке x . Примеры:
При x = 1, |1 − 2|=|−1| = −(−1) = 1
При x = 0, |0 − 2|=|−2| = −(−2) = 2
При x = −1, |−1 − 2|=|−3| = −(−3) = 3
При x = −9,|−9 − 2|=|−11| = −(−11) = 11
Число 2 является своего рода точкой перехода, в которой модуль |x − 2| меняет свой порядок раскрытия.
Можно представить как модуль |x − 2| двигался по маршруту от минус бесконечности до числа 2, раскрываясь в каждой точке с минусом. Попав в точку 2, модуль поменял свой порядок раскрытия — а именно раскрывшись в точке 2 с плюсом, он далее стал раскрываться с плюсом, двигаясь в правую часть к плюс бесконечности.
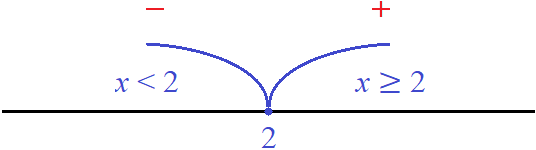
С помощью координатной прямой это можно представить так:
Красные знаки минуса и плюса указывают, как будет раскрываться модуль |x − 2| на промежутках x и x ≥ 2 .
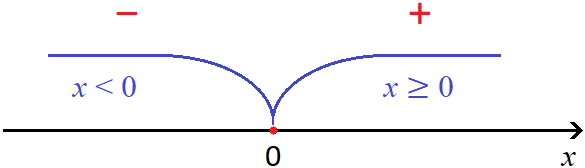
Точку перехода можно найти для любого модуля. Для этого нужно узнать при каких x подмодульное выражение равно нулю. Ноль это то значение, до и после которого модуль всегда сохраняет свой знак. Это следует из правила раскрытия модуля:
В этом примере в момент когда x станет равным нулю, модуль |x| раскроется с плюсом и далее при всех x , бóльших нуля, будет раскрываться с плюсом. Напротив, при всех x , мéньших нуля модуль будет раскрываться с минусом:
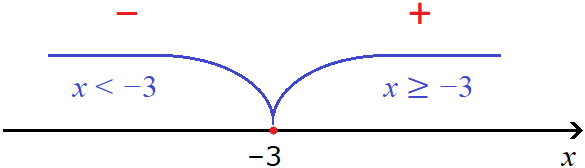
А например для модуля |2x + 6| точкой перехода будет число −3 , потому что при его подстановке в подмодульное выражение 2x + 6 вместо x, данное подмодульное выражение станет равно нулю. Изобразим это на рисунке:
При всех x, бóльших либо равных −3 , модуль будет раскрываться с плюсом. Примеры:
При x = −3, |2 × (−3) + 6| = |0| = 0
При x = 4, |2 × 4 + 6| = |14| = 14
При x = 5, |2 × 5 + 6| = |16| = 16
А при всех x, мéньших 3, модуль будет раскрываться с минусом. Примеры:
При x = −4, |2 × (−4) + 6| = |−2| = −(−2) = 2
При x = −5, |2 × (−5) + 6| = |−4| = −(−4) = 4
При x = −6, |2 × (−6) + 6| = |−6| = −(−6) = 6
Пример 2. Решить уравнение |x| + 3x = −2
Решение
Раскроем модуль, который содержится в левой части уравнения:
Если x ≥ 0 , то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 3x = −2 . Сразу решим это уравнение:
Теперь рассмотрим второй случай — когда x −x + 3x = −2 . Решим и это уравнение:
Получили корни 
Выполним проверку, подставив найденные корни в исходное уравнение. Проверим корень
Видим, что при подстановке корня 

Проверим теперь корень −1
Получили верное равенство. Значит из двух найденных решений только −1 является корнем уравнения.
Ответ: −1.
Здесь можно сделать важный вывод. В уравнениях с модулем найденные корни не всегда удовлетворяют исходному уравнению. Чтобы убедиться в правильности своего решения, нужно выполнять проверку, подставляя найденные корни в исходное уравнение.
Кроме того, проверить является ли найденное значение корнем уравнения можно с помощью условия, согласно которому был раскрыт модуль.
Так, в данном примере мы раскрывали модуль |x| для случаев когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля:
Условия x≥0 и x x + 3x = −2 . Корнем этого уравнения стало число 

А при раскрытии модуля со знаком минус, получилось уравнение −x + 3x = −2 . Корнем этого уравнения стало число −1 . Это число удовлетворяет условию x −x + 3x = −2 . Действительно, при подстановке числа −1 в неравенство x получается верное неравенство.
Пример 3. Решить уравнение |1 − 2x| − 4x = −6
Решение
При раскрытии модуля |1 − 2x| со знаком плюс, получим уравнение 1 − 2x − 4x = −6 . Решим его:
При раскрытии модуля |1 − 2x| со знаком минус, получим уравнение −1 + 2x − 4x = −6. Решим его:
Получили корни 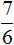

Корень 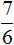
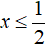
Корень 
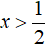
Ответ: 
Пример 4. Решить уравнение | x 2 − 3x | = 0
Решение
Если модуль числа равен нулю, то подмодульное выражение тоже равно нулю:
То есть можно не раскрывать модуль. Достаточно узнать при каких значениях x подмодульное выражение равно нулю. В данном случае для этого нужно решить неполное квадратное уравнение:
Получили корни 0 и 3. Оба корня удовлетворяют исходному уравнению. Проверка показывает это:
Пример 5. Решить уравнение x 2 − 5|x| + 6 = 0
Выпишем отдельно модуль |x| и раскроем его:
При раскрытии модуля |x| со знаком плюс, исходное уравнение примет вид x 2 − 5x + 6 = 0 . Это квадратное уравнение. Решим его с помощью дискриминанта:
Оба корня удовлетворяют условию x ≥ 0 , значит являются корнями исходного уравнения.
При раскрытии модуля |x| со знаком минус, исходное уравнение примет вид x 2 + 5x + 6 = 0 . Это тоже квадратное уравнение. Решим его как и предыдущее:
При условии x ≥ 0 , модуль из уравнения раскрылся с плюсом, получились корни 3 и 2. Оба корня удовлетворяют условию x ≥ 0 , значит удовлетворяют и исходному уравнению.
При условии x , модуль из уравнения раскрылся с минусом, получились корни −2 и −3. Оба корня удовлетворяют условию x , значит удовлетворяют и исходному уравнению.
Ответ: 3, 2, −2 и −3.
Сведéние уравнения с модулем в совокупность
Большинство элементарных уравнений с модулем можно решить сведéнием их к так называемой совокупности уравнений.
Элементарными мы будем называть те уравнения с модулем, в которых левая часть является модулем из какого-то выражения, а правая часть — числом. Например, |x| = 3 или |2x − 1| = 3.
Решим наше самое первое уравнение |x − 2| = 5 сведéнием его к совокупности уравнений. Корнями этого уравнения были числа 7 и −3. Это уравнение тоже считается элементарным.
Если раскрыть модуль |x − 2| со знаком плюс, то уравнение |x − 2| = 5 примет вид x − 2 = 5 .
Если раскрыть модуль |x − 2| со знаком минус, то уравнение |x − 2| = 5 примет вид −(x − 2) = 5 , то есть −x + 2 = 5 .
Видим, что из уравнения |x − 2| = 5 получилось два уравнения: x − 2 = 5 и −x + 2 = 5 . Причём каждое из уравнений имеет свой собственный корень. Уравнение x − 2 = 5 имеет корень 7, а уравнение −x + 2 = 5 — корень −3
Выпишем уравнения x − 2 = 5 и −x + 2 = 5 и объединим их квадратной скобкой:
Такой вид записи называют совокупностью уравнений.
Совокупность уравнений — это несколько уравнений, объединённых квадратной скобкой, и имеющих множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Так, число 7 является решением совокупности 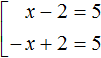
Число −3 тоже является решением данной совокупности, поскольку удовлетворяет второму уравнению − х + 2 = 5.
Вместе же числа 7 и −3 образуют множество решений данной совокупности.
В отличие от системы уравнений, совокупность состоит из уравнений, которые не зависят друг от друга. Для каждого уравнения, входящего в совокупность, значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет как первому уравнению, так и второму.
Решить совокупность уравнений означает найти множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Решим каждое уравнение совокупности 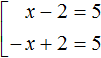
Символ ⇔ как было ранее сказано означает равносильность. В данном случае он указывает на то, что все получающиеся совокупности равносильны друг другу.
Итак, мы получили корни 7 и −3. Поскольку эти два числа являются решениями совокупности 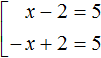
В исходную совокупность можно включать условия, согласно которым был раскрыт модуль. В этом случае каждое уравнение вместе со своим условием обрамляется знаком системы.
Дополним предыдущую совокупность условиями, согласно которым был раскрыт модуль. К первому уравнению x − 2 = 5 добавим условие x − 2 ≥ 0 , а ко второму уравнению −x + 2 = 5 добавим условие x − 2
Решение каждого уравнения должно удовлетворять своему условию. Поэтому условия и уравнения обрамлены знáком системы.
Решим получившуюся совокупность с условиями. Условия являются неравенствами, которые тоже можно решать:
В первом случае получили корень 7 , который удовлетворяет своему условию x ≥ 2 . Во втором случае получили корень −3 , который удовлетворяет своему условию x .
Не следует бояться таких записей. Это лишь подробное решение, показывающее что откуда взялось. Чаще всего решение можно записать покороче.
Существует схема для сведéния в совокупность уравнения вида |x| = a . Выглядит эта схема так:
Данная схема легко позволяет свести уравнение с модулем в совокупность. Эту схему можно прочитать так: « Если выражение |x| равно a, то подмодульное выражение равно a или −a »
Квадратная скобка в совокупностях заменяет собой слово «или».
Например, уравнение |x| = 5 можно свести в совокупность, рассуждая так: если выражение |x| равно 5, то подмодульное выражение равно 5 или −5 .
А применительно к нашему предыдущему примеру можно рассуждать так: если |x − 2| равно 5 , то подмодульное выражение равно 5 или −5
Это та же самая совокупность, что и в прошлый раз. Убедитесь в этом, умножив обе части второго уравнения на −1.
В уравнениях где слева модуль, а справа число, мы будем чаще использовать именно такой способ записи совокупности. Он позволяет не прибегать к правилу раскрытия модуля, а сразу получить совокупность.
Но надо помнить, что эта схема будет работать только для уравнений вида |x| = a . То есть для уравнений, у которого слева модуль, а справа число.
Пример 2. Решить уравнение |2x − 1| = 3
Решение
У этого уравнения слева модуль, а справа число. Значит его можно свести в совокупность, воспользовавшись схемой
Если выражение |2x − 1| равно 3, то подмодульное выражение 2x − 1 равно 3 или −3
Теперь решим каждое уравнение совокупности по отдельности:
Ответ: 2 и −1.
Пример 3. Решить уравнение |x + 2| − 3 = 8
Решение
В некоторых случаях прежде чем свести исходное уравнение в совокупность, его следует упростить.
Так, в данном случае −3 следует перенести в правую часть, изменив знак:
Получили уравнение |x + 2| = 11 . Если выражение |x + 2| равно 11, то подмодульное выражение x + 2 равно 11 или −11
Решим данную совокупность:
Ответ: 9 и −13.
Пример 4. Решить уравнение 4|x| + 4 = 2|x| + 10
Решение
Перенесём 2|x| из правой части в левую часть, а 4 перенесём из левой части в правую часть:
Разделим обе части получившегося уравнения на 2. Тогда получится простое уравнение с модулем:
Ответ: 3 и −3.
Пример 5. Решить уравнение
Решение
Если выражение |2 − 5x 2 | равно 3, то подмодульное выражение 2 − 5x 2 равно 3 или −3
В обоих уравнениях перенесём 2 в правую часть, изменив знак:
В первом уравнении разделим обе части на −5. Во втором уравнении так же разделим обе части на −5. Тогда получим два квадратных уравнения
Первое уравнение не имеет корней, потому что квадрат любого числа положителен, а в данном случае он равен отрицательному числу. Корнями второго уравнения являются числа 1 и −1, поскольку вторая степень этих чисел равна единице.
Ответ: 1 и −1.
Пример 6. Решить уравнение |x + 6| + 4x = 5
Решение
Данное уравнение не является уравнением вида |x| = a , значит не получится воспользоваться схемой 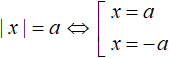
Чтобы свести данное уравнение в совокупность, нужно сначала раскрыть его модуль, затем записать совокупность из получившихся уравнения.
Раскроем модуль |x + 6|
Если x + 6 ≥ 0 , то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 6 + 4x = 5
Если x + 6 , то модуль раскроется со знаком минус и тогда исходное уравнение примет вид − x − 6 + 4x = 5. Получим следующую совокупность:
Дальнейшее решение элементарно:
Из найденных корней только 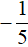
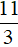
Ответ:
Наиболее простой вид
Наиболее простой вид уравнения с модулем выглядит так:
где x — корень уравнения, a — произвольное число, бóльшее или рáвное нулю. То есть a ≥ 0
Если условие a ≥ 0 не выполнено, то уравнение |x|= a корней не имеет. Это следует из определения модуля. Действительно, модуль всегда неотрицателен.
Приведем несколько примеров уравнений вида |x| = a
Пример 1. Решить уравнение |x| = 2
Решение
В данном случае сразу видно, что корнями являются числа 2 и −2. Ведь если вместо x подставить эти числа, то получим верное равенство: |−2| = 2 и |2| = 2. Решение для этого уравнения можно записать, сведя его в совокупность:
«Если выражение |x| равно 2, то подмодульное выражение x равно 2 или −2«
Ответ: 2 и −2
Пример 2. Решить уравнение |−x| = 4
Решение
Если выражение |−x| равно 4, то подмодульное выражение равно 4 или −4
Умножим оба уравнения на −1
Ответ: −4 и 4.
Пример 3. Решить уравнение |x| = −7
В данном случае корней нет, поскольку модуль всегда неотрицателен. А в данном случае модуль равен отрицательному числу.
Если уравнение с модулем не имеет корней, обычно пишут что x принадлежит пустому множеству:
Напомним, что пустым называют множество, не имеющее элементов.
Модуль внутри модуля
В этом уравнении слева располагается модуль, который в свою очередь содержит внутри себя другой модуль, а справа уравнения располагается число. Такой вид уравнения с модулем можно решить, сведя его в совокупность с помощью схемы, которую мы рассмотрели ранее:
В нашем случае если выражение 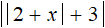
В получившейся совокупности имеется два уравнения с модулем. Эти уравнения тоже в свою очередь следует свести в совокупность. Но сначала немного упростим эти уравнения. В первом и во втором уравнении перенесем 3 в правую часть, изменив знак. Тогда получим:
Теперь сведём эти уравнения в совокупности. Первое уравнение распадётся на следующую совокупность:
Сразу решим совокупность 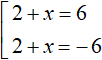
Теперь решим второе уравнение |2 + x| = −12 . Но замечаем, что его правая часть равна отрицательному числу. Это уравнение не имеет корней, потому что модуль не может равняться отрицательному числу.
Значит уравнение 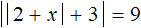
В данном случае оба корня удовлетворяют исходному уравнению.
Ответ: 4 и −8 .
Вообще, уравнение с модулем внутри которого содержится другой модуль, тоже решается различными способами. Какой способ использовать зависит от самогó уравнения. Решим например следующее уравнение:
Здесь уже нельзя использовать схему 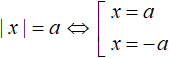
Но тогда справа появляется переменная x, на которую нужно будет вводить дополнительное ограничение, чтобы правая часть уравнения не стала отрицательной. Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.
Чтобы раскрыть модули данного уравнения нужно сначала определиться где внешний и где внутренний модуль.
В уравнении 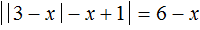
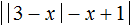
Значение внешнего модуля зависит от внутреннего модуля, и раскрываться внешний модуль будет исходя от результата который получился в результате вычисления его подмодульного содержимого.
Например, если x = 3 , то внутренний модуль |3 − x| примет значение 0, и в результате всё подмодульное выражение внешнего модуля станет равно −2 . А это значит что внешний модуль будет раскрываться с минусом.
||3 − x| − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2
А если например x = −2 , то внутренний модуль |3 − x| примет значение 5, и в результате всё подмодульное выражение внешнего модуля станет равно 8. А это значит что внешний модуль будет раскрываться с плюсом:
||3 − x| − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8
Поэтому решение будем начинать с раскрытия внутреннего модуля.
Если внутренний модуль раскроется с плюсом, то есть если 3 − x ≥ 0 (что равносильно неравенству x ≤ 3 ), то исходное уравнение примет вид:
Теперь уравнение имеет только внешний модуль. Решим его раскрыв модуль:
Если −2x + 4 ≥ 0, то:
Сейчас нас интересуют только те значения x при которых внутренний модуль раскрывается с плюсом, а это произойдет при условии x ≤ 3. Поэтому для наглядности рядом с найденным корнем указано, что он удовлетворяет условию x ≤ 3
Решаем далее. Если −2x + 4 , то:
Несмотря на то, что оба найденных корня удовлетворяют уравнению |−2x+4|=6−x , мы исключаем корень 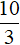
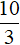
Итак, если внутренний модуль раскрывается с плюсом, исходное уравнение принимает вид |−2x + 4| = 6 − x и корнем этого уравнения является число −2 .
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда 3 − x (что равносильно неравенству x > 3 ). Внутренний модуль будет раскрываться с минусом при всех значениях x больших 3.
Если внутренний модуль раскроется с минусом, то исходное уравнение примет вид:
Модуль −2 равен 2 . Тогда получаем простейшее линейное уравнение, корень которого равен 4
Получили корень 4 , который удовлетворяет условию x > 3 .
В итоге корнями уравнения являются числа −2 и 4.
Ответ: 2 и 4.
Пример 3. Решить уравнение ||x − 1| − 7| = 10
Решение
Слева располагается модуль, а справа число, значит можно применить схему:
В данном случае если выражение ||x − 1| − 7| равно 10, то подмодульное выражение |x − 1| − 7 равно 10 или −10. Получится совокупность из двух уравнений:
Упростим получившиеся уравнения. Перенесём число −7 в обоих уравнениях в правую часть, изменив знак:
Второе уравнение корней не имеет. Первое уравнение распадется на совокупность 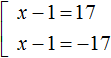
Ответ: 18 и −16 .
Решим это же уравнение с помощью раскрытия модулей. Начнем с внутреннего модуля.
Если x − 1 ≥ 0 (что равносильно x ≥ 1 ), то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда x − 8 ≥ 0 и x − 8
Сейчас нас интересуют те значения, при которых внутренний модуль исходного уравнения раскрывается с плюсом. А это будет при условии, что x ≥ 1 . Этому условию удовлетворяет только значение 18 , поэтому мы пометили его зеленой галочкой для наглядности.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда x − 1 (или что равносильно неравенству x ).
Если x − 1 , то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда −x − 6 ≥ 0 и −x − 6
Из найденных корней только −16 удовлетворяет условию x .
В итоге корнями уравнения ||x − 1| − 7| = 10 являются числа 18 и −16 .
Видно, что с помощью схемы 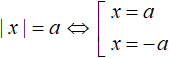
Слева модуль, а справа выражение с переменной
Решим следующее уравнение с модулем:
Здесь так же применима схема:
То есть, если выражение |4x − 3| равно 3x, то подмодульное выражение 4x − 3 должно равняться 3x или −3x.
Но в исходном уравнении переменная x содержится не только под знáком модуля, но и в правой части. Нам пока неизвестно какое значение примет переменная x . Если x примет отрицательное значение, то правая часть станет полностью отрицательной. В этом случае корней не будет, потому что модуль не может равняться отрицательному числу.
Поэтому, если мы хотим решить данное уравнение, то при сведéнии его в совокупность, дополнительно следует ввести ограничение в виде условия 3x ≥ 0 . Это будет означать, что правая часть уравнения |4x − 3| = 3x должна быть больше либо равна нулю:
Совокупность и условие обрамлены знаком системы, потому что решения совокупности должны удовлетворять условию 3x ≥ 0.
Итак, решим совокупность. Условие 3x ≥ 0 является неравенством, которое тоже можно решить:
Получившиеся корни можно подставить в условие x ≥ 0 и посмотреть выполняется ли оно. Если выполняется, то найденные корни удовлетворяют уравнению. В данном случае при подстановке обеих корней в неравенство, оно выполняется. Проверка также показывает, что корни удовлетворяют уравнению:
Пример 2. Решить уравнение |2x − 1| = 5x − 10
Решение
Решим это уравнение таким же образом, как и предыдущее. Введём условие, требующее чтобы правая часть была больше либо равна нулю:
В данном случае только значение 3 удовлетворяет условию x ≥ 2 . Оно же является единственным корнем исходного уравнения. Проверка показывает это:
А число 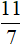
Видим, что модуль стал равен отрицательному числу, а это противоречит определению модуля и нашему условию x ≥ 2 .
Пример 3. Решить уравнение
Решение
Это уравнение мы решили, когда учились решать уравнения с модулем внутри которых другой модуль. Теперь данное уравнение можно решить, сведя его в совокупность.
Для начала перенесём x в правую часть, изменив знак:
Теперь сведём данное уравнение в совокупность. Дополнительно введём условие в виде неравенства 6 − x ≥ 0
В левой части первого уравнения оставим модуль, остальные члены перенесём в правую часть. Тоже самое сделаем и со вторым уравнением. Также будем решать неравенство 6 − x ≥ 0 , оно позволит в конце проверять найденные корни на соответствие:
Решим первое уравнение. Оно распадётся на следующую совокупность:
Получились корни −2 и 8 . Из них только −2 удовлетворяет условию x ≤ 6 .
Теперь решим второе уравнение. Оно является уравнением, содержащим переменную в правой части. При сведении его в совокупность дополним его условием −7 + 2x ≥ 0
При решении второго уравнения получились корни 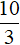
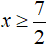
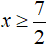
В итоге корнями исходного уравнения 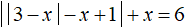
Пример 4. Решить уравнение |4x + 20| = −6x
Решение
На первый взгляд покажется, что данное уравнение не имеет решений, потому что правая часть отрицательна. Но это не совсем так. Правая часть содержит переменную x, которая может принять отрицательное значение или ноль, и это приведёт к тому что правая часть станет положительной либо равной нулю. А такое уравнение имеет право на существование.
В данном случае мы решим это уравнение, сведя его в совокупность. Но при этом укажем, что правая часть должна быть больше или равна нулю:
Из найденных корней только корень −2 удовлетворяет исходному уравнению. Также он удовлетворяет нашему условию x ≤ 0 .
Ответ: −2.
Когда обе части — модули
Решим следующее уравнение:
Обе части этого уравнения являются модулями. Раскроем эти модули. Будем учитывать все возможные случаи при их раскрытии.
Случай 1. Если x + 7 ≥ 0 и 1 + 3x ≥ 0 , то модули в обеих частях раскроются со знаком плюс и тогда исходное уравнение примет вид:
Это простейшее линейное уравнение. Решим его:
Случай 2. Если x + 7 и 1 + 3x то модули в обеих частях раскроются со знаком минус и тогда исходное уравнение примет вид:
Раскроем скобки, получим:
Замечаем, что если умножить обе части этого уравнения на −1 , то получается уравнение x + 7 = 1 + 3 x . А это уравнение мы получали в результате раскрытия модулей со знаком плюс.
То есть уравнения x + 7 = 1 + 3x и −x − 7 = −1 − 3x являются равносильными, а значит имеют одни и те же корни. Убедимся в этом, решив уравнение −x − 7 = −1 − 3x
Поэтому, раскрыв модули со знаком плюс, нет необходимости раскрывать их со знаком минус, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Следующий случай это когда x + 7 ≥ 0 и 1 + 3x . Тогда исходное уравнение примет вид x + 7 = −1 − 3x. Найдём корень этого уравнения:
И последний случай это когда x + 7 и 1 + 3x ≥ 0 . Тогда уравнение примет вид −x − 7 = 1 + 3 x . Если умножить это уравнение на −1 , то получим уравнение x + 7 = −1 − 3x. А это уравнение мы получали, когда рассматривали предыдущий случай (случай x + 7 ≥ 0 и 1 + 3x ).
Следовательно, уравнение −x − 7 = 1 + 3x равносильно предыдущему уравнению x + 7 = −1 − 3 x . Убедимся в этом решив уравнение −x − 7 = 1 + 3x
Значит раскрыв левую часть со знаком плюс, а правую часть со знаком минус, нет необходимости раскрывать левую часть со знаком минус, а правую часть со знаком плюс, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Вообще, если в уравнении обе части являются модулями как в данном примере, то это уравнение можно свести в следующую совокупность:
В этой конструкции уравнение вида |a| = |b| сведено в совокупность из двух уравнений a = b и a = −b . Видно что первое уравнение получается путем раскрытия обоих модулей со знаком плюс, а второе уравнение — путем раскрытия модуля |a| со знаком плюс, а модуля |b| — со знаком минус.
Важно. Данная схема работает только тогда, когда обе части являются модулями без посторонних членов. Проще говоря, если будет дано уравнение, например |a| = |b| + c , то приведенную схему использовать нельзя.
Пример 2. Решить уравнение |2 − 3x| = |x + 5|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс, во втором уравнении — модуль |2 − 3x| будет раскрыт со знаком плюс, а модуль |x + 5| со знаком минус:
Ответ: 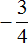
Пример 3. Решить уравнение |x 2 − 13x + 35|=|35 − x 2 |
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс. Во втором уравнении — модуль |x 2 − 13x + 35| будет раскрыт со знаком плюс, а модуль |35 − x 2 | со знаком минус:
Приведём подобные члены в обоих уравнениях:
Первое уравнение является неполным квадратным. Решим его, вынеся x за скобки. Второе уравнение решается элементарно:
Ответ: 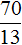
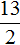
Когда решение — числовой промежуток
Нередко приходиться решать уравнения с модулем, где корнями являются не один или два числа, а числовой промежуток. Таковым, например, является уравнение:
Раскроем модуль этого уравнения:
Если раскрыть модуль со знаком плюс, то получается уравнение 5x + 3 = −5x − 3 . Решим его:
А если раскрыть модуль со знаком минус, то получится уравнение −5x − 3 = −5x − 3 . В этом уравнении обе части являются одинаковыми, а значит данное равенство является тождеством. Оно будет верно при любом значении x . Значит корнями уравнения −5x − 3 = −5x − 3 являются все числа от минус бесконечности до плюс бесконечности:
Но надо помнить про условия, согласно которым были раскрыты модули. В первом случае мы получили корень 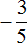
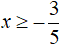
Значит один из корней уравнений равен
Во втором случае мы получили множество корней от минус бесконечности до плюс бесконечности. Но это будет верно только при условии что
Например, если взять любое число из промежутка (−∞; +∞) , но которое не будет удовлетворять условию 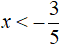
Например, число 2 принадлежит промежутку (−∞; +∞), но не удовлетворяет условию 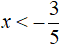
А если взять к примеру число −5 , то оно будет принадлежать промежутку (−∞; +∞) и удовлетворять условию 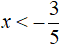
Поэтому ответ надо записать так, чтобы были выполнены оба условия 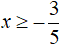
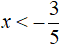

Раскрыв модуль со знаком минус и решив получившееся уравнение, мы получили в ответе множество всех чисел от минус бесконечности до плюс бесконечности, но при этом было дано условие 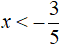
Корнями уравнения −5x − 3 = −5x − 3 при условии 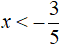
Значит на координатной прямой нужно заштриховать область слева от числа 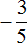
Число 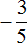
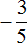
Тогда окончательный ответ будет выглядеть так:
Ответ:
Также, можно решить это уравнение сведя его в совокупность, дополнительно указав, что правая часть должна быть больше либо равна нулю:
Пример 2. Решить уравнение |2x − 3| = 3 − 2x
Решение
Решим исходное уравнение для случаев когда 2x − 3 ≥ 0 и 2x − 3
Ответ:
Использование координатной прямой
Рассмотрим ещё один способ решения элементарных уравнений с модулем — с помощью координатной прямой. Этот способ используется редко, но знать о нём не помешает.
Решим наше самое первое уравнение |x − 2| = 5 с помощью координатной прямой. Напомним, что корнями этого уравнения были числа 7 и −3.
Модуль есть расстояние от начала координат до точки A . Либо расстояние между двумя числами на координатной прямой.
Расстояние между двумя числами выражается в виде разности |x1 − x2| , где x1 — первое число, x2 — второе число.
Если внимательно посмотреть на уравнение |x − 2|= 5 , то можно увидеть что его левая часть это расстояние от x до 2 (или от 2 до x) и это расстояние равно 5. Отмéтим на координатной прямой число x и число 2
Правая часть уравнения |x − 2|= 5 говорит о том, что расстояние от x до 2 составляет пять единиц:
Если расстояние от x до 2 равно 5, то и расстояние от 2 до x тоже равно 5. Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x
Видно, что отсчитав пять шагов влево мы попали в точку с координатой −3. А это один из корней, который мы находили для уравнения |x − 2|= 5.
Но пять целых шагов от числа 2 можно отсчитать не только влево, но и вправо:
Если отсчитать пять целых шагов вправо, то попадём в точку с координатой 7. Это тоже был корень уравнения |x − 2|= 5
Несколько модулей в одной части
Решим следующее уравнение:
Это уравнение содержит два модуля в левой части. Чтобы решить данное уравнение нужно раскрыть его модули. Рассмотреть нужно каждый из случаев:
- когда оба модуля больше либо равны нулю;
- когда оба модуля меньше нуля;
- когда первый модуль больше либо равен нулю, а второй модуль меньше нуля;
- когда первый модуль меньше нуля, а второй модуль больше либо равен нулю.
Не будем комментировать каждый случай, а сразу приведём решение:
Первые два случая корней не дали. В третьем случае нашелся корень 3, но он не удовлетворяет условиям x − 5 ≥ 0 и x , поэтому не является корнем исходного уравнения.
В четвёртом случае нашёлся корень 2, который удовлетворяет условиям x − 5 и x ≥ 0 . Также он удовлетворяет исходному уравнению.
Заметно, что такой способ решения уравнения неудобен. Если модулей в уравнении будет три, четыре или более, то придётся рассматривать намного больше случаев. Человек запутавшись, может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.
Поэтому такой вид уравнения как в данном примере удобнее решать методом интервалов. Об этом мы поговорим в следующем уроке.
источники:
http://ege-study.ru/ru/ege/materialy/matematika/uravneniya-i-neravenstva-s-modulem/
http://spacemath.xyz/uravnenie-s-modulem/
Уравнение с модулем достаточно сложная тема для начинающих. Учитывая это обстоятельство, в данный урок войдут только элементарные уравнения.
Что такое уравнение с модулем и как его решить?
В уравнениях с модулем неизвестное значение содержится под знáком модуля. Например:
|x − 2| = 5
Уравнения с модулем бывают разными и решаются они различными методами. Нельзя сказать что какой-то метод наиболее рационален. Всё зависит от исходного уравнения.
Например, в каких-то уравнениях можно просто угадать корень, в то время как в других нужно логически мыслить, раскрывать модули, выполнять тождественные преобразования. Человек волен выбирать каким методом решения пользоваться.
К примеру, решим вышеприведённое уравнение |x − 2| = 5. Допустим, что мы не знаем ни одного метода решения. Как бы мы его решили?
Прежде всего заметим, что правая часть данного уравнения равна числу 5. Слева же располагается модуль из выражения |x − 2|. Это означает что подмодульное выражение x − 2 должно равняться числу 5 или −5
Значит нужно выяснить при каких значениях переменной x подмодульное выражение x − 2 будет обращаться в число 5 или −5.
Искомые значения x найдутся если приравнять подмодульное выражение к числу 5 и −5, а затем поочерёдно решить каждое из уравнений:
Значит корнями уравнения |x − 2| = 5 являются числа 7 и −3.
Большинство элементарных уравнений с модулем можно решить используя правило раскрытия модуля. Для этого раскрывают модуль содержащийся в уравнении, затем получившееся выражение подставляют в исходное уравнение вместо выражения с модулем.
Раскрывать модуль нужно для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля.
Решим наше уравнение |x − 2| = 5 с помощью правила раскрытия модуля. Выпишем отдельно его модуль и раскроем его:
В этой конструкции говорится, что если подмодульное выражение x − 2 больше или равно нулю, то модуль раскроется как x − 2, и тогда исходное уравнение примет вид x − 2 = 5, откуда x = 7
А если же подмодульное выражение x − 2 меньше нуля, то модуль раскроется как −(x − 2). Тогда исходное уравнение примет вид −(x − 2) = 5, откуда x = −3
Итак, уравнение |x − 2|= 5 имеет корни 7 и −3. Для проверки подстáвим числа 7 и −3 в исходное уравнение вместо x. Тогда получим верное равенство:
Подмодульное выражение как правило содержит такое x, которое может обращать всё подмодульное выражение как в положительное число, так и в отрицательное, либо вообще в ноль.
Поэтому модуль и раскрывается для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля. Каждый из случаев будет давать независимое уравнение со своим корнем.
Вернёмся теперь к моменту, где мы раскрывали модуль:
Условия x − 2 ≥ 0 и x − 2 < 0 являются неравенствами, которые можно решить, тем самым приведя их к простому виду:
Символ ⇔ означает равносильность. В данном случае указывается, что условие x − 2 ≥ 0 равносильно условию x ≥ 2, а условие x − 2 < 0 равносильно условию x < 2.
Такой вид записи условий позволяет однозначно сказать при каких x модуль будет раскрываться с плюсом, а при каких с минусом.
В первом случае получилось условие x ≥ 2. Это значит что при всех x бóльших либо равных 2, модуль |x − 2| будет раскрываться с плюсом. Так, при x = 7, подмодульное выражение станет равно 5
|7 − 2| = |5|
А значит дальнейшее раскрытие будет с плюсом
|7 − 2| = |5| = 5
Таким же образом модуль |x − 2| будет вести себя и с другими значениями x на промежутке x ≥ 2. То есть, будет раскрываться с плюсом. Примеры:
При x = 3, |3 − 2|=|1| = 1
При x = 4, |4 − 2|=|2| = 2
При x = 2, |2 − 2|=|0| = 0
При x = 13, |13 − 2|=|11| = 11
А во втором случае получилось условие x < 2. Это значит что при всех x мéньших 2, модуль будет раскрываться с минусом. Так, при x = −3, подмодульное выражение опять же станет равно 5. Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:
|−3 − 2| = |−5| = −(−5) = 5
Модуль |x − 2| будет вести себя так же и с другими значениями x на промежутке x < 2. Примеры:
При x = 1, |1 − 2|=|−1| = −(−1) = 1
При x = 0, |0 − 2|=|−2| = −(−2) = 2
При x = −1, |−1 − 2|=|−3| = −(−3) = 3
При x = −9,|−9 − 2|=|−11| = −(−11) = 11
Число 2 является своего рода точкой перехода, в которой модуль |x − 2| меняет свой порядок раскрытия.
Можно представить как модуль |x − 2| двигался по маршруту от минус бесконечности до числа 2, раскрываясь в каждой точке с минусом. Попав в точку 2, модуль поменял свой порядок раскрытия — а именно раскрывшись в точке 2 с плюсом, он далее стал раскрываться с плюсом, двигаясь в правую часть к плюс бесконечности.
С помощью координатной прямой это можно представить так:
Красные знаки минуса и плюса указывают, как будет раскрываться модуль |x − 2| на промежутках x < 2 и x ≥ 2.
Точку перехода можно найти для любого модуля. Для этого нужно узнать при каких x подмодульное выражение равно нулю. Ноль это то значение, до и после которого модуль всегда сохраняет свой знак. Это следует из правила раскрытия модуля:
В этом примере в момент когда x станет равным нулю, модуль |x| раскроется с плюсом и далее при всех x, бóльших нуля, будет раскрываться с плюсом. Напротив, при всех x, мéньших нуля модуль будет раскрываться с минусом:
А например для модуля |2x + 6| точкой перехода будет число −3, потому что при его подстановке в подмодульное выражение 2x + 6 вместо x, данное подмодульное выражение станет равно нулю. Изобразим это на рисунке:
При всех x, бóльших либо равных −3, модуль будет раскрываться с плюсом. Примеры:
При x = −3, |2 × (−3) + 6| = |0| = 0
При x = 4, |2 × 4 + 6| = |14| = 14
При x = 5, |2 × 5 + 6| = |16| = 16
А при всех x, мéньших 3, модуль будет раскрываться с минусом. Примеры:
При x = −4, |2 × (−4) + 6| = |−2| = −(−2) = 2
При x = −5, |2 × (−5) + 6| = |−4| = −(−4) = 4
При x = −6, |2 × (−6) + 6| = |−6| = −(−6) = 6
Пример 2. Решить уравнение |x| + 3x = −2
Решение
Раскроем модуль, который содержится в левой части уравнения:
Если x ≥ 0, то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 3x = −2. Сразу решим это уравнение:
Теперь рассмотрим второй случай — когда x < 0. В этом случае модуль в исходном уравнении раскроется со знаком минус, и тогда получится уравнение −x + 3x = −2. Решим и это уравнение:
Получили корни и −1.
Выполним проверку, подставив найденные корни в исходное уравнение. Проверим корень
Видим, что при подстановке корня исходное уравнение не обращается в верное равенство. Значит
не является корнем исходного уравнения.
Проверим теперь корень −1
Получили верное равенство. Значит из двух найденных решений только −1 является корнем уравнения.
Ответ: −1.
Здесь можно сделать важный вывод. В уравнениях с модулем найденные корни не всегда удовлетворяют исходному уравнению. Чтобы убедиться в правильности своего решения, нужно выполнять проверку, подставляя найденные корни в исходное уравнение.
Кроме того, проверить является ли найденное значение корнем уравнения можно с помощью условия, согласно которому был раскрыт модуль.
Так, в данном примере мы раскрывали модуль |x| для случаев когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля:
Условия x≥0 и x<0 являются неравенствами. В эти неравенства можно подставлять найденные корни. Если неравенства окажутся верными, значит корни удовлетворяют исходному уравнению.
Так, при раскрытии модуля со знаком плюс, получилось уравнение x + 3x = −2. Корнем этого уравнения стало число . Это число не удовлетворяет условию x ≥ 0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение x + 3x = −2. Действительно, при подстановке числа
в неравенство x ≥ 0 получается неверное неравенство.
А при раскрытии модуля со знаком минус, получилось уравнение −x + 3x = −2. Корнем этого уравнения стало число −1. Это число удовлетворяет условию x<0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение −x + 3x = −2. Действительно, при подстановке числа −1 в неравенство x < 0 получается верное неравенство.
Пример 3. Решить уравнение |1 − 2x| − 4x = −6
Решение
Раскроем модуль:
При раскрытии модуля |1 − 2x| со знаком плюс, получим уравнение 1 − 2x − 4x = −6. Решим его:
При раскрытии модуля |1 − 2x| со знаком минус, получим уравнение −1 + 2x − 4x = −6. Решим его:
Получили корни и
.
Корень не удовлетворяет условию
, значит не является корнем исходного уравнения.
Корень удовлетворяет условию
, значит является корнем исходного уравнения. Проверка также покажет это:
Ответ: .
Пример 4. Решить уравнение |x2 − 3x| = 0
Решение
Если модуль числа равен нулю, то подмодульное выражение тоже равно нулю:
То есть можно не раскрывать модуль. Достаточно узнать при каких значениях x подмодульное выражение равно нулю. В данном случае для этого нужно решить неполное квадратное уравнение:
Получили корни 0 и 3. Оба корня удовлетворяют исходному уравнению. Проверка показывает это:
Пример 5. Решить уравнение x2 − 5|x| + 6 = 0
Выпишем отдельно модуль |x| и раскроем его:
При раскрытии модуля |x| со знаком плюс, исходное уравнение примет вид x2 − 5x + 6 = 0. Это квадратное уравнение. Решим его с помощью дискриминанта:
Оба корня удовлетворяют условию x ≥ 0, значит являются корнями исходного уравнения.
При раскрытии модуля |x| со знаком минус, исходное уравнение примет вид x2 + 5x + 6 = 0. Это тоже квадратное уравнение. Решим его как и предыдущее:
При условии x ≥ 0, модуль из уравнения раскрылся с плюсом, получились корни 3 и 2. Оба корня удовлетворяют условию x ≥ 0, значит удовлетворяют и исходному уравнению.
При условии x < 0, модуль из уравнения раскрылся с минусом, получились корни −2 и −3. Оба корня удовлетворяют условию x < 0, значит удовлетворяют и исходному уравнению.
Ответ: 3, 2, −2 и −3.
Сведéние уравнения с модулем в совокупность
Большинство элементарных уравнений с модулем можно решить сведéнием их к так называемой совокупности уравнений.
Элементарными мы будем называть те уравнения с модулем, в которых левая часть является модулем из какого-то выражения, а правая часть — числом. Например, |x| = 3 или |2x − 1| = 3.
Решим наше самое первое уравнение |x − 2| = 5 сведéнием его к совокупности уравнений. Корнями этого уравнения были числа 7 и −3. Это уравнение тоже считается элементарным.
Если раскрыть модуль |x − 2| со знаком плюс, то уравнение |x − 2| = 5 примет вид x − 2 = 5.
Если раскрыть модуль |x − 2| со знаком минус, то уравнение |x − 2| = 5 примет вид −(x − 2) = 5, то есть −x + 2 = 5.
Видим, что из уравнения |x − 2| = 5 получилось два уравнения: x − 2 = 5 и −x + 2 = 5. Причём каждое из уравнений имеет свой собственный корень. Уравнение x − 2 = 5 имеет корень 7, а уравнение −x + 2 = 5 — корень −3
Выпишем уравнения x − 2 = 5 и −x + 2 = 5 и объединим их квадратной скобкой:
Такой вид записи называют совокупностью уравнений.
Совокупность уравнений — это несколько уравнений, объединённых квадратной скобкой, и имеющих множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Так, число 7 является решением совокупности 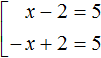
Число −3 тоже является решением данной совокупности, поскольку удовлетворяет второму уравнению −х + 2 = 5.
Вместе же числа 7 и −3 образуют множество решений данной совокупности.
В отличие от системы уравнений, совокупность состоит из уравнений, которые не зависят друг от друга. Для каждого уравнения, входящего в совокупность, значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет как первому уравнению, так и второму.
Решить совокупность уравнений означает найти множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Решим каждое уравнение совокупности 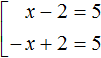
Символ ⇔ как было ранее сказано означает равносильность. В данном случае он указывает на то, что все получающиеся совокупности равносильны друг другу.
Итак, мы получили корни 7 и −3. Поскольку эти два числа являются решениями совокупности 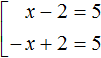
В исходную совокупность можно включать условия, согласно которым был раскрыт модуль. В этом случае каждое уравнение вместе со своим условием обрамляется знаком системы.
Дополним предыдущую совокупность условиями, согласно которым был раскрыт модуль. К первому уравнению x − 2 = 5 добавим условие x − 2 ≥ 0, а ко второму уравнению −x + 2 = 5 добавим условие x − 2 < 0
Решение каждого уравнения должно удовлетворять своему условию. Поэтому условия и уравнения обрамлены знáком системы.
Решим получившуюся совокупность с условиями. Условия являются неравенствами, которые тоже можно решать:
В первом случае получили корень 7, который удовлетворяет своему условию x ≥ 2. Во втором случае получили корень −3, который удовлетворяет своему условию x < 2.
Не следует бояться таких записей. Это лишь подробное решение, показывающее что откуда взялось. Чаще всего решение можно записать покороче.
Существует схема для сведéния в совокупность уравнения вида |x| = a. Выглядит эта схема так:
Данная схема легко позволяет свести уравнение с модулем в совокупность. Эту схему можно прочитать так: «Если выражение |x| равно a, то подмодульное выражение равно a или −a»
Квадратная скобка в совокупностях заменяет собой слово «или».
Например, уравнение |x| = 5 можно свести в совокупность, рассуждая так: если выражение |x| равно 5, то подмодульное выражение равно 5 или −5.
А применительно к нашему предыдущему примеру можно рассуждать так: если |x − 2| равно 5, то подмодульное выражение равно 5 или −5
Это та же самая совокупность, что и в прошлый раз. Убедитесь в этом, умножив обе части второго уравнения на −1.
В уравнениях где слева модуль, а справа число, мы будем чаще использовать именно такой способ записи совокупности. Он позволяет не прибегать к правилу раскрытия модуля, а сразу получить совокупность.
Но надо помнить, что эта схема будет работать только для уравнений вида |x| = a. То есть для уравнений, у которого слева модуль, а справа число.
Пример 2. Решить уравнение |2x − 1| = 3
Решение
У этого уравнения слева модуль, а справа число. Значит его можно свести в совокупность, воспользовавшись схемой
Если выражение |2x − 1| равно 3, то подмодульное выражение 2x − 1 равно 3 или −3
Теперь решим каждое уравнение совокупности по отдельности:
Ответ: 2 и −1.
Пример 3. Решить уравнение |x + 2| − 3 = 8
Решение
В некоторых случаях прежде чем свести исходное уравнение в совокупность, его следует упростить.
Так, в данном случае −3 следует перенести в правую часть, изменив знак:
Получили уравнение |x + 2| = 11. Если выражение |x + 2| равно 11, то подмодульное выражение x + 2 равно 11 или −11
Решим данную совокупность:
Ответ: 9 и −13.
Пример 4. Решить уравнение 4|x| + 4 = 2|x| + 10
Решение
Перенесём 2|x| из правой части в левую часть, а 4 перенесём из левой части в правую часть:
4|x| − 2|x| = 10 − 4
2|x| = 6
Разделим обе части получившегося уравнения на 2. Тогда получится простое уравнение с модулем:
Ответ: 3 и −3.
Пример 5. Решить уравнение
Решение
Если выражение |2 − 5x2| равно 3, то подмодульное выражение 2 − 5x2 равно 3 или −3
В обоих уравнениях перенесём 2 в правую часть, изменив знак:
В первом уравнении разделим обе части на −5. Во втором уравнении так же разделим обе части на −5. Тогда получим два квадратных уравнения
Первое уравнение не имеет корней, потому что квадрат любого числа положителен, а в данном случае он равен отрицательному числу. Корнями второго уравнения являются числа 1 и −1, поскольку вторая степень этих чисел равна единице.
Ответ: 1 и −1.
Пример 6. Решить уравнение |x + 6| + 4x = 5
Решение
Данное уравнение не является уравнением вида |x| = a, значит не получится воспользоваться схемой 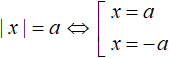
Чтобы свести данное уравнение в совокупность, нужно сначала раскрыть его модуль, затем записать совокупность из получившихся уравнения.
Раскроем модуль |x + 6|
Если x + 6 ≥ 0 , то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 6 + 4x = 5
Если x + 6 < 0, то модуль раскроется со знаком минус и тогда исходное уравнение примет вид −x − 6 + 4x = 5. Получим следующую совокупность:
Дальнейшее решение элементарно:
Из найденных корней только является корнем исходного уравнения, поскольку удовлетворяет условию x ≥ −6. А корень
не является корнем уравнения, поскольку не удовлетворяет условию x < −6.
Ответ:
Наиболее простой вид
Наиболее простой вид уравнения с модулем выглядит так:
| x | = a
где x — корень уравнения, a — произвольное число, бóльшее или рáвное нулю. То есть a ≥ 0
Если условие a ≥ 0 не выполнено, то уравнение |x|= a корней не имеет. Это следует из определения модуля. Действительно, модуль всегда неотрицателен.
Приведем несколько примеров уравнений вида |x| = a
Пример 1. Решить уравнение |x| = 2
Решение
В данном случае сразу видно, что корнями являются числа 2 и −2. Ведь если вместо x подставить эти числа, то получим верное равенство: |−2| = 2 и |2| = 2. Решение для этого уравнения можно записать, сведя его в совокупность:
«Если выражение |x| равно 2, то подмодульное выражение x равно 2 или −2«
Ответ: 2 и −2
Пример 2. Решить уравнение |−x| = 4
Решение
Если выражение |−x| равно 4, то подмодульное выражение равно 4 или −4
Умножим оба уравнения на −1
Ответ: −4 и 4.
Пример 3. Решить уравнение |x| = −7
В данном случае корней нет, поскольку модуль всегда неотрицателен. А в данном случае модуль равен отрицательному числу.
Если уравнение с модулем не имеет корней, обычно пишут что x принадлежит пустому множеству:
x ∈ ø
Напомним, что пустым называют множество, не имеющее элементов.
Модуль внутри модуля
Рассмотрим уравнение:
В этом уравнении слева располагается модуль, который в свою очередь содержит внутри себя другой модуль, а справа уравнения располагается число. Такой вид уравнения с модулем можно решить, сведя его в совокупность с помощью схемы, которую мы рассмотрели ранее:
В нашем случае если выражение равно 9, то подмодульное выражение |2 + x| + 3 равно 9 или −9
В получившейся совокупности имеется два уравнения с модулем. Эти уравнения тоже в свою очередь следует свести в совокупность. Но сначала немного упростим эти уравнения. В первом и во втором уравнении перенесем 3 в правую часть, изменив знак. Тогда получим:
Теперь сведём эти уравнения в совокупности. Первое уравнение распадётся на следующую совокупность:
Сразу решим совокупность 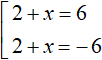
Теперь решим второе уравнение |2 + x| = −12. Но замечаем, что его правая часть равна отрицательному числу. Это уравнение не имеет корней, потому что модуль не может равняться отрицательному числу.
Значит уравнение имеет корни 4 и −8. Проверим эти корни, подставив их в исходное уравнение
В данном случае оба корня удовлетворяют исходному уравнению.
Ответ: 4 и −8.
Вообще, уравнение с модулем внутри которого содержится другой модуль, тоже решается различными способами. Какой способ использовать зависит от самогó уравнения. Решим например следующее уравнение:
Здесь уже нельзя использовать схему 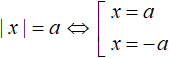
Но тогда справа появляется переменная x, на которую нужно будет вводить дополнительное ограничение, чтобы правая часть уравнения не стала отрицательной. Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.
Чтобы раскрыть модули данного уравнения нужно сначала определиться где внешний и где внутренний модуль.
В уравнении внешним модулем является полностью левая часть
, а внутренним модулем — выражение
Значение внешнего модуля зависит от внутреннего модуля, и раскрываться внешний модуль будет исходя от результата который получился в результате вычисления его подмодульного содержимого.
Например, если x = 3, то внутренний модуль |3 − x| примет значение 0, и в результате всё подмодульное выражение внешнего модуля станет равно −2. А это значит что внешний модуль будет раскрываться с минусом.
||3 − x| − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2
А если например x = −2, то внутренний модуль |3 − x| примет значение 5, и в результате всё подмодульное выражение внешнего модуля станет равно 8. А это значит что внешний модуль будет раскрываться с плюсом:
||3 − x| − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8
Поэтому решение будем начинать с раскрытия внутреннего модуля.
Если внутренний модуль раскроется с плюсом, то есть если 3 − x ≥ 0 (что равносильно неравенству x ≤ 3), то исходное уравнение примет вид:
Теперь уравнение имеет только внешний модуль. Решим его раскрыв модуль:
Если −2x + 4 ≥ 0, то:
Сейчас нас интересуют только те значения x при которых внутренний модуль раскрывается с плюсом, а это произойдет при условии x ≤ 3. Поэтому для наглядности рядом с найденным корнем указано, что он удовлетворяет условию x ≤ 3
Решаем далее. Если −2x + 4 < 0, то:
Несмотря на то, что оба найденных корня удовлетворяют уравнению |−2x+4|=6−x, мы исключаем корень из решений, потому что нас сейчас интересуют только те значения x, при которых внутренний модуль изначального уравнения раскрывается с плюсом. Поэтому рядом с корнем
указано, что он не удовлетворяет условию x ≤ 3.
Итак, если внутренний модуль раскрывается с плюсом, исходное уравнение принимает вид |−2x + 4| = 6 − x и корнем этого уравнения является число −2.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда 3 − x < 0 (что равносильно неравенству x > 3). Внутренний модуль будет раскрываться с минусом при всех значениях x больших 3.
Если внутренний модуль раскроется с минусом, то исходное уравнение примет вид:
Модуль −2 равен 2. Тогда получаем простейшее линейное уравнение, корень которого равен 4
Получили корень 4, который удовлетворяет условию x > 3.
В итоге корнями уравнения являются числа −2 и 4.
Ответ: 2 и 4.
Пример 3. Решить уравнение ||x − 1| − 7| = 10
Решение
Слева располагается модуль, а справа число, значит можно применить схему:
В данном случае если выражение ||x − 1| − 7| равно 10, то подмодульное выражение |x − 1| − 7 равно 10 или −10. Получится совокупность из двух уравнений:
Упростим получившиеся уравнения. Перенесём число −7 в обоих уравнениях в правую часть, изменив знак:
Второе уравнение корней не имеет. Первое уравнение распадется на совокупность 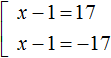
Ответ: 18 и −16.
Решим это же уравнение с помощью раскрытия модулей. Начнем с внутреннего модуля.
Если x − 1 ≥ 0 (что равносильно x ≥ 1), то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда x − 8 ≥ 0 и x − 8 < 0
Сейчас нас интересуют те значения, при которых внутренний модуль исходного уравнения раскрывается с плюсом. А это будет при условии, что x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы пометили его зеленой галочкой для наглядности.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда x − 1 < 0 (или что равносильно неравенству x < 1).
Если x − 1 < 0, то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда −x − 6 ≥ 0 и −x − 6 < 0
Из найденных корней только −16 удовлетворяет условию x < 1.
В итоге корнями уравнения ||x − 1| − 7| = 10 являются числа 18 и −16.
Видно, что с помощью схемы 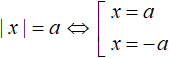
Слева модуль, а справа выражение с переменной
Решим следующее уравнение с модулем:
|4x − 3| = 3x
Здесь так же применима схема:
То есть, если выражение |4x − 3| равно 3x, то подмодульное выражение 4x − 3 должно равняться 3x или −3x.
Но в исходном уравнении переменная x содержится не только под знáком модуля, но и в правой части. Нам пока неизвестно какое значение примет переменная x. Если x примет отрицательное значение, то правая часть станет полностью отрицательной. В этом случае корней не будет, потому что модуль не может равняться отрицательному числу.
Поэтому, если мы хотим решить данное уравнение, то при сведéнии его в совокупность, дополнительно следует ввести ограничение в виде условия 3x ≥ 0. Это будет означать, что правая часть уравнения |4x − 3| = 3x должна быть больше либо равна нулю:
Совокупность и условие обрамлены знаком системы, потому что решения совокупности должны удовлетворять условию 3x ≥ 0.
Итак, решим совокупность. Условие 3x ≥ 0 является неравенством, которое тоже можно решить:
Получившиеся корни можно подставить в условие x ≥ 0 и посмотреть выполняется ли оно. Если выполняется, то найденные корни удовлетворяют уравнению. В данном случае при подстановке обеих корней в неравенство, оно выполняется. Проверка также показывает, что корни удовлетворяют уравнению:
Пример 2. Решить уравнение |2x − 1| = 5x − 10
Решение
Решим это уравнение таким же образом, как и предыдущее. Введём условие, требующее чтобы правая часть была больше либо равна нулю:
В данном случае только значение 3 удовлетворяет условию x ≥ 2. Оно же является единственным корнем исходного уравнения. Проверка показывает это:
А число не удовлетворяет условию x ≥ 2 и не является корнем исходного уравнения. Проверка также показывает это:
Видим, что модуль стал равен отрицательному числу, а это противоречит определению модуля и нашему условию x ≥ 2.
Пример 3. Решить уравнение
Решение
Это уравнение мы решили, когда учились решать уравнения с модулем внутри которых другой модуль. Теперь данное уравнение можно решить, сведя его в совокупность.
Для начала перенесём x в правую часть, изменив знак:
Теперь сведём данное уравнение в совокупность. Дополнительно введём условие в виде неравенства 6 − x ≥ 0
В левой части первого уравнения оставим модуль, остальные члены перенесём в правую часть. Тоже самое сделаем и со вторым уравнением. Также будем решать неравенство 6 − x ≥ 0, оно позволит в конце проверять найденные корни на соответствие:
Решим первое уравнение. Оно распадётся на следующую совокупность:
Получились корни −2 и 8. Из них только −2 удовлетворяет условию x ≤ 6.
Теперь решим второе уравнение. Оно является уравнением, содержащим переменную в правой части. При сведении его в совокупность дополним его условием −7 + 2x ≥ 0
Дальнейшее элементарно:
При решении второго уравнения получились корни и 4. Прежде чем сверять их с условием x ≤ 6 следует сверить их с условием
под которое решалось уравнение |3 − x| = −7 + 2x. Условию
удовлетворяет только корень 4.
В итоге корнями исходного уравнения являются числа −2 и 4.
Пример 4. Решить уравнение |4x + 20| = −6x
Решение
На первый взгляд покажется, что данное уравнение не имеет решений, потому что правая часть отрицательна. Но это не совсем так. Правая часть содержит переменную x, которая может принять отрицательное значение или ноль, и это приведёт к тому что правая часть станет положительной либо равной нулю. А такое уравнение имеет право на существование.
В данном случае мы решим это уравнение, сведя его в совокупность. Но при этом укажем, что правая часть должна быть больше или равна нулю:
Из найденных корней только корень −2 удовлетворяет исходному уравнению. Также он удовлетворяет нашему условию x ≤ 0.
Ответ: −2.
Когда обе части — модули
Решим следующее уравнение:
|x + 7| = |1 + 3x|
Обе части этого уравнения являются модулями. Раскроем эти модули. Будем учитывать все возможные случаи при их раскрытии.
Случай 1. Если x + 7 ≥ 0 и 1 + 3x ≥ 0, то модули в обеих частях раскроются со знаком плюс и тогда исходное уравнение примет вид:
x + 7 = 1 + 3x
Это простейшее линейное уравнение. Решим его:
Случай 2. Если x + 7 < 0 и 1 + 3x < 0, то модули в обеих частях раскроются со знаком минус и тогда исходное уравнение примет вид:
−(x + 7) = −(1 + 3x)
Раскроем скобки, получим:
−x − 7 = −1 − 3x
Замечаем, что если умножить обе части этого уравнения на −1, то получается уравнение x + 7 = 1 + 3x. А это уравнение мы получали в результате раскрытия модулей со знаком плюс.
То есть уравнения x + 7 = 1 + 3x и −x − 7 = −1 − 3x являются равносильными, а значит имеют одни и те же корни. Убедимся в этом, решив уравнение −x − 7 = −1 − 3x
Поэтому, раскрыв модули со знаком плюс, нет необходимости раскрывать их со знаком минус, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Следующий случай это когда x + 7 ≥ 0 и 1 + 3x < 0. Тогда исходное уравнение примет вид x + 7 = −1 − 3x. Найдём корень этого уравнения:
И последний случай это когда x + 7 < 0 и 1 + 3x ≥ 0. Тогда уравнение примет вид −x − 7 = 1 + 3x. Если умножить это уравнение на −1, то получим уравнение x + 7 = −1 − 3x. А это уравнение мы получали, когда рассматривали предыдущий случай (случай x + 7 ≥ 0 и 1 + 3x < 0).
Следовательно, уравнение −x − 7 = 1 + 3x равносильно предыдущему уравнению x + 7 = −1 − 3x. Убедимся в этом решив уравнение −x − 7 = 1 + 3x
Значит раскрыв левую часть со знаком плюс, а правую часть со знаком минус, нет необходимости раскрывать левую часть со знаком минус, а правую часть со знаком плюс, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Вообще, если в уравнении обе части являются модулями как в данном примере, то это уравнение можно свести в следующую совокупность:
В этой конструкции уравнение вида |a| = |b| сведено в совокупность из двух уравнений a = b и a = −b. Видно что первое уравнение получается путем раскрытия обоих модулей со знаком плюс, а второе уравнение — путем раскрытия модуля |a| со знаком плюс, а модуля|b|— со знаком минус.
Важно. Данная схема работает только тогда, когда обе части являются модулями без посторонних членов. Проще говоря, если будет дано уравнение, например |a| = |b| + c, то приведенную схему использовать нельзя.
Пример 2. Решить уравнение |2 − 3x| = |x + 5|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс, во втором уравнении — модуль |2 − 3x| будет раскрыт со знаком плюс, а модуль |x + 5| со знаком минус:
Выполним проверку:
Ответ: и
Пример 3. Решить уравнение |x2 − 13x + 35|=|35 − x2|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс. Во втором уравнении — модуль |x2 − 13x + 35| будет раскрыт со знаком плюс, а модуль |35 − x2| со знаком минус:
Приведём подобные члены в обоих уравнениях:
Первое уравнение является неполным квадратным. Решим его, вынеся x за скобки. Второе уравнение решается элементарно:
Ответ: ,
, 0.
Когда решение — числовой промежуток
Нередко приходиться решать уравнения с модулем, где корнями являются не один или два числа, а числовой промежуток. Таковым, например, является уравнение:
|5x + 3| = −5x − 3
Раскроем модуль этого уравнения:
Если раскрыть модуль со знаком плюс, то получается уравнение 5x + 3 = −5x − 3. Решим его:
А если раскрыть модуль со знаком минус, то получится уравнение −5x − 3 = −5x − 3. В этом уравнении обе части являются одинаковыми, а значит данное равенство является тождеством. Оно будет верно при любом значении x. Значит корнями уравнения −5x − 3 = −5x − 3 являются все числа от минус бесконечности до плюс бесконечности:
x ∈ (−∞; +∞)
Но надо помнить про условия, согласно которым были раскрыты модули. В первом случае мы получили корень . Он будет верен только при условии что
. Это условие соблюдено. Проверка также показывает что корень подходит:
Значит один из корней уравнений равен
Во втором случае мы получили множество корней от минус бесконечности до плюс бесконечности. Но это будет верно только при условии что
Например, если взять любое число из промежутка (−∞; +∞), но которое не будет удовлетворять условию , то это число не будет обращать наше уравнение в верное равенство.
Например, число 2 принадлежит промежутку (−∞; +∞), но не удовлетворяет условию , а значит число 2 не является корнем исходного уравнения. Проверка также покажет это:
А если взять к примеру число −5, то оно будет принадлежать промежутку (−∞; +∞) и удовлетворять условию , а значит будет обращать исходное уравнение в верное равенство:
Поэтому ответ надо записать так, чтобы были выполнены оба условия и
. Для наглядности нарисуем координатную прямую и обозначим её как x

Раскрыв модуль со знаком минус и решив получившееся уравнение, мы получили в ответе множество всех чисел от минус бесконечности до плюс бесконечности, но при этом было дано условие . Значит более точным ответ в этом случае будет таким:
Корнями уравнения −5x − 3 = −5x − 3 при условии являются все числа от минус бесконечности до
Значит на координатной прямой нужно заштриховать область слева от числа . Они будут иллюстрировать числа, меньшие
Число тоже является верным корнем исходного уравнения. Он был получен при раскрытии модуля со знаком плюс. Поэтому на координатной прямой пустой кружок нужно закрасить. Так мы включим число
во множество решений:
Тогда окончательный ответ будет выглядеть так:
Ответ:
Также, можно решить это уравнение сведя его в совокупность, дополнительно указав, что правая часть должна быть больше либо равна нулю:
Пример 2. Решить уравнение |2x − 3| = 3 − 2x
Решение
Решим исходное уравнение для случаев когда 2x − 3 ≥ 0 и 2x − 3 < 0
Ответ:
Использование координатной прямой
Рассмотрим ещё один способ решения элементарных уравнений с модулем — с помощью координатной прямой. Этот способ используется редко, но знать о нём не помешает.
Решим наше самое первое уравнение |x − 2| = 5 с помощью координатной прямой. Напомним, что корнями этого уравнения были числа 7 и −3.
Модуль есть расстояние от начала координат до точки A. Либо расстояние между двумя числами на координатной прямой.
Расстояние между двумя числами выражается в виде разности |x1 − x2|, где x1 — первое число, x2 — второе число.
Если внимательно посмотреть на уравнение |x − 2|= 5, то можно увидеть что его левая часть это расстояние от x до 2 (или от 2 до x) и это расстояние равно 5. Отмéтим на координатной прямой число x и число 2
Правая часть уравнения |x − 2|= 5 говорит о том, что расстояние от x до 2 составляет пять единиц:
Если расстояние от x до 2 равно 5, то и расстояние от 2 до x тоже равно 5. Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x
Видно, что отсчитав пять шагов влево мы попали в точку с координатой −3. А это один из корней, который мы находили для уравнения |x − 2|= 5.
Но пять целых шагов от числа 2 можно отсчитать не только влево, но и вправо:
Если отсчитать пять целых шагов вправо, то попадём в точку с координатой 7. Это тоже был корень уравнения |x − 2|= 5
Несколько модулей в одной части
Решим следующее уравнение:
|x − 5| − |x| = 1
Это уравнение содержит два модуля в левой части. Чтобы решить данное уравнение нужно раскрыть его модули. Рассмотреть нужно каждый из случаев:
- когда оба модуля больше либо равны нулю;
- когда оба модуля меньше нуля;
- когда первый модуль больше либо равен нулю, а второй модуль меньше нуля;
- когда первый модуль меньше нуля, а второй модуль больше либо равен нулю.
Не будем комментировать каждый случай, а сразу приведём решение:
Первые два случая корней не дали. В третьем случае нашелся корень 3, но он не удовлетворяет условиям x − 5 ≥ 0 и x < 0, поэтому не является корнем исходного уравнения.
В четвёртом случае нашёлся корень 2, который удовлетворяет условиям x − 5 < 0 и x ≥ 0. Также он удовлетворяет исходному уравнению.
Заметно, что такой способ решения уравнения неудобен. Если модулей в уравнении будет три, четыре или более, то придётся рассматривать намного больше случаев. Человек запутавшись, может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.
Поэтому такой вид уравнения как в данном примере удобнее решать методом интервалов. Об этом мы поговорим в следующем уроке.
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Задание 2. Решить уравнение:
Решение:
Задание 3. Решить уравнение:
Решение:
Задание 4. Решить уравнение:
Решение:
Ответ: 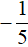
Задание 5. Решить уравнение:
Решение:
Ответ: 
Задание 6. Решить уравнение:
Решение:
Ответ: 
Задание 7. Решить уравнение:
Решение:
Ответ: 
Задание 8. Решить уравнение:
Решение:
Ответ: 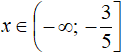
Задание 9. Решить уравнение:
Решение:
Ответ: 
Задание 10. Решить уравнение:
Решение:
Ответ: 
Задание 11. Решить уравнение:
Решение:
Ответ: 
Задание 12. Решить уравнение:
Решение:
Ответ: 0, 5.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Чтобы найти множество значений функции, сначала необходимо узнать множество значений аргумента, а затем с использованием свойств неравенств отыскать соответственные наибольшее и наименьшее значения функции. К этому сводится решение многих практических задач.
Инструкция
Выполните нахождение наибольшего значения функции, которая на отрезке имеет конечное число критических точек. Для этого вычислите ее значение
во всех точках, а также на концах отрезка. Из полученных чисел выберите наибольшее. Метод поиска наибольшего значения выражения
используется для решения различных прикладных задач.
Выполните для этого следующие действия: переведите задачу на язык функции, выберите параметр x, через него выразите нужную величину как функцию f(x). Используя средства анализа, найдите наибольшее и наименьшее значения функции на определенном промежутке.
Воспользуйтесь следующими примерами для нахождения значения функции. Найти значения функции y=5-корень из (4 – x2). Следуя определению квадратного корня, получим 4 – x2 > 0. Решите квадратичное неравенство, в результате получите, что -2
Возведите в квадрат каждое из неравенств, затем умножьте все три части на –1, прибавьте к ним 4. Затем введите вспомогательную переменную и сделайте предположение, что t = 4 – x2, где 0 значение функции получится на окончаниях промежутка.
Произведите обратную замену переменных, в результате вы получите следующее неравенство: 0 значение, соответственно, 5.
Воспользуйтесь методом применения свойств непрерывной функции, чтобы определить наибольшее значение
выражения
. В данном случае используйте числовые значения, которые принимаются выражением на заданном отрезке. Среди них всегда присутствует наименьшее значение
m и наибольшее значение
M. Между этими числами заключается множество значений функции.
Инструкция
Выполните нахождение наибольшего , которая на отрезке имеет конечное число критических точек. Для этого вычислите ее значение
во всех точках, а также на концах отрезка. Из полученных выберите наибольшее. Метод поиска наибольшего значения выражения
для решения различных прикладных задач.
Выполните для этого следующие действия: переведите задачу на язык функции, выберите параметр x, через него выразите нужную величину как функцию f(x). Используя средства анализа, найдите наибольшее и наименьшее значения функции на определенном промежутке.
Посчитайте количество необходимых действий и подумайте, в каком порядке их следует выполнять. Если вас затрудняет данный вопрос, обратите внимание, что прежде других выполняются действия, заключенные в скобки, затем – деление и умножение; и вычитание производятся в последнюю очередь. Чтобы было легче запомнить алгоритм выполняемых действий, в выражении над каждым знаком-оператором действий (+,-,*,:) тонким карандашом проставьте цифры, соответствующие выполнения действий.
Приступайте к выполнению первого действия, придерживаясь установленного порядка. Считайте в уме, если действия легко выполнить устно. Если же требуются вычисления (в столбик), осуществляйте их запись под выражением, указывая порядковый номер действия.
Четко отслеживайте последовательность выполняемых действий, оценивайте, что из чего нужно вычесть, что на что разделить и т.п. Очень часто ответ в выражении получается неверным из-за допущенных ошибок на данном этапе.
Если вы выполнили
предложенную вам работу, я предлагаю
вам проверить правильность ее выполнения:
№ 1. Решение: а) sin
α
= -т.к
cos
α
= 0,6, 1,5 πб)
tg
(π/2
+α)
= – ctg
α
= –
№
2. Решение:
№ 3. Решение: 6 sinα
, т.к. -1 ≤ sinα
≤ 1, то -6 ≤ 6 sinα
≤ 6. Значит наименьшее значение функции
равно -6, а наибольшее значение функции
равно 6.
№
4. Решение: а)150 0
=
б) 270 0
=
№ 5. Решение: а)
№ 6.
Решение:
(1 – sin 2
α):
(1- cos 2
α)
= cos 2 x: sin 2 x
= ctg 2 x
Надеюсь, что вы не
нашли ошибочных решений у себя или их
было очень мало!
-
«Преобразование тригонометрических выражений», практическая часть, 10 класс. Вариант Вариант Часть А
Документ
Найти наименьшее
значение
выражения
А5. Найти наибольшее
значение
выражения
3 sin
α – 2. 1,5 – 1,5sinα. 1) -7; 2) -5; 3) -3; 4) -1. 1) 1; 2) 2; 3) 3; 4) 4. А6. Найдите
значение
выражения
ctg 150°∙cos120° А6. Найдите
значение
выражения
cos210°/sin
… -
Задачи для самостоятельного решения. Упростить выражения
Документ
Найти наименьшее
значение
выражения
. Найти наименьшее
значение
выражения
. Найти наибольшее
значение
выражения
. Найти наименьшее
значение
выражения
, если. Переменные и положительны, при этом. Найдите
наименьшее
значение
выражение
суммы… -
Линейные и квадратные неравенства (повторение) (3 ч) Урок 1 Цели
Урок
Y = –x4; б) y = (x – 3)5 – 2. 2. Найдите
наименьшее
и наибольшее
значения
функции y = x6 на отрезке [– 2; 1]. 3. Определите… самостоятельно. в) S50
= 3175. г) S50
= –245 … . 4. При каком значении
х значение
выражения
является числом иррациональным? … -
Тема: “Применение производной к решению экстремальных задач”
Документ
BL=h, AC=b, то у= исключая у из выражения
для S находим S = Ищем максимум для… Найдите
наименьшее
и наибольшее
значения
функции: +sin2x на (0 😉 Решение: D (f)=R Найдем
производную: f” (x) = – cos x +2 sinxcosx = cos x (2 sin
x-) Найдем
критические…
Как решать уравнения с модулем: основные правила
30 декабря 2016
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft( x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft( x right) right|=a]
Ну и как такое решать? Напомню: $fleft( x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
или:
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left( 2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
[2x+1=5Rightarrow 2x=4Rightarrow x=2]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 \& 2x+1 lt 0 \end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft( x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; \& 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. \end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; \& 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. \end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft( x right)$ и $gleft( x right)$ :
[left| fleft( x right) right|=gleft( x right)Rightarrow left{ begin{align}& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, \& 2xge 0. \end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2xRightarrow 3x-2x=2Rightarrow x=2; \& 3x-2=-2xRightarrow 5x=2Rightarrow x=frac{2}{5}. \end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5};$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft( x right) right|=gleft( x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left( x-{{x}^{3}} right), \& x-{{x}^{3}}ge 0. \end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; \& 2{{x}^{3}}-3{{x}^{2}}=0; \end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left( 2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 \& 2x-3=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left( x-{{x}^{3}} right); \& {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; \& -3{{x}^{2}}+2x=0; \& xleft( -3x+2 right)=0. \end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 \& -3x+2=0 \end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
[x-{{x}^{3}}ge 0]
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; \& x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; \& x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; \end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft( x right) right|=left| gleft( x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left( x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
[x-1=pm left( {{x}^{2}}-3x+2 right)]
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]
[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft( x right) right|=gleft( x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, \& -a,quad a lt 0. \end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac{5}{3}]
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
[x=frac{5}{3}Rightarrow 3x-5=3cdot frac{5}{3}-5=5-5=0]
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
[5-3x=5-3x]
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac{5}{3}]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
[xin left( -infty ;frac{5}{3} right)]
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
[3x-5=0Rightarrow left| 3x-5 right|=0]
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
[0=3x-5Rightarrow 3x=5Rightarrow x=frac{5}{3}]
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Итого окончательный ответ: $xin left( -infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Смотрите также:
- Простейшие уравнения с модулем
- Уравнение с двумя модулями
- Сложные выражения с дробями. Порядок действий
- Сводный тест по задачам B15 (2 вариант)
- Как решать биквадратное уравнение
- B4: счетчики на электричество
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».