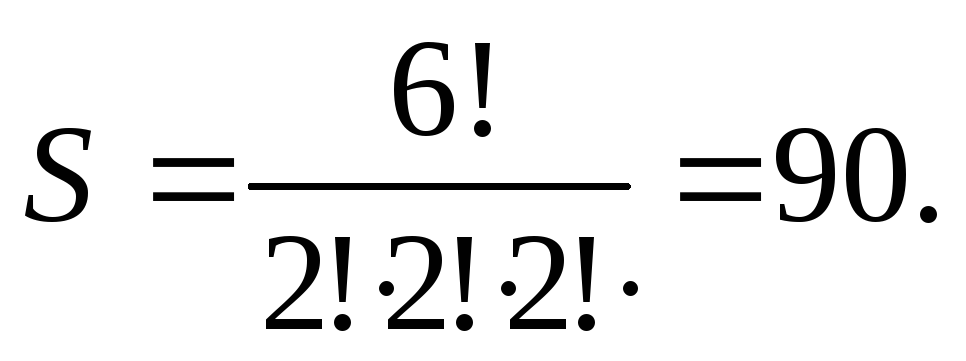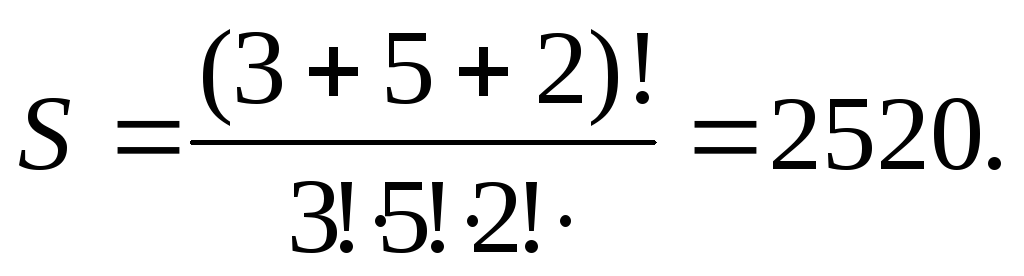Как найти наибольший биномиальный коэффициент разложения - Сайт, где вы сможете решить свои вопросы

Пусть
множество,
состоящее изэлементов. Любое подмножество(включая и пустое подмножество), содержащееэлементов, называетсясочетаниемпоэлементов из
(или комбинацией поэлементов из₎,
при этом, разумеется,,
т.е.

сочетанияминазывают комбинации,
составленные изnразличных элементов поmэлементам. Сочетания считаются различными,
если их состав отличаются друг от друга
хотя бы одним элементом.

Теорема 2. Число сочетаний из n
элементов по m
определяется равенством:

(3)
.

Доказательство.Пустьзаданное
множество, состоящее изэлементов,–
какое либо подмножество,
содержащееэлементов. Составим всевозможные
перестановки из элементов,
получимразличных строк длиной.
Если указанную операцию произвести с
каждымэлементным
подмножеством множества,
то получим всегоразличных строк длиной.
Естественно, таким способом должны
получиться без исключения все строки

длиной
без
повторений, которые можно составить из
элементов множества.
Поскольку, по теореме 1, число таких
строкто имеем равенство,
из которого следует доказательство
теоремы.Подчеркнем, что
числа размещений, перестановок и
сочетаний связаны равенствами

т.е.
с учетом равенство (2) получаем (3). В
частности,

Далее,
рассмотрим несколько примеров на
применение комбинаторных понятий.

Пример 7. Сколько трехзначных
чисел можно составить из цифр 1, 2, 3, если
каждая цифра входит в изображение числа
только один раз?

Решение: Искомое число трехзначных
чисел:

Выпишите
самостоятельно эти наборы чисел.

Пример 8. Сколько можно составить
сигналов из 6 флажков различного цвета,
взятых

по 2?

Решение: Искомое число сигналов

Пример 9. Сколькими способами
можно выбрать две детали из ящика,
содержащего 10 деталей?

Решение: Искомое число способов.

Пример 10. Какое количество партий
сыграли 8 шахматистов, встречаясь с
каждым партнером только один раз.

Решение. В данной задаче набор
пар несущественен.

Двухэлементное
множество можно упорядочить только
2!=2 способами (число
перестановок). Следовательно, общее
число партий (пар) будет в 2! меньше, чем
число размещений.
Поэтому, общее число партий равно.

Решение этой задачи можно изящно
иллюстрировать геометрически (см.
Рис.4). Рассмотрим выпуклый восьмиугольник
.
С каждой любой вершины восьмиугольника
можно провести к другим вершинам семь
отрезков, т.е. количество встреч партий
шахматистов с другими партнерами равно
числу отрезков, соединяющих с остальными.
Общее число вершин (шахматистов) равно
8, а так как отрезкиАВиВАи т.д.
являются равными, то различных отрезков
(партий) будет равно.

Задания. 1.Эту же задачу решите, с
помощью турнирной таблицу встреч.

Бином Ньютона. Пустьитакие величины, для которых имеет место
равенство.
Из школьного курса известны алгебраические
тождества:

Продолжая, этот процесс, т.е. пользуясь
равенствами
можно написать следующее равенство:

Данное равенство называется
формулой бинома Ньютона. При этом мы
воспользовались равенствами:
=1.
Неотрицательные целые числа(обычно называют их биномиальными
коэффициентами) определены равенствами:

если
ипри остальных значениях.
Напомним, что принято 0!=1.

В
частности, имеют место равенства:

Обычно
формула бинома Ньютона доказывается
методом математической индукции с
учетом равенств:

Основные свойства бинома Ньютона.

1. В разложении
содержитсяслагаемых.

2. Показатель степени параметра
убывает отnдо 0,
напротив, показатель степенивозрастает от 0 до n,
в любом случае сумма показателей
степени величин (параметров)иравнаn – показателю
степени бинома.

3. Биномиальные коэффициенты, равноудаленные
от концов разложения, равны между собой,
т.е.
А также верно и другое разложение

(1)

4. Для биномиальных коэффициентов
верно равенство

Некоторые непосредственные выводы.

5. Из общей формулы (1) непосредственно
выводятся следующие равенства:

а. Если сумма чисел,
то имеет место равенство

В
дальнейшем это равенство играет важную
роль в теории вероятностей.

в. Если
,
то сумма биномиальных коэффициентов
равно,
т.е. верна формула

с. Если
,
то сумма биномиальных коэффициентов
всегда равна нулю.

В частности, полагая
,
получим равенство

Формулу
(1) можно переписать в виде:

6. Биномиальные коэффициенты сначала
возрастают, а затем, убывают. При этом:

– если показатель степени бинома
четный, то биномиальный коэффициент
среднего слагаемого разложения
наибольший;

– если же показатель степени бинома
нечетный, то биномиальные коэффициенты
двух средних слагаемых равны между
собой и являются наибольшими;

– на основании свойства 4.биномиальные
коэффициентымогут быть вычислены с помощью так
называемого «треугольника Паскаля»

В этих «треугольных» таблицах
легко заметить, что каждое число, кроме
крайних единиц, является суммой двух
вышерасположенных чисел.

7. Поскольку биномиальный коэффициент
начинается с нулевого члена, то в общем
виде принято ()
– ое слагаемоесчитать
–
им членом разложения, и обозначается:

Задача 1. Для выражениянайти
шестое слагаемое.

Решение.Нужно воспользоваться
биномиальной формулой, когда.

Ответ.
.

Задача 2..Найдите наибольший член
разложения

Решение.Для решения этой задачи
необходимо выяснить для каких
выполняется неравенства:

Рассмотрим отношение

Отсюда
следует, что при

т.е.,
при
коэффициенты убывают. Значит, для номеранаибольший
член разложения бинома и он же будетдесятым слагаемым

Задача 3. Найти член разложения,
не содержащий положительной степени(т.е. найти слагаемое содержащее).

Решение. Так как,тогда выписывая показатель степени,
после несложных упрощений получим:

Следовательно, четвёртый
член разложения (он же пятое
слагаемое) является
решением задачи.

Ниже предложим некоторые сведения из
теории арифметических функций.

Упражнения:
А. Докажите,
что

1.
При
любом простом

биномиальные
коэффициенты
делятся
на число
.

2.
Докажите
тождества:

,
еслилюбое
нечётное простое число..

В.
Дополнительные сведения. Пусть
–
каноническое представление натурального
числа,
определим классическую функцию Мебиусас помощью комбинаторных коэффициентов

равенством:

(**)

Докажите, что

1. Для
любых взаимно простых натуральных

,
(свойство
мультипликативности)

2.(свойство ортогональности)

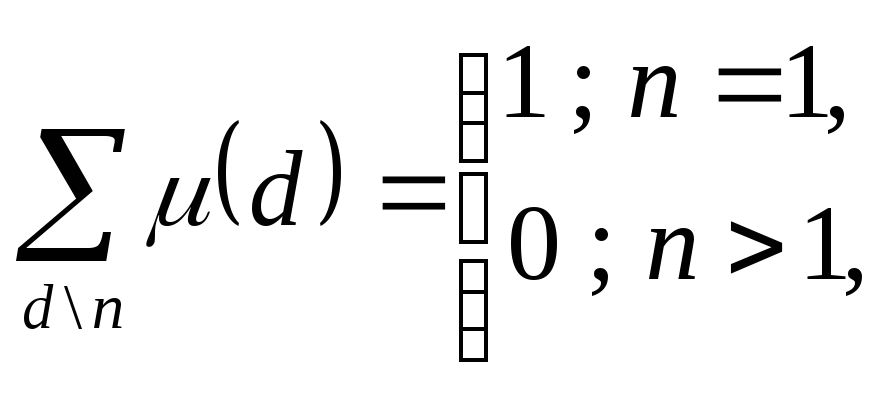
где
суммирование ведётся по всем положительным
целым делителям числа
.

3.
Вычислите функцию

Примечание.
Классическая
функция Мебиуса определяется несколько
иначе. По этому поводу можно обратиться,
например, к известным учебникам по
теории чисел
[3;4].
Определение
(**) предложенное здесь выгодно по
многим причинам. Во – первых, функция
определена одной формулой, во – вторых,
легко определяются различные обобщения
(речь идёт о функциях

которая
равна 0 или 1, смотря по тому, делится
или не делится число
натую степень числа,
а также других арифметических функций,
связанные с функцией Мебиуса). Подробные
сведения о функции Мебиуса и её свойства
можно найти в учебниках по теории чисел
[3;4].

Читателям
интересующихся более обстоятельно
этими вопросами, рекомендуем обратиться
к фундаментальным источникам по
аналитической теории чисел [5-7].

Рассмотрим ещё
одну тематику,
обобщающую
понятие размещения.

8.
Размещения данного состава. Полиномиальная
формула.

Начнём со следующей
простой задачи

.
Состав строки.
Размещение
данного состава. Рассмотрим
наборы (строки)
и.
Очевидно, что они различны, но имеют
один и тот же «состав»
– в каждую из них входят три буквы
и две буквы.
Далее, уточним понятиесостава
строки.
Пусть
некоторое
членное
множество,
строка длиной,
составленная из элементов множества.
Тогда каждому номеруиз совокупностибудет
соответствовать число
указывающее, на количество участия
элементовв строке
.
Выписывая по порядку эти числа, получаем
новую строку,
которую и называют составом строки.

Например, если
и
,
то строкаимеет следующий состав.
Следовательно, в строкеэлементучаствует три раза, элементне участвует, элементучаствует два раза, элементучаствует один раз. Две строки, имеющие
один и тот же состав, могут отличаться
друг от друга лишь порядков элементов.
Их называютразмещениями
с повторениями данного состава.

Рассмотрим следующую
комбинаторную задачу:
найти
число размещений, имеющий данный состав
.

Приведём
основное утверждение о числе составов

Теорема
3.
Количество

–
различных
последовательностей (составов),
составленных из элементов
,
в которых
каждый элемент
встречается

раз
(равно

(4)
.

Доказательство.
Обозначим
количество
составов указанных в формулировке
теоремы 1 буквой
.
А так же, положим.
Введём в рассмотрениепроизвольных
различных элементов:

.
Для любой исходной последовательности

строим различные перестановки из
указанных
элементов, заменяя элементы по следующему
правилу. На тех местах исходной
последовательности, где стояло одно и
то же(этот элемент встречалсяраз), записываем какой-нибудь перестановку
изэлементов
.
Согласно
равенству (2) такое действие для одного
можно осуществлять в точностиразличными способами. Проделав такое
действие для каждого(),
мы получим некоторую перестановку изиз указанных выше элементов. На основании
формулы умножения (см. пункт)
для любой последовательности строки
получим всего указанным способом
различных перестановок из
элементов. Для различных исходных
последовательностей вышеуказанным
способом мы, естественно, получаем
различные перестановки из взятыхэлементов.
При этом любая из выбранныхэлементов может быть получена этим
способом, если в качестве начальной
последовательности выбрать ту строку,
которая образуется в результате замены
всех элементов
во
взятой перестановке одним элементом
для кахдого.
Таким образом, с учётом равенства (2)
получаем:,
следовательно,

И с учётом нашего
обозначения
,
теорема доказана.

Пример 1. Количество
различных 6 – значных натуральных чисел,
которые можно записать с помощью цифр
1,2,3 так, чтобы каждая цифра встречалась
в записи по два раза, равно:

Пример 2. В
наличии имеются книги трёх наименований,
причём имеется три экземпляра книг
одного наименования, пять экземпляров
другого и два экземпляра третьего.
Количество различных размещений этих
книг на одной полке составляет:

Если в наличии
имеются книги
различных наименований, причём поэкземпляров книг каждого наименования,
то всеэкземпляров
книг могут быть размещены на полке

способами.

Пример 3. В
одном ряду шахматной доски располагаются:
1 король, 1
ферз, 2 слона, 2 коня, 2 ладьи. Количество
всевозможных расположения этих фигур
в одном ряду равно:

.
Полиномиальная формула. Обобщением
формулы Бинома Ньютона является так
называемая полиномиальная формула,
которую приведём без доказательства.

Пусть
любые
числа (или произвольные комутативные
объекты). Имеет место

следующее утверждение

Теорема 4.
Справедлива
полиномиальная формула

(4)

где
суммирование распространяется на
всевозможные целые числа
,
для которых

Следствие.

1) Для
случая
,
получаем формулу

(5)

2) Для случая
имеет
место равенство

Задания:
1. На
основании равенство (5) проверьте
тождество

2.
Пусть
,
тогда при целомсправедливо
неравенство

Это
известное неравенство Бернулли.

Указание.
Используйте
метод математической индукции.

В
завершении этого раздела сформулируем
известную формулу Стирлинга без
доказательства.

где
основание
натурального логарифма. Эта формула
обычно применяется при больших значениях.
В частности, из неё вытекает, чтос точностью доприближается выражением

Другими
словами, справедливо (с учётом свойства
логарифмической функции) неравенство

Источник

Биномиальный коэффициент — коэффициент перед членом разложения бинома Ньютона $(1+x)^{n}$ по степеням . Коэффициент при $x^{k}$ обозначается или и читается «биномиальный коэффициент из по » (или «число сочетаний из по »):

${displaystyle (1+x)^{n}={binom {n}{0}}+{binom {n}{1}}x+{binom {n}{2}}x^{2}+ldots +{binom {n}{n}}x^{n}=sum _{k=0}^{n}{binom {n}{k}}x^{k}}$

для натуральных степеней .

Биномиальные коэффициенты могут быть также определены для произвольных действительных показателей . В случае произвольного действительного числа биномиальные коэффициенты определяются как коэффициенты разложения выражения $(1+x)^{n}$ в бесконечный степенной ряд:

${displaystyle (1+x)^{n}=sum _{k=0}^{infty }{binom {n}{k}}x^{k}}$

где в случае неотрицательных целых все коэффициенты при k>n обращаются в нуль и поэтому данное разложение является конечной суммой.

В комбинаторике биномиальный коэффициент для неотрицательных целых чисел и интерпретируется как количество сочетаний из по , то есть как количество всех (нестрогих) подмножеств (выборок) размера в -элементном множестве.

Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.

Явные формулы[править | править код]

Вычисляя коэффициенты в разложении $(1+x)^{n}$ в степенной ряд, можно получить явные формулы для биномиальных коэффициентов .

Для всех действительных чисел и целых чисел :

${displaystyle {binom {n}{k}}={begin{cases}{frac {n(n-1)(n-2)cdot ldots cdot (n-k+1)}{k!}},&kgeqslant 0\0,&k<0end{cases}}}$

где обозначает факториал числа .

Для неотрицательных целых и также справедливы формулы:

${displaystyle {binom {n}{k}}={begin{cases}{frac {n!}{k!(n-k)!}},&0leqslant kleqslant n\0,&k>nend{cases}}}$

Для целых отрицательных показателей коэффициенты разложения бинома ${displaystyle (1+x)^{-n}}$ равны:

${displaystyle {binom {-n}{k}}={begin{cases}(-1)^{k}cdot {frac {(n+k-1)!}{k!(n-1)!}},&kgeqslant 0\0,&k<0end{cases}}}$

Треугольник Паскаля[править | править код]

Визуализация биномиального коэффициента до 4 степени

Тождество:

{n choose k}={n-1 choose k-1}+{n-1 choose k}

позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел , в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:

${begin{matrix}n=0:&&&&&1&&&&\n=1:&&&&1&&1&&&\n=2:&&&1&&2&&1&&\n=3:&&1&&3&&3&&1&\n=4:&1&&4&&6&&4&&1\vdots &&vdots &&vdots &&vdots &&vdots &end{matrix}}$

Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от той, что выписана здесь, поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, Омару Хайяму).

Если в каждой строке треугольника Паскаля все числа разделить на $2^{n}$ (это сумма всех чисел в строке), то все строки при стремлении к бесконечности примут вид функции нормального распределения.

Свойства[править | править код]

Производящие функции[править | править код]

Для фиксированного значения производящей функцией последовательности биномиальных коэффициентов является:

${displaystyle sum _{k=0}^{infty }{binom {n}{k}}x^{k}=(1+x)^{n}}$

Для фиксированного значения производящая функция последовательности коэффициентов равна:

${displaystyle sum _{n}{binom {n}{k}}y^{n}={frac {y^{k}}{(1-y)^{k+1}}}}$

Двумерной производящей функцией биномиальных коэффициентов для целых n,k является:

${displaystyle sum _{n,k}{binom {n}{k}}x^{k}y^{n}={frac {1}{1-y-xy}}}$

, или ${displaystyle sum _{n=0}^{infty }sum _{k=0}^{n}{binom {n}{k}}x^{k}y^{n}={frac {1}{1-y-xy}}}$

Делимость[править | править код]

Из теоремы Люка следует, что:

Основные тождества[править | править код]

.
${displaystyle {binom {n}{k}}=(-1)^{k}{binom {-n+k-1}{k}}}$ .
(правило симметрии).
${displaystyle {n choose k}={frac {n}{k}}{n-1 choose k-1}}$ (вынесение за скобки).
(замена индексов).
.

Бином Ньютона и следствия[править | править код]

а более общем виде

${displaystyle sum _{k=-a}^{a}(-1)^{k}{a+b choose a+k}{b+c choose b+k}{c+a choose c+k}={frac {(a+b+c)!}{a!,b!,c!}}}$

Свёртка Вандермонда и следствия[править | править код]

Свёртка Вандермонда:

${displaystyle sum _{k}{r choose m+k}{s choose n-k}={r+s choose m+n}}$

где а . Это тождество получается вычислением коэффициента при ${displaystyle x^{m+n}}$ в разложении ${displaystyle (1+x)^{r}(1+x)^{s}}$ с учётом тождества ${displaystyle (1+x)^{r+s}=(1+x)^{r}(1+x)^{s}}$ . Сумма берётся по всем целым , для которых . Для произвольных действительных , число ненулевых слагаемых в сумме будет конечно.

Следствие свёртки Вандермонда:

${n choose 0}{a choose a}-{n choose 1}{a+1 choose a}+ldots +(-1)^{n}{n choose n}{a+n choose a}=(-1)^{n}{a choose n}$

Более общее тождество:

$sum _{{i=0}}^{{p}}(-1)^{i}{p choose i}prod _{{m=1}}^{{n}}{i+s_{m} choose s_{m}}=0$

, если $sum _{{m=1}}^{n}{s_{m}}<p$

Ещё одним следствием свёртки является следующее тождество:
${displaystyle {n choose 0}^{2}+{n choose 1}^{2}+ldots +{n choose n}^{2}={2n choose n}}$ .

Другие тождества[править | править код]

${displaystyle {binom {n}{t}}+{binom {n}{t+s}}+{binom {n}{t+2s}}+ldots ={frac {1}{s}}sum _{j=0}^{s-1}left(2cos {frac {pi j}{s}}right)^{n}cos {frac {pi (n-2t)j}{s}}}$

Также имеют место равенства:

${displaystyle {begin{alignedat}{2}{binom {n}{3}}&={frac {n(n-1)(n-2)}{color {Green}2}}-sum _{i=2}^{n-1}{(n-i)(n-i+1)}=\&=n(n-1)(n-2)-sum _{i=2}^{n-1}{(n-i)({color {Green}2}n-i+1)}=\&=3{binom {n}{3}}-2{binom {n}{3}};\end{alignedat}}}$

${displaystyle {begin{alignedat}{2}{binom {n}{4}}&={frac {n(n-1)(n-2)(n-3)}{color {Green}2}}-sum _{i=3}^{n-1}{(n-i)left(n(n-1)-sum _{i_{0}=1}^{i-2}i_{0}right)}=\&=n(n-1)(n-2)(n-3)-sum _{i=3}^{n-1}{(n-i)left({color {Green}2}n(n-1)-sum _{i_{0}=1}^{i-2}i_{0}right)}=\&=24{binom {n}{4}}-23{binom {n}{4}};\end{alignedat}}}$

${displaystyle {begin{alignedat}{2}{binom {n}{5}}&={frac {n(n-1)(n-2)(n-3)(n-4)}{color {Green}2}}-\&-sum _{i=4}^{n-1}{(n-i)left(n(n-1)(n-2)-sum _{i_{0}=1}^{i-3}sum _{i_{1}=1}^{i_{0}}i_{1}right)}=\&=n(n-1)(n-2)(n-3)(n-4)-\&-sum _{i=4}^{n-1}{(n-i)left({color {Green}2}n(n-1)(n-2)-sum _{i_{0}=1}^{i-3}sum _{i_{1}=1}^{i_{0}}i_{1}right)}=\&=120{binom {n}{5}}-119{binom {n}{5}}.end{alignedat}}}$

Откуда следует:

${displaystyle {binom {n}{3}}={frac {sum limits _{i=2}^{n-1}{(n-i)(2n-i+1)}}{2}}={frac {sum limits _{i=2}^{n-1}{(n-i)left(2A_{n}^{1}-{binom {i-1}{1}}right)}}{2}};}$

${displaystyle {binom {n}{4}}={frac {sum limits _{i=3}^{n-1}{(n-i)left(2n(n-1)-sum limits _{i_{0}=1}^{i-2}i_{0}right)}}{23}}={frac {sum limits _{i=3}^{n-1}{(n-i)left(2A_{n}^{2}-{binom {i-1}{2}}right)}}{23}};}$

${displaystyle {begin{alignedat}{2}&{binom {n}{5}}={frac {sum limits _{i=4}^{n-1}{(n-i)left(2n(n-1)(n-2)-sum limits _{i_{0}=1}^{i-3}sum limits _{i_{1}=1}^{i_{0}}i_{1}right)}}{119}}=\&={frac {sum limits _{i=4}^{n-1}{(n-i)left(2A_{n}^{3}-{binom {i-1}{3}}right)}}{119}};\end{alignedat}}}$

${displaystyle {binom {n}{k}}={frac {sum limits _{i=k-1}^{n-1}{(n-i)left(2A_{n}^{k-2}-{binom {i-1}{k-2}}right)}}{k!-1}}}$

где $A_{n}^{k}$ — количество размещений из по .

Матричные соотношения[править | править код]

Если взять квадратную матрицу, отсчитав элементов по катетам треугольника Паскаля и повернув матрицу на любой из четырёх углов, то детерминант этих четырёх матриц равен ±1 при любом , причём детерминант матрицы с вершиной треугольника в верхнем левом углу равен 1.

В матрице числа на диагонали повторяют числа строк треугольника Паскаля (). Её можно разложить в произведение двух строго диагональных матриц: нижнетреугольной и получаемой из неё транспонированием:

${displaystyle {begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}=UU^{T}}$

где . Обратная матрица к имеет вид:

${displaystyle U^{-1}={begin{bmatrix}(-1)^{i+j}{binom {i}{j}}end{bmatrix}}}$

Таким образом, можно разложить обратную матрицу к в произведение двух строго диагональных матриц: первая матрица — верхнетреугольная, а вторая получается из первой путём транспонирования, что позволяет дать явное выражение для обратных элементов:

${begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}}=sum _{{k=0}}^{{p}}(-1)^{{m+n}}{binom {k}{m}}{binom {k}{n}}$

, где

Элементы обратной матрицы меняются при изменении её размера и, в отличие от матрицы , недостаточно приписать новую строку и столбец. Столбец матрицы есть многочлен степени по аргументу , следовательно, первые p столбцов образуют полный базис в пространстве векторов длины +1, чьи координаты могут быть интерполированы многочленом равной или меньшей степени p-1 . Нижняя строка матрицы ${begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}}$ ортогональна любому такому вектору.

${begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{p,n}}^{{-1}}=sum _{{k=0}}^{{p}}(-1)^{{p+n}}{binom {k}{p}}{binom {k}{n}}=(-1)^{{p+n}}{binom {p}{n}}$

$sum _{{n=0}}^{{p}}(-1)^{{p+n}}{binom {p}{n}}{P}_{{a}}(n)=0$

при

, где ${P}_{{a}}(n)$

многочлен степени

Если произвольный вектор длины p+1 можно интерполировать многочленом степени i<p , то скалярное произведение со строками (нумерация с 0) матрицы ${begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}}$ равно нулю.
Используя тождество выше и равенство единицы скалярного произведения нижней строки матрицы ${begin{bmatrix}{binom {i+j}{i}}end{bmatrix}}_{{m,n}}^{{-1}}$ на последний столбец матрицы , получаем:

${displaystyle sum _{n=0}^{p}(-1)^{p+n}{binom {p}{n}}{n}^{p}=p!}$

Для показателя большего можно задать рекуррентную формулу:

${displaystyle sum _{n=0}^{p}(-1)^{p+n}{binom {p}{n}}{n}^{p+a}=p!{P}_{2a}(p)={f}_{a}(p)}$

где многочлен

${displaystyle {P}_{2a+2}(p)=sum _{x=1}^{p}x{P}_{2a}(x);quad ageqslant 0;quad {P}_{0}(p)=1}$

Для доказательства сперва устанавливается тождество:

${displaystyle {f}_{a}(p+1)=sum _{x=0}^{a}{(p+1)}^{x+1}{f}_{a-x}(p)}$

Если требуется найти формулу не для всех показателей степени, то:

${displaystyle {P}_{2a}(p)={frac {p}{{2}^{a}}}{binom {p+a}{a}}{Q}_{a-1}(p);quad a>0}$

Старший коэффициент ${Q}_{{a-1}}(p)$ равен 1, потребуется a-1 значений, чтобы найти другие коэффициенты:

${Q}_{{a-1}}(p)=p(p+1){T}_{{a-3}}(p)$

для

{displaystyle aequiv 1{pmod {2}};ageqslant 3}

Асимптотика и оценки[править | править код]

Непосредственно из формулы Стирлинга следует, что для верно $C_{n}^{{alpha n}}sim {sqrt {{frac {1}{2pi alpha (1-alpha )n}}}}left({{frac {1}{alpha }}}right)^{{alpha n}}left({{frac {1}{1-alpha }}}right)^{{(1-alpha )n}}=left({{frac {1}{alpha ^{alpha }{(1-alpha )}^{{(1-alpha )}}}}+o(1)}right)^{{n}}$ .

Целозначные полиномы[править | править код]

Биномиальные коэффициенты ${displaystyle {tbinom {x}{0}}=1,{tbinom {x}{1}}=x,{tbinom {x}{2}}={tfrac {x^{2}}{2}}-{tfrac {x}{2}}}$ , … являются целозначными полиномами от , то есть принимают целые значения при целых значениях , — это нетрудно понять, например, по треугольнику Паскаля. Более того, они образуют базис целозначных полиномов, в котором все целозначные полиномы выражаются как линейные комбинации с целыми коэффициентами.^[1]

В то же время стандартный базис ${displaystyle 1,x,x^{2}}$ , … не позволяет выразить все целочисленные полиномы, если использовать только целые коэффициенты, так как уже ${displaystyle {tbinom {x}{2}}={tfrac {x^{2}}{2}}-{tfrac {x}{2}}}$ имеет дробные коэффициенты при степенях .

Этот результат обобщается на полиномы многих переменных. А именно, если полином степени имеет вещественные коэффициенты и принимает целые значения при целых значениях переменных, то

${displaystyle R(x_{1},dots ,x_{m})=Pleft({binom {x_{1}}{1}},dots ,{binom {x_{1}}{k}},dots ,{binom {x_{m}}{1}},dots ,{binom {x_{m}}{k}}right)}$

где — полином с целыми коэффициентами.^[2]

Алгоритмы вычисления[править | править код]

Биномиальные коэффициенты можно вычислить с помощью рекуррентной формулы , если на каждом шаге хранить значения при . Этот алгоритм особенно эффективен, если нужно получить все значения при фиксированном . Алгоритм требует O(n) памяти ( $O(n^{2})$ при вычислении всей таблицы биномиальных коэффициентов) и $O(n^{2})$ времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени), где — «» большое.

При фиксированном значении биномиальные коэффициенты могут быть вычислены по рекуррентной формуле ${displaystyle {tbinom {n}{k}}={tfrac {n}{n-k}}cdot {tbinom {n-1}{k}}}$ с начальным значением . Для вычисления значения этот метод требует O(1) памяти и O(n) времени.

Если требуется вычислить коэффициенты при фиксированном значении , можно воспользоваться формулой ${displaystyle {tbinom {n}{k}}={tfrac {n-k+1}{k}}cdot {tbinom {n}{k-1}}}$ при начальном условии . При каждом шаге итерации числитель уменьшается на (начальное значение равно ), а знаменатель соответственно увеличивается на (начальное значение — ). Для вычисления значения этот метод требует O(1) памяти и O(k) времени.

Примечания[править | править код]

↑ Прасолов В. В. Глава 12. Целозначные многочлены // Многочлены. — М.: МЦНМО, 1999, 2001, 2003. Архивная копия от 21 января 2022 на Wayback Machine
↑ Ю. Матиясевич. Десятая проблема Гильберта. — Наука, 1993.

Литература[править | править код]

Биномиальные коэффициенты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17—25.
Кузьмин О. В. Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6, № 5. — С. 101—109.
Ландо С. К. Теневое исчисление // VIII летняя школа «Современная математика». — Дубна, 2008.
Винберг Э. Б. Удивительные арифметические свойства биномиальных коэффициентов // Математическое просвещение. — 2008. — Вып. 12. — С. 33–42.
Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Математические основы информатики = Concrete Mathematics. A Foundation for Computer Science. — 2-е. — М.: Мир; Бином. Лаборатория знаний; «Вильямс», 1998—2009. — 703, 784 с. — ISBN 95-94774-560-7, 78-5-8459-1588-7.

Источник

Бином Ньютона

Авторы
Руководители
Файлы работы
Наградные документы

Скукин Д.И. 1

1МАОУ “Гимназия №1”

Дятел О.И. 1

1МАОУ “ГИМНАЗИЯ №1”

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Вступление

Формула бинома Ньютона для целых положительных показателей была известна задолго до Исаака Ньютона, но он в 1676 году указал на возможность распространения этого разложения и на случай дробного или отрицательного показателя. Строгое обоснование указанных Ньютоном возможностей дал Н. Абель в 1826 году. В случае дробного или отрицательного n все биномиальные коэффициенты отличны от нуля, а правая часть формулы получает бесконечный ряд членов (биномиальный ряд). Бином Ньютона играет роль во многих областях математики, в частности в алгебре и теории чисел.

Бином Ньютона — формула разложения произвольной натуральной степени двучлена (a+b)n в многочлен. Каждый из нас знает наизусть формулы «квадрата суммы» (a+b)2 и «куба суммы» (a+b)3,но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности, которые я рассматриваю в своей работе.

План

1. Вступление

2. Цели и задачи

3. История бинома Ньютона

4. Бином Ньютона

5. Свойства разложения бинома Ньютона

6. Решение задач с применением бинома Ньютона

7. Заключение

8. Список используемой литературы

Цели и задачи

Изучить бином Ньютона и его свойства

Показать применение данных свойств при решении задач

Показать применение бинома Ньютона при решении технических задач

История бинома Ньютона

Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю (англ.), жившему в XIII веке, а также исламским математикам ат-Туси (XIII век) и ал-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.

Исаак Ньютон около 1677 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.

Что означает фразеологизм «Бином Ньютона»?

Шутливая фраза, применяется по отношению к плевому делу, простой задаче, которую некоторые ошибочно считают непосильной для выполнения или архисложной.

Возникновение фразы: из романа Михаила Булгакова (1891 – 1940 гг.) «Мастер и Маргарита» (1940 г.).

Слова Коровьева, которые решил прокомментировать разговор Воланда с буфетчиком Соковым. Буфетчик жалуется на зрителей, которые расплатились с ним фальшивыми деньгами, чем «на сто девять рублей наказали буфет».

« – Ну, конечно, это не сумма, – снисходительно сказал Воланд своему гостю, – хотя, впрочем, и она, собственно, вам не нужна. Вы когда умрете?

Тут уж буфетчик возмутился.

– Это никому не известно и никого не касается, – ответил он.

– Ну да, неизвестно, – послышался все тот же дрянной голос (Коровьева) из кабинета, – подумаешь, бином Ньютона! Умрет он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвертой палате».

В художественной литературе

В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.

В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о математике профессоре Мориарти:

Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая карьера.

В романе «Мастер и Маргарита» М. А. Булгакова:

«подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».

Позже это же выражение «Подумаешь, бином Ньютона!». упомянуто в фильме «Сталкер» А. А. Тарковского.

Роман Е. Н. Вильмонт получил название «Мимолетности, или Подумаешь, бином Ньютона!».

Бином Ньютона

Рассмотрим произведения двух, трех и четырех биномов (двучленов) вида х-{- а. После умножения и приведения подобных членов по х получим

(х + а) (х + b) = x² + (а + Ь) х + ab

(х + а) (х + b) (х + с) = x³ + (а + Ь + с) х² + (аb + ас + bс) х + abc

(х + а) (х + b) (х + с) (х + d) = x⁴ + (а + Ь + с + d) x³ + (ab + ac + ad + bc + bd + cd) x² + (abc + abd + acd + bcd) x + abcd.

Рассматривая эти произведения, легко заметить, что произведение биномов, отличающихся только вторыми членами, есть многочлен, упорядоченный по убывающим степеням первого члена х, степень которого равна числу перемножаемых биномов. Коэффициент первого члена многочлена равен 1, а последующие образуются так: второй коэффициент равен сумме всех вторых членов биномов, третий — сумме всевозможных произведений вторых членов по два, четвертый — сумме всевозможных произведений вторых членов по три и т. д. 11оследний член многочлена равен произведению всех вторых членов биномов.

Методом математической индукции можно доказать, что правило образования произведения биномов, отличающихся только вторыми членами, установленное из рассмотрения произведений двух, трех II четырех биномов, верно для произведения любого конечного числа биномов.

Для произведения n биномов справедлива формула:

(x+a₁) (x+a₂) (x+a₃)… (x+a_n-1) (x+a_n)=xⁿ+S₁x^n-1+S₂x^n-2+…S_n-1x+S_n

S₁=a₁+a₂+a₃+…+a_n

S₂=a₁a₂+a₁a₃+…+a_n-2a_n+a_n-1a_n

S₃=a₁a₂a₃+a₁a₂a₄+…+a_n-2a_n-1a_n

……………………………………………..

S_n-1=a₁a₂a₃…a_n-1+…+a₂a₃a₄…a_n

S_n=a₁a₂a₃…a_n-1a_n

Эта формула верна и в том случае, если вторые члены равны между собой.

Если в формуле для произведения n биномов положить a₁=a₂=a₃=…=a_n=a, то получим

(x+a)ⁿ=xⁿ=S₁x^n-1+S₂x^n-2+…+S_n-1x+S_n

Окончательныйвидформулы

(x+a)ⁿ=xⁿ+C¹_nax^n-1+…+C^k_na^kx^n-k+…+C^n-1_na^n-1x+aⁿ

Это формула называется формулой бинома Ньютона, а правая ее часть – разложением бинома.

Свойства разложения бинома Ньютона

1) Количество членов разложения бинома на единицу больше показателя степени бинома.

2) Все члены разложения имеют одну и ту же степень n относительно первого и второго членов бинома, т. е. разложение есть однородный многочлен, причем показатели первого члена убывают от n до 0, а показатели второго члена возрастают от 0 до п.

3) Коэффициенты разложения следуют так: первый равен 1 = C⁰_n и последующие соответственно равны C¹_n ,C²_n,… Cⁿ_n = 1 т. е. коэффициент (k + 1)-го члена равен C^k_n. Эти коэффициенты называются биномиальными. Заметим, что биномиальные коэффициенты всегда натуральные числа, если показатель бинома есть натуральное число.

4) Биномиальные коэффициенты, равноотстоящие от концов разложения, равны между собой: C⁰_n= Cⁿ_n, C¹_n= Cⁿ^-1_n , C^k_n= Cⁿ^–^k_n

5) Из свойств 1 и 4 следует, что если показатель бинома четный, то в разложении бинома средний член имеет наибольший биномиальный коэффициент, а если показатель бинома нечетный, то в разложении имеется два средних члена с одинаковым наибольшим коэффициентом.

6) Последующий биномиальный коэффициент разложения равен предыдущему, умноженному на показатель первого члена бинома и предыдущем члене и деленному на число предыдущих членов

C^k⁺¹_n= n-1/k+1 * C^k_n

Сумма всех биномиальных коэффициентов равна 2^п, где п — показатель бинома.

Если в формуле бинома Ньютона положить х = а = 1, то получим

2ⁿ= C⁰_n⁺ C¹_n+…+ Cⁿ_n

Если в формуле бинома Ньютона заменить а на -а, то получим

(x-aⁿ)=xⁿ-C¹_nax^n-1+C²_nax^n-2-…+(-1)^kC^k_na^kx^n-k+…+(-1)ⁿaⁿ

Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах.

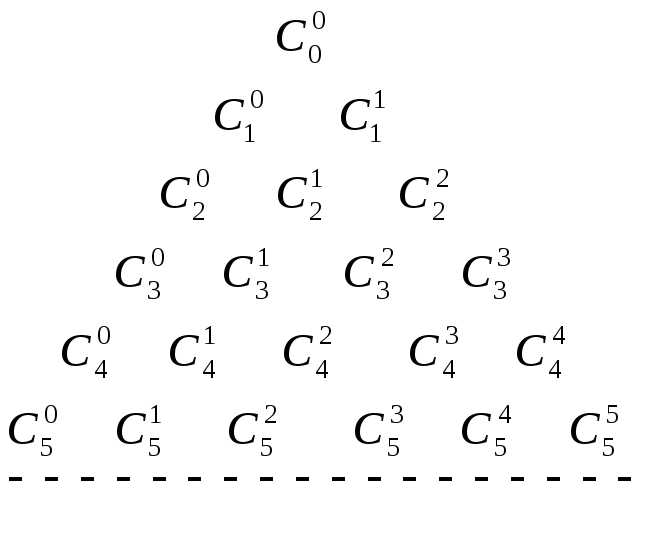
Для определения биномиальных коэффициентов удобно пользоваться так называемым треугольником Паскаля или арифметическим треугольником. Это треугольная таблица биномиальных коэффициентов, составленная так, что каждый ее элемент равен сумме двух над ним стоящих.

Решение задач с применением бинома Ньютона

Пример 1

Возведите в степень: (u – v)5.

Решение У нас есть (a + b)n, где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:

1 5 10 10 5 1

Тогда у нас есть

(u – v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 – 5u4v + 10u3v2 – 10u2v3 + 5uv4 – v5.

Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.

Пример 2

Возведите в степень: (2t + 3/t)4.

Решение У нас есть (a + b)n, где a = 2t, b = 3/t, и n = 4. Мы используем 5-й ряд треугольника Паскаля:

1 4 6 4 1

Тогда мы имеем

Пример 3

Найдите 5-й член в выражении (2x – 5y)6.

Решение Во-первых, отмечаем, что 5 = 4 + 1. Тогда k = 4, a = 2x, b = -5y, и n = 6. Тогда 5-й член выражения будет

Пример 4

Найдите 8-й член в выражении (3x – 2)10.

Решение Во-первых, отмечаем, что 8 = 7 + 1. Тогда k = 7, a = 3x, b = -2 и n = 10. Тогда 8-й член выражения будет

Пример 5 Сеть ресторанов Венди предлагает следующую начинку для гамбургеров:

{кетчуп, горчица, майонез, помидоры, салат, лук, грибы, оливки, сыр}.

Сколько разных видов гамбургеров может предложить Венди, исключая размеры гамбургеров или их количество?

Решение:

Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно

Таким образом, Венди может предложить 512 различных гамбургеров.

Решение технических задач

Задача 1

Тяга воздушного винта и потребляемая им мощность вычисляются по формулам: P=apn²_sD⁴N=bpn³_sD⁵

Где D-диаметр винта; n_s-число оборотов винта в секунду, p– плотность воздуха , a и b – коэффициенты зависящие от конструкции винта.

При ремонте винта для удаления с его концов царапин и зазубрин пришлось уменьшить его диаметр на величину ∆D, которая значительно меньше диаметраD.

Определить, на сколько снизилась тяга этого винта и потребляемая им Мощность при тех же секундных оборотах, если полагать все остальные параметры, входящие в формулы, неизменными.

Решение:

Пусть Q₂=Q₁+ ∆Q, T₂₌T₁-∆T, где ∆T-искомое уменьшение долговечности.

Тогда T₁/T₁-∆T =(Q₁+∆Q/Q₁)⁹= (1+∆Q/Q₁)⁹

откуда ∆T= T₁[1- 1/(1+∆Q/Q₁)⁹]=T₁[1-1/1+9∆Q/Q₁+36(∆Q/Q₁)²+82(∆Q/Q₁)³+126(∆Q/Q₁)⁴+126(∆Q/Q₁)⁵+82(∆Q/Q₁)⁶+36(∆Q/Q₁)⁷+9(∆Q/Q₁)⁸+(∆Q/Q₁)⁹]

Если ∆Q/Q₁<<1 формула может быть упрощена, так как степени ∆Q/Q₁ выше первой очень малы. В Этом случае ∆T≈T₁(1-1/1+9∆Q/Q₁)= 9T₁ *∆Q/Q₁ /1+9∆Q/Q₁

Задача 2

Газ сжимается в сосуде, стенки которого хорошо проводят тепло. При этом абсолютная температура и давление газа связаны следующим уравнением:

p₂/p₁=(T₂/T₁)ⁿ^/ⁿ^-1

где п= 1,2—показатель политропы; р₁ и р₂ — соответственно давления первого и второго состояния; T₁и T₂— соответственно абсолютные температуры первого и второго состояния.

Температура в сосуде измеряется посредством помещенной в нем термопары. Пусть во втором состоянии при сжатии температура получила небольшое приращение ∆t = 5° против первого состояния. Определить, какое приращение получило при этом давление. Температура Т₁ = 300° и давление р₁ = 2 кГ/см²— первого состояния известны.

Решение:

Подставляя значения T₂и p₂ в формулу, получаем:

p₁+∆p/p₁ = (T₁+∆t/T₁)^1.2/1.2-1=

(1+∆t/T₁)⁶=1+6+∆t/T₁+15(∆t/T₁)²+20(∆t/T₁)³+6(∆t/T₁)⁵+(∆t/T₁)⁶

Так как ∆t<<T₁,то ∆t/T₁<<1, следовательно, все степени ∆t/T₁ выше первой малы сравнительно с единицей и ими можно пренебречь без ущерба для точности расчета. Тогда p₁+∆p/p₁ = 1+∆p/p₁≈1+∆t/T₁ , откуда ∆p≈6 p₁/T₁*∆t= 6* 2/300 *5 = 0.2 кГ/ см²

Задача 3

Известно, что Т₁—долговечность вала, вращающегося с постоянной угловой скоростью, при приложении к нему поперечной нагрузки , равной Q₁. Определить, на сколько уменьшится долговечность вала, если нагрузка увеличится на ∆Q. Зависимость между нагрузкой и долговечностью устанавливается формулой: T₁/T₂=(Q₂/Q₁)⁹

Решение:

Пусть Q₂=Q₁+ ∆Q, T₂₌T₁-∆T, где ∆T-искомое уменьшение долговечности.

Тогда T₁/T₁-∆T =(Q₁+∆Q/Q₁)⁹= (1+∆Q/Q₁)⁹

Задача 4

Усилие в ходовом конце каната полиспаста: P=kⁿ(k-1)*Q/ kⁿ-1

где Q—вес поднимаемого груза; k= 1,02 — коэффициент сопротивления блока; n — число ветвей полиспаста. Вывести упрощенную формулу для вычисления Р и, применив ее, определить Р, если Q = 1500 кГ и п = 5.

Решение:

P=1.02ⁿ(1.02-1)Q/1.02ⁿ-1=1.02ⁿ*0.02*Q/(1+0.02)ⁿ-1=

1.02ⁿ*0.02*Q/1+n*1*0.02+n(n-1)/2 * 1*0.02²….0.02ⁿ-1

Заметим, что 0.02²=0.0004; 0.02³=0.000008 и т.д.

Видно, что члены разложения по формуле Ньютона быстро убывают. Для практики достаточно учесть первые 3 числа разложения, пренебрегая следующими. Тогда получаем:

P≈1.02ⁿ *0.02*Q/n*0.02+n(n-1)/2 *0.62² = 1.02n*Q/n[1+(n-1)0.01]

Использование этой приближенной формулы обеспечит точность и простоту в расчетах, так как в ней нет высоких степеней, близких величин (kⁿ-1)ⁿ имеющихся в точной формуле и крайне не удобных для расчетов.

Для нас получаем : P=1.02⁵*1500/5[1+(5-1)*0.01]≈ 318 кГ

Заключение

При изучении математики решение задач играет огромную роль. И не только потому,что необходимо выработать умение применять полученные знания на практике (а ведь это одна из основных целей изучения математики в школе). Без решения задач нельзя владеть и теорией. Именно в процессе решения задач математические понятия, аксиомы и теоремы, формулы и правила, геометрические фигуры предстают перед нами в самых разнообразных ракурсах, не в застывшем виде, а в движении, в различных связях и взаимозависимостях, которые отображают диалектику самой действительности. Подобно тому, как грамматическими правилами можно овладеть лишь в процессе живой языковой практики, так и математическую теорему, определение, формулу можно усвоить по-настоящему, научиться применять на практике только в процессе решения задач.

Используемая литература

1. А.Б. Шкарин, А.М. Федянов, Б.Г. Сандлер «алгебраические задачи в технике»

2. А.П. Савин «Энциклопедический словарь»

3. Г.И. Глейзер «История математики в школе»

4. Ф.П. Яремчук, П.А. Рудченко «Алгебра и элементарные функции»

5. Интернет-энциклопедия ru.wikipedia.org

Просмотров работы: 9306

Источник

Бинома Ньютона

Это формула, представляющая выражение ( a + b ) ⁿ при натуральном n в виде многочлена:

(a+b)ⁿ=aⁿ+C_n¹·a^n-1·b+C_n²·a^n-2·b²+

+C_n³·a^n-3·b³+…+C_n^n-1· a· b^n-1+bⁿ

Заметим, что сумма показателей степеней для a и b постоянна и равна n, т.е. все одночлены, входящие в это разложение имеют одинаковую степень n.

Числа С_n¹; C_n²; C_n³;… C_nⁿ называются биномиальными коэффициентами.
Т.о., член разложения бинома ( a + b ) ⁿ , стоящий на (к+1)-ом месте, выражается следующим образом:
T_k+1=C_n^k·b^k·a^n-k,
а если учесть, что разложение может быть такого вида ( a – b ) ⁿ, то
T_k+1=(-1)^k·C_n^k·b^k·a^n-k, где k может принимать все значения от 0 до n.
Всего в разложении бинома (n+1) слагаемое.
Напомним формулу числа сочетаний

Из этой формулы ясно, что C_n^k=C_n^n-k

Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все n элементов. Значит, C_nⁿ=1; C_n⁰=1

Происходит это потому, что 0!=1 по определению.

Треугольник Паскаля

Биномиальные коэффициенты можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая – для n = 2; третья – для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

( a + b )⁷ ,

мы можем получить результат моментально, используя таблицу:

(a+b)⁷=a⁷+7a⁶b+21a⁵b²+35a⁴b³+35a³b⁴+21a²b⁵+7ab⁶+b⁷

Свойства биномиальных коэффициентов
1. Сумма коэффициентов разложения ( a + b ) ⁿ равна 2 ⁿ .
2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения: C_n^k=C_n^n-k

3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна 2^n-1

С использованием материалов сайта http://www.bymath.net/studyguide/alg/sec/alg31.html

Домашнее задание по теме Бином Ньютона. Срок выполнения 31.01.2017
Как обычно, ответы заносим в googleформу. Удачи)))
Для справки (потребуется при решении задачи):
Каждый член арифметической прогрессии является средним арифметическим между своими соседними членами.

Источник

Явные формулы[править | править код]

Треугольник Паскаля[править | править код]

Свойства[править | править код]

Производящие функции[править | править код]

Делимость[править | править код]

Основные тождества[править | править код]

Бином Ньютона и следствия[править | править код]

Свёртка Вандермонда и следствия[править | править код]

Другие тождества[править | править код]

Матричные соотношения[править | править код]

Асимптотика и оценки[править | править код]

Целозначные полиномы[править | править код]

Алгоритмы вычисления[править | править код]

Примечания[править | править код]

Литература[править | править код]

Бином Ньютона

Вам также может понравиться

Как найти уголь для кузнеца

Как правильно составить декларацию за учебу

Ошибка данных crc на sd карте как исправить

Добавить комментарий Отменить ответ